【全国百强校】山西省忻州市第一中学2017届高考数学(理)一轮复习预学案(学生版)6.5 立体
山西省忻州市第一中学2017届高考数学理一轮复习测标题
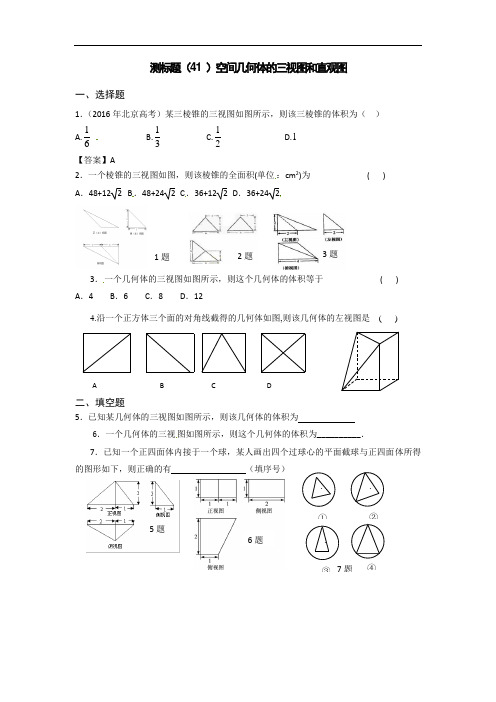
测标题(41 )空间几何体的三视图和直观图一、选择题1.(2016年北京高考)某三棱锥的三视图如图所示,则该三棱锥的体积为( ) A.16 B.13 C.12D.1 【答案】A2.一个棱锥的三视图如图,则该棱锥的全面积(单位:cm 2)为 ( ) A .48+12 2 B .48+24 2 C .36+12 2 D .36+2423.一个几何体的三视图如图所示,则这个几何体的体积等于 ( )A .4B .6C .8D .124.沿一个正方体三个面的对角线截得的几何体如图,则该几何体的左视图是 ( )二、填空题5.已知某几何体的三视图如图所示,则该几何体的体积为6.一个几何体的三视图如图所示,则这个几何体的体积为__________.7.已知一个正四面体内接于一个球,某人画出四个过球心的平面截球与正四面体所得的图形如下,则正确的有 (填序号)A B C D5题66题3 43 41题 3题2题8.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为 . 三、解答题9.一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.请画出该几何体的直观图,并求出它的体积;10.四棱锥P -ABCD 的直观图如图1所示,三视图如图2所示,E ,F 分别为PC ,BD 的中点.①求证平面PAD ⊥平面PDC ;②求三棱锥E -AFB 的体积.附加题10分(2016年山东高考)有一个半球和四棱锥组成的几何体,其三视图如右图所示,则该几何体的体积为2AB CD P EF1(A )π32+31 (B )π32+31 (C )π62+31 (D )π62+1【答案】C。
山西省忻州市第一中学2017届高考数学理一轮复习预学案

10.1 极坐标与参数方程(总第96课时)【考纲要求】1.了解坐标系的作用,了解平面直角坐标系下伸缩变换作用下平面图形的变化情况.2.了解极坐标的基本概念,会在极坐标系中用极坐标刻画点的位置,能进行极坐标和直角坐标互化.3.能在极坐标系中给出简单图形表示的极坐标方程.【基础必备】1.极坐标定义___________________________________________.2.极坐标与直角坐标的互化:⎩⎨⎧x=_____y=_____或⎩⎨⎧ρ2=_____tan θ=______. 3.(1)θ=α( ρ>0)表示的图形是_____________________.θ=α( ρ∈R)表示的图形是_____________________.(2)过点A(a,0)(a >0),且垂直于极轴的直线的极坐标方程为__________.过点A(-a, π)(a >0),且垂直于极轴的直线的极坐标方程为__________.过点A(a,π2)(a >0),且平行于极轴的直线的极坐标方程为__________.过点A(a,3π2)(a >0),且平行于极轴的直线的极坐标方程为__________.(3)ρ=r(r >0)表示的图形是_____________________.圆心在C(a,0)(a >0),半径为a(a >0)的圆的极坐标方程为_______.圆心在C(a,π2) (a >0),半径为a(a >0)的圆的极坐标方程为_______.圆心在C(a, π)(a >0),半径为a(a >0)的圆的极坐标方程为_______.圆心在C(a,3π2) (a >0),半径为a(a >0)的圆的极坐标方程为_______.注意:处理极坐标系中弦长、弦中点、三角形面积等问题可直接在极坐标系中借助平面几何知识解决,比化为直角坐标方便、简洁.【小组互查】【课前测验】1.点M 的直角坐标是(-1,3),则点M 的极坐标为 ( )A .(2, π3)B .(2, -π3)C .(2, 2π3)D .(2, 2k π+π3)(k ∈Z)2.在极坐标系中,两点的极坐标是M(6,π3),N(-8,5π6),求M 、N 两点间的距离.3.极坐标方程ρcos2θ=0表示的曲线为 ( )A .极点B .极轴C .一条直线D .两条相交直线4.曲线的极坐标方程ρ=2cos 2θ2-1的直角坐标方程为 ( )A .x 2+(y -12)2=14B .(x -12)2+y 2=14C .x 2+y 2=14D .x 2+y 2=1【查漏补缺】。
山西省忻州市第一中学2017届高考数学文一轮复习学案随

随机抽样【三维目标】知识与技能1.理解随机抽样的必要性和重要性;2.会用简单随机抽样方法从总体中抽取样本;了解分层抽样和系统抽样方法;3.了解分布的意义和作用,能根据频率分布表画频率分布直方图、频率折线图、茎叶图,体会它们各自的特点;4.理解样本数据标准差的意义和作用,会计算数据标准差;5.能从样本数据中提取基本的数字特征(如平均数、标准差),并给出合理的解释;6.会用样本的频率分布估计总体分布,会用样本的基本数字特征估计总体的基本数字特征,理解用样本估计总体的思想;7.会用随机抽样的基本方法和样本估计总体的思想解决一些简单的实际问题;过程与方法通过复习,进一步提高同学统计数据,整理数据,分析数据的能力.情感、态度与价值观通过学习使学生进一步认识,统计在日常生活中的重要性。
【题型归类】例1.某单位在岗职工共624人,为了调查工人用于上班途中的时间,该单位工会决定抽取10%的工人进行调查,请问:如何采用系统抽样法完成这一抽样?例2.某校共有学生2 000名,各年级男、女生人数如表.已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.19,现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为()A. 24B. 18C. 16D. 12例3.交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查.假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为()A、101B、808C、1212D、2012【课堂练习】1.为了考察某校的教学水平,将抽查这个学校高三年级的部分学生本年度的考试成绩.为了全面反映实际情况,采取以下三种方式进行抽查(已知该校高三年级共有20个班,并且每个班内的学生已经按随机方式编好了学号,假定该校每班学生的人数相同):①从高三年级20个班中任意抽取一个班,再从该班中任意抽取20名学生,考察他们的学习成绩;②每个班抽取1人,共计20人,考察这20名学生的成绩;③把学生按成绩分成优秀、良好、普通三个级别,从其中共抽取100名学生进行考察(已知该校高三学生共1 000人,若按成绩分,其中优秀生共150人,良好生共600人,普通生共250人).根据上面的叙述,试回答下列问题:(1)上面三种抽取方式的总体、个体、样本分别是什么?每一种抽取方式抽取的样本中,样本容量分别是多少?(2)上面三种抽取方式各自采用的是何种抽取样本的方法?(3)试分别写出上面三种抽取方式各自抽取样本的步骤.2.某市有大型超市200家、中型超市400家、小型超市1400家.为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市_______家.。
山西省忻州市第一中学2017届高考数学文一轮复习学案数

数列通项
【三维目标】
知识与技能:
1.能通过观察、归纳,构造等差数列、等比数列,求数列通项公式,进而求数列某一项.
2.能利用推导等差数列,等比数列通项公式的方法(累加、累乘、迭代)、求数列通项公式.
过程与方法:
通过求数列通项公式,学会归类整理,化归转化的方法
情感、态度、价值观:
等差数列、等比数列知识在高考中属于必考内容,中高档题常考查函数与数列结合.【题型归类】
例1.数列{a n}的前n项和为S n,a1=1,a n+1=2S n(n∈N+).求数列{a n}的通项a n.
例2.(1)数列{a n}中,a n+1= a n+4n+1,a1=2,求a n.
(2)数列{a n}中,a1=2,a n+1=2a n+3,求a n.
(3)数列{a n}中,a1=2,a n+1=2a n+3n,求a n.
例3.设s n 是等差数列{a n }的前n 项和,已知13S 3与14S 4的等比中项为15S 5,又13S 3与14S 4的等差
中项为1,求等差数列的通项a n .
【课堂练习】
1.数列{a n }中,a 1=12,a 1+a 2+…+a n =n 2a n ,求a n。
山西省忻州市第一中学2017届高考数学理一轮复习测标题

测标题 ( 26 ) 向量的平行、垂直与综合一.选择题(每小题5分)1.已知向量a →=(-5,6),b →=(6,5),则a →与b → ( )A .垂直B .不垂直也不平行C .平行且同向D .平行且反向 2.若|a →|=1,|b →|=2,c →=a →+b →,且c →⊥a →,则向量a →与b →的夹角为 ( )A .30ºB .60ºC .120ºD .150º3.已知向量a →=(8,12x),b →=(x ,1) (x>1),若(2a →+b →)∥b →,则x 的值为 ( )A .0B .2C .4D .84.已知平面向量a →=(1,2),b →=(-2,n),且 a →∥b →,则2a →+3b → = ( )A .(-5,-10)B .(-4,-8)C .(-3,-6)D .(-2,-4)5.在∆ABO 中,OA →=a →,OB →=b →,OD 是边AB 上的高,若AD →=λAB →,则实数λ等于 ( )A .a →⋅(b →-a →)|a →-b →|2B . a →⋅(a →-b →)|a →-b →|2C .a →⋅(b →-a →)|a →-b →|D .a →⋅(a →-b →)|a →-b →|二.填空题(每小题5分)6.在平行四边形ABCD 中,AD=1,∠BAD=60°,E 为CD 的中点.若AC →·BE →=1则AB 的长为____________.7.已知向量a →=(cos θ,sin θ),θ∈[0,π],向量b →=(3,-1),若|2a →-b →|<m 恒成立,则实数m 的取值范围为____________.三.解答题(每小题10分)8.在∆ABC 中,已知2AB →•AC →=3|AB →|•|AC →|=3BC →2.(1)求角A;(2)求sinB ⋅sinC 的值.9.已知a →,b →,c →是同一平面内的三个向量,其中a →=(1,2)(1)若|c →|=25,且c →∥a →,求c →的坐标.(2)若|b →|=52,且a →+2b →与2a →-b →垂直,求a →与b →的夹角θ.附加题:10.(2016年山东高考)已知非零向量m ,n 满足4│m │=3│n │,cos<m ,n >=13. 若n ⊥(t m +n ),则实数t 的值为 ( )A .4B .–4C .94D .–94 【答案】B11.(2016年四川高考)在平面内,定点A ,B ,C ,D 满足DA =DB =DC , DA •DB =DB •DC =DC •DA =-2,动点P ,M 满足AP =1,PM =MC ,则2BM 的最大值是 ( )A .434B .494CD 【答案】B。
山西省忻州市第一中学2017届高考数学理一轮复习测标题

测标题 (25) 平面向量的数量积一.选择题(每小题5分)1.边长为1的正∆ABC 中,AB →=a →,BC →=b →,CA →=c →,则a →⋅b →+b →⋅c →+c →⋅a →=( )A .32B .-32C .3D .02.向量a →=(cos16︒,sin16︒),b →=(cos136︒,sin136︒),则向量a →与a →+b →的夹角为 ( )A .15︒B .60︒C .45︒D .30︒3.已知向量a →=(2,1),a →·b →=10,|a →+b →|=52,则|b →|= ( )A . 5B .10C .5D .254.设a →,b →是两个非零向量. 下列说法正确的是 ( )A .若|a →+b →|=|a →|-|b →|,则a →⊥b →B .若a →⊥b →,则|a →+b →|=|a →|-|b →|C .若|a →+b →|=|a →|-|b →|,则存在实数λ,使得b →=λa →D .若存在实数λ,使得b →=λa →,则|a →+b →|=|a →|-|b →|5.已知a →,b →是单位向量,a →•b →=0,若向量c →满足|c →-a →-b →|=1,则|c →|的最大值为( )A .2-1B . 2C .2+1 C .2+26.设a →、b →、c →是单位向量,且a →·b →=0→,则(a →-c →)·(b →-c →)的最小值为 ( )A .-2B .2-2C .-1D .1- 2二.填空题(每小题5分)7.已知非零向量a →,b →满足|a →|=3|b →|=|a →+2b →|,则a →与b →夹角的余弦值为 .8.已知向量a →与b →的夹角为120︒,且|a →|=|b →|=4,那么b →·(2a →+b →)的值为 .9.已知△ABC 为等边三角形,AB =2.设点P ,Q 满足AP =λAB ,AQ =(1-λ) AC ,λ∈R .若32BQ CP ⋅=-,则λ= .三.解答题(每小题10分)10.(1)已知平面向量α→,β→,|α→|=1,|β→|=2,α→⊥(α→-2β→),求|2α→+β→|.(2)已知向量a →=(x 2,x+1), b →=(1-x ,t),若函数f(x)=a →⋅b →在区间(-1,1)上是增函数,求t 的取值范围.附加题:11.已知向量a →=(cos α,sin α),b →=(cos β,sin β),且a →, b →满足|k a →+b →|=3|a →-k b →|,k ∈N *.(1)求证:(a →+b →)⊥(a →-b →);(2)将a →与b →的数量积表示为关于k 的函数f(k);(3)求函数f(k)的最小值,以及取得最小值时向量a →与b →的夹角θ.f(k)=(k 2+1)/4k 12,60︒。
山西省忻州市第一中学2017届高考数学理一轮复习测标题
测标题 (24) 平面向量的基本定理及坐标运算一.选择题(每小题5分)1.下列向量组中,能作为表示它们所在平面内所有向量的一组基底的是 ( )A .a →=(1,2),b →=(0,0) B .a →=(1,-2),b →=(3,5) C .a →=(3,2),b →=(9, 6)D .a →=(-34, 12),b →=(3,-2)2.设x,y ∈R ,向量a →=(x,1),b →=(1,y),c →=(2,-4)且a →⊥c →,b →∥c →,则|a →+b →|=( ) A . 5 B .10 C .2 5 D .103.若向量BA →=(2,3),CA →=(4,7),则BC →= ( ) A .(-2,-4)B .(2,4)C .(6,10)D .(-6,-10)4.已知点A,B 的坐标分别为(2,-2),(4,3),向量p →的坐标为(2k-1,7),且p →∥AB →,则k 的值为 ( )A .-910B .910C .-1910D .19105.在平面直角坐标系xoy 中,已知A(1,0),B(0,1),点C 在第二象限内,∠AOC =5π6,且|OC →|=2,若OC →=λOA →+μOB →,则λ,μ的值是 ( ) A .3,1 B .1, 3C .-1, 3D .-3,1二.填空题(每小题5分)6.在平面直角坐标系中,O 为坐标原点,已知A(3,1),B(-1,3)两点,若C 满足OC →=αOA →+βOB →,其中α,β∈R,且α+β=1,则点C 的轨迹方程为 .7.已知向量OA →=(k,12), OB →=(4, 5), OC →=(-k, 10), 且A,B,C 三点共线,则k=8.在ΔABC 中,∠A =90º,AB =1,AC =2,设点P ,Q 满足AP →=λAB →,AQ →=(1-λ)AC →,λ∈R ,若BQ →•CP →=-2,则λ= .三.解答题(每小题10分)A B P Q C9.设a →=(6,3a),b →=(2,x 2-2x),如果存在实数x 使a →∥b →,求实数a 的取值范围.10.已知两定点F 1(-2,0),F 2(2,0),满足条件|PF 2→|-|PF 1→|=2的点P 的轨迹是曲线E ,直线y=kx -1与曲线E 交于A ,B 两点.如果|AB|=63,且曲线E 上存在点C,使OA →+OB →=mOC →,求m 的值和∆ABC 的面积S. 附加题:11.(10分)已知a =(1,2),b =(x,1), (1)若(2a +b )∥(a -b ),求x 的值;(2)若2a +b 与a -b 的夹角是锐角,求x 的取值范围. 【解】:(1)∵a =(1,2),b =(x,1),∴2a +b =(2+x,5),a -b =(1-x,1).由(2a +b )∥(a -b ),可知2+x =5-5x .解得x =12.(2)由题意可知:(2a +b )·(a -b )>0且2a +b 与a -b 不共线, ∴⎩⎪⎨⎪⎧(2+x )(1-x )+5>0,x ≠12,∴-1-292<x <-1+292且x ≠12. 即所求x 的取值范围是⎝ ⎛⎭⎪⎫-1-292,12∪⎝ ⎛⎭⎪⎫12,-1+292.。
山西省忻州市第一中学2017届高考数学理一轮复习测标题
测标题( 27 ) 极坐标与参数方程一.选择题(每小题5分)1.在直角坐标系xOy 中,直线l 的参数方程为⎩⎨⎧x=ty=4+t (t 为参数),以原点为极点,以x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ=42sin(θ+π4),则直线l 和曲线C 的公共点有 ( ) A .0个B .1个C .2个D .无数个2.在极坐标系中,点P(2,-π6)到直线l :ρsin(θ-π6)=1的距离是 ( )A .3+1B . 2C . 6D .3+2二.填空题(每小题5分)3.在平面直角坐标中,已知直线l 与曲线C 的参数方程分别为l :⎩⎨⎧x=1+s y=1-s(s 为参数)和C :⎩⎨⎧x=t+2y=t 2(t 为参数),若l 与C 相交于A 、B 两点,则|AB|_______.4.在极坐标系中,曲线ρ=asin θ与ρ=acos θ (a >0,ρ>0,0≤θ<2π)的交点的极坐标为__________.二.解答题(每小题10分)5.已知圆O 1和圆O 2的极坐标方程分别为ρ=2,ρ2-22ρcos(θ-π4)=2. (1)把圆O 1和圆O 2的极坐标方程化为直角坐标方程; (2)求经过两圆交点的直线的极坐标方程.6.在直角坐标系xOy 中,直线l 的参数方程为1cos ,2sin x t y t αα=+⎧⎨=+⎩(t 为参数)在极坐标系(与直角坐标系xOy 取相同的长度单位.且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为6sin .ρθ=(1)求圆C 的直角坐标方程;(2)设圆C 与直线l 交于点A ,B .若点P 的坐标为(1,2),求||||PA PB +的最小值.7.已知曲线C 的极坐标方程是4cos ρθ=.以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,直线l 的参数方程是1cos sin x t y t αα=+⎧⎨=⎩(t 为参数).(1)将曲线C 的极坐标方程化为直角坐标方程;(2)若直线l 与曲线C 相交于A 、B 两点,且AB ,求直线的倾斜角α的值.8.已知曲线C 的极坐标方程为ρ=4cos θ,直线l 的参数方程是:⎩⎨⎧x =-5+22t ,y =5+22t (t为参数).(1)求曲线C 的直角坐标方程,直线l 的普通方程;(2)将曲线C 横坐标缩短为原来的12,再向左平移1个单位,得到曲线C 1,设点P 在1C 上,点Q 在直线l 上,求PQ 的最小值及此时点P 的直角坐标.附加题1.在极坐标系中,已知圆C 的圆心C ⎝⎛⎭⎫3,π3,半径r =3. (1)求圆C 的极坐标方程;(2)若点Q 在圆C 上运动,点P 在OQ 的延长线上,且OQ →=2QP →,求动点P 的轨迹方程.。
山西省忻州市第一中学2017届高考数学理一轮复习测标题
测标题( 12 )指数与指数函数一.选择题(每小题5分)1.已知函数f(x)=a x -b 的图象如图,其中a,b 为常数,则下列结论正确的是 ( ) A.a>1,b<0 B.a>1,b>0 C.0<a<1,b>0D.0<a<1,b<02.若10a -<<,则式子1333,,aa a 的大小关系是( ) A .1333aa a >>B .1333aa a >>C .1333aa a >> D .1333aa a >> 3.(2013浙江理)已知x ,y 为正实数,则 ( )A .2lgx+lgy=2lgx +2lgy B .2lg(x +y )=2lg x ∙2lg yC .2lg x ∙ lg y=2lg x +2lg yD .2lg(xy )=2lg x ∙2lg y4.设3x =17,则 ( ) A.-2<x<-1 B.-3<x<-2C.-1<x<0D.0<x<15.已知f(x)=23x -1+m 是奇函数,则实数m 的值( )A.-1B.0C.1D.2二.填空题(每小题5分)6.若函数f(x)=2x 2-2ax -a -1的定义域是R ,则a 的取值范围是___________.7.(2012上海理)已知函数||)(a x ex f -=(a 为常数),若f(x)在区间),1[+∞上是增函数,则a 的取值范围是___________.8.化简11410104848++的值等于___________.三.解答题(每小题10分)9.画出函数y =|3x -1|的图象,并利用图象回答:k 为何值,方程|3x -1|=k 无解?有一解?有两解?10.已知9x -10×3x +9≤0,求函数y=(14)x -1-4(12)x +2的最大值和最小值.附加题11.已知函数f (x )=2a ·4x -2x -1.(1)当a =1时,求函数f (x )在x ∈[-3,0]的值域; (2)若关于x 的方程f (x )=0有解,求a 的取值范围. 【解】 (1)当a =1时,f (x )=2·4x -2x -1=2(2x )2-2x -1, 令t =2x,x ∈[-3,0],则t ∈⎣⎡⎦⎤18,1.故y =2t 2-t -1=2⎝⎛⎭⎫t -142-98,t ∈⎣⎡⎦⎤18,1,故值域为⎣⎡⎦⎤-98,0(2)关于x 的方程2a (2x )2-2x -1=0有解,等价于方程2ax 2-x -1=0在(0,+∞)上有解.解法一:记g (x )=2ax 2-x -1, 当a =0时,解为x =-1<0,不成立.当a <0时,开口向下,对称轴x =14a <0,过点(0,-1),不成立.当a >0时,开口向上,对称轴x =14a >0,过点(0,-1),必有一个根为正,所以,a >0.解法二:方程2ax 2-x -1=0 可化为a =x +12x 2=12⎝⎛⎭⎫1x +122-18,∴a 的范围即为函数g (x )=12⎝⎛⎭⎫1x +122-18在(0,+∞)上的值域 所以,a >0.。
山西省忻州市第一中学2017届高考数学理一轮复习测标题
测标题( 17 )导数概念及其运算一.选择题(每小题5分)1.若f (x )=2xf ′(1)+x 2,则f ′(0)等于 ( )A .2B .0C .-2D .-4【答案】 D2.已知函数f(x)=x •lnx ,若f '(x 0)=2.则x 0= ( )A .e 2B .eC .ln22D .ln2 3.如果函数y=f(x)的图象如右图,那么导函数y=f '(x)的图象可能是 ( )4.点p 在曲线y=x 3-x+7上移动,过点p 的切线的倾斜角的取值范围是 ( )A .[0,π]B .[0,π2)∪[3π4,π)C .[0,π2)∪[π2,π)D .[0,π2]∪[3π4,π)5.设函数f(x)=g(x)+x 2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为 ( )A .4B .-14C .2D .-126.曲线y=1-x 2与曲线y=1+x 3在x=x 0处的切线互相垂直,则x 0等于 ( ) A .136 B .-136 C .23 D .-23或07.已知函数f(x)在R 上满足f(x)=2f(2-x)-x 2+8x -8,则曲线y=f(x)在点(1,f(1))处的切线方程是 ( )A .y=2x -1B .y=xC .y=3x -2D .y=-2x+3二.填空题(每小题5分)8.设函数f(x)=(1+2x)(1+x) 5,则导函数f '(x)的展开式中的常数项是____________.9.函数y=f(x)的图像过原点,且它的导函数g=f '(x)的图像是如图所示的一条直线,则y=f(x)图像的顶点在第____________.象限.10.某运动员参加100m 赛跑,最后10m 离开起点的距离s=t 2+9t +90(t 的单位是s ),他冲过终点线瞬间的速度为____________.三.解答题(每小题10分)11.已知曲线C :y=x 3+3x 2-5 ,求(1)曲线C 在点M(1,-1)处的切线方程;(2)曲线C 过点M(1,-1)的切线方程.附加题:12.已知函数f (x )=x 3+(1-a )x 2-a (a +2)x +b (a ,b ∈R ).(1)若函数f (x )的图象过原点,且在原点处的切线斜率为-3,求a ,b 的值;(2)若曲线y =f (x )存在两条垂直于y 轴的切线,求a 的取值范围.【解】 f ′ (x )=3x 2+2(1-a )x -a (a +2).(1)由题意得⎩⎪⎨⎪⎧f (0)=b =0,f ′(0)=-a (a +2)=-3, 解得b =0,a =-3或a =1.(2)∵曲线y =f (x )存在两条垂直于y 轴的切线,∴关于x 的方程f ′(x )=3x 2+2(1-a )x -a (a +2)=0有两个不相等的实数根,∴Δ=4(1-a )2+12a (a +2)>0,即4a 2+4a +1>0,∴a ≠-12. ∴a 的取值范围为⎝⎛⎭⎫-∞,-12∪⎝⎛⎭⎫-12,+∞.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.5 立体几何综合(总第65课时)
【考纲要求】
综合处理空间几何体中线线,线面,面面平行,垂直的关系.
【基础必备】
1、总结证明平行的方法______________________________
2、总结证明垂直的方法______________________________
【小组互查】
【课前测验】
1.若某几何体的三视图如图所示,已知该几何体的体积是2,则俯
视图中的x=_____
2.已知三棱锥O-ABC中,OA、OB、OC两两互相垂直,OC=1,OA=x,OB=y,若
x+y=4,则三棱锥O-ABC体积的最大值是 ( )
A.1 B.13 C.23 D.33
3.给出下列命题
①在空间里,垂直于同一平面的两个平面平行
②设l,m是不同的直线,是一个平面,若l⊥,l∥m,则m⊥
③已知,表示两个不同平面,m为平面内一条直线,则“⊥”是“m⊥”的充
要条件
④若点P到三角形三个顶点的距离相等,则点P在该三角形所在平面内的射影是该三角
形的外心
⑤a,b是两条异面直线,P是一点,过P总可以作一个平面与a,b之一垂直,与另一
个平行
其中正确的命题是_______________________
4.如图,四边形ABCD与AABB都是边长为a的正方形,点E是AA的中点,AA⊥平
面ABCD
(1)求证:AC∥平面BDE.
B
A C D
A
B
E
2
2
1
x
(2)求证:平面AAC⊥平面BDE
【查漏补缺】
