《名校推荐》山西省忻州市第一中学2017届高考数学(理)一轮复习测标题(14)函数的图象
山西省忻州市第一中学2017届高考数学理一轮复习测标题14 函数的图象 精品
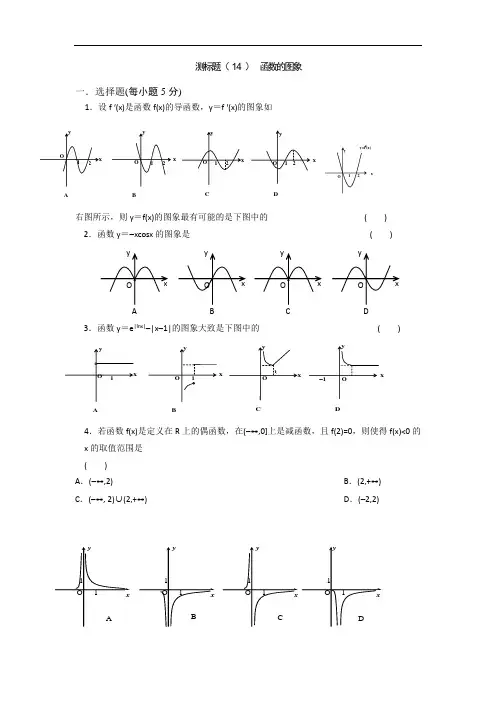
测标题( 14 ) 函数的图象一.选择题(每小题5分)1.设f '(x)是函数f(x)的导函数,y =f '(x)的图象如右图所示,则y =f(x)的图象最有可能的是下图中的 ( ) 2.函数y =-xcosx 的图象是 ( )3.函数y =e |lnx|-|x -1|的图象大致是下图中的 ( )4.若函数f(x)是定义在R 上的偶函数,在(-∞,0]上是减函数,且f(2)=0,则使得f(x)<0的x 的取值范围是( ) A .(-∞,2) B .(2,+∞) C .(-∞, 2)∪(2,+∞)D .(-2,2)5.(2012全国理)已知函数1()ln(1)f x x x=+-;则()y f x =的图像大致为 ( )6.若函数y=f(x+1)是偶函数,则函数y=f(x)的图象关于 ( ) A .y 轴对称B .x 轴对称C .原点对称D .直线x=1对称7.函数f (x )=e x1+x 的图象大致是 ( )【答案】 B8.(2016年全国I 高考))函数y =2x 2–e |x |在[–2,2]的图像大致为 ( )(B )【答案】D【解析】()22288 2.80f e =->->,排除A ,()22288 2.71f e =-<-<,排除B0x >时,()22x f x x e =-()4x f x x e '=-,当10,4x ⎛⎫∈ ⎪⎝⎭时,()01404f x e '<⨯-=因此()f x 在10,4⎛⎫⎪⎝⎭单调递减,排除C 故选D . 二.填空题(每小题5分)9.函数y=2-xx -1的图象关于点__________对称.AB C D10.函数f(x)=|4x -x 2|+a 有二个零点. 则a 的取值范围为__________.三.解答题(每小题10分)11.(2012福建理)对于实数a 和b ,定义运算“﹡”:⎪⎩⎪⎨⎧>-≤-=*ba ab b ba ab a b a ,,22,设)1()12()(-*-=x x x f ,且关于x 的方程为f(x)=m(m ∈R)恰有三个互不相等的实数根x 1,x 2,x 3,求x 1x 2x 3的取值范围.附加题12.(2010理11).已知函数|lg |,010,()16,10.2x x f x x x <≤⎧⎪=⎨-+>⎪⎩若a,b,c 互不相等,且f(a)=f(b)=f(c),则abc 的取值范围是( ) (A)(1,10) (B)(5,6)(C)(10,12) (D)(20,24)。
山西省忻州市第一中学2017届高考数学理一轮复习测标题

测标题( 14 ) 圆一.选择题(每小题5分)1.方程x 2+y 2+Dx +Ey +F=0(D2+E2-4F>0)表示的曲线关于x +y =0成轴对称图形,则 ( )A .D +E =0B .D +F =0C .E +F =0D .D +E +F =02.(2012∙广东)平面直角坐标系xOy 中,直线3x+4y -5=0与圆x 2+y 2=4相交于A,B 两点,则弦AB 的长等于 ( )A .3 3B .2 3C . 3D .13.已知关于x 、y 的方程x 2+y 2+kx +2y +k 2=0所表示的曲线是一个圆,当这个圆取到最大面积时,圆心的坐标是 ( )A .(0,-1)B .(-1,0)C .(1,-1)D .(-1,1)4.已知圆的方程为x 2+y 2-6x -8y=0,设圆中过点(2,5)的最长弦与最短弦分别为AB 、CD ,则直线AB 与CD 的斜率之和为 ( )A .-1B .0C .1D .-25.垂直于直线1y x =+且与圆221x y +=相切于第一象限的直线方程是 ( )A .0x y +=B .10x y ++=C .10x y +-=D .0x y +=6.若圆x 2+y 2-2mx+m 2-4=0与圆x 2+y 2+2x -4my+4m 2-8=0相切,则实数m 的取值集合是( )A .{-125,2}B .{0,-25}C .{0,2}D .{-125,-25,0,2}二.填空题(每小题5分)7.(2010•全国理)过点A(4,1)的圆C 与直线x -y -1=0相切于点B (2,1),则圆C 的方程为_________.8.设圆(x -3)2+(y+5)2=r 2(r>0)上有且仅有两个点到直线4x -3y -2=0的距离等于1,则圆半径r 的取值范围是________________.三.解答题(每小题10分)9.已知圆C :x 2+y 2+2x -4y +3=0.(1)若圆C 的切线在x 轴和y 轴上的截距相等,求此切线的方程;(2)从圆C 外一点P (x 1,y 1)向该圆引一条切线,切点为M ,O 为坐标原点,且有|PM |=|PO |,求使得|PM |取得最小值的点P 的坐标.10.(2012江苏12)在平面直角坐标系xOy 中,圆C 的方程为228150x y x +-+=,若直线2y kx =-上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,求k 的最大值.附加题1.已知点P 是圆C :x 2+y 2-2x+2y=0上的一个动点,点Q 是直线l :x+y=0上的一个动点,O为坐标原点,则OP →·OQ →|OQ →|的最大值是___________。
山西省忻州市第一中学2017届高考数学理一轮复习测标题

测标题( 23 ) 几何概型一.选择题(每小题5分)1.在区间[]0,2上随机地取一个数x ,则事件“121-1log 2x ≤+≤()1”发生的概率为( ) A.34B.23 C .13 D.142.已知区域A={(x,y)|x+y≤6,x≥0,y≥0},区域B={ (x,y)|x-2y≥0,x≤4,y≥0},若向区域A 内随机地投一点P ,则点P 落在区域B 内的概率为 ( ) A .13B .23C .19D .293.将一枚骰子抛掷两次,向上所得的点数分别为m 和n ,则函数y=23mx 3-nx+1 在[1,+∞)上为增函数的概率是 ( ) A .12B .56C .34D .234.设复数(1)z x yi =-+(,)x y R ∈,若||1z ≤,则y x ≥的概率 ( ) A .3142π+ B .112π+ C .1142π- D .112π- 5.在区间[0,1]上随机取两个数,x y ,记1p 为事件“12x y +≤”的概率,2p 为事件“12xy ≤”的概率,则 ( ) A .1212p p << B .1212p p << C .2112p p <<D .2112p p << 二.填空题(每小题5分)6.如图,在矩形区域ABCD 的A , C 两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE 和扇形区域CBF (该矩形区域内无其他信号来源, 基站工作正常). 若在该矩形区域内随机地选一地点, 则该地点无.信号的概率是 7.在直角三角形ABC 中,∠A=90°,AB=1,BC=2,在BC 边上取一点M ,则∠AMB ≥90°的概率为_________A BCM1三.解答题(每小题10分)8.某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售。
如果当天卖不完,剩下的玫瑰花做垃圾处理。
山西省忻州市第一中学2017届高考数学理一轮复习测标题

测标题( 15 )方程的根与函数的零点一.选择题(每小题5分)1.下列说法不正确的是 ( )A .方程f(x)=0有实根⇔函数y=f(x)有零点B .函数f(x)=-x 2+3x+5有两个零点C .y=f(x)在[a,b]上满足f(a)⋅f(b)<0,则y=f(x)在(a,b)内有零点D .单调函数若有零点,至多有一个2.函数f(x)=ln(x+1)-1x 的零点所在的大致区间是( ) A .(0,1) B .(1,2) C .(2,e) D .(3,4)3.若函数f(x)的零点与g(x)=4x +2x -2的零点之差的绝对值不超过0.25,则f(x)可以是( ) A .f(x)=4x -1 B .f(x)=(x -1)2 C .f(x)=e x -1 D .f(x)=ln(x -12)4.(2012天津理)函数22)(3-+=x x f x 在区间(0,1)内的零点个数是 ( )A .0 B. 1 C.2 D.35.设函数f (x )的定义域为R ,f (x )=⎩⎪⎨⎪⎧x ,0≤x ≤1,⎝⎛⎫12x -1,-1≤x <0.且对任意的x ∈R 都有 f (x +1)=f (x -1),若在区间[-1,3]上函数g (x )=f (x )-mx -m 恰有四个不同零点,则实数m 的取值范围是 ( )A.⎣⎡⎦⎤0,12 B.⎣⎡⎭⎫0,14 C.⎝⎛⎦⎤0,12 D.⎝⎛⎦⎤0,14 【答案】 D二.填空题(每小题5分)6.用二分法求方程3250x x --=在区间[2,3]上的近似解,取区间中点x 0=2.5,那么下一个有解区间为 .7.(2011陕西理)函数()cos f x x =在[0,)+∞内有 个零点8.若函数y =f (x )(x ∈R ) 满足f (x +2)=f (x )且x ∈[-1,1]时,f (x )=1-x 2;函数g (x )=lg|x |,则函数y =f (x )与y =g (x )的图象在区间[-5,5]内的交点个数共有________个.【答案】 8三.解答题(每小题10分)9.m 为何值时,f(x)=x 2+2mx+3m+4的两个零点且都比-1大.10.已知函数f(x)=x 2-x+k ,k ∈Z ,若方程f(x)=2在(-1,32)上有两个不相等的实数根.(1)确定k 的值;(2)求[f(x)]2+4f(x)的最小值及对应的x 值.附加题:11.已知函数f (x )=4x +m ·2x +1有且仅有一个零点,求m 的取值范围.并求出该零点.【解】 ∵f (x )=4x +m ·2x +1有且仅有一个零点,即方程(2x )2+m ·2x +1=0仅有一个实根.设2x =t (t >0),则t 2+mt +1=0.当Δ=0时,即m 2-4=0,∴m =-2时,t =1;m =2时,t =-1(不合题意,舍去).∴2x =1,x =0符合题意.当Δ>0时,即m >2或m <-2时,t 2+mt +1=0有两正或两负根,即f (x )有两个零点或没有零点.∴这种情况不符合题意.综上可知:m =-2时,f (x )有唯一零点,该零点为x =0.。
山西省忻州市第一中学2017届高考数学理一轮复习预学案

10.1 极坐标与参数方程(总第96课时)【考纲要求】1.了解坐标系的作用,了解平面直角坐标系下伸缩变换作用下平面图形的变化情况.2.了解极坐标的基本概念,会在极坐标系中用极坐标刻画点的位置,能进行极坐标和直角坐标互化.3.能在极坐标系中给出简单图形表示的极坐标方程.【基础必备】1.极坐标定义___________________________________________.2.极坐标与直角坐标的互化:⎩⎨⎧x=_____y=_____或⎩⎨⎧ρ2=_____tan θ=______. 3.(1)θ=α( ρ>0)表示的图形是_____________________.θ=α( ρ∈R)表示的图形是_____________________.(2)过点A(a,0)(a >0),且垂直于极轴的直线的极坐标方程为__________.过点A(-a, π)(a >0),且垂直于极轴的直线的极坐标方程为__________.过点A(a,π2)(a >0),且平行于极轴的直线的极坐标方程为__________.过点A(a,3π2)(a >0),且平行于极轴的直线的极坐标方程为__________.(3)ρ=r(r >0)表示的图形是_____________________.圆心在C(a,0)(a >0),半径为a(a >0)的圆的极坐标方程为_______.圆心在C(a,π2) (a >0),半径为a(a >0)的圆的极坐标方程为_______.圆心在C(a, π)(a >0),半径为a(a >0)的圆的极坐标方程为_______.圆心在C(a,3π2) (a >0),半径为a(a >0)的圆的极坐标方程为_______.注意:处理极坐标系中弦长、弦中点、三角形面积等问题可直接在极坐标系中借助平面几何知识解决,比化为直角坐标方便、简洁.【小组互查】【课前测验】1.点M 的直角坐标是(-1,3),则点M 的极坐标为 ( )A .(2, π3)B .(2, -π3)C .(2, 2π3)D .(2, 2k π+π3)(k ∈Z)2.在极坐标系中,两点的极坐标是M(6,π3),N(-8,5π6),求M 、N 两点间的距离.3.极坐标方程ρcos2θ=0表示的曲线为 ( )A .极点B .极轴C .一条直线D .两条相交直线4.曲线的极坐标方程ρ=2cos 2θ2-1的直角坐标方程为 ( )A .x 2+(y -12)2=14B .(x -12)2+y 2=14C .x 2+y 2=14D .x 2+y 2=1【查漏补缺】。
《名校推荐》山西省忻州市第一中学2017届高考数学(理)一轮复习测标题(2)命题与简单逻辑联结词

测标题命题与简单逻辑联结词一.选择题(每小题5分)1.(2013·课标全国卷1)已知命题p:∀x∈R,2x<3x;命题q:∃x∈R,x3=1-x2,则下列命题中为真命题的是( ) A.p∧q B.非p∧qC.p∧非q D.非p∧非q【答案】 B2.(2016年浙江高考)命题“,使得n≥x2”的否定形式是( )A.,使得B.,使得C.,使得D.,使得【答案】D3.(2015浙江)命题“且的否定形式是()A.,且B.或C.且D.或4.已知下列四个命题:①“若xy=0,则x=0且y=0”的逆否命题;②“正方形是菱形”的否命题;③“若ac2>bc2,则a>b” 的逆命题④命题“若m>2,则不等式x2-2x+m>0的解集为R”其中正确的命题个数为( )A.1个B.2个C.3个D.0个5.命题P:若a,b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件.命题q:函数y=|x-1|-2的定义域是(-∞,-1]∪[3,+∞),则( ) A.“p或q”为假B.“p且q”为真C.p真q假D.p假q真6.命题“若函数f(x)=log a x(a>0且a≠1)在其定义域内是减函数,则log a2<0”的逆否命题是( ) A.“若log a2<0,则函数f(x)=log a x(a>0,a≠1)在其定义域内不是减函数”B.“若log a2≥0,则函数f(x)=log a x(a>0,a≠1)在其定义域内不是减函数”C.“若log a2<0,则函数f(x)=log a x(a>0,a≠1)在其定义域内是减函数”D.“若log a2≥0,则函数f(x)=log a x(a>0,a≠1)在其定义域内是减函数”7.给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行; ②若一个平面经过另一个平面的垂线,那这两个平面相互垂直;③垂直于同一直线的两直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直;其中,为真命题的是( )A .①②B .②③C .③④D .②④8.(2012江西理5)下列命题中,假命题为( ) A .存在四边相等的四边形不是..正方形 B .为实数的充分必要条件是为共轭复数C .若R ,且则至少有一个大于1D .对于任意n ∈N*,都是偶数 二.填空题(每小题5分)9.(2015山东)若“x[0,],tanxm ”是真命题,则实数m 的最小值为10.(2010全国理5)已知命题:函数在R 为增函数,:函数在R 为减函数,则在命题:,:,:和:中,真命题有___________.三.解答题(每小题10分)11.已知,p :|3x -4|>2,q :1x 2-x -2>0,求⌝p 和⌝q 对应的x 的值的集合,并具体写出若p 则q 这个命题逆否命题.附加题12.已知c >0,设命题p :函数y =c x 为减函数.命题q :∀x ∈⎣⎡⎦⎤12,2,x +1x>c .如果p ∨q 为真命题,p ∧q 为假命题,求实数c 的取值范围.【解】若命题p 为真,则0<c <1.若命题q 为真,则c <⎝⎛⎭⎫x +1x min , 又当x ∈⎣⎡⎦⎤12,2时,2≤x +1x ≤52, 则必须且只需2>c ,即c <2.因为p ∨q 为真命题,p ∧q 为假命题,所以p 、q 必有一真一假.当p 为真,q 为假时,⎩⎪⎨⎪⎧ 0<c <1,c ≥2,无解; 当p 为假,q 为真时,⎩⎪⎨⎪⎧c ≥1,c <2,所以1≤c <2. 综上,c 的取值范围为[1,2).。
山西省忻州市第一中学2017届高考数学文一轮复习学案算
算法与程序框图
【三维目标】
知识与技能
1.了解算法的含义,了解算法的思想.
2.理解程序框图的三种基本逻辑结构:顺序、条件分支、循环.并能读懂程序框图.
方法与过程:读图能力、计算能力及推理能力;
情感、态度与价值观:
高考必考知识点,必须熟练掌握.
【题型归类】
例1.【2012高考湖北理11】阅读左图所示的程序框图,运行相应的程序,输出的结果s=.
例2.【2012高考陕西理10.】右图是用模拟方法估计圆周率π的程序框图,P表示估计结果,
则图中空白框内应填
入( )
A .1000N P =
B .41000N P =
C .1000M P =
D .41000
M P =
【课堂练习】
1.如果执行如图6的程序框图,输入n=6,m=4,那么输出的P 等于 ( )
A .720
B .360
C .240
D .120 2.如果执行下边的程序框图,输入正整数N (N ≥2)和实数a 1,a 2,…,a N ,输出A ,B ,则
( )
A .A +
B 为a 1,a 2,…,a N 的和
B .A+B 2
为a 1,a 2,…,a N 的算术平均数 C .A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数
D .A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数
图6。
山西省忻州市第一中学2017届高考数学文一轮复习学案数
数列通项
【三维目标】
知识与技能:
1.能通过观察、归纳,构造等差数列、等比数列,求数列通项公式,进而求数列某一项.
2.能利用推导等差数列,等比数列通项公式的方法(累加、累乘、迭代)、求数列通项公式.
过程与方法:
通过求数列通项公式,学会归类整理,化归转化的方法
情感、态度、价值观:
等差数列、等比数列知识在高考中属于必考内容,中高档题常考查函数与数列结合.【题型归类】
例1.数列{a n}的前n项和为S n,a1=1,a n+1=2S n(n∈N+).求数列{a n}的通项a n.
例2.(1)数列{a n}中,a n+1= a n+4n+1,a1=2,求a n.
(2)数列{a n}中,a1=2,a n+1=2a n+3,求a n.
(3)数列{a n}中,a1=2,a n+1=2a n+3n,求a n.
例3.设s n 是等差数列{a n }的前n 项和,已知13S 3与14S 4的等比中项为15S 5,又13S 3与14S 4的等差
中项为1,求等差数列的通项a n .
【课堂练习】
1.数列{a n }中,a 1=12,a 1+a 2+…+a n =n 2a n ,求a n。
山西省忻州市第一中学2017届高考数学文一轮复习学案等
等差数列与等比数列
【三维目标】
知识与技能:
1.理解等差数列、等比数列的概念;
2.掌握等差数列、等比数列的通项公式与前n项和公式;
3.能在具体的问题情境中识别数列的等差关系或等比关系,并能用等差数列、等比数列的有关知识解决相应的问题;
4.了解等差数列与一次函数、等比数列与指数函数的关系.
过程与方法:
等差数列、等比数列问题解题常用方法:基本量法,性质法,函数法
情感、态度、价值观:
等差数列、等比数列知识在高考中是必考内容,一般直接考查等差、等比数列的通项公式,前n项公式,和性质的题目为容易题.
【题型归类】
例1.已知数列{a n}的前n项和S n=12n-n2,
(1)求S n的最大值.
(2)求数列{|a n|}的前n项和T n.
例2.在等差数列{a n}中,已知a1=20,前n项和为S n,且S15=S10,求当n取何值时,S n取得最大值,并求出它的最大值.
例3.已知等差数列{a n}的首项a1=1,公差d>0,且第2项,第5项,第14项分别是等比数列{b n}的第2项,第3项,第4项.
(1)求数列{a n},数列{b n}的通项公式;
(2)设数列{c n}对n N*,均有c1
b1+
c2
b2+…+
c n
b n=a n+1成立,求c1+c2+…+c2013.
【课堂练习】
1.设数列{a n}对所有正整数n都满足a1+2a2+22a3+…+2n-1a n=8-5n,求数列{a n}的通项公式以及其前n项和S n.。
山西省忻州市第一中学2017届高考数学理一轮复习预学案
6.5 立体几何综合(总第65课时)
【考纲要求】
综合处理空间几何体中线线,线面,面面平行,垂直的关
系.
【基础必备】
1、总结证明平行的方法______________________________
2、总结证明垂直的方法______________________________
【小组互查】
【课前测验】
1.若某几何体的三视图如图所示,已知该几何体的体积是2,则俯视图中的x=_____
2.已知三棱锥O-ABC 中,OA 、OB 、OC 两两互相垂直,OC =1,OA =x ,OB =y ,若x+y=4,则三棱锥O-ABC 体积的最大值是 ( )
A .1
B .13
C .23
D .33
3.给出下列命题
①在空间里,垂直于同一平面的两个平面平行
②设l ,m 是不同的直线,α是一个平面,若l ⊥α,l ∥m ,则m ⊥α
③已知α,β表示两个不同平面,m 为平面α内一条直线,则“α⊥β”是“m ⊥β”的充要条件
④若点P 到三角形三个顶点的距离相等,则点P 在该三角形所在平面内的射影是该三角形的外心
⑤a ,b 是两条异面直线,P 是一点,过P 总可以作一个平面与a ,b 之一垂直,与另一个平行
其中正确的命题是_______________________
4.如图,四边形ABCD 与AA 'B 'B 都是边长为a 的正方形,点E 是AA '的中点,AA '⊥平面ABCD
(1)求证:A 'C ∥平面BDE .
B
A
C D A '
B '
E
(2)求证:平面A AC⊥平面BDE 【查漏补缺】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
测标题( 14 ) 函数的图象
一.选择题(每小题5分)
1.设f '(x)是函数f(x)的导函数,y =f '(x)的图象如
右图所示,则y =f(x)的图象最有可能的是下图中的 ( ) 2.函数y =-xcosx 的图象是 ( )
3.函数y =e |lnx|-|x -1|的图象大致是下图中的 ( )
4.若函数f(x)是定义在R 上的偶函数,在(-∞,0]上是减函数,且f(2)=0,则使得f(x)<0的x 的取值范围是
( ) A .(-∞,2) B .(2,+∞) C .(-∞, 2)∪(2,+∞)
D .(-2,2) 5.(2012全国理)已知函数;则的图像大致为 ( )
6.若函数y=f(x+1)是偶函数,则函数y=f(x)的图象关于 ( ) A .y 轴对称
B .x 轴对称
C .原点对称
D .直线x=1对称
7.函数f (x )=e
x
1+x 的图象大致是 ( )
【答案】 B
8.(2016年全国I 高考))函数y =2x 2–e |x |在[–2,2]的图像大致为 ( )
(B )
【答案】D
【解析】,排除A ,,排除B
时, ,当时,
因此在单调递减,排除C 故选D . 二.填空题(每小题5分)
9.函数y=2-x
x -1的图象关于点__________对称.
10.函数f(x)=|4x -x 2|+a 有二个零点. 则a 的取值范围为__________.
三.解答题(每小题10分)
11.(2012福建理)对于实数a 和b ,定义运算“﹡”:,
设,且关于x 的方程为f(x)=m(m ∈R)恰有三个互不相等的实数根x 1,x 2,x 3,求x 1x 2x 3的取值范围.
附加题
12.(2010理11).已知函数若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是()(A) (B) (C) (D)。
