圆柱圆锥的有关计算题
圆柱与圆锥的认识与计算测验题及答案

圆柱与圆锥的认识与计算测验题及答案题目一:判断题(每题5分,共10分)()1. 圆柱的侧面是由圆和一个平行于它的平面围成的。
()2. 圆锥的侧面是由圆和多个平行于它的平面围成的。
题目二:选择题(每题10分,共30分)1. 对于一个圆锥,下面哪个说法是正确的?A. 圆锥的底面是一个圆B. 圆锥的底面是一个矩形C. 圆锥的底面是一个三角形D. 圆锥没有底面2. 如图所示,一个圆柱的高为4cm,半径为2cm,求圆柱的体积是多少?A. 8π cm³B. 4π cm³C. 16π cm³D. 32π cm³3. 如图所示,一个圆锥的底面半径为4cm,高为6cm,求圆锥的表面积是多少?A. 48π cm²B. 24π cm²C. 96π cm²D. 12π cm²题目三:计算题(每题10分,共30分)1. 如图所示,一个圆柱的底面半径为3cm,高为8cm,求圆柱的体积和表面积分别是多少?2. 如图所示,一个圆锥的底面半径为5cm,高为10cm,求圆锥的体积和表面积分别是多少?3. 如图所示,一个圆锥的底面半径为6cm,高为9cm,现在将它的高减半,求减半后圆锥的体积和表面积分别是多少?答案:题目一:1.√ 2.√题目二:1.A 2.C 3.C题目三:1.体积:216π cm³,表面积:162π cm²2.体积:83.33π cm³,表面积:157.08π cm²3.体积:54π cm³,表面积:141π cm²。
圆柱圆锥练习题和答案

圆柱圆锥练习题和答案一、选择题1. 圆柱的体积公式是()A. V = πr²hB. V = πr² + hC. V = πr² - hD. V = πrh2. 圆锥的体积公式是()A. V = 1/3πr²hB. V = 3πr²hC. V = πr²h/3D. V = πr²h3. 圆柱的表面积公式是()A. S = 2πrh + 2πr²B. S = πrh + πr²C. S = 2πrhD. S = πr²4. 圆锥的侧面展开图是()A. 圆形B. 长方形C. 扇形D. 三角形5. 圆柱和圆锥的底面都是()A. 圆形B. 长方形C. 扇形D. 三角形二、填空题6. 一个圆柱的底面半径为3厘米,高为5厘米,其体积是_________立方厘米。
7. 一个圆锥的底面半径为4厘米,高为9厘米,其体积是_________立方厘米。
8. 一个圆柱的底面周长为12.56厘米,高为4厘米,其表面积是_________平方厘米。
9. 一个圆锥的底面半径为2厘米,高为6厘米,其表面积是_________平方厘米。
三、计算题10. 一个圆柱形容器的底面直径为20厘米,高为30厘米,求其容积。
11. 一个圆锥形沙堆,底面半径为5米,高为3米,如果将沙堆铺在长10米,宽6米的长方形地面上,求铺成的沙堆高度。
四、解答题12. 一个圆柱形油桶,底面半径为0.8米,高为1.5米,求油桶的表面积和体积。
13. 一个圆锥形漏斗,底面半径为0.6米,高为0.9米,求漏斗的体积。
答案:1. A2. A3. A4. C5. A6. 141.37. 75.368. 150.729. 37.6810. 圆柱形容器的容积为3.14 × (20/2)² × 30 = 3000π 立方厘米。
11. 圆锥形沙堆的体积为1/3 × 3.14 × 5² × 3 = 78.5π 立方米。
圆柱圆锥练习题以及答案

圆柱圆锥练习题以及答案一、选择题1. 一个圆柱的底面半径为3厘米,高为5厘米,其体积为:A. 141.3立方厘米B. 282.6立方厘米C. 94.2立方厘米D. 47.1立方厘米2. 一个圆锥的底面半径为4厘米,高为9厘米,其体积为:A. 75.36立方厘米B. 100.48立方厘米C. 50.24立方厘米D. 37.68立方厘米3. 圆柱的侧面积公式是:A. 2πr²B. πr²C. 2πrhD. πrh4. 圆锥的侧面积公式是:A. πr²B. πrlC. πr²+πrlD. 2πrh二、填空题1. 一个圆柱的底面直径为6厘米,高为10厘米,其侧面积为______平方厘米。
2. 一个圆锥的底面半径为5厘米,高为12厘米,其体积为______立方厘米。
三、解答题1. 一个圆柱形水桶的底面直径为40厘米,高为60厘米,求这个水桶的容积。
2. 一个圆锥形沙堆,底面半径为3米,高为4米,如果每立方米沙重1.5吨,求这堆沙的重量。
四、计算题1. 一个圆柱形油桶,底面直径为50厘米,高为80厘米,求油桶的表面积。
2. 一个圆锥形粮仓,底面直径为20米,高为15米,如果每立方米粮食重750千克,求粮仓的容积以及能装多少千克的粮食。
答案:一、选择题1. B2. B3. C4. C二、填空题1. 376.82. 188.4三、解答题1. 水桶的容积为:V=πr²h=π×(20)²×60=37680立方厘米。
2. 圆锥形沙堆的体积为:V=1/3πr²h=1/3×π×(3)²×4=12.56立方米。
沙堆的重量为:12.56×1.5=18.84吨。
四、计算题1. 油桶的表面积为:A=2πr(h+r)=2π×25(80+25)=4712.5平方厘米。
2. 圆锥形粮仓的体积为:V=1/3πr²h=1/3×π×(10)²×15=1570立方米。
六年级圆柱圆锥练习题

六年级圆柱圆锥练习题一、选择题(每题2分,共20分)1. 圆柱的体积公式是:A. V = πr²hB. V = πr² dC. V = πr²lD. V = πr² b2. 圆锥的体积公式是:A. V = 1/3πr²hB. V = πr²hC. V = 1/3πr²lD. V = πr² b3. 圆柱的侧面积公式是:A. S = 2πrhB. S = πr²hC. S = πr²D. S = πrh4. 圆锥的底面积公式是:A. S = πr²B. S = 2πrhC. S = πrhD. S = πr²h5. 如果圆柱的底面半径是圆锥底面半径的2倍,那么圆柱的体积是圆锥体积的:A. 1/3倍B. 2倍C. 4倍D. 8倍二、填空题(每题2分,共20分)6. 一个圆柱的底面半径是3厘米,高是10厘米,它的体积是________立方厘米。
7. 一个圆锥的底面半径是4厘米,高是12厘米,它的体积是________立方厘米。
8. 圆柱的底面积是28.26平方厘米,高是5厘米,它的体积是________立方厘米。
9. 一个圆锥的底面周长是12.56厘米,高是9厘米,它的体积是________立方厘米。
10. 圆柱的侧面积是62.8平方厘米,底面半径是2厘米,它的高是________厘米。
三、计算题(每题10分,共30分)11. 一个圆柱形容器,底面半径为5厘米,高为15厘米,求它的体积和侧面积。
12. 一个圆锥形的沙堆,底面半径为6米,高为10米,求它的体积。
13. 一个圆柱形的油桶,底面直径为0.8米,高为1.2米,求它的体积和侧面积。
四、应用题(每题15分,共30分)14. 一个圆柱形的蓄水池,底面直径为20米,深为5米,如果每小时向池中注水20立方米,需要多少小时才能将池子注满?15. 一个圆锥形的粮仓,底面半径为5米,高为10米,如果每立方米粮食重750千克,这个粮仓最多可以装多少吨粮食?五、拓展题(10分)16. 一个圆柱形的花瓶,底面半径为4厘米,高为20厘米。
小学数学圆柱圆锥练习题

小学数学圆柱圆锥练习题 1. 圆柱体 (1) 问题:若圆柱的底面半径为3cm,高度为8cm,求圆柱的体积和表面积。
解析:圆柱的体积公式为V = πr²h,表面积公式为A = 2πrh + 2πr²。 (2) 问题:圆柱的体积为108π cm³,底面半径为6cm,求圆柱的高度。
解析:根据圆柱的体积公式V = πr²h,可以得到 h = V / (πr²)。 (3) 问题:圆柱的表面积为144π cm²,底面半径为4cm,求圆柱的高度。
解析:根据圆柱的表面积公式A = 2πrh + 2πr²,可以得到 h = (A - 2πr²) / (2πr)。
2. 圆锥体 (1) 问题:若圆锥的底面半径为6cm,高度为10cm,求圆锥的体积和表面积。
解析:圆锥的体积公式为V = (1/3)πr²h,表面积公式为A = πr(r + l),其中 l 为斜高。
(2) 问题:圆锥的体积为140π/3 cm³,底面半径为5cm,求圆锥的高度。 解析:根据圆锥的体积公式V = (1/3)πr²h,可以得到 h = 3V / (πr²)。 (3) 问题:圆锥的表面积为100π cm²,底面半径为3cm,求圆锥的高度。
解析:根据圆锥的表面积公式A = πr(r + l),可以得到 l = A / (πr) - r,然后可以利用勾股定理得到圆锥的高度。
3. 综合练习 (1) 问题:一个圆柱的表面积是圆锥的表面积的2倍,且圆柱的高度是圆锥的高度的2倍,已知圆锥的底面半径为4cm,求圆柱的底面半径。
解析:设圆柱的底面半径为 r,则圆柱的表面积为2πr(r + h),圆锥的表面积为πr(r + l)。根据题目中的条件,可以列出方程 2πr(r + h) = πr(r + l)。带入已知条件并求解方程,可以得到圆柱的底面半径。
(2) 问题:一个圆锥的表面积是圆柱的表面积的3倍,且圆锥的高度是圆柱的高度的2倍,已知圆柱的底面半径为5cm,求圆锥的底面半径。
圆柱与圆锥专项练习题

六年级圆柱与圆锥专项练习题1、为了测定一根圆柱的底面半径,用细绳绕其一周,测得它的长度是251.2厘米,这根圆柱木材的底面半径是多少厘米?2、一个圆柱罐头的四周贴了一圈商标纸,将其撕下后是一个长为25.12厘米,宽为5厘米的长方形。
这个罐头的店面半径和高是多少厘米?3、某种饮料罐的形状是圆柱形,底面直径是7厘米,高是12厘米,将24罐这种饮料按如图所示的方式放入箱内,这个纸箱的长、宽、高至少各是多少厘米?4、妈妈过生日时爸爸买了一个大蛋糕,蛋糕盒是圆柱形,底面半径和高都是18厘米。
售货员阿姨用漂亮的红丝带把它捆起来,并在上面结了一个16厘米的蝴蝶结。
你知道这根红丝带有多长吗?5、一个圆柱形的废旧油桶的底面半径是1米,高是1.5米。
如果把它的侧面沿高剪开,得到的长方形的铁皮长和宽各是多少米?面积是多少平方米?6、鸿瑞小区要挖一个直径20米,深3米的圆柱形游泳池,这个游泳池的占地面积是多少?7、用一根长为18.84厘米,宽为10厘米的长方形彩纸沿长卷起来做成一个底面积最大的圆柱,如果要将两底封起来,需要密封的底面积是多少平方厘米?8、计算下列圆柱的表面积。
(1)底面半径3厘米,高6厘米。
(2)底面直径14厘米,高5厘米。
9、一种压路机的滚筒直径是1.2米,长3米,每分钟转10周,每分钟压路机前进多少米?每分钟压路多少平方米?10、一个圆柱形水池,水池内壁和底面都要镶上瓷砖,水池底面直径是6米,池深2米,镶瓷砖的面积是多少平方米?11、一个无盖圆柱形笔筒的侧面包装是一张边长为15.7厘米的正方形彩纸,求这个笔筒的表面积。
12、把一根长6米的圆柱形木材分成三段,表面积增加了3.14平方米,这根木材原来的底面积是多少平方米?13、一个圆柱原来的高是12厘米,如果它的高增加3厘米,它的表面积就增加37.68平方厘米。
原来这个圆柱的表面积是多少平方厘米?14、一个圆柱的侧面积是376.8平方厘米,高是20厘米。
圆柱圆锥的表面积与体积练习题
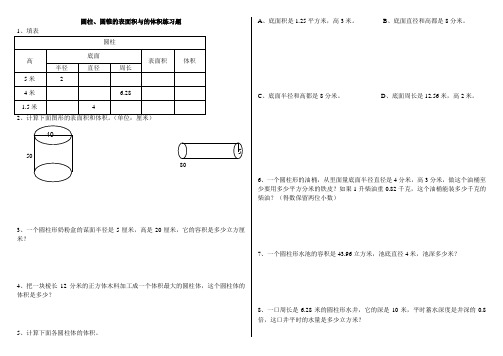
圆柱、圆锥的表面积与的体积练习题2、计算下面图形的表面积和体积。
(单位:厘米)803、一个圆柱形奶粉盒的谋面半径是5厘米,高是20厘米,它的容积是多少立方厘米?4、把一块棱长12分米的正方体木料加工成一个体积最大的圆柱体,这个圆柱体的体积是多少?A、底面积是1.25平方米,高3米。
B、底面直径和高都是8分米。
C、底面半径和高都是8分米。
D、底面周长是12.56米,高2米。
6、一个圆柱形的油桶,从里面量底面半径直径是4分米,高3分米,做这个油桶至少要用多少平方分米的铁皮?如果1升柴油重0.82千克,这个油桶能装多少千克的柴油?(得数保留两位小数)7、一个圆柱形水池的容积是43.96立方米,池底直径4米,池深多少米?8、一口周长是6.28米的圆柱形水井,它的深是10米,平时蓄水深度是井深的0.8倍,这口井平时的水量是多少立方米?9、一个长8分米,宽6分米,高4分米的长方体与一个圆柱体的体积相等,高相等,这个圆柱的底面积是多少?10、一段圆柱形钢材,长50厘米,横截面半径是4厘米,如果每立方厘米钢是7.9克,这段钢材的重量是多少千克?(得数保留一位小数)11、求下面图形的表面积和体积(单位:分米)12、有一段底面是环形的钢管,外圆直径是40厘米,内圆直径是20厘米,这根钢管长250厘米,求这根钢管的体积是多少立方厘米?圆柱的体积练习二1、一个圆柱的底面半径是6厘米,高是2分米,求这个圆柱的体积。
2、小刚有一个圆柱形的水杯,水杯的底面半径是5厘米,高是10厘米,有资料显示:每人每天的正常饮水量大约是1升,小刚一天要喝几杯水?3、一个圆柱形水桶,底面直径和高都是40厘米,用这个水桶容积的85%装水,每升水重1千克,桶中的水大约有多少千克?4、一个底面半径是10米的圆柱形蓄水池,能蓄水2512立方米,若再挖深2米,可蓄水多少立方米?5、一个圆柱形油桶,内底面直径是40厘米,高是50厘米,它的容积是多少升?如6、一个圆柱形玻璃杯底面半径是10厘米,里面装不水,水的高度是12厘米,把一小块铁块放进杯中,水上升到15厘米,这块铁块重多少克?(每立方厘米铁重7.8克)7、下图是一个长15厘米,宽6厘米、高15个底面半径为5厘米的圆柱形空洞,求这个零件的体积。
【数学】圆柱与圆锥综合练习题(提高篇)

【数学】圆柱与圆锥综合练习题(提高篇)一、圆柱与圆锥1.计算下面圆柱的表面积和体积,圆锥的体积。
(1)(2)【答案】(1)解:表面积:3.14×52×2+3.14×5×2×13=157+408.2=565.2(cm2)体积:3.14×52×13=1020.5(dm3)(2) ×3.14×82×15= ×3.14×64×15=1004.8(cm3)【解析】【分析】(1)圆柱的表面积=底面积×2+侧面积,侧面积=底面周长×高,圆柱的体积=底面积×高,根据公式计算即可;(2)圆锥的体积=底面积×高×,根据公式计算体积即可。
2.一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm。
把瓶口塞紧后使其瓶口向下倒立,这时酒深25cm。
求酒瓶的容积。
【答案】解:3.14×(10÷2)2×[15+(30-25)]=1570(cm3)答:酒瓶的容积是1570 cm3。
【解析】【分析】酒瓶的容积相当于高15厘米的圆柱形酒的体积,和高是(30-25)厘米的圆柱形空气的体积,把这两部分体积相加就是酒瓶的容积。
3.一个圆锥形沙堆,占地面积是30平方米,高2.7米,每立方米沙重1.7吨。
如果用一辆载重8吨的汽车把这些沙子运走,至少需要运多少次?【答案】解:30×2.7× ×1.7÷8≈6(次)答:至少需要运6次。
【解析】【分析】根据圆锥的体积公式V=×底面积×高求出这个沙堆的体积,然后乘 1.7吨求出沙堆的重量,最后根据沙堆总重量÷每次载重量=运输次数,代入数据即可求出需要运多少次。
4.一个圆锥形沙堆,底面积是45.9m2,高1.2m.用这堆沙在12m宽的路面上铺3cm厚的路基,能铺多少米?【答案】解:3厘米=0.03米×45.9×1.2÷(12×0.03)=18.36÷0.36=51(米)答:能铺51米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱、圆锥的侧面展开图
一、选择题
1. 已知圆柱的底面半径为2cm,高为5cm,则圆柱的侧面积是( )
A.20cm2 B.20πcm2 C.10πcm2 D.5πcm2
2. 已知圆柱的底面半径为1,母线长为2,则圆柱的侧面积为( )
A、2 B、4 C、2π D、4π
3. 如图所示,圆柱的底面周长为6cm,AC是底面圆的直径,高BC= 6cm,点P是母线BC上
一点且PC=23BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是
( )
A.(64)cm B.5cm C.35cm D.7cm
4. 露露从纸上剪下一个圆形和一个扇形的纸片(如图),用它们恰好能围成一个圆锥模型,若圆的半径为1.扇形的圆
心角等于120°,则此扇形的半径为( )
A、31 B、 C、3 D、6
5. 一个几何体的三视图如下:其中主视图和左视图都是腰长为4,底边为2的等腰三角形,则这个几何体侧面展开图
的面积为( )
A、2π B、 12π C、4π D、8π
6.如图,将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,这个棱柱的侧面积为( )
A.9 B.339 C.3259 D.3239
7. 一个圆锥的底面圆的周长是2π,母线长是3,则它的侧面展开图的圆心角等于( )
A、150° B、120° C、90° D、60°
8. 若一个圆锥的侧面积是10,则下列图象中表示这个圆锥母线l与底面半径r之间的函数关系的是( )
A、 B、C、D、
9.一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是( )
A、1 B、34 C、12 D、13
10.将一个圆心角是90°的扇形围成一个圆锥的侧面,则该圆锥的侧面积S侧和底面积S底的关系是( )
A、S侧=S底 B、S侧=2S底 C、S侧=3S底 D、S侧=4S
底
11. 如图是一圆锥的主视图,则此圆锥的侧面展开图的圆心角的是( )
A、60° B、90° C、120° D、180°
6
第11题 第12题
12. 如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所
示的一个圆锥,则圆锥的高为( )
A. 17cm B. 4cm C. 15cm D. 3cm
13. 一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是( )
A.5π B.4π C.3π D.2π
14.如图,矩形ABCD中,AB=4,以点B为圆心,BA为半径画弧交BC于点E,以点O为圆心的⊙O与弧AE,边AD,
DC都相切.把扇形BAE作一个圆锥的侧面,该圆锥的底面圆恰好是⊙O,则AD的长为( )
A.4 B.92 C.112 D.5
15. 如果圆锥的底面周长为20π,侧面展开后所得扇形的圆心角为120°,则该圆锥的全面积为( )
A.100π B.200π C.300π D.400π
16. 已知圆锥底面圆的半径为6厘米,高为8厘米,则圆锥的侧面积为( )
A.48厘米2 B. 48π厘米2 C. 120π厘米2 D. 60π厘米
17. 如图,Rt△ABC中,∠ACB=90°,AC=BC=22,若把Rt△ABC绕边AB所在直线旋转一周,
则所得几何体的表面积为( )A、4π B、42π C、8π D、82π
二、填空题
1. 如图,把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形
纸筒的侧面(衔接处无缝隙且不重叠),则圆锥底面半径是 cm.
2. 如图是一个几何体的三视图,这个几何体的全面积为 .( π取3.14)
3. 如图,圆柱底面半径为2cm,高为9cm,点AB、分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一
棉线从A顺着圆柱侧面绕3圈到B,求棉线最短为 cm.
4. 母线长为2,底面圆的半径为1的圆锥的侧面积为 .
5.已知一个圆锥形的零件的母线长为3cm,底面半径为2cm,则这个圆锥形的零件的侧面积为 cm2.(用π表示).
6.如果圆锥的底面周长是20π,侧面展开后所得的扇形的圆心角为120°.则圆锥的母线是
7.用半径为9cm,圆心角为120°的扇形纸片围成一个圆锥,则该圆锥的高为 cm.
8.一个圆锥形的零件的母线长为4,底面半径为1,则这个圆锥形零件的全面积是 .
9.在Rt△ABC中,∠C=90°,AC=3,BC=4,将△ABC绕边AC所在直线旋转一周得到圆锥,则该圆锥的侧面积是 .
10.若圆锥的侧面展开时一个弧长为l6π的扇形,则这个圆锥的底面半经是 .
11.将一个半径为6cm,母线长为15cm的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是 度.
12.已知一个圆锥的底面半径长为3cm、母线长为6cm,则圆锥的侧面积是 cm2.
13.如图是一个圆锥形型的纸杯的侧面展开图,已知圆锥底面半径为5cm,母线长为15cm,那么纸杯的侧面积
为 cm2.
14.若用半径为12,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥底面圆的半径的长 .
15.如图,将半径为3cm的圆形纸片剪掉三分之一,余下部分围成一个圆锥的侧面,则这个圆锥的高是
三、解答题
1.如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(1)请完成如下操作:
①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长,建立平面直角坐标系;②用直尺和圆规
画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连结AD、CD.
(2)请在(1)的基础上,完成下列问题:
①写出点的坐标:C 、D ;②⊙D的半径= (结果保留根号);
③若扇形ADC是一个圆锥的侧面展开图,则该圆锥的底面面积为 (结果保留π);
④若E(7,0),试判断直线EC与⊙D的位置关系并说明你的理由.
2.在△ABC中,AB= 3,AC= 2,BC=1.
(1)求证:∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.
答案:1-5 BDBCC 6-10 BDCDB 11-15 BCCDD 16 DB
填空题: 1-5题 4 ; ;15 ;2 ; 6 ;
6-10 30 ; 62 ; 5 ; 20 ;8 ;
11-15 144; 18 ;75 ;4 ;5cm
解答题:
第一题
A
B
C
O
C点(6,2);D(2,0) ; 圆D的半径为25 ;圆锥底面积为; 相切
第二题:(6+2)
