阴影部分面积ppt课件
合集下载
花瓣形阴影面积计算

花瓣形阴影部分的画法及面积计算
1、分别以正方形四条边的中点为圆心; 2、以正方形边长的一半为半径; 3、在正方形内部画出四个半圆;
阴影部分面积计算-------化整为零(作差)
空白部分的面积: (5X5—3.14X5²X )X2=10.75 (CM²) 一个花瓣的面积:
5X5—10.75=14.25(CM²) 四个花瓣的面积: 14.25X4=57(CM²)
阴影部分面积计算-------变换转化(平移)
空白部分的面积: (10X10—3.14X5²)X2 =43 (CM²) 阴影部分的面积:
10X10—43=57(CM²)
Байду номын сангаас
阴影部分面积计算-------追根溯源(重叠)
3.14X5²X2—10X10 =57(CM²)
阴影部分面积计算-------总结
阴影部分面积计算-------化整为零(做差)
空白部分的面积: (5X5—3.14X5²X )X2=10.75 (CM²) 一个花瓣的面积:
5X5—10.75=14.25(CM²) 四个花瓣的面积: 14.25X4=57(CM²)
阴影部分面积计算-------化整为零(分解)
半个花瓣的面积: 3.14X5²X —5X5X =7.125 (CM²) 一个花瓣的面积:
转化
割补
等积变换
平移
旋转
重叠
7.125X2=14.25(CM²) 四个花瓣的面积: 14.25X4=57(CM²)
阴影部分面积计算-------化整为零(重叠)
两个四分之一圆的面积: 3.14X5²X X2=39.25(CM²) 一个花瓣的面积:
39.25—5X5=14.25(CM²) 四个花瓣的面积: 14.25X4=57(CM²)
1、分别以正方形四条边的中点为圆心; 2、以正方形边长的一半为半径; 3、在正方形内部画出四个半圆;
阴影部分面积计算-------化整为零(作差)
空白部分的面积: (5X5—3.14X5²X )X2=10.75 (CM²) 一个花瓣的面积:
5X5—10.75=14.25(CM²) 四个花瓣的面积: 14.25X4=57(CM²)
阴影部分面积计算-------变换转化(平移)
空白部分的面积: (10X10—3.14X5²)X2 =43 (CM²) 阴影部分的面积:
10X10—43=57(CM²)
Байду номын сангаас
阴影部分面积计算-------追根溯源(重叠)
3.14X5²X2—10X10 =57(CM²)
阴影部分面积计算-------总结
阴影部分面积计算-------化整为零(做差)
空白部分的面积: (5X5—3.14X5²X )X2=10.75 (CM²) 一个花瓣的面积:
5X5—10.75=14.25(CM²) 四个花瓣的面积: 14.25X4=57(CM²)
阴影部分面积计算-------化整为零(分解)
半个花瓣的面积: 3.14X5²X —5X5X =7.125 (CM²) 一个花瓣的面积:
转化
割补
等积变换
平移
旋转
重叠
7.125X2=14.25(CM²) 四个花瓣的面积: 14.25X4=57(CM²)
阴影部分面积计算-------化整为零(重叠)
两个四分之一圆的面积: 3.14X5²X X2=39.25(CM²) 一个花瓣的面积:
39.25—5X5=14.25(CM²) 四个花瓣的面积: 14.25X4=57(CM²)
人教版六年级数学上册第五单元《圆与正方形组合的面积问题的应用》课件

3.14
r
2-
1 2
2r
r
2
=
1.14r
2
这节课你有什么收获?
1 “外方内圆” 图形中,圆的直径等于正方形的边长。 如果圆的半径为r,那么正方形和圆之间部分的面 积为0.86r2。
2 “外圆内方”图形中,这个正方形的对角线等于圆 的直径。如果圆的半径为r,那么圆和正方形之间 部分的面积为1.14r2。
易错辨析
选一选。 下面三个正方形的边长都是4 cm,阴影部分的面积相比,( D )。 A.第一个大 B.第二个大 C.第三个大 D.一样大
辨析:第一个图形是挖去一个完整的圆,第二个图形是挖 去两个半圆,第三个图形是挖去了四个四分之一圆, 所以剩余的阴影部分的面积是一样的。
3.圆的面积
5圆
第3课时 外方内圆和外圆内方图形面积的计算方法
7.求图中阴影部分面积。 4×4=16(cm2) 3.14×(4÷2)2=12.56(cm2) (16-12.56)×2=6.88(cm2) 16-6.88=9.12(cm2) 答:阴影部分的面积是9.12 cm2。
题目中都告诉 了我们什么?
上图中两个圆的半 径都是1 m,怎样
求正方形和圆之间 部分的面积呢?
左图求的是正
方形比圆多的
面积,右图求 的是……
你)可以看出: 2×2=4(m²) 3.14×1²=3.14(m²) 4-3.14=0.86(m²)
夯实基础
1. 右图是一面我国唐代外圆内方的铜镜。铜镜的 直径是24 cm。外面的圆与内部的正方形之间的 面积是多少?(选题源于教材P70做一做) 1.14×(24÷2)²=164.16(cm²) 答:外面的圆与内部的正方形之间的面积是164.16cm²。
关于求阴影部分面积圆

= 100 – 78.5 = 21.5 cm2
图中阴影部分的面积是4平方厘米, 圆环的面积是多少?
3.14×4=12.56(平方厘米)
图中圆环的面积是314平方厘米, 阴影部分的面积是多少?
314÷3.14=100(平方厘米)
求阴影部分面积。
4m
4m
求阴影部分面积。(单位:dm)
o 10
求阴影部分的面积。(单位:厘米)
3.右面图形的中间是一个 边长为4厘米的正方形。 计算整个图形的面积是 多少平方厘米?
14 求阴影部分面积。2cmຫໍສະໝຸດ 求下列各图中阴影部分面积。
S = 3.14 ×(22 - 12)÷2 = 3.14 × 3÷2 = 4.71 cm2
S = 10×10 – 3.14 × 102÷4 = 100 – 314÷4
求阴影部分的面积:
右图圆的周长是62.8厘米,它的面积与长方形的 面积相等。
2021年1月22日星期五
竹溪县实验小学 吴怀忠
8
2021年1月22日星期五
竹溪县实验小学 吴怀忠
圆单元整理与复习
灵活应用
1、如下图,绳长4米,问小狗的活动面积有多 大?
2、一个圆形花圃的周长是50.24米,在它 里面留出1/8的面积种菊花。菊花的占地面 积是多少?
2021年1月22日星期五
竹溪县实验小学 吴怀忠
11 求阴影部分周长和 面积。(单位:cm)
4
2021年1月22日星期五
2
竹溪县实验小学 吴怀忠
13 跑道外圈长多少米?内圈长 多少米?(两端各是半圆) 跑道和草坪面积分别是多少?
2021年1月22日星期五
100米
竹溪县实验小学 吴怀忠
求阴影面积:
图中阴影部分的面积是4平方厘米, 圆环的面积是多少?
3.14×4=12.56(平方厘米)
图中圆环的面积是314平方厘米, 阴影部分的面积是多少?
314÷3.14=100(平方厘米)
求阴影部分面积。
4m
4m
求阴影部分面积。(单位:dm)
o 10
求阴影部分的面积。(单位:厘米)
3.右面图形的中间是一个 边长为4厘米的正方形。 计算整个图形的面积是 多少平方厘米?
14 求阴影部分面积。2cmຫໍສະໝຸດ 求下列各图中阴影部分面积。
S = 3.14 ×(22 - 12)÷2 = 3.14 × 3÷2 = 4.71 cm2
S = 10×10 – 3.14 × 102÷4 = 100 – 314÷4
求阴影部分的面积:
右图圆的周长是62.8厘米,它的面积与长方形的 面积相等。
2021年1月22日星期五
竹溪县实验小学 吴怀忠
8
2021年1月22日星期五
竹溪县实验小学 吴怀忠
圆单元整理与复习
灵活应用
1、如下图,绳长4米,问小狗的活动面积有多 大?
2、一个圆形花圃的周长是50.24米,在它 里面留出1/8的面积种菊花。菊花的占地面 积是多少?
2021年1月22日星期五
竹溪县实验小学 吴怀忠
11 求阴影部分周长和 面积。(单位:cm)
4
2021年1月22日星期五
2
竹溪县实验小学 吴怀忠
13 跑道外圈长多少米?内圈长 多少米?(两端各是半圆) 跑道和草坪面积分别是多少?
2021年1月22日星期五
100米
竹溪县实验小学 吴怀忠
求阴影面积:
求阴影部分面积(圆)

13
跑道外圈长多少米?内圈长 多少米?(两端各是半圆) 跑道和草坪面积分别是多少?
100米
2015年1月8日星期四 竹溪县实验小学 吴怀忠
15
求阴影部分面积。
4cm
2015年1月8日星期四
竹溪县实验小学 吴怀忠
16
求阴影部分面积。
4m
2015年1月8日星期四
4m
竹溪县实验小学 吴怀忠
8
2015年1月8日星期四
8分米
3分米
15分米
2
求阴影部分的周长与面积。(单位:cm)
4
10
2015年1月8日星期四
竹溪县实验小学 吴怀忠
3
求阴影部分周长和 面积。(单位:dm)
3
5
2015年1月8日星期四
竹溪县实验小学 吴怀忠
4
求阴影部分面积。(单位:dm)
1
3
2015年1月8日星期四
竹溪县实验小学 吴怀忠
图中阴影部分的面积是5平方厘米, 圆环的面积是多少?
10
S=3.14 ×10×10÷2 = 314÷2 = 157(平方米)
10
9
求阴影部分周长和 面积。(单位:cm)
20
3.右面图形的中间是一个 边长为4厘米的正方形。 计算整个图形的面积是 多少平方厘米?
求阴影面积:
4cm 4cm
2.求阴影部分的面积。(单位:厘米)
求下列各图中阴影部分面积。
2015年1月8日星期四
竹溪县实验小学 吴怀忠
8
求月8日星期四 竹溪县实验小学 吴怀忠
14
求阴影部分面积。
2cm
2015年1月8日星期四
竹溪县实验小学 吴怀忠
4.微专题 三种方法求阴影部分面积
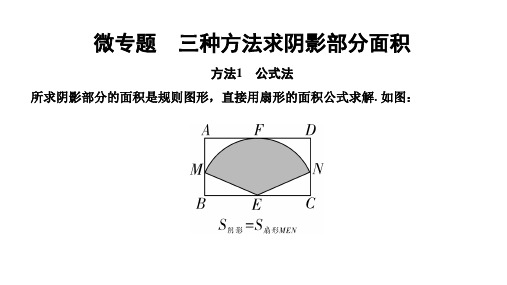
第4题图
综合训练
1. 如图,在半径为4的⊙O 中,CD 是直径,AB是弦,且CD⊥AB,垂足为点E, ∠AOB=90°,则阴影部分的面积是___2_π____. 2. 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E.若∠AOC=60°,OC=2,则 阴影部分的面积是__2__- __2___3_c_m__2__.
针对训练 2. 如图,正方形ABCD的边长为4,以BC为直径的半圆O交对角线线BD于点E, 则阴影部分的面积为__8_-__π___.
第2题图
二、构造和差法 先设法将不规则阴影部分与空白部分组合或将阴影部分进行分割,构造规则图形, 再进行面积和差计算.如图:
针对训练 3. 如图,在扇形AOB 中,∠AOB=90°,正方形CDEF的顶点C是 »AB 的中点, 点D在OB上,点E在OB的延长线上.当正方形CDEF的边长为2 2 时,则图中 阴影部分的面积为_2_π__-__4__.第1题图第2题图
3. 如图,菱形ABCD的边长为2,∠A=60°,B»D是以点A为圆心,AB长为半径的 弧,C»D 是以点B为圆心,BC长为半径的弧,则阴影部分的面积为___3_____cm2. 4. 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4 2 ,O是AB的中点, 以O为圆心,线段OC的长为半径画圆心角为90°的扇形EOF,E¼F 经过点C,则阴 影部分的面积为__2_π_-__4__.
第3题图
第4题图
微专题 三种方法求阴影部分面积
方法1 公式法 所求阴影部分的面积是规则图形,直接用扇形的面积公式求解. 如图:
针对训练 1. 如图,在▱ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是 ___3_π____.
第1题图
综合训练
1. 如图,在半径为4的⊙O 中,CD 是直径,AB是弦,且CD⊥AB,垂足为点E, ∠AOB=90°,则阴影部分的面积是___2_π____. 2. 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E.若∠AOC=60°,OC=2,则 阴影部分的面积是__2__- __2___3_c_m__2__.
针对训练 2. 如图,正方形ABCD的边长为4,以BC为直径的半圆O交对角线线BD于点E, 则阴影部分的面积为__8_-__π___.
第2题图
二、构造和差法 先设法将不规则阴影部分与空白部分组合或将阴影部分进行分割,构造规则图形, 再进行面积和差计算.如图:
针对训练 3. 如图,在扇形AOB 中,∠AOB=90°,正方形CDEF的顶点C是 »AB 的中点, 点D在OB上,点E在OB的延长线上.当正方形CDEF的边长为2 2 时,则图中 阴影部分的面积为_2_π__-__4__.第1题图第2题图
3. 如图,菱形ABCD的边长为2,∠A=60°,B»D是以点A为圆心,AB长为半径的 弧,C»D 是以点B为圆心,BC长为半径的弧,则阴影部分的面积为___3_____cm2. 4. 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4 2 ,O是AB的中点, 以O为圆心,线段OC的长为半径画圆心角为90°的扇形EOF,E¼F 经过点C,则阴 影部分的面积为__2_π_-__4__.
第3题图
第4题图
微专题 三种方法求阴影部分面积
方法1 公式法 所求阴影部分的面积是规则图形,直接用扇形的面积公式求解. 如图:
针对训练 1. 如图,在▱ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是 ___3_π____.
第1题图
《小学奥数》专题:求阴影部分面积的技巧
割补法
学而优教育 求阴影面积方法之六
例题6:如图,已知正方形的 边长为3,求图形的阴影部分 面积。
3
3
3
3
割补法
解:S阴
1 2
33
9. 2
学而优教育 求阴影面积方法之六
例题6:如图,已知正方形的 边长为3,求图形的阴影部分 面积。
3
3
割补法
学而优教育 求阴影面积方法之六
例题6:如图,已知正方形的 边长为3,求图形的阴影部分 面积。
2
2
学而优质教mn 育 难 例题8:如图,已知直角三角 分 形的直角边长为2,求图形的 析 阴影部分面积。
2
2
学而优质教mn 育 难 例题8:如图,已知直角三角 分 形的直角边长为2,求图形的 析 阴影部分面积。
4
重新组合法 4
解:S阴 S正 S圆 42 22 16 4.
学而优教育
求阴影面积方法之四
mn
例题4: 如图,已知正方形的
边长为4,求图形的阴影部分
面积。
4
重新组
4
合法
解:S阴 S圆 S正 42 22 16 4.
学而优教育 求阴影面积方法之五
例题5: 如图,已知大正方形 的边长为4,小正方形的边长 为2,求图形的阴影部分面积。
2 4
2
解:S阴
1 2
2
4
4.
学而优教育
求阴影面积方法之四
例题4: 如图,已知正方形的 边长为4,求图形的阴影部分 面积。
4
学而优教育
求阴影面积方法之四
例题4: 如图,已知正方形的边长为4, 求图形的阴影部分面积。
4
重新组合法
4
圆的周长和面积组合图形2讲PPT课件
学习目标:
1.掌握含有圆的组合图形面积 的计算方法。
2.准确计算含有圆的组合图形 的面积。
温故知新
新知探究
边学边做
堂清测试
求
环
.8cm
O
形 的
12cm
面
积
图片什么欣是组赏合图形呢?
v像这样由几个简单的图形 组合而成的图形叫做组合 图形
求红色部分面积。
S 红=S大半圆
解:S阴=102×3.14×
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人:XXXXXX 时 间:XX年XX月XX日
15
1 2
10cm
=157米 6厘米
求阴影部分面积。
r=5m
S阴= S三角形
求阴影部分面积。
4m
求阴影部分面积。
解:
S阴影 =
3 ×(3.14 ×52 )+ 52 4
=58.875+25
=83.875cm 2
r=5cm
S阴影=
3 4
S圆+S小正
这三个方法有什么区别呢?
堂清测试
我会填:
1.圆周率是指(
)
的比值,用字母(
)表示,它
是一个(
)小数.
2.正方形的边长和圆的直径相等,它
们的周长比是(
).
竹溪县实验小学 吴怀忠
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
14
结束语
当你尽了自己的最大努力时,失败也是伟大的, 所以不要放弃,坚持就是正确的。
1.掌握含有圆的组合图形面积 的计算方法。
2.准确计算含有圆的组合图形 的面积。
温故知新
新知探究
边学边做
堂清测试
求
环
.8cm
O
形 的
12cm
面
积
图片什么欣是组赏合图形呢?
v像这样由几个简单的图形 组合而成的图形叫做组合 图形
求红色部分面积。
S 红=S大半圆
解:S阴=102×3.14×
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人:XXXXXX 时 间:XX年XX月XX日
15
1 2
10cm
=157米 6厘米
求阴影部分面积。
r=5m
S阴= S三角形
求阴影部分面积。
4m
求阴影部分面积。
解:
S阴影 =
3 ×(3.14 ×52 )+ 52 4
=58.875+25
=83.875cm 2
r=5cm
S阴影=
3 4
S圆+S小正
这三个方法有什么区别呢?
堂清测试
我会填:
1.圆周率是指(
)
的比值,用字母(
)表示,它
是一个(
)小数.
2.正方形的边长和圆的直径相等,它
们的周长比是(
).
竹溪县实验小学 吴怀忠
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
14
结束语
当你尽了自己的最大努力时,失败也是伟大的, 所以不要放弃,坚持就是正确的。
六年级 求阴影部分面积 圆和扇形
求阴影部分的面积。
| ← 15厘米 →|
求阴影部分面积。
10cm
求阴影部分的面积。
1 求阴影部分面积。(单位:cm)
8 8
求圆的面积:
O·
正方形的面积是12平方厘米
2 下图中,正方形面积 为10m2,求圆的面积。
2020年3月30日星期一
10m2
竹溪县实验小学 吴怀忠
求圆的面积:
O
三角形的面积是4平方厘米
求阴影部分周长和 面积。(单位:cm)
20
右面图形的中间是一个 边长为4厘米的正方形。 计算整个图形的面积是 多少平方厘米?
=
+
求阴影面积: 直接算呢?有简便方法吗?
4cm 4cm
求阴影部分的面积。(单位:厘米)
求下列各图中阴影部分面积。
阴影部分的面积 =大半圆的面积 -小半圆的面积
阴影部分的面积 =正方形的面积 -直角扇形的面积
2020年3月30日星期一
100米
竹溪县实验小学 吴怀忠
10 求阴影部分面积。
2020年3月30日星期一
4cm
竹溪县实验小学 吴怀忠
11 求阴影部分面积。
2020年3月30日星期一
4m
4m
竹溪县实验小学 吴怀忠
8
2020年3月30日星期一
竹溪县实验小学 吴怀忠
5
竹溪县实验小学 吴怀忠
5 求阴影部分面积。(单位:dm)
1
3
2020年3月30日星期一
竹溪县实验小学 吴怀忠
图中圆与长方形面积相等,圆的周 长是6.28米。阴影部分面积多少平 方米?
2020年3月30日星期一
竹溪县实验小学 吴怀忠
求阴影部分面积
阴影部分面积= 正方形面积
4×4—3.14×2× 2
=16—12.56 =3.44cm2
4dm
阴影部分面积=
四分之一圆面积
—
三角形面积
3.14×4× 4÷4
=12.56 —8
4×4÷2
=4.56 (平方分米)
a米
a米
一个正方形面积
阴影部分面积=
R=4cm 阴影部分面积=
R=4cm 一个三角形的面积
你会找它的高和底吗? 4×2× 4 ÷2=16(平方厘米)
5dm 2dm
阴影部分面积= 5×5 正方形面积 3.14× 2 × 2 ÷2 半圆面积
=25 —6.28 =18.72(平方分米)
8cm
8cm
通过割补把两个阴影部分变成一个等腰直角三角形 阴影部分面积= 等腰直角三角形面积 正方形的边长等于圆的半径 等腰直角三角形的底和高等于正方形的 边长 8÷2=4 CM 4 × 4÷2=8 CM2
6dm
10dm 4cm 4cm 8cm 10cm
R=4cm
8cm
10cm
a米 a米
10cm
6cm
5cm
8cm
4dm 4dm
8cm
2 1 2 1
1cm
10cm
12cm 1cm
1cm 5cm 5cm 4cm 4cm 20cm
3cm 5cm
2cm
20米 12米 2m
2m
4cm
圆半径:4÷2=2cm 圆面积
4cm
8cm
梯形上底=半径=4cm 梯形高=半径=4cm
梯形面积:(4+8)×4 ÷2 =12×4 ÷2 =24cm2 四分之一圆面积:3.14 ×4 ×4 ÷4=12.56cm2
人教版六年级数学上册第五单元第6课时《圆与正方形组合的面积问题的应用》课件
4.土楼是福建、广东等地 区的一种建筑形式,被列入 “世界物质文化名录”,土 楼的外围形状有圆形、方形、 椭圆形等。圭峰楼和德逊楼 是福建省南靖县两座地面是 圆环形的土楼,
圭峰楼外直径33 m,内直 径14 m;德逊楼外直径 26.4 m,内直径14.4 m。 两座土楼的房屋占地面积 相差多少? (选题源于教材P73第12题)
6.篮球场上的3 分线是由 两条平行线段和一个半 圆组成的。请你根据图 中的数据计算出3 分线 的长度和3 分线内区域 的面积。 (选题源于教材P73第14题)
半圆的弧长:3.14×6.75=21.195(m) 3分线的长度:21.195+2×1.575≈24.35(m) 半圆的面积:(3.14×6.752)÷2=71.533125(m2) 长方形的面积:6.75×2×1.575=21.2625(m2) 3分线内区域的面积:71.533125+21.2625≈92.80(m2) 答:3 分线的长度和3 分线内区域的面积是92.80m2。
3.14×(34÷2)2-3.14×(14÷2)2=753.6(m2) 3.14×(26÷2)2-3.14×(14÷2)2=376.8(m2) 753.6-376.8=376.8(m2)答:占地面积相差376m2。
5.一个圆的周长是62.8 m,半径增加了2 m 后,面积 增加了多少?(选题源于教材P73第13题) 62.8÷3.14÷2=10(m) 10+2=12(m) 3.14×122-3.14×102 =138.16(m2) 答:面积增加了138.16m2
(2)
4×4-3.14×(4÷2)2 =3.44(cm2)
(5×2)2-3.14×52 =21.5(m2)
3.解决问题 (1)在一块边长为20 cm的正方形铁片中,截取如图
