天津大学弹性力学试卷A
硕士研究生入学考试弹性力学试题

(50 分)
1、悬臂梁在端部受集中力
M、F,上面受有分布载荷 q0
l x
,下面受有均布剪力 0
;
2、楔形体在一面受有均布压力 q 和楔顶受有一集中载荷 P 的作用。
y
o
P
q
r
x
三、试推导出按位移求解弹性力学问题时所用的基本微分方程(Lame 方程)。(30 分) 四、在已知扭矩 M 的作用下,半径为 a 的圆截面扭杆,有半径为 b 的圆弧槽, 取坐
硕士研究生入学考试弹性力学试题
试题(A)
一、试述五个基本假定在建立弹性力学基本方程时有什么用途?(30 分)
二、试用应力函数 Ax3 Bx2 y Cxy2 Dy3 求解只受重力作用的三角形悬
臂梁的各应力分量,如图所示,已知梁的密度为ρ 。
(30 分)
O
α ρɡ
x
y
三、设有半平面体,体力不计,在其边界面上受有 2 个相距 3 D 的法向
y q
O q
α /2
α /2
x
2、矩形薄板,三边固定,一边受有均布压力 q
q
x o
b a
b a
y
(40 分)
试题(B)
一、如图所示为平面应力状态下的细长薄板条,上下边界受均布力 q 的作用,其余边
界上均无面力作用,试说明 A,B,C 点处的应力状态。 q
(20 分)
C o
B y
q
A
x
二、试给出如图所示平面应力问题的定解条件
a
a
a
O
x
a
ρg
y
4
集中力 P 的作用,试求 600 ,r D 处的应力分量。
2
(10 分)
天津大学在线考试题库及答案[理论力学]
![天津大学在线考试题库及答案[理论力学]](https://img.taocdn.com/s3/m/aeb0b4984431b90d6d85c736.png)
理论力学一、单选题1. 质点M 的质量为m ,受有二个力F 和R 的作用,产生水平向左的加速度a ,质点M 的运动微分方程为( ) MC aA.R F x m -=&&B.R F x m -=-&&C.F R x m -=&&D.F R x m -=-&&[答案]:A2. 重为W 的货物由电梯载运下降,当电梯加速下降、匀速下降及减速下降时,货物对地板的压力分别为R 1、R 2、R 3,它们之间的关系为( )A.R 1 = R 2 = R 3B.R 1 > R 2 > R 3C.R 1 < R 2 < R 3D.R 1 < R 3 > R 2[答案]:C3. 质量为m 的小球,放在倾角为 α 的光滑面上,并用平行于斜面的软绳将小球固定在图示位置。
如斜面与小球均以a 的加速度向左运动,则小球受到斜面的约束力为( )A.cos sin mg ma αα-B.cos sin mg ma αα+C.cos mg αD.sin ma α[答案]:B4. 提升矿石用的传送带与水平面成倾角α。
设传送带与矿石之间的摩擦系数为f ,为保持矿石不在带上滑动,则所需的加速度a 至少为多大( )A.)sin cos (αα+=f g aB.)sin cos (αα-=f g aC.αcos gf a =D.αsin g a =[答案]:B5. 质量为m 的物块A ,置于物块B 上,如图所示。
A 与B 间的摩擦系数为f ,为保持A 与B 一起以加速度a 水平向右运动。
则所需的加速度a 至少为多大( )A.gB.2gC.2gfD.gf[答案]:D6. 汽车重P ,以匀速v 驶过拱桥,在桥顶处曲率半径为R ,在此处桥面给汽车的约束力大小为( )A.PB.gRPv P 2+ C.gR Pv P 2- D.gRPv P - [答案]:C7. 质量为m 的物体M 在地面附近自由降落,它所受的空气阻力的大小为F R = Kv 2,其中K 为阻力系数,v 为物体速度,该物体所能达到的最大速度为( )A.Kmg v = B.mgK v = C.Kg v = D.gK v =[答案]:A8. 在图示圆锥摆中,球M 的质量为m ,绳长l ,若α角保持不变,则小球的法向加速度为( )A.αsin gB.a g cosC.αtan gD.αtan c g[答案]:C9. 起重机起吊重量25=Q kN 的物体,要使其在25.0=t s 内由静止开始均匀的加速到0.6m/s 的速度,则重物在起吊时的加速度和绳子受的拉力为( )A.2.4 m/s 2;25.38kNB.0.15 m/s 2;31.12kNC.2.4 m/s 2;31.12kND.0.15 m/s 2;25.38kN[答案]:C10. 已知A 物重N 20=P ,B 物重N 30=Q ,滑轮C 、D 不计质量,并略去各处摩擦,则绳水平段的拉力为( )A.30NB.20NC.16ND.24N[答案]:D11. 图示均质圆轮,质量为m ,半径为r ,在铅垂图面内绕通过圆盘中心O 的水平轴以匀角速度ω转动。
《弹性力学》试题

《弹性力学》试题(答题时间:100分钟)一、填空题(每小题4分)1.以应力表示的相容方程其适用性: , 。
2.一组可能的应力分量应满足 , 。
3.等截面直杆扭转问题中,方程0=s ϕ的物理意义是 。
4.应力函数ϕ在边界上值的物理意义是 ,y x ∂∂∂∂ϕϕ,在边界上值的物理意义是 。
5.由平面应力到平面应变问题,其材料弹性常数的转换关系为: ,。
二、简述题(每小题7分)1.图示矩形弹性薄板,沿对角线方向作用一对拉力P ,板的几何尺寸如图,材料的弹性模量E 、泊松比 μ 已知。
试求薄板面积的改变量S ∆。
2.图示两楔形体,试分别用直角坐标和极坐标写出其应力函数ϕ的形式。
题二(1)图 题二(2)图 3.图示曲杆,在b r =边界均布拉应q ,在自由端作用有水平集中力P 。
试写出其边界条件(除固定端外)。
题二(3)图4.下面给出平面应力问题(单连通域)一组应力分量和一组应变分量,试判断它们是否可能。
(1),21y C x C x +=σ,43y C x C y -=σy C x C xy 14-=τ;(2)),(22y x C x +=ε,2Cy y =εCxy xy 2=γ。
5.试用笛卡尔张量写出弹性力学平衡微分方程、几何方程、形变比能1U 的表达式。
三、计算题1.图示顶角为α的楔形体,下端无限长,受水平方向的常体力作用,设单位体积的水平力为p ,试用纯三次多项式为应力函数ϕ求其应力分量。
(15分)2.已知圆环在a r =的内边界上被固定,在b r =的圆周上作用着均匀分布剪应力0τ,如图所示。
试确定圆环内的应力与位移。
(提示:取应力函数θϕA =) (15分)3.一端固定,另一端自由的梁,其跨度为l ,抗弯刚度EI 为常数,分别承受均匀分布载荷q 、集中力P 的作用,如图所示。
若用Ritz 法(或最小势能原理)求解,试:(1)构造两种形式的挠度近似函数)(x w (三角函数形式、多项式);(2)在上述)(x w 中,任选一种求梁的挠度(取一项待定系数)。
弹性力学试卷题库原版
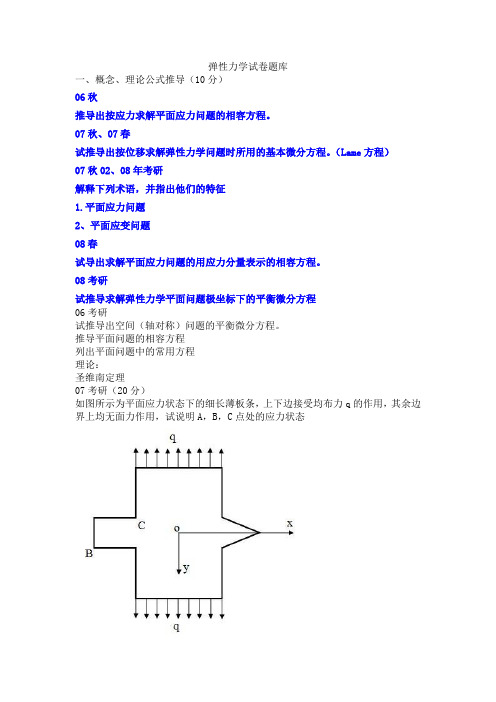
弹性力学试卷题库一、概念、理论公式推导(10分)06秋推导出按应力求解平面应力问题的相容方程。
07秋、07春试推导出按位移求解弹性力学问题时所用的基本微分方程。
(Lame方程)07秋02、08年考研解释下列术语,并指出他们的特征1.平面应力问题2、平面应变问题08春试导出求解平面应力问题的用应力分量表示的相容方程。
08考研试推导求解弹性力学平面问题极坐标下的平衡微分方程06考研试推导出空间(轴对称)问题的平衡微分方程。
推导平面问题的相容方程列出平面问题中的常用方程理论:圣维南定理07考研(20分)如图所示为平面应力状态下的细长薄板条,上下边接受均布力q的作用,其余边界上均无面力作用,试说明A,B,C点处的应力状态二、定界条件(10分*2)06秋、07秋、07秋02、07春、08春1、(10分)楔型体双边受对称均布剪力q 。
Oy xq qα/2α/2xy o C Bqq06秋、 2、(10分)矩形截面挡水墙的密度为ρ,厚度为h ,水的密度为γ。
07秋、08考研3、(10分)下图所示楔形体,试分别写出极坐标和直角坐标下的定解条件。
07秋02、07春4、设有矩形截面的长竖柱,密度为ρ,在一边侧面上受均布剪力q 。
γgρgxy O2h 2h08春、07考研5、(10分)楔形体在一面受有均布压力q 和楔顶受有一集中载荷P 的作用。
08考研简支梁受均布荷载q 作用,ρgyxObqP xy r θα β q o xqLqLLLy07考研悬臂梁在端部受集中力M 、F ,上面受有分布载荷xlq 0,下面受有均布剪力006考研矩形薄板,三边固定,一边受有均布压力qhlMxl q 0Oxyxboa baq如图所示为一矩形截面水坝,其左侧面受静水压力,顶部受集中力P 作用。
试写出定界条件,固定边不考虑。
图示水坝,顶面受有均布压力q ,斜面受静水压力作用,底部固定,写出定解条件。
(下载的图一中)三、平面(直角或极坐标)(20分) 06秋、08考研等厚度薄板沿周边承受均匀压力q 的作用,若O 点不能移动和转动,试求板内任意一点A(x,y)处的位移。
试卷A-2021

北京航空航天大学2019-2020 学年第二学期期末《弹性力学》A卷班级______________学号 _________姓名______________成绩 _________2020年6月10日班号 学号 姓名 成绩《 弹性力学 》期末考试卷2、请字迹工整,以便拍照。
题目:一、分析计算题…………………………………………………………(本题18分)(1)图1所示为三角形薄板,请在图中画出正的面力和正的体力的方向。
(4分)图1 图2 图3(2)图2所示的单位宽度的梁在x =0处受集中力和力矩的作用,需要应用圣维南原理来处理,请说出圣维南原理的内容,并给出x =0面上满足静力等效的三个积分表示的边界条件。
(6分)(3)设A 是薄板上一点,A 点应力为x σ,y σ,xy τMPa ,请在过A 点的微元体(图3所示)上画出这三个应力的方向。
问过A 点与坐标轴为45°夹角的斜面(BC 边)上的应力是多少?请在图3中BC 边上标出你计算得到的应力方向。
(8分)二、简答题………………………………………………………………(本题12分) 试比较平面应力问题与平面应变问题的相同和不同之处。
三、简答题………………………………………………………………(本题10分) 若不计体力,不同材料组成的同样结构受同样的载荷,其应力分布是否相同?其应变是否相同?为什么?四、简答题………………………………………………………………(本题10分) 什么是薄膜比拟?它与等截面杆的扭转问题有什么关系?五、简答题………………………………………………………………(本题10分) 什么是薄板弯曲问题?描述它的微分方程与边界条件是什么样的?六、推导题………………………………………………………………(本题11分) 等厚薄圆盘以角速度ω旋转,分析其应力、位移分布特点,试导出圆盘二维极坐标下的平衡微分方程(材料常数E 、μ、ρ为已知)。
七、分析题………………………………………………………………(本题15分) 判断3ax y ϕ=,能否作为应力函数?如果能,对下图所示的矩形板,请画出矩形板边界上的面力分布(不计体力,且0a >)。
弹性力学试卷供参习

一、计算题(共15分)
简易起重设备的计算简图如图所示,已知斜杆AB用两根63mm⨯40mm⨯4mm不等边角钢组成,钢的许用应力[σ]=170MPa。
试问在提起重量为P=15kN的重物时,斜杆AB是否满足强度条
件?
二、计算题(共10分)
如图所示阶梯状圆轴,AB段直径d1=120mm,BC段直径d2=100mm。
扭转力偶矩为M A=22kN⋅m,M B=36 kN⋅m,M C=14 kN⋅m。
已知材料的许用切应力[τ]=80MPa,试校核该轴的强度。
三、计算题(共15分)
受力体某点两平面上的应力如图示,求其主应力大小。
四、计算题(共15分)
图示圆轴直径d=20mm,受弯矩My及扭矩Mx作用。
若由实验测得轴表面上A点沿轴线方向的线应变ε0=6×10-4,B点沿轴线成45°方向的线应变ε-45︒=4×10-4,已知材料的E=200GPa,υ=0.25,[σ]=160MPa。
试求My及Mx,并按第四强度理论校核轴的强度。
五、计算题(共15分)
图示槽形截面悬臂梁,已知惯性矩I Z=1.02×108mm4,y c=96.4mm。
P=10KN,m=70KN·m。
试求梁的最大拉应力(σt )max 和最大压应力(σc )max (C为形心)。
3m m
单位:mm
3m C
250y c
六、计算题(共15分)
图示由A3钢制成的1、2两杆,弹性模量为E ,1、2两杆均为方形,边长分别是2a 和a 。
已知l=10a ,适用欧拉公式的临界柔度值为100。
试求2杆失稳时载荷P 的临界值。
弹性力学试卷及答案4套
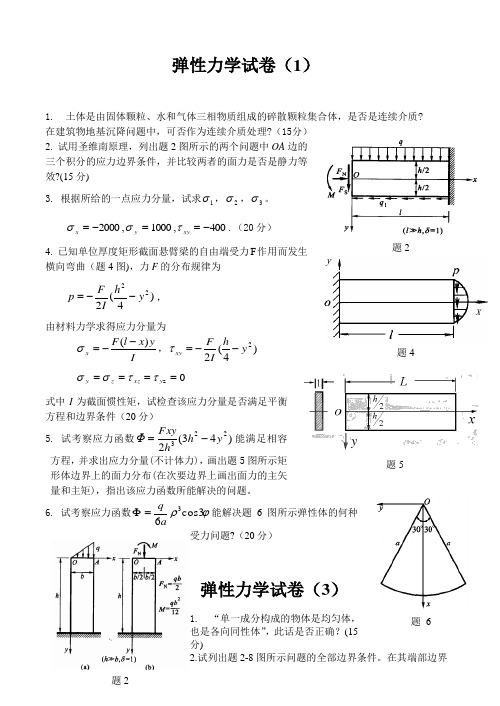
弹性力学试卷(1)1. 土体是由固体颗粒、水和气体三相物质组成的碎散颗粒集合体,是否是连续介质? 在建筑物地基沉降问题中,可否作为连续介质处理?(15分)2. 试用圣维南原理,列出题2图所示的两个问题中OA边的三个积分的应力边界条件,并比较两者的面力是否是静力等效?(15分)3. 根据所给的一点应力分量,试求1σ,2σ,3σ。
400,1000,2000-==-=xyyxτσσ.(20分)4. 已知单位厚度矩形截面悬臂梁的自由端受力F作用而发生横向弯曲(题4图),力F的分布规律为)4(222yhIFp--=,由材料力学求得应力分量为IyxlFx)(--=σ,)4(22yhIFxy--=τz====yxzzyττσσ式中I为截面惯性矩,试检查该应力分量是否满足平衡方程和边界条件(20分)5. 试考察应力函数)43(2223yhhFxyΦ-=能满足相容方程,并求出应力分量(不计体力),画出题5图所示矩形体边界上的面力分布(在次要边界上画出面力的主矢量和主矩),指出该应力函数所能解决的问题。
6.试考察应力函数ϕρcos363aq=Φ能解决题6图所示弹性体的何种受力问题?(20分)弹性力学试卷(3)1. “单一成分构成的物体是均匀体,也是各向同性体”,此话是否正确?(15分)2.试列出题2-8图所示问题的全部边界条件。
在其端部边界题2题2题4y题5题 6上,应用圣维南原理列出三个积分的应力边界条件。
(15分) 3. 根据所给的一点应力分量,试求1σ,2σ,3σ。
1010,50,100===xy y x τσσ.(20分)4. 检验下列应力分量是否是题4图所示问题的解答:q b y x 22=σ,0===yx xy yττσ。
(20分)5. 试证)2(10)134(4332332h y h y qy h y h y qx Φ-+-+-=能满足相容方程,并考察它在题5图所示矩形板和坐标系中能解决什么问题(设矩形板的长度为L ,深度为h ,体力不计)。
弹性力学2010试卷A

,考试作弊将带来严重后果!华南理工大学期末考试《弹性力学》试卷(A)1. 考前请将密封线内各项信息填写清楚;2. 所有答案请直接答在试卷上; 3.考试形式:闭卷;5分,共8小题,合计40分):1.何谓理想弹性体?微小位移和形变的假定在推导弹性力学基本方程时起2.根据应力符号规定,在图中标出极坐标下任意一点处各坐标面上应力分量ρϕτ和ϕρτ的不同。
3.应力分量除了满足平衡微分方程之外,还需满足什么才是正确的解答?4.下面的应变状态是否能存在?为什么?22,,0x y xy Axy Bx y εεγ===。
其中,A 、B 为非零常数。
5.如果某一应力边界问题中有m 个主要边界和n 个次要边界,试问在主要边界、次要边界上各应满足什么类型的应力边界条件?各有几个条件?6.何谓极小势能原理?7.为了能从有限单元法得出正确的解答,单元位移模式必须满足哪些条件?8.在应用有限单元法求解时,为什么在计算对象的厚度突变处或弹性有突变的地方,应当把单元取得较小些并将突变线作为单元的界线(即不要使突变线穿过单元)?二、取满足相容方程的应力函数Φ=Axy2,其中A>0为常数,试求出应力分量(不计体力),并画出该应力函数在图示弹性体(厚度为1)边界上的面力分布,在次要边界上表示出面力的主矢量和主矩。
(10分)三、设单位厚度矩形截面的悬臂梁在自由端受集中力偶M作用,如图所示,试用应力函数Φ=Axy+Bxy3+Cy3+Dy2求其应力分量(不计体力),并确定常数A、B、C、D。
(20分)x四、图中所示厚度为t 的狭长矩形薄板右端完全固定左端受均匀面力x f q =-作用。
在板的中部A 、B 两点有半径为A R 和B R 的圆形小孔,其中点A 位于x 轴上、点B 可能在x 轴和边线之间的任何位置。
(15分) 1. 只有孔A 的情况(即0,0A B R R >=时的情况)。
在什么条件下我们可以估算出A 点处的最大和最小孔边应力?为什么?给出此时的最大和最小孔边应力、对应的直角坐标下的分量值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学院专业年级学号姓名
2019〜2020学年第2学期期末考试试卷《弹性力学1》(A卷共3页)
(考试时间:2020年6月12日)4.矩形薄板受到如图1所示的外力作用,若要分析板内的应力分布情况,应该采用下列()作为应力函数。
A. p = ax2 + bxy + cy+d
B.中=ay + bxy+ cx+ d
C.中=ax3 + bxy + cy2
D.中=ax2 + bxy2 + cy
题号一二三四成绩核分人签字
得分
一、判断题(下面各小题正确的划",错误的划X,每小题3分,共18分)
1.弹性力学是从微分体dV入手分析弹性体,而材料力学是从有限体A V入手分析,因此弹性力学的计算结果相比材料力学更为精确。
()
2.不同坐标系下,应力分量的值不同,但是描述的一点受力的应力状态是确定的。
(
)
3.对于承受均布荷载的简支梁来说,弹性力学的应力分量解答与材料力学的相应解答均不相同。
()
4.用应力分量表示的相容方程等价于几何方程和物理方程。
()
5.为了保证平面有限元离散模型的连续性,应使所选择的位移模式以及相应的应变、应力等函数在单元内部以及相邻单元的边界上均满足连续性条件。
()
6.平面六结点三角形单元在其自重作用下的等效结点荷载是将总重W平均分配到各个结点上,方向向下。
()
二、选择题(下面各小题仅有一个答案是正确的,每小题4分,共32分)
1.在常体力情况下,用应力函数中表示的相容方程是()。
A.泊松方程
B.重调和方程
C.欧拉方程
D.调和方程
2.无限长的圆筒承受均布内压力q作用时,其内部任意点沿圆筒轴向方向处于()。
A.受拉状态
B.受压状态
C.无受力状态
D.三种情况都有可能
3.半空间体在边界上受竖直向下的集中力F作用,其边界上的沉陷量随着与集中力F的距离的增大而呈现()。
A.指数型函数衰减
B.自然对数型函数衰减
B.常用对数型函数衰减 D.反比例型函数衰减
£
b
标
rrrnzdrrrn
1
0X
1
-
5.两个等截面直杆,如图2所示,一个横截面为椭圆,a = 2b;另一个横截面为长方形,l = 2m,p = 0.246,p广0.229。
已知l = 2a,且二者的单位扭角K相同,则其最大剪应
力()。
A. T椭圆<T长方形
6.在有限元法中,
B. T椭圆=T长方形
C. T椭圆>T长方形
D.无法比较
将作用于单元的外荷载应用()转化为单元的等效结点荷载。
椭圆
A.刚性体静力等效原则
B.虚功原理
C.变形体静力等效原则
D.达朗贝尔原理
7.平面六结点三角形单元(T6单元,厚度f = 1)的面积为A,质量密度为p,在jm边上承受竖向均布荷载q作用,如图3所示,则其在自重和边界面力共同作用下jm边上三个结点处的竖向等效结点荷载为()。
A.F =-州+", F。
初,F =-ql+2p g A
Ljy 6 L1y 3 Lm y 6
C. F =-义,F =-心翌,F =旦 D
Lj y 6 L1y 3 Lm y 6
B. F 顼,F =-^P^, F 顼
Lj y 3 L1y 3 Lm y 3
_ q l +p gA ql ql +P gA
Ljy"—'命=一孑F my=一
8.在平面四结点矩形单元(R4单元)中,右,点发生向右的水平位移u , m点发生向左的水平位移u,而其匕所有的结点位移分量均为0,则此时该单元的位移形态为(
)。
A.双线性曲面
B.双曲面
C.椭球面
D.线性平面
学院专业班年级学号姓名共3页第2页
1.试写出图4所示浸在液体中的梯形结构的边界条件,液体质量密度为p。
三、简答题(每小题8分,共16分) 1.简述圣维南原理,并举例说明。
四、计算题(第1小题10分,第2、3小题每题12分,共34分)
2.在体力为常量的平面应力问题中,应力分量b = 2kx2y,b = —ky3,T = 3ky3(k为常数,且k。
0)是否真实存在?为什么?' "
2. 一个任意形状的薄板在某一面力作用下,其内部距离边界较远的某一点A处的应力分
3 1
量为b =b = —q,T = —q,如图5所示,若将直角坐标系的坐标原点设置在A点处,并以A点为圆心、c为半径开凿一个小圆孔,试求该圆孔与x轴交点B处的最大、最小正应力。
3.如图6所示的单位厚度的悬臂梁在左端受到竖向集中力尸作用,体力不计,/>>们若用应力函数中=axy + bxy3求解,试确定系数a、b的数值以及最终的应力分量。
>
°
k h_ f2
"h_
<2 _____ l
学院专业年级学号姓名图5。
