介电常数
介电强度和介电常数
介电强度和介电常数介电强度和介电常数是电学中的重要概念，它们在电场中的行为以及材料性质的研究中都扮演着至关重要的角色。
本文将从概念解释、应用举例等方面，生动地介绍介电强度和介电常数，旨在为读者提供全面且具有指导意义的知识。
首先，介电强度是介电材料在电场中的响应能力的度量。
它代表了单位电场下介质所能储存的电能。
介电强度可以用下式表示：D=εE其中，D是介电强度，ε是介电常数，E是电场强度。
从式子中可以看出，介电强度与电场强度成正比，而介电常数则是介电强度和电场强度之比。
其次，介电常数是介质相对于真空的电容量大小。
它是介质在电场中的响应能力与真空的相对比值。
介电常数可以通过以下公式表示：ε=ε0*εr其中，ε是介电常数，ε0是真空中的介电常数（常数值），εr 是相对介电常数。
介电常数的大小与介质的特性有关。
对于不同的介质，其介电常数的数值不同，代表着介质对电场的响应能力。
例如，对于真空而言，其介电常数为ε0=8.854x10^-12F/m，这意味着真空的电场强度和介电强度之间的比值为1。
而对于一些常见的介质，如玻璃、空气、水等，它们的相对介电常数介于1和100之间。
介电常数的重要性体现在它对电容器的性能有着直接影响。
电容器的电容量是通过介电常数来决定的，电场强度越大，介质对电荷的响应能力越强，电容量也会越大。
因此，在设计和选择电容器时，需要根据实际需求考虑材料的介电常数。
此外，介电强度和介电常数还与介质的极化现象密切相关。
当介质处于电场中时，其分子或原子会发生极化，即电荷的重新分布，导致正负电荷的分离。
通过介电强度和介电常数的概念，我们可以更好地理解并描述这一过程，并可以预测材料在电场中的行为。
综上所述，介电强度和介电常数是电学中的重要概念。
通过介电强度和介电常数的理解，我们可以更好地研究材料在电场中的性质和行为，以及电容器的设计和选择。
因此，对这两个概念的全面理解和应用能够在电学研究和应用中发挥重要的指导作用。
(完整版)介电常数
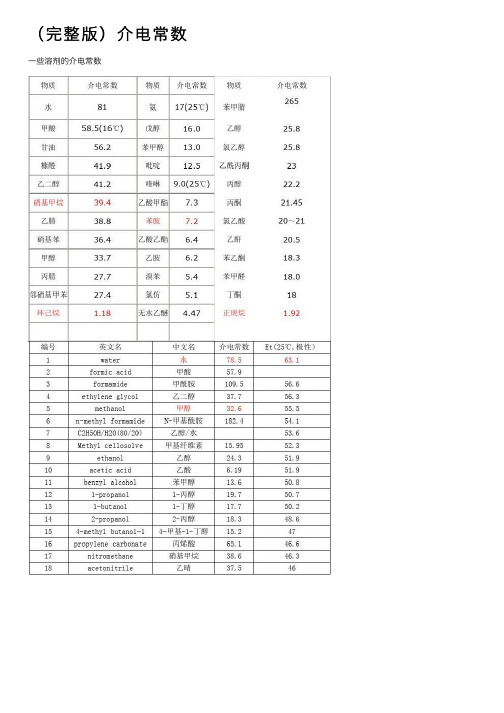
（完整版）介电常数⼀些溶剂的介电常数介电常数(Dielectric constants)表1列出常见⽓体在20℃，101 325 Pa条件下的介电常识（ε）。
数据中的有效数字表⽰测试精度，其中Ar，H2，He，N2，O2，CO2等被推荐为参⽐数据，其精度为百万分之⼀或更⾼。
1 ⽓体的介电常数（Dielectric constants of gases）表1 ⽓体的介电常数Table 1 Dielectric constants of gases2 饱和⽔蒸⽓的介电常数（Dielectric constants of saturated water vapor）表2给出不同温度下的液态⽔成平衡的⽔蒸⽓的介电常数。
表2 饱和⽔蒸⽓的介电常数Table 2 Dielectric constants of saturated water vapor3 液体的介电常数（Dielectric constants of liquid）表3给出常见液体在指定温度下的介电常数（ε），测试压⼒为101325Pa。
加*表⽰测试压⼒为液体的饱和蒸⽓压（该温度下其饱和蒸⽓压⼤于101325Pa）。
表3 液体的介电常数Table3 Dielectric constants of liquid3 2.58 He 氦-269 1.408I2 碘118 11.1 NH3 氨-77 25 N2氮-195 1.433 N2H4 肼20 52.9 N2O ⼀氧化⼆氮0 1.61114.9 CH2Br2 ⼆溴甲烷10 7.77 CH2Cl2⼆氯甲烷20 9.08 CH2I2⼆碘甲烷25 5.32 CH2O2甲酸16 58.5 CH3Br 溴甲烷0 9.82 CH3Cl 氯甲烷-20 *12.6 CH3I 碘甲烷20 7.00242C2H4Cl21，1-⼆氯⼄烷18 10.0 C2H4Cl21，2-⼆氯⼄烷25 10.37 C2H4O ⼄醛20 21.1 C2H4O 环氧⼄烷-1 13.9 C2H4O2⼄酸20 6.15 C2H4O2甲酸甲酯20 8.5 C2H5Br 溴⼄烷20 9.39 C2H5CI 氯⼄烷0 12.2536C3H6O 丙醛17 18.5 C3H6O2 甲酸⼄酯25 7.16 C3H6O2⼄酸甲脂25 6.68 C3H6O2丙酸40 3.30 C3H6O3 乳酸18 22 C3H7Br 1-溴丙烷25 8.09 C3H7Br 2-溴丙烷25 9.46 C3H7Cl 1-氯丙烷20 7.7 C3H7I 1-碘丙烷20 7.00410C4H10O 2-丁醇25 15.8 C4H10O 2-甲基-2-丙醇30 10.9 C4H10O2-甲基-1-丙醇25 17.7 C4H10O ⼆⼄基醚20 4.335 C4H10O2 1，4丁⼆醇30 30.2 C4H11S 1-丁硫醇25 4.95 C4H11S2过硫化⼆⼄基25 5.72 C4H11N 丁胺21 5.3 C4H11N 异丁胺21 4.4C4H11N ⼆⼄基胺22 3.6 C5feO5五羰基铁20 2.60511C5H11Cl 1-氯戊烷11 6.6 C5H11Cl 1-氯-3-甲基丁烷20 6.05 C5H11I 1-碘戊烷20 5.81 C5H11N 哌啶22 5.8 C5H12戊烷20 1.844 C5H12异戊烷20 1.843 C5H12O 1-戊醇25 13.9 C5H12O 2-甲基-2-丁醇25 5.82 C5H12O 3-甲基-1-丁醇25 14.7C5H12S 1-戊硫醇25 4.55 C5H13N 戊胺22 4.5 C6H4ClNO2o-氯硝基苯50 37.7610C6H10O 环⼰酮20 18.6 C6H10O 异亚丙基丙酮0 15.6 C6H10O ⼄酰⼄酸⼄酯22 15.7 C6H10O 丙酸酐16 18.3 C6H10O 草酸⼆⼄酯21 8.1 C6H11Cl 氯代环⼰烷25 7.6 C6H12环⼰烷25 2.016 C6H12甲基环戊烷20 1.985 C6H12⼄基环丁烷20 1.965C6H12O 环⼰醇25 15.0 C6H12O 2-⼰酮14 14.6 C6H12O 4-甲基-2-丁酮20 13.1 C6H12O 3，3-⼆甲基-2-丁酮14 13.1614C6H15N ⼆丙基胺21 2.9 C6H18Osi2六甲基⼆硅氧烷20 2.17 C7H5ClO 苯甲酰氯20 23 C7H6N 苄腈25 25.20 C7H6Cl22，4-⼆氯甲苯20 6.9 C7H6O 苯甲醛20 17.8 C7H7O ⽔杨醛30 17.1 C7H7Br p-溴甲苯58 5.49 C7H7Cl o-氯甲苯20 4.45 C7H7Cl m-氯甲苯20 5.55 C7H7Cl o-氯甲苯20 6.08 C7H7Cl 苄基氯13 7.0 C7H7F o-氟甲苯30 4.22 C7H7F m-氟甲苯30 5.42714C7H141-庚烯20 2.05 C7H14O 2-庚酮20 11.95 C7H14O2⼄酸戊酯20 4.75 C7H14O2⼄酸异戊酯30 4.63 C7H14O2戊酸⼄酯18 4.71 C7H14O2丁酸⼄酯20 4.3 C7H14O2庚酸71 2.59 C7H15Br 1-溴庚烷25 5.33 C7H15Cl 1-氯庚烷22 5.48 C7H16庚烷20 1.924 C7H162-甲基已烷20 1.919 C7H163-甲基已烷20 1.927 C7H162，2-⼆甲基戊烷20 1.912 C7H162，3-⼆甲基戊烷20 1.939 C7H162，4-⼆甲基戊烷20 1.914811C8H11N N-⼄基苯胺20 5.76 C8H14O3丁酸酐20 12.9 C8H16O2⾟酸20 2.45 C8H16O2丁酸异丁酯20 4.1 C8H16O2丙酸异戊酯20 4.2 C8H17Br 1-溴⾟烷25 5.00 C8H17Cl 1-氯⾟烷25 5.05 C8H18⾟烷20 1.948 C8H182，2，3-三甲基戊烷20 1.96C8H182，2，4-三甲基戊烷20 1.940 C8H18O 1-⾟醇20 10.34 C8H18O 2-⾟醇20 8.20 C8H18O 4-甲基-3-庚醇20 5.25C8H18O 5-甲基-3-庚醇20 6.13 C8H18O ⼆丁基醚25 3.06 C8H19N ⼆异丁基胺22 2.7107C10H8萘85 2.54 C10H10O4邻苯⼆甲酸⼆甲酯24 8.5 C10H121，2，3，4-四氢化萘20 2.757 C10H14异丁基苯17 2.35C10H14叔丁基苯20 2.38 C10H14p-甲基异丙基苯20 2.243 C10H18顺⼗氢化萘20 2.197 C10H18反⼗氢化萘20 2.172C10H20O 薄荷醇42 3.95 C10H22癸烷20 1.991 C10H22O 1-癸烷20 1.983 C11H101-甲基萘20 2.71 C11H24⼗⼀烷20 2.005 C12H10联苯75 2.53 C12H10N2O 氧化偶氮苯40 5.1 C12H10O ⼆苯醚30 3.65 C12H11N ⼆苯胺53 3.34 固体的介电常数（Dielectric constants of solid）表4给出常见⽆机固体的介电数（e），对于各向异性的材料则给出⼏个独⽴的介电常数。
介电常数ε0
介电常数ε0电场是电荷所产生的一种物理量，它是描述电荷附近空间中电场强度和方向的物理量。
介电常数是介质对电场的响应程度的度量，它描述了电场作用下介质中电荷的离散程度。
介电常数的定义是介质的相对电容率与真空的相对电容率之比。
真空的相对电容率是1，所以真空中的介电常数被定义为ε0（读作epsilon-zero），其值约为8.854 × 10^-12 F/m (法拉每米)。
介电常数可以用来计算电场强度和电势能的关系。
根据库仑定律，电荷之间的相互作用力正比于电荷的乘积，和它们之间的距离的倒数。
公式为F = k * q1 * q2 / r^2，其中F是电场强度，q1和q2是电荷，r是它们之间的距离，k是库仑常数。
根据电场的定义，电场强度E等于F除以电荷q1，所以E = k * q2 /r^2。
根据电势能的定义，电势能U等于电场强度E乘以电荷q1，所以U = k * q1 * q2 / r。
可以将这两个公式结合起来，得到U = E * q1 * r。
如果将介质引入，根据介电常数的定义，我们可以将公式改写为U = (E / ε0) * (q1 * q2 / r) * ε0。
这样，介质的影响就体现在了E / ε0这个比值上。
介质的电容率是介质的一种性质，它可以用来描述电荷在介质中的分布情况。
电荷越容易在介质中被离子化，电容率就越大，介电常数也就越大。
在真空中，由于没有任何跟电荷相互作用的离子，电容率为0，介电常数为1。
而在有介质存在的情况下，电场作用下的电容率会发生变化，电荷分布情况也会受到影响，从而导致电场强度的改变。
在电路中，介电常数在电容器中起到重要作用。
电容器是一种储存电荷的装置，它由两个导体板之间的介质隔离而成。
介质的介电常数决定了电容器的电容值，即储存电荷的能力。
常用的电容器材料包括空气、陶瓷、塑料等，它们的介电常数不同，导致了电容器的电容值也不同。
在电磁学和场论中，介电常数是研究电磁波在介质中传播速度的重要参量。
常用填料介电常数计算公式
常用填料介电常数计算公式介电常数是描述物质在电场中响应能力的物理量，它是介质中电场强度与介质中电极化强度之比。
在工程实践中，常常需要计算填料的介电常数，以便进行材料选择、设计和工艺控制。
本文将介绍常用填料介电常数的计算公式，并对其应用进行讨论。
1. 理论背景。
介电常数是描述介质对电场的响应能力的物理量，它是介质中电场强度与介质中电极化强度之比。
介质的介电常数通常用ε表示，其计算公式如下：ε = ε0 εr。
其中，ε0是真空介电常数，其数值约为8.85×10^-12 F/m；εr是相对介电常数，是介质相对于真空的介电常数。
在工程实践中，常用填料的介电常数通常是通过实验测定或者计算得到的。
2. 常用填料介电常数的计算公式。
常用填料的介电常数可以通过以下几种方式进行计算：（1）经验公式。
一些常用填料的介电常数可以通过经验公式进行估算。
例如，对于混凝土材料，可以使用如下经验公式进行计算：ε = ε0 (1 + 0.02f)。
其中，f为混凝土的含水率。
这种经验公式虽然简单，但在工程实践中具有一定的适用性。
（2）复合材料的混合规则。
对于复合材料而言，其介电常数可以通过混合规则进行计算。
例如，对于由两种介质混合而成的复合材料，其介电常数可以通过加权平均的方式进行计算：ε = φ1 ε1 + φ2 ε2。
其中，φ1和φ2分别为两种介质的体积分数，ε1和ε2分别为两种介质的介电常数。
这种计算方法适用于介电常数相差较大的复合材料。
（3）有限元模拟。
对于复杂的填料结构或者复合材料，可以通过有限元模拟的方法进行介电常数的计算。
有限元模拟是一种基于数值计算的方法，可以较准确地计算复杂结构的介电常数。
这种方法的优点是可以考虑材料的微观结构和非均匀性，但缺点是计算复杂度较高，需要较多的计算资源。
3. 应用讨论。
填料的介电常数在工程实践中具有重要的应用价值。
首先，填料的介电常数直接影响着材料的电学性能，例如绝缘性能、电容性能等。
介电常数
29
离子间作用力强，相同外电场使离 子产生位移困难； 离子间作用力弱，相同外电场使离 子产生位移容易。 离子位移极化所需的时间10-12 10-13秒。
30
外电场频率>1013赫兹时，时间 <10-13秒，离子位移极化来不及完成， 不再产生离子位移极化，而产生电 子位移极化。（极化时间10-14 10-15秒）
14
如下图被电场极化了的介质表面
出现感应电荷，这些电荷不会跑到
极板上而被束缚在介质表面，称为 表面束缚电荷。
15
16
极化的微观本质就是介质内部带电质点产 生位移。但由于介质内部质点的束缚力很强， 在电场作用下沿一定方向的相对位移是有限 度的，是在平衡位置附近的很小的位移，因 而它不是载流子，不形成电流。
33
与离子位移极化的区别： 离子位移极化只在平衡位置附 近移动。 离子松弛极化，离子是从一个 平衡位置运动到另一个新的平衡 位置。
34
离子松弛极化可用下述过程描 述，若在某缺陷附近有两个平衡 位置1及2，中间隔有势垒u(下图 a)，当离子热运动能超过势垒高 度u时，离子就从1迁移至2，反之， 离子也可以从2迁移至1．在一定 温度下离子迁移的几率与势垒u有 关。
6
各种材料室温时的介电常数为： 装置瓷、电阻瓷及电真空瓷：212 Ⅰ型电容器瓷：6 1500； Ⅱ型电容器瓷：200 3万； Ⅲ型电容器瓷：7000 几十万； 压电陶瓷：50 20000 干燥空气；1.000585； 真空：1。
7
由上可知，电子陶瓷的介电 常数数值范围很大。介电常数大 的材料，可以制造容量大、体积 小的电容器；介电常数小的材料， 用来制造装置另件。
第二节
介电常数
电子陶瓷除具有绝缘性质外，还能储 存电荷。 介电常数就是衡量其储存电荷能力的 参数，又叫介电系数或电容率。 一、介质极化和介电常数 设有一个真空中的平行板电极系统，电 极面积为s，两极板间的距离为 l ，在两 极板间加上直流电压U，则极板上将充有 电荷Q0一 陶瓷介质，而极板的面积s和距离l不变； 或在厚度为l的平板形陶瓷介质两面被上 面积为s的电极。在电压U不变的情况下， 极板上电荷由Q0增加到Q。 电荷增加是由于陶瓷介质在电场作 用下发生极化的结果。这一现象叫介质 的宏观极化。它是介质微观质点极化的 外部表现。极板上电荷增加的过程也就 是微观质点极化的过程。
化学中介电常数定义
化学中介电常数定义
在化学中，介电常数是衡量物质极化程度的物理量，通常表示为ε。
它定义为媒质（如溶液）中电场强度与所施加电场强度之比，即：ε = E / E0
其中，E是媒质中的电场强度，E0是该电场在真空中的强度。
介电常数的单位为法拉第/米（F/m）或库仑/伏特·米（C/V·m）。
介电常数与物质的极化程度有密切关系。
当电场作用于物质时，物质中的电子会受到力的作用而发生偏移。
这个偏移会使物质内部出现极化，从而产生电偶极子。
电偶极子的存在又会影响电场的分布，从而影响整个介质中的电场强度。
介电常数的大小与物质中的电偶极子密度有关，电偶极子密度越大，介电常数越大。
介电常数在化学中有着广泛的应用，例如用于计算溶液中分子间相互作用的强度、计算电化学反应的速率常数等。
在材料科学中，介电常数也是一个重要的参数，因为它决定了材料在电场下的响应性能。
- 1 -。
介电常数
介电常数一、介电常数的基本简介介质在外加电场时会产生感应电荷而削弱电场，在相同的原电场中真空中的电场与某一介质中的电场的比值即为相对介电常数(permittivity),又称相对电容率，以εr表示。
如果有高介电常数的材料放在电场中，场的强度会在电介质内有可观的下降。
介电常数（又称电容率），以ε表示，ε=εr*ε0，ε0为真空绝对介电常数，ε0=8.85*e-12,F/m。
一个电容板中充入介电常数为ε的物质后电容变大ε倍。
电介质有使空间比起实际尺寸变得更大或更小的属性。
例如，当一个电介质材料放在两个电荷之间，它会减少作用在它们之间的力，就像它们被移远了一样。
当电磁波穿过电介质，波的速度被减小，有更短的波长。
二、介电常熟的解释“介电常数”在工具书中的解释1．又称电容率或相对电容率，表征电介质或绝缘材料电性能的一个重要数据，常用ε表示。
它是指在同一电容器中用同一物质为电介质和真空时的电容的比值，表示电介质在电场中贮存静电能的相对能力。
相对介电常数愈小绝缘性愈好。
空气和CS2的ε值分别为1.0006和2.6左右，而水的ε值特别大，10℃时为 83.83，与温度有关。
2．介电常数是物质相对于真空来说增加电容器电容能力的度量。
介电常数随分子偶极矩和可极化性的增大而增大。
在化学中，介电常数是溶剂的一个重要性质，它表征溶剂对溶质分子溶剂化以及隔开离子的能力。
介电常数大的溶剂，有较大隔开离子的能力，同时也具有较强的溶剂化能力。
介电常数用ε表示。
“介电常数”在学术文献中的解释1.介电常数是指物质保持电荷的能力，损耗因数是指由于物质的分散程度使能量损失的大小。
理想的物质的两项参数值较小。
k2.介质常数具有复数形式，实数部分称为介电常数，虚数部分称为损耗因子.通常用损耗正切值(损耗因子与介电常数之比)来表示材料与微波的耦合能力，损耗正切值越大，材料与微波的耦合能力就越强3．介电常数是指在同一电容器中用某一物质为电介质与该物质在真空中的电容的比值.在高频线路中信号传播速度的公式如下：V=K4.通常将相对介电常数均称为介电常数.反射脉冲信号的强度，与界面的波反射系数和透射波的衰减系数有关，主要取决于周围介质与反射体的电导率和介电常数。
元素的介电常数表
元素的介电常数表
以下是一些常见元素的介电常数：
1.氢 0 1.00026
2.聚苯乙烯 20 24
3.空气 0 1.000585
4.硬橡胶 4.3
5.硫化氢 0 1.004
6.纸 2.5
7.真空 - -
8.干砂 - -
9.乙醴 - 4.335
10.15%K湿砂 -9 -
11.液态二氧化碳 -20 1.585
12.木头 -25 -
13.甲醇 -25 -33.7
14.琥珀 -33 -
15.乙醇 -16 -25.7
16.冰 -30 -28
17.水 -81 -4
18.虫胶 -4 -4
19.液态氨 -270.8 -16.2
20.赛璐璐 -33 -4
21.液态氮 -253 -1.058
22.玻璃 -4 -8
23.液态氢 -182 -1.22
24.黄磷 -4 -4
25.液态氧 -185 -1.465
26.硫 -4 -4
27.液态氮 0 -2.28
28.碳（金刚石） -5 ?-
介电常数是描述电介质在电场中极化行为的物理量。
具体到元素或材料的介电常数，可能受温度、频率等多种因素影响，并且具体数值可能需要更详细的实验测定。
因此，上表所提供的介电常数仅供参考，具体数值可能需要根据实际情况进行测量和确认。
介电常数与真空介电常数和相对介电常数公式
介电常数与真空介电常数和相对介电常数公式介电常数是描述材料中电场作用下电荷极化程度的物理量。
它与真空介电常数和相对介电常数有密切关系。
真空介电常数，通常用符号ε0表示，是自然界中的一个常数。
它定义为真空中单位体积的电容率，其数值约为8.85×10-12 F/m。
真空介电常数是一个普遍适用于所有材料的参考值，因为在真空中不存在其他物质，因此电场作用下电荷极化的唯一影响来自于空气中的电荷。
相对介电常数，通常用符号εr表示，是一种材料特有的物理量。
它定义为材料在电场作用下电容率与真空电容率之比。
相对介电常数是描述材料对电场的响应能力的一个参数。
对于相同的电场强度，材料的相对介电常数越大，说明材料极化程度越高。
根据介电常数的定义，可以将材料中的电场作用下的电荷极化过程分为两个部分：一部分是电场作用下电子的位移极化，另一部分是电场作用下离子的位移极化。
对于电子的位移极化，当材料中存在电场时，电子会受到电场力的作用，发生位移。
这种位移导致电子云的形状发生变化，从而使材料中的电子产生了极化。
电子的位移极化可以通过介电常数来描述，其数值与材料的相对介电常数有关。
对于离子的位移极化，当材料中存在电场时，离子会受到电场力的作用，发生位移。
这种位移导致离子云的形状发生变化，从而使材料中的离子产生了极化。
离子的位移极化同样可以通过介电常数来描述，其数值与材料的相对介电常数有关。
通过介电常数的定义可以看出，介电常数与真空介电常数和相对介电常数之间存在着密切的关系。
真空介电常数是一个普遍适用于所有材料的参考值，而相对介电常数则是描述材料特性的一个参数。
在实际应用中，通过测量材料的相对介电常数，可以间接地得到材料中的电子和离子的位移极化程度，从而进一步了解材料的电学性质。
介电常数是描述材料中电场作用下电荷极化程度的物理量，它与真空介电常数和相对介电常数密切相关。
真空介电常数是一个普遍适用于所有材料的参考值，而相对介电常数则是描述材料特性的一个参数。
介电常数 电压分布
介电常数电压分布介电常数是描述材料对电场响应的重要物理量，它决定了材料在电场中的行为。
电压分布是指在给定的电场情况下，各点的电势值的分布情况。
本文将围绕介电常数和电压分布展开详细阐述，从宏观和微观两个角度来解释它们的原理和应用。
一、介电常数的概念和影响因素介电常数是材料对电场的响应能力的度量，它描述了材料中电荷的受力情况和电场的传播速度。
介电常数的大小决定了材料的电容性质，即材料在电场中储存电荷的能力。
介电常数大的材料具有较高的电容性质，可以储存更多的电荷，而介电常数小的材料则相反。
介电常数的大小受到多种因素的影响，包括材料的化学成分、晶体结构、温度等。
一般来说，离子晶体的介电常数较大，而共价晶体和金属的介电常数较小。
此外，温度的变化也会对介电常数产生影响，一般情况下，随着温度升高，介电常数会减小。
二、电压分布的原理和计算方法电压分布是指在给定电场情况下，各点的电势分布情况。
电势是描述电场能量分布的物理量，它与电荷和电场之间的相互作用密切相关。
在一个均匀的电场中，电势随着距离的增加呈线性变化，即电场强度乘以距离。
计算电压分布的方法有多种，其中最常见的是使用电势分布的微分方程进行求解。
通过求解该微分方程，可以得到电势随空间的分布关系。
此外，还可以使用有限元法等数值方法进行计算，通过离散化空间，将微分方程转化为代数方程，再求解得到电势分布。
三、介电常数与电压分布的应用介电常数和电压分布在电子学、材料科学等领域有着广泛的应用。
下面分别介绍它们在这些领域的具体应用。
1.电子学中的应用在电子学中，介电常数和电压分布常用于设计和优化电子器件。
例如，在集成电路中，通过控制介电常数的大小和分布，可以实现电磁屏蔽、降噪和信号传输的优化。
此外，在电容器和电感器等被动元件中，介电常数也是决定其性能的重要参数之一。
2.材料科学中的应用在材料科学中，介电常数和电压分布被广泛用于研究材料的电学性质和应用。
例如，在光学材料中，通过调节介电常数的大小和分布，可以实现对光的反射、吸收和透射的调控，从而实现光学器件的设计和优化。
介电常数
介电常数介质在外加电场时会产生感应电荷而削弱电场，介质中电场与原外加电场(真空中)的比值即为相对介电常数(permittivity，不规范称dielectric constant)，又称诱电率，与频率相关。
介电常数是相对介电常数与真空中绝对介电常数乘积。
如果有高介电常数的材料放在电场中，电场的强度会在电介质内有可观的下降，理想导体内部由于静电屏蔽场强总为零，故其介电常数为无穷。
介电常数(又称电容率)，以ε表示，ε=εr*ε0，ε0为真空绝对介电常数，ε0=8.85*10^(-12)F/m。
需要强调的是，一种材料的介电常数值与测试的频率密切相关。
一个电容板中充入介电常数为ε的物质后电容变大εr倍。
电介质有使空间比起实际尺寸变得更大或更小的属性。
例如，当一个电介质材料放在两个电荷之间，它会减少作用在它们之间的力，就像它们被移远了一样。
当电磁波穿过电介质，波的速度被减小，有更短的波长。
根据物质的介电常数可以判别高分子材料的极性大小。
通常，介电常数大于3.6的物质为极性物质;介电常数在2.8~3.6范围内的物质为弱极性物质;介电常数小于2.8为非极性物质。
测量方法相对介电常数εr可以用静电场用如下方式测量:首先在两块极板之间为真空的时候测试电容器的电容C0。
然后，用同样的电容极板间距离但在极板间加入电介质后测得电容Cx。
然后相对介电常数可以用下式计算εr=Cx/C0在标准大气压下，不含二氧化碳的干燥空气的相对电容率εr=1.00053.因此，用这种电极构形在空气中的电容Ca来代替C0来测量相对电容率εr时，也有足够的准确度。
(参考GB/T 1409-2006)对于时变电磁场，物质的介电常数和频率相关，通常称为介电系数。
"介电常数" 在工具书中的解释:1.又称电容率或相对电容率，表征电介质或绝缘材料电性能的一个重要数据，常用ε表示。
它是指在同一电容器中用同一物质为电介质和真空时的电容的比值，表示电介质在电场中贮存静电能的相对能力。
介电常数
介电常数介质在外加电场时会产生感应电荷而削弱电场，原外加电场(真空中)与最终介质中电场比值即为介电常数(permittivity)，又称诱电率，与频率相关。
如果有高介电常数的材料放在电场中，场的强度会在电介质内有可观的下降。
电介质经常是绝缘体。
其例子包括瓷器(陶器)，云母，玻璃，塑料，和各种金属氧化物。
有些液体和气体可以作为好的电介质材料。
干空气是良好的电介质，并被用在可变电容器以及某些类型的传输线。
蒸馏水如果保持没有杂质的话是好的电介质，其相对介电常数约为80。
介电常数是相对介电常数与真空中绝对介电常数乘积。
如果有高介电常数的材料放在电场中，电场的强度会在电介质内有可观的下降，理想导体内部由于静电屏蔽场强总为零，故其介电常数为无穷。
一个电容板中充入介电常数为ε的物质后电容变大ε倍。
电介质有使空间比起实际尺寸变得更大或更小的属性。
例如，当一个电介质材料放在两个电荷之间，它会减少作用在它们之间的力，就像它们被移远了一样。
当电磁波穿过电介质，波的速度被减小，有更短的波长。
相对介电常数εr可以用静电场用如下方式测量：首先在其两块极板之间为空气的时候测试电容器的电容C0。
然后，用同样的电容极板间距离但在极板间加入电介质后侧得电容Cx。
然后相对介电常数可以用下式计算εr=Cx/C0。
真空介电常数：ε0＝8.854187817×10-12F／m。
ε0和真空磁导率μ0以及电磁波在真空传播速率c之间的关系为。
真空平行板电容器的电容为，若取S为单位面积，d为单位距离，则C＝ε0，真空电容率的名称即源于此。
介电常数又叫介质常数，介电系数或电容率，它是表示绝缘能力特性的一个系数，以字母ε表示，单位为法/米。
需要强调的是，一种材料的介电常数值与测试的频率密切相关。
介电常数愈小，说明此介质产生的感应电荷削弱原外加电场的能力愈小（有可能此介质在外加电场时产生的感应电荷少），即原外加电场减少的愈少，原外加电场与削弱后的原外加电场的比值愈小，此介质的绝缘性愈好，导电性愈弱。
介电常数和介电损耗
介电常数和介电损耗介电常数和介电损耗是材料科学中的两个重要概念，它们在电学、光学、声学等领域都有着广泛的应用。
本文将从介电常数和介电损耗的定义、性质和测量方法等方面进行介绍和分析。
一、介电常数的定义和性质介电常数是指在电场作用下，材料中电荷与电场之间相互作用的程度，它是介电性质的重要参数。
介电常数的定义为：$$epsilon_r=frac{epsilon}{epsilon_0}$$其中，$epsilon_r$为相对介电常数，$epsilon$为介电常数，$epsilon_0$为真空介电常数。
介电常数的物理意义是材料中电场的传递速度，它决定了材料对电场的响应速度和电场的分布。
介电常数越大，材料对电场的响应速度越慢，电场分布也越均匀；介电常数越小，材料对电场的响应速度越快，电场分布也越不均匀。
介电常数与材料的分子结构、化学成分、晶体结构等有关。
例如，金属的介电常数非常小，接近于零；而绝缘体的介电常数较大，一般在2-10之间；半导体的介电常数介于金属和绝缘体之间，一般在10-100之间。
二、介电损耗的定义和性质介电损耗是指材料在电场作用下发生的能量损耗，它是介电性质的另一个重要参数。
介电损耗的定义为：$$tandelta=frac{Im(epsilon)}{Re(epsilon)}$$其中，$tandelta$为介电损耗角，$epsilon$为介电常数，$Re(epsilon)$为介电常数的实部，$Im(epsilon)$为介电常数的虚部。
介电损耗的物理意义是材料中电场能量的转化和散失，它决定了材料对电场的响应精度和能量损失程度。
介电损耗越小，材料对电场的响应精度越高，能量损失也越少；介电损耗越大，材料对电场的响应精度越低，能量损失也越多。
介电损耗与材料的分子结构、化学成分、晶体结构、温度等有关。
例如，晶体结构对介电损耗的影响较大，一般情况下，非晶态材料的介电损耗较小，而晶态材料的介电损耗较大。
三、介电常数和介电损耗的测量方法介电常数和介电损耗的测量方法有多种，下面介绍几种常用的方法：1. 热释电法热释电法是一种通过测量材料在电场作用下的温度变化来确定介电常数和介电损耗的方法。
介电常数百科
介电常数百科
介电常数是描述材料在电场中对电能储存和损耗能力的物理量，通常用符号ε表示。
介电常数是一个无量纲的测量值，它定义为介质中的电场强度与真空中电场强度的比值。
介电常数的大小反映了材料对电场的削弱程度，即介质内部感应电荷的产生能力。
介电常数越大，表明材料内部的电场被削弱得越多，也就是说，该材料能够储存更多的静电能。
此外，介电常数还可以分为相对介电常数（εr）和绝对介电常数（ε）。
相对介电常数是材料的介电常数与真空中介电常数的比值，而绝对介电常数则是材料本身的介电常数。
自由空间的介电常数（ε0）是一个基本物理常数，其值为8.85 x 10^-12 F/m（法拉每米）。
总的来说，介电常数的概念对于理解和应用电磁学、电子工程以及材料科学等领域至关重要。
常用材料的介电常数
常用材料的介电常数介电常数是材料对电场的响应能力的度量，它反映了材料中电荷的移动性和电场的传播性。
常用材料的介电常数因其化学成分、结构和物理性质的不同而有所差异。
以下将介绍一些常见材料的介电常数。
1.空气（二氧化碳）：空气是一种常见的绝缘体，其介电常数约为1、这意味着空气对电场的响应很弱，相对来说不会对电场产生太大的影响。
2.玻璃：玻璃是一种非晶态固体，其介电常数通常在5到10之间。
玻璃在电子器件和光学设备中广泛应用，其相对较高的介电常数使得它成为一种良好的电绝缘体。
3.陶瓷：陶瓷是一种晶体或非晶态的材料，其介电常数因其具体的组成和制备方法而有所不同。
一般来说，陶瓷的介电常数在5到100之间，因此陶瓷既具有绝缘体的特点，又具有一定的电导能力。
4.金属：金属是一种具有高导电性的材料，其介电常数通常非常大且为实数。
实数介电常数意味着金属对电场的响应是强烈而立即的，电场几乎能够在金属中自由传播。
5.水：水是一种极好的电导体，其介电常数约为80。
这意味着水对电场的响应非常强烈，电场能够迅速传播并引起水中电荷的移动。
6.聚合物：聚合物是一类包含大量重复单元的大分子材料，其介电常数通常在2至10之间。
聚合物的介电常数取决于其化学结构以及晶型与非晶态之间的比例。
7.石英：石英是一种天然的晶体，具有较高的介电常数，约为4、石英对电场有较强的响应能力，且具有较低的电导率，因此常被用于制造高频电子设备的基板。
总的来说，不同的材料具有不同的介电常数，这是由其结构和物理性质所决定的。
了解各种材料的介电常数对于设计和开发电子设备、光学仪器等有重要的意义。
介电常数
4～5
矿石
25～30
奶粉
1.8～2.2
水泥
4～6
丙酮
20～30
汽油
1.9
甲醚
5
甲醇
30
环乙醇
2
异氰酸脂
7.5
甘油
37
柴油
2.1
丁醇
11
2．常见物质介电常数表
2材料
介电常数
材料
介电常数
材料
介电常数
ABS颗粒
1.5~2.5
环氧树脂
2.5~6.0
氯化钾
4.6
丙酮
19.5~20
乙醇
24
PVC粉末
1.4
丙烯酸树脂糖3Fra bibliotek氯化钙
11.8
盐酸
4~12
硫酸
84
硫酸钙
5.6
氧化铁
14.2
甲苯，液体
2.0~2.4
二氧化碳
1.6
液氮
1.4
尿烷
6.5~7.1
水泥
1.5~2.1
煤油
2.8
植物油
2.5~3.5
氯水
2
矿物油
2.1
玉米废渣
2.3~2.6
煤粉
1.2~1.8
尼龙
4~5
小麦粉
2.2~2.6
变压器油
2.2~2.4
油漆
5~8
二甲苯，液体
1．常见物质介电常数表
1介质名称
介电常数
介质名称
介电常数
介质名称
介电常数
空气
1
干燥煤粉
2.2
湿沙
15～20
聚苯乙烯颗粒
1.05～1.5
介电常数测量原理
介电常数测量原理
介电常数测量是指测量材料的介电常数，也称为相对介电常数或电容率。
介电常数是材料对电场的响应能力的度量，反映了材料中电场的传播速度和能量储存能力的大小。
一种常用的测量介电常数的方法是使用介电恒压法。
该方法基于平行板电容器的原理，利用电容器的电场分布和存储电荷的能力来确定介电常数。
在实验中，首先将待测材料作为绝缘板插入平行板电容器中。
然后，通过连接电源，施加恒定的电压使电容器充电至一定电势差。
接下来，测量电容器的电荷量和电场强度，从而计算出材料的介电常数。
该方法的原理是电场在电介质中的形成。
当电场作用于电介质时，电介质内的电荷会重新分布，形成电介质的极化。
电介质的极化导致了电容器的电场分布发生变化，从而影响了电容器的电容量和储能能力。
通过测量电容器的电荷量和电场强度，可以确定电介质的介电常数。
需要注意的是，在进行介电常数测量时应控制其他因素的影响，例如温度、湿度等。
另外，不同频率下的电场对材料的极化方式也会不同，因此在测量时需要选择合适的频率。
通过介电常数的测量，可以对材料的电学性质进行评估和比较。
此外，介电常数在电磁场分析、电路设计和电磁波传播等领域中也具有重要的应用价值。
介电常数单位和测试标准
介电常数单位和测试标准介电常数是一个描述电介质在电场中储存电能能力的物理量。
它的大小取决于电介质的性质、形状和大小，以及测试时所用的频率、温度和湿度等因素。
因此，介电常数的单位和测试标准是至关重要的。
一、单位介电常数的单位通常使用“法拉/米”（F/m）或“真空介电常数”（ε0）来表示。
其中，真空介电常数是一个无量纲的常数，其值为8.854187817×10^{-12} F/m。
在许多情况下，介电常数的大小与频率有关，因此有时也会使用“频率相关介电常数”（frequency-dependent permittivity）来表示。
二、测试标准介电常数的测试标准包括以下步骤：1.准备样品：选择具有代表性的样品，并将其形状和大小调整为适合测试的规格。
2.设定测试条件：确定测试时的频率、温度和湿度等条件。
这些条件会影响介电常数的值，因此必须严格控制。
3.准备测试设备：使用高精度的介电常数测试设备进行测量，设备应具备足够的稳定性和精确度。
4.进行测试：将样品放置在测试设备中，并按照设定的条件进行测量。
通常需要进行多次测量以获得准确的结果。
5.数据处理：对测量数据进行处理和分析，以获得样品的介电常数值。
这些数据需要进行修正和校准，以消除测试条件和设备误差的影响。
在测试过程中，需要注意以下几点：1.样品准备要充分，以保证其具有代表性。
样品的形状和大小应与测试设备相匹配，以确保测试结果的准确性。
2.测试条件要严格控制，以消除其对介电常数值的影响。
特别是温度和湿度，必须保持在设定的范围内。
3.测试设备应具备高精度和高稳定性，以确保测量结果的准确性。
在测试前应对设备进行检查和校准，以确保其性能正常。
4.测量数据需要进行修正和校准，以消除测试条件和设备误差的影响。
修正和校准的方法和技术需要根据具体的测试条件和设备进行调整。
5.在数据处理和分析过程中，需要使用合适的统计方法和技术，以确保获得准确的介电常数值。
这些数据需要进行详细的检查和分析，以获得有意义的结果。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
介电常数
介电常数又叫介质常数，介电系数或电容率，它是表示绝缘能力特性的一个系数，以字母ε表示，单位为法/米(F/m)
定义为电位移D和电场强度E之比，ε=D/Ε。
电位移D的单位是库/二次方米(C ／m^2)。
某种电介质的介电常数ε与真空介电常数ε0之比称为该电介质的相对介电常数εr，εr＝ε／ε0是无量纲的纯数，εr与电极化率χe的关系为εr＝1＋χe。
真空介电常数：ε0= 8.854187817×10^-12 F/m
介质在外加电场时会产生感应电荷而削弱电场，原外加电场(真空中)与最终介质中电场比值即为相对介电常数(permittivity),
如果有高相对介电常数的材料放在电场中，场的强度会在电介质内有可观的下降。
电介质经常是绝缘体。
其例子包括瓷器(陶器)，云母，玻璃，塑料，和各种金属氧化物。
有些液体和气体可以作为好的电介质材料。
干空气是良好的电介质，并被用在可变电容器以及某些类型的传输线。
蒸馏水如果保持没有杂质的话是好的电介质，其相对介电常数约为80。
一个电容板中充入相对介电常数为ε的物质后电容变大ε倍。
故相对介电常数εr 可以用如下方式测量:首先在其两块极板之间为真空的时候测试电容器的电容C0。
然后，用同样的电容极板间距离但在极板间加入电介质后侧得电容Cx。
然后相对介电常数可以用下式计算
εr=Cx/C0
电介质有使空间比起实际尺寸变得更大或更小的属性。
例如，当一个电介质材料放在两个电荷之间，它会减少作用在它们之间的力，就像它们被移远了一样。
当电磁波穿过电介质，波的速度被减小，有更短的波长。
对于时变电磁场，物质的介电常数和频率相关，通常称为介电系数。
附常见溶剂的介电常数
H2O (水) 78.5
HCOOH (甲酸) 58.5
HCON(CH3)2 (N,N-二甲基甲酰胺)36.7
CH3OH (甲醇) 32.7
C2H5OH (乙醇) 24.5
CH3COCH3 (丙酮) 20.7
n-C6H13OH （正己醇）13.3
CH3COOH (乙酸或醋酸) 6.15
C6H6 (苯) 2.28
CCl4 (四氯化碳) 2.24
n-C6H14 （正己烷）1.88。