河北省保定市高阳中学2013-2014学年高一数学下学期第十五次周练试题新人教A版
河北省保定市高阳中学2013-2014学年高二数学下学期第九次周练试题新人教A版

河北省保定市高阳中学2013-2014学年高二数学下学期第九次周练试题新人教A版1.一物体运动方程为〔其中单位是米,单位是秒〕,那么物体在秒末的瞬时速度是A.米/秒 B.米/秒 C.米/秒 D.米/秒2.假设函数在区间内可导,且如此的值为A. B. C. D.3.函数的递增区间是A. B. C. D.4.,假设,如此的值等于〔〕A. B. C. D.5.函数在一点的导数值为是函数在这点取极值的A.充分条件 B.必要条件 C.充要条件 D.必要非充分条件6.函数在区间上的最小值为〔〕A.72 B.36 C.12 D.07.曲线在处的切线平行于直线,如此点的坐标为A. B. C.和 D.和8.函数的最大值为A. B. C. D.9.假设函数的图象的顶点在第四象限,如此函数的图象是〔〕10.函数的定义域为区间,导函数在内的图象,如此函数在开区间内有极小值点A.个 B.个 C.个 D.个11.假设,如此的值为_________________;12.曲线在点处的切线倾斜角为__________;13.函数的导数为_____________________;14.函数的单调递增区间是____________________;15.如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个一样的小正方形,制成一个无盖的小盒子,问小正方形的边长为____________时,盒子容积最大,最大容积是____________.16.求垂直于直线并且与曲线相切的直线方程.17.求函数在区间上的最大值与最小值.18.函数,当时,有极大值;〔1〕求的值;〔2〕求函数的极小值.19.的图象经过点,且在处的切线方程是.〔1〕求的解析式;〔2〕求的单调递增区间.20.函数在与时都取得极值.(1)求的值与函数的单调区间;(2)假设对,不等式恒成立,求的取值范围.答案二、填空题11.12.13.14.15.1cm18cm3三、解答题16.解:设切点为,函数的导数为切线的斜率,得,代入到得,即,.17.解:,当得,或,或,∵,,+ +↗↗列表:又;右端点处;∴函数在区间上的最大值为,最小值为.〔2〕,令,得.19.解:〔1〕的图象经过点,如此,切点为,如此的图象经过点得;〔2〕单调递增区间为.20.解:〔1〕由,得,函数的单调区间如下表:极大值极小值所以函数的递增区间是与,递减区间是;。
河北省保定市高阳中学2013-2014学年高一下学期第十七次周练数学试题

一、选择题1.sin (-11400)的值是( )A21 B 21- C 23 D 23-2.已知b a ,为单位向量,则下列正确的是( )A 0=-b aB b a b a 22==+C 0||||=-b aD 1=⋅b a 3.设)33,24(),2,1(+=+=k b k a ,若b a 与共线,则k 等于( ) A 3 B 0 C -5 D 3或-5 4.的值是)55sin()35sin()55cos()35cos(0x x x x -+--+( ) A 0 B -1 C 1± D 1 5.函数x y 2sin 32+=的最小正周期是( ) A π4 B π2 C π D2π6.有以下结论:(1)若c a b a ⋅=⋅,且0≠a ,则;c b =(2);0,(21211=+=y y x x x a(3)||b a =+ (4)函数102lg -=x y 的图象可由函数x y lg =的图象按向量)1,2(-=a 平移而得到。
其中错误的结论是( ) A (1)(2) B (3)(4) C (1)(3) D (2)(4) 7.三角形ABC 中,,2||,1||||===AB BC AC 则CA CB BC AB ⋅+⋅的值是( )A 1B -1C 0D 28.已知=(-2,-3)、ON =(1,1),点)21(,x P 在线段MN 的中垂线上,则x 等于( ).A .25-B .23-C .27- D .3- 9.在三角形ABC 中,02cos 2cos <-B A 是B-A<0的( )A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要的条件)(0,,1||,2||.10的取值范围是,则且角,是某锐角三角形的最大的夹角与若已知λλθλλ<-+⊥==b a b a b a b a A02<<-λ B 2-<λ C 3322-≤<-λ D 0332<≤-λ 11.在三角形ABC 中,已知,10,4:3:2sin :sin :sin =+=b a C B A 且则向量AB 在向量AC的投影是( )A 7B 6C 5D 412.把函数x x y sin cos 3-=的图象向右平移a 个单位,所得图象关于y 轴对称,则a 的最大负值是( )A 6π-B 3π-C 32π-D 65π- 二、填空题13.=-=a a a 2tan ,54cos 是第三象限的角,则且已知_____________________ . ;的取值范围是则,满足,若正数________________3.14ab b a ab b a ++= ._________________的取值范围是b a +15.已知三角形ABC 中,,5||,3||,415,0,,===<⋅==∆b a S b a b AC a AB ABC则a 与b 的夹角是_________________________ .16.给出下列8种图象的变换方法:(1) 将图象上所有点的横坐标缩短到原来的21倍(纵坐标不变)。
河北省保定市高阳中学2013-高一下学期第十八次周练数学试题
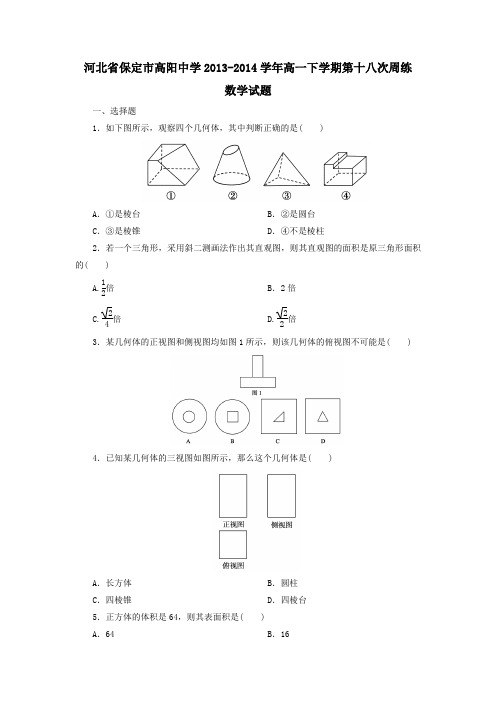
河北省保定市高阳中学2013-2014学年高一下学期第十八次周练数学试题一、选择题1.如下图所示,观察四个几何体,其中判断正确的是( )A.①是棱台B.②是圆台C.③是棱锥D.④不是棱柱2.若一个三角形,采用斜二测画法作出其直观图,则其直观图的面积是原三角形面积的( )A.12倍B.2倍C.24倍 D.22倍3.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )4.已知某几何体的三视图如图所示,那么这个几何体是( )A.长方体B.圆柱C.四棱锥D.四棱台5.正方体的体积是64,则其表面积是( )A.64 B.16C .96D .无法确定6.圆锥的高扩大到原来的2倍,底面半径缩短到原来的12,则圆锥的体积( )A .缩小到原来的一半B .扩大到原来的2倍C .不变D .缩小到原来的167.三个球的半径之比为1:2:3,那么最大球的表面积是其余两个球的表面积之和的( )A .1倍B .2倍 C.95倍 D.74倍 8.有一个几何体的三视图及其尺寸如下图(单位:cm),则该几何体的表面积为( )A .12πcm 2B .15πcm 2C .24πcm 2D .36πcm 29.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )A .7B .6C .5D .310.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为( )A.32,1 B.23,1C.32,32D.23,3211.某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为5的等腰三角形.则该几何体的体积为( )A.24 B.80C.64 D.24012.如果用表示1个立方体,用表示两个立方体叠加,用表示3个立方体叠加,那么图中由7个立方体摆成的几何体,从正前方观察,可画出平面图形是( )二、填空题13.圆台的底半径为1和2,母线长为3,则此圆台的体积为________.14.一个几何体的三视图如图所示,则这个几何体的体积为___________________ __________________________________________________.15.圆柱的侧面展开图是边长为6π和4π的矩形,则圆柱的表面积为________.16.一个几何体的三视图及其尺寸如下图所示,其中主视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是________.三、解答题17.画出如图所示几何体的三视图.18.圆柱的高是8cm,表面积是130πcm2,求它的底面圆半径和体积.19.如下图所示是一个空间几何体的三视图,试用斜二测画法画出它的直观图(尺寸不限).20.如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为7m,制造这个塔顶需要多少铁板?21.如下图,在底面半径为2、母线长为4的圆锥中内接一个高为3的圆柱,求圆柱的表面积.22.如图所示(单位:cm),四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.答案1 C2 C3 D4 A5 C6 A7 C8 C9 A 10 C 11 B 12 B13 142 3π14 3615 24π2+8π或24π2+18π16 2(1+3)π+4 21718 V =πr 2h =π×52×8=200π(cm 3). 1920制造这个塔顶需要82m 2铁板.21 S 表面积=2S 底+S 侧=2πr 2+2πrh ′=2π+2π×3=2(1+3)π. 22 V 圆台-V 半球=52π-16π3=140π3(cm 3).。
河北省保定市高阳中学2013-2014学年高二数学下学期第九次周练试题新人教A版

河北省保定市高阳中学2013-2014学年高二数学下学期第九次周练试题新人教A版1.一物体运动方程为(其中单位是米,单位是秒),那么物体在秒末的瞬时速度是A.米/秒 B.米/秒 C.米/秒 D.米/秒2.若函数在区间内可导,且则的值为A. B. C. D.3.函数的递增区间是A. B. C. D.4.,若,则的值等于()A. B. C. D.5.函数在一点的导数值为是函数在这点取极值的A.充分条件 B.必要条件 C.充要条件 D.必要非充分条件6.函数在区间上的最小值为()A.72 B.36 C.12 D.07.曲线在处的切线平行于直线,则点的坐标为A. B. C.和 D.和8.函数的最大值为A. B. C. D.9.若函数的图象的顶点在第四象限,则函数的图象是()10.函数的定义域为区间,导函数在内的图象,则函数在开区间内有极小值点A.个 B.个 C.个 D.个11.若,则的值为_________________;12.曲线在点处的切线倾斜角为__________;13.函数的导数为_____________________;14.函数的单调递增区间是____________________;15.如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为____________时,盒子容积最大,最大容积是____________.16.求垂直于直线并且与曲线相切的直线方程.17.求函数在区间上的最大值与最小值.18.已知函数,当时,有极大值;(1)求的值;(2)求函数的极小值.19.已知的图象经过点,且在处的切线方程是.(1)求的解析式;(2)求的单调递增区间.20.已知函数在与时都取得极值.(1)求的值与函数的单调区间;(2)若对,不等式恒成立,求的取值范围.答案二、填空题11.12.13.14.15.1cm 18cm3三、解答题16.解:设切点为,函数的导数为切线的斜率,得,代入到得,即,.17.解:,当得,或,或,∵,,+ +↗↗列表:又;右端点处;∴函数在区间上的最大值为,最小值为.(2),令,得.19.解:(1)的图象经过点,则,切点为,则的图象经过点得;(2)单调递增区间为.20.解:(1)由,得,函数的单调区间如下表:极大值极小值所以函数的递增区间是与,递减区间是;。
河北省保定市高阳中学2013-2014学年高二数学下学期第十四次周练试题新人教A版

高二下学期第十四次周练数学试题1.集合{|18}A x x =<<,{|60}B x x =-<,如此A B =.2.设复数z 满足(i)i i 1z +=-〔i 是虚数单位〕,如此z =.3.||1,||2==a b ,且+a b 与a 垂直,如此a 与b 的夹角是.4.曲线3y x x =+在1x =处的切线方程为.420--=x y5.在ABC △中,AD 为BC 边上的中线,AB =BD =2AD =,如此ADC △ 的面积ADC S =△.6.集合{}2|230A x x x =-+≤,{}2|(2)[(1)]0B x x a x a =--+≤,假设“x A ∈〞是“x B ∈〞的充分不必要条件,如此实数a 的取值范围是. 7.假设1sin 63πα⎛⎫+= ⎪⎝⎭,如此2cos 23πα⎛⎫- ⎪⎝⎭=. 8. 向量(12)a =,,(4)b x =,,假设向量a b ⊥,如此x =____________9. 在R 上定义运算⊗:()(1)1.x y x y ⊗=--假设不等式()()1x a x a -⊗+<对任意实数x 成立,如此a 的取值范围为______________.10. 奇函数()()f x x R ∈满足:()30f -=,且在区间[]0,2与[)2,+∞上分别递减和递增,如此不等式()0xf x <的解集为______________.11.假设a 为正整数,2()(2)1f x ax a x =-++在[0,1]上的最小值为1-,如此a =_____________ .12.命题P :“对x ∀∈R ,∃m ∈R ,使22cos sin 20x x m -+=〞,假设命题P ⌝是假命题,如此实数m 的取值范围是____________________.13. 函数21,0()1,0x x f x x ⎧+≤=⎨>⎩,如此满足不等式2(1)(2)f x f x ->的实数x 的取值范围是___________________.14. ABC ∆ 的一个内角为120,并且三边长构成公差为4的等差数列,如此ABC ∆的面积为_______________.答案1.〔1,6〕2.13.23π4.420--=x y5.26.3(,]27.79-8.-89.(1,1)--10.(3,0)(0,3)11.1或2---+12.[11-∞-⋃+∞13.(,1(1,)14.。
河北省保定市高阳中学2014届高三数学下学期周练试题(二十五)新人教版

高三数学周练二十五圆22410x y y +--=的圆心和半径是:A (2,0),5C r =B (0,2),C r = C (0,2).C r -=D (2,0),5C r -= 已知AB ∥PQ ,BC ∥QR ,∠ABC =30,则∠PQR 等于( )A 30oB 0030150或C 0150D 以上都不对若,,a b x y >>则下列不等式中正确的是( )....a b A a x b y B ax by C D x b y ay x ->- > > ->-若A (-2,3),B (3,-2),C (21,m)三点共线,则m的值为( ) A 21 B 21-C -2D 2经平面外一点和平面内一点与平面α垂直的平面有A 1个B 0 个C 无数个D 1个或无数个直线032=--y x 与圆9)3()2(22=++-y x 交于E 、F 两点,则∆EOF (O 为原点)的面积为( ) A 23 B 43 C 52 D 556a ,b ,c 表示直线,M 表示平面,给出下列四个命题:①若a ∥M ,b ∥M ,则a ∥b ;②若b ⊂M ,a ∥b ,则a ∥M ;③若a ⊥c ,b ⊥c ,则a ∥b ;④若a ⊥M ,b ⊥M ,则a ∥b.其中正确命题的个数有A 0个B 1个C 2个D 3个 设26,37,2-=-==c b a ,则c b a ,,的大小顺序是( )A a b c >>B a c b >>C a c b d +>+D a c b d ->-在空间直角坐标系中,点M (1,-2,3)关于xoy 平面及z 轴对称的点的坐标分别为 ,等体积的球和正方体,它们的表面积的大小关系是S 球_____S 正方体(填”大于、小于或等于”).正方体1111ABCD A B C D -,那么△11AB D , 三棱锥A -A1B1D1的体积为设直线20mx y -+=与圆221x y +=相切,则实数m 的值为 过点(1,2)且在两坐标轴上的截距相等的直线的方程________ ___已知PA 垂直平行四边形ABCD 所在平面,若PC BD ⊥,平行则四边形ABCD 一定是 .15.已知0,0a b >>且1a b +=,求证:114a b +≥16.体积为V 的圆柱中,底面半径r 和圆柱的高h 为多少时,其表面积S 最小?17.已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.1A 求证:(1)1C O 面11AB D ; (2)1A C ⊥面11AB D . (3)111AB D C BD 平面平面18.已知圆22:6440C x y x y +--+=,直线1l 被圆所截得的弦的中点为(5,3)P 。
河北省保定市高阳中学2013-2014学年高二数学下学期第三次周练试题新人教A版
河北省保定市高阳中学2013-2014学年高二数学下学期第三次周练试题新人教A 版一、选择题1.假设()sin cos f x x α=-,如此'()f α等于〔 〕 A .sin αB .cos α C .sin cos αα+D .2sin α2.假设函数2()f x x bx c =++的图象的顶点在第四象限,如此函数'()f x 的图象是〔 〕3.函数1)(23--+-=x ax x x f 在),(+∞-∞上是单调函数,如此实数a 的取值范围是〔 〕A .),3[]3,(+∞--∞B .]3,3[-C .),3()3,(+∞--∞D .)3,3(-4.对于R 上可导的任意函数()f x ,假设满足'(1)()0x f x -≥,如此必有〔 〕A . (0)(2)2(1)f f f +< B. (0)(2)2(1)f f f +≤ C.(0)(2)2(1)f f f +≥ D.(0)(2)2(1)f f f +>5.假设曲线4y x =的一条切线l 与直线480x y +-=垂直,如此l 的方程为〔 〕A .430x y --=B .450x y +-=C .430x y -+=D .430x y ++= 6.函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如下列图,如此函数)(x f 在开区间),(b a 内有极小值点〔 〕A .1个B .2个C .3个D .4个 二、填空题 1.假设函数2f xx x c 在2x =处有极大值,如此常数c 的值为_________;2.函数x x y sin 2+=的单调增区间为。
3.设函数())(0)f x ϕϕπ=+<<,假设()()f x f x '+为奇函数,如此ϕ=__________ 4.设321()252f x x x x =--+,当]2,1[-∈x 时,()f x m <恒成立,如此实数m 的取值范围为。
河北省保定市高阳中学2013-高一下学期第五次周练数学试题
高一下学期第五次周练数学试题1. 若数列的前5项为6,66,666,6666,66666,……,写出它的一个通项公式是 。
2.,则是这个数列的第 项。
3.已知数列{}n a ,11a =,112n n na a a +=+(*n N ∈),写出这个数列的前4项,并根据规律,写出这个数列的一个通项公式. 4. 数列 ,17164,1093,542,211的一个通项公式是 。
5. 数列 ,54,43,32,21--的一个通项公式是 。
6.将正偶数按下表排成5列:第1列 第2列 第3列 第4列 第5列 第1行 2 4 6 8第2行 16 14 12 10第3行 18 20 22 24 …… …… 28 26则2006在第 行,第 列。
7.已知{a n }是递增数列,且对任意n ∈N +,都有a n =n 2+λn 恒成立,则实数λ的取值范围是 。
8.观察下列不等式:112>,111123++>,111312372++++>,111122315++++>,1115123312++++>,,由此猜想第n 个不等式为 ▲ .9.若数列{a n }满足a n+1=,76,)121(12)210(21=⎪⎪⎩⎪⎪⎨⎧<≤-<≤a a a a a n n n n 若则a 20的值是 10.已知数列{a n }中,a n =()*15.6n n N n ∈-,求数列{a n }的最大项. 11.设向量a =(2,x ),b =(12,-+x n x )(n N +∈),函数=y a ·b 在上的最小值与最大值的和为n a ,又数列{n b }满足:1109)109()109(2)1(21121++++=+++-+--- n n n n b b b n nb . (1)求证:1+=n a n ;(2)求n b 的表达式;(3)n n n b a c ⋅-=,试问数列{n c }中,是否存在正整数k ,使得对于任意的正整数n ,都有n c ≤k c 成立?证明你的结论.12.数列{a n }满足a 1=2,a n+1=-11na +,求a 2008。
河北省保定市高阳中学高三数学下学期周练(二十六)试题
河北省保定市高阳中学2014届高三数学下学期周练(二十六)试题新人教A 版1.已知集合}01211|{2<--=x x x A ,集合}),13(2|{Z n n x x B ∈+==,则B A ⋂等于2.为了得到函数y=cos(2x+4π)的图象,可以将函数y=sin (2x+2π)的图象向 平移 个单位长度3.函数y =cos3x +sin2x -cosx 的最大值等于4.设ax x f x 21)13(log )(3++=是偶函数,则a 的值为5.已知函数f(x)=32x 3+32x ,则f(1101)+f(2101)+……+f(100101)=________________. 6.曲线)4cos()4sin(2ππ-+=x x y 和直线21=y 在y 轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于7.正弦曲线y=sinx 上一点P ,正弦曲线的以点P 为切点的切线为直线l ,则直线l 的倾斜角的范围是8.已知命题p :函数)2(log 25.0a x x y ++=的值域为R.命题q :函数x a y )25(--=是R 上的减函数.若p 或q 为真命题,p 且q 为假命题,则实数a 的取值范围是9.已知函数y=f(x)(x ∈R )满足f(x+1)=f(x —1),且x ∈[—1,1]时,f(x)=x2,则y=f(x)与y=log5x 的图象的交点个数为10.若ABC ∆的内角满足,0sin tan ,0cos sin <->+A A A A 则角A 的取值范围是______11.定义运算b a *为:()(),⎩⎨⎧>≤=*b a b b a a b a 例如,121=*,则函数f(x)=x x cos sin *的值域为 .12、点P 是曲线2ln y x x =-上任意一点,则点P 到直线2y x =-的最小距离为 13.函数)(x f 是R 上的单调函数且对任意的实数都有1)()()(-+=+b f a f b a f .,5)4(=f 则不等式3)23(2<--m m f 的解集为 14.已知函数)(|2|)(2R x b ax x x f ∈+-=.给下列命题:①)(x f 必是偶函数;②当)2()0(f f =时,)(x f 的图像必关于直线x =1对称;③若02≤-b a ,则)(x f 在区间[a ,+∞)上是增函数;④)(x f 有最大值||2b a -.其中正确的序号是________.答案1. {2,8}2. 4π3. 32274. 21-5. ________50________.6. π7. ),43[]4,0[πππ⋃8. 1<a<29. 410. ⎪⎭⎫⎝⎛43,2ππ11. [-1,2 .12、13. (-1,34)14. ___③_____.。
河北省保定市高阳中学2013-2014学年高二数学下学期第四次周练试题新人教A版
河北省保定市高阳中学2013-2014学年高二数学下学期第四次周练试题新人教A 版一、选择题1.数列2,5,11,20,,47,x …中的x 等于〔 〕 A .28 B .32 C .33 D .27 2.设,,(,0),a b c ∈-∞如此111,,a b c b c a+++〔 〕 A .都不大于2- B .都不小于2-C .至少有一个不大于2-D .至少有一个不小于2-3.正六边形ABCDEF ,在如下表达式①EC CD BC ++;②DC BC +2;③ED FE +;④FA ED -2中,与AC 等价的有〔 〕 A .1个 B .2个 C .3个 D .4个 4.函数]2,0[)44sin(3)(ππ在+=x x f 内〔 〕 A .只有最大值 B .只有最小值 C .只有最大值或只有最小值 D .既有最大值又有最小值5.如果821,,a a a ⋅⋅⋅为各项都大于零的等差数列,公差0≠d ,如此〔 〕 A .5481a a a a > B .5481a a a a <C .5481a a a a +>+D .5481a a a a =6. 假设234342423log [log (log )]log [log (log )]log [log (log )]0x x x ===,如此x y z ++=〔 〕A .123B .105C .89D .58 7.函数xy 1=在点4=x 处的导数是 ( )A .81 B .81- C .161 D .161-二、填空题1.从222576543,3432,11=++++=++=中得出的一般性结论是_____________。
2.实数0≠a ,且函数)12()1()(2ax x a x f +-+=有最小值1-,如此a =__________。
3.b a ,是不相等的正数,b a y b a x +=+=,2,如此y x ,的大小关系是_________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 河北省保定市高阳中学2013-2014学年高一生物下学期第十五次周练试题新人教版 一、单选题 1.数列na的通项公式11nnan,则该数列的前( )项之和等于9。 A.98 B.99 C.96 D.97 2.设m、m+1、m+2是钝角三角形的三边长,则实数m的取值范围是( ) A.0<m<3 B.1<m<3 C.3<m<4 D.4<m<6 3.已知三角形的三边构成等比数列,且它们的公比为q,则q的取值范围是( )
A.15(0,)2 B.15(,1]2 C.15[1,)2 D.)251,251( 4.在△ABC中,若22tantanbaBA,则△ABC的形状是( ) A.直角三角形 B.等腰或直角三角形 C.等腰三角形 D.不能确定 5.在△ABC中,若b=22,a=2,且三角形有解,则A的取值范围是( ) A.0°<A<30° B.0°<A≤45° C.0°<A<90° D.30°<A<60°
6(理). 等差数列na中,若11a,815a,则122311aaaa…1001011aa( )
A.200199 B.100199 C.200201 D.100201 (文)若实数a,b,c成等比数列,则函数f(x)=ax2+bx+c的图像与x轴交点的个数为( ) A 0个 B 1个 C 2个 D 不能确定 7. 如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( ) (A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 由增加的长度决定 8(理).等差数列{}na,{}nb的前n项和分别为nS,nT,若7453nnSnTn,则使nnab为整数的正整数
n的取值个数是( ) A 3 B 4 C 5 D 6
(文).等差数列{}na,{}nb的前n项和分别为nS,nT,若231nnSnTn,则nnab=( )
A 23 B 2131nn C 2131nn D 2134nn 9(理).设a、b、c为同平面内具有相同起点的任意三个非零向量,且满足a与b不共线,ac,ac,则bc的值一定等于( )
A.以a、b为两边的三角形面积; B.以a、b为邻边的平行四边形的面积; C.以b、c为两边的三角形面积; D.以b、c为邻边的平行四边形的面积. 2
(文).在△ABC中,AB=5,BC=7,AC=8,则BCAB的值为( ) A.79 B.69 C.5 D.-5
10(理).已知正项数列na满足:2*113,2122181,nnananannnN ,设
,1nnab数列nb的前n项的和nS,则nS的取值范围为 ( )
A.10,2 B.11,32 C.11,32 D.11,32 (文).已知数列2004,2005,1,-2004,-2005,…,这个数列的特点是从第二项起,每一项都等于它的前后两项之和,则这个数列的前2004项之和2004S等于( ) A.2005 B.2004 C.1 D.0 二. 填空题: 11(理).在△ABC中,A=60°,b=1,其面积为3,则CBAcbasinsinsin=_____________ (文). 在△ABC中,已知sinA∶sinB∶sinC=3∶5∶7,则此三角形的最大内角等于________. 12.等差数列nan的前}{项和为nS,若m>1,211210,78,mmmmaaaS则m=_____。
13.数列),60cos1000lg(),...60cos1000lg(),60cos1000lg(,1000lg01020n…的前_____项和为最大? 14(理).不等式log2 (2x-1)·log2 (2x1-2)<2的解集是_______________。 (文).已知22,,21211,xyRxxyy则32xy 15(理). 已知an=100241n(n=1, 2, …),则S99=a1+a2+…+a99=
(文). 设f(x)=221x,利用课本中推导等差数列前n项和的求和公式的方法, 可求得f(-8)+f(-7)+…+f(0)+…+f(8)+f(9)的值为___________________. 三. 解答题 16. 在锐角三角形中,边a、b是方程x2-23 x+2=0的两根,角A、B满足2sin(A+B)-3 =0,求角C的度数,边c的长度及△ABC的面积. (本题满分12分)
17.(理)已知集合3(x-1)2x-2x-3211331A=x|2<,B=x|log(9-x)3
B={x|x2+ax+b<0},求a+b的值。(本题满分12分) (文)(1)若02522xx,化简:221442xxx (2)求关于x的不等式(k2-2k+25)x<(k2-2k+25)1ˉx的解集
18.在△ABC中,已知角A、B、C所对的边分别是a、b、c,边c=72 ,且tanA+tanB=3 tanA·tanB-3 ,又△ABC的面积为S△ABC=332 ,求a+b的值。
19.设数列}{na的前n项和为nS,101a,1091nnSa. ⑴求证:数列}{lgna是等差数列.
⑵设nT是数列))(lg(lg31nnaa的前n项和,求使)5(412mmTn 对所有的Nn都成立的最大正整数m的值.
20. 2(4)nn个正数排成n行n列: 111213141naaaaa 212223242naaaaa 313233343naaaaa
1234nnnnnnaaaaa 其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知241a,4218a,43316a,试求1122nnaaa的值. 4
21.设fk是满足不等式122loglog52kxx≥2kkN的自然数x的个数. (1)求fk的函数解析式; (2)12nSfffn,求nS;
(3)设123nnPn,由(2)中nS及nP构成函数nT,2211loglog10.5nnnnnSPTSP,求nT的最小值与最大值.
答案 1---5. B B D B B 6.(理)D (文)A , 7 .A , 8(理)C (文)B 9(理)B(文)D , 10(理)B (文)D
11. (理) 2393 (文)23 12. 20 13. 10
14. (理)(㏒254,㏒23)(文) –2 或0 15. (理) 10199.2(文)42 5
16.解:由2sin(A+B)-3 =0,得sin(A+B)=32 , ∵△ABC为锐角三角形 ∴A+B=120°, C=60°.………………………………………………………………(4分) 又∵a、b是方程x2-23 x+2=0的两根,∴a+b=23 ,a·b=2, ……………….(6分) ∴c2=a2+b2-2a·bcosC=(a+b)2-3ab=12-6=6, ∴c=6 , …………….…….(10分)
S△ABC=12 absinC=12 ×2×32 =32 . …………….…….(12分)
17. (理)解:∵32Axx, 2291219022120xxBxxxxx…(6分) ∴A∩B={x|x2+ax+b<0}=122xx, ………………………(8分) ∴2和12即为方程x2+ax+b=0的两根,∴132221(2)12ab ∴a+b=12.………(12分) (文)解:(1)∵12,2x原式=221222122xxxx…(5分) 12222xx=12232xx………………………(8分)
(2)2253211,22kkk原不等式等价于1xx, 此不等式的解集为12xx………………………(12分)
18.解:由tanA+tanB=3 tanA·tanB-3 可得tantan1tantanABAB=-3 ,………(3分) 即tan(A+B)=-3 …………………….(4分) ∴tan(π-C)= -3 , ∴-tanC=-3 , ∴tanC=3
∵C∈(0, π), ∴C=3……………………………………………………….(6分)
又△ABC的面积为S△ABC=332 ,∴12 absinC=332 即12 ab×32 =332 , ∴ab=6…….(8分) 又由余弦定理可得c2=a2+b2-2abcosC ∴(72 )2= a2+b2-2abcos3∴(72 )2= a2+b2-ab=(a+b)2-3ab∴(a+b)2=1214 , …….(11分)
∵a+b>0, ∴a+b=112 ……………………………………………………. (12分) 19.解:⑴依题意,10010912aa,故1012aa,………………………………. (2分) 当2n时,1091nnSa ① 又1091nnSa ② ………………….…………. (4分)
②―①整理得:101nnaa,故}{naNn为等比数列,
