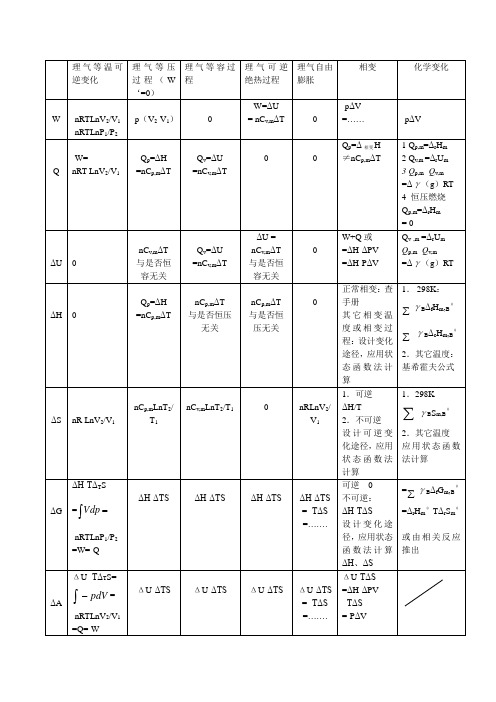
热力学知识:热力学中的热力学计算和热力图表
热力学计算公式小结表
∆H
0
nCp,m∆T 与是否恒压 无关
0
正常相变:查 手册 其它相变温 度或相变过 程:设计变化 途径,应用状 态函数法计 算 1.可逆 ∆H/T 2.不可逆 设计可逆变 化途径,应用 状态函数法 计算 可逆 0 不可逆: ∆H-T∆S 设计变化途 径,应用状态 函数法计算 ∆H、∆S ΔU-T∆S =∆H-∆PV - T∆S =-P∆V
θ ∑ γB∆fHm,B
Q
Qp=∆H =nCp,m∆T
Qv=∆U =nCv,m∆T
0
0
∆U
0
nCv,m∆T 与是否恒 容无关 Qp=∆H =nCp,m∆T
Qv=∆U =nCv,m∆T
∆U = nCv,m∆T 与是否恒 容无关 nCp,m∆T 与是否恒 压无关
0
W+Q 或 =∆H-∆PV =∆H-P∆V
= ∑ γB∆fGm,B
θ
θ
=∆rHm -T∆rSm
θ
-nRTLnP1/P2 =W=-Q ΔU- T∆TS= ∆A
或由相关反应 推出
∫ − pdV =
-nRTLnV2/V1 =Q=-W
ΔU-∆TS
ΔU-∆TS
ΔU-∆TSΔU-∆TS =Fra bibliotek-T∆S =…….
理气等温可 逆变化
理气等压 过程(W ‘=0) -p(V2-V1)
理气等容过 程
理气可逆 绝热过程 W=∆U = nCv,m∆T
理气自由 膨胀
相变
化学变化
W
-nRTLnV2/V1 -nRTLnP1/P2 -W= nRT LnV2/V1
0
0
-p∆V =…… Qp=∆ 相变 H ≠nCp,m∆T
热力学 表

热力学表以下是一些热力学表:
1.热容量表。
物质热容量(J/g·K)。
水4.18。
氧气0.918。
氢气14.30。
氧化铁0.80。
铜0.385。
2.熵表。
物质熵(J/mol·K)。
水69.9。
氧气205。
氢气131。
氧化铁87.4。
铜33.1。
3.焓表。
物质焓(kJ/mol)。
水40.7。
氧气0。
氢气0。
氧化铁-822。
铜0。
4.热力学稳定性表。
物质ΔG(kJ/mol)。
H2O-237。
O20。
FeO-271。
Cu0。
5.可逆热力学过程表。
过程ΔSΔH。
等温过程0q/T。
等压过程qP。
等容过程qVq。
绝热过程-q/T-q。
6.热力学常数表。
常数值。
玻耳兹曼常数1.381×10^-23J/K。
阿伏伽德罗常数6.022×10^23/mol 。
普朗克常数6.626×10^-34J·s。
理想气体常数 R 8.31 J/mol.K 。
注意:此表并不是所有热力学量的完整列表,只是涵盖了一些重要的量。
此表中的值可能因不同数据源而略有差异。
第十三章 热力学基础1

解 氮气可视为理想气体, 其液化过程为绝热过程.
p1 = 50 × 1.01× 105 Pa
p2 = 1.01× 10 Pa
5
T1 = 300K
氮气为双原子气体由表查得 γ = 1.40
p2 (γ −1) / γ T2 = T1 ( ) = 98.0K p1
第十三章:热力学基础
例3 一汽缸内有一定的水,缸壁由良导热材料 制成. 作用于活塞上的压强 1 .013 × 10 5 Pa ,摩擦不计. 开始时,活塞与水面接触. 若环境 (热源) 温度非常 缓慢地升高到 100o C . 求把单位质量的水汽化为水 蒸气,内能改变多少?
2 (p , , ) 2 V T 2 2
p2
W
( p2, 2, 2 ) V T 2
p1
W
( p1, 1 ,T1 ) V 1
o V1
V2 V
o V2
V1 V
E1
W
E2
E2
E1
W
第十三章:热力学基础
绝热线和等温线
绝热过程曲线的斜率 pV γ = 常量
γpV γ −1dV + V γ dp = 0
dp pA ( ) a = −γ dV VA
p
p2
' p2
2 T 2
T2' = T1 Q=0
2'
p1
T1
o V = V ' = V 10 V V 2 2 1 1
第十三章:热力学基础
T = 常量
1
ν 已知: = 5 mol T0 = 293 K
P0 = 1.013 × 105 Pa V = 0.1V0
解 (1)等温过程
V2′ ′ W12 = νRT ln = −2.80×104 J V1
热力学参数和热力学循环的计算

热力学参数和热力学循环的计算在现代工业中,热力学参数和热力学循环的计算在许多领域具有重要的应用价值。
热力学参数是描述物质状态的基本参数,包括温度、压力、体积、熵等。
热力学循环是指在发电、制冷、加热等过程中,物质的热力学状态变化的过程。
本文将探讨如何计算热力学参数和热力学循环的计算方法。
一、热力学参数的计算1、温度温度是物质内部分子热运动的强弱指标,常用的温度单位有摄氏度、华氏度、开氏度等。
对于一个物体温度的测量,可通过浸温法、电阻计法、红外测温法等方法进行。
2、压力压力是指物质分子对单位面积的压力,通常用帕斯卡(Pa)和标准大气压(101325 Pa)表示。
压力的测量方法有静压法、量筒法、毛细法等方法。
3、体积体积是指物质所占据的空间大小,通常以立方米为单位。
物体体积的测量有水滴法、毛细法、位移法等。
4、熵熵是描述系统混乱程度的一个物理量,通常以焦耳/开尔文表示。
熵的计算需要考虑系统的起始状态和末状态,在具体的应用中,常常采用某些热力学循环或过程的参数来计算。
二、热力学循环的计算热力学循环是指在特定条件下,物质所经历的一系列热力学变化过程。
常见的热力学循环包括卡诺循环、布雷顿循环等。
1、卡诺循环的计算卡诺循环是一种理论上最为完美的热力学循环,通过计算卡诺循环的效率可得到能源转化的最大效率。
卡诺循环是一个理想循环,基于以下假设:1)工作物质是均匀、不可压缩的理想气体。
2)热源和冷源之间没有热损失。
3)工作物质需要足够的时间来达到热源和冷源的温度。
4)气缸和环境之间没有热损失。
卡诺循环的效率公式为:η = 1 - T2/T1,其中T2为冷源温度,T1为热源温度。
通过计算得知,卡诺循环的效率是不能达到100%的,但其效率越接近1,能源转换的效率就越高。
2、布雷顿循环的计算布雷顿循环是现代蒸汽动力机的基本循环,包括四个过程:加热、膨胀、冷却、压缩。
通过计算布雷顿循环的效率可以得到汽轮机或发电机的最大效率。
第五章 热力学计算

第五章 热力学计算热力学以及化学热力学是迄今发展得最为完善和普遍适用的一门理论性学科,在包括无机非金属材料在内的众多学科领域中有着广泛的应用。
它在理论上解决了有关体系复杂过程发生的方向性和平衡条件,以及伴随该过程体系能量变化等问题。
它对探讨各种无机材料系统的具体过程,如烧成、烧结、腐蚀、水化反应等进行的方向及可能性,都有着巨大的科学研究和生产实践方面的指导意义。
应用热力学方法可以判断过程进行的方向和可能,而不能判断过程进行的速度和时间。
过程进行的速度和时间问题属动力学范畴。
第一节:热化学计算 一. 热效应 1.热效应的定义在恒温条件下只作体积功而不作其他功,系统吸热或放热的现象称为热效应,如化学反应和相变中吸热或放热。
恒容热效应:Q V =△U+P △V=△U恒压热效应:Q P =△U+P △V=△(U+PV)= △H 热焓是在恒压条件下发挥作用的特性函数。
∑∑∆-∆=∆反应物产物)H ()H (H 0i,298f ,i 0i,298f ,i298R,γγ2.盖斯定律32123222212222H H H H SiO2CaO - H 2CaO SiO-SiO- H O Si 2CaO H O 2Ca SiO 2CaO -SiO2CaO - H 2O Si 2Ca ∆+∆+∆=∆⋅∆+∆+∆+⋅⋅∆++根据盖斯定律:应来生成:也可以通过下列几步反反应:βββββ3.热效应与温度的关系⎰∑∑⎰⋅∆=∆H-∆H∆+∆+∆=-=∆++==∆=∆--2112P,R ,R 2i P,iP,P 2P P R CcTbT a )C ()C (C cT bT a (T)C )(C dT H d T T T T iidT反应物产物恒压热容γγ三.热化学计算举例7654321)(27)(26)(2521)(24)(23)(2)()(2)(2)(221323 2298 2298 2.21323 21100 2110022∆H+∆H=∆H+∆H+∆H+∆H+∆H⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡⋅∆H ⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡⋅∆H ⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡-+∆H ↓∆H ↑∆H ↑⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡⋅∆H ⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡⋅∆H ⎥⎦⎤⎢⎣⎡-+⋅→+l b l bS b S bS b S S b l b S S b SiO O P K SiO O P K SiO O P KSiO O P K SiO O P K SiO O P K SiOO P SiOO P αα第二节 热力学计算 一.熵判据1.对于孤立系统,当熵变△S >0时,过程自发进行。
热力学

热力学:是一门研究物质的能量、能量传递和转换以及能量与物质性质之间普遍关系的科学。
工质:工程热力学中把实现热能与机械能相互转换的工作物质称为工质。
温度是表示物体的冷热程度。
摄氏温度t 与热力学温度的关系:K=t+273.15比体积是表示单位质量物质所占的体积v熵是表示单位质量物质,在某一温度下,发生单位热量传递时,转化为工质内部低级能量的数量焓是流动工质所具有的能量热量的传递是由于分子热运动导致的,它包括热传导、热辐射以及电磁辐射能量转换与守恒定律:1: 自然界中的一切物质都具有能量,能量不可能被创造和消灭,但可以转换和转移。
2:当能量发生形式转换和在物体间转移时,能量的总和保持不变热力学第一定律: 在热能与其他形式的能的互相转换过程中能量的总和保持不变。
系统与外界之间仅有热量和功量的交换,没有物质交换的系统称之为闭口系统系统与外界之间不仅有热量和功量的交换,而且还有物质交换的系统称之为开口系统pv=RT R=Rm/µ Rm=8.31kJ/(kmol.K)cp/ cv=K cp-cv=R 单元子气体k=1.66;双原子气体k=1.4;多原子气体k=1.29比热容是单位量的物质发生单位温度变化时所吸收或放出的热量。
实际热力过程可用pvn=常数来表达=cons闭口系统的膨胀功 w )(121T T n R --= P-v 图由体积功的表达式可以看出:任意热力过程体积对压力的积分就是热力过程所完成的体积功最理想的热机是由2个定温过程和2个等熵过程组成的循环,即卡诺循环能量守恒定律(热力学第一定律): dq=du+dw=du+pdv=dh-vdp内燃机性能指标很多,主要有:1: 动力性指标—功率/Pe 、扭矩/Ttq 、转速/n ;2: 经济性指标—热效率η、燃油消耗率be ;3: 运转性能指标—冷启动性、噪声和排气品质内燃机的实际热力循环: 是燃料的热能转变为机械能的过程,由进气、压缩、燃烧、膨胀和排气等5个过程所组成。
热力学

等压过程的热力学第一定律: p
Qp E W
po
V1
V2 V
等压过程的功:
W
V2 V1
pdV
p(V2 V1)
因为
PV1
m M
RT1
m PV2 M RT2
W
m M
R(T2
T1)
内能增量:
ΔE
m M
i 2 R(T2
T1)
m
吸收热量: Qp M Cp,m (T2 T1)
dQ dT V,mol
i 2
R
定压摩尔热容: 1mol 理想气体
在压强不变的状态下,温度升 Cp,m
高一度所需要吸收的热量。
dQ dT p,mol
i 2
1R
热量计算式:
Q m M
CmdT
热容量与系统 经过的过程有关。
(3)内能变化的计算
(3)p 不变,热量变为什么?氢气的T,V各为多少?
解: (1)Q = E,热量转变为内能
ΔE
QV
m M
CV ,m (T
To )
n
i 2
R(T
To )
T
2QV inR
To
2500 273 285K 5 28.31
(2)T 不变,热量变为什么?氢的p,V各为多少?
热力学基础
§1 热力学第一定律
热力学第一定律: Q (E2 E1) W
Q 表示系统吸收的热量,W 表示系统所作的功,
E 表示系统内能的增量。
符号规定: 1、系统吸收热量Q为正,系统放热Q为负。 2、系统对外作功W为正,外界对系统作功W为负。
热力学知识:热力学与热力学计算

热力学知识:热力学与热力学计算热力学是研究热现象和能量转换的物理学科,是研究物质内部运动和相互作用的科学。
热力学广泛应用于各种领域,从工业和机械制造到生命科学和化学,以及天文学和宇宙学。
热力学的基本概念包括热、温度、热量、功、热力学第一定律、热力学第二定律、熵等。
其中,热是指能够转移到其他物体并使其发生温度变化的能量;温度是物体内分子运动平均动能的量度;热量是物体内部分子的热运动所带来的能量变化;功是物质所做的有用的活动,例如机械力、电力和化学能,它们都可以转化为热能来维持生命。
热力学计算是研究能量转换和处理的数学方法。
在工业和化学过程中,热力学计算被广泛应用于设计和优化燃气轮机、重要化学反应和蒸汽涡轮等设施。
热力学计算的主要任务是确定给定系统的热性质和能量特性,以此确定物质特性以及系统的最大效率和能量转换率。
在热力学计算中使用了许多数学工具,例如微积分、差分、代数和几何。
早期的热力学计算使用的是手工计算和试验研究结合的方法,而今天,随着计算机技术的发展,热力学计算使用了更多计算机程序和数值模拟方法。
热力学计算的一个重要应用是工程热力学。
这种热力学应用于设计和优化化学反应器、蒸汽动力机、燃气动力机和核燃料处理装置以及其他工业过程。
热力学计算还应用于天文学和宇宙学,用于研究天体中的物质的物理和化学性质。
热力学计算包括反应热力学和相行平衡热力学。
反应热力学研究反应热、速率和平衡常数;相行平衡热力学研究相变和物质在两相之间的平衡。
这些理论在各个领域中都有广泛的应用。
总之,热力学和热力学计算是研究能量转换和处理的科学方法和数学方法。
在工业、化学、宇宙学和天文学等领域中广泛应用,在减少能源浪费和提高生产效率方面发挥着重要作用。
热力学的理论和热力学计算的方法不断发展,将继续为人类社会的发展和繁荣作出贡献。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热力学知识:热力学中的热力学计算和热力
图表
热力学是一门能够描述物质能量转化和传递的物理学科,它研究的是热量、功、能量和熵等基本的物理量之间的相互关系。
在实际应用中,热力学常常被用来计算各种体系的热力学性质,例如热容、热力学势函数、化学反应平衡等等。
在热力学计算中,热力图表也是非常常用的工具,它可以直观地描述各种体系的物理和化学性质,便于我们进行分析和研究。
一、热力学计算
1、热力学基本量
在热力学的计算中,热量、功、能量和熵是最基本的物理量,它们之间的关系可以表示为:
ΔU=Q-W
其中,ΔU表示系统内能的变化,Q表示系统所吸收的热量,W表示系统所做的功。
另外,在热力学中还有几个重要的热力学量,例如热容、热力学
势函数、化学反应平衡等等。
这些量的计算也是非常重要的,它们可
以反映出体系的热力学性质和稳定性。
2、热力学循环
在热力学循环中,热量和功的转化可以循环进行,从而实现能量
的连续转化和利用。
例如,蒸汽动力发电机系统中,水被加热蒸发,
蒸汽驱动涡轮机运转产生功,然后通过冷凝器进行冷却回到水箱中,
从而循环再次加热。
在这个过程中,热量和功的变化可以通过热力学
计算进行分析和优化,以达到最高的能量转化效率。
3、化学反应
化学反应是热力学计算中的一个重要应用,它可以研究各种化学
反应的平衡状态和反应能量。
在化学反应中,物质的热化学态函数是
计算反应热量和反应平衡的重要工具。
例如,在S→SO2的氧化反应中,热化学态函数可以表示为:
ΔH=-297 kJ/mol(S)+0 kJ/mol(O2)-395 kJ/mol(SO2)
其中,ΔH表示反应热量,单位为kJ/mol。
二、热力图表
1、热力图
热力图是一种图形化表示热力学性质的图表,它直观地展示了各种变量之间的相互关系。
在热力学中,常用的热力图有比热容图、热力学势函数图、化学反应热图等等。
这些图表可以帮助我们更好地理解和分析热力学性质,以便制定更好的计算和实验方案。
2、比热容图
比热容图是一种描述物质热力学性质的图表,它可以直观地显示出不同物质在不同温度下的比热容变化。
比热容是物质吸收的热量与温度变化之间的比率,它是反映物质热学性质的重要物理量。
比热容图也是设计各种加热、冷却设备以及热力学循环系统等的重要工具。
3、热力学势函数图
热力学势函数图是一种描述体系稳定状态的图表,它可以直观地显示出不同条件下体系自由能、焓、熵等物理量的变化情况。
在热力学计算中,热力学势函数是非常重要的工具,它可以帮助我们确定体
系的稳定状态以及最佳的热力学条件。
在化学反应热力学计算中,常
用的热力学势函数有Gibbs自由能、Helmholtz自由能等等。
总之,在热力学中,热力学计算和热力图表都是非常重要的工具,它们可以帮助我们更好地理解和分析物质能量转化和传递的规律。
随
着人类对物质世界认知的不断深入,热力学的应用范围也将越来越广泛。
