课时作业4:7.2.1 三角函数的定义
7.2.3 三角函数的诱导公式 2023-2024学年高中数学苏教版必修第一册

图示
角π-α与角α
的终边关于
y轴对称
公式
sin(π-α)= sin α ,cos(π-α)= -cos α ,tan(π-α)= -tan α
4.诱导公式四
终边关系
图示
角π+α与角α
的终边关于
原点对称
公式
sin(π+α)= -sin α ,cos(π+α)= -cos α ,tan(π+α)= tan α
解 由
=3+2√2,
1-tan(-360°)
1+tan
2
得
=3+2√2,∴tan θ= 2 .
1-tan
cos2 +sincos+2sin2
2
原式=
=1+tan
θ+2tan
θ
2
cos
2
22
2
=1+ +2×( ) =2+ .
2
2
2
素养形成
思想方法——分类讨论思想在诱导公式中的应用
cos(π-)sin(π-)
-sin(-sin)cos sin
=
==-tan α.
cos
cos(-cos)sin
1+2sin(360°-70°)cos(360°+70°)
(2)原式= sin(180°+70°)+cos(720°+70°)
1-2sin70°cos70°
|cos70°-sin70°|
变式训练2化简下列各式:
cos(π+)cos(3π-)tan(π+)
(1)
;
《三角函数的定义》人教版数学高一下册PPT课件

第一章 三角函数
〔跟踪练习 3〕求值: (1)sin(-1 740°)cos1 470°+cos(-660°)sin750°+tan405°; (2)sin2174π+tan2(-116π)tan94π.
(4)若 sinα=sinβ,则必有 α=β.( × )
(5)若 α 是第二象限角,且 P(x,y)是其终边上一点,则 cosα=-
x .( ×
x2+y2
)
2
2
2.若角 α 的终边与单位圆相交于点( 2 ,- 2 ),则 sinα 的值为( B )
2 A. 2
2 B.- 2
1 C.2
D.-1
2
2
2
y (2)若已知角 α 终边上一点 P(x,y)(x≠0)是单位圆上点,则 sinα=y,cosα=x,tanα=x.
(3)若已知角 α 终边上一点 P(x,y)不是单位圆上一点,则先求 r= x2+y2,再求
ቤተ መጻሕፍቲ ባይዱ
y
x
sinα= r,cosα= r.
(4)若已知角 α 终边上点的坐标含参数,则需进行分类讨论.
y
y
___x___叫做 α 的正切,记作 tanα,即 tanα=x(x≠0).
第一章 三角函数
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值 的函数.
③由三角形相似的知识,我们也可以利用角 α 终边上任意一点的坐标来定义三角函 数.
2021_2022学年新教材高中数学第7章三角函数7.27.2.1任意角的三角函数学案苏教版必修第一
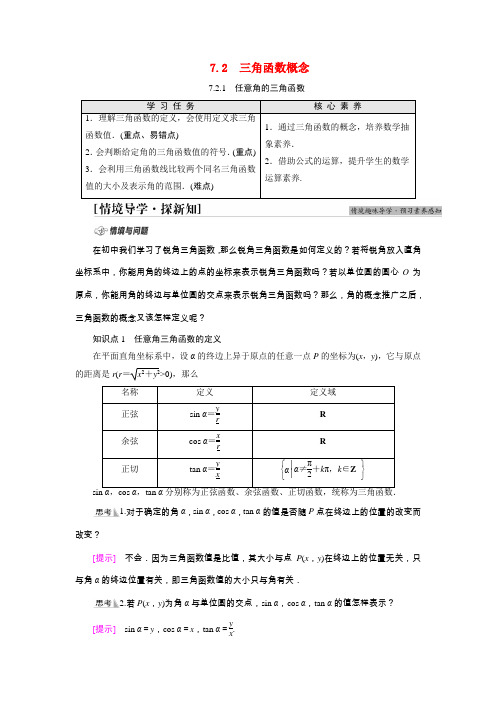
7.2 三角函数概念7.2.1任意角的三角函数学习任务核心素养1.理解三角函数的定义,会使用定义求三角函数值.(重点、易错点)2.会判断给定角的三角函数值的符号.(重点)3.会利用三角函数线比较两个同名三角函数值的大小及表示角的范围.(难点)1.通过三角函数的概念,培养数学抽象素养.2.借助公式的运算,提升学生的数学运算素养.在初中我们学习了锐角三角函数,那么锐角三角函数是如何定义的?若将锐角放入直角坐标系中,你能用角的终边上的点的坐标来表示锐角三角函数吗?若以单位圆的圆心O为原点,你能用角的终边与单位圆的交点来表示锐角三角函数吗?那么,角的概念推广之后,三角函数的概念又该怎样定义呢?知识点1任意角三角函数的定义在平面直角坐标系中,设α的终边上异于原点的任意一点P的坐标为(x,y),它与原点的距离是r(r=x2+y2>0),那么名称定义定义域正弦sin α=yr R余弦cos α=xr R正切tan α=yx⎩⎨⎧⎭⎬⎫α⎪⎪α≠π2+kπ,k∈Z1.对于确定的角α,sin α,cos α,tan α的值是否随P点在终边上的位置的改变而改变?[提示]不会.因为三角函数值是比值,其大小与点P(x,y)在终边上的位置无关,只与角α的终边位置有关,即三角函数值的大小只与角有关.2.若P(x,y)为角α与单位圆的交点,sin α,cos α,tan α的值怎样表示?[提示]sin α=y,cos α=x,tan α=yx.1.若角α的终边经过点P ⎝ ⎛⎭⎪⎫22,-22,则sin α=________;cos α=________;tan α=________.-2222-1 [由题意可知 |OP |=⎝⎛⎭⎫22-02+⎝⎛⎭⎫-22-02=1, ∴sin α=-221=-22;cos α=221=22;tan α=-2222=-1.]知识点2 三角函数在各象限的符号2.(1)若α在第三象限,则sin αcos α________0;(填“>”或“<”)(2)cos 3tan 4________0.(填“>”或“<”) (1)> (2)< [(1)∵α在第三象限, ∴sin α<0,cos α<0,∴sin αcos α>0. (2)∵π2<3<π,π<4<3π2,∴3是第二象限角,4是第三象限角. ∴cos 3<0,tan 4>0.∴cos 3tan 4<0.] 知识点3 三角函数线(1)有向线段:规定了方向(即规定了起点和终点)的线段;有向直线:规定了正方向的直线;有向线段的数量:若有向线段AB 在有向直线l 上或与有向直线l 平行,根据有向线段AB 与有向直线l 的方向相同或相反,分别把它的长度添上正号或负号,这样所得的数,叫作有向线段的数量,记为AB .(2)三角函数线3.思考辨析(正确的打“√”,错误的打“×”)(1)α一定时,单位圆的正弦线一定.( ) (2)在单位圆中,有相同正弦线的角必相等.( ) [答案] (1)√ (2)×类型1 三角函数的定义及应用【例1】 (1)在平面直角坐标系中,角α的终边在直线y =-2x 上,求sin α,cos α,tan α的值.(2)当α=-π3时,求sin α,cos α,tan α的值.[解] (1)当α的终边在第二象限时,在α终边上取一点P (-1,2),则r =(-1)2+22=5,所以sin α=25=255,cos α=-15=-55,tan α=2-1=-2.当α的终边在第四象限时, 在α终边上取一点P ′(1,-2), 则r =12+(-2)2=5,所以sin α=-25=-255,cos α=15=55,tan α=-21=-2.(2) 当α=-π3时,设α的终边与单位圆的交点坐标为P (x ,y ),(x >0,y <0)根据直角三角形中锐角π3的邻边是斜边的一半,得x=12,由勾股定理得⎝⎛⎭⎫122+y2=1,y<0,解得y=-32,所以P⎝⎛⎭⎫12,-32.因此sin α=-321=-32,cos α=121=12,tan α=-3212=- 3.1.将本例(1)的条件“y=-2x”改为“3x+y=0”其他条件不变,结果又如何?[解]直线3x+y=0,即y=-3x,当α的终边在第二象限时,在α的终边上取一点P(-1,3),则r=2,所以sin α=32,cos α=-12,tan α=-3;当α的终边在第四象限时,在α终边上取一点P′(1,-3),则r=2,所以sin α=-32,cos α=12,tan α=- 3.2.将本例(1)的条件“在直线y=-2x上”,改为“过点P(-3a,4a)(a≠0)”,求2sin α+cos α.[解]因为r=(-3a)2+(4a)2=5|a|,①若a>0,则r=5a,角α在第二象限,sin α=yr=4a5a=45,cos α=xr=-3a5a=-35,所以2sin α+cos α=85-35=1.②若a<0,则r=-5a,角α在第四象限,sin α=4a-5a=-45,cos α=-3a-5a=35,所以2sin α+cos α=-85+35=-1.1.已知角α终边上任意一点的坐标求三角函数值的方法(1)先利用直线与单位圆相交,求出交点坐标,然后再利用正、余弦函数的定义求出相应的三角函数值.(2)在α的终边上任选一点P (x ,y ),设P 到原点的距离为r (r >0),则sin α=y r ,cos α=xr .当已知α的终边上一点求α的三角函数值时,用该方法更方便.2.已知特殊角α,求三角函数值的方法(1)先设出角α的终边与单位圆交点坐标,由锐角三角形的定义结合勾股定理求出该点的坐标.(2)利用三角函数的定义,求出α的三角函数值.(此时P 到原点的距离r =1)3.当角α的终边上点的坐标以参数形式给出时,要根据问题的实际情况对参数进行分类讨论.[跟进训练]1.已知角θ终边上一点P (x,3)(x ≠0),且cos θ=1010x ,求sin θ,tan θ. [解] 由题意知r =x 2+9,由三角函数定义得cos θ=xr=x x 2+9.又∵cos θ=1010x , ∴xx 2+9=1010x . ∵x ≠0,∴x =±1. 当x =1时,P (1,3), 此时sin θ=312+32=31010, tan θ=31=3.当x =-1时,P (-1,3), 此时sin θ=3(-1)2+32=31010,tan θ=3-1=-3.2. 当α=4π3时,求sin α,cos α,tan α的值.[解] 当α=4π3时,设α的终边与单位圆的交点坐标为P (x ,y ),(x <0,y <0)根据直角三角形中锐角π3的邻边是斜边的一半,得x =-12,由勾股定理得⎝⎛⎭⎫-122+y 2=1,y <0,解得y =-32, 所以P ⎝⎛⎭⎫-12,-32.因此sin α=-321=-32,cos α=-121=-12,tan α=-32-12= 3.类型2 三角函数值的符号【例2】 (1)若角θ同时满足sin θ<0且tan θ<0,则角θ的终边一定位于( ) A .第一象限 B .第二象限 C .第三象限D .第四象限(2)判断下列各式的符号. ①sin 2 015° cos 2 016° tan 2 017°; ②tan 191°-cos 190°; ③sin 2 cos 3 tan 4.(1)D [由sin θ<0,可知θ的终边可能位于第三或第四象限,也可能与y 轴的负半轴重合.由tan θ<0,可知θ的终边可能位于第二象限或第四象限,故θ的终边只能位于第四象限.](2)[解] ①∵2 015°=1 800°+215°=5×360°+215°, 2 016°=5×360°+216°,2 017°=5×360°+217°, ∴它们都是第三象限角,∴sin 2 015°<0,cos 2 016°<0,tan 2 017°>0, ∴sin 2 015° cos 2 016° tan 2 017°>0.②∵191°角是第三象限角,∴tan 191°>0,cos 191°<0, ∴tan 191°-cos 191°>0.③∵π2<2<π,π2<3<π,π<4<3π2,∴2是第二象限角,3是第二象限角,4是第三象限角, ∴sin 2>0,cos 3<0,tan 4>0, ∴sin 2 cos 3 tan 4<0.判断三角函数值在各象限符号的攻略(1)基础:准确确定三角函数值中各角所在象限. (2)关键:准确记忆三角函数在各象限的符号.(3)注意:用弧度制给出的角常常不写单位,不要误认为角度制导致象限判断错误.[跟进训练]3.判断下列式子的符号:(1)tan 108°·cos 305°;(2)cos 5π6·tan11π6sin2π3;(3)tan 120°·sin 269°.[解] (1)∵108°是第二象限角,∴tan 108°<0. ∵305°是第四象限角,∴cos 305°>0. 从而tan 108°·cos 305°<0.(2)∵5π6是第二象限角,11π6是第四象限角,2π3是第二象限角,∴cos5π6<0,tan 11π6<0,sin 2π3>0. 从而cos 5π6·tan11π6sin2π3>0.(3)∵120°是第二象限角,∴tan 120°<0, ∵269°是第三象限角,∴sin 269°<0. 从而tan 120°·sin 269°>0.类型3 应用三角函数线解三角不等式【例3】 在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合: (1)sin α≥32;(2)cos α≤-12.1.在单位圆中,满足sin α=32的正弦线有几条?试在图中明确. [提示] 两条,如图1所示,MP 1与NP 2都等于32. 2.在单位圆中,满足cos α=-12的余弦线有几条?在图中明确.[提示] 一条,如图2所示,OM =-12.图1 图2[解] (1)作直线y =32交单位圆于A ,B 两点,连接OA ,OB ,则OA 与OB 围成的区域(图①阴影部分)即为角α的终边的范围,故满足条件的角α的集合为⎩⎨⎧⎭⎬⎫α⎪⎪2k π+π3≤α≤2k π+2π3,k ∈Z .(2)作直线x =-12交单位圆于C ,D 两点,连接OC ,OD ,则OC 与OD 围成的区域(图②阴影部分)即为角α终边的范围,故满足条件的角α的集合为⎩⎨⎧⎭⎬⎫α⎪⎪2k π+23π≤α≤2k π+43π,k ∈Z .利用三角函数线解三角不等式的方法(1)正弦、余弦型不等式的解法对于sin x ≥b ,cos x ≥a (sin x ≤b ,cos x ≤a ),求解的关键是恰当地寻求点,只需作直线y =b 或x =a 与单位圆相交,连接原点与交点即得角的终边所在的位置,此时再根据方向即可确定相应的范围.(2)正切型不等式的解法对于tan x ≥c ,取点(1,c ),连接该点和原点并反向延长,即得角的终边所在的位置,结合图象可确定相应的范围.[跟进训练]4.求函数f (x )=1-2cos x +ln ⎝⎛⎭⎫sin x -22的定义域. [解] 由题意,自变量x 应满足不等式组⎩⎪⎨⎪⎧1-2cos x ≥0,sin x -22>0,即⎩⎨⎧cos x ≤12,sin x >22.则不等式组的解的集合如图(阴影部分)所示,∴函数f (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪2k π+π3≤x <2k π+34π,k ∈Z .1.若sin α<0,tan α>0,则α终边所在象限是( ) A .第一象限 B .第二象限 C .第三象限D .第四象限C [由sin α<0可知α的终边落在第三、四象限及y 轴的负半轴上. 由tan α>0可知α的终边落在第一、三象限内. 故同时满足sin α<0,tan α>0的角α为第三象限角.] 2.(多选题)下列三角函数判断错误的是( ) A .sin 165°>0 B .cos 280°<0 C .tan 170°>0D .tan 310°>0BCD[∵90°<165°<180°∴sin 165°>0.又270°<280°<360°,∴cos 280°>0.又270°<310°<360°.∴tan310°<0,90°<170°<180°∴tan 170°<0.]3.已知角α终边过点P (1,-1),则tan α的值等于________. -1 [由三角函数定义知tan α=-11=-1.]4.已知角α终边过P ⎝⎛⎭⎫32,12,则cos α等于________.32 [由三角函数定义可知,角α的终边与单位圆交点的横坐标为角α的余弦值,故cos α=32.] 5.已知sin θ·tan θ<0,那么θ是第________象限角.二或三 [因为sin θ·tan θ<0,所以sin θ<0,tan θ>0或sin θ>0,tan θ<0,若sin θ>0,tan θ<0,所以θ在第二象限.若sin θ<0,tan θ>0,则θ在第三象限.]回顾本节知识,自我完成以下问题.1.三角函数值的大小与取点有关吗?与什么有关?[提示] 三角函数值的大小与终边所在的位置有关,与取点无关. 2.求一个角的三角函数值需确定几个量?分别是什么?[提示] 确定三个量,角的终边上异于原点的点的横、纵坐标及其到原点的距离. 3.已知角的大小,怎样利用定义求三角函数值? [提示] 确定出角的终边与单位圆的交点坐标.。
高中数学第7章三角函数7.2任意角的三角函数7.2.4第1课时诱导公式①②③④课件新人教B版必修第三

南京眼的桥身的完美对称 辽宁生命之环的完美对称
问题 你能否利用这种对称性,借助单位圆,讨论任意角 α 的终 边与 π±α,-α 有什么样的对称关系?
提示 π+α 的终边与 α 的终边关于原点对称;π-α 的终边与 α 的终边关于 y 轴对称;-α 的终边与 α 的终边关于 x 轴对称.
1.诱导公式① sin(α+k·2π)= sin α (k∈Z), cos(α+k·2π)= cos α (k∈Z), tan(α+k·2π)= tan α (k∈Z).
[解] (1)cos 210°=cos(180°+30°)
=-cos
30°=-
3 2.
(2)sin 114π=sin2π+34π
=sin 34π=sinπ-π4
=sin
π4=
2 2.
(3)sin-436π=-sin6π+76π =-sin 76π=-sinπ+π6=sin π6=12. (4)cos(-1 920°)=cos 1 920° =cos(5×360°+120°) =cos 120°=cos(180°-60°)=-cos 60° =-12.
3 .
解决给值求值问题的策略 1解决给值求值问题,首先要仔细观察条件式与所求式之间的 角、函数名称及有关运算之间的差异及联系. 2可以将已知式进行变形向所求式转化,或将所求式进行变形 向已知式转化.
[跟进训练]
2.已知 sin β=13,cos(α+β)=-1,则 sin(α+2β)的值为( )
=cosπ+π6=-cos π6=- 23.
法二:cos-316π=cos-6π+56π =cosπ-π6=-cos π6=- 23. (3)tan(-945°)=-tan 945°=-tan(225°+2×360°) =-tan 225°=-tan(180°+45°)=-tan 45°=-1.
高中数学第1章三角函数7.1正切函数的定义7.2正切函数的图像与性质高一数学

确;当点 P 在G︵H上时,tanα>0,sinα<0,cosα<0,故 D 选项错误.综
上,故选 C.
12/8/2021
第十二页,共十四页。
12/8/2021
第十三页,共十四页。
内容(nèiróng)总结
第一章 三角函数(sānjiǎhánshù)
No Image
12/8/2021
第十四页,共十四页。
D.xx∈R,x≠kπ+34π,k∈Z
12/8/2021
第九页,共十四页。
解析:选 D y=tanπ4-x=-tanx-π4,
由 x-π4≠kπ+π2(k∈Z),得 x≠kπ+34π(k∈Z).所以函数的定
义域为x|
x∈R,x≠kπ+34π,k∈Z.
12/8/2021
第十页,共十四页。
5.(2018·北京卷)在平面直角坐标系中,
A︵B,C︵D,E︵F,G︵H是圆 x2+y2=1 上的四段弧
(如图),点 P 在其中一段上,角 α 以 Ox 为始
边,OP 为终边,若 tanα<cosα<sinα,则 P 所
在的圆弧是( )
A.A︵B
B.C︵D
C.E︵F
D.G︵H
12/8/2021
第十一页,共十四页。
解析:选 C 逐个分析 A、B、C、D 四个选项,利用三角函
数的定义可得正确结论.当点 P 在A︵B上时,cosα=x,sinα=y,
∴cosα>sinα,故 A 选项错误;当点 P 在C︵D上时,cosα=x,sinα
=y,tanα=yx,∴tanα>sinα>cosα,故 B 选项错误;当点 P 在E︵F上
时,cosα=x,sinα=y,tanα=yx,∴sinα>cosα>tanα,故 C 选项正
高中数学 第一章 三角函数 1.2.1.1 三角函数的定义课时作业(含解析)新人教A版必修4-新人教

课时作业3 三角函数的定义——基础巩固类——一、选择题1.sin(-1 305°)的值是( B ) A.12B.22 C .-22D .-12解析:sin(-1 305°)=sin(-4×360°+135°)=sin135°=22. 2.已知角α的终边经过点P (m ,-3),且cos α=-45,则m 等于( C )A .-114B.114C .-4D .4解析:由题意可知,cos α=mm 2+9=-45,又m <0,解得m =-4.3.若sin θ<cos θ,且sin θ·cos θ<0,则角θ的终边位于( D ) A .第一象限 B .第二象限 C .第三象限 D .第四象限解析:由条件可知cos θ>0,sin θ<0,则θ为第四象限角,故选D. 4.如果角α的终边过点P (2sin30°,-2cos30°),则sin α的值等于( C ) A.12B .-12 C .-32D .-33解析:由题意得P (1,-3),它与原点的距离r =12+(-3)2=2,∴sin α=-32. 5.设a <0,角α的终边经过点P (-3a,4a ),则sin α+2cos α的值等于( A ) A.25B .-25 C.15D .-15解析:∵a <0,角α的终边经过点P (-3a,4a ),∴点P 与原点的距离r =-5a ,sin α=-45,cos α=35,∴sin α+2cos α=25,选A.6.已知点P ⎝⎛⎭⎫sin 3π4,cos 3π4落在角θ的终边上,且θ∈[0,2π],则θ的值为( D )A.π4B.3π4C.5π4D.7π4解析:θ∈[0,2π],根据三角函数定义可知sin θ=cos 3π4=sin ⎝⎛⎭⎫2π+π2-3π4=sin 7π4,cos θ=sin 3π4=cos ⎝⎛⎭⎫2π+π2-3π4=cos 7π4,故θ=7π4,故选D. 二、填空题7.已知角α的终边经过点M (π,-2),则sin 2α+cos 2α=1. 解析:x =π,y =-2,r =π2+2,∴sin 2α+cos 2α=⎝⎛⎭⎫y r 2+⎝⎛⎭⎫x r 2=2π2+2+π2π2+2=1.8.已知角α的终边落在直线y =-3x (x <0)上,则|sin α|sin α-|cos α|cos α=2.解析:角α的终边落在直线y =-3x (x <0)上, 在角α的终边上取一点P (x 0,-3x 0)(x 0<0), 有-3x 0>0.故P 在第二象限.所以|sin α|sin α-|cos α|cos α=sin αsin α--cos αcos α=1+1=2.9.函数y =sin x |sin x |+|cos x |cos x +tan x|tan x |的值域是{-1,3}.解析:当x 是第一象限角时,y =sin x sin x +cos x cos x +tan xtan x =3;当x 是第二象限角时,y =sin x sin x +-cos x cos x +tan x-tan x =-1;当x 是第三象限角时,y =sin x -sin x +-cos x cos x +tan xtan x =-1;当x 是第四象限角时,y =sin x -sin x +cos x cos x +tan x-tan x =-1.三、解答题10.已知角θ的终边上一点P (-3,m ),且sin θ=24m .求cos θ与tan θ. 解:由题意得sin θ=m m 2+3=24m , 若m =0,则cos θ=-1,tan θ=0. 若m ≠0,则m =±5.当m =5时,cos θ=-64,tan θ=-153; 当m =-5时,cos θ=-64,tan θ=153. 11.计算:(1)sin(-1 395°)cos1 110°+cos(-1 020°)sin750°. (2)已知tan α=13且0<α<π2,求sin (α-2π)·cos (2π+α)tan (α+4π)的值.解:(1)原式=sin(45°-4×360°)cos(30°+3×360°)+cos(60°-3×360°)sin(30°+2×360°)=sin45°cos30°+cos60°sin30°=22×32+12×12=6+14. (2)sin (α-2π)·cos (2π+α)tan (α+4π)=sin α·cos αtan α.因为tan α=13,且0<α<π2,所以可设α终边上一点坐标为(3x ,x ),x >0, 所以sin α=x (3x )2+x 2=1010, cos α=3x (3x )2+x 2=31010. 所以原式=1010×3101013=910.——能力提升类——12.若sin αtan α<0,且cos αtan α<0,则角α是( C )A .第一象限角B .第二象限角C .第三象限角D .第四象限角解析:由sin αtan α<0可知sin α,tan α异号,从而α是第二或第三象限角.由cos αtan α<0可知cos α,tan α异号,从而α是第三或第四象限角.综上可知,α是第三象限角.13.在△ABC 中,若sin A cos B tan C <0,则△ABC 是( C ) A .锐角三角形 B .直角三角形 C .钝角三角形D .锐角三角形或钝角三角形解析:因为sin A >0,所以cos B ,tan C 中一定有一个小于0,即B ,C 中一定有一个钝角,故△ABC 是钝角三角形.14.已知角α的终边经过点(3a -9,a +2),且sin α>0,cos α≤0,则实数a 的取值X 围是(-2,3].解析:∵点(3a -9,a +2)在角α的终边上,sin α>0,cos α≤0,∴⎩⎪⎨⎪⎧a +2>0,3a -9≤0,解得-2<a ≤3.15.已知角α的终边在直线y =-3x 上,求10sin α+3cos α的值. 解:设角α的终边上任一点为P (k ,-3k )(k ≠0), 则x =k ,y =-3k ,r =k 2+(-3k )2=10|k |.当k >0时,r =10k ,α是第四象限角,sin α=y r =-3k 10k =-31010,1cos α=r x =10k k =10,所以10sin α+3cos α=10×⎝⎛⎭⎫-31010+310=-310+310=0;当k <0时,r =-10k ,α为第二象限角,sin α=y r =-3k -10k =31010,1cos α=r x =-10kk =-10,所以10sin α+3cos α=10×31010+3×(-10)=310-310=0. 综上,10sin α+3cos α=0.。
高中数学第七章三角函数7.2任意角的三角函数7.2.4第3课时诱导公式习题课作业b

12/12/2021
第五页,共二十八页。
2.若 cos(π+α)=-13,那么 sin32π-α等于( A )
A.-13
B.13
C.2 32
D.-2 3 2
解析:∵cos(π+α)=-cosα=-13, ∴cosα=13,∴sin32π-α=-cosα=-13.
12/12/2021
第六页,共二十八页。
12/12/2021
第七页,共二十八页。
4.已知 a=tan-76π,b=cos234π,c=sin-334π,则 a,b,c 的
大小关系是( A )
A.b>a>c
B.a>b>c
C.b>c>a
D.a>c>b
解析:∵a=tan-76π=-tan6π=- 33,b=cos234π=cos4π= 22,
∴α 的终边位于第一象限内,∴α=31π0+2kπ(k∈Z),故选 C.
12/12/2021
第九页,共二十八页。
6.若 sin(π+α)+cosπ2+α=-m,则 cos32π-α+2sin(6π-α)的
值为( B )
A.-23m
B.-32m
C.23m
D.32m
12/12/2021
第十页,共二十八页。
第二十四页,共二十八页。
∴sin2α=12,∴sinα=±
2 2.
∵-π2<α<2π,∴α=4π或 α=-π4.
(1)当
α=4π时,由②,得
cosβ=
3 2.
∵β∈(0,π),∴β=π6;
12/12/2021
第二十五页,共二十八页。
(2)当
α=-4π时,由②,得
2016高中数学 三角函数 7.1正切函数的定义、7.2正切函数的图像与性质、7.3正切函数的诱导公式课件

1.对正切函数图像的理解 π (1)正切函数的图像是由被互相平行的直线 x= +kπ (k∈ Z) 2 所隔开的无数多支曲线组成的, 这些直线叫作正切曲线各支的 渐近线. π (2)正切函数的图像向上、向下无限延伸,但永远不和 x= + 2 kπ (k∈ Z)相交,与 x 轴交于点(kπ ,0)(k∈ Z).
π 2tan x, <x≤ π , 2
正切函数的性质
π 求函数 f(x)= tan 2x- 的定义域、 最小正周期和单调 3 区间. (链接教材 P40 练习 T2)
π π [解 ] 由题意,知 2x- ≠kπ + (k∈ Z), 3 2 kπ 5π 所以 x≠ + (k∈ Z), 2 12
第一章
三角函数
§7
正切函数
7.1 正切函数的定义
7.2 正切函数的图像与性质
7.3 正切函数的诱导公式
1.问题导航 (1)用正切线作正切函数的图像与作哪个三角函数的图像的方 法类似?该方法有什么优缺点? π π (2)正切函数的定义域能写成 - + kπ , + kπ (k∈ Z) 2 2 吗?为什么? (3)正切函数的诱导公式的实质是什么?
(3)正切函数的简图可用“三点两线”画出来, “三点”是指(0, π π π π 0), - ,-1 , , 1 ;“两线”是指 x= 和 x=- . 2 2 4 4 π 作简图时只需先作出一个周期中的两条渐近线 x=- , x= 2 π π π ,然后描出三点 (0,0), , 1 , - ,-1,用光滑的 2 4 4 曲线连接得一条曲线,再平行移动至各个周期内即可.
3π 3π 1. (1)函数 y= sin x 与 y=tan x 在区间 - 上的交点个 , 2 2 数是( A ) A. 3 C. 5 B.4 D. 6
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.2.1 三角函数的定义
一、选择题
1.下列三角函数判断错误的是( )
A.sin 165°>0 B.cos 280°>0
C.tan 170°>0 D.tan 310°<0
2.已知角α终边上异于原点的一点P且|PO|=r,则点P坐标为( )
A.P(sin α,cos α) B.P(cos α,sin α)
C.P(rsin α,rcos α) D.P(rcos α,rsin α)
3.角α的终边上有一点(-a,2a)(a<0),则sin α的值为( )
A.-55 B.255
C.55 D.-255
4.若θ是第二象限角,则( )
A.sin θ2>0 B.cos θ2<0
C.tan θ2>0 D.以上均不对
5.使得lg(cos αtan α)有意义的角α是( )
A.第一或第二象限角 B.第二或第三象限角
C.第三或第四象限角 D.第一或第四象限角
二、填空题
6.设α为第二象限角,则点P(cos α,sin α)在第________象限.
7.已知角α的终边经过点(3a-9,a+2),且cos α≤0,sin α>0,则实数a的取值范围是________.
8.若角α终边经过点P(-3,y),且sin α=34y(y≠0),则cos α=________.
三、解答题
9.已知角α的终边经过点P(1,3),
(1)求sin α+cos α的值;
(2)写出角α的集合S.
10.在平面直角坐标系中,角α的终边在直线3x+4y=0上,求sin α-3cos α+tan α的值.
参考答案
一、选择题
1.【答案】C
【解析】∵90°<165°<180°,∴sin 165°>0;
又270°<280°<360°,∴cos 280°>0;
又90°<170°<180°,∴tan 170°<0;
又270°<310°<360°,∴tan 310°<0,故选C.
2.【答案】D
【解析】设P(x,y),则sin α=yr,∴y=rsin α,又cos α=xr,x=rcos α,∴P(rcos α,rsin α),
故选D.
3.【答案】D
【解析】因为a<0,所以sin α=2a(-a)2+(2a)2=2a-5a=-
25
5
.
4.【答案】C
【解析】∵θ是第二象限角,∴2kπ+π2<θ<2kπ+π,∴kπ+π4<θ2
θ
2
>0.
5.【答案】A
【解析】要使原式有意义,必须cos αtan α>0,即需cos α,tan α同号,所以α是第一或第二
象限角.
二、填空题
6.【答案】二
【解析】∵α为第二象限角,∴cos α<0,sin α>0.
7.【答案】-2<a≤3
【解析】由 cos α≤0,sin α>0,得 3a-9≤0,a+2>0,
解得-2<a≤3.
8.【答案】-
3
4
【解析】∵过点P(-3,y),∴sin α=y3+y2=
3
4
y.
又y≠0,∴13+y2=34,
∴|OP|=3+y2=43=433=r,
∴cos α=xr=-3433=-
3
4
.
三、解答题
9.解:(1)由点P的坐标知,r=|OP|=2,x=1,y=3,
∴sin α=32,cos α=12,
∴sin α+cos α=
3+1
2
.
(2)由(1)知,在0~2π内满足条件的角α=
π
3
,
∴角α的集合S=α α=2kπ+π3,k∈Z.
10.解:①当α的终边在第二象限时,取终边上的点P(-4,3),OP=5,
sin α=
35,cos α=-45=-45,tan α=3-4=-3
4
,
所以sin α-3cos α+tan α=35+125-34=
9
4
.
②当α的终边在第四象限时,取终边上的点P(4,-3),OP=5,
sin α=-
35,cos α=45,tan α=-34=-3
4
,
所以sin α-3cos α+tan α=-35-125-34=-
15
4
.
