02电工学(电工技术)第二版魏佩瑜第二章电路的分析方法答案
电工技术第2章习题答案
2.1.1 选择题（1）在图2-73所示电路中，发出功率的元件是Ａ。
（Ａ）仅是5Ｖ的电源（Ｂ）仅是2Ｖ的电源（Ｃ）仅是电流源（Ｄ）电压源和电流源都发出功率（Ｅ）条件不足图2-73题2.1.1（1）图图2-74题2.1.1（2）图（2）在图2-74所示电路中，当增大时，恒流源两端的电压Ｕ。
（A）不变（B）升高（C）降低（3）在图2-75所示电路中，当开关S闭合后，P点的电位。
（A）不变（B）升高（C）为零（4）在图2-76所示电路中，对负载电阻R而言，点画线框中的电路可用一个等效电源代替，该等效电源是。
（A）理想电压源（B）理想电流源（C）不能确定图2-75题2.1.1（3）图图2-76题2.1.1（4）图(5) 实验测的某有源二端线性网络的开路电压为10V，当外接3Ω的电阻时，其端电压为6V，则该网络的戴维南等效电压的参数为(C)。
(a)6V，R0=3Ω(b)8V，R0=3Ω (c)10V，R0=2Ω(6) 实验测得某有源二端线性网络的开路电压为6V，短路电流为3A。
当外接电阻为4Ω时，流过该电阻的电流I为( A )。
(a)1A (b)2A (c)3A(7) 在图2-77所示电路中，已知1=4V，2=4V，当2单独作用时，电阻R中的电流为1，那么当1单独作用时，电压是（A）（A）1V （B）3V （C）-3V图2-77题2.1.1（7）图（8）一个具有几个结点，b条支路的电路，其独立的方程为（B）a)（1）个 b)（1）个（9）一个具有几个结点，b条支路的电路，要确定全部支路电流，最少要测量（B）a)（1）次 b)（1）次（10）一个具有n个结点，b条支路的电路，要确定全部支路电压，最少要测量（A）a)（1）次 b)（1）次（11）电阻并联时，电阻值越大的电阻：（A）a)消耗功率越小； b)消耗功率越大。
（12）两个电阻并联时，电阻值，越小的电阻（B）a)该支路分得的电流愈小； b)该支路分得的电流愈大。
《电路与模拟电子技术》第二版第二章习题解答
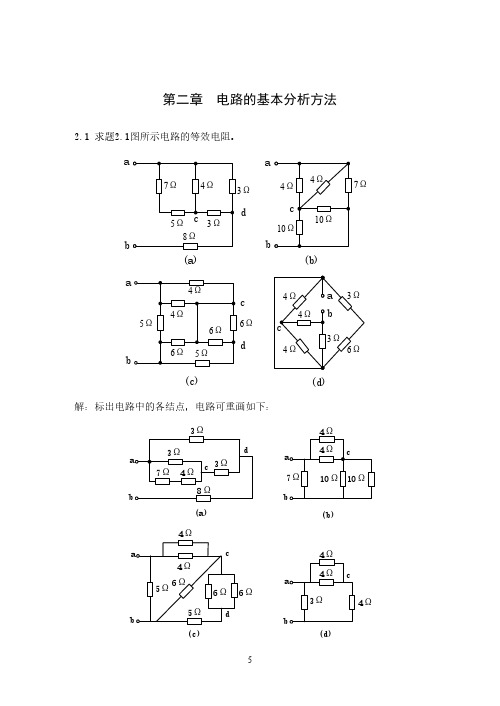
第二章电路的基本分析方法2.1 求题2.1图所示电路的等效电阻。
解：标出电路中的各结点，电路可重画如下：(b)(a)(c)(d)6Ω7Ω3Ωa aabbbddcb(a)(d)(c)(b)6Ωb4Ω（a ）图 R ab =8+3||[3+4||（7+5）]=8+3||（3+3）=8+2=10Ω（b ）图 R ab =7||(4||4+10||10)=7||7=3.5Ω（c ）图 R ab =5||[4||4+6||(6||6+5)]=5||(2+6||8)=5||(2+3.43)=2.6Ω（d ）图 R ab =3||(4||4+4)=3||6=2Ω（串联的3Ω与6Ω电阻被导线短路）2.2 用电阻的丫-△的等效变换求题2.2图所示电路的等效电阻。
解：为方便求解，将a 图中3个6Ω电阻和b 图中3个2Ω电阻进行等效变换，3个三角形连接的6Ω电阻与3个星形连接的2Ω电阻之间可进行等效变换，变换后电路如图所示。
（a ）R ab =2+(2+3)||(2+3)=4.5Ω（b ） R ab =6||(3||6+3||6)=6||4=2.4Ω2.3 将题2.3图所示电路化成等效电流源电路。
baba(b)(a)题2.2图(b)(a)题2.3图b abΩ(b)解：（a ）两电源相串联，先将电流源变换成电压源，再将两串联的电压源变换成一个电压源，最后再变换成电流源；等效电路为（b ）图中与12V 恒压源并联的6Ω电阻可除去（断开），与5A 恒流源串联的9V 电压源亦可除去（短接）。
两电源相并联，先将电压源变换成电流源，再将两并联的电流源变换成一个电流源，等效电路如下：2.4 将题2.4图所示电路化成等效电压源电路。
解：（a ）与10V 电压源并联的8Ω电阻除去（断开），将电流源变换成电压源，再将两串联的电压源变换成一个电压源，再变换成电流源，最后变换成电压源，等效电路如下：（b ）图中与12V 恒压源并联的6Ω电阻可除去（断开），与2A 恒流源串联的4Ω亦可(a)(b)题2.4图aa bababababbbb b除去（短接），等效电路如下：2.5 用电源等效变换的方法，求题2.5图中的电流I 。
电工技术 第2版 第二章 电路的分析方法
第一节 支路电流法 第二节 回路电流法 第三节 节点电压法 第四节 叠加定理 第五节 等效电源定理
第一节 支路电流法
支路电流法以n个支路电流为未知量， 基本思路是 应用基尔霍夫定律列出与支路电流数目相等的n个独立方 程式，再联立求解出支路电流。
应用支路电流法解题步骤： （1）首先标明各待求支路电流参考方向，并规定回 路绕行方向； （2）应用基尔霍夫电流定律列出（m－1）个节点电 流方程； （3）应用基尔霍夫电压定律列出［n－(m－1)］个 独立的回路电压方程式； （4）联立这n个方程组求解各支路电流。 （5）根据已求得的支路电流，计算其他电量，比如 元件的电压和功率等。
设方两向， 个，闭根合据回基, 路尔的霍绕夫行电方压向定为律顺（时KV针L）, 对回路Ⅰ，有
对回路Ⅱ，有
代入各项数据： 解方程组，得：
根据支路电流和回路电流的关系可得：
[例2-4]如图2-4所示电路，已知Us1=10V，Us2=2V，Is=5A，R1=1 ，R2=R3=R4=2 。用回路电流法求支路电流。
（3）联立方程组，求解回路电流；
（4）依据支路电流与回路电流的关系，求解各支 路电流和其他电量。
[例2-3]如图2-3所示电路为例，已知Us1=20V，Us2=30V， Us3=10V，R1=10 ，R2=20 ，R3=10 ，R4=50 。用回路电 流法求支路电流。 [解]：选取两个网孔作为回路，以顺时针为参考方向，标出回 路电流 Il1 ，Il 2以及各支路电流I1 ，I2 ，I3 。
E1 E2 I1R1 I2 R2
对回路Ⅱ，有
E2 I 2 R2 I3R3
解方程组，得： 1=0.667A,2=1.333A,3=2A
电阻上消耗的功率： I12 R1 0.667 2 6 2.7W
《电工学》电路的分析方法习题答案
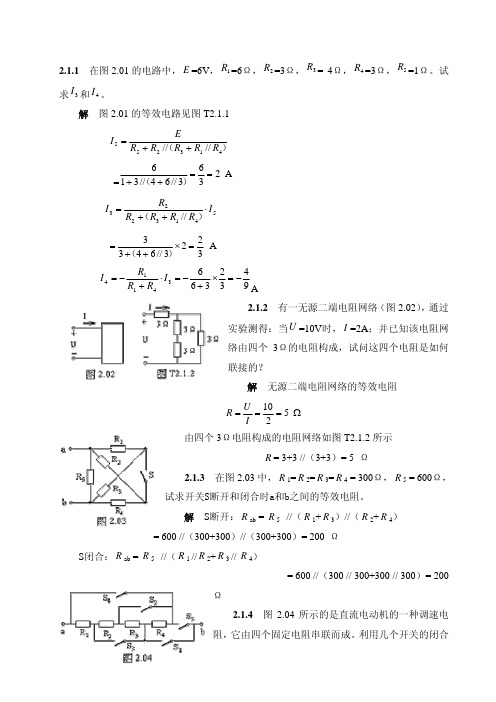
2.1.1 在图2.01的电路中，E =6V ，=6Ω，=3Ω，= 4Ω，=3Ω，=1Ω。
试求和。
1R 2R 3R 4R 5R 3I 4I 解 图2.01的等效电路见图T2.1.1）（413255////R R R R R EI ++==A2363//64//316==++）（5413223//I R R R R R I ⋅++=）（A3223//6433=×++=）（943236634114−=×+−=⋅+−=I R R R I A 2.1.2 有一无源二端电阻网络（图2.02），通过实验测得：当U =0V时，1I =2A ；并已知该电阻网络由四个3Ω的电阻构成，试问这四个电阻是如何联接的？解 无源二端电阻网络的等效电阻Ω===5210I U R由四个3Ω电阻构成的电阻网络如图T2.1.2所示R = 3+3 //（3+3）= 5 Ω2.1.3 在图2.03中，R 1=R 2=R 3=R 4 = 300Ω，R 5 = 600Ω，试求开关S断开和闭合时a和b之间的等效电阻。
解 S 断开：R ab = R 5 //（R 1+R 3）//（R 2+R 4）= 600 //（300+300）//（300+300）= 200 Ω S 闭合：R ab = R 5 //（R 1 //R 2+R 3 // R 4）= 600 //（300 // 300+300 // 300）= 200 Ω2.1.4 图2.04所示的是直流电动机的一种调速电阻，它由四个固定电阻串联而成。
利用几个开关的闭合或断开，可以得到多种电阻值。
设四个电阻都是1Ω，试求在下列三种情况下a，b两点间的电阻值：（1）S 1和S 5闭合，其他断开；（2）S 2，S 3和S 5闭合，其他断开；（3）S 1，S 3和S 4闭合，其他断开。
解 （1）S 1和S 5闭合：R ab =R 1 +R 2 +R 3 = 3 Ω （2）S 2，S 3和S 5闭合： R ab =R 1 +R 2 //R 3 //R 4 =Ω311（3）S 1，S 3和S 4闭合：R ab = R 1 //R 4 = 0.5 Ω2.1.5 图2.05是一衰减电路，共有四档。
电力电子技术(第二版)第2章答案
电力电子技术 ( 第二版 ) 第 2 章答案第 2 章可控整流器与有源逆变器习题解答2-1 拥有续流二极管的单相半波可控整流电路，电感性负载，电阻为5Ω,电感为 0.2H，电源电压U2为 220V，直流均匀电流为10A，试计算晶闸管和续流二极管的电流有效值，并指出其电压定额。
解：由直流输出电压均匀值U d的关系式：1 cosU d0.45U 22已知直流均匀电流I d为10A，故得：U d I d R 10 5 50A能够求得控制角α为：2U d1250cos0.451 00.45U2220则α =90°。
因此，晶闸管的电流有效值求得，I VT1I d2d t I d 2I d1I d 5A2222续流二极管的电流有效值为： I VD R I d 8.66 A2晶闸管蒙受的最大正、反向电压均为电源电压的峰值U M2U2，考虑 2~3 倍安全裕量，晶闸管的额定电压为U TN 2~ 3U M 2~ 3 311 622~ 933V续流二极管蒙受的最大反向电压为电源电压的峰值U M2U2，考虑 2~3 倍安全裕量，续流二极管的额定电压为U TN2~ 3U M2~ 3 311 622~ 933V2-2 拥有变压器中心抽头的单相双半波可控整流电路如图2-44 所示，问该变压器能否存在直流磁化问题。
试说明晶闸管蒙受的最大反向电压是多少？当负载是电阻或许电感时，其输出电压和电流的波形与单相全控桥时能否相同。
解：因为单相双半波可控整流电路变压器二次测绕组中，正负半周内上下绕组内电流的方向相反，波形对称，其一个周期内的均匀电流为零，故不会有直流磁化的问题。
剖析晶闸管蒙受最大反向电压及输出电压和电流波形的状况：（1）以晶闸管VT2为例。
当VT1导通时，晶闸管VT2经过VT1与2个变压器二次绕组并联，因此 VT2蒙受的最大电压为 2 2U 2。
（2）当单相全波整流电路与单相全控桥式整流电路的触发角相同时，关于电阻负载：（0 ~ ）时期无晶闸管导通，输出电压为0；（~）时期，单相全波电路中 VT1 导通，单相全控桥电路中VT1、VT4导通，输出电压均与电源电压u2相等；(~)时期，均无晶闸管导通，输出电压为0；(~ 2)时期，单相全波电路中VT2导通，单相全控桥电路中VT2、VT3导通，输出电压等于u2。
电工技术第二章 电路的分析方法习题解答
第二章电路的分析方法本章以电阻电路为例，依据电路的基本定律，主要讨论了支路电流法、弥尔曼定理等电路的分析方法以及线性电路的两个基本定理：叠加定理和戴维宁定理。
1．线性电路的基本分析方法包括支路电流法和结点电压法等。
（1）支路电流法：以支路电流为未知量，根据基尔霍夫电流定律（KCL）和电压定律(KVL)列出所需的方程组，从中求解各支路电流，进而求解各元件的电压及功率。
适用于支路较少的电路计算。
（2）结点电压法：在电路中任选一个结点作参考结点，其它结点与参考结点之间的电压称为结点电压。
以结点电压作为未知量，列写结点电压的方程，求解结点电压，然后用欧姆定理求出支路电流。
本章只讨论电路中仅有两个结点的情况，此时的结点电压法称为弥尔曼定理。
2 ．线性电路的基本定理包括叠加定理、戴维宁定理与诺顿定理，是分析线性电路的重要定理，也适用于交流电路。
（1）叠加定理：在由多个电源共同作用的线性电路中，任一支路电压（或电流）等于各个电源分别单独作用时在该支路上产生的电压（或电流）的叠加（代数和）。
①“除源”方法（a）电压源不作用：电压源短路即可。
（b）电流源不作用：电流源开路即可。
②叠加定理只适用于电压、电流的叠加，对功率不满足。
（2）等效电源定理包括戴维宁定理和诺顿定理。
它们将一个复杂的线性有源二端网络等效为一个电压源形式或电流源形式的简单电路。
在分析复杂电路某一支路时有重要意义。
①戴维宁定理：任何一个线性含源的二端网络，对外电路来说，可以用一个理想电压源和一个电阻的串联组合来等效代替，其中理想电压源的电压等于含源二端网络的开路电压，电阻等于该二端网络中全部独立电源置零以后的等效电阻。
②诺顿定理：任何一个线性含源的二端网络，对外电路来说，可以用一个理想电流源和一个电阻的并联组合来等效代替。
此理想电流源的电流等于含源二端网络的短路电流，电阻等于该二端网络中全部独立电源置零以后的等效电阻。
3 ．含受控源电路的分析对含有受控源的电路，根据受控源的特点，选择相应的电路的分析方法进行分析。
电工学-第二章习题答案
第二章 电路的分析方法2.1.1 在图2.01的电路中，V 6=E ，Ω=61R ，Ω=32R ，Ω=43R ，Ω=34R ，Ω=15R 。
试求3I 和4I 。
4I ↓图2.01解：图2.01电路可依次等效为图（a ）和图（b ）。
R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。
Ω=1R A2S =图2.12解：根据电压源与电流源的等效变换，图2.12所示电路可依次等效为图（a ）和图（b ），由图（b ）可求得A 2.15.023=+=I由图（a ）可求得：A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中，（1）当将开关S 合在a 点时，求电流1I ，2I 和3I ；（2）当将开关S 合在b 点时，利用（1）的结果，用叠加定理计算电流321,I I I 和 。
I图2.19I (a)I (b)解：（1）当将开关S 合在a 点时，图2.19所示电路即为图（a ），用支路电流法可得：=+=+=+12042130423231321I I I I I I I 解得：===A 25A 10A 15321I I I(2)开关S 合在b 点时，利用叠加原理图2.19所示电路可等效为图（a ）和图（b ），其中图（a ）电路中130V 和120V 两个电压源共同作用时所产生的电流已在（1）中求得，即：A 151=,I A 102=,I A 253=,I由图3（b ）可求得：A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则：A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20（a ）所示，V 10ab ,,V 124321=====U R R R R E 。
电工技术习题答案第二章
第二章电路的分析方法习题参考答案1.用支路电流法求I1、I2、I3, U1、U2、U3。
图2-12 习题1的电路解：根据KCL 列方程组：123112312134 I A I AI A =--=-=-==--=-根据KVL列方程组123642628426 U V U V U V =-==+==+=所以得：I1=-2A、I2=2A、I3=-4A, U1=2V、U2=8V、U3=6V 2.求图2-13所示电路中的I S和U 。
图2-13 习题2的电路解：如图所示设流过2Ω电流为I 1,流过5Ω电流为I 2,得：()12126323*361515356155*615ABS AB AC I A U V I A I I I AU U U V===+===∴=+==-=--=-则3.电路如图2-14所示，已知E 1=8V ，E 2=4V ，E 3=6V ，R 1=2Ω，R 2=4Ω，R 3=1Ω，求各支路电流。
图2-14 习题3的电路解：根据KCL,KVL 列方程组 11222133311321R I E R I E E R I I E I I I +-=++=+=把已知条件代入，解方程组得：I 1=1.429A, I 2=2.286A, I 3=-0.857A4.电路如图2-15所示，用叠加原理求各支路电流。
(I 1=0.2A, I 2=1.2A)图2-15 习题4的电路解：原图可以等效为以下两个电路的叠加：则有：''12200.81015I I A ===+ 及 ''''12''''1210151I I I I =-+=得''''120.6,0.4I A I A =-= '''111'''2220.21.2I I I AI I I A ∴=+==+=5. 如图2-16所示电路，已知U S1=U S2=U S3=1V ，R 1=R 2=R 3=1Ω，用叠加定理求流过Ｒ1的电流。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 电路的分析方法
P39 习题二 2-1
题2-1图 题2-1等效图 解：
334424144I R R I R I R R I ⋅=⋅+⎪⎪⎭
⎫
⎝⎛+⋅ ①
33341445I R E I I R R I R ⋅-=⎥⎦
⎤
⎢⎣⎡++ ② 344443363I I I I =+⎪⎭⎫
⎝⎛+，344215I I = 34815I I =
①
33444621I I I I -=⎪⎭
⎫
⎝⎛++，345623I I -=
3410123I I -=，34506015I I -=，A 29
30
,302933=
=I I 代入 ①A 29
16,
29
3081544=
⨯=⨯I I 另外，戴维南等效图
A 29549
296I 5==
回归原图 3355I R I R E ⋅=⋅-，所以 A 29
3042954
163=⨯
-=I 2-2答 由并联输出功率400w 所以每个R
获得功率R
U P 2
,W 1004400==
)(484,2201002
Ω==R R
改串联后：W 254
22220P P 222=⨯===总消耗输出R U 2-3
题2-3等效图
Ω=++⨯=++⋅=
313212123121112111R R R R R R ，Ω=++⨯=++⨯=13213
223121123122R R R R R R
Ω=++⨯=++⋅=
2
1
3213123121123133R R R R R R
)(913910312
953125225
231ab Ω=+=+=+
⨯
+
=R 2-4
题2-4 △-Y 变换（一）图
1Ω
a
2
b
c
题2-4 △-Y 变换（二）图
题2-4 △-Y 变换（三）图
题2-4 等效星型图
2-5 解：
c
题2-5 （a)图
2-6 用两种电源等效互换的方法，求电路中5Ω电阻上消耗的功率。
题2-5 （b）图
题2-5 （c）图
题2-5 （d）图
习题2-6图
解：由两源互换，原图可变为下图
A 19
4
215=--，所以：W 551252=⨯=⋅=R I P 2-7
题2-7 图
21I
解：① I
I I
I
I I 44.011648.012010221=--=++
I
I I I I I I 102905150102121=-=-=++ I I I 15)(44021=+-，I 16450=
A 8
225
A 16450==
I 16
2250
1501=-I 所以 ：A 8
75A 1615016225024001==-=I
16
4500
292=-I A 435161401645004640164500401162==-=-⨯=I
② i
sg i
R I R E U 12
∑∑+∑
=
V 2225418.0310290150414.018.0110
4.0116
8.0120=+++=++++=U
所以：A 8
225414450=⨯==R U I
W 3164162254822522
2
R ≈=
⨯⎪⎭
⎫
⎝⎛==R I P 2-8 试用支路电流法和节点电压法求如图所示各支路的电流。
题2-8图
①
1
2133215050251000I I I I I I I =-=-=++ 1
1331)3(1015)(507502I I I I I -⨯=-==+
A 1,A 2
1
321=-==I I I
② i
sg i
R I R E U 12
∑∑+∑
=
V 5050
3501505015015010
5010050255025==+++++=U
所以： 123A 2
1
5025,A 150
100I U I U
I =-=-=
=-= 2-9 用叠加原理求图中的电流I 。
U
25V
题 2-8参考方向图
题2-9 图
解：由叠加原理可知原图可变为下（a ）、（b ）两图之和。
"'I I I +=
（a)中 A 5
2
232'-=+-
=I （b)中 A 5
9A 3233"=⨯+=I
所以 A 5
11-=I
2-10 用叠加原理求如图所示电路中的电压ab U 及元件ab 消耗的功率。
（电阻单位为Ω）
（a ）
)(b
题2-10图
解：由叠加原理可有：
（a)图中：A 16
612'=+=
I ，
（b ）图中A 5.256
66
"=⨯+=I 所以：A 5.3"'=+=I I I
故 W 5.735.321V ;2165.32ab ab =⨯==-=⨯-=R I P U
2-11 题图a ）中，V 10,,V 12ab 4321=====U R R R R E 。
若将理想电压源去掉后，如图b ），试问此时=ab U ？
Ω
Ω （a)
+
（b
解：由叠加原理可知，b)图等于a)图减c)图，即：两电流源共同作用的响应，等于总的响应减去电压源单独作用的响应。
由已知，V 10=U 而C)图中 ，V 34"=⨯=R R
E
U 所以：V 7310"'=-=-=U U U
2-12 求：（1）题图中端点a 、b 处的戴维南和诺顿等效电路。
（2）如果用1Ω电流表跨接在a 、b 处，将通过多大电流？
R
=
—
c)
题2-12图 解：
Ω=+⨯⨯=3
4
21212ab R V 3
10
1211022110b a ab
=⨯+-⨯+=-=V V U
所以，等效戴维南电路与诺顿电路如下：
Ω=12R 时 A 7103
4113
10ab =+⨯=
I
所以电流表的读数约为1.43A
2-13 应用戴维南定理求图中1Ω电阻的电流。
解： 由于1Ω为研究对象，所以与电流源串联的2Ω和理想电压源并联的5Ω每个电阻对1Ω不起作用，因此电路图为（b ）
a
b
a
b
等效戴维南电路
等效诺顿电路
图
①将1Ω电阻开路，如（c ）图，V 3010104b a ab =-⨯=-=V V U
②去源后，如（d ）图：
Ω=4ab R
戴维南等效电路如（e ）图
A 61
430
=+=
I 2-14 试用戴维南定理和诺顿定理求图中负载L R 上的电流。
Ω
(b)
4
Ω
（c ）
4Ω
（d ）
1Ω I
（e ）
题2-14图
解：由戴维南定理，等效图如下图（a ），
①V 1102
220ab ==U
②去源 Ω=⨯=25100
5050ab R
化简后见（b ）图
A 15
22
5025110L =+=
I 而诺顿等效电路如图（c ）：A 5
2250
2200==I
a b
ab +
-
（a ）
50Ω b a
（b ）
A 15
22
522315025250=⨯=+=
I I 2-15
解：
题2-15图 ①当V 120,==U I ②当0=U ，A 310412
3
m I =⨯=
故当),0(+∞∈R 时，R 中的I 与U 的点的轨迹为直线中在第一象限中的线段。
50Ω
b
a
I （c ）
a ）
b ）。