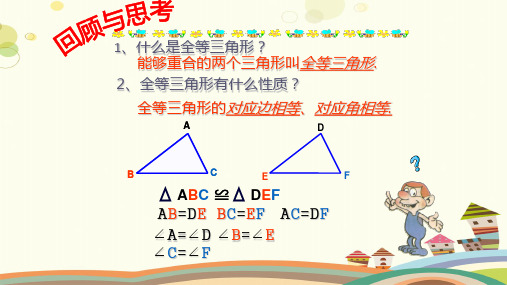
北师大版七年级数学下册 第4章 百分导学 P50 4.3 探索三角形全等的条件(第2课时) 练习答案
七年级数学下册 4.3《探索三角形全等的条件》教案 北师大版(2021学年)

七年级数学下册4.3《探索三角形全等的条件》教案(新版)北师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(七年级数学下册4.3《探索三角形全等的条件》教案(新版)北师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为七年级数学下册4.3《探索三角形全等的条件》教案(新版)北师大版的全部内容。
《探索三角形全等的条件》教学目标一、知识与技能1.掌握三角形全等的条件;2.会证明简单的三角形全等问题;二、过程与方法1.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;2.通过观察、动手操作、类比、推断等数学活动,积累数学活动经验,感受数学思考过程的条理性,发展形象思维;三、情感态度和价值观1.通过自主学习的发展体验获取数学知识的感受,培养学生勇于创新,多方位审视问题的创造技巧;2.通过分组讨论学习,体会合作学习的兴趣;教学重点探究三角形全等的条件;教学难点寻求三角形全等的条件;教学方法引导发现法、启发猜想课前准备教师准备课件、多媒体学生准备练习本课时安排3课时教学过程一、导入小明作业本上画的三角形被墨迹污染了,她想画一个与原来完全一样的三角形,她该怎么办?请你帮助小颖想一个办法,并说明你的理由?注意:与原来完全一样的三角形,即是与原来三角形全等的三角形.要画一个三角形与小明画的三角形全等。
需要几个与边或角的大小有关的条件呢?一个条件?两个条件?三个条件?···让我们一起来探索三角形全等的条件二、新课做一做1.只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?2.给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做.(1)三角形的一个内角为30° ,一条边为3cm;(2)三角形的两个内角分别为30°和50° ;(3)三角形的两条边分别为4cm,6cm.结论:只给出一个条件或两个条件时,都不能保证所画出的三角形一定全等.议一议如果给出三个条件画三角形,你能说出有哪几种可能的情况?有四种可能:三条边、三个角、两边一角和两角一边.做一做(1)已知一个三角形的三个内角分别为40° ,60°和80° ,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?结论:三个内角对应相等的两个三角形不一定全等.(2)已知一个三角形的三条边分别为4 cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?754三边分别相等的两个三角形全等,简写为“边边边"或“SSS”。
北师版数学七年级下册 利用“角边角”“角角边”判定三角形全等

1. 在△ABC 和△DEF 中,AB=DE,∠B=∠E,要使
△ABC≌△DEF,则下列补充的条件中错误的是( A )
A.AC=DF
B.BC=EF
C.∠A=∠D
D.∠C=∠F
2. 在△ABC 与△A′B′C′ 中,已知∠A=44°,∠B=67°,
∠C′=69°,∠A′=44°,且 AC=A′C′,那么这两个三角
∠B =∠B' (全等三角形对应角相等).
因所在为以△∠AABDAD⊥D和BBC=△∠,AAA'B''DD'D''B⊥' 中'.B,'C',全边等上的三高角也形B相对等应.
∠ADB =∠A'D'B' (已证),
DC A′
∠B =∠B' (已证),
AB = AB (已证),
B′
D′ C′
所以△ABD≌△A'B'D'(AAS). 所以 AD = A'D'.
几何语言: 在△ABC 和△A′B′C′ 中,
∠A =∠A′(已知),
A
A′
AB = A′B′(已知),
∠B =∠B′(已知),
B
C B′
C′
所以△ABC≌△A′B′C′(ASA).
典例精析
例1 已知:∠ABC=∠DCB,∠ACB=∠DBC.
试说明:△ABC≌△DCB. 解:在△ABC 和△DCB 中,
3 cm
60°
45°
思考: 这里的条件与问题 1 中的条件有什么相同点与不同
点?你能将它转化为问题 1 中的条件吗?
60°
75°
归纳总结
北师大版初中数学七年级下册《探索三角形全等的条件》(第二课时)说课稿

《探索三角形全等的条件》(第二课时)说课稿一个好的数学问题,既能揭示课堂的教学内容,又能充分调动学生的积极性。
本节设置了问题,把知识串联起来,以引导学生的思维。
学生在思考问题的过程中,探索掌握全等三角形的判别条件,从而完成本节的教学目标。
新课标下的数学教学,既要为学生的今天的学习服务,又要为学生明天的学习奠基,新课改倡导学生主动参与、乐于探究、勤于动手,获取新知的能力、分析和解决问题的能力,以及合作与交流的能力。
坚持“以学生发展为本”的教学设计理念,把学生的起点作为教师的起点,把传授知识服务于学生有个性、可持续、全面和谐的发展,使每一堂课都成为不可重复的激情与智慧综合的过程。
一、教材分析1、教学内容《探索三角形全等的条件》是北师大版初中数学七年级下册第五章第四节的内容。
本节共三课时,我所说的第二课时的内容包括(1)经历问题探索三角形全等的条件归纳总结出“角边角、角角边”定理(2)“角边角、角角边”定理的运用,(3)掌握判定三角形全等的另外两个条件。
2、教学内容的地位及作用(1)三角形全等的判定是中学数学十分重要内容之一,是证明线段相等、角相等的重要方法,是今后几何学习的基础。
本节课是探索三角形全等条件的第二课时,在前面的认知基础上展开继续探索,学好了将为下节课探索三角形全等的其他条件打下坚实的基础;同时为今后探索直角三角形全等的条件以及三角形相似的条件提供很好模式和方法,由于几何证明在新课标中要求不同,本内容在学生学习证明的思想方法中显出更加重要的作用。
(2)通过探索三角形全等的“角边角、角角边”条件,可以让学生经历和体验知识的形成过程,了解数学研究问题的方法,领会数学思想,获得数学活动的经验;同时发展学生的空间观念,培养学生推理意识和对推理过程的理解,发展推理能力。
3、教学目标由于教学的学生是初一的孩子,对几何的认识还很限,这是第一次系统的学习三角形,所以根据所教的学生已有的认知基础,以及教学内容的地位和作用,我拟定以下教学目标:(1)知识目标:经历探索三角形全等条件的过程,掌握三角形全等的“角边角、角角边”条件并初步学会运用。
初中数学北师大七年级下册第四章三角形探索三角形全等条件PPT
3000
60o 60o 60o
结论:三个内角对应相等的两个三角形
不一定全等.
探索三角形全等的条件
三个条件 --三条边
2、已知三角形三条边分别是 4cm,5cm,7cm,画出这个三角形,把所画的
三角形分别剪下来,并与同伴比一比,你会发现什么?
三边对应相等的两个三角形全等!
简写为:“边边边”或“SSS”
300
60o 60o
60o
探索三角形全等的条件
两个条件--两条边
2、三角形的两条边分别是:4cm,6cm
探索三角形全等的条件
两个条件--一角一边
3、 三角形的一个角为30°,一条边为6cm
30o
6cm
论画归
?
三 角 形 , 你 得 出 了 怎 样 的 结
纳
: 通 过 探 究 给 出 两 个 条 件
你能用三角形的稳定性来 说明SSS公理吗?
四边形不具有稳定性,你能想出什么方法 让它们的形状不发生改变吗?
通过这节课的学习活动你有哪些收获?
(1)只给出一个条件或两个条件时,都不能保 证两个三角形全等.
(2)三个内角对应相等的两个三角形不一 定全等.
(3)边边边公理:三边对应相等的两个三 角形全等,简写为“边边边”或“SSS”.
A
证明:∵D是BC的中点
∴BD=CD 在△ABD与△ACD中
B
C
D
结论:从这题的证明中
AB=AC(已知)
可以看出,证明是由题
BD=CD(已证) AD=AD(公共边) ∴△ABD≌△ACD(SSS)
设(已知)出发,经过一 步步的推理,最后推出 结论正确的过程.
A
A
D
(北师大版)七年级数学下册:第四章三角形4.3第2课时利用“角边角”“角角边”判定三角形全等授课典案

图4-1-29处理方式:可让学生快乐地回答.【师】同学们都非常喜欢读书,那你们家里一定有漂亮的典案二导学设计4.3探索三角形全等的条件(2)一、学习目标1、探索出三角形全等的条件“ASA ”和“AAS ”并能应用它们来判定两个三角形 是否全等。
2、体会利用转化的数学思想和方法解决问题的过程。
3、能够有条理的思考和理解简单的推理过程,并运用数学语言说明问题。
4、敢于面对数学活动中的困难,并能通过合作交流解决遇到的问题。
二、学习重点掌握三角形全等条件“ASA ”和“AAS ”,并能应用它们来判定两个三 角形是否全等。
三、学习难点 探索 “AAS ”的条件 四、学习设计: 1.温故而知新如图,在△ABC 中,AB =AC ,AD 是BC 边上的中线,△ABD 和△ACD 全等吗? 你能说明理由吗? 2、创设情景,引入新课提问:一张三角形的纸片,被斯成三部分,究竟用那部分可 画出原图一样的三角形? 探究练习1. 两角和它们的夹边将学生分组小组分工合作完成下列问题: 画一个△ABC 使它满足以下条件: 第一组:∠A=90°, ∠B=30°,AB=10cm 第二组: ∠A=60°, ∠B=45°,AB=9cm学生动手操作,完成问题后,小组交流比较,看看能得到什么结论?学生表述,老师板书: ________________________对应相等的两个三角形全等;(简写为_____________或者 ______________) 探究练习2.如果“两角及一边”条件中的边是其中一角的对边,比如三角形的两个内角分别是60° 和45°,一条边长为10cm ,情况会怎样呢?ABCD(1) 如果角60°所对的边为10cm ,你能画出这个三角形吗?(2) 如果角45°所对的边为10cm ,那么按这个条件画出的三角形都全等吗?结论___________________________对应相等的两个三角形全等简写为________________________________思考:若两个三角形具备两角和其中一个角的对边分别相等,哪么这两个三角形全等,你认为对吗?能举例说明吗?3.举例应用:例1.如图,已知AO=DO ,∠AOB 与∠DOC 是对顶角,还需补充条件______________=_______________,就可根据“ASA ”说明△AOB ≌△DOC ;或者补充条件_______________=_______________,就可根据“AAS ”,说明△AOB ≌△DOC 。
北师大版七年级数学下册4.3 第2课时 利用“角边角”“角角边”判定三角形全等(导学案)

4.3 第2课时 利用“角边角”“角角边”判定三角形全等【学习目标】1.掌握“角边角”、“角角边”作为条件判断两个三角形全等; 2.利用“角边角”、“角角边”的判定方法解决简单的实际问题。
【使用说明与学法指导】1.先精读一遍教材P100-P101页,利用“角边角”、“角角边”的判定方法解决简单的实际问题。
针对课前预习二次阅读教材,并回答问题.2.找出自己的疑惑和需要讨论的问题,随时记录在课本或导学案上,准备课上讨论质疑.【课前预习】1.下列三角形全等的是2. 三边对应相等的两个三角形全等,简写为 或 3. 如图,已知DB AC DC AB ==,,那么A ∠与D ∠相等吗?3.自主预习书本P100-P101页.【课堂探究】专题一、探究“角角边”的判定方法1.若三角形的两个内角分别是 60和 80,它们所夹的边为2cm 。
你能用量角器和刻度尺画出这个三角形吗?54 2 5424 2342 3(1)(2)(3) (4)AD2.你画的三角形与同伴画的一定全等吗?专题二、探究“角角边”的判定方法1.若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?3cm2.你画的三角形与同伴画的一定全等吗?由此我们得到两种新的判定三角形全等的方法:▲规律整理表述:(1)对应相等的两个三角形全等,简写成“”或“”(2)对应相等的两个三角形全等,简写成“”或“”专题三、三角形全等的条件的应用例1:如图,AB与CD相交于点O,O是AB的中点,∠A=∠B,△AOC≌△BOD吗?为什么?例2:如图,∠B=∠C ,AD平分∠BAC,你能证明△ABD≌△ACD?若BD=3cm,则CD有多长?【学习小结】1.判定两个三角形全等,我们学习了哪些方法?【课堂检测】1.如图所示,∠B=∠C,AB=AC,则△ABE≌△ACD吗?请说明理由。
★2.图中的两个三角形全等吗? 请说明理由。
北师大版数学教材七年级下册 第四章三角形 4.3.1探索三角形全等的条件
A1
B
C
B1
C1
AB = A1B1 BC = B1C1 AC = A1C1
∠A =∠A1 ∠B =∠B1 ∠C =∠C1
4.3.1探索三角形全等的条件(1)
单击页面即可演示
问题引入:
想一想:要画一个三角形与小明画的三角形全等. 需要几个与边或角的大小有关的条件?只知道一个条件 (一角或一边)行吗?两个条件呢?三个条件呢?
挑战自我:
四边形不具有稳定性,你有办法让它们稳定吗?
反 思 小 结
①本节课我们探讨了什么问题?
②得到了什么结论?
③运用了什么数学思想方法?
练. 已知:在△ABC和△DEF中, AB=DE,AC=DF,BF=EC,
这两个三角形全等吗?为什么?
证明:
全等
∵ BF=EC ∴ BF+FC=EC+CF ∴ BC=EF 在△ABC和△DEF中
AB=DE AC=DF BC=EF ∴△ABC≌△DEF (SSS)
练习:1、如图,AB=AC,BD=CD,BH
=CH,图中有几组全等的三角形?它们全等
的条件是什么?
A
解:有三组。
在△ABH和△ACH中
∵ AB AC(已知)
BH CH(已知)
B
AH AH(公共边)
∴△ABH≌△ACH(SSS);
7cm 5cm
有两个角对应相等的两个三角形
30°
45°
有一条边和一个角对应相等的两个三角形
30°
探索的结论:
只给出两个条件,不能保证所画出的三角形一定全等
30°
45°
30°
智者探宝3:
七年级数学下册 第4章 三角形 4.3 探索三角形全等的条件课件 (新版)北师大版
知识详解
(1)用“ASA”判定两个三角形全等的条件是两角及这两个角的夹边对应相等.因此列举两个三角形全等 的条件时,一定要把夹边写在中间,以突出边角的位置及对应关系,避免出错. (2)用“AAS”来判定两个三角形全等时,要注意边是其中一角的对边,三个条件一定要对应,按“角角边” 的顺序列出全等的三个条件. (3)“AAS”与“ASA”的联系 结合三角形的内角和定理可知,“AAS”可由“ASA”推导得出,将两者结合起来可得出:两个三角形,如 果具备两个角和一边对应相等,就可判定其全等.其中“对应”必不可少.如图,△ABC与△DEF不全等
DE CF,
DEB AFC, ∴△DEB≌△CFA(SAS),
BE AF,
∴∠B=∠A,∴AC∥DB.
知识点四 全等三角形判定方法的灵活运用 判定两个三角形全等时,如果给出的条件不全面,则需要根据已知的条 件结合相应的判定方法进行分析,先找出所缺的条件再说明全等. 具体思路如下:
(1)已知两边
解析 ∵BE=CF, ∴BE+EF=CF+EF,即BF=CE.
AB DC,
在△ABF和△DCE中,
AF
DE,
BF CE,
∴△ABF≌△DCE(SSS).
知识点二 判定三角形全等的条件——角边角、角角边
角边角 (ASA)
内容
应用格式
两角和它们的夹边分别相等的两 个三角形全等(可以简写成“角 边角”或“ASA”)
在△ABC和△A'B'C'中,
AB A ' B ',
∵ B B ', ∴△BACBCB≌'C ', △A'B'C'(SAS)
图形表示
七年级数学下册4.3探索三角形全等的条件(第2课时)导学案(无答案)(新版)北师大版
1 探索三角形全等的条件(二) 课题 探索三角形全等的条件(二) 授课教师 学习 目标 1、记住“ASA”和“AAS”,证三角形全等探索过程。 2、会运用本节知识进行三角形全等的证明。
学习 重难点 学习重点:“ASA”和“AAS”,证三角形全等探索过程。 学习难点:运用本节知识进行三角形全等的证明。
学法 指导 讲练结合法 多媒体演示法 探究法 尝试指导法
学 习 过 程
独 立 尝 试
学 案 导 案 探究练习1. 两角和它们的夹边,将学生分组小组分工合作完成下列问题: 画一个△ABC使它满足以下条件: 第一组:∠A=90°, ∠B=30°,AB=10cm 第二组: ∠A=60°, ∠B=45°,AB=9cm 学生动手操作,完成问题后,小组交流比较,看看能得到什么结论?学生表述,老师板书: ________________________对应相等的两个三角形全等; (简写为_____________或者 ______________) 探究练习2. 如果“两角及一边”条件中的边是其中一角的对边,比如三角形的两个内角分别是60° 和45°,一条边长为10cm,情况会怎样呢? ①如果角60°所对的边为10cm,你能画出这个三角形吗? ②如果角45°所对的边为10cm,那么按这个条件画出的三角形都全等吗? 结论_______________________对应相等的两个三角形全等 简写为________________________________ 2
合作探究 如图,OP是∠MON的角平分线, C是OP上一点,CA⊥OM,CB⊥ON, 垂足分别为A、B,△AOC≌△BOC吗? 为什么?
自我挑战 如图:已知BD=CE,∠B=∠C, △ABD与△ACE全等吗?为什么?
堂清试题 1、如图,AB=DC,∠A=∠D.试说明:∠1=∠2。 2、如图,ΔABC中,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G。 ⑴图中有全等三角形吗?请找出来,并证明你的结论。 ⑵若连结DE,则DE与AB有什么关系?并说明理由。
七年级数学下册北师大版课件:4.3.2探索三角形全等的条件
2. 都给边:给三条边
请画出三条边分 别为4cm、5cm和 7cm的三角形。
点拨二:(7分钟) 1、已知一个三角形的三个内角 分别为300,
600,900,请画出这个三角
300
600 300
600
300
600
结论:三个内角对应相等的两个三角形 不一定全等.
2.给出三条边
(5)两边对应相等的两个三角形全等( × )
件
(1)
(2)
(3) (4)
(5)
只给出一个条件或两个条件时,都不
能保证所画出的三角形全等.
自学指导2:(1分钟)
认真阅读教材P97议一议至P98,思考下面问题: 1. 若给出三个条件画三角形,你能说出有哪
几种可能情况?
1. 都给角:给三个角
2. 都给边:给三条边
2、已知三角形的三条边分 别为4cm、5cm和 7cm,请画出这个三角形。
4
5
7
4
5
7
三边分别相等的两个三角形全等, 简写为“边边边”或“SSS”
3、如图,当 AB=CD,BC=DA时,图中的 △ABC与△CDA是否全等?并说明理由。
解:△ABC≌△CDA
理由:在△ABC与△CDA中
AB=CD (已知)
(4)三角形具有稳定性.四边形等具有不稳定性。
(给出两个条件画三角形) (1)给出两条边长3cm和5cm (2)给出两个内角分别为300和600 分组画图 (3)给出一条边3cm和一个内角为300
画好后与你同桌交流,看看你们画的三 角形大小完全相同吗?
学生自学,教师巡视(5分钟)
自学检测1(4分钟)
判断:
(1)一边对应相等的两个三角形全等( × ) (2)一内角对应相等的两个三角形全等( × ) (3)一边和一内角对应相等的两个三角形全等 (× (4)两内角对应相等的两个三角形全等( × )
