上海中考一模数学考试范围
(完整版)上海中考数学考试大纲
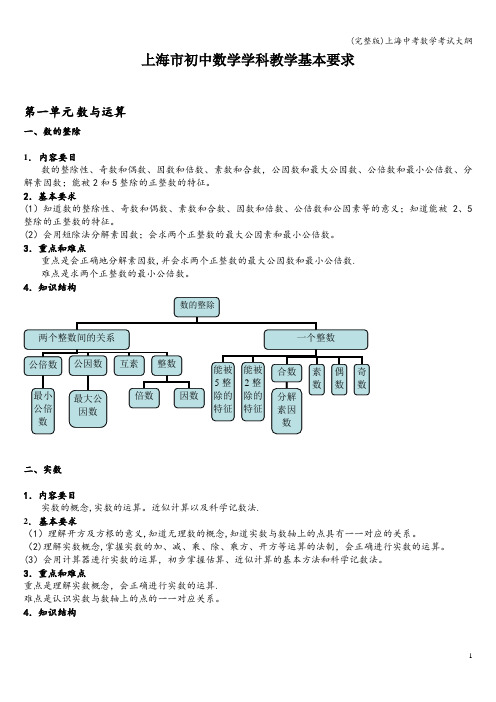
上海市初中数学学科教学基本要求第一单元数与运算一、数的整除1.内容要目数的整除性、奇数和偶数、因数和倍数、素数和合数,公因数和最大公因数、公倍数和最小公倍数、分解素因数;能被2和5整除的正整数的特征。
2.基本要求(1)知道数的整除性、奇数和偶数、素数和合数、因数和倍数、公倍数和公因素等的意义;知道能被2、5整除的正整数的特征。
(2)会用短除法分解素因数;会求两个正整数的最大公因素和最小公倍数。
3.重点和难点重点是会正确地分解素因数,并会求两个正整数的最大公因数和最小公倍数.难点是求两个正整数的最小公倍数。
4.知识结构二、实数1.内容要目实数的概念,实数的运算。
近似计算以及科学记数法.2.基本要求(1)理解开方及方根的意义,知道无理数的概念,知道实数与数轴上的点具有一一对应的关系。
(2)理解实数概念,掌握实数的加、减、乘、除、乘方、开方等运算的法制,会正确进行实数的运算。
(3)会用计算器进行实数的运算,初步掌握估算、近似计算的基本方法和科学记数法。
3.重点和难点重点是理解实数概念,会正确进行实数的运算.难点是认识实数与数轴上的点的一一对应关系。
4.知识结构第二单元 方程与代数一、整式与分式 1.内容要目代数式,整式的加减法,同底数幂的乘法和除法,幂的乘方,积的乘方。
单项式的乘法和除法,单项式与多项式的乘法,多项式除以单项式,多项式的乘法。
乘法公式:22222()();()2a b a b a b a b a ab b +-=-±=±+因式分解:提取公因式法,公式法,十字相乘法,分组分解法。
分式,分式的基本性质,约分,最简分式,通分,分式的乘除法,分式的加减法,整数的指数幂,整数指数幂的运算。
2.基本要求(1)理解用字母表示数的意义;理解代数式的有关概念。
(2)通过列代数式,掌握文字语言与数学式子的表述之间的转换,领悟字母“代”数的数学思想;会求代数式的值。
(3)掌握整式的加、减、乘、除及乘方的运算法则,掌握平方差公式、两数和(差)的平方公式.(4)理解因式分解的意义,掌握提取公因式法、公式法、二次项系数为1时的十字相乘法、分组分解法等因式分解的基本方法.(5)理解分式的有关概念及其基本性质,掌握分式的加、减、乘、除运算。
2024届上海市宝山区初三一模数学试卷(含答案)

图 2 第1页 共12页2024届上海市宝山区初三一模数学试卷考生注意:1.本试卷共25题.2.试卷满分150分.考试时间100分钟.3.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.4.除第一、二大题外,其余各题如无特殊说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.下列各组中的四条线段成比例的是( ▲ )(A )2cm ,3cm ,4cm ,5cm ;(B )2cm ,3cm ,4cm ,6cm ; (C )1cm ,2cm ,3cm ,2cm ; (D )3cm ,2cm ,6cm ,3cm .2.已知线段AB =2,点P 是线段AB 的黄金分割点,且AP >BP ,则AP 的长是( ▲ )(A )253−;(B )53−; (C)215−; (D )15−.3.许多大型商场购物中心为了引导人流前往目标楼层,会考虑使用“飞梯”(可以跨楼层抵达的超高超长的自动扶梯).上海大悦城的“飞梯”从3层直达7层,“飞梯”的截面如图1,AB 的长为50米,AB 与AC 的夹角为24°,则高BC 是( ▲ )(A ) 2450sin 米; (B ) 2450cos 米; (C )︒2450sin 米; (D )︒2450cos 米. 4.在四边形ABCD 中,如果BC AD 32=,|AB DA +|=|DA DC −|,那么四边形ABCD 是( ▲ )(A )矩形; (B )菱形; (C )正方形; (D )等腰梯形.5.二次函数y =ax 2+bx 的图像如图2所示,则一次函数y =ax +b 的图像不.经过( ▲ )(A )第一象限; (B )第二象限; (C )第三象限; (D )第四象限.图3图16.如图3,在正方形网格中,A 、B 、C 、D 、M 、N 都是格点,从A 、B 、C 、D 四个格点中选取三个构成一个与△AMN 相似的三角形,某同学得到两个三角形:①△ABC ;②△ABD .关于这两个三角形,下列判断正确..的是( ) (A )只有①是; (B )只有②是; (C )①和②都是; (D )①和②都不是.二、填空题:(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置上】7.已知线段a =2,b =4,如果线段c 是a 和b 的比例中项,那么c = ▲ .8.比例尺为1:100000的地图上,A 、B 两地的距离为2cm ,那么A 、B 两地的实际距离为 ▲ km .9.计算:sin 30°-sin 45°.cos 45°= ▲.10.二次函数()20y ax bx c a =++≠图像上部分点的坐标(x ,y )对应值如表1所示,那么该函数图像的对称轴是直线 ▲ .11.直径是2的圆,当半径增加x 时,面积的增加值s 与x 之间的函数关系式是 ▲. 12.在△ABC 中,∠BAC =90°,点G 为重心,联结AG 并延长,交BC 于点F ,如果BC =6,那么GF 的长是 ▲ .13.如图4,斜坡AB ,坡顶B 离地面的高度BC 为30m ,如果坡比i =1:3,那么这个斜坡的长度AB = ▲ m .14.在△ABC 中,如果2BC =,7AB =,3AC =,那么cos A = ▲.15.如果二次函数)0()2(<−=a x a y 2的图像上有两点),(149y 和),(237y , 那么y 1 ▲ y 2.(填“>”、“=”或“<”)16.如图5,已知正方形DEFG 的边EF 在△ABC 的边BC 上,顶点D 、G 分别在边AB 、AC 上,如果BC = 6,△ABC 的面积为12,那么EF 的长为 ▲ .17.平面直角坐标系中,在x 轴上,且到一条抛物线的顶点及该抛物线与y 轴的交点的距离..之和..最小的点,称为这条抛物线与x 轴的“亲密点”.那么抛物线2245y x x =++与x 轴的“亲密点”的坐标是 ▲ .18.已知AC 和BD 是矩形ABCD 的两条对角线,将△ADC 沿直线AC 翻折后,点D 落在点E 处,三角形AEC 与矩形的重叠部分是三角形ACF ,联结DE .如果AB =6,BF =2,那么∠BDE 的正切值是 ▲ .图5表1图4三、解答题:(本大题共7题,满分78分)19.(本题满分10分)如图6,在△ABC 中,∠C = 90︒,sinB = 54,AB =10,点D 是AB 边上一点, 且BC = BD .(1)求BD 的长;(2)求∠ACD 的余切值. 20.(本题满分10分)如图7,在△ABC 中,AB =5,BC =4,BD 平分∠ABC 交AC 于点D ,DE ∥BC 交AB 于点E .(1)求DE 的长;(2)联结CE 交BD 于点F ,设a AB =,b AD =,用a 、b 的线性组合表示向量BD = ▲ ,BF = ▲ .21.(本题满分10分)在平面直角坐标系xOy 中,已知二次函数c bx x y ++=2的图像经过点A (1,0)和B (0,3).(1)求该二次函数的表达式;(2)如果点E (4,m )在该函数图像上,求△ABE 的面积.图6图722.(本题满分10分)综合实践活动中,某小组利用木板和铅锤自制了一个简易测高仪测量塔高.测高仪ABCD 为矩形,CD =30cm ,顶点D 处挂了一个铅锤H .图8是测量塔高的示意图,测高仪上的点C 、D 与塔顶G 在一条直线上,铅垂线DH 交BC 于点M .经测量,点D 距地面1.9m ,到塔EG 的距离DF =13m ,CM =20cm .求塔EG 的高度(结果精确到1m ).23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)如图9,在正方形ABCD 中,点E 、F 分别在边CD 、BC 上,且CE =BF ,DF 分别交AE 、AC 于点P 、Q .(1)求证:AE ⊥DF ;(2)求证:DFPQ BF AQ ⋅=⋅2.图8图924.(本题满分12分,每小题满分各4分)如图10,在平面直角坐标系xOy 中,将抛物线221x y =平移,使平移后的抛物线仍经过原点O ,新抛物线的顶点为M (点M 在第四象限),对称轴与抛物线221x y =交于点N ,且MN =4.(1)求平移后抛物线的表达式;(2)如果点N 平移后的对应点是点P ,判断以点O 、M 、N 、P 为顶点的四边形的形状,并 说明理由;(3)抛物线221x y =上的点A 平移后的对应点是点B ,BC ⊥MN ,垂足为点C ,如果△ABC是等腰三角形,求点A 的坐标.图1025.(本题满分14分,第(1)小题满分4分,第(2)(3)小题满分各5分)如图11,已知△ABC中,AB=AC=1,D是边AC上一点,且BD=AD,过点C作CE∥AB,并截取CE=AD,射线AE与BD的延长线交于点F.2;(1)求证:BF=DFAF⋅(2)设AD=x,DF=y,求y与x的函数关系式;(3)如果△ADF是直角三角形,求DF的长.图11参考答案一、选择题:(本大题共6题,每题4分,满分24分)1.B ;2.D ;3.A ;4.D ;5.C ;6.B .二、填空题:(本大题共12题,每题4分,满分48分) 7.22;8.2;9.0;10.x =2 ;11.S =πx 2+2πx ; 12. 1;13.1030; 14.37; 15.>;16.2.4 17. ),085(−; 18. 31或33. 三、解答题:(本大题共7题,满分78分)19.解:(1)∵在Rt △ABC 中,sinB =ABAC ,又∵sinB = 54,AB =10, ∴AC =8,…………………………………………………………………………2分 ∵∠C = 90︒,∴,222AB BC AC =+∴BC =6,…………………………………………………………………………2分 ∵BC = BD ,∴BD =6.………………………………………………………………………… 1分(2)过点D 作DE ⊥AC ,垂足为点E .………………………………………………………1分又由∠C = 90︒,可得DE ∥BC , ∴,ABAD BC DE = ∵BC =6,A D =4,AB =10,∴DE =2.4, ………………………………………………………………………1分 同理可得EC =4.8,………………………………………………………………1分 ∵在Rt △DEC 中,cot ∠ACD = DEEC , …………………………………………1分∴cot ∠ACD = 2. …………………………………………………………………1分20.解:(1)∵BD 平分∠ABC ,∴∠1=∠2,∵DE ∥BC ,∴∠2=∠3,∴∠1=∠3, ………………………………………………………………………1分 ∴DE =BE , ………………………………………………………………………1分 设DE =BE =x ,则AE =5-x , ……………………………………………………1分 ∵DE ∥BC ,∴ABAE BC DE =, ……………………………………………………1分 ∴,554x x −= ………………………………………………………………………1分解得920=x ,所以,.920=DE …………………………………………………1分(2)BD =a b −, ……………………………………………………………………2分BF =.149149a b −…………………………………………………………………2分21.解:(1)由图像经过点B (0,3),可知c =3, ………………………………………2分再由图像经过点A (1,0),可得0312=++b ,解得b =-4, ……………………2分所以,该二次函数的表达式为.342+−=x x y …………………………………1分(2)把x =4代入342+−=x x y ,得y =3,……………………………………1分由B (0,3)、E (4,3)可知BE ∥x 轴,……………………………………………1分 于是BE =4,BE 边上的高为3,…………………………………………………2分∴.63)04(21=⋅−⋅=∆ABE S …………………………………………………1分22.解:在Rt △CDM 中,cot ∠CDM =CMCD , ……………………………………………1分又∵CD =30cm ,CM =20cm , ………………………………………………………1分 ∴cot ∠CDM = 23, ……………………………………………………………………1分∵DF ⊥EG ,∴∠DGF +∠GDF =90°,……………………………………………………………1分 又由题意可得∠CDM +∠GDF =90°,∴ ∠CDM =∠DGF , …………………………………………………………………1分在Rt △DGF 中,cot ∠DGF = DFGF ,…………………………………………………1分又∵DF =13m ,∴GF =m 239, ………………………………………………………………………1分∴EG =GF+EF =m 219.1239≈+, ……………………………………………………2分 答:塔EG 的高度约为21m . …………………………………………………………1分23.证明:(1)∵在正方形ABCD 中,∴CD =BC ,AD =CD ,∠ADE =∠DCF =90°, …………………………………1分又∵CE =BF ,∴CD -CE =BC -BF ,即DE =CF , …………………………………………………………………………1分 ∴△ADE ≌△CDF ,∴∠1=∠2, …………………………………………………………………………1分 ∵∠ADE =90°∴∠1+∠3=90°,∴∠2+∠3=90°, ……………………………………………………………………1分 ∵∠APQ =∠2+∠3,∴∠APQ =90°,………………………………………………………………………1分 ∴AE ⊥DF.(2)过点E 作EG ⊥AC ,垂足为点G . ………………………………………………1分 ∵∠APQ =90°,∴∠APQ =∠AGE ,又∵∠PAQ =∠EAG ,∴△APQ ∽△AEG ,……………………………………………………………………1分 ∴EGAE PQ AQ =,…………………………………………………………………………1分 ∵在正方形ABCD 中,∴ 45214=∠=∠DCF , 在Rt △CDM 中,cot ∠4= 22=CE EG , ∴CE EG 22=, ………………………………………………………………………1分 ∵CE =BF ,∴BF EG 22=,………………………………………………………………………1分 ∵△ADE ≌△CDF ,∴AE =DF , …………………………………………………………………………1分 ∴BF DF PQ AQ 22=, ∴DF PQ BF AQ ⋅=⋅2.……………………………………………………………1分24.解:(1),,设)0)(21(2>t t t N )421(2−t t M ,则,……………………………………………………1分于是平移后抛物线的表达式是421)(2122−+−=t t x y , ………………………………1分由平移后抛物线经过原点O (0,0),可得t =2(负值不合题意舍去),………………1分所以,平移后抛物线的表达式是2)2(212−−=x y . ……………………………………1分(2)四边形OMPN 是正方形.根据题意可得O (0,0),M (2,-2),N (2,2),P (4,0), …………………………1分记MN 与OP 交于点G ,则G (2,0),∴OG =GP =2,MG =NP =2,MN =OP =4,22==NP NO ,∴四边形OMPN 是平行四边形, ……………………………………………………1分 ∵MN =OP =4,∴四边形OMPN 是矩形, ……………………………………………………………1分 ∵22==NP NO ,∴四边形OMPN 是正方形. ……………………………………………………………1分(3),,设)21(2a a A ,,则)2212(2−+a a B )2212(2−a C ,,222,2)2(22a BC a AC AB =+−==,可得,……………………………………1分;,(舍去①)84(),0,4,04,2)2(22,11222A a a a a a AC AB ===−+−==…………1分 ;,或,②)422()422(,22,22,22,112−−====A A a a a BC AB ………………1分 ;,,,③)22(2,2)2(222A a a a BC AC ==+−=……………………………………1分所以,点A 的坐标是)2,2()422()422()8,4(、,、,、−.25.(1)证明:∵CE ∥AB ,∴∠1=∠2,………………………………………………………………………………1分又∵AB =AC ,CE =AD ,∴△ABD ≌△AEC ,………………………………………………………………………1分 ∴∠3=∠4,又∵∠AFB =∠AFD ,∴△ABF ∽△ADF ,………………………………………………………………………1分 ∴AFBF DF AF =,∴BF DF AF ⋅=2.…………………………………………………………………………1分 解:(2)过点D 作DG ∥AB ,交AE 于点G. ………………………………………………1分又∵CE ∥AB ,∴DG ∥CE , ∴AC AD CE DG =,……………………………………………………………………………1分由AD =x ,则CE =x ,CD =1-x ,∴2x DG =,………………………………………………………………………………1分∵DG ∥AB , ∴BF DF AB DG =,……………………………………………………………………………1分∴y x y x +=12, ∴231x x y −=. ……………………………………………………………………………1分(3)①∠DAF =ABD ≠90°,………………………………………………………………1分 ②如果∠AFD =90°,由∠1=∠3=∠4,∠1+∠3+∠4=90°,可得∠3=∠4=30°,……………………1分 设DF =m ,则AD =BD =2m ,在Rt △ABF 中,cos ∠3=ABBF , ∴2312=+m m ,63=m .………………………………………………………………1分③如果∠ADF =90°,由∠1=∠3=∠4,∠1+∠3=90°,可得∠3=∠4=45°,……………………………1分 设DF =m ,AD =BD =m ,在Rt △ABF 中,cos ∠3=BFAB , ∴221=+m m ,22=m . ………………………………………………………………1分 所以,当△ADF 是直角三角形时,DF 的长为63或22.。
上海市静安区2023届九年级初三数学一模试卷+答案

2023年上海市静安区中考数学一模试卷本试卷共有25道试题,满分150分,考试时间100分钟一、选择题(本大题共6题,每题4分,满分24分)1、下列实数中,无理数是(▲)C. 0(2)π+ D.872、计算32x x⋅所得的结果是(▲)A. 9xB. 6xC. 5xD. x3、如果非零向量a、b互为相反向量,那么下列结论中错误的是(▲)A. a∥bB. a b= C. 0a b+= D. a b=−4、如图,已知ABC∆与DEF∆,下列条件一定能推得它们相似的是(▲)A. A D∠=∠,B E∠=∠ B. A D∠=∠且AB BCDF EF=C. A B∠=∠,D E∠=∠ D. A E∠=∠且AB ACDE DF=5、如果060A︒<∠<︒,那么sin A与cos A的差(▲)A. 大于0B. 小于0C. 等于0D. 不能确定6、如图,在ABC∆中,中线AD与中线BE相交于点G,联结DE.下列结论成立的是(▲)A.13DG AG= B.BG DEEG AB= C.14DEGAGBSS∆∆= D.12CDEAGBSS∆∆=二、填空题(本大题共12题,每题4分,满分48分)7、13的倒数是_____▲_____. 8、计算:4222aa a +=++_____▲_____.9、已知:2:3a b =,那么aa b+的值是_____▲_____.10、抛物线2(1)2y x =+−与y 轴的交点坐标是_____▲_____.11、请写出一个以直线3x =为对称轴,且在对称轴左侧部分是下降的抛物线,这条抛物线的表达式可以是_____▲_____(只要写出一个符合条件的抛物线表达式).12、有一座拱桥的截面图是抛物线形状,在正常水位时,桥下水面AB 宽20米,拱桥的最高点O 距离水面AB 为3米,如图建立直角坐标平面xOy ,那么此抛物线的表达式为 _____▲_____.13、一水库的大坝横断面是梯形,坝顶、坝底分别记作BC 、AD ,且迎水坡AB 的坡度为1:2.5,背水坡CD 的坡度为1:3,则迎水坡AB 的坡角_____▲_____背水坡CD 的坡角(填“大于”或“小于”).14、已知111222ABC A B C A B C ∆∆∆∽∽,ABC ∆与111A B C ∆的相似比为15,ABC ∆与222A B C ∆的相似比为23,那么111A B C ∆与222A B C ∆的相似比为_____▲_____.15、在矩形ABCD 内作正方形AEFD (如图所示),矩形的对角线AC 交正方形的边EF 于点P .如果点F 恰好是边CD 的黄金分割点(DF FC >),且2PE =,那么PF = _____▲_____.16、在ABC ∆中,6AB =,5AC =,点D 、E 分别在边AB 、AC 上,当4AD =,ADE C ∠=∠时,DEBC=_____▲_____. 17、如图,ABC ∆绕点C 逆时针旋转90︒后得DEC ∆,如果点B 、D 、E 在一直线上,且60BDC ∠=︒,3BE =,那么A 、D 两点间的距离是_____▲_____.18、定义:把二次函数2()y a x m n =++与2()y a x m n =−−−(0a ≠,m 、n 是常数)称作互为“旋转函数”.如果二次函数2322y x bx =+−与214y x cx c =−−+(b 、c 是常数)互为“旋转函数”,写出点(,)P b c 的坐标_____▲_____. 三、解答题(本大题共7题,满分78分) 19、(本题满分10分)2cot 45sin 45tan 45︒−︒⎛⎫+ ⎪︒⎝⎭.如图,已知在ABC ∆中,点D 、E 分别在边AB 、AC 上,且2BD AD =,12AE EC =. (1)求证:DE ∥BC ;(2)设BE a =,BC b =,试用向量a 、b 表示向量AC .21、(本题满分10分,每小题各5分)如图,已知在ABC ∆中,B ∠为锐角,AD 是BC 边上的高,5cos 13B =,13AB =,21BC =.(1)求AC 的长; (2)求BAC ∠的正弦值.有一把长为6米的梯子AB ,将它的上端A 靠着墙面,下端B 放在地面上,梯子与地面所成的角为α,地面与墙面互相垂直(如图1所示).一般满足5075α︒≤≤︒时,人才能安全地使用这架梯子.(1)当梯子底端B 距离墙面2.5米时,求α的度数(结果取整数),此时人是否能安全地使用这架梯子?(2)当人能安全地使用这架梯子,且梯子顶端A 离开地面最高时,梯子开始下滑,如果梯子顶端A 沿着墙面下滑1.5米到墙面上的D 点处停止,梯子底端B 也随之向后平移到地面上的点E 处(如图2所示),此时人是否能安全使用这架梯子?请说明理由.如图,在梯形ABCD 中,AD ∥BC ,DF 分别交对角线AC 、底边BC 于点E 、F ,且AD AC AE BC ⋅=⋅.(1)求证:AB ∥FD ;(2)点G 在底边BC 上,10BC =,3CG =,联结AG ,如果AGC ∆与EFC ∆的面积相等,求FC 的长.24、(本题满分12分,第(1)小题4分,第(2)①、②小题各4分)如图所示,在平面直角坐标系xOy 中,抛物线26y ax bx =+−(0a ≠)与x 轴交于点A 、B (点A 在点B 的左侧),交y 轴与点C ,联结BC ,ABC ∠的余切值为13,8AB =,点P 在抛物线上,且PO PB =.(1)求上述抛物线的表达式;(2)平移上述抛物线,所得新抛物线过点O 和点P ,新抛物线的对称轴与x 轴交于点E . ①求新抛物线的对称轴;②点F 在新抛物线对称轴上,且EOF PCO ∠=∠,求点F 的坐标.25、(本题满分14分,第(1)①、②小题各5分,第(2)小题4分)在等腰直角ABC ∆中,90C ∠=︒,4AC =,点D 为射线CB 上一动点(点D 不与点B 、C 重合),以AD 为腰且在AD 的右侧作等腰直角ADF ∆,90ADF ∠=︒,射线AB 与射线FD 交于点E ,联结BF .(1)如图1所示,当点D 在线段CB 上时, ①求证:ACD ABF ∆∆∽;②设CD x =,tan BFD y ∠=,求y 关于x 的函数解析式,并写出x 的取值范围; (2)当2AB BE =时,求CD 的长.2023年上海市静安区中考数学一模试卷参考答案1-6、BCCADC 7、38、29、2510、(0,1)−11、2(3)y x =−(答案不唯一,形为2(3)y a x c =−+(0a >)的均为正确答案)12、23100y x =−13、大于 14、103151−16、451718、1,23P ⎛⎫− ⎪⎝⎭19、3220、(1)证略;(2)3322b a − 21、(1)20;(2)636522、(1)65α≈︒,此时人可以安全地使用这架梯子;(2)不能,此时46α≈︒23、(1)证略;(224、(1)21262y x x =+−;(2)①对称轴直线4x =;②84,5F ⎛⎫ ⎪⎝⎭或84,5F ⎛⎫− ⎪⎝⎭25、(1)①证略;②44xy x−=+(04x <<);(2)3。
上海市闵行区2023届九年级初三数学一模试卷+答案

2023年上海市闵行区中考数学一模试卷本试卷共有25道试题,满分150分,考试时间100分钟一、选择题(本大题共6题,每题4分,满分24分) 1、下列各组图形一定相似的是( ▲ ) A. 两个直角三角形 B. 两个菱形C. 两个矩形D. 两个等边三角形2、如图,已知AB ∥CD ∥EF ,它们依次交直线1l 、2l 于点A 、C 、E 和点B 、D 、F ,如果:3:1AC CE =,10BF =,那么DF 等于( ▲ )A.103B.203C.52D.1523、如图,已知在Rt ABC ∆中,90ACB ∠=︒,B β∠=,CD AB ⊥,垂足为点D ,那么下列线段的比值不一定等于sin β的是( ▲ )A.ADBDB.ACABC.ADACD.CDBC4、下列说法正确的是( ▲ ) A. 如果e 为单位向量,那么a a e =B. 如果a b =−,那么a ∥bC. 如果a 、b 都是单位向量,那么a b =D. 如果a b =,那么a b =5、抛物线22y x =向下平移3个单位长度后所得新抛物线的顶点坐标为( ▲ ) A. (3,0)−B. (3,0)C. (0,3)−D. (0,3)6、如图,某零件的外径为10cm ,用一个交叉卡钳(两条尺长AC 和BD 相等)可测量零件的内孔直径AB .如果3AC BDOC OD==,且量得4CD =cm ,则零件的厚度x 为( ▲ )A. 2cmB. 1.5cmC. 0.5cmD. 1cm二、填空题(本大题共12题,每题4分,满分48分) 7、如果3a b =(0b ≠),那么a bb+=_____▲_____. 8、化简:()22333a b b −+−=_____▲_____. 9、已知2()2f x x x =+,那么(1)f 的值为_____▲_____.10、抛物线22y x =在对称轴的左侧部分是_____▲_____的(填“上升”或“下降”). 11、已知两个相似三角形的相似比为2:3,那么这两个三角形的面积之比为_____▲_____. 12、设点P 是线段AB 的黄金分割点(AP BP >),2AB =,那么线段AP 的长是 _____▲_____.13、在直角坐标平面内有一点(5,12)A ,点A 与原点O 的连线与x 轴的正半轴的夹角为θ,那么sin θ的值为_____▲_____.14、已知D 、E 分别是ABC ∆的边AB 、AC 上的点(不与端点重合),要使得ADE ∆与ABC ∆相似,那么添加一个条件可以为_____▲_____(只填一个).15、已知一斜坡的坡角为30︒,则它的坡度i =_____▲_____.16、如图,一艘船从A 处向北偏西30︒的方向行驶5海里到B 处,再从B 处向正东方向行驶8千米到C 处,此时这艘船与出发点A 处相距_____▲_____海里.17、如图,在Rt ABC ∆中,90ACB ∠=︒,9AB =,cot 2A =,点D 在边AB 上,点E 在边AC 上,将ABC ∆沿着折痕DE 翻折后,点A 恰好落在线段BC 的延长线上的点P 处,如果BPD A ∠=∠,那么折痕DE 的长为_____▲_____.18、阅读:对于线段MN 与点O (点O 与MN 不在同一直线上),如果同一平面内点P 满足:射线OP 与线段MN 交于点Q ,且12OQ OP =,那么称点P 为点O 关于线段MN 的“准射点”.问题:如图,矩形ABCD 中,4AB =,5AD =,点E 在边AD 上,且2AE =,联结BE .设点F 是点A 关于线段BE 的“准射点”,且点F 在矩形ABCD 的内部或边上,如果点C 与点F 之间距离为d ,那么d 的取值范围为_____▲_____.三、解答题(本大题共7题,满分78分)19、(本题满分10分))11311cos308−⎛⎫−+︒⎪⎝⎭.20、(本题满分10分,第(1)小题4分,第(2)小题6分)如图,已知ABC∆中,点D、E分别在边AB和AC上,DE∥BC,且DE经过ABC∆的重心,设AB a=,AC b=.(1)DE=_____▲_____(用向量a、b表示);(2)求作:13a b+(不要求写作法,但要指出所作图中表示结论的向量).21、(本题满分10分,每小题各5分)已知在平面直角坐标系xOy 中,抛物线223y x x =−++与y 轴交于点A ,其顶点坐标为B .(1)求直线AB 的表达式;(2)将抛物线223y x x =−++沿x 轴正方向平移m (0m >)个单位后得到的新抛物线的顶点C 恰好落在反比例函数16y x=的图像上,求ACB ∠的余切值.22、(本题满分10分)2022年11月12日10时03分,搭载天舟五号货运飞船的长征七号遥六运载火箭,在海南文昌航天发射场成功发射.天舟五号货运飞船重约13.6吨,长度10.6BD =米,货物仓的直径可达3.35米,是世界现役货物运输能力最大、在轨支持能力最全面的货运飞船,堪称“在职最强快递小哥”.已知飞船发射塔垂直于地面,某人在地面A 处测得飞船底部D 处的仰角为45︒,顶部B 处的仰角为53︒,求此时观测点A 到发射塔CD 的水平距离(结果精确到0.1米).(参考数据:sin 530.80︒≈,cos530.60︒≈,tan 53 1.33︒≈)23、(本题满分12分,第(1)小题5分,第(2)小题7分)已知:如图,在ABC ∆中,AB AC =,点D 、E 分别是边AC 、AB 的中点,DF AC ⊥,DF 与CE 相交于点F ,AF 的延长线与BD 相交于点G .(1)求证:ABD ACE ∠=∠; (2)求证:2CD DG BD =⋅.24、(本题满分12分,每小题各4分)在平面直角坐标系xOy 中,抛物线2y ax bx =+经过(1,3)A −、(2,0)B ,点C 是该抛物线上的一个动点,联结AC ,与y 轴的正半轴交于点D .设点C 的横坐标为m . (1)求该抛物线的表达式; (2)当32DC AD =时,求点C 到x 轴的距离; (3)如果过点C 作x 轴的垂线,垂足为点E ,联结DE ,当23m <<时,在CDE ∆中是否存在大小保持不变的角?如果存在,请指出并求其度数;如果不存在,请说明理由.25、(本题满分14分,第(1)小题3分,第(2)小题5分,第(3)小题6分) 如图1,点D 为ABC ∆内一点,联结BD ,CBD BAC ∠=∠,以BD 、BC 为邻边作平行四边形DBCE ,DE 与边AC 交于点F ,90ADE ∠=︒. (1)求证:ABC CEF ∆∆∽;(2)延长BD ,交边AC 于点G ,如果CE FE =,且ABC ∆的面积与平行四边形DBCE 面积相等,求AGGF的值; (3)如图2,联结AE ,若DE 平分AEC ∠,5AB =,2CE =,求线段AE 的长.2023年上海市闵行区中考数学一模试卷参考答案1-6、DCABCD 7、48、2a −9、310、下降11、4:9121−13、121314、ADE B ∠=∠(或DE ∥BC 等,答案不唯一)15、16、717、 18、5d ≤≤19、20、(1)2233b a −;(2)图略 21、(1)3y x =+;(2)4 22、32.1米23、(1)证略;(2)证略 24、(1)22y x x =−;(2)34;(3)45DEC EDO ∠=∠=︒25、(1)证略;(2)2;(3)2。
2024年上海市奉贤区中考一模 数学 试题(学生版+解析版)

2024年上海市奉贤区中考一模数学试题一、选择题(本大题共6题,每题4分,满分24分)l下列函数中是二次函数的是()A.y=2x+lB.y =—2xC.y=x 2 +22.将抛物线y=x 2向右平移3个单位长度得到的抛物线是(A. y=x 2+3B. y=x 2-3C. y =(x -3)2D.y=启D.y=(x +3)23在Rt丛ABC 中,乙C=90气AC=S ,乙4=a ,那么BC 的长是()A.St an aB. 5c ot aC. 5sin aD. Sc os a4如图,在心灶死中,点D、E 分别在AB、AC 的反向延长线上,已知AB =2AD,下列条件中能判定DEii BC 的是()EDBAC l DEl AC 2 A.—=-B.—=-C —= -AE2BC 2EC 3s.已知同=5,例=3'且b 与a 方向相反,下列各式正确的是()3.3.5.5 A .b=::...aB. b=-::...aC. b=::...aD.b=-::...a5 5 336如图,将"访C 绕点8顺时针旋转,使得点A 落在边AC 上,点A、C 的对应点分别为D、E ,边DE 交AE 2D.—=-EC 3BC 千点F,连接CE.下列两个三角形不一定相似的是(BCA.6BAD 与_BCEB.VBDF 与1:::,.ECFC.. DCF 与6.BEFD. 6DBF 与.DEB二、填空题(本大题共12题,每题4分,满分48分)x-y 7.如果x :y =5:3,那么——-=8计算3(2a+b)-4a=9已知抛物线y =(a-2)入3-x开口向上,那么a的取值范围是10已知抛物线y =-2x 2 +l在对称轴左侧部分是的.(填“上升”或“下降”)ll.如果P是线段AB的黄金分割点,AB=2cm,那么较长线段AP的长是12.某人顺着坡度为1:✓3的斜坡滑雪,下滑了120米,那么商度下降了一米.cm13如图,已知ADIi BEi/CF,它们依次交直线l 1千点A 、B、C,交直线l 2千点D 、E 、F,已知AB:AC=3:5, DF=lO,那么EF的长为14如图,已知6.ABC的周长为15,点E、F是边BC的三等分点,DEii AB, DF I I AC,那么心DEF 的周长是.ABc15如图,已知"ABC 在边长为1个单位的方格纸中,三角形的顶点在小正方形顶点位置,那么L.ABC 的正切值为.广六----,-勹,B[----';--7.y..-斗I --4AC石16在1.A BC中,乙4=45°'cos乙B =—-(乙B是锐角),BC=✓S ,那么AB的长为517如图是某幢房屋及其屋外遮阳篷,已知遮阳篷固定点A距离地面4米(即AB=4米),遮阳篷的宽度5AC为2.6米,遮阳篷与房屋墙壁的夹角a的余弦值为—,当太阳光与地面的夹角为60°时,遮阳篷在地13面上的阴影宽度BD 为米.18如图,在梯形ABCD 中,ADIi BC, BC=3AD,点E 是AB中点,如果点F在DC 上,线段EF 把梯形分成而积相等的两个部分,那么——=DF DC8A D三、解答题(本大题共7题,满分78分)19.计算tan45° -l cot 30°-l l .2 s in 60°-2cos 60° 20已知抛物线y=x 2+bx+c 经过点A(3,0), B(O, -3).(])求抛物线表达式并写出顶点坐标;(2)联结AB,与该抛物线的对称轴交千点P,求点P的坐标.2]如图,在ABC 中,G 是,ABC 的重心,联结AG 并延长交BC 千点D.AC(I)如果AB动,万它=石,那么AD =(用向榄;、b 表示);(2)已知AD=6,AC=8,点E 在边AC 上,且LAGE =乙C,求AE 的长.22.如图l,某小组通过实验探究凸透镜成像规律,他们依次在光具座上垂直放趾发光物箭头、凸透镜和光屏,并调整到合适的窝度.如图2,主光轴/垂直千凸透镜MN,且经过凸透镜光心O,将长度为8厘米的发光物箭头AB 进行移动,使物距oc 为32厘米,光线AO 、BO 传播方向不变,移动光屏,直到光屏上呈现一个消晰的像A'Ir,此时测得像距OD 为12.8厘米.4,`'I尤I\片Pl(I)求像A'B'的长度.(2)已知光线AP平行千主光轴l,经过凸透镜MN折射后通过焦点F,求凸透镜焦距OF的长.l'&!l23如图,在J访C中,AB=AC,点D在边BC上,已知LAFD=乙B,边DF交AC千点E.(I)求证:AF·CE=CD-FE:AB BC(2)连接AD,如果—-=——,求证:AD2=AEAC.AF DF24在平面直角坐标系中,如果两条抛物线关千直线x=m对称,那么我们把一条抛物线称为另一条抛物线关千直线·x=I/1的镜像抛物线(I)如图,已知抛物线y=x2-2x顶点为A.yiXA@求该抛物线关千y轴的镜像抛物线的表达式;I@已知该抛物线关千直线x=rn的镜像抛物线的顶点为B,如果tanL.OB A=..:.(乙OBA是锐角),求m的4仙I(2)已知抛物线y=-:;-x2 +bx+ c(b >0) 顶点为C,它的一条镜像抛物线的顶点为D,这两条抛物线4的交点为E(2,l).如果CDE是直角三角形,求该抛物线的表达式25在直角梯形ABCD中,ADIi BC,乙8=90°,AD=6, AB=4, BC> AD, LADC 平分线交边BC于点E,点F在线段DE上,射线CF与梯形ABCD的边相交千点G.4(l )如图1,如果点G 与A 重合,当tan 乙BCD =一时,求BE 的长;B二C3(2)如图2,如果点G 在边AD 上,联结BG,当DG =4,且YCGB cn VBAG 时,求sin 乙BCD 的值;B A穹三(3)当F 是D E 中点,且AG =l 时,求CD 的长.2024年上海市奉贤区中考一模数学试题一、选择题(本大题共6题,每题4分,满分24分)l下列函数中是二次函数的是(A. y=2x+l 【答案】C 【解析)B. y=—2xC.y=x2 +2D.y=启【分析】木题考查了二次函数的定义,根据二次函数的定义逐项分析即可,熟练掌握其定义是解决此题的关键.【详解】A.y=2x+l是一次函数,故不符合题意:B.y=—是反比例函数,故不符合题意:2xC.y= x2 +2是二次函数,故符合题意:D. y=石了不是二次函数,故不符合题意,故选:C.2.将抛物线y=x2向右平移3个单位长度得到的抛物线是(A. y= x2 +3【答案)C【解析】B. y=x2-3C. y =(x-3)2【分析】根据抛物线平移规律:上加下减,左加右减解答即可D.y=(x+3)2【详解】解:抛物线y= x2向右平移3个单位长度得到的抛物线是y=(x-3)2.故选:C【点睛】本题考查了二次函数图象的平移,理解乎移规律是解题的关键.3在Rt丛ABC中,乙C=90°,AC=S, LA=a,那么BC的长是()A.Stana【答案】A【解析)B. ScotaC. SsinaD. Scosa【分析】木题考查了正切定义,正切等千对边比邻边,先画出图形,再根据正切三角函数的定义即可得.【详解】由题意,画出图形如下:AB C BC 则tan A =—一,即tan a =一—,AC 5 解得BC=5tana,故选:A .4如图,在心钮C 中,点D、E 分别在AB、AC 的反向延长线上,已知AB =2AD,下列条件中能判定DEii BC的是()E DBACl A—=-AE2【答案]C 【解析]【分析】木题考查了相似三角形的判定及性质,利用相似三角形的判定及性质逐一判断即可求解,熟练掌握DEl B —=-BC 22-3= AC -EC c AE 2D.—=-EC 3相似三角形的判定及性质是解题的关键.AB【详解】解:AB=2AD ,...—-=2,ADAC 1.... ABA、巾—=-,及—-=2不能判定DEii BC,故不符合题意;AE 2AD DE IAB B、巾—-=一,—-=2不能判定DEii BC,则错误,故不符合题意;BC 2 AD AC 2 C、—=-,EC 3 AC 2 ·-=-=2,AE 1AB ·—=2,AD :心EO公ABC,:.乙ADE=乙ABC,:.DEii BC,故符合题意;AE 2 ABD、巾—=-、—=2不能判定DEii BC,故不符合题意EC 3 AD 故选:C5.已知忖=5,树=3,且E与;的方向相反,下列各式正确的是()3-A . b =::...a【答案l B 【解析l【分析】本题考查了平面向见的线性运算由b与a的方向相反,且lal=S,I 叶=3'可得b和a的关系.3 -B.b = --aa 5-3= bcta 5-3= -b D 【详解】解:·:1111=5,I 叶=3,. ·. I 叶=3忆I,5... b与a的方向相反,�3-:.b=-::....a .故选:B .6如图,将.ABC 绕点B 顺时针旋转,使得点A 落在边AC 上,点A、C 的对应点分别为D、E,边D E 交BC千点F,连接CE.下列两个三角形不一定相似的是(B CA.6BAD 与.c.BCEB.VBDF与6.ECFC.DCF与6.BEFD. DBF 与...D邸【答案】D 【解析】【分析】本题考查相似三角形的判定、旋转性质、等腰三角形的性质,根据旋转的性质和相似三角形的判定逐项判断即可.熟练掌握相似三角形的判定是解答的关键.【详解】解:如图,BE由旋转性质得AB=BD, BC= B E, L.ABD=乙CBE,乙4=乙BDE,乙4CB=乙DEB AB BD BCBE:.,6.BAJ)v>心BCE,故选项A不符合题意;.:乙ABD=乙CBE,AB=BD, BC=BE, :.丛=丛DB =纽CE=纽EC ,:.乙BDF =乙BCF,又LDFB=乙CFE,:.D:.BDFV>D:.ECF,故选项B 不符合题意;.:乙DCF=乙FEB,又乙DFC=乙BFE,:. e.DCF (/)t.BEF,故选项C 不符合题意;根据题意,无法证明DBF 与..DEB 相似,故选项D 符合题意,故选:D .二、填空题(本大题共12题,每题4分,满分48分)x-y 7.如果x:y=S :3,那么一一-=【答案]23【解析]5【分析】根据x :y =5:3得到x =-:-Y,把它代入后而的式子求出比值.3 【详解】解:·:x: y =5:3, 5 :. 3x=5y ,即x = - y ,35 -y-y :.江立=3=3.yy3故答案是:一.23【点睛】木题主要考查了比例的性质,解题的关键是掌握比例基本的性质.8.计算3(2a+b)-4a =【答案】2a+3h【解析】【分析】木题主要考查了平面向揽,利用平面向量的定义与运算性质解答即可,熟练掌握平面向量的运算性质是解题的关键.【详解】3(2a+E)-4a=6a+3b-4a=2a+3l1:故答案为:2a+3b.9.已知抛物线y=(a-2)入3_x开口向上,那么a的取值范围是【答案l a>2##2<a令【解析】【分析】本题主要考查了二次函数的性质,熟练掌握二次函数的性质是解题的关键.利用二次函数y= ax2 +bx+c的性质:a>o时,抛物线开口向上,列出不等式解答即可.【详解】解:?抛物线y=(a-2)x2-x开口向上,:. a-2>0,:. a>2.:. a的取值范围是:a>2.故答案为:a>2.10已知抛物线y=-2x2+]在对称轴左侧部分是的.(填“上升”或“下降”)【答案】上升【解析】【分析】本题考查了二次函数图象的性质,熟练掌握二次函数y=ax2 +k的性质是解答本题的关键.根据性质解答即可.【详解)解:·:y=-2x2+1, a=-2<0,:.抛物线升口向下.对称轴是直线y轴,..在对称轴左侧部分是上升的.故答案为:上升.l l.如果P是线段AB的黄金分割点,AB=2cm,那么较长线段AP的长是【答案】(-1+石)【解析J【分析】木题考查了黄金分割的定义,关键是明确黄金分割所涉及的线段的比根据黄金分割的定义解答.【详解】解:设AP=xcm,根据题意列方程得,X2=2(2-X),即x2+2x-4=0,解得X1=-1+✓5心2=-l-石(负值舍去)故答案为:(-l+..f.订12.某人顺着坡度为1:.f_诈筛斜坡滑雪,下滑了120米,那么商度下降了一米.【答案)60【解析)cm【分析】此题考查了解直角三角形的应用——坡度坡角问题,设垂直高度,表示出水平距离,利用勾股定理求解即可,解题的关键是掌握坡度坡角的定义.【详解】?坡度为l:✓3,...设高度下降了x(x>O)米,则水平前进了石x米,由勾股定理得:x2+(✓3x) 2+ 3x =120气解得:x=60,故答案为:60.13.如图,已知ADIi BEi/CF,它们依次交直线l1千点A、B、c.交直线l2千点D、E、F,已知AB:AC=3:5, DF=lO,那么EF的长为【答案】4【解析)【分析】木题考查的是平行线分线段成比例定理,根据平行线分线段成比例定理列出比例式,代入已知数据计算即可,灵活运用定理、找准对应关系是解题的关键.【详解】?AD I BE CF, AB: AC=3:5,AB DE 3= =-,AC DF 5·: DF=lO,DE 3=-,l0 5:. D E=6,:. EF=l0-6=4.故答案为:4.14如图,已知6.ABC的周长为15,点E、F是边BC的三等分点,DEii AB, DF II AC,那么丛DEF 的周长是.AB c【答案)5【解析)【分析】本题主要考查了相似三角形的判定与性质,平行线的性质,利用平行线的性质和相似三角形的判定与性质解答即可,熟练掌握相似三角形的判定与性质是解题的关键.【详解】解:?点E,F是边BC的三等分点,I:.EF =..:.B e.'."DE II AB, DF II AC,:.乙DEF=乙B,. ·..• DEF C/)•ABC,..七DEF 的周长:心FE=乙C,E F I 凇C的周长=—-=-,B C 3:. DEF的周长=-xl5=5.3故答案为: 5.l5.如图,已知乙ABC 在边长为1个单位的方格纸中,三角形的顶点在小正方形顶点位置,那么LABC 的正切值为广.十六.勹,B:: , , , AC 【答案)-##0.5【解析)【分析】本题考查勾股定到及三角形函数的性质等知识点,构建合适的直角三角形即可解决问题,构造出合适的直角三角形是解题的关键.【详解】连接CD,如图所示,r····r····,....-,.B , : ::····! ,...,...,.1.] A C易得6.BCD是直角三角形,由勾股定理得,CD=扩了F=丘,在R t 矗BCD 中,BD=卢=2石,CD 扛1tan乙ABC =—=—=-.BD 2石2故答案为:一.I 16.在..ABC 中,石乙A=45°,cos乙B=—(乙B是锐角),【答案】3BC=石,那么AB的长为.【解析)【分析】本题主要考查了解直角三角形,勾股定理,过点C作CD.L AB寸-/),先解Rt b.DBC得到BD=l,即可利用勾股定理求出CD=2,再解Rt七ADC求出AD=2,则AB=AD+BD=3.【详解】解:如图所示,过点C作CD上AB-=f D,在R心DBC中,cosB=壁汇正,BC=石,B C 5:. B D=l,:.CD=�=2•CD在R t1,.AD C中,tan A=一—=1,AD:. AD=2,:. AB=AD+BD=3,故答案为:3.ABD17如图是某幢房屋及其屋外遮阳篷,已知遮阳篷的固定点A距离地面4米(即AB=4米),遮阳篷的宽度5AC为2.6米,遮阳篷与房屋墙壁的夹角a的余弦值为—,当太阳光与地面的夹角为60°时,遮阳篷在地13面上的阴影宽度BD为米.【答案】(2.4-石)【解析)【分析】本题考查解直角三角形的应用,先作CF上AB千点F,作CE上BD,交BD的延长线千点E,然后根据锐角三角函数和勾股定理,可以求得BE和DE的值,从而可以求得BD的值.【详解】解:作CF上AB千点F,作C E.L BD,交BD的延长线千点E,如图,5 由已知可得,AC=2.6米,cosa=—,LAFC=9()气AB=4米,13:. AF= AC-cos a = 2.6x —= 1 13...CF=J AC 2 -AF 2 =五言=2.4(米),BF=AB-AF = 4-1= 3(米),:.CE=BF=3米,CF=BE=2.4米,.乙CDE =60°,乙CED =90气:.DE= C E 3= = tan60°石石:. BD= B E-DE= (2.4-和(米)故答案为:(2.4-打)18如图,在梯形ABCD 中,ADIi BC, BC=3AD,点E 是AB 中点,如果点F 在DC 上,线段EF 把梯形分成而积相等的两个部分,那么——=DF D CA DB3 【答案l .:..##0.754【解析】【分析】木题考查梯形,相似三角形的判定和性质,三角形的面积,关键是由三角形的面积公式得到CFM=3FN,证明VFDM戎FCN,即可求解连接AF ,BF,过F 作MN_j_BC交BC 于N,交AD 延长线千M,由ADIi BC,得到MN_j_AD,由点E 是AB 中点,得到屾FAE 的面积=VFBE 的面积,由线段EF 把梯形分成面积相等的两个部分,得到6ADF 的面积=心BCF 的面积,由三角形面积公式得到FM=3FN,由YFDMcnYFCN,得到FD MF DF 3 —=—=3,即可求出——=-.FC NF DC 4【详解】解:连接AF ,BF ,过F作MN..1BC交BC于N,交AD延长线千M,A D M...夕.--�·: ADIi BC,:.MN..1.AD,了点E是AB中点,:..,.FAE 的面积=VFBE 的面积线段EF把梯形分成面积相等的两个部分,:.心AD F的面积=纽CF的面积,.. -AD· FM =-BC·FN , 2 2·: BC=3AD,:. FM =3FN,·: DMIICN,:. V FDM戎FCN,FD MF :.—=—=3, FC NFDF 3 ·-=-DC 4故答案为:一.34 三、解答题(本大题共7题,满分78分)19.计算即145°2 s in 60° -2cos 60°-lcot30°-ll.3-【答案)石2【解析)【分析】本题考查了实数的运算原式利用特殊角的三角函数值计算即可求出值,熟练掌握运算法则和特殊角的三角函数值是解本题的关键.【详解】tan45° 2si n 60°-2cos60°石l l -I石-112x 一-2x-2 2 =古-(石-I)=罕-扣l3-石=- -!cot 30° -II 20.已知抛物线y= x 2 +bx+c 经过点A(3,0),B(0,-3)(1)求抛物线表达式并写出顶点坐标;(2)联结AB,与该抛物线的对称轴交千点P,求点P的坐标.【答案】(1)抛物线表达式为y =x2-2.x -3;顶点坐标为(1,--4);(2)P (l ,-2)【解析J【分析】木题主要考查了二次函数的图象与性质,一次函数的图象与性质.(L)利用待定系数法和配方法解答即可;(2)利用待定系数法求得直线AB 的解析式,令x=l,求得Y 值,则结论可得.【小问l详解】解:抛物线y= x 2+bx+c 经过点A(3,0),B(0,-3), 9+3b =0{�::+c =O , b =-2 •{c =-3''...抛物线表达式为y="y =x " -2x -3;y = x 2 -2x -3= (x -1)2-4, .抛物线的顶点坐标为(1,-4);【小问2详解】解:设直线AB的解析式为y=kx+n,3k+n=0•{n= -3'{: :1-3直线AB的解析式为y=x-3. A B与该抛物线的对称轴交千点p,抛物线的对称轴为直线x=l,..当x=l时,y=1-3=-2.:. P(I,-2).2]如图,在ABC中,G是乙ABC的重心,联结AG并延长交BC千点D.AC(I)如果AB=a,A C =b,那么AD=(用向量a、b表示);(2)已知AD=6,AC=8,点E在边AC上,且L A GE=乙C,求AE的长.1 I2 2【答案】(l)-a+-b(2)3;【解析】【分析】本题主要考查了平面向量,三角形的巫心,相似三角形的判定与性质,(l)利用平面向量的定义解答即可;(2)利用三角形的重心的定义和相似三角形的判定与性质解答即可.【小问l详解】解:AB=a,AC=b,:. BC=B A+AC=-a+b·G是ABC的重心,联结AG并延长交BC千点D,:.A D为心ABC的BC边上的中线,即点D为BC的中点,1 1 -l -.. B D =-B C =--a .十-b2 2 2 __ _ _ _ 1-l -l -i -:. AD=AB+BD=a-.:...a+.:...b=.:...a+.:...b 2 2 2 2故答案为: 1 l-a+-b .2 2【小问2详解】·G 是._ABC 的重心,2 2 . ·. AG = -AD = -x6=4.3 3·LAGE=乙C,:._GAE c.n 1..CAD,AE AD :.-= AGAC AE 6 ..= - 4 8:. A E =3乙GAE =LCAD,22如图],某小组通过实验探究凸透镜成像的规律,他们依次在光具座上垂直放趾发光物箭头、凸透镜和光屏,并调整到合适的商度.如图2,主光轴l垂直千凸透镜MN,且经过凸透镜光心O,将长度为8匣米的发光物箭头AB进行移动,使物距oc 为32匣米,光线AO、BO传播方向不变,移动光屏,直到光屏上呈现一个清晰的像A'B',此时测得像距OD为12.8匣米.儿八牲广I(I)求像A'B'的长度,,.A[H2 (2)已知光线AP 平行干主光轴I'经过凸透镜MN 折射后通过焦点F,求凸透镜焦距OF 的长.【答案】(1)3.2厘米64 (2)—厘米.【解析l【分析】本题主要考查了相似三角形的应用,平行四边形的判定与性质等知识点,(I )利用相似三角形的判定与性质,通过证明丛OAB丑�O A'B'与6.0AC v>,OA'D 解答即可;(2)过点A'作A'E I OD交1\tlN于点E,利用平行四边形的判定与性质和相似三角形的判定与性质解答即可,熟练掌握相似三角形的判定与性质是解题的关键.【小问l详解】巾题意得:AB I MN I A'B', OC=32cm,OD=l2.8cm,AB=8cm,·: AB/I AB',:. LOAB-LOA'B',. AB OA..=A,B OA',·: AB/I AB',:. "OAC v>•QA'D,OA OCOA'OD. AB OCA'B'OD8 32A'B'12.8:. A'B'=3.2.占像A'B'的长度3.2厘米.【小问2详解】过点A'作A'E I OD交MN于点E,如图,`'I •';,·: A'E I OD, MN A'B',...四边形A'EOD为平行四边形,:. A'E=OD=l2.8cm,OE=A'D.同理:四边形ACOP为平行四边形,:. AP=0C=32cm,·: AP I CD, A'E I OD,:. AP J A'E,:.6AP沪ti.A'EO,PO AP 32 5=-=-=-,OE A'E 12.8 2PO 5=-A'D 2·: MN j: A'B',:. �PQF cn�'DF,PO OF 5= =-,A'D DF 25 64:. OF=-=-OD=—(厘米).7 7:.凸透镜焦距OF的长为—-厘米.723如图,在..ABC中,AB=AC,点D在边BC上,已知LAFD=乙B,边DF交AC千点E.(1)求证:AFCE=CD·FE;AB BC(2)连接AD,如果—-=——,求证:AD2 =AEAC.AF DF【答案】(l)见详解(2)见详解【解析】【分析】木题主要考查了等腰三角形的性质,相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.(I)利用等腰三角形的性质和相似三角形的判定与性质解答即可;(2)利用相似三角形判定与性质解答即可.【小问l详解】证明:·:AB=AC,..乙ABC=乙ACB,·:乙AFD=乙B,:.乙AFD=乙ACB.:乙AEF=乙DEC,:心AEF0立EC,AF FE :.-=— DC CE':.AF-CE=CD-FE;【小问2详解】AB BC ·:—=—乙AFD=乙B ,AF DF':.L:::,.ABC夕心AFD,...乙ACB=乙ADF,乙DAC=乙EAD,. ·. µADC O µAED,AD AC :.-= AE AD':. AD 2 = AE·AC.24在平面直角坐标系中,如果两条抛物线关千直线x=m对称,那么我们把一条抛物线称为另一条抛物线关千直线x=m的镜像抛物线(I)如图,已知抛物线y=x 2-2x顶点为A.XA@求该抛物线关千y轴的镜像抛物线的表达式;@已知该抛物线关千直线x=m 的镜像抛物线的顶点为B,如果tan LOBA =.:.(乙OBA 是锐角),求m 的4值.(2)已知抛物线y=�x 2 +bx+c(b> 0)的顶点为C,它的一条镜像抛物线的顶点为D,这两条抛物线4的交点为E(2,l ).如果CDE 是直角三角形,求该抛物线的表达式3 5 【答案J Cl) (D y = x 2 + 2x ;@--或-(2)y=�(x+2)2-34【解析】2 2【分析】Cl )@由y=x 2 -2x=(x-1) -1,可得A(l,-1),则该抛物线关千y 轴的镜像抛物线的顶点为A(-1,-1),然后求镜像抛物线的表达式即可:@当X=/11.在点A 左侧时,该抛物线关千直线X=m.的镜像抛物线的顶点为B(2m-l,-l),如图1-l ,连接AB 交Y 轴于点E,则OE=I,由tan 乙OBA =-,可4得BE=-2m+l=4,计算求解即可;如图1-2,当x=m 在点A 右侧时,同理可得,2m-1=4,计算求解即可;(2)如图2,由题意知,若A CDE 是直角三角形,则"CDE 是等腰直角三角形,则EH =CH =DH,设EH=CH =DH= t,由£(2,1),可得C(2-t,l -t),即抛物线表达式为4 y=�(x-2+t)2 +1-t,将E(2,J )代入得,l =�(2-2+t)2+1-t,求出满足要求的t.进而可得抛物4线的表达式.【小问l详解】@解:·:y=x 2-2x=(x-1}2-l, :. A(l,-1),...该抛物线关于y 轴的镜像抛物线的顶点为A(-1,-1),:.该抛物线关千y 轴的镜像抛物线的表达式为y=(x+Jf-1.即y=X 2 +2X;@当x =m 在点A 左侧时,·: A(l,-1),该抛物线关千直线x=m 的镜像抛物线的顶点为B,:. B(2m-l,-l),如图1-1,连接AB 交Y 轴千点E,则OE =l,vxx=m图1-1·: tan 乙OB A=.:....,1 4:. BE=-2m +l=4,3解得,m =-一;2如图1-2,当x=m在点A右侧时,I , , ,,, A x=m图1-2同理可得,2m-l =4,5解得,m =一;23.. 5 综上所述,m 的值为--或-;2 2【小问2详解】解:如图2,y,图2由题意知,若CDE是直角三角形,则CDE是等腰直角三角形,则EH=CH=DH,设EH=CH=DH=t,·: E(2,1),:. C(2-t,1-t), :.抛物线的表达式为= y -(x-2+t)2+l -t ,4 将E (2,l )代入y =�(4 �(x -2+t)2+1-t 得,I =�(2-2+1/ +1-t ,4 解得,t=4或t=O (舍去),:.抛物线的表达式为1=) -(x+2)2 -3.4 【点睛】木题考查了二次函数解析式,轴对称的性质,等腰三角形的判定与性质,正切等知识,熟练掌握二次函数解析式,轴对称的性质,等腰三角形的判定与性质,正切是解题的关键.25在直角梯形ABCD 中,ADI/BC,乙B=90°,AD=6, AB=4, BC> AD,乙ADC 的平分线交边BC 于点E,点F在线段DE 上,射线CF 与梯形ABCD 的边相交千点G.4(I)如图I,如果点G 与A 重合,当tan乙BCD =一时,求BE 的长:勹三C (2)如图2,如果点G在边AD 上,联结BG,当DG=4,且VCGBcnVBAG 时,求sin 乙BCD 的值;B 三((3)当F 是D E 中点,且AG =l 时,求CD 的长【答案](I) 4石(2)—(3)CD 的长为5或9+寸7【解析】【分析】(I )过点D 作DH .L BC 千点H,利用且角梯形的性质,矩形的判定与性质求得DH,利用直角三角形的边角关系定理求得CH,利用勾股定理求得CD,利用角平分线的定义和平行线的性质得到CD=CE,则BE=BC-CE,(2)过点D作DM..LBC千点M,利用(I)结论,勾股定理和相似三角形的判定与性质求得BC,CM,再利用等腰直角三角形的判定与特殊角的三角函数值解答即可;(3)利用分类讨论的方法分两种情况讨论解答:@当点G在AD上时,利用等腰三角形的三线合一的性质,全等三角形的判定与性质解答即可;@当点G在AB上时,连接DG,GE,延长DG,CG交千点N,利用勾股定理求得BE,利用相似三角形的判定与性质求得AN,再利用全等三角形的判定与性质解答即可.【小问l详解】尸`C·: A D Ii BC,乙B=90°,解:过点D作DH..L BC千点H,如图,:.乙BAD=90°,·:DH.LBC,:.四边形ABHD为矩形,:. DH= A B= 4, BH =AD= 6,4tan乙BCD=_:_,DH 4=-,CH 3:.CH =3,:.CD=�=S,QADII BC,...乙ADE=乙DEC,Q乙心E=乙CDE,...乙CDE=乙CED,:.CE=CD=S,:. BC=BH +CH =9,.·.BE= BC -CE= 9-5 =4:【小问2详解】过点D作DM..l BC千点M,如图,产三c由(1)知:AD=BM =6, DM =AB= 4, CD= C E,QDG=4,AD=6,:.AG=2,:.BG=�=2乔·: VCGB=VBAG,BG BC...乙BAG=乙CGB=90°,—=—AG BG'2石BC· ·. =2 2石':.BC=lO,:.CM=BC-BM=4,:.DM=CM=4,: ..,.D MC为等腰直角三角形,...乙BCD=乙CDM=45°,:.sin乙BCD=sin45°=—;【小问3详解】@当点G在AD上时,如图,三c由(1)知:CD=C E,·: F是DE中点,:.CF..l DE,『DF G:F D;乙CDF在6DGF几DCF中,乙DF G=乙DFC=90°.」氏F车DCF(ASA),:. DG =DC,QAG=l,A D=6,:.DG=5,:. C D=DG=5:@当点G在AB上时,连接DG,GE,延长DG,CG交于点N,如图,A D人'-二二2..-.一.一一··一G I''、·. 、·``、、、、`、E C由(1)知:CD=CE,·: F是D E中点,:.CF上DE,:.cc为DE的垂直平分线,:.GD=GE,:. G D2 =GE2,:. A G2 +A D2 = B G2 +BE2,:. 12 +62 =32 + B E2,:. BE=2打,·: ADIi BC,:. V A NGv>VBCG,AG ANBG B CI AN..-=3 BC在l::JJNF和"DCF中,{;:D F D F乙CDF,乙NFD=乙CF D=90°:.,.DNF轧DCF(AAS),:. CD=ND,设CD=x,则BC=CE+ B E= x+ 2打,AN=DN -DA= CD-DA= x-6,1x-6-=.. 3-x+2打':. x=9+打,:. CD=9+打,综上,CD的长为5或9+.J了【点睛】木题主要考查了直角梯形的性质,平行线的性质,矩形的判定与性质,直角三角形的性质,直角三角形的边角关系定理,勾股定理,全等三角形的判定与性质,相似三角形的判定与性质,角平分线的定义,等腰三角形的判定与性质,过梯形的上底的一点作高线是解决此类问题常添加的辅助线.。
2023年上海市杨浦区中考数学一模试卷及答案解析

2023年上海市杨浦区中考数学一模试卷一、选择题:(本大题共6题,每题4分,满分24分)1.(4分)下列函数中,二次函数是()A.y=x+1B.y=x(x+1)C.y=(x+1)2﹣x2D.2.(4分)已知点A(1,2)在平面直角坐标系xOy中,射线OA与x轴正半轴的夹角为α,那么cosα的值为()A.B.2C.D.3.(4分)已知一个单位向量,设、是非零向量,下列等式中,正确的是()A.B.C.D.4.(4分)如图,传送带和地面所成斜坡的坡度为1:3,它把物体从地面点A处送到离地面3米高的B处,则物体从A到B所经过的路程为()A.3米B.2米C.米D.9米5.(4分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,下列结论中,错误的是()A.B.C.D.6.(4分)如图,在△ABC中,AG平分∠BAC,点D在边AB上,线段CD与AG交于点E,且∠ACD=∠B,下列结论中,错误的是()A.△ACD∽△ABC B.△ADE∽△ACG C.△ACE∽△ABG D.△ADE∽△CGE二、填空题:(本大题共12题,每题4分,满分48分)7.(4分)求值:cot30°=.8.(4分)计算:=.9.(4分)如果函数f(x)=2x2﹣3x+1,那么f(2)=.10.(4分)如果两个相似三角形的周长比为2:3,那么它们的对应高的比为.11.(4分)已知点P是线段MN的黄金分割点(MP>NP),如果MN=10,那么线段MP =.12.(4分)已知在△ABC中,AB=13,BC=17,tan B=,那么AC=․13.(4分)已知抛物线y=ax2在对称轴左侧的部分是下降的,那么a的取值范围是.14.(4分)将抛物线y=x2﹣2x+3向下平移m个单位后,它的顶点恰好落在x轴上,那么m =.15.(4分)广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠与喷头的水平距离x(米)的函数解析式是y=﹣x2+6x(0≤x≤4).水珠可以达到的最大高度是(米).16.(4分)如图,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度为50厘米,小球在左右两个最高位置时,细绳相应所成的角为74°,那么小球在最高和最低位置时的高度差为厘米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)17.(4分)如图,已知在四边形ABCD中,∠DAB=90°,∠ABC=60°,AB=CB,点E、F分别在线段AB、AD上.如果CE⊥BF,那么的值为.18.(4分)如图,已知在矩形ABCD中,AB=6,BC=8,将矩形ABCD绕点C旋转,使点B恰好落在对角线AC上的点B′处,点A、D分别落在点A′、D′处,边A′B′、A′C分别与边AD交于点M、N,那么线段MN的长为.三、解答题:(本大题共7题,满分78分)19.(10分)在平面直角坐标系xOy中,点A(1,m)、B(3,n)在抛物线y=ax2+bx+2上.(1)如果m=n,那么抛物线的对称轴为直线;(2)如果点A、B在直线y=x﹣1上,求抛物线的表达式和顶点坐标.20.(10分)如图,已知△ABC中,点D、E分别在边AB和AC上,DE∥BC,且DE经过△ABC的重心G.(1)设,=(用向量表示);(2)如果∠ACD=∠B,AB=9,求边AC的长.21.(10分)如图,某条道路上通行车辆限速为60千米/小时,在离道路50米的点P处建一个监测点,道路的AB段为监测区.在△ABP中,已知∠A=45°,∠B=30°,车辆通过AB段的时间在多少秒以内时,可认定为超速?(精确到0.1秒)(参考数据:=1.732)22.(10分)新定义:由边长为1的小正方形构成的网格图形中,每个小正方形的顶点称为格点.如图,已知在5×5的网格图形中,△ABC的顶点A、B、C都在格点上.请按要求完成下列问题:=;sin∠ABC=;(1)S△ABC=S△ABC.(不要求写作法,(2)请仅用无刻度的直尺在线段AB上求作一点P,使S△ACP但保留作图痕迹,写出结论)23.(12分)已知:如图,在△ABC中,点D、E、F分别在边AC、BD、BC上,AB2=AD•AC,∠BAE=∠CAF.(1)求证:△ABE∽△ACF;(2)联结EF,如果BF=CF,求证:EF∥AC.24.(12分)已知在平面直角坐标系xOy中,抛物线x2+bx+c与x轴交于点A(﹣4,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求抛物线的表达式;(2)点P是直线AC上方抛物线上一点,过点P作PG⊥x轴,垂足为点G,PG与直线AC交于点H.如果PH=AH,求点P的坐标;(3)在第(2)小题的条件下,联结AP,试问点B关于直线CD对称的点E是否恰好落在直线AP上?请说明理由.25.(14分)已知在正方形ABCD中,对角线BD=4,点E、F分别在边AD、CD上,DE =DF.(1)如图,如果∠EBF=60°,求线段DE的长;(2)过点E作EG⊥BF,垂足为点G,与BD交于点H.①求证:;②设BD的中点为点O,如果OH=1,求的值.2023年上海市杨浦区中考数学一模试卷参考答案与试题解析一、选择题:(本大题共6题,每题4分,满分24分)1.【分析】利用二次函数定义进行解答即可.【解答】解:A、y=x+1是一次函数,不是二次函数,故此选项不合题意;B、y=x(x+1)是二次函数,故此选项符合题意;C、y=(x+1)2﹣x2可化为y=2x+1,不是二次函数,故此选项不合题意;D、y=不是二次函数,故此选项不符合题意.故选:B.【点评】此题主要考查了二次函数定义,关键是掌握二次函数的定义,一次函数、反比例函数定义.2.【分析】根据题意,画出相应的平面直角坐标系,然后根据勾股定理可以得到OA的长,从而可以计算出cosα的值.【解答】解:连接OA,作AB⊥x轴于点B,则∠ABO=90°,∵点A(1,2)∴OB=1,AB=2,∴OA===,∵射线OA与x轴正半轴的夹角为α,∴cosα===,故选:C.【点评】本题考查解直角三角形、坐标与图形的性质,解答本题的关键是明确题意,求出OA的长.3.【分析】长度不为0的向量叫做非零向量,向量包括长度及方向,而长度等于1个单位长度的向量叫做单位向量,注意单位向量只规定大小没规定方向,则可分析求解.【解答】解:A、得出的是向量n的方向不是单位向量,故不符合题意;B、符合向量的长度及方向,故符合题意;C、由于单位向量只限制长度,不确定方向,故不符合题意;D、左边得出的是向量m的方向,右边得出的是向量n的方向,两者方向不一定相同,故不符合题意.故选:B.【点评】本题考查了向量的性质.注意:平面向量既有大小,又有方向.4.【分析】由题意可得物体从A到B所经过的路程为AB的长,根据坡比求出AC的长,再根据勾股定理求出AB的长即可.【解答】解:∵BC:AC=1:3,∴3:AC=1:3,∴AC=9,∴AB===3,∴物体从A到B所经过的路程为3,故选:A.【点评】本题考查了轨迹,解直角三角形,知道坡比的概念是解题的关键.5.【分析】根据题意,易证明△ADC∽△ACB,△ADC∽△CDB,根据相似三角形的性质即可选择.【解答】解:∵CD⊥AB,∴∠ADC=∠ACB=90°,∵∠A=∠A,∴△ADC∽△ACB,∴,故A、B选项正确,不符合题意;故C选项错误,符合题意;∵CD⊥AB,∴∠ADC=∠CDB=90°,∵∠A+∠B=90°,∠DCB+∠B=90°,∴∠A=∠DCB,∴△ADC∽△CDB,∴,故D选项正确,不符合题意.故选:C.【点评】本题主要考查相似三角形的判定与性质,三角形相似的判定一直是中考考查的热点之一,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.6.【分析】根据相似三角形的判定逐一判定即可.【解答】解:∵∠ACD=∠B,∠CAD=∠BAC,∴△ACD∽△ABC,故A正确;∵△ACD∽△ABC,∴∠ADC=∠ACB,又∵∠BAG=∠CAE,∴△ADE∽△ACG,故B正确;∵AG平分∠BAC,∴∠BAG=∠CAE,又∵∠ACD=∠B,∴△ACE∽△ABG,故C正确;由已知条件无法证明△ADE∽△CGE,故D错误;故选:D.【点评】本题考查了相似三角形的判定,熟练掌握相似三角形的判定是解题的关键.二、填空题:(本大题共12题,每题4分,满分48分)7.【分析】根据特殊角的三角函数值直接写出即可.【解答】解:根据特殊角的三角函数值知:cot30°=,故答案为:.【点评】本题考查了特殊角的三角函数值,解题时牢记特殊角的三角函数值是关键.8.【分析】根据平面向量的加法法则计算即可.【解答】解:(﹣2)+=﹣+=+.故答案为:+.【点评】本题考查平面向量的加法法则,解题的关键是掌握平面向量的加法法则,属于中考常考题型.9.【分析】计算自变量为2对应的函数值即可.【解答】解:把x=2代入f(x)=2x2﹣3x+1得:f(2)=2×22﹣3×2+1=3.故答案为:3.【点评】本题考查了函数值:函数值是指自变量在取值范围内取某个值时,函数与之对应唯一确定的值.10.【分析】根据相似三角形的周长比等于相似比可求得其相似比,再根据对应高线的比等于相似比可得到答案.【解答】解:∵两个相似三角形的周长比为2:3,∴这两个相似三角形的相似比为2:3,∴它们的对应高的比为:2:3,故答案为:2:3.【点评】本题主要考查相似三角形的性质,掌握相似三角形的周长比、对应高线比等于相似比是解题的关键.11.【分析】由黄金分割的定义得PM=MN,即可得出结论.【解答】解:∵点P是线段MN的黄金分割点,MP>PN,MN=10,∴PM=MN=×10=5﹣5,故答案为:5﹣5.【点评】本题考查的是黄金分割的概念,把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,比值叫做黄金比.12.【分析】过A作AD⊥BC于D,解直角三角形求出BD和AD,求出CD,再根据勾股定理求出AC即可.【解答】解:过A作AD⊥BC于D,则∠ADB=∠ADC=90°,∵tan B=,AB=13,BC=17,∴设AD=5x,则BD=12x,在Rt△ABD中,AD2+BD2=AB2,即(5x)2+(12x)2=132,解得x=1(负值舍去),∴AD=5x=5,BD=12x=12,∴CD=BC﹣BD=17﹣12=5,由勾股定理得:AC===5.故答案为:5.【点评】本题考查了解直角三角形和勾股定理,能熟记锐角三角形函数的定义和勾股定理解此题的关键.13.【分析】由题意可得抛物线开口向上,进而求解.【解答】解:∵抛物线y=ax2在对称轴左侧的部分是下降的,∴抛物线开口向上,∴a>0,故答案为:a>0.【点评】本题考查二次函数的性质,解题关键是掌握二次函数图象与系数的关系.14.【分析】利用平移的性质得出平移后解析式,进而得出其顶点坐标.【解答】解:y=x2﹣2x+3=(x﹣1)2+2,∴将抛物线y=x2﹣2x+3沿y轴向下平移2个单位,使平移后的抛物线的顶点恰好落在x 轴上,∴m=2,故答案为:2.【点评】此题主要考查了二次函数的平移以及图形的旋转以及配方法求二次函数顶点坐标等知识,正确记忆二次函数平移规律是解题关键.15.【分析】先把函数关系式配方,求出函数的最大值,即可得出水珠达到的最大高度.【解答】解:∵y=﹣x2+6x,=﹣(x2﹣4x),=﹣[(x﹣2)2﹣4],=﹣(x﹣2)2+6,∴当x=2时,y有最大值6,∴水珠可以达到的最大高度为6米.故答案为:6.【点评】本题考查了二次函数的实际应用,关键是把二次函数变形,求出函数的最大值,此题为数学建模题,借助二次函数解决实际问题.16.【分析】当小球在最高位置时,过小球作小球位置最低时细绳的垂线,在构建的直角三角形中,可根据偏转角的度数和细绳的长度,求出小球最低位置时的铅直高度,进而可求出小球在最高位置与最低位置时的高度差.【解答】解:如图:过A作AB⊥OC于B.Rt△OAB中,OA=50厘米,∠AOB=74°÷2=37°,∴OB=OA•cos37°=50×cos37°.∴BC=OC﹣OB=50﹣50×cos37°=50(1﹣cos37°)≈50×0.2=10(厘米).故答案为:10.【点评】此题考查了三角函数的基本概念,主要是余弦概念及运算,关键把实际问题转化为数学问题加以计算.17.【分析】连接AC,过C作CG⊥AB于G,由AB=BC,∠ABC=60°,可得△ABC是等边三角形,即可得==,根据∠DAB=90°,CE⊥BF,可证△ABF∽△GCE,故==.【解答】解:连接AC,过C作CG⊥AB于G,如图:∵AB=BC,∠ABC=60°,∴△ABC是等边三角形,∴AG=AC=AB,∴CG==AG,∴==,∵∠DAB=90°,CE⊥BF,∴∠AFB+∠AEC=180°,∵∠AEC+∠CEG=180°,∴∠AFB=∠CEG,∵∠FAB=90°=∠CGE,∴△ABF∽△GCE,∴==,故答案为:.【点评】本题考查等边三角形的性质,涉及相似三角形的判定与性质,解题的关键是作辅助线,构造相似三角形解决问题.18.【分析】过点A′作A′E⊥AD于点E,先根据勾股定理求出AC=10,再根据旋转的性质可得BC=B′C=8,AB=A′B'=6,∠B=∠AB′M=∠A′B′C=90°,则AB′=2,再证明△AB′M∽△ADC,由相似三角形的性质求出B′M=,AM=,则A′M=,再证明△A′ME∽△AMB′,由相似三角形的性质求出A′E=,ME=,则DE=,设EN=x,则DN=,易证明△A′NE∽△CND,相似三角形的性质列出方程求解即可.【解答】解:如图,过点A′作A′E⊥AD于点E,∵在矩形ABCD中,AB=6,BC=8,∴AC=,∵将矩形ABCD绕点C旋转,使点B恰好落在对角线AC上的点B′处,∴BC=B′C=8,AB=A′B′=6,∠B=∠AB′M=∠A′B′C=90°,∵AB′=AC﹣B′C=10﹣8=2,∵∠AB′M=∠D,∠B′AM=∠CAD,∴△AB′M∽△ADC,∴,即,∴B′M=,AM=,∴A′M=A′B′﹣B′M=,∵A′E⊥AD,∴∠A′EM=∠AB′M,∵∠A'ME=∠AMB′,∴△A′ME∽△AMB′,∴,即,∴A′E=,ME=,∴AE=AM+ME=,∴DE=AD﹣AE=8﹣=,设EN=x,则DN=,∵∠A′EN=∠D=90°,∠A′NE=∠CND,∴△A′NE∽△CND,∴,即,解得:x=,∴EN=,∴MN=ME+EN==.故答案为:.【点评】本题主要考查矩形的性质、旋转的性质、勾股定理,相似三角形的判定与性质,正确作出辅助线,熟练掌握相似三角形的性质是解题关键.三、解答题:(本大题共7题,满分78分)19.【分析】(1)当m=n时,则点A和点B为抛物线上的对称点,然后利用抛物线的对称性确定对称轴;(2)先利用一次函数解析式确定点A、B的坐标,再把点A、B的坐标分别入y=ax2+bx+2得a、b的方程组,则解方程可得到抛物线解析式,然后把一般式配成顶点式得到抛物线的顶点坐标.【解答】解:(1)∵A(1,m)、B(3,n),m=n,∴点A和点B为抛物线上的对称点,∴抛物线的对称轴为直线x=2;故答案为:x=2;(2)把A(1,m)、B(3,n)分别代入y=x﹣1得m=0,n=2,∴A(1,0)、B(3,2),把A(1,0)、B(3,2)分别代入y=ax2+bx+2得,解得,∴抛物线解析式为y=x2﹣3x+2,∵y=x2﹣3x+2=(x﹣)2﹣,∴抛物线的顶点坐标为(﹣,﹣).【点评】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.也考查了二次函数的性质.20.【分析】(1)连接AG并延长交BC于M,由G是△ABC的重心,DE∥BC,可得===,而=,即得=;(2)证明△ACD∽△ABC,可得AC2=AB•AD,即得AC=3.【解答】解:(1)连接AG并延长交BC于M,如图:∵G是△ABC的重心,∴AG=2MG,∴=,∵DE∥BC,∴△ADG∽△ABM,△ADE∽△ABC,∴===,∴DE=BC,∵=,DE∥BC,∴=;故答案为:;(2)∵AB=9,由(1)知=,∴AD=6,∵∠A=∠A,∠ACD=∠B,∴△ACD∽△ABC,∴=,即AC2=AB•AD,∴AC2=9×6,解得AC=3(负值已舍去),∴边AC的长为3.【点评】本题考查平面向量和相似三角形的判定与性质,解题的关键是掌握相似三角形的判定定理.21.【分析】过P作PH⊥AB于H,由已知可得,PH=50米,在Rt△APH中,AH=PH=50米,在Rt△BPH中,BH==50≈86.6米,可得AB=AH+BH≈136.6米,而136.6÷=8.196(秒),即可得到答案.【解答】解:过P作PH⊥AB于H,如图:由已知可得,PH=50米,在Rt△APH中,∵∠PAH=45°,∴∠APH=∠PAH=45°,∴AH=PH=50米,在Rt△BPH中,tan30°=,∴BH==50≈86.6米,∴AB=AH+BH≈136.6米,∵60千米/小时=米/秒,而136.6÷≈8.2(秒),∴车辆通过AB段的时间在8.2秒以内时,可认定为超速.【点评】本题考查解直角三角形的应用,解题的关键是作辅助线,构造直角三角形解决问题.22.【分析】(1)由正方形面积减去三个直角三角形面积可求S△ABC,过A作AD⊥BC于D,用面积法可求AD的长,在Rt△ABD中可得sin∠ABC;(2)取格点E,F,连接EF交AB于P,由AE=BF可知AP=BP,从而AP=AB,=S△ABC,故P是满足条件的点.即可得S△ACP【解答】解:(1)由图可得:S△ABC=3×3﹣×1×3﹣×3×1﹣×2×2=4,过A作AD⊥BC于D,如图:∵וAD=4,∴AD=,∴sin∠ABC===,故答案为:4,;(2)如图:点P即为所求点.【点评】本题考查作图﹣应用与设计作图,设计三角形面积,锐角三角函数等知识,解题的关键是掌握相似三角形的性质和判定定理.23.【分析】(1)由AB2=AD•AC可得△ABC∽△ADB,有∠ACB=∠ABD,又∠BAE=∠CAF,故△ABE∽△ACF;(2)由△ABC∽△ADB,△ABE∽△ACF,可得=,=,即得=,而BF=CF,可得=,△EBF∽△DBC,从而∠BEF=∠BDC,EF∥AC.【解答】证明:(1)如图:∵AB2=AD•AC,∴=,∵∠BAC=∠DAB,∴△ABC∽△ADB,∴∠ACB=∠ABD,∵∠BAE=∠CAF,∴△ABE∽△ACF;(2)如图:由(1)知△ABC∽△ADB,△ABE∽△ACF,∴=,=,∴=,∵BF=CF,∴=,即=,∵∠EBF=∠DBC,∴△EBF∽△DBC,∴∠BEF=∠BDC,∴EF∥AC.【点评】本题考查相似三角形的判定与性质,解题的关键是掌握相似三角形的判定定理.24.【分析】(1)用待定系数法可得y=﹣x2﹣x+3;(2)由A(﹣4,0),C(0,3)可得直线AC解析式为y=x+3,AC==5,设P(m,﹣m2﹣m+3),可得PH=﹣m2﹣3m,由△AHG∽△ACO,可得AH=m+5,故﹣m2﹣3m=m+5,即可解得P(﹣,);(3)作B关于直线CD的对称点E,过E作EW⊥x轴于W,设BE交CD于K,由y=﹣x2﹣x+3得抛物线对称轴为直线x=﹣,B(1,0),证明△BDK∽△CDO,可得BK=,DK=,从而BE=2BK=2,又△EWB∽△DKB,即可得EW=2,BW =4,E(﹣3,2),由A(﹣4,0),P(﹣,)得直线AP解析式为y=2x+8,故E 在直线直线AP上.【解答】解:(1)把A(﹣4,0),C(0,3)代入x2+bx+c得:,解得,∴y=﹣x2﹣x+3;(2)如图:由A(﹣4,0),C(0,3)可得直线AC解析式为y=x+3,AC==5,设P(m,﹣m2﹣m+3),则H(m,m+3),∴PH=(﹣m2﹣m+3)﹣(m+3)=﹣m2﹣3m,HG=m+3,∵∠HAG=∠CAO,∠AGH=90°=∠AOC,∴△AHG∽△ACO,∴=,即=,∴AH=m+5,∵PH=AH,∴﹣m2﹣3m=m+5,解得m=﹣或m=﹣4(与A重合,舍去),∴P(﹣,);(3)点B关于直线CD对称的点E恰好落在直线AP上,理由如下:作B关于直线CD的对称点E,过E作EW⊥x轴于W,设BE交CD于K,如图:由y=﹣x2﹣x+3得抛物线对称轴为直线x=﹣,B(1,0),∴D(﹣,0),BD=,∵C(0,3),∴CD=,∵B,E关于直线CD对称,∴∠BKD=90°=∠DOC,BK=EK,∵∠CDO=∠BDK,∴△BDK∽△CDO,∴==,即==,∴BK=,DK=,∴BE=2BK=2,∵∠EWB=90°=∠DKB,∠WBE=∠DBK,∴△EWB∽△DKB,∴==,即==,∴EW=2,BW=4,∴OW=BW﹣OB=3,∴E(﹣3,2),由A(﹣4,0),P(﹣,)得直线AP解析式为y=2x+8,在y=2x+8中,令x=﹣3得y=2,∴E在直线直线AP上,即B关于直线CD对称的点E恰好落在直线AP上.【点评】本题考查二次函数的综合应用,涉及待定系数法,相似三角形的判定与性质,解题的关键是掌握相似三角形的判定定理.25.【分析】(1)可推出△BEF是等边三角形,从而BE=EF,设DE=DF=x,从而表示出EF和BE,进一步得出结果;(2)①延长EG,交BC于T,作CR∥ET,可证得△BCF≌△CDR,进而得出BE=ET,根据AD∥BC得出,从而得出;②作EQ⊥BD于Q,设DE=2a,从而AE=2﹣2a,EQ=DQ=a,在Rt△ABE 中可表示出BE2=4a2﹣8a+16,在Rt△EQH中,EH2=EQ2+HQ2=4a2﹣6a+9,由①知,,从而,从而得出,求得a的值,从而得出EQ,BE,EH,根据△BHG∽△EHQ可得出BG=,进一步得出结果.【解答】(1)解:如图1,连接EF,∵四边形ABCD是正方形,BD=4,∴AB=AD=CD=BC=2,∠A=∠C=∠ADC=90°,∵BE=BF,∴△ABE≌△CBF(HL),∴BE=BF,AE=CF,∴DE=DF,∵∠EBF=60°,∴BE=EF=BF,设DE=DF=x,则AE=2﹣x,EF=x,∴BE2=(2)2+(2﹣x)2=x2+16﹣4x,∴(x)2=x2+16﹣4x,∴x1=2﹣2,x2=﹣2﹣2(舍去),∴DE=2﹣2;(2)①证明:如图2,延长EG,交BC于T,作CR∥ET,∵ET⊥BF,∴CR⊥BF,∴∠RCD+∠BFC=90°,∵四边形ABCD是正方形,∴AD∥BC,∠ADC=∠BCD=90°,AD=CD,∴四边形CTER是平行四边形,∠DRC+∠RCD=90°,∴CR=ET,∠BFC=∠DRC,∴△BCF≌△CDR(AAS),∴CR=BF,∴ET=BF,∵BE=BF,∴BE=ET,∵AD∥BC,∴,∴;②如图3,作EQ⊥BD于Q,设DE=2a,则AE=2﹣2a,EQ=DQ=a,在Rt△ABE中,BE2=AB2+AE2=(2)2+(2﹣2a)2=4a2﹣8a+16,在Rt△EQH中,HQ=BD﹣DQ﹣BH=3﹣a,EH2=EQ2+HQ2=()2+(3﹣a)2=4a2﹣6a+9,由①知,,∴,∴,∴a1=0(舍去),a2=,∴EQ==,EH2=4×=,BE2=4×=,∴EH=,BE=,∵∠EQH=∠HGB=90°,∠EHQ=∠BHG,∴△BHG∽△EHQ,∴,∴,∴BG=,∵BF=BE=,∴FG=BF﹣BG==,∴=.【点评】本题考查了正方形的性质,等边三角形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解决问题的关键是作辅助线,构造全等三角形和相似三角形.。
上海市松江区2024年中考数学一模试卷和参考答案

松江区2024届第一学期期末质量监控试卷初三数学(满分150分,完卷时间100分钟) 2024.01考生注意:1.本试卷含三个大题,共25题;没有特殊说明,几何题均视为在同一个平面内研究问题.2.答题时,务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】 1. 下列函数中,属于二次函数的是(▲)(A )2y x =−;(B )2y x =; (C )221)y x x =−+(; (D )22y x =. 2. 在Rt △ABC 中,已知∠C =90°,∠A =α, BC =a ,那么AB 的长为(▲)(A )a sin α; (B )cos aα; (C )a sin α; (D )a cos α.3.关于二次函数22(1)y x 的图像,下列说法正确的是(▲)(A )开口向上; (B )经过原点;(C )对称轴右侧的部分是下降的; (D )顶点坐标是(1,0).4. 下列条件中,不能判定a ∥b 的是(▲)(A )a ∥c ,b ∥c ,其中0c ≠;(B )a c =−,2b c =;(C )2a b =− ;(D )||3||a b =. 5. 如图,在Rt △ABC 中,∠BAC =90°,斜边BC 上的高AH =3, 矩形DEFG 的边DE 在边BC 上,顶点G 、F 分别在边AB 、AC 上, 如果GF 正好经过△ABC 的重心,那么BD ·EC 的积等于( ▲ ) (A )4; (B )1; (C )1625; (D )925.6. 某同学对“两个相似的四边形”进行探究.四边形ABCD 和四边形A 1B 1C 1D 1是相似的图形,点A 与点A 1、点B 与点B 1、点C 与点C 1、点D 与点D 1分别是对应顶点,已知k B A AB=11.(第5题图)H G F AE CB D该同学得到以下两个结论:①四边形ABCD 和四边形A 1B 1C 1D 1的面积比等于2k ;②四边形ABCD 和四边形A 1B 1C 1D 1的两条对角线的和之比等于k . 对于结论①和②,下列说法正确的是( ▲ ) (A )①正确,②错误; (B )①错误,②正确; (C )①和②都错误;(D )①和②都正确.二、填空题(本大题共12题,每题4分,满分48分)7. 若12y x = ,则y x y =+ ▲ . 8.A 、B 两地的实际距离AB =250米,画在地图上的距离A ′B ′=5厘米,那么地图上的距离与实际距离的比是 ▲ .9. 某印刷厂一月份印书50万册,如果第一季度从2月份起,每月印书量的增长率都为x ,三月份的印书量为y 万册,写出y 关于x 的函数解析式是 ▲ .10.已知点P 是线段AB 的黄金分割点,且AP >BP ,如果AB =5,那么AP = ▲ . 11.在直角坐标平面中,将抛物线2(1)2y x =−++,先向左平移1个单位,再向下平移2个单位,那么平移后的抛物线表达式是 ▲ .12.如果一个二次函数图像的顶点在x 轴上,且在y 轴的右侧部分是上升的.请写出一个符合条件的函数解析式: ▲ .13.如图,一辆小车沿着坡度为1: 2.4的斜坡从A 点向上行驶了50米,到达B 点,那么此时该小车上升的高度为 ▲ 米.14.如图,梯形ABCD 中,AB ∥CD ,且43AB CD =,若AB m =, AD n =.请用m ,n 来表示AC = ▲ .15.如图,已知直线l 1、l 2、l 3分别交直线m 于点A 、B 、C ,交直线n 于点D 、E 、F ,且l 1∥l 2∥l 3,AB =2BC ,DF =6,那么EF = ▲ .16.如图,在梯形ABCD 中,AD ∥BC ,点E 是AD 的中点,BE 、CD 的延长线交于点F ,如果AD :BC =2:3,那么:EDF AEB S S △△= ▲ .nmA DE BCF(第15题图)l 3l 2 l 1 DBA(第18题图)(第14题图) C BAD (第16题图)(第13题图)水平面ABACB15° (第22题图)30°M17.在△ABC 中,AB = AC ,点D 、E 分别是边AB 、AC 的中点,BE 与CD 相交于点O ,如果△OBC 是等边三角形,那么tan ∠ABC = ▲ .18.如图,在矩形ABCD 中,AB =2,BC =3,将边AB 绕点A 逆时针旋转,点B 落在B '处,联结BB '、CB ',若90BB C ∠'=︒,则BB '= ▲ . 三、解答题(本大题共7题,满分78分) 19.(本题满分10分)二次函数y =ax 2+bx +c (a ≠0)的图像上部分点的横坐标x 、纵坐标y 的对应值如下表.x … 0 1 2 3 4 … y…3-1?3…(1)由表格信息,求出该二次函数解析式,并写出该二次函数图像的顶点D 的坐标;(2)如果该二次函数图像与y 轴交于点A ,点P (5,t )是图像上一点,求△P AD 的面积.20.(本题满分10分)如图,在△ABC 中,点D 、E 、F 分别在边AB 、AC 、BC 上,联结DE 、EF .已知ED BC ∥,EF AB ∥,AD =3,9DB =.(1)求BFFC的值; (2)若△ABC 的面积为16,求四边形BFED 的面积.21.(本题满分10分)已知:如图,△ABC 中,AB =15,BC =14, 4sin 5B =,AD ⊥BC 于D . (1)求AC 的长;(2)如果点E 是边AC 的中点,求cot ∠EBC 大小.22.(本题满分10分)如图,A 处有一垂直于地面的标杆AM ,热气球沿着 与AM 的夹角为15°的方向升空,到达B 处,这时 在A 处的正东方向200米的C 处测得B 的仰角为30° (AM 、B 、C 在同一平面内).求A 、B 之间的距离.(结果精确到1米,2 1.414)≈(第20题图)(第19题图)y xO (第21题图)CA23.(本题满分12分,其中每小题各6分)已知:如图,在△ABC 中,点D 、E 分别在边AB 、AC 上,DE ∥BC ,∠BDC =∠DEC . 求证:(1)△ADE ∽△ACD ;(2)AC AEBCCD =22.24.(本题满分12分,其中第(1)小题3分,第(2)小题4分,第(3)小题5分)在平面直角坐标系xOy 中,抛物线2(0)y ax bx+c a =+>的图像经过原点O (0, 0)、点A (1,3a ),此抛物线的对称轴与x 轴交于点C ,顶点为B . (1)求抛物线的对称轴;(2)如果该抛物线与x 轴负半轴的交点为D ,且∠ADC 的正切值为2,求a 的值; (3)将这条抛物线平移,平移后,原抛物线上的点A 、B 分别对应新抛物线上的点E 、P .联结P A ,如果点P 在y 轴上,P A ∥x 轴,且∠EP A =∠CBO ,求新抛物线的表达式.25.(本题满分14分,其中第(1)小题4分,第(2)小题第5分、第(3)题5分)在△ABC 中,AC =BC .点D 是射线AC 上一点(不与A 、C 重合),点F 在线段BC 上,直线DF 交直线AB 于点E ,2CD CF CB =⋅. (1)如图,如果点D 在AC 的延长线上. ①求证:DE BD =;②联结CE ,如果CE ∥BD ,CE =2,求EF 的长. (2)如果DF :DE =1:2,求:AE :EB 的值.(第23题图)AD BCE (第24题图)yxO DAB C EF(第25题图)(第25题备用图)BCA2023届第一学期九年级期末数学练习卷参考答案一、选择题(本大题共6题,每题4分,满分24分) 1.B 2. A 3. C 4. D 5. B 6. D二、填空题(本大题共12题,每题4分,满分48分)7.13; 8. 1:5000; 9. 250(1)y x =+; 10. 5552−; 11. 2(2)y x =−+; 12. 2=y x (答案不唯一); 13. 2501314. 34+m n ; 15. 2; 16. 12;17. 33 ; 18. 125.三、解答题(本大题共7题,满分78分)19.解:(1)∵图像过(0,3)、(4,3)∴该二次函数图像的对称轴为直线x =2, ∴顶点坐标为D (2,-1),设该二次函数的解析式为2(2)1y a x =−−, ∵当x =1时,y =0,∴0=a -1,得a =1.∴二次函数的解析式为2(2)1y x =−−,顶点D 的坐标为(2,-1). (2)当x =5时,y =8, ∴点P (5,8), 当当x =0时,y =3,∴A (0,3)分别过点P ,D 作y 轴的垂线,垂足分别为点B 、点C ,则16325922PBCD S =+⨯=梯形()12442ACD S =⨯⨯=△;1255522ABP S =⨯⨯=△∴6325415.22APD S =−−=△ 20.解:(1)∵DE ∥BC ,∴=AD AE BD EC∵AD =3,BD =9,∴31.93==AE EC ∵EF ∥AB , ∴1.3AE BF EC FC ==(2)∵DE ∥BC ,∴ADE ABC △∽△ ∴2()ADE ABC S AD S AB=△△, ∵△ABC S =16,∴21().164ADE S =△ 1.ADE S =△ (第19题图)yxO DPAB C(第20题图)同理可得23().164EFC S =△∴9.EFC S =△ ∴1619 6.BFED S =−−=21.解:(1)∵AD ⊥BC, AB =15,4sin 5B =,∴AD =15sin B=12. ∴BD =9, ∵BC =14,∴CD =5 ∴AC =13(2)联结BE ,过点E 作EH ⊥BC ,垂足为H ∵ E 为AC 的中点 EH ∥AD ,∴.EH EC CH ADACCD==∴ EH =6, CH =DH =2.5,∴BH =11.5∴ cot ∠EBC =11.523.612==BH EH 22(本题满分10分)解:过点A 作AH ⊥BC ,垂足为H .∵ ∠C =30°,AC =200,∴ AH =12AC =100∵AM ⊥AC ,∠BAM =15°∴ ∠BAC =105°, ∠ABC =45° ∴AB =°1002141sin 45AH =≈米答:A 、B 之间的距离约为141米.23. 证明:(1)∵∠BDC =∠DEC ∴∠ADC =∠AED ∵∠A =∠A ∴△ADE ∽△ACD (2)∵DE ∥BC ∴∠EDC =∠DCB ∵∠BDC =∠DEC ∴△BDC ∽△CED∴22=△△CDE BDC S CD S BC ∵DE ∥BC ∴=△△CDE BDC S DE S BC , =DE AE BC AC ∴ 22=CD AEBC AC24. 解(1)∵抛物线2(0)y ax bx+c a =+>的图像经过原点O (0, 0)、点A (1,3a ),CB AD EH ACB15° (第22题图)30°MH(第23题图)AD BCE∴3⎧⎨++=⎩c =0a b c a ∴2=⎧⎨⎩b ac =0∴抛物线的表达式22=+y ax ax ∵2122−=−=−b aa a∴抛物线的对称轴是:直线x =-1 (2)∵O (0, 0)对称轴是直线x =-1 ∴D (-2,0)过点A 作AH ⊥x 轴,垂足为H ,则AH =3a ,DH =3∴t a n ∠ADC =323==AH aDH∴ a =2(3)过点E 作EF ⊥P A ,垂足为F 当x =-1时,y =-a ,∴B (-1,-a ) ∵P A ∥x 轴 ∴P (0,3a )点B 到P 向右平移1个单位向上平移4a 个单位, ∴ PF =2,EF =4a∵tan ∠CBO =1=OC BC a tan ∠EP A =422==EF aa PF∵∠EPA =∠CBO∴12,=a a2=a∴新抛物线的表达式是2=+y 25.(1)①∵2CD CF CB =⋅ ∴=CF CDCD CB又∵∠DCB =∠FCD ∴△DCB ∽△FCD ∴∠DBC =∠FDC题图))DABCEF(第25题图)∵AC =BC ,∴∠A =∠CBA∠DEB =∠A +∠EDA ∠DBA =∠CBA +∠DBC ∴∠DEB = ∠DBA ∴DE =BD(1)②∵CE ∥DB ∴∠BDF =∠DEC 又∵DB =DE ,∠DBF =∠EDC ∴△DBF ≌△EDC ∴CE =DF =2 DE =DB =2+EF ∵=CE EF BD DF ∴222=+EFEF EF1− (EF=1舍去) (2)1º当点D 在AC 延长线上时 过点D 作DH ∥AB 交BC 的延长线于点H∵DH ∥AB DF :DE =1:2 ∴DH =EB ∠H =∠HBA =∠A 又∵∠DBH =∠EDA BD =DE ∴△BHD ≌△DAE ∴DH =AE =EB AE :EB =1 2º当点D 在边AC 上时过点D 作DG ∥AB 交BC 于点G同理△DCB ∽△FCD ∴∠DBC =∠FDC =∠EDA ∵∠CBA =∠CAB =∠E +∠EDA ∴∠E =∠DBA =∠GDB ∴DE =DB △BGD ≌△DAE ∴DG =AE又∵DF :DE =1:2,13==DG DF BE EF ∴AE :EB=13DABCE F (第25(2)题图)H(第25题备用图)BC ADFEG。
2023上海普陀区中考初三一模数学试题及答案

2023年上海市普陀区中考数学一模试卷一、选择题(共6题,每题4分,满分24分).1.(4分)下列函数图象中,与y 轴交点的坐标是(0,1)的是()A .2y x =B .21y x =-C .221y x =+D .22(1)y x =+2.(4分)在Rt ABC ∆中,已知90ACB ∠=︒,2tan 3B =,4AC =,那么BC 的长是()A .6B .3C .D .3.(4分)如果二次函数2()y x m k =-+的图象如图所示,那么下列说法中正确的是()A .0m >,0k >B .0m >,0k <C .0m <,0k >D .0m <,0k <4.(4分)如图,已知D 是AB 的中点,EA AB ⊥,CB AB ⊥,2AE AB BC ==,那么下列结论中错误的是()A .ED AC =B .EDAC ∠=∠C .ED AC ⊥D .30CAB ∠=︒5.(4分)已知k 为实数,a 是非零向量,下列关于ka 的说法中正确的是()A .如果0k =,那么0ka = B .如果k 是正整数,那么ka 表示k 个a 相加C .如果0k ≠,那么||||ka k a = D .如果0k ≠,ka 与a 的方向一定相同6.(4分)在ABC ∆和DEF ∆中,已知AB AC =,DE DF =,如果从下列条件中增添一个条件,ABC ∆与DEF ∆仍不一定相似,那么这个条件是()A .A D ∠=∠B .B E ∠=∠C .A E ∠=∠D .AB DE BC EF=二、填空题:(本大题共12题,每题4分,满分48分)7.(4分)已知32x y =,10x y +=,那么x y -=.8.(4分)已知反比例函数(0)k y k x =≠的图象在第一、三象限,如果120x x <<,那么1y 2y (填“>”、“<”或“=“)9.(4分)已知二次函数2(1)31y a x x =-+-的图象有最高点,那么a 的取值范围是.10.(4分)已知抛物线2(2)y mx m x =-+的对称轴是直线1x =,那么m 的值等于.11.(4分)已知点(1,)A a 在抛物线221y x =-+上,将此抛物线沿着y 轴向上平移3个单位,点A 随之平移到点A '的位置,那么点A '的坐标是.12.(4分)已知C 是线段AB 的中点,设AB a = ,那么AB BC +=.(用向量a 表示)13.(4分)在ABC ∆中,5AC =,12BC =,13AB =,那么sin B =.14.(4分)如图,在四边形ABCD 中,//AD BC ,BAC ADC ∠=∠,如果2AD =,5BC =,那么AC =.15.(4分)如图,方格纸上各小正方形的边长都为1,点A 、B 、C 、D 都在小正方形顶点的位置上,AD 与BC 交于点E ,那么BE 的长是.16.(4分)如图,ABC ∆中的一边BC 与双边平行且单位相同的刻度尺的一边重合,边AB 、AC 分别与刻度尺的另一边交于点D 、E ,点B 、C 、D 、E 在刻度尺上的读数分别为0、5、1、3,如果刻度尺的宽度为3,那么ABC ∆的面积是.17.(4分)如图,点D 、E 在ABC ∆的边BC 上,BAD C ∠=∠,B EAC ∠=∠,如果4BD =,3EC =,那么AB AC 的值是.18.(4分)如图,在ABC ∆中,AD 为边BC 上的中线,2BC AC =,6BC =,2AD =.将ADC ∆绕点D 以逆时针方向旋转得到△A DC '',点A '、C '分别与点A 、C 对应.联结BC ',BC '与线段AD 交于点G .如果点A '、A 、C '在同一条直线上,那么C G '=.三、解答题:(本大题共7题,满分78分)19.(10分)计算:22sin 604cot 30cos 302sin 45tan 45︒-︒⋅︒︒+︒.20.(10分)如图,已知梯形ABCD 中,//AD BC ,E 是BC 上一点,//AE CD ,AE 、BD 相交于点F ,:1:3EF CD =.(1)求BE AD的值;(2)联结FC ,设AB a = ,FE b = ,那么BF =,FC = .(用向量a 、b 表示)21.(10分)如图,在平面直角坐标系xOy 中,正比例函数(0)y kx k =≠的图象与反比例函数3(0)y x x=>的图象交于点(3,)A a .(1)求这个正比例函数的解析式;(2)将这个正比例函数的图象向上平移(0)m m >个单位,新函数的图象与反比例函数3(0)y x x=>的图象交于点B ,如果点B 的纵坐标是横坐标的3倍,求m 的值.22.(10分)如图,光从空气斜射入水中,入射光线AB射到水池的水面B点后折射光线BD 射到池底点D处,入射角30∠=︒;入射光线AC射到水池的水∠=︒,折射角22DBNABM面C点后折射光线CE射到池底点E处,入射角60ACM∠'=︒,折射角DE BC,MN、M N''为法线.入射光线AB、AC和折射光线BD、CE ∠'=︒.//40.5ECN及法线MN、M N''都在同一平面内,点A到直线BC的距离为6米.(1)求BC的长;(结果保留根号)(2)如果8.72DE=米,求水池的深.取1.41取1.73,sin22︒取0.37,cos22︒取0.93,tan22︒取0.4,sin40.5︒取0.65,cos40.5︒取0.76,tan40.5︒取0.85)⋅=⋅,ABE AED∠=∠.(1)求证:ABE ECD∆∆∽;(2)如果F 、G 、H 分别是AE 、DE 、AD 的中点,联结BF 、HF 、HG 、CG .求证:BF HF CG HG ⋅=⋅.24.(12分)在平面直角坐标系xOy 中(如图),抛物线22(0)y ax x c a =++≠与x 轴交于点A 、B ,其中点A 的坐标为(1,0),与y 轴交于点(0,3)C -.抛物线的顶点为D .(1)求抛物线的表达式,并写出点D 的坐标;(2)抛物线的对称轴上有一点M ,且点M 在第二象限,如果点M 到x 轴的距离与它到直线BD 的距离相等,求点M 的坐标;(3)抛物线上有一点N ,直线ON 恰好经过OBD ∆的重心,求点N 到x 轴的距离.25.(14分)如图,在矩形ABCD 中,3tan 4ABD ∠=,E 是边DC 上一动点,F 是线段DE延长线上一点,且EAF ABD∠=∠,AF与矩形对角线BD交于点G.(1)当点F与点C重合时,如果6AD=,求DE的长;(2)当点F在线段DC的延长线上,①求AGAE的值;②如果3DE CF=,求AED∠的余切值.参考答案一、选择题(共6题,每题4分,满分24分).1.(4分)下列函数图象中,与y 轴交点的坐标是(0,1)的是()A .2y x =B .21y x =-C .221y x =+D .22(1)y x =+【分析】把(0,1)代入解析式,解答即可.解:A .当0x =时,2001y =⨯=≠,不符合题意;B .当0x =时,20111y =⨯-=-≠,不符合题意;C .当0x =时,2011y =⨯+=,符合题意;D .当0x =时,22(01)21y =⨯+=≠,不符合题意;故选:C .【点评】本题考查的是二次函数图象上点的坐标特征,二次函数图象上的点都在该函数的图象上.2.(4分)在Rt ABC ∆中,已知90ACB ∠=︒,2tan 3B =,4AC =,那么BC 的长是()A .6B .3C .D .【分析】根据三角函数中正切值的定义解决此题.解:如图.在Rt ABC ∆中,90ACB ∠=︒,2tan 3B =,4AC =,42tan 3AC B BC BC ∴===.6BC ∴=.故选:A .【点评】本题主要考查正切值,熟练掌握正切值的定义是解决本题的关键.3.(4分)如果二次函数2()y x m k =-+的图象如图所示,那么下列说法中正确的是()A .0m >,0k >B .0m >,0k <C .0m <,0k >D .0m <,0k <【分析】根据解析式知,m ,k 是抛物线的顶点坐标,再根据函数图象得出结论.解:2()y x m k =-+ ,顶点坐标为(,)m k ,由图象可得,0m >,0k <,故选:B .【点评】本题考查了二次函数图象和系数的关系,解题的关键是能根据图象找出二次函数的顶点存在的特点、性质.4.(4分)如图,已知D 是AB 的中点,EA AB ⊥,CB AB ⊥,2AE AB BC ==,那么下列结论中错误的是()A .ED AC =B .EDAC ∠=∠C .ED AC ⊥D .30CAB ∠=︒【分析】用SAS 证明EAD ABC ∆≅∆,得ADE C ∠=∠,可证90AFD ∠=︒,从而说明A 、B 、C 正确.解:设AC 交DE 于点F .点D 是AB 的中点,AD DB ∴=,2AE AB BC == ,AD BC ∴=,EA AB ⊥ ,CB AB ⊥,90EAD B ∴∠=∠=︒,在EAD ∆和ABC ∆中,90AE BA EAD B AD BC =⎧⎪∠=∠=︒⎨⎪=⎩,()EAD ABC SAS ∴∆≅∆,ED AC ∴=,ADE C ∠=∠,90A C ∠+∠=︒ ,90A ADE ∴∠+∠=︒,AC DE ∴⊥,故选项A ,B ,C 正确.故选:D .【点评】本题主要考查了全等三角形的判定与性质,含30︒角的直角三角形的性质等知识,证明DAE ABC ∆≅∆是解题的关键.5.(4分)已知k 为实数,a 是非零向量,下列关于ka 的说法中正确的是()A .如果0k =,那么0ka = B .如果k 是正整数,那么ka 表示k 个a 相加C .如果0k ≠,那么||||ka k a = D .如果0k ≠,ka 与a 的方向一定相同【分析】若0k =,则0ka = ;当0k <时,||||ka k a =- ;当0k <时,ka 与a 的方向相反,由此可得答案.解:A .若0k =,则0ka = ,故A 选项错误,不符合题意;B .若k 是正整数,则ka 表示k 个a 相加,故B 选项正确,符合题意;C .当0k <时,||||ka k a =- ,故C 选项错误,不符合题意;D .当0k <时,ka 与a 的方向相反,故D 选项错误,不符合题意.故选:B .【点评】本题考查平面向量,熟练掌握平面向量的性质是解答本题的关键.6.(4分)在ABC ∆和DEF ∆中,已知AB AC =,DE DF =,如果从下列条件中增添一个条件,ABC ∆与DEF ∆仍不一定相似,那么这个条件是()A .A D ∠=∠B .B E ∠=∠C .A E ∠=∠D .AB DE BC EF=【分析】利用等腰三角形的性质以及相似三角形的判定解决问题即可.解:A 、由A D ∠=∠,可以根据两边成比例夹角相等,推出两三角形相似.本选项不符合题意;B 、由B E ∠=∠,可以推出A D ∠=∠根据两边成比例夹角相等,推出两三角形相似.本选项不符合题意;C 、由A E ∠=∠,不能判定两三角形相似.本选项符合题意;D 、由AB DE BC EF =,可以推出AB AC BC DE DF EF==,根据三边成比例两三角形相似,本选项不符合题意.故选:C .【点评】本题考查相似三角形的判定,等腰三角形的性质等知识,解题的关键是掌握相似三角形的判定方法,属于中考常考题型.二、填空题:(本大题共12题,每题4分,满分48分)7.(4分)已知32x y =,10x y +=,那么x y -=2.【分析】直接利用已知代入求出y 的值,即可得出x 的值,进而得出答案.解: 32x y =,10x y +=,32x y ∴=,则3102y y +=,解得:4y =,故6x =,那么642x y -=-=.故答案为:2.【点评】此题主要考查了比例的性质,正确将已知代入是解题关键.8.(4分)已知反比例函数(0)k y k x =≠的图象在第一、三象限,如果120x x <<,那么1y >2y (填“>”、“<”或“=“)【分析】先根据反比例函数(0)k y k x=≠的图象在第一、三象限可知0k >,故在每一象限内y 随x 的增大而减小,据此可得出结论.解: 反比例函数(0)k y k x=≠的图象在第一、三象限,0k ∴>,在每一象限内y 随x 的增大而减小.120x x << ,12y y ∴>.故答案为:>.【点评】本题考查的是反比例函数图象上点的坐标特点,先根据题意判断出函数的增减性是解题的关键.9.(4分)已知二次函数2(1)31y a x x =-+-的图象有最高点,那么a 的取值范围是1a <.【分析】根据二次函数的图象与性质即可求出答案.解:由题意可知:10a -<,1a ∴<,故答案为:1a <.【点评】本题考查二次函数图象与系数关系,解题的关键是熟练运用二次函数的图象与性质,本题属于中等题型.10.(4分)已知抛物线2(2)y mx m x =-+的对称轴是直线1x =,那么m 的值等于2.【分析】由对称轴公式可得到关于m 的方程,可求得答案.解:2(2)y mx m x =-+ 的对称轴是直线1x =,(2)12m m -+∴-=,解得:2m =.故答案为:2.【点评】本题主要考查二次函数的性质,掌握二次函数的对称轴公式是解题的关键,即2y ax bx c =++的对称轴为2b x a=-.11.(4分)已知点(1,)A a 在抛物线221y x =-+上,将此抛物线沿着y 轴向上平移3个单位,点A 随之平移到点A '的位置,那么点A '的坐标是(1,2).【分析】确定平移后得顶点坐标,再根据顶点式写出最后抛物线的解析式,进而解答即可.解:抛物线221y x =-+上,将此抛物线沿着y 轴向上平移3个单位,得到的抛物线是2213y x =-++,即224y x =-+,把1x =,y a =代入221y x =-+中,可得:21a -+=,解得:1a =-,∴点A '的坐标是(1,2),故答案为:(1,2).【点评】本题考查了二次函数的图象与几何变换,关键是根据平移的规律解答.12.(4分)已知C 是线段AB 的中点,设AB a = ,那么AB BC += 12a .(用向量a 表示)【分析】由题意得12BC a =- ,则11()22AB BC a a a +=+-= .解:C 是线段AB 的中点,AB a = ,∴12BC a =- ,∴11()22AB BC a a a +=+-= .故答案为:12a .【点评】本题考查平面向量,熟练掌握平面向量的加法运算法则是解答本题的关键.13.(4分)在ABC ∆中,5AC =,12BC =,13AB =,那么sin B =513.【分析】首先根据题意得出ABC ∆为直角三角形,再画出图形,其中5AC =,12BC =,13AB =;然后根据sin AC B AB=计算即可.解:5AC = ,12BC =,13AB =,222AC BC AB ∴+=,ABC ∴∆是直角三角形,如图所示:在Rt ABC ∆中,5AC =,12BC =,13AB =,则5sin 13AC B AB ==.【点评】本题考解直角三角形,牢记锐角三角函数的定义是解题关键.14.(4分)如图,在四边形ABCD 中,//AD BC ,BAC ADC ∠=∠,如果2AD =,5BC =,那么AC =【分析】先根据平行线的性质得到DAC ACB ∠=∠,加上BAC ADC ∠=∠,则利用相似三角形的判定方法可判断ABC DCA ∆∆∽,然后利用相似比可求出AC 的长.解://AD BC ,DAC ACB ∴∠=∠,BAC ADC ∠=∠ ,ABC DCA ∴∆∆∽,::AC AD BC AC ∴=,即:25:AC AC =,解得AC =,即AC ..【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.在应用相似三角形的性质时利用相似比进行几何计算.15.(4分)如图,方格纸上各小正方形的边长都为1,点A、B、C、D都在小正方形顶点的位置上,AD与BC交于点E,那么BE的长是 2.5.【分析】先根据勾股定理,得5BC=,再根据比例线段求出BE.解:连接BD,根据勾股定理,得5BC==,//AB CD,ABE DEC∴∆∆∽,∴AB BE CD EC=,∴245BE =,解得: 2.5BE=,故答案为:2.5.【点评】本题考查了相似三角形的判定与性质、勾股定理,掌握两个知识点的应用,推出比例线段是解题关键.16.(4分)如图,ABC∆中的一边BC与双边平行且单位相同的刻度尺的一边重合,边AB、AC分别与刻度尺的另一边交于点D、E,点B、C、D、E在刻度尺上的读数分别为0、5、1、3,如果刻度尺的宽度为3,那么ABC∆的面积是252.【分析】过点A作AF DE⊥,垂足为G,并延长AG交BC于点H,根据题意得:2DE=,5BC=,3GH=,//DE BC,从而可得ADE ABC∠=∠,AED ACB∠=∠,然后证明A字模型相似三角形ADE ABC∆∆∽,从而利用相似三角形的性质求出AH的长,最后利用三角形的面积公式进行计算,即可解答.解:过点A作AF DE⊥,垂足为G,并延长AG交BC于点H,由题意得:2DE=,5BC=,3GH=,//DE BC,ADE ABC∴∠=∠,AED ACB∠=∠,ADE ABC∴∆∆∽,∴DE AG BC AH=,∴23 5AHAH-=,解得:5AH =,ABC ∴∆的面积112555222BC AH =⋅=⨯⨯=,故答案为:252.【点评】本题考查了相似三角形的判定与性质,三角形的面积,平行线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.17.(4分)如图,点D 、E 在ABC ∆的边BC 上,BAD C ∠=∠,B EAC ∠=∠,如果4BD =,3EC =,那么AB AC 的值是233.【分析】由BAD C ∠=∠,B B ∠=∠,得BAD BCA ∆∆∽,有2AB BC BD =⋅,同理可得2AC BC CE =⋅,故2243AB BC BD BD AC BC CE CE ⋅===⋅,即可得答案.解:BAD C ∠=∠ ,B B ∠=∠,BAD BCA ∴∆∆∽,∴AB BD BC AB=,2AB BC BD ∴=⋅,B EAC ∠=∠ ,C C ∠=∠,ACE BCA ∴∆∆∽,∴AC CE BC AC=,2AC BC CE ∴=⋅,∴2243AB BC BD BD AC BC CE CE ⋅===⋅,∴3AB AC =,故答案为:3.【点评】本题考查相似三角形的判定与性质,解题的关键是掌握相似三角形的判定定理.18.(4分)如图,在ABC ∆中,AD 为边BC 上的中线,2BC AC =,6BC =,2AD =.将ADC ∆绕点D 以逆时针方向旋转得到△A DC '',点A '、C '分别与点A 、C 对应.联结BC ',BC '与线段AD 交于点G .如果点A '、A 、C '在同一条直线上,那么C G '=7.【分析】以D 为原点,DC 所在直线为x 轴建立直角坐标系,过A 作AH DC ⊥于H ,设A C ''交y 轴于M ,由AD 为边BC 上的中线,2BC AC =,6BC =,可得3BD CD AC ===,(3,0)B -,设DH m =,由22222AD DH AH AC CH -==-,可得23m =,故23DH =,423AH =,2(3A ,423,直线DA解析式为y =,根据将ADC ∆绕点D 以逆时针方向旋转得到△A DC '',可证//A C DC '',得四边形AMDH 是矩形,从而求得7(3C ',423,直线BC '解析式为23244y x =+,联立44y x y ⎧=+⎪⎨⎪=⎩得3(7G ,62)7,即可得到答案.解:以D 为原点,DC 所在直线为x 轴建立直角坐标系,过A 作AH DC ⊥于H ,设A C ''交y 轴于M,如图:AD 为边BC 上的中线,2BC AC =,6BC =,3BD CD AC ∴===,(3,0)B ∴-,设DH m =,则3CH m =-,22222AD DH AH AC CH -==- ,222223(3)m m ∴-=--,解得23m =,23DH ∴=,423AH =,2(3A ∴,423,由(0,0)D ,2(3A ,3得直线DA 解析式为y =, 将ADC ∆绕点D 以逆时针方向旋转得到△A DC '',AD A D '∴=,CAD C A D ''∠=∠,AA D A AD ''∴∠=∠,CAD A AD '∴∠=∠,AC CD = ,CAD ADC ∴∠=∠,A AD ADC '∴∠=∠,//A C DC ''∴,∴四边形AMDH 是矩形,23AM DH ∴==,423DM AH ==,AD A D '= ,23A M AM '∴==,27333C M A C A M ''''∴=-=-=,7(3C '∴,由(3,0)B -,7(3C '得直线BC '解析式为y =+联立23244y x y ⎧=+⎪⎨⎪=⎩得37627x y ⎧=⎪⎪⎨⎪=⎪⎩,3(7G ∴,)7,7C G '∴==,故答案为:7.【点评】本题考查三角形中的旋转问题,解题的关键是建立直角坐标系,求出相关点的坐标.三、解答题:(本大题共7题,满分78分)19.(10分)计算:22sin 604cot 30cos 302sin 45tan 45︒-︒⋅︒︒+︒.【分析】把特殊角的三角函数值代入计算即可.解:原式34=-==-=.【点评】本题考查了特殊角的三角函数值,熟练掌握特殊角的三角函数值是解题的关键.20.(10分)如图,已知梯形ABCD 中,//AD BC ,E 是BC 上一点,//AE CD ,AE 、BD 相交于点F ,:1:3EF CD =.(1)求BE AD的值;(2)联结FC ,设AB a = ,FE b = ,那么BF =2b a -,FC = .(用向量a 、b 表示)【分析】(1)根据题意可证明四边形AECD 为平行四边形,得到AE CD =,则:1:3EF AE =,:1:2EF AF =,易证明BEF DAF ∆∆∽,由相似三角形的性质即可求解;(2)由2AF EF =得2AF b =,3AE b =,由三角形法则求出BF 和BE ,再求出BC ,最后利用三角形法则即可求出FC .解://AD BC ,//AE CD ,∴四边形AECD 为平行四边形,AE CD ∴=,:1:3EF CD = ,:1:3EF AE ∴=,:1:2EF AF =,//AD BC ,BEF DAF ∴∆∆∽,∴12BE EF AD AF ==;(2)联结FC ,如图,由(1)可得2AF EF =,FE b = ,∴2AF b =,3AE b =,∴2BF AF AB b a =-=-,3BE AE AB b a =-=-,12BE AD =,AD EC =,∴2(3)62EC b a b a =-=-,∴36293BC BE EC b a b a b a =+=-+-=-,∴93272FC BC BF b a b a b a =-=--+=-.故答案为:2b a -,72b a -.【点评】本题主要考查平行四边形的判定与性质、相似三角形的判定与性质、平面向量,熟练三角形法则是解题关键.21.(10分)如图,在平面直角坐标系xOy中,正比例函数(0)y kx k=≠的图象与反比例函数3(0)y xx=>的图象交于点(3,)A a.(1)求这个正比例函数的解析式;(2)将这个正比例函数的图象向上平移(0)m m>个单位,新函数的图象与反比例函数3(0)y xx=>的图象交于点B,如果点B的纵坐标是横坐标的3倍,求m的值.【分析】(1)将点(3,)A a代入反比例函数3yx=,求出a的值,再待定系数法求正比例函数解析式即可;(2)设点B横坐标为t,则纵坐标为3t,根据点B的纵坐标是横坐标的3倍,列方程求出t的值,即可确定点B坐标,再将点B坐标代入13y x m=+,即可求出m的值.解:(1)根据题意,将点(3,)A a代入反比例函数3 yx =,得33a=,解得1a=,∴点A坐标为(3,1),将点(3,1)A代入正比例函数y kx=,得31k=,解得13 k=,∴正比例函数解析式为13y x =;(2)这个正比例函数的图象向上平移(0)m m>个单位,得13y x m =+,设点B横坐标为t,则纵坐标为3 t,点B的纵坐标是横坐标的3倍,∴33t t=,解得1t=或1t=-(舍),∴点B坐标为(1,3),将点B坐标代入13y x m =+,得133m =+,解得83 m=.【点评】本题考查了反比例函数与一次函数的交点问题,待定系数法求解析式,一次函数的图象与几何变换,熟练掌握待定系数法求解析式是解题的关键.22.(10分)如图,光从空气斜射入水中,入射光线AB射到水池的水面B点后折射光线BD 射到池底点D处,入射角30ABM∠=︒,折射角22DBN∠=︒;入射光线AC射到水池的水面C点后折射光线CE射到池底点E处,入射角60ACM∠'=︒,折射角40.5ECN∠'=︒.//DE BC,MN、M N''为法线.入射光线AB、AC和折射光线BD、CE 及法线MN、M N''都在同一平面内,点A到直线BC的距离为6米.(1)求BC的长;(结果保留根号)(2)如果8.72DE =米,求水池的深.取1.41取1.73,sin 22︒取0.37,cos 22︒取0.93,tan 22︒取0.4,sin 40.5︒取0.65,cos 40.5︒取0.76,tan 40.5︒取0.85)【分析】(1)根据题意和锐角三角函数,可以求得CF 和BF 的值,然后即可计算出BC 的值;(2)根据(1)中的结果和锐角三角函数,可以求得水池的深.解:(1)作AF BC ⊥,交CB 的延长线于点F ,则////AF MN M N '',ABM BAF ∴∠=∠,ACM CAF ∠'=∠,30ABM ∠=︒ ,60ACM ∠'=︒,30BAF ∴∠=︒,60CAF ∠=︒,6AF = 米,tan 3063BF AF ∴=⋅︒=⨯=(米),tan 606CF AF =⋅︒==(米),BC CF BF ∴=-=-=),即BC 的长为米;(2)设水池的深为x 米,则BN CN x ='=米,由题意可知:22∠'=︒.8.72DE=米,ECN∠=︒,40.5DBNN E CN x'='⋅︒≈(米),∴=⋅︒≈(米),tan40.50.85DN BN xtan220.4,+=+'DN DE BC N E∴+=+,0.48.720.85x x解得4x≈,即水池的深约为4米.【点评】本题考查解直角三角形的应用,解答本题的关键是明确题意,利用数形结合的思想解答.23.(12分)已知:如图,在四边形ABCD中,E为BC上一点,AB DE AE EC⋅=⋅,∠=∠.ABE AED(1)求证:ABE ECD∽;∆∆(2)如果F、G、H分别是AE、DE、AD的中点,联结BF、HF、HG、CG.求证:BF HF CG HG⋅=⋅.【分析】(1)将AB DE AE EC ⋅=⋅变形为AB AE EC DE=,由ABE AED ∠=∠,根据三角形的内角和定理推导出BAE CED ∠=∠,即可证明ABE ECD ∆∆∽;(2)根据三角形的中位线定理得//HF ED ,12HF ED =,12EG ED =,2AE AF =,2DE EG =,可证明四边形EFHG 是平行四形,则AF EF HG ==,再证明ABF ECG ∆∆∽,得BF AF HG CG EG HF==,所以BF HF CG HG ⋅=⋅.【解答】证明:(1)如图1,AB DE AE EC ⋅=⋅ ,∴AB AE EC DE =,ABE AED ∠=∠ ,180180ABE AEB AED AEB ∴︒-∠-∠=︒-∠-∠,180BAE ABE AEB ∠=︒-∠-∠ ,180CED AED AEB ∠=︒-∠-∠,BAE CED ∴∠=∠,ABE ECD ∴∆∆∽.(2)如图2,F 、G 、H 分别是AE 、DE 、AD 的中点,//HF ED ∴,12HF ED =,12EG ED =,2AE AF =,2DE EG =,//HF EG ∴,HF EG =,∴四边形EFHG 是平行四形,AF EF HG ∴==, 22AB AE AF AF EC DE EG EG===,BAF CEG ∠=∠,ABF ECG ∴∆∆∽,∴BF AF CG EG=,∴BF HG CG HF=,BF HF CG HG ∴⋅=⋅.【点评】此题重点考查三角形的内角和定理、相似三角形的判定与性质、三角形的中位线定理、平行线边形的判定等知识,证明四边形EFHG 是平行四形及ABF ECG ∆∆∽是解题的关键.24.(12分)在平面直角坐标系xOy 中(如图),抛物线22(0)y ax x c a =++≠与x 轴交于点A 、B ,其中点A 的坐标为(1,0),与y 轴交于点(0,3)C -.抛物线的顶点为D .(1)求抛物线的表达式,并写出点D 的坐标;(2)抛物线的对称轴上有一点M ,且点M 在第二象限,如果点M 到x 轴的距离与它到直线BD 的距离相等,求点M 的坐标;(3)抛物线上有一点N ,直线ON 恰好经过OBD ∆的重心,求点N 到x 轴的距离.【分析】(1)用待定系数法即可求解;(2)设点(1,)M m -,则MH m MN ==,在Rt BDH ∆中,21tan 42BH BDH DH ∠===,则sin4m BDH m ∠=+,即可求解;(3)直线ON 恰好经过OBD ∆的重心,则ON 为BD 边上的中线,由点B 、D 的坐标得BD 的中点坐标为(2,2)--,进而求解.解:(1)由题意得:320c a c =-⎧⎨++=⎩,解得:13a c =⎧⎨=-⎩,故抛物线的表达式为:223y x x =+-,则抛物线的对称轴为1x =-,则点(1,4)D --;(2)设抛物线的对称轴交x 轴于点R ,过点M 作MR BC ⊥于点R ,设点(1,)M m -,则MH m MR ==,在Rt BDH ∆中,21tan 42BH BDH DH ∠===,则sin 4MR m BDH MD m ∠==+,解得:1m =+,即点M的坐标为:(1)-+;(3) 直线ON 恰好经过OBD ∆的重心,则ON 为BD 边上的中线,由点B 、D 的坐标得BD 的中点坐标为(2,2)--,则直线ON 的表达式为:y x =,联立223y x x =+-和y x =并解得:x y ⎧=⎪⎪⎨⎪=⎪⎩,即点N 的坐标为113(2-,1132+-,故点N 到x轴的距离为:12+.【点评】本题考查了二次函数综合运用,涉及到重心的定义、解直角三角形、一次函数的应用等知识点,数形结合是本题解题的关键.25.(14分)如图,在矩形ABCD 中,3tan 4ABD ∠=,E 是边DC 上一动点,F 是线段DE 延长线上一点,且EAF ABD ∠=∠,AF 与矩形对角线BD 交于点G .(1)当点F 与点C 重合时,如果6AD =,求DE 的长;(2)当点F 在线段DC 的延长线上,①求AG AE的值;②如果3DE CF =,求AED ∠的余切值.【分析】(1)设DE x =,根据矩形的性质即解直角三角形推出8CD AB ==,8AE CE x ==-,根据勾股定理得到2226(8)x x +=-,据此求解即可;(2)①AE 交BD 于点M ,连接EG ,根据相似三角形的判定与性质推出AMG DME ∆∆∽,AMD GME ∆∆∽,ABD GAE ∆∆∽,根据相似三角形的性质得出AB AG BD AE=,设3AD a =,则4AB a =,根据勾股定理求出5BD a =,据此求解即可;②设3AD a =,则4CD AB a ==,设CF x =,且0a >,0x >,则4DF a x =+,根据锐角三角函数得到cot DE x AED AD a∠==,根据勾股定理求出AE =,AF =DGF BGA ∆∆∽,根据相似三角形的性质得AG AB FG DF =,进而求出13x a =,据此即可得解.解:(1)如图,当点F 与点C 重合时,设DE x =,四边形ABCD 是矩形,//AB CD ∴,AC BD =,12DG BD =,12CG AC =,90ADC BAD ∠=∠=︒,AB CD =,ABD BDC ∴∠=∠,DG CG =,683tan 4AD CD AB ABD ====∠,ACD BDC ∴∠=∠,EAF ABD ∠=∠ ,EAF ACD ∴∠=∠,8AE CE x ∴==-,90ADC ∠=︒ ,222AD DE AE ∴+=,即2226(8)x x +=-,74x ∴=,74DE ∴=;(2)①如图,AE 交BD 于点M ,连接EG ,由(1)得,EAF BDC ∠=∠,AMG DME ∠=∠ ,AMG DME ∴∆∆∽,∴AM GM DM EM=,又AMD GME ∠=∠ ,AMD GME ∴∆∆∽,ADB GEA ∴∠=∠,ABD EAF ∠=∠ ,ABD GAE ∴∆∆∽,∴AB AG BD AE=,3tan 4AD ABD AB ∠== ,∴设3AD a =,则4AB a =,5BD a ∴===,∴4455AG AB a AE BD a ===;②如图,连接EG ,3tan 4AD ABD AB ∠== ,∴设3AD a =,则4CD AB a ==,设CF x =,且0a >,0x >,则4DF a x =+,3DE CF = ,3DE x ∴=,3cot 3DE x xAED AD a a ∴∠===,AE ==,AF ,//AB CD ,DGF BGA ∴∆∆∽,∴AG ABFG DF =,44aa x =+,AG ∴=,由①得,45 AGAE=,54AG AE∴=,54∴=,两边平方并整理得,22(3)(7)(3287)0x a x a x ax a-+++=,a>,0x>,30x a∴- ,2232870x ax a++>,30x a∴-=,∴13xa=,1 cot3AED∴∠=,即AED∠的余切值1 3.【点评】此题是相似综合题,考查了相似三角形的判定与性质、矩形的性质、解直角三角形等知识,熟练掌握相似三角形的判定与性质、矩形的性质、解直角三角形并作出合理的辅助线是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于上海中考一模数学考试范围的解读
上海中考一模数学考试范围包括但不限于以下几个方面:
1. 数学基础知识:包括数与式的运算、函数和函数的相关概念、方程与不等式、初步统计、相交线与平行线、相似三角形、四边形、圆与正方形等。
这些知识点会以选择题和填空题的形式进行考查,题量通常为4道选择题和12道填空题。
例如,可能会考查学生对三角形全等的判定方法、勾股定理的应用、一次函数的性质和图像、二次函数的图像和性质等基础知识的理解和掌握程度。
2. 数学运算能力:包括数值计算、代数式的化简求值、函数的求值等。
这些知识点会以选择题、填空题和解答题的形式进行考查,其中解答题的难度相对较大。
例如,可能会考查学生对有理数的加减乘除、乘方和开方等基本运算的掌握程度,或者考查学生根据函数图像求函数解析式等问题的解决能力。
3. 数学思维能力:包括逻辑推理、归纳分类、化归思想等。
这些知识点通常以选择题和填空题的形式进行考查,但也有可能在解答题中出现。
例如,可能会考查学生根据已知条件推导出结论、对不同情况进行分析和分类、利用化归思想解决复杂问题的能力等。
【总结】
总的来说,上海中考一模数学考试范围非常广泛,需要学生全面掌握初中数学的基础知识和基本技能,同时注重数学思维能力的培养和提高。
建议学生在备考期间多做历年真题和模拟题,了解考试形式和难度,同时加强数学基础知识的巩固和复习。
