【免费下载】统计学专业经典案例分析
医学统计学案例分析2

案例分析—四格表确切概率法【例1-5】为比较中西药治疗急性心肌梗塞的疗效,某医师将27例急性心肌梗塞患者随机分成两组,分别给予中药和西药治疗,结果见表1-4。
经检验,得连续性校正χ22=3.134,P>0.05,差异无统计学意义,故认为中西药治疗急性心肌梗塞的疗效基本相同。
表1-4两种药物治疗急性心肌梗塞的疗效比较药物有效无效合计有效率(%)中药12(9.33)2(4.67)1485.7西药6(8.67)7(4.33)1346.2合计1892766.7【问题1-5】(1)这是什么资料?(2)该资料属于何种设计方案?(3)该医师统计方法是否正确?为什么?【分析】(1)该资料是按中西药的治疗结果(有效、无效)分类的计数资料。
该资料是按中西药的治疗结果(有效、无效)分类的计数资料完全随机设计方案。
(2)27例患者随机分配到中药组和西药组,属于例患者随机分配到中药组和西药组,属于完全随机设计方案(3)患者总例数n=27<40,该医师用χ2检验是不正确的。
当n<40或T<1时,不宜计算χ2值,需采用四格表确切概率法(exact probabilities in2×2table)直接计算概率案例分析-卡方检验(一)【例1-1】某医师为比较中药和西药治疗胃炎的疗效,随机抽取140例胃炎患者分成中药组和西药组,结果中药组治疗80例,有效64例,西药组治疗60例,有效35例。
该医师采用成组t检验(有效=1,无效=0)进行假设检验,结果t=2.848,P=0.005,差异有统计学意义检验,故认为中西药治疗胃炎的疗效有差别,中药疗效高于西药。
【问题1-1】(1)这是什么资料?(2)该资料属于何种设计方案?(3)该医师统计方法是否正确?为什么?(4)该资料应该用何种统计方法?【分析】(1)该资料是按中西药疗效(有效、无效)分类的该资料是按中西药疗效(有效、无效)分类的二分类资料,即计二分类资料,即计数资料。
(2)随机抽取140例胃炎患者分成西药组和中药组,属于属于完全随机设完全随机设计方案。
医学统计学案例分析(1)

案例分析—四格表确切概率法【例1-5】为比较中西药治疗急性心肌梗塞的疗效,某医师将27例急性心肌梗塞患者随机分成两组,分别给予中药和西药治疗,结果见表1-4。
经检验,得连续性校正χ2=3.134,P>0.05,差异无统计学意义,故认为中西药治疗急性心肌梗塞的疗效基本相同。
表1-4 两种药物治疗急性心肌梗塞的疗效比较药物有效无效合计有效率(%)中药12(9.33)2(4.67)1485.7西药 6(8.67)7(4.33)1346.2合计1892766.7【问题1-5】(1)这是什么资料?(2)该资料属于何种设计方案?(3)该医师统计方法是否正确?为什么?【分析】(1) 该资料是按中西药的治疗结果(有效、无效)分类的计数资料。
(2) 27例患者随机分配到中药组和西药组,属于完全随机设计方案。
(3) 患者总例数n=27<40,该医师用χ2检验是不正确的。
当n<40或T<1时,不宜计算χ2值,需采用四格表确切概率法(exact probabilities in 2×2 table)直接计算概率案例分析-卡方检验(一)【例1-1】某医师为比较中药和西药治疗胃炎的疗效,随机抽取140例胃炎患者分成中药组和西药组,结果中药组治疗80例,有效64例,西药组治疗60例,有效35例。
该医师采用成组t检验(有效=1,无效=0)进行假设检验,结果t=2.848,P=0.005,差异有统计学意义检验(有效=1,无效=0)进行进行假设检验,结果t=2.848,P=0.005,差异有统计学意义,故认为中西药治疗胃炎的疗效有差别,中药疗效高于西药。
【问题1-1】(1)这是什么资料?(2)该资料属于何种设计方案?(3)该医师统计方法是否正确?为什么?(4)该资料应该用何种统计方法?【分析】(1) 该资料是按中西药疗效(有效、无效)分类的二分类资料,即计数资料。
(2) 随机抽取140例胃炎患者分成西药组和中药组,属于完全随机设计方案。
统计学教学案例(精选)

用于研究不同组别间均值差异的显著性,判断因素对结果的影响是 否显著。
回归分析
用于研究变量之间的关系,通过建立回归方程预测因变量的取值。
应用实例
在农业生产中,通过方差分析比较不同施肥方案对作物产量的影响 ,利用回归分析预测未来产量趋势。
04 非参数统计案例
非参数检验方法简介
非参数检验的定义与特点
先验概率
根据以往经验和分析得到的概率。
似然函数
表示在给定参数下,观测数据出现的概率。
后验概率
在得到新的观测数据后,对先验概率进行更新得到的概率。
贝叶斯网络模型构建与评估
贝叶斯网络
一种概率图模型,用于表示变 量间的依赖关系。
网络结构学习
通过数据学习贝叶斯网络的结 构,即变量间的依赖关系。
参数学习
在已知网络结构的情况下,通 过数据学习变量的条件概率分 布。
提高统计软件应用能力
通过实践操作,学生应熟练掌握至少一种统计软 件(如SPSS、R、Python等),提高数据处理 和分析效率。
统计学发展趋势探讨
大数据与人工智能融合
随着大数据和人工智能技术的不 断发展,统计学将更加注重与这 些技术的融合,提高数据处理和 分析的智能化水平。
跨领域应用拓展
统计学将在更多领域发挥重要作 用,如生物医学、环境科学、社 会科学等,为跨学科研究提供有 力支持。
频数分布表
通过分组整理数据,展示 各组数据的频数,直观反 映数据的分布情况。
直方图与条形图
利用图形展示数据的分布 情况,便于观察数据的分 布规律。
概率密度函数
描述连续型随机变量的分 布情况,反映数据在不同 取值范围内的概率大小。
数据集中趋势度量
统计学案例分析

52
案例 讨论 二
构成比
某组成部分的观察单位 各组成部分的观察单位
数 数
*100 %
率
发生某事件的观察单位 数 可能发生某事件的观察 单位总数
*100
%
发病率
观察期内新发病的例数 同期内可能发生该病的 平均人数
*
K
患病率
时点现患病人数 检查人口数
案例 讨论 二
首先,通过题目分析可知该题测得的不是发病率,而是相
95.8 98.3 98.7
均数为 S
S2
(X - X)2
n -1
2614.92 3.32 238-1
17.5~
18.5
0
0
235Leabharlann 98.7=1699/238=7.14(μ mol∕kg)
19.5~21.5
20.5
3
1.3
238
100
合计
—
238
100
—
— 标准差为
x
案例
讨论
一
经案例分析可知该发汞结果测定为 偏态分布,因为均数(average)适用于对 称分布或偏度不大的资料,尤其适合正 态分布。标准差(standard deviations)同 样适用于近似正态分布。所以不能选用 均数与标准差来计算该企业法功的平均 水平与变异程度。
患病
20~
333
3
0.9
712
11
1.5
率
30~
301
4
1.3
142
9
6.3
40~
517
64
12.4
185
27
统计学案例
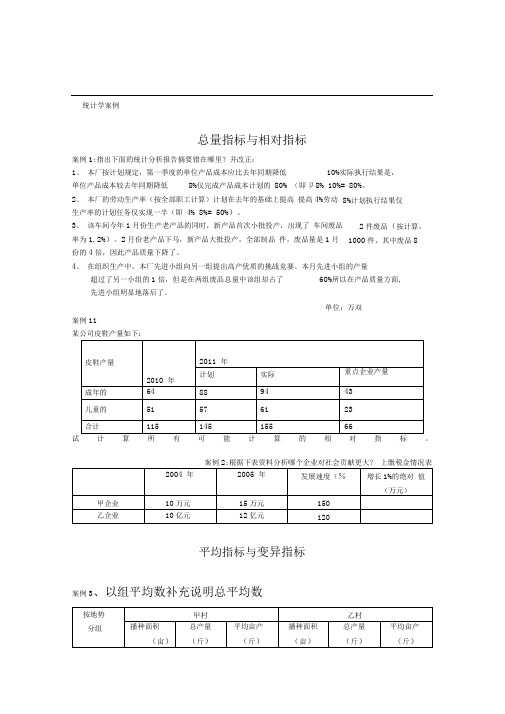
总量指标与相对指标案例1:指出下面的统计分析报告摘要错在哪里?并改正:1、 本厂按计划规定,第一季度的单位产品成本应比去年同期降低10%实际执行结果是,单位产品成本较去年同期降低8%仅完成产品成本计划的 80% (即卩8% 10%= 80%。
2、 本厂的劳动生产率(按全部职工计算)计划在去年的基础上提高 提高4%劳动生产率的计划任务仅实现一半(即 4% 8%= 50%)。
3、 该车间今年1月份生产老产品的同时,新产品首次小批投产,出现了 车间废品率为1.2%)。
2月份老产品下马,新产品大批投产,全部制品 件,废品量是1月份的4倍,因此产品质量下降了。
4、 在组织生产中,本厂先进小组向另一组提出高产优质的挑战竞赛。
本月先进小组的产量超过了另一小组的1倍,但是在两组废品总量中该组却占了 60%所以在产品质量方面,先进小组明显地落后了。
单位:万双案例11某公司皮鞋产量如下:试。
案例2:根据下表资料分析哪个企业对社会贡献更大? 上缴税金情况表平均指标与变异指标案例3、以组平均数补充说明总平均数统计学案例8%计划执行结果仅 2件废品(按计算, 1000件,其中废品8案例4:某单位有10个人,其中1人月工资为10万元,9人每人月工资为1000元。
该单位 职工月平均工资为 10900元。
即:100000 1000 9 “ccc" 10900(兀)以上报告所用平均指标是否恰当?如果不恰当应如何改正?案例6、变异指标与平均指标的结合运用案例6-1 :根据下表资料分析哪个企业平均工资更有代表性?案例7、录取中有无歧视?财经系(文科)和工程系(理科)。
该校报考及录取的总体表某高校的报考及录取情况10你认为这个平均数有代表性吗?如果缺乏代表性应如何改正? 案例5:以下是各单位统计分析报告的摘录本局所属30个工厂,本月完成生产计划的情况是不一致的。
完成计划90%勺有3个,完 成96%勺有5个,完成102%勺有10个,完成110%勺有8个,完成120%的有4个。
医学统计学案例分析.

Thanks!
•
(4)确定P值做出推断
•
在进行统计学分析过程中,一定要熟悉资料类型,什么
•
资料要用什么统计方法,各种检验方法的使用条件,且不能
•
乱用,或在用时犯一的错误。
案例分析四
据表资料,问三种产妇在产后一个月内泌乳量有无差别
乳量 无 少 多
合计
早产 30 36 31 97
足月产 132 292 414 838
住院日、费用。等级“很好、好、一般、差”的定义见表一,病人医 疗质量各等级频数分布见下表二。
指标
表一 很好、好、一般、差的标准
很好
好
一般
疗效
治愈
显效
好转
住院日(天)
≤15
16-20
21-25
差 无效 >25
费用(元)
≤1400 1400-1800 1800-2200
>2200
• 1.本题的研究员用卡方检验对本题做了统计推断而我们知道卡方检验 用于计数或计量资料,而本题是一个等级资料。
1 n2
v 8,t0.05/2 2.036, P 0.05,按照 0.05 的水准,不能拒绝H 0 ,差异无统计
学意义,上不能认为饲养中添加熊去氧胆酸对大鼠脂肪肝有预防作用。
而另一位研究者采用两独立样本的秩和检验,T=39查界值
表,得0.01<P<0.02,按 0.05的水准,拒绝 H0,差异有统计
• 小结
• 卡方检验的用途: • (1)比较两个或多个独立样本频率或独立样本频率分布。
(2)比较配对设计两样本频率分布。 (3)单样本分布的拟合优度。、 注意事项:单项有序的行X列表,不宜用卡方检验比较两组效应,若做卡
卫生统计学案例分析二
总体均数的置信区间与参考值范围的区别联系
• 参考值范围:
案例二
• 已知正常成年男子血红蛋白均值为140g/L,今随机调 查某厂成年男子60人,测其血红蛋白均值为125g/L, 标准差15g/L。故认为该厂成年男子血红蛋白均值低于 一般成年男子。 • (1)该结论是否正确?为什么? • (2)有研究者根据该资料估计该地成年男子血红蛋白 均值为125g/L,该结论是否正确?为什么?(解法如第一题) • (3)解决此类问题可采用哪些统计分析方法?这些方 法有什么区别和联系?
• 3.男性血红蛋白含量的参考值范围:
• 女性血红蛋白含量的参考值范围:
• 制定参考值范围需要注意:
• 1.所谓正常人不是指完全正常的人,而是指排除了影响所研究指标的 疾病和有关因素的同质人群。 • 2.选择足够大的人群为调查对象, • 3.样本数量足够大(n》100) • 4.确定去单侧还是双侧正常值范围, • 5.选择适当的百分界限, • 6.选择正确的方法(百分位数法或近似正态法)。
谢 谢!
• (1)这是什么资料?该资料属于何种设计方案? • (2)拟比较三组小鼠细胞免疫功能是否有差异,可以采用哪些 统计方法?用该方法的条件是什么?思想是什么? • (3)如果想知道党参组和黄芪组小鼠细胞免疫功能是否有差异, 可以采用哪些统计方法? • (4)该研究者的统计处理方法是否正确?为什么?
案例六
• • •
• • • •
(1)该资料属于什么资料类型? (2)该资料属于何种设计方案? (3)比较治疗前后血红蛋白是否有差别可采用什么 统计方法?用该方法的条件是什么? (4)该医生的结论是否正确?为什么?
案例四
• 分别测得13名健康人和13名Ⅲ度肺气肿病人痰中抗胰蛋白酶含 量(g/L)如下表。某研究者根据此资料先计算差值并进行正态性 检验,服从统计后应用配对t检验:t=-5.276,P=0.000,故认为 Ⅲ度肺气肿病人痰中抗胰蛋白酶含量高于健康人。 • 健康人:2.7 2.2 4.1 4.3 2.6 1.9 1.7 0.6 1.9 1.3 1.5 1.7 1.3 • Ⅲ度肺气肿患者 :3.6 3.4 3.7 5.4 3.6 6.8 4.7 2.9 4.8 5.6 4.1 3.3 4.3 • • (1)请用excel计算健康人和Ⅲ度肺气肿病人痰中抗胰蛋白酶 含量的均数和标准差(请注明步骤)。 • (2)欲比较两组抗胰蛋白酶含量是否有差异,可以采用哪些统 计方法?用该方法的条件是什么?T 检验相关内容 (3)该医生的统计处理方法是否正确?为什么?(两独立样本 资料的t检验)
统计学数据分析案例
统计学数据分析案例在统计学中,数据分析是一项重要的工作。
通过对数据的收集、整理、分析和解释,我们可以发现数据背后的规律和趋势,为决策提供支持和参考。
下面,我们将通过几个实际案例来展示统计学数据分析的应用。
案例一,销售数据分析。
某公司在过去一年的销售数据显示,不同产品的销售额有所不同。
为了更好地了解产品销售情况,我们对销售额进行了统计分析。
通过对比不同产品销售额的均值、中位数和标准差,我们发现其中一款产品的销售额波动较大,而另一款产品的销售额相对稳定。
结合市场情况和产品特点,我们提出了针对性的销售策略建议,以优化产品组合和提高销售效益。
案例二,用户行为数据分析。
某互联网平台收集了大量用户的行为数据,包括浏览量、点击量、购买量等。
我们通过对用户行为数据的分析,发现了不同用户群体的行为特点。
通过构建用户行为模型,我们可以预测用户的行为偏好和购买意向,为平台运营和营销活动提供了有力的数据支持。
案例三,医疗数据分析。
在医疗领域,数据分析对于疾病预测、诊断和治疗具有重要意义。
通过对患者的临床数据进行统计分析,我们可以发现不同疾病的发病规律和影响因素。
同时,结合医学知识和统计模型,我们可以建立疾病预测和诊断模型,为临床决策提供科学依据。
通过以上案例,我们可以看到统计学数据分析在不同领域的广泛应用。
通过对数据的深入挖掘和分析,我们可以发现隐藏在数据背后的规律和价值,为决策和实践提供有力支持。
因此,数据分析不仅是统计学的重要内容,也是现代社会决策和管理的重要工具。
希望通过本文的案例分析,能够加深对统计学数据分析的理解,提高数据分析能力,为工作和生活带来更多的价值和意义。
统计学案例分析
统计学案例分析统计学是一门研究数据收集、分析、解释和呈现的学科,它在各个领域都有广泛的应用。
在本文中,我们将通过一个实际的案例来展示统计学在实际问题中的应用和分析过程。
案例背景:假设我们是一家电商公司的数据分析师,我们的公司最近推出了一款新产品,但是销售情况并不理想。
我们需要通过统计学的方法来分析销售数据,找出问题所在,并提出改进方案。
数据收集:首先,我们需要收集相关的销售数据。
这包括产品的销售数量、销售地区、销售渠道、促销活动等信息。
通过这些数据,我们可以对销售情况进行全面的分析。
数据分析:接下来,我们将对收集到的数据进行分析。
首先,我们可以通过统计学的方法计算产品在不同地区的销售数量和销售额。
然后,我们可以利用统计学的假设检验方法来判断不同促销活动对销售情况的影响。
此外,我们还可以利用统计学的回归分析方法来找出影响销售的关键因素。
问题发现:通过数据分析,我们发现产品在某些地区的销售情况并不理想,而在其他地区表现良好。
同时,我们还发现某些促销活动对销售额的提升效果并不明显。
通过回归分析,我们找出了影响销售的关键因素,如产品定价、市场竞争情况等。
改进方案:基于数据分析的结果,我们提出了一些改进方案。
首先,我们可以针对销售不理想的地区调整市场策略,比如增加广告投放、调整产品定价等。
其次,我们可以重新评估促销活动的效果,并对不同促销活动进行优化。
最后,我们还可以根据回归分析的结果,调整产品定价和销售策略,以提升销售额。
结论:通过统计学的案例分析,我们发现了产品销售不理想的原因,并提出了相应的改进方案。
统计学在实际问题中的应用可以帮助我们更好地理解数据,发现问题,并提出解决方案。
希望本文的案例分析能够对读者有所启发,也希望大家能够在实际工作中更多地运用统计学的方法来解决问题。
总结:统计学作为一门重要的学科,对于数据分析和问题解决起着至关重要的作用。
通过本文的案例分析,我们可以看到统计学在实际问题中的应用和价值。
统计学研究报告分析案例
统计学研究报告分析案例引言统计学是一门研究数据收集、分析和解释的学科。
在研究领域中,统计方法被广泛应用于数据分析和决策制定。
本文以某研究机构进行的一项关于消费者购买行为的统计学研究报告为案例进行分析。
背景该研究报告旨在了解消费者在购买某电子产品时的决策因素和购买意愿。
研究机构通过在不同地区选择了一定数量的受访者,并设计了一份问卷调查,以收集有关消费者购买行为的数据。
在收集到足够的样本后,研究机构对数据进行了统计学分析,并将结果整理成报告。
方法研究机构使用了随机抽样的方法,选择了来自不同地区的1000名消费者作为受访者。
问卷包括了关于消费者个人信息、购买偏好和购买决策的问题。
在收集到问卷数据后,研究机构对数据进行了整理、清洗和编码。
然后,应用统计学方法对数据进行了描述性统计和推断统计分析。
结果描述性统计分析在对问卷中的个人信息问题进行描述性统计时,发现约占调查对象总数28%的受访者年龄在18-25岁之间,占据了受访者的最大比例。
而男性和女性受访者的比例相对均衡,分别占调查对象总数的52%和48%。
此外,大部分受访者在教育程度上具备大学本科或以上的学历。
在购买行为方面,分析结果显示,大多数受访者的购买决策受到产品质量、价格和品牌声誉等因素的共同影响。
此外,在线评价和媒体广告也对一部分受访者的购买决策产生一定的影响。
在购买偏好方面,统计结果表明,受访者更愿意购买具备先进技术和多功能性的电子产品。
推断统计分析为了对调查结果进行推断统计分析,研究机构使用了卡方检验和回归分析等方法。
卡方检验的结果表明,消费者的购买决策与年龄、性别和教育程度之间存在显著的相关性。
回归分析则进一步揭示了购买决策因素与购买意愿之间的关联。
例如,产品质量、价格和品牌声誉被发现对购买意愿有较大的正向影响。
除了以上的统计分析,研究机构还对调查结果进行了可视化处理,通过绘制柱状图和饼图等图表,使得数据更加直观和易于理解。
结论通过对统计学研究报告的分析,可以得出以下结论:1.统计数据表明,年龄、性别和教育程度是影响消费者购买行为的重要因素。
