第8章-遗传算法【精品毕业设计】(完整版)
数学建模遗传算法与优化问题【精品毕业设计】(完整版)
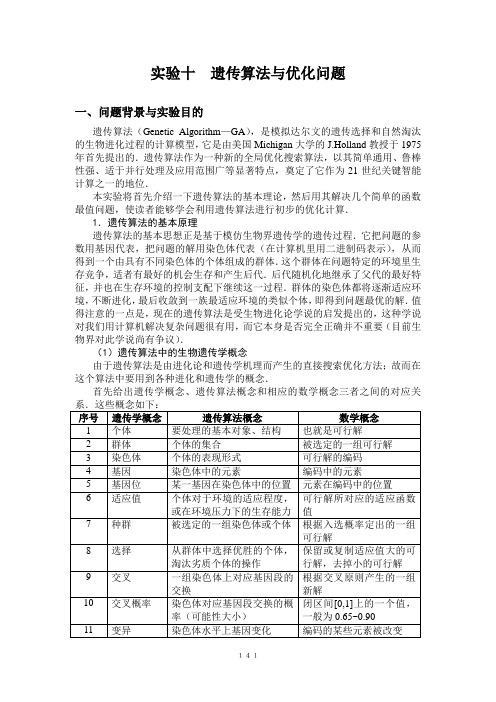
实验十遗传算法与优化问题一、问题背景与实验目的遗传算法(Genetic Algorithm—GA),是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,它是由美国Michigan大学的J.Holland教授于1975年首先提出的.遗传算法作为一种新的全局优化搜索算法,以其简单通用、鲁棒性强、适于并行处理及应用范围广等显著特点,奠定了它作为21世纪关键智能计算之一的地位.本实验将首先介绍一下遗传算法的基本理论,然后用其解决几个简单的函数最值问题,使读者能够学会利用遗传算法进行初步的优化计算.1.遗传算法的基本原理遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程.它把问题的参数用基因代表,把问题的解用染色体代表(在计算机里用二进制码表示),从而得到一个由具有不同染色体的个体组成的群体.这个群体在问题特定的环境里生存竞争,适者有最好的机会生存和产生后代.后代随机化地继承了父代的最好特征,并也在生存环境的控制支配下继续这一过程.群体的染色体都将逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,即得到问题最优的解.值得注意的一点是,现在的遗传算法是受生物进化论学说的启发提出的,这种学说对我们用计算机解决复杂问题很有用,而它本身是否完全正确并不重要(目前生物界对此学说尚有争议).(1)遗传算法中的生物遗传学概念由于遗传算法是由进化论和遗传学机理而产生的直接搜索优化方法;故而在这个算法中要用到各种进化和遗传学的概念.首先给出遗传学概念、遗传算法概念和相应的数学概念三者之间的对应关遗传算法计算优化的操作过程就如同生物学上生物遗传进化的过程,主要有三个基本操作(或称为算子):选择(Selection)、交叉(Crossover)、变异(Mutation).遗传算法基本步骤主要是:先把问题的解表示成“染色体”,在算法中也就是以二进制编码的串,在执行遗传算法之前,给出一群“染色体”,也就是假设的可行解.然后,把这些假设的可行解置于问题的“环境”中,并按适者生存的原则,从中选择出较适应环境的“染色体”进行复制,再通过交叉、变异过程产生更适应环境的新一代“染色体”群.经过这样的一代一代地进化,最后就会收敛到最适应环境的一个“染色体”上,它就是问题的最优解.下面给出遗传算法的具体步骤,流程图参见图1:第一步:选择编码策略,把参数集合(可行解集合)转换染色体结构空间;第二步:定义适应函数,便于计算适应值;第三步:确定遗传策略,包括选择群体大小,选择、交叉、变异方法以及确定交叉概率、变异概率等遗传参数;第四步:随机产生初始化群体;第五步:计算群体中的个体或染色体解码后的适应值;第六步:按照遗传策略,运用选择、交叉和变异算子作用于群体,形成下一代群体;第七步:判断群体性能是否满足某一指标、或者是否已完成预定的迭代次数,不满足则返回第五步、或者修改遗传策略再返回第六步.图1 一个遗传算法的具体步骤遗传算法有很多种具体的不同实现过程,以上介绍的是标准遗传算法的主要步骤,此算法会一直运行直到找到满足条件的最优解为止.2.遗传算法的实际应用例1:设2()20.5f x x x =-++,求 max (), [1,2]f x x ∈-.注:这是一个非常简单的二次函数求极值的问题,相信大家都会做.在此我们要研究的不是问题本身,而是借此来说明如何通过遗传算法分析和解决问题.在此将细化地给出遗传算法的整个过程.(1)编码和产生初始群体首先第一步要确定编码的策略,也就是说如何把1-到2这个区间内的数用计算机语言表示出来.编码就是表现型到基因型的映射,编码时要注意以下三个原则:完备性:问题空间中所有点(潜在解)都能成为GA 编码空间中的点(染色体位串)的表现型;健全性:GA 编码空间中的染色体位串必须对应问题空间中的某一潜在解; 非冗余性:染色体和潜在解必须一一对应.这里我们通过采用二进制的形式来解决编码问题,将某个变量值代表的个体表示为一个{0,1}二进制串.当然,串长取决于求解的精度.如果要设定求解精度到六位小数,由于区间长度为2(1)3--=,则必须将闭区间 [1,2]-分为6310⨯等分.因为216222097152231024194304=<⨯<= 所以编码的二进制串至少需要22位.将一个二进制串(b 21b 20b 19…b 1b 0)转化为区间[1,2]-内对应的实数值很简单,只需采取以下两步(Matlab 程序参见附录4):1)将一个二进制串(b 21b 20b 19…b 1b 0)代表的二进制数化为10进制数:21212019102100()(2)'i i i b b b b b b x =⋯=⋅=∑2)'x 对应的区间[1,2]-内的实数:12)1(2'122---⋅+-=x x 例如,一个二进制串a=<1000101110110101000111>表示实数0.637197.'x =(1000101110110101000111)2=2288967637197.01232288967122=-⋅+-=x 二进制串<0000000000000000000000>,<1111111111111111111111>,则分别表示区间的两个端点值-1和2.利用这种方法我们就完成了遗传算法的第一步——编码,这种二进制编码的方法完全符合上述的编码的三个原则.首先我们来随机的产生一个个体数为4个的初始群体如下:pop(1)={<1101011101001100011110>, %% a1<1000011001010001000010>, %% a2<0001100111010110000000>, %% a3<0110101001101110010101>} %% a4(Matlab 程序参见附录2)化成十进制的数分别为:pop(1)={ 1.523032,0.574022 ,-0.697235 ,0.247238 }接下来我们就要解决每个染色体个体的适应值问题了.(2)定义适应函数和适应值由于给定的目标函数2()20.5f x x x =-++在[1,2]-内的值有正有负,所以必须通过建立适应函数与目标函数的映射关系,保证映射后的适应值非负,而且目标函数的优化方向应对应于适应值增大的方向,也为以后计算各个体的入选概率打下基础.对于本题中的最大化问题,定义适应函数()g x ,采用下述方法:min min (), ()0()0,f x F f x F g x -->⎧=⎨⎩若其他 式中min F 既可以是特定的输入值,也可以是当前所有代或最近K 代中()f x 的最小值,这里为了便于计算,将采用了一个特定的输入值.若取min 1F =-,则当()1f x =时适应函数()2g x =;当() 1.1f x =-时适应函数()0g x =.由上述所随机产生的初始群体,我们可以先计算出目标函数值分别如下(Matlab 程序参见附录3):f [pop(1)]={ 1.226437 , 1.318543 , -1.380607 , 0.933350 }然后通过适应函数计算出适应值分别如下(Matlab 程序参见附录5、附录6): 取min 1F =-,g[pop(1)]= { 2.226437 , 2.318543 , 0 , 1.933350 }(3)确定选择标准这里我们用到了适应值的比例来作为选择的标准,得到的每个个体的适应值比例叫作入选概率.其计算公式如下:对于给定的规模为n 的群体pop={123,,,,n a a a a },个体i a 的适应值为()i g a ,则其入选概率为1()(),1,2,3,,()i s i n ii g a P a i n g a ===⋯∑由上述给出的群体,我们可以计算出各个个体的入选概率.首先可得 41() 6.478330ii g a ==∑, 然后分别用四个个体的适应值去除以41()i i g a =∑,得:P (a 1)=2.226437 / 6.478330 = 0.343675 %% a 1P (a 2)=2.318543 / 6.478330 = 0.357892 %% a 2P (a 3)= 0 / 6.478330 = 0 %% a 3P (a 4)=1.933350 / 6.478330 = 0.298433 %% a 4(Matlab 程序参见附录7)(4)产生种群计算完了入选概率后,就将入选概率大的个体选入种群,淘汰概率小的个体,并用入选概率最大的个体补入种群,得到与原群体大小同样的种群(Matlab 程序参见附录8、附录11).要说明的是:附录11的算法与这里不完全相同.为保证收敛性,附录11的算法作了修正,采用了最佳个体保存方法(elitist model),具体内容将在后面给出介绍.由初始群体的入选概率我们淘汰掉a3,再加入a2补足成与群体同样大小的种群得到newpop(1)如下:newpop(1)={<1101011101001100011110>,%% a1<1000011001010001000010>,%% a2<1000011001010001000010>,%% a2<0110101001101110010101>} %% a4(5)交叉交叉也就是将一组染色体上对应基因段的交换得到新的染色体,然后得到新的染色体组,组成新的群体(Matlab程序参见附录9).我们把之前得到的newpop(1)的四个个体两两组成一对,重复的不配对,进行交叉.(可以在任一位进行交叉)<110101110 1001100011110>,<1101011101010001000010>交叉得:<100001100 1010001000010>,<1000011001001100011110><10000110010100 01000010>,<1000011001010010010101>交叉得:<01101010011011 10010101>,<0110101001101101000010>通过交叉得到了四个新个体,得到新的群体jchpop (1)如下:jchpop(1)={<1101011101010001000010>,<1000011001001100011110>,<1000011001010010010101>,<0110101001101101000010>}这里采用的是单点交叉的方法,当然还有多点交叉的方法,不过有些烦琐,这里就不着重介绍了.(6)变异变异也就是通过一个小概率改变染色体位串上的某个基因(Matlab程序参见附录10).现把刚得到的jchpop(1)中第3个个体中的第9位改变,就产生了变异,得到了新的群体pop(2)如下:pop(2)= {<1101011101010001000010>,<1000011001001100011110>,<1000011011010010010101>,<0110101001101101000010> }然后重复上述的选择、交叉、变异直到满足终止条件为止.(7)终止条件。
grasshopper-galapagos遗传算法【精品毕业设计】(完整版)

Evolutionary Principles applied toProblem Solving遗传算法There is nothing particularly new about Evolutionary Solvers or Genetic Algorithms. The first references to this field of computation stem from the early 60's when Lawrence J. Fogel published the landmark paper "On the Organization of Intellect" which sparked the first endeavours into evolutionary computing. The early 70's witnessed further forays with seminal work produced by -among others- Ingo Rechenberg and John Henry Holland. Evolutionary Computation didn't gain popularity beyond the programmer world until Richard Dawkins' book "The Blind Watchmaker" in 1986, which came with a small program that generated a seemingly endless stream of body-plans called "Bio-morphs" based on human selection. Since the 80's the advent of the personal computer has made it possible for individuals without government funding to apply evolutionary principles to personal projects and they have since made it into the common parlance.其实在遗传算法和基因算法里并什么特别新的理论出现,该领域的第一篇文献出现在六十年代由Lawrence J. Fogel 出版的具有里程碑意义的论文“智能组织”,这篇论文使人们开始致力于研究遗传算法。
遗传算法简介及sga流程【精品毕业设计】(完整版)

遗传算法:遗传算法(Genetic Algorithm)是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法。
遗传算法(Genetic Algorithms简称GA)是由美国Michigan大学的John Holland教授于20世纪60年代末创建的。
它来源于达尔文的进化论和孟德尔、摩根的遗传学理论,通过模拟生物进化的机制来构造人工系统。
遗传算法作为一种全局优化方法,提供了一种求解复杂系统优化问题的通用框架,它不依赖于问题的具体领域,对优化函数的要求很低并且对不同种类的问题具有很强的鲁棒性,所以广泛应用于计算机科学、工程技术和社会科学等领域。
John Holland教授通过模拟生物进化过程设计了最初的遗传算法,我们称之为标准遗传算法。
标准遗传算法流程如下:1)初始化遗传算法的群体,包括初始种群的产生以及对个体的编码。
2)计算种群中每个个体的适应度,个体的适应度反映了其优劣程度。
3)通过选择操作选出一些个体,这些个体就是母代个体,用来繁殖子代。
4)选出的母代个体两两配对,按照一定的交叉概率来进行交叉,产生子代个体。
5)按照一定的变异概率,对产生的子代个体进行变异操作。
6)将完成交叉、变异操作的子代个体,替代种群中某些个体,达到更新种群的目的。
7)再次计算种群的适应度,找出当前的最优个体。
8)判断是否满足终止条件,不满足则返回第3)步继续迭代,满足则退出迭代过程,第7)步中得到的当前最优个体,通过解码,就作为本次算法的近似最优解。
早熟收敛:一般称之为“早熟”,是遗传算法中的一种现象。
指在遗传算法早期,在种群中出现了超级个体,该个体的适应值大大超过当前种群的平均个体适应值。
从而使得该个体很快在种群中占有绝对的比例,种群的多样性迅速降低,群体进化能力基本丧失,从而使得算法较早收敛于局部最优解的现象。
早熟收敛的本质特征是指群体中的各个个体非常相似,群体的多样性急剧减少,当前群体缺乏有效等位基因(最优解位串上的等位基因),在遗传算子作用下不能生成高阶竞争模式。
遗传算法解决TSP问题【精品毕业设计】(完整版)

GA(Fitness,Fitness_threshold,p,r,m)
Fitness:适应度评分函数,为给定假设赋予一个评估分数
Fitness_threshold:指定终止判据的阈值
p:群体中包含的假设数量
r:每一步中通过交叉取代群体成员的比例
m:变异率
初始化群体:P←随机产生的p个假设
在本程序的TSP问题中一共有20个城市,也就是在图模型中有20个顶点,因此一个染色体的长度为20。
3.3适应函数f(i)
对具有n个顶点的图,已知各顶点之间( , )的边长度d( , ),把 到 间的一条通路的路径长度定义为适应函数:
对该最优化问题,就是要寻找解 ,使f( )值最小。
3.4选择操作
选择作为交叉的双亲,是根据前代染色体的适应函数值所确定的,质量好的个体,即从起点到终点路径长度短的个体被选中的概率较大。
(2)交叉(Crossover):对于选中进行繁殖的两个染色体X,Y,以X,Y为双亲作交叉操作,从而产生两个后代X1,Y1.
(3)变异(Mutation):对于选中的群体中的个体(染色体),随机选取某一位进行取反运算,即将该染色体码翻转。
用遗传算法求解的过程是根据待解决问题的参数集进行编码,随机产生一个种群,计算适应函数和选择率,进行选择、交叉、变异操作。如果满足收敛条件,此种群为最好个体,否则,对产生的新一代群体重新进行选择、交叉、变异操作,循环往复直到满足条件。
3.变异:使用均匀的概率从Ps中选择m%的成员.对于选出的每个成员,在它表示中随机选择一个为取反
4.更新:P←Ps
5.评估:对于P中的每个h计算Fitness(h)
从P中返回适应度最高的假设
3.
3.1 TSP问题的图论描述
基本遗传算法【精品毕业设计】(完整版)

基本遗传算法【精品毕业设计】(完整版)遗传算法1、遗传算法⽣物学基础和基本理论达尔⽂⾃然选择学说认为,⽣物要⽣存下去,就必须进⾏⽣存⽃争。
⽣存⽃争包括种内⽃争、种间⽃争以及⽣物跟⽆机环境之间的⽃争三个⽅⾯。
在⽣存⽃争中,具有有利变异(mutation)的个体容易存活下来,并且有更多的机会将有利变异传给后代;具有不利变异的个体就容易被淘汰,产⽣后代的机会也少得多。
因此,凡是在⽣存⽃争中获胜的个体都是对环境适应性⽐较强的。
达尔⽂把这种在⽣存⽃争中适者⽣存,不适者淘汰的过程叫做⾃然选择。
达尔⽂的⾃然选择学说表明,遗传和变异是决定⽣物进化的内在因素。
遗传是指⽗代与⼦代之间,在性状上存在的相似现象。
变异是指⽗代与⼦代之间,以及⼦代的个体之间,在性状上或多或少地存在的差异现象。
在⽣物体内,遗传和变异的关系⼗分密切。
⼀个⽣物体的遗传性状往往会发⽣变异,⽽变异的性状有的可以遗传。
遗传能使⽣物的性状不断地传送给后代,因此保持了物种的特性,变异能够使⽣物的性状发⽣改变,从⽽适应新的环境⽽不断地向前发展。
⽣物的各项⽣命活动都有它的物质基础,⽣物的遗传与变异也是这样。
根据现代细胞学和遗传学的研究得知,遗传物质的主要载体是染⾊体(chromsome),染⾊体主要是由DNA(脱氧核糖核酸)和蛋⽩质组成,其中DNA⼜是最主要的遗传物质。
现代分⼦⽔平的遗传学的研究⼜进⼀步证明,基因(gene)是有遗传效应的⽚段,它储存着遗传信息,可以准确地复制,也能够发⽣突变,并可通过控制蛋⽩质的合成⽽控制⽣物的性状。
⽣物体⾃⾝通过对基因的复制(reproduction)和交叉(crossover),即基因分离、基因⾃由组合和基因连锁互换)的操作使其性状的遗传得到选择和控制。
同时,通过基因重组、基因变异和染⾊体在结构和数⽬上的变异产⽣丰富多采的变异现象。
需要指出的是,根据达尔⽂进化论,多种多样的⽣物之所以能够适应环境⽽得以⽣存进化,是和上述的遗传和变异⽣命现象分不开的。
遗传算法-JAVA【精品毕业设计】(完整版)

java常用代码---遗传算法标签:javadistancecalendarstringrandom算法2011-11-17 18:23 5815人阅读评论(1) 收藏举报分类:数据结构与算法实践(23)import java.util.*;public class Tsp {private String cityName[]={"北京","上海","天津","重庆","哈尔滨","长春","沈阳","呼和浩特","石家庄","太原","济南","郑州","西安","兰州","银川","西宁","乌鲁木齐","合肥","南京","杭州","长沙","南昌","武汉","成都","贵州","福建","台北","广州","海口","南宁","昆明","拉萨","香港","澳门"}; //private String cityEnd[]=new String[34];private int cityNum=cityName.length; //城市个数private int popSize = 50; //种群数量private int maxgens = 20000; //迭代次数private double pxover = 0.8; //交叉概率private double pmultation = 0.05; //变异概率private long[][] distance = new long[cityNum][cityNum];private int range = 2000; //用于判断何时停止的数组区间private class genotype {int city[] = new int[cityNum]; //单个基因的城市序列long fitness; //该基因的适应度double selectP; //选择概率double exceptp; //期望概率int isSelected; //是否被选择}private genotype[] citys = new genotype[popSize];/*** 构造函数,初始化种群*/public Tsp() {for (int i = 0; i < popSize; i++) {citys[i] = new genotype();int[] num = new int[cityNum];for (int j = 0; j < cityNum; j++)num[j] = j;int temp = cityNum;for (int j = 0; j < cityNum; j++) {int r = (int) (Math.random() * temp);citys[i].city[j] = num[r];num[r] = num[temp - 1];temp--;}citys[i].fitness = 0;citys[i].selectP = 0;citys[i].exceptp = 0;citys[i].isSelected = 0;}initDistance();}/*** 计算每个种群每个基因个体的适应度,选择概率,期望概率,和是否被选择。
使用遗传算法求解函数最大值【精品毕业设计】(完整版)
使用遗传算法求解函数最大值题目使用遗传算法求解函数f(x,y)=x∗sin(6∗y)+y∗cos(8∗x)在x∈[1,2]及y∈[1,2]的最大值。
解答算法使用遗传算法进行求解,篇末所附源代码中带有算法的详细注释。
算法中涉及不同的参数,参数的取值需要根据实际情况进行设定,下面运行时将给出不同参数的结果对比。
定义整体算法的结束条件为,当种群进化次数达到maxGeneration时停止,此时种群中的最优解即作为算法的最终输出。
设种群规模为N,首先是随机产生N个个体,实验中定义了类型Chromosome表示一个个体,并且在默认构造函数中即进行了随机的操作。
然后程序进行若干次的迭代,在每次迭代过程中,进行选择、交叉及变异三个操作。
一选择操作首先计算当前每个个体的适应度函数值,这里的适应度函数即为所要求的优化函数,然后归一化求得每个个体选中的概率,然后用轮盘赌的方法以允许重复的方式选择选择N个个体,即为选择之后的群体。
但实验时发现结果不好,经过仔细研究之后发现,这里在x、y取某些值的时候,目标函数计算出来的适应值可能会出现负值,这时如果按照把每个个体的适应值除以适应值的总和的进行归一化的话会出现问题,因为个体可能出现负值,总和也可能出现负值,如果归一化的时候除以了一个负值,选择时就会选择一些不良的个体,对实验结果造成影响。
对于这个问题,我把适应度函数定为目标函数的函数值加一个正数,保证得到的适应值为正数,然后再进行一般的归一化和选择的操作。
实验结果表明,之前的实验结果很不稳定,修正后的结果比较稳定,趋于最大值。
二交叉操作首先是根据交叉概率probCross选择要交叉的个体进行交叉。
这里根据交叉参数crossnum进行多点交叉,首先随机生成交叉点位置,允许交叉点重合,两个重合的交叉点效果互相抵消,相当于没有交叉点,然后根据交叉点进行交叉操作,得到新的个体。
三变异操作首先是根据变异概率probMutation选择要变异的个体。
基于遗传算法的自动排课系统毕业设计【精品毕业设计】(完整版)
随着人工智能的发展,特别是在计算智能领域的拓展,借鉴于生物界进化思想和遗传算法,由于其超强的并行搜索能力,以及在解决优化问题中表现出来的高度鲁棒性,它已经被广泛应用于各个领域。目前,很多研究人员已使用遗传算法来求解排课问题,如文献[20]使用遗传算法优化教室的合理利用,文献[21]的用自适应的遗传算法求解大学课表安排问题,文献[22]的基于遗传算法排课系统的设计与实现等等。这些应用说明,使用遗传算法来解决排课问题,其结果还是令人较为满意的。
1.
回溯算法也叫试探法.它是一种系统地搜索问题的解的方法,可以被认为是一个有过剪枝的DFS(深度优先搜索)过程。它按优先条件向前搜索,以达到目标,但当搜索到某一步时.发现原先的选择并不优或达不到目标。就退回一步重新选择。而满足回溯条件的某个状态点称之为回溯点。具体到计算机智能排课系统中,选优条件即为排课数学模型中的约束条件群(需求集中的元素特征与资源集中的元素特征相互作用形成的数学关系)若不满足约束条件群,该选择即为不优或达不到目标当遍历该步骤的所有可能仍未满足约束条件群.则该状态满足了回溯条件,该状态点即为回溯点。
关键词:遗传算法、自动排课、Java。
Abstract
Along with science technical and community information technical increases continuously,calculator science is gradually mature, its mighty function has behaved deep cognition, and it has entered the human social each realm erupts to flick the more and more important function, bringing our life biggest of convenience.Curriculum arrangement is an important and complicated workinginschool,so solving the problem is of great importance for teaching programming.Investigatedand studied the algorithm existed,determinethatadoptgenetic algorithm.ThroughDesign ImplementationtheAutoCourseArrangementManagementSystemBaseonGeneticAlgorithm,researched theapplicationofgenetic algorithmin theCourseArrangementManagementSystem.
R语言GA遗传算法【精品毕业设计】(完整版)
GA包遗传算法最大化使用遗传算法的适应度函数。
默认求最大值。
用法:ga(type = c("binary", "real-valued", "permutation"), fitness, ..., min, max, nBits, population = gaControl(type)population,<br/>selection=gaControl(type)selection, crossover = gaControl(type)crossover,<br/> mutation=gaControl(type)mutation, popSize = 50, pcrossover = 0.8, pmutation = 0.1, elitism = base::max(1, round(popSize*0.05)), maxiter = 100, run = maxiter, maxfitness = Inf, names = NULL, suggestions = NULL, keepBest = FALSE, parallel = FALSE, monitor = gaMonitor, seed = NULL)参数说明•type: 解得编码类型–binary :二进制编码–real-valued:实数浮点编码–permutation:问题涉及到重新排序的列表,字符串编码。
可求解TSP 问题•fitness:适应度函数•min:解得下界(多元变量为一个向量)•max:解得上界(多元变量为一个向量)•nBits:一个种群用二进制编码的长度是多少(长度越大代表精度越高) •population:初始种群•selection:选择•crossover: 交叉•crossover:变异•popsize:种群大小•pcrossover: 交叉概率(默认0.8)•pmutation:变异概率(默认0.1)•elitism: 代沟(默认情况下,前5%个体将在每个迭代中保留)•maxiter:最大迭代次数(默认100)•maxfitness:适应度函数的上界,GA搜索后中断•keepBest:是否保留每一代的最优解•parallel:是否采用并行运算•monitor:绘图用的,监控遗传算法的运行状况•seed:一个整数值包含随机数发生器的状态。
遗传算法新论文【精品毕业设计】(完整版)
学校代码 10126 学号 00708037 分类号密级本科毕业论文基于遗传算法的图像阈值分割学院、系数学科学学院计算数学系专业名称信息与计算科学年级 2007级学生姓名刘家祥指导教师曹军2011年 5月 20 日内容摘要图像分割就是指把图像分成各具特性的区域并提取出感兴趣目标的技术和过程。
图像的分割是以灰度值作为分割的依据,通过各个像素的灰度值和事先确定的阈值的比较来分割图像。
如何确定最合适的阈值是处理好图像分割的关键,这自然成为一直以来分割算法研究的焦点。
遗传算法是对生物进化论中自然选择和遗传学机理中生物进化过程的模拟来计算最优解的方法。
遗传算法具有众多的优点,如鲁棒性、并行性、自适应性和快速收敛,可以应用在图像处理技术领域中图像分割技术来确定分割阈值。
本文主要介绍基于遗传算法的最小误差阈值法、最大类间方差法(Otsu法)以及最佳直方图熵法(KSW熵法)等三种方法分割图像。
关键词:图像分割,遗传算法,阈值分割AbstractImage segmentation refers to the image into regions each with characteristics and goals of the technology to extract and process of interest. Segmentation is a segmentation based on gray value, gray value of each pixel through the predetermined threshold value and comparing the image segmentation. How to determine the most appropriate threshold is the key to handling image segmentation, which has naturally become the focus of segmentation algorithms.Genetic algorithm is a biological theory of evolution and genetic mechanism of natural selection in biological evolution simulation method to calculate the optimal solution. Genetic algorithm has many advantages, such as robustness, parallel, adaptive, and fast convergence, can be used in the field of image processing image segmentation technique to determine the split threshold.In this paper, genetic algorithm based on minimum error threshold, the largest class variance (Otsu method) and the best histogram entropy (KSW entropy method) are three ways to split the image.Keywords : Image segmentation, genetic algorithms, threshold目录第一章绪论 .................................................. - 1 - 第二章遗传算法概述 ........................................ . - 2 -2.1遗传算法的研究历史....................................... - 2 -2.2生物背景................................................. - 2 -2.3遗传算法的基本思想....................................... - 3 -2.4遗传算法的几个概念....................................... - 4 -2.4.1适应度函数......................................... - 4 -2.4.2遗传算法最常用的算子............................... - 4 -2.5遗传算法运算的基本流程................................... - 5 - 第三章图像分割的现状 ........................................ - 7 -3.1图像分割简介............................................. - 7 -3.2图像分割方法............................................. - 8 -3.2.1基于边缘检测的分割................................. - 8 -3.2.2基于区域的分割..................................... - 8 -3.2.3边缘与区域相结合的分割............................. - 9 -3.3阈值选取................................................. - 9 - 第四章基于遗传算法的图像阈值分割 ........................... - 10 -4.1图像阈值................................................ - 10 -4.2阈值分割的原理.......................................... - 10 -4.3最小误差阈值法.......................................... - 11 -4.3.1最小误差法图像阈值分割............................ - 11 -4.3.2 利用遗传算法来改进最小误差法...................... - 12 -4.4 最大类间方差法(Otsu法)............................... - 13 -4.4.1最大类间方差法(Otsu法)阈值分割.................. - 13 -4.4.2 Otsu阈值分割的遗传算法设计........................ - 15 -4.5 KSW熵法................................................ - 17 -4.5.1 KSW熵阈值分割................................... - 17 -4.5.2 KSW单阈值分割的遗传算法设计..................... - 18 -4.5.3 KSW双阈值分割的遗传算法设计..................... - 19 - 第五章基于新的遗传算法的图像分割 ........................... - 25 -5.1混沌遗传算法............................................ - 25 -5.2量子遗传算法............................................ - 25 -5.3免疫遗传算法............................................ - 25 - 结论 .......................................................... - 26 - 致谢 .......................................................... - 27 - 参考文献: ..................................................... - 28 -内蒙古大学本科学年论文第- 1 - 页基于遗传算法的图像阈值分割第一章绪论图像分割是图像处理与计算机视觉的基本问题之一,是图像处理到图像分析的关键步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8章遗传算法
1.引言
遗传算法(GeneticAlgorithms简称GA)是由美国Michigan大学的JohnHolland教授创建的。
它来源于达尔文的进化论、魏茨曼的物种选择学说和孟德尔的群体遗传学说。
其基本思想是模拟自然界遗传机制和生物进化论而形成的一种过程搜索最优解的算法。
其特点是几乎不需要所求问题的任何信息而仅需要目标函数的信息,不受搜索空间是否连续或可微的限制就可找到最优解。
依据它的并行性,非常适用于大规模并行计算机。
因此,遗传算法广泛的应用于自动控制、计算科学、模式识别、工程设计、智能故障诊断、管理科学和社会科学领域,适用于解决复杂的非线性和多维空间寻优问题。
2.遗传算法的发展
1)20世纪60年代,John Holland教授和他的数位博士受到生物模拟技术的启发,认识到自然遗传可以转化为人工遗传算法。
1962年John Holland提出了利用群体进化模拟适应性系统的思想,引进了群体、适应值、选择,变异、交叉等基本概念。
2)1967年,J.D.Bagely在其博士论文中首次提出了“遗传算法”的概念。
3)1975年,Holland出版了《自然与人工系统中的适应性行为》(Adaptation in Natural and Artificial System)。
该书系统地阐述了遗传算法的基本理论和方法,提出了遗传算法的基本定理—模式定理,从而奠定了遗传算法的理论基础。
同年,De Jong在其博士论文中首次把遗传算法应用于函数优化问题,对遗传算法的机理与参数进行了较为系统地研究,并建立了著名的五函数测试平
台。
4)20世纪80年代初,Holland教授实现了第一个基于遗传算法的机器学习系统—分类器系统(Classifier System简称CS),开创了基于遗传算法的机器学习的新概念。
5)1989年,David Goldberg出版了《搜索、优化和机器学习中的遗传算法》(Genetic Algorithms in Search Optimization and Machine Learning)。
该书全面系统地总结了当时关于遗传算法的研究成果,结合大量的实例,完整的论述了遗传算法的基本原理及应用,奠定了现代遗传算法的基础。
6)1992年,John R.Koza出版了专著《遗传编程》(GeneticProgramming),提出了遗传编程的概念,并成功地把遗传编程的方法应用于人工智能、机器学习、符号处理等方面。
随着遗传算法的不断深入和发展,关于遗传算法的国际学术活动越来越多,遗传算法已成为一个多学科、多领域的重要研究方向。
3.遗传算法的特点
1)直接处理的对象是决策变量的编码集而不是决策变量的实际值本身,搜索过程既不受优化函数的连续性约束,也没有优化函数导数必须存在的要求。
3)遗传算法是一种自适应搜索技术,其选择、交叉、变异等运算都是以一种概率方式来进行,从而增加了搜索过程的灵活性,同时能以很大的概率收敛于最优解,具有较好的全局优化求解能力。
4)遗传算法直接以目标函数值为搜索信息,对函数的性态无要求,具有较好的普适性和易扩充性;同时,我们可以把搜索范围集中到适应度较高的部分搜索空间中,从而提高了搜索效率。
1.遗传算法从问题解的串集开始嫂索,而不是从单个解开始。
这是遗传算法与传统优化算法的极大区别。
传统优化算法是从单个初始值迭代求最优解的;容易误入局部最优解。
遗传算法从串集开始搜索,复盖面大,利于全局择优。
2.遗传算法求解时使用特定问题的信息极少,容易形成通用算法程序。
由于遗传算法使用适应值这一信息进行搜索,并不需要问题导数等与问题直接相关的信息。
遗传算法只需适应值和串编码等通用信息,故几乎可处理任何问题。
遗传算法的基本思想简单,运行方式和实现步骤规范,便于具体使用。
3.遗传算法有极强的容错能力
遗传算法的初始串集本身就带有大量与最优解甚远的信息;通过选择、交叉、变异操作能迅速排除与最优解相差极大的串;这是一个强烈的滤波过程;并且是一个并行滤波机制。
故而,遗传算法有很高的容错能力。
4.遗传算法中的选择、交叉和变异都是随机操作,而不是确定的精确规则。
这说明遗传算法是采用随机方法进行最优解搜索,选择体现了向最优解迫近,交叉体现了最优解的产生,变异体现了全局最优解的复盖。
5.遗传算法采用多点搜索或者说是群体搜索,具有很高的隐含并行性。
术语说明
遗传算法的基本思想是基于Darwin进化论和Mendel的遗传学说的。
Darwin进化论最重要的是适者生存原理。
它认为每一物种在发展中越来越适应环境。
物种每个个体的基本特征由后代所继承,但后代又会产生一些异于父代的新变化。
在环境变化时,只有那些熊适应环境的个体特征方能保留下来。
Mendel遗传学说最重要的是基因遗传原理。
它认为遗传以密码方式存在细胞中,并以基因形式包含在染色体内。
每个基因有特殊的位置并控制某种特殊性质;所以,每个基因产生的个体对环境具有某种适应性。
基因突变和基因杂交可产生更适应于环境的后代。
经过存优去劣的自然淘汰,适应性高的基因结构得以保存下来。
由于遗传算法是由进化论和遗传学机理而产生的直接搜索优化方法;故而在这个算法中要用到各种进化和遗传学的概念。
这些概念如下:
一、串(String)
它是个体(Individual)的形式,在算法中为二进制串,并且对应于遗传学中的染色体(Chromosome)。
二、群体(Population)
个体的集合称为群体,串是群体的元素
三、群体大小(Population Size)
在群体中个体的数量称为群体的大小。
一、染色体(Chronmosome)
染色体又可以叫做基因型个体(individuals),一定数量的个体组成了群体(population),群体中个体的数量叫做群体大小。
二、基因(Gene)
基因是串中的元素,基因用于表示个体的特征。
例如有一个串S=1011,则其中的1,0,1,1这4个元素分别称为基因。
它们的值称为等位基因(Alletes)。
三、基因地点(Locus)
基因地点在算法中表示一个基因在串中的位置称为基因位置(Gene Position),有时也简称基因位。
基因位置由串的左向右计算,例如在串S=1101 中,0的基
因位置是3。
四、基因特征值(Gene Feature)
在用串表示整数时,基因的特征值与二进制数的权一致;例如在串S=1011 中,基因位置3中的1,它的基因特征值为2;基因位置1中的1,它的基因特征值为8。
五、适应度(Fitness)
各个个体对环境的适应程度叫做适应度(fitness)。
为了体现染色体的适应能力,引入了对问题中的每一个染色体都能进行度量的函数,叫适应度函数. 这个函数是计算个体在群体中被使用的概率。
七、串结构空间S S
在串中,基因任意组合所构成的串的集合。
基因操作是在结构空间中进行的。
串结构空间对应于遗传学中的基因型(Genotype)的集合。
八、参数空间S P
这是串空间在物理系统中的映射,它对应于遗传学中的表现型(Phenotype)的集合。
九、非线性
它对应遗传学中的异位显性(Epistasis)
遗传算法的目的
典型的遗传算法CGA(Canonical Genetic Algorithm)通常用于解决下面这一类的静态最优化问题:
考虑对于一群长度为L的二进制编码b i,i=1,2,…,n;有b i∈{0,1}L。
