1随机过程实验报告-副本
随机过程1(1.1) (2)

离散型随机变量:
Geometric Random Variable
Poisson Random Variable
当二项随机变量中参数n很大,p很小时, 二项随机变量可以近似看作是Poisson随 机变量。
连续型随机变form Random Variable
T=[0,24,……)
4.根据参数集与状态空间离散与否,随机过程可分为
●离散参数,离散状态的随机过程 (例3)
● 离散参数,连续状态的随机过程 (例4)
● 连续参数,离散状态的随机过程 (例1)
● 连续参数,连续状态的随机过程 (例2)
参数集为离散的随机过程也称为随机序列, 或时间序列.
§2 随机过程的有限维分布函数族
随机过程基本概念 随机分析 平稳过程 马尔科夫过程(链)
教材
《随机过程》张卓奎 陈慧婵 西安电子科技大学出版社 2003 《随机过程 同步学习指导》 张卓奎 陈慧婵
西安电子科技大学出版社 2004
参考教材
1.《随机过程》毛用才 胡奇英 西安电子科技大学出版社 1998 2.《随机过程理论》 周荫清 电子工业出版社 第二版 2006 3.《 An introduction to stochastic processes 》 Edward P.C. kao Thomson 2003
n 1 n 1
则称P为E的概率。
概率的性质:
(1) P( ) 0 ; (2) Monotonicity: 若E F, P( E ) P( F ) (3) P(E c ) 1 P(E) P( En ) P( En ) (4) Subadditivity: 布尔不等式: n 1 n 1 n n (5) P( Ei ) P( Ei ) P( Ei E j )
随机信号实验报告(模板)(1)

随机信号实验报告学院通信工程学院专业信息工程班级 1401051班制作人文杰制作人晓鹏一、 摘要根据实验的要求与具体容,我们组做了一下分工,XXX 完成了本次的第一组实验即基于MATLAB 的信号通过线性系统与非线性系统的特性分析,具体容有(高斯白噪声n ,输入信号x ,通过线性与非线性系统的信号a,b,y1,y2的均值,均方值,方差,自相关函数,概率密度,功率谱密度以及频谱并把它们用波形表示出来),XXX 和XXX 两人合力完成了基于QUARTUS II 的2ASK 信号的产生及测试实验具体容有(XXX 负责M 序列发生器以及分频器,XXX 负责载波的产生以及开关函数和管脚配置),最后的示波器调试以及观察2ASK 信号的FFT 变换波形由我们组所有人一起完成的。
二、实验原理及要求实验一、信号通过线性系统与非线性系统的特性分析1、实验原理① 随机过程的均值(数学期望):均值表示集合平均值或数学期望值。
基于随机过程的各态历经性,可用时间间隔T 的幅值平均值表示,即:均值表达了信号变化的中心趋势,或称之为直流分量。
② 随机过程的均方值:信号x(t)的均方值,或称为平均功率,其表达式为:均方值表达了信号的强度,其正平方根值,又称为有效值,也是信号的平均能量的一种表达。
③ 随机信号的方差: 信号x(t)的方差定义为:描述了信号的静态量,方差反映了信号绕均值的波动程度。
在已知均值和均方值的前提下,方差就很容易求得了。
④随机信号的自相关函数信号的相关性是指客观事物变化量之间的相依关系。
对于平稳随机过程X(t)和Y(t)在两个不同时刻t和t+τ的起伏值的关联程度,可以用相关函数表示。
在离散情况下,信号x(n)和y(n)的相关函数定义为:τ,t=0,1,2,……N-1。
⑤随机过程的频谱:信号频谱分析是采用傅立叶变换将时域信号x(t)从另一个角度来了解信号的特征。
时域信号x(t)的傅氏变换为:⑥随机过程的功率谱密度:随机信号的功率普密度是随机信号的各个样本在单位频带的频谱分量消耗在一欧姆电阻上的平均功率的统计均值,是从频域描述随机信号的平均统计参量,表示X(t)的平均功率在频域上的分布。
随机过程上机实验报告讲解

2015-2016第一学期随机过程第二次上机实验报告实验目的:通过随机过程上机实验,熟悉Monte Carlo计算机随机模拟方法,熟悉Matlab的运行环境,了解随机模拟的原理,熟悉随机过程的编码规律即各种随机过程的实现方法,加深对随机过程的理解。
上机内容:(1 )模拟随机游走。
(2)模拟Brown运动的样本轨道。
(3)模拟Markov过程。
实验步骤:(1)给出随机游走的样本轨道模拟结果,并附带模拟程序。
①一维情形%—维简单随机游走% “从0开始,向前跳一步的概率为p,向后跳一步的概率为1-p”n=50;p=0.5;y=[0 cumsum(2.*(rand(1,n-1)v=p)-1)]; % n 步。
plot([0:n-1],y); %画出折线图如下。
w%一维随机步长的随机游动%选取任一零均值的分布为步长,比如,均匀分布。
n=50;x=rand(1,n)-1/2;y=[0 (cumsum(x)-l)];plot([0:n],y);②二维情形%在(u, v)坐标平面上画出点(u(k), v(k)), k=1:n,其中(u(k)) 和(v(k))是一维随机游动。
例%子程序是用四种不同颜色画了同一随机游动的四条轨道。
n=100000;colorstr=['b' 'r' 'g' 'y'];for k=1:4z=2.*(rand(2,n)<0.5)-1;x=[zeros(1,2); cumsum(z')];col=colorstr(k);plot(x(:,1),x(:,2),col);③%三维随机游走 ranwalk3dp=0.5;n=10000; colorstr=['b' 'r' 'g' 'y'];for k=1:4z=2.*(rand(3,n)v=p)-1; x=[zeros(1,3); cumsum(z')];col=colorstr(k);plot3(x(:,1),x(:,2),x(:,3),col);hold on end gridhold onendgrid4:04003?0-200-300-400-2OD20050、-100-200 -20D⑵给出一维,二维Brown运动和Poisson过程的模拟结果,并附带模拟程序,没有结果的也要把程序记录下来。
随机过程1(1)

4.根据参数集与状态空间离散与否,随机过程可分为
●离散参数,离散状态的随机过程 (例3)
● 离散参数,连续状态的随机过程 (例4)
● 连续参数,离散状态的随机过程 (例1)
● 连续参数,连续状态的随机过程 (例2)
参数集为离散的随机过程也称为随机序列, 或时间序列.
二
随机过程的有限维分布函数族
设X={X(t),t∈T}是S.P.
2 0 2 0
0 h( x ) 1 其它
0 2x 1 其它
2
x0
2 其它
(3)
t
2
时,X (t ) V cos
2
0,
此时X (
2
)是单点分布, 则
F
ห้องสมุดไป่ตู้X(
2
( x ) P{ X (
)
2
) x}
1 x 0 0 x 0
特别注意: 一族随机变量X(t) 的两个特点:随机性与函数性
随机过程定义
设(Ω,F,P)为一概率空间,T为一参数集,T R,
若对每一 t ∈T,均有定义在(Ω,F,P)上的一个 随机变量X(ω,t),(ω∈Ω)与之对应, 则称X(ω,t)为(Ω,F,P)上的一个随机过程(S.P.) 记X={X(ω,t), ω∈Ω,t∈T},
注意: 设{X(ω,t), ω∈Ω, t∈T}为一S.P.
1. X(ω ,t),实质上为定义在T×Ω上的二元单值函数. 2.对每一个固定的t, X(t)为一随机变量. 随机变量X(t) (t∈T)所有可能取值的集合,称为随机过 程X(ω,t),的状态空间.记为S. S中的元素称为状态. 3.对每一个ω0∈Ω,X(ω0,t)是定义在T上的普通函数. 记为 x(ω0,t), 称为为随机过程的一个样本函数.也称轨 道或实现. 样本函数的图形称为样本曲线.
随机过程第三版课后答案

随机过程第三版课后答案【篇一:随机过程习题答案】们的均值分别为mx和my,它们的自相关函数分别为rx(?)和ry(?)。
(1)求z(t)=x(t)y(t)的自相关函数;(2)求z(t)=x(t)+y(t)的自相关函数。
答案:(1)rz(?)?e?z(t??)z(t)??e?x(t??)y(t??)x(t)y(t)?利用x(t)和y(t)独立的性质:rz(?)?e?x(t??)x(t)?e?y(t??)y(t)???rx(?)ry(?)(2)rz(?)?e?z(t??)z(t)??e??x(t??)?y(t??)???x(t)?y(t)?? ?e?x(t??)x (t)?x(t??)y(t)?y(t??)x(t)?y(t??)y(t)?仍然利用x(t)和y(t)互相独立的性质:rz(?)?rx(?)?2mxmy?ry(?)2、一个rc低通滤波电路如下图所示。
假定输入是均值为0、双边功率谱密度函数为n0/2的高斯白噪声。
(1)求输出信号的自相关函数和功率谱密度函数;(2)求输出信号的一维概率密度函数。
电流:i(t)电压:y(t)答案:(1)该系统的系统函数为h(s)?y(s)1? x(s)1?rcs则频率响应为h(j?)?11?jrc?n02而输入信号x(t)的功率谱密度函数为px(j?)?该系统是一个线性移不变系统,所以输出y(t)的功率谱密度函数为:py(j?)?px(j?)h(j?)?2n0/21?rc?2对py(j?)求傅里叶反变换,就得到输出的自相关函数:1ry(?)?2?????py(j?)ej??1d??2?n0/2j?????1?rc?2ed??(2)线性系统输入为高斯随机过程,则输出也一定是高斯的。
因此,为了求输出的一维概率密度函数,仅需知道输出随机过程的均值和方差即可。
均值:已知输入均值mx=0,则输出均值my=mxh(0)=02方差:ry(0)?var(y)?my因为均值为0,所以方差var(y)?ry(0)?一维pdf:略12?n0/2???1?rc2?2d??3、理想带通滤波器的中心频率为fc、带宽为b,其在通带的频率增益为1。
随机过程实验

实验名称:随机变量的仿真与实验实验内容:用MATLAB 分别产生服从(二项分布、泊松分布、正态分布、均匀分布、指数分布、瑞利分布)的随机变量,并分析他们的:1、分布函数或概率密度函数2、均值、方差1、服从二项分布的随机变量理论分析如果随机变量X 的分布律为k n k k n k q p C k X P p -===}{0<p<1, q=1-p, k=0,1,2,…n,则称X 服从参数为n ,p 的二项分布,记为X~B(n ,p)。
其期望和方差分别为E(X) = np ,D(X)=npq 。
随机变量X~B(20,0.4),可以通过matla b 计算其期望和方差,绘制分布律和分布函数。
程序如下:n = 20;p = 0.4;[E,D] = binostat(n ,p); %计算期望和方差f = binopdf(1:21, n, p); %计算分布律F = binocdf(1:21, n, p); %计算分布函数subplot(2,2,1); stem(f); %绘制分布律title('二项分布理论分布律 n=20 p=0.4');xlabel('x');ylabel('p');subplot(2,2,3); stem(F); %绘制分布函数title('二项分布理论分布函数 n=20 p=0.4');xlabel('x');ylabel('f');计算得结果E(X) = 8,D(X) = 4.800,分布律和分布函数如图1。
图1 X~B(20,0.4)的分布律和分布函数样本分析利用matlab中binornd函数产生一个X~B(20,0.4)的样本,样本点总数为20000。
计算其均值和方差,计算分布律和分布函数,并与理论结果进行比较。
程序如下:n = 20;p = 0.4;R = binornd(n,p,1,20000);e = mean(R); %期望d = var(R); %方差f = zeros (1,21);F = zeros (1,21);for j = 1:21 %计算统计分布律for i=1:20000if j == R(i)f(1,j) = f(1,j) + 1;endendf(1,j) = f(1,j) / 20000;endsubplot(2,2,1);stem(f);title('二项分布样本分布律 n=20 p=0.4');xlabel('x');ylabel('p');for j = 1:21 %计算分布函数for i = 1:jF(1, j) = F(1, j) + f(1,i);endendsubplot(2,2,3);stem(F);title('二项分布样本分布函数 n=20 p=0.4');xlabel('x');ylabel('f');计算结果为e=8.0218,d=4.7760,与理论值(E(X)=8,D(X)=4.8)基本接近。
随机过程实验
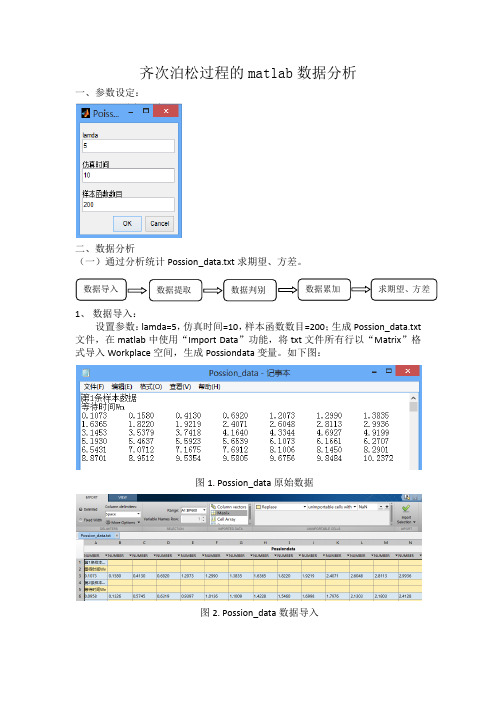
齐次泊松过程的matlab数据分析一、参数设定:二、数据分析(一)通过分析统计Possion_data.txt求期望、方差。
1、数据导入:设置参数:lamda=5,仿真时间=10,样本函数数目=200;生成Possion_data.txt 文件,在matlab中使用“Import Data”功能,将txt文件所有行以“Matrix”格式导入Workplace空间,生成Possiondata变量。
如下图:图1. Possion_data原始数据图2. Possion_data数据导入图3. 生成Possiondata2、数据提取编程将Possiondata数组中的第3,6,9…300行提取出来形成一个新的数值poiss。
图4. 提取有效数据3、数据判别(1)、按照试验指导大纲,将时间间隔设成0.1,将每一条样本函数按照0.1的时间间隔进行统计,将在同一个0.1间隔内的数据归为一类。
得到“t1”图5. 数据判别归类(2)、采用“length”函数将上表中的数据进行计数得到以下参数:图6. 统计类中数量(3)、将“t2”进行累加,并同样的方法计算所有样本函数得到“s”:图7. 得到样本计数样本图8. 第一条样本计数过程图9. SJGC生成的第一条样本函数4、计算期望、方差使用“mean”函数计算期望值,使用“var”函数计算方差得到下图:图10. 均值_方差图从图中可以看出,泊松过程的均值与方差具有一致性。
图11. SJGC生成的均值函数图(二)求泊松过程的速率方法1根据所得到的的均值函数,使用“polyfit”函数采用一次函数模拟得到斜率4.9138,即为泊松速率。
方法2考虑到泊松事件的时间间隔是指数分布,且均值为泊松过程速率的倒数。
对样本函数进行处理,将两次到达时间相减得到每相邻两次事件发生的时间间隔,使用“expfit”函数得到估计的均值,对其求倒得到泊松速率。
使用循环语句得到每一条样本函数的速率,最后求平均得到要求的泊松速率。
3.随机过程的模拟与特征估计-随机信号分析实验报告

计算机与信息工程学院验证性实验报告专业: 通信工程 年级/班级:2011级 第3学年 第1学期实验目的1、 了解随机过程特征估计的基本概念和方法2、 学会运用MATLAB^件产生各种随机过程3、 学会对随机过程的特征进行估计4、 通过实验了解不同估计方法所估计出来的结果之间的差异 实验仪器或设备 1、 一台计算机 2、 M ATLAB r2013a实验原理1、 高斯白噪声的产生:利用 MATLAB!数randn 产生2、 自相关函数的估计:MATLAB!带的函数:xcorr3、功率谱的估计:MATLAB!带的函数为pyulear先估计自相关函数R x (m),再利用维纳—辛钦定理,功率谱为自相关函数的傅立叶变N 1G x ( X 'R x (m)e”(3.2)m=N 4)4、 均值的估计:MATLAB!带的函数为mean1 N 4m x 二一' x(n)(3.3 )N n =15、 方差的估计:MATLAB!带的函数为var1 N -1「[x(n) -mi x ]2 (3.4 ) N n#6 AR(1)模型的理论自相关函数和理论功率谱 对于AR(1)模型X(n) =aX(n-1) W(n)自相关函数R x (m)二1 N-|m|N 4m|_JZ x(n + m)x (n)n =0(3.1 )换: (3.5)功率谱为四、实验内容(1)按如下模型产生一组随机序列x(n) =ax(n_1)・w(n),其中w(n)为均值为1,方差 为4的正态分布白噪声序列。
1、 产生并画出a=°.8和a=°.2的x(n)的波形;2、 估计x(n)的均值和方差;3、 估计x(n)的自相关函数。
(2)设有AR(1)模型,X(n) »°.8X(n -1) W(n),1、 W (n)是零均值正态白噪声,方差为 4。
2、 用MATLA 模拟产生X(n)的500个样本,并估计它的均值和方差;3、 画出X(n)的理论的自相关函数和功率谱;4、 估计X(n)的自相关函数和功率谱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1随机过程实验报告 - 副本__________________________________________________________________________________随机过程试验报告班级:姓名:学号:____________________________________________________________________ ____________________________________________________________________________________________ ______________________________________________________________________________________实验一实验题目 Xtxwt()cos(),描绘出随机过程的图像实验目的 Xtxwt()cos(),利用MATLAB编程描绘出随机过程的图像实验地点及时间信息楼127机房 2012.5.31实验内容Xtxwt()cos(),绘制随机过程的图像实验习题,函数z=xcos(wt)中,w为常量,设为2;自变量为x和t,其中t[-1,1],x服从[-1,1]上的标准正态分布;y是因变量。
用Matlab编程如下:t=-1:0.01:1;>> x=normpdf(t);//x服从标准正态分布。
>> z=x.*cos(1*t);>> plot3(t,x,z);如下图所示;实验总结理解随机过程的本质含义,并学会运用MATLAB语言编程描绘在随机过程函数图像。
实验成绩评阅时间评阅教师____________________________________________________________________ ____________________________________________________________________________________________ ______________________________________________________________________________________实验二实验题目 Xtwt()cos(),,,,绘制随机相位正弦波的均值,方差和自相关函数的图像实验目的通过绘制图像,深入理解随机相位正弦波的均值,方差和自相关函数实验地点及时间信息楼127机房 2012.5.31Xtwt()cos(),,,,实验内容:绘制随机相位正弦波的均值,方差和自相关函数的图像实验习题,cos(,t,,),,,,函数z=中,令=2,=2,服从(0,2)上的均匀分布,,,t(0,2)。
经过计算其均值u=0, 方差为2,自相关函数为R=2cos(t2-t1)。
运用Matlab编写程序绘制图像如下:绘制函数图像程序为:t=0:pi/100:2*pi;,>> x=unifpdf(t,0,2*pi);//x服从(0,2)上的均匀分布。
>> z=2.*cos(2*t+x);>> plot3(t,x,z);函数图像如图(1):---------图(1)绘制均值函数程序如下:x=-1:0.01:1;____________________________________________________________________ ____________________________________________________________________________________________ ______________________________________________________________________________________>> u=0;>> plot(x,u);均值函数图像如图(2):------------图(2)绘制方差函数程序如下: x=-2:0.01:2;>> y=2;>> plot(x,y);方差函数图像如图(3):-------------图(3)____________________________________________________________________ ____________________________________________________________________________________________ ______________________________________________________________________________________,,,,,在自相关函数R=2cos(t2-t1)中, t1(0,2),t2(0,2),t2-t1,,(-2,2)绘制自相关函数程序如下:t=-2*pi:pi/100:2*pi;>> r=2.*cos(2*t);>> plot(t,r);自相关函数图像如图(4):----------图(4)实验总结1、深刻理解了随机相位正弦波的均值,方差和自相关函数的含义。
2、掌握了随机相位正弦波的均值,方差和自相关函数的计算方法;2(学会了运用Matlab编写程序绘制随机相位正弦波函数、均值函数、方差函数和自相关函数的图像。
____________________________________________________________________ ____________________________________________________________________________________________ ______________________________________________________________________________________实验成绩评阅时间评阅教师实验三实验题目模拟Possion流实验目的用Matlab语言产生随机数,了解 Possion流实验地点及时间信息楼机房121 2012.6.4实验内容用Matlab语言产生随机数,并编程实现possion流的模拟实验内容:用Matlab中的randn函数利用计算机产生伪随机数。
x=randn(1,N)产生长度为N且具有零均值和单位方差的正态分布的随机信号。
利用函数X=-a^(-1)*log(U)模拟泊松流。
利用Matlab编写函数绘制函数图像程序如下:U=randn(1,40); //产生均值为0,方差为1,长度为40的高斯白噪声。
>> a=2;X=-a^(-1)*log(U);>> S=zeros(1,42);>> d=zeros(1,42);>> S(1)=0;S(2)=X(1);for n=3:41S(n)=S(n-1)+X(n-1);endfor i=0:41if 0<=i<S(2)d(i+1)=0;elsefor j=2:41if (S(j)<=i)&(S(j+1)<i)d(i+1)=j;endendendend %-------------plot(d); //绘制泊松流图像>>如图(1)所示:____________________________________________________________________ ____________________________________________________________________________________________ ______________________________________________________________________________________--------图(1)实验总结1、学会了几种用Matlab产生随机数的方法,2、根据课本知识的学习掌握了泊松流的产生原理。
3、会编写用Matab模拟泊松流并绘制图像的程序。
____________________________________________________________________ ____________________________________________________________________________________________ ______________________________________________________________________________________实验成绩评阅时间评阅教师实验四实验题目求Markov链的极限分布实验目的用Matlab语言求Markov遍历链的极限分布实验地点及时间信息楼机房121 2012.6.6实验内容判定一个Markov链是否是遍历的,若是遍历的,求其极限分布。
并能从实际问题中抽象出Markov链,并求出其极限分布,并理解其实际意义。
实验习题为适应日益扩大的旅游事业的需要,某城市的A,B,C三个照相馆组成一个联营部,联合经营出租相机的业务,旅游者可由A,B,C三处任何一处租出相机,用完后还到A,B,C三处的任何一处即可.估计转移概率如表所示,今欲选择A,B,C之一附设租机维修点,问该点设在何处为好?还相机处A B C 租相机处 A 0.2 0.8 0B 0.8 0 0.2C 0.1 0.3 0.6 问题分析:转移概率矩阵P为:0.20.800.680.160.16,,,,,,,,2P,0.800.2P,0.180.70.12,,,,,,,,0.10.30.60.320.260.42,,,,2PP因为的所有元素都大于零,所以为正规矩阵。
当A,B,C三还相机处业务开,pppp,(,,)123展一定时期时会达到平衡条件,这样就可以得到一固定概率,使,,ppp,得成立,即____________________________________________________________________ ____________________________________________________________________________________________ ______________________________________________________________________________________0.20.80,,,,pppppp,,0.800.2,,,,,,,123123,,,,0.10.30.6,, -------------------(1) ppp,,,,1123 -------------------------------(2) (1)、(2)式同时成立运用Matlab编写程序,程序及结果如下:>> p=[0.2 0.8 0;0.8 0 0.2; 0.1 0.3 0.6];>> p2=p^2p2 =0.6800 0.1600 0.16000.1800 0.7000 0.12000.3200 0.2600 0.4200>> a=[p'-eye(3);ones(1,3)];b=[0 0 0 1]';T=a\bT =0.41460.39020.1951所以ppp,,0.4146,0.3902,0.1951,,,,,123由程序运行结果可知在稳定状态相机还到A处得概率为0.4146,在稳定状态相机还到B处得概率为0.3902,在稳定状态相机还到C处得概率为0.1951,A处的概率最大,因此相机维修点设在A处是最佳得选择。
