组合逻辑电路 习题课
第四章组合逻辑电路-习题PPT课件

大数 输 出
A0
A0
A1
A 1 7485
A2 A3
A2
A3
F A>B
0
(A>B) i
1
(A=B) i F A=B
0
B0
(A<B) i B0
B1
B1
F A<B
B2
B2
B3
B3
B0 1D0 A0 1D1
1Y
B1 2D0 A1 2D1
2Y
B2 A2
3D0 3D1
74157
3Y
B3 4D0 A3 4D1
(3)画逻辑电路,如下图所示:
2021/2/12
2021/2/12
D
&
B
&
C
A
&
& F
题4.4 图
F = A + BD + BC =A+B(D+C) = A + B D ·C = A ·B D ·C
2021/2/12
4.10 电话室需要对三种电话编码控制,按紧急 次序排列优先权高低是:火警电话、急救电话 、普通电话,分别编码为11,10,01。试设计 该编码电路。
的9,不需要修正。 A+B = COS3S2S1S0 ≤ (1001)2= (9)10 ,不需要修正。
2021/2/12
(1)10+(8)10= (9)10
2)若相加之和在10 ~ 15 之间,本位还要进行加6修正,
而进位是在进行加6修正时产生的。 10 ≤ A + B = COS3S2S1S0 ≤ 15 ,需要修正+6。
CD AB 00 01 11 10
第十一章组合逻辑电路习题及答案

第十一章组合逻辑电路习题及答案一、填空题1、数字电路中的逻辑电路按功能可分为电路和电路两种类型。
2、组合电路的特点:输出状态仅仅取决于输入值的组合,而与无关。
3、电路结构看,组合电路具有两个特点:(1)电路由电路组成,不包含任何元件,(2)电路中不存在任何回路。
4、电路的分析,是根据给定的电路,写出表达式,并以此来描述它的,确定对于的关系。
5、不考虑进位输入,只将本位两数相加,称为。
6、组合逻辑电路的分析,一般按以下步骤进行:第一步:根据给定的逻辑电路,写出。
第二步:化简逻辑电路的。
第三步:根据化简后的逻辑函数表达式列。
第四步:描述。
7、当两个本位数相加,再考虑进位数时,叫。
8、全加器有个输入,个输出。
9、全加器一个输出为,另一个输出为。
10、全加器的本位和输出表达式S n= ,进位输出表达式C n= 。
11、一个输出N位代码的二进制编码器,可以表示种输入信号。
12、二进制编码器是将输入信号编成的电路。
13、二进制译码器是将翻译成相对应的的电路。
14、二一十进制编码器是将,分别编成对应的的电路。
15、二一十进制译码器是将翻译成相对应的。
二、选择题1、组合电路的输出取决于()A、输入信号的现态B、输出信号的现态C、输入信号的现态和输出信号变化前的状态2、3线—8线译码器电路是()A、3位二进制B、三进制C、三--八进制3、七段数码显示译码电路应有()个输出端。
A、8个B、7个C、16个4、译码电路的输出量是()A、二进制代码B、十进制数C、某个特定的控制信息5、译码器可以将()的状态翻译成相应的输出信号。
A、输入代码B、输入数字C、输入信号D、输入脉冲6、七段字符显示器电路中a、b、c、d、g段发光是显示数字()。
A、6B、5C、4D、37、如图所示,BA为()。
A、00B、01C、10D、118、一个四输入端的与非门,它的输出有()种状态。
A、1B、2C、4D、169、能实现对两个一位二进制数及低位的进位数进行加法运算的电路称为()。
组合逻辑电路习题(附答案)

例1 指出下图1所示电路的输出逻辑电平是高电平、低电平还是高阻态。
已知图(a)中的门电路都是74系列的TTL门电路,图(b)中的门电路为CC4000系列的CMOS门电路。
图1解: TTL门电路的输入端悬空时,相当于高电平输入,输入端接有电阻时,其电阻阻值大于1.4K时,该端也相当于高电平,电阻值小于0.8K时,该端才是低电平。
而CMOS逻辑门电路,输入端不管是接大电阻还是接小电阻,该端都相当于低电平(即地电位)。
所以有如下结论:(a) 1L为低电平状态;2L是低电平状态;3L是高电平状态;4L 输出为高阻状态;(b) 1L输出为高电平;2L输出是低电平状态;3L输出是低电平状态;例2 图例2所示为用三态门传输数据的示意图,图中n 个三态门连到总线BUS ,其中D 1、D 2、…、D n 为数据输入端,EN 1、EN 2、…、ENn 为三态门使能控制端,试说明电路能传输数据的原理。
图例2 解:由三态门电路符号可知,当使能端低电平时,三态门输出为高阻阻态,所以,只要给各三态门的使能端n EN EN EN ,,,21 依次为高电平时,则,1n D D 的数据就依次被传输到总线上去。
例3 某功能的逻辑函数表达式为L=∑m(1,3,4,7,12,14,15);(1)试用最少量的“与-非”门实现该函数;(2)试用最少量的“或-非”门实现该函数;解: (1)设变量为A 、B 、C 、D ,用卡诺图化简,结合“1”方格得:DBACDAABCDCBDBACDAABCDCBDCBAfL=+++==),,,((2)卡诺图中结合“0”方格,求最简的“或—与”表达式,得:DCADCBDBBADCADCBDBBAL+++++++++=++++++=))()()((例4 试用一片八选一数据选择器74LS151实现逻辑函数。
(1) ACD D ABC CD B A D C B A Z ++=),,,( (2) C B A C B A C B A C B A Z ++=),,(解:解例基本思路:选定多路选择器的地址输入变量,列出卡诺图,求出数据输入端的函数关系式;(1) 选定四变量函数中的ABC(A 2A 1A 0)为地址输入,卡诺图为画出的电路图为:(2) 选定多路选择器的地址变量为)(012A A A ABC ,由于地址数正好是变量数,所以数据输入端的逻辑关系一定是常量“0”和“1”。
苏教版(2019) 选择性必修1 课时6 组合逻辑电路分析 练习(含答案)

课时6 组合逻辑电路分析一、基础巩固篇1.下列门电路可以实现F =A +B ________的是( )2.如图所示电路,输出函数F 为( )A.F =0B.F =1C.F =D.F =ABC3.如图所示为甲、乙两个逻辑电路,下列关于这两个逻辑电路的说法中,正确的是( )①甲逻辑电路可依据灯亮判断出输入信号A 、B 相同 ②甲逻辑电路可依据灯亮判断出输入信号A 、B 相异 ③乙逻辑电路可依据灯亮判断出输入信号A 、B 相同 ④乙逻辑电路可依据灯亮判断出输入信号A 、B 相异 A.①③ B.②③ C.①④D.②④4.如图所示为一组合逻辑电路,其中A 、B 是信号输入端,M 是控制信号端,F 是输出端。
下列关于电路的分析中不正确...的是( )A.当M 输入高电平时,F 的输出信号与A 的输入信号一致B.当A 、B 输入低电平时,F 输出低电平C.当M 输入低电平时,F 的输出信号与B 的输入信号一致D.F 输出的信号始终与M 控制信号相反5.如图所示的逻辑电路所对应的逻辑函数是( )A.Y =A -+B -B.Y =B A -+A B -C.Y =AB +A -·B -D.Y =AB +AB ——6.如图所示的控制电路,S 1、S 2按下时接通,松开后断开,初始状态S 1、S 2都断开。
下列说法不正确...的是( )A.初始状态时,LED1不亮,LED2亮B.只按下S 1时,LED1亮,LED2不亮C.只按下S 2时,LED1不亮,LED2亮D.同时按下S 1、S 2时,LED1亮,LED2不亮7.如图所示是一个由基本逻辑门组成的逻辑电路,下列关于该电路的说法,错误..的是( )A.当B的信号为1时,F的输出和A的输入相反B.当A的信号为0时,F的输出和B的输入相反C.当B的信号为0时,不管A的信号是什么,F的输出都不会改变D.当A的信号为1时,不管B的信号是什么,F的输出都不会改变8.某逻辑电路如图所示,在其真值表中,出现输出信号F为1的次数为()A.1次B.2次C.3次D.4次9.如图所示是小明设计的密码锁控制电路,开锁条件:①拨对密码;②钥匙插入锁眼使开关S闭合。
第04章 组合逻辑电路习题解

4.7写出下图所示电路的逻辑函数表达式,其中以S3,S2, 写出下图所示电路的逻辑函数表达式,其中以 , , 写出下图所示电路的逻辑函数表达式 S1,S0作为控制信号,A,B作为输入数据,列表说明输出 作为控制信号, , 作为输入数据 列表说明输出Y 作为输入数据, , 作为控制信号 的作用下与A, 的关系 的关系. 在S3–S0的作用下与 ,B的关系. 的作用下与
4.12试画出用 线-8线译码器 试画出用3线 线译码器 线译码器74LSl38和门电路产生如下多输 试画出用 和门电路产生如下多输 出逻辑函数的逻辑图. 出逻辑函数的逻辑图.
Y1 = AC Y2 = AB C + AB C + BC Y3 = B C + AB C
C B A 1
A0 A1 A2 S1 & S2 S3 EN
1,由波形图得到真值表 ,
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F 0 0 1 1 0 0 1 0 1 1 1 1 1 1 1 0
能对输入信号设置优先级并总是对优先级最高的一 个输入信号进行编码的编码器称作优先编码器. 个输入信号进行编码的编码器称作优先编码器. 变量处打" 表示该变量不管取什么值对输出没有 变量处打"X"表示该变量不管取什么值对输出没有 影响, 影响,在写出函数与或式中表示这是一个并项后消 去的因子. 去的因子.
(完整版)组合逻辑电路习题及答案.
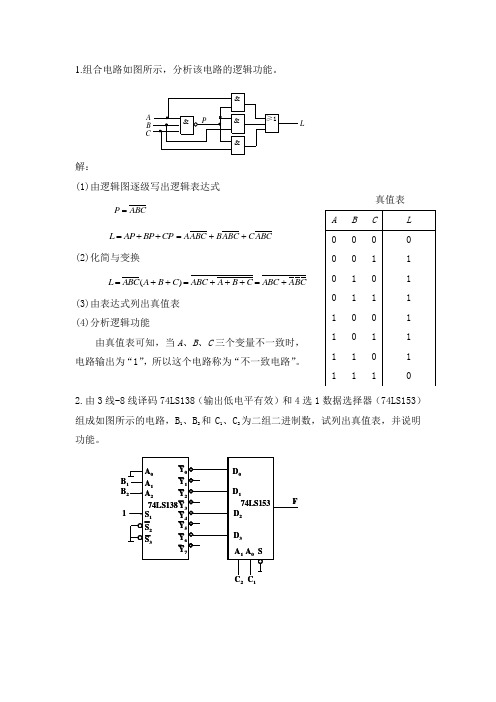
1.组合电路如图所示,分析该电路的逻辑功能。
解:(1)由逻辑图逐级写出逻辑表达式ABC P =CP BP AP L ++=ABC C ABC B ABC A ++= (2)化简与变换CB A ABC C B A ABC C B A ABC L +=+++=++=)((3)由表达式列出真值表(4)分析逻辑功能由真值表可知,当A 、B 、C 三个变量不一致时,电路输出为“1”,所以这个电路称为“不一致电路”。
2.由3线-8线译码74LS138(输出低电平有效)和4选1数据选择器(74LS153)组成如图所示的电路,B 1、B 2和C 1、C 2为二组二进制数,试列出真值表,并说明功能。
真值表A B CL解: 输出表达式: 212101122321F D C C D C C D C C D C C =+++021*********Y C C Y C C Y C C Y C C =⋅+⋅+⋅+⋅21021210212102121021A A A C C A A A C C A A A C C A A A C C =⋅+⋅+⋅+⋅2121212121212121B BC C B B C C B B C C B B C C =⋅+⋅+⋅+⋅功能说明:由地址码C 2C 1选择B 2B 1的最小项的反变量输出3.设计一个监视交通信号灯工作状态的逻辑电路。
正常情况下,红、黄、绿灯只有一个亮,否则视为故障状态,发出报警信号,提醒有关人员修理。
要求:(1)用门电路实现(2)用3-8线译码器实现(3)用4选1数据选择器实现。
解:(1)用门电路实现真值表B 2C 1C 0 00 11 01 1F21B B 21B B 21B 21B B①逻辑抽象输入变量:R 、A 、G ,红、黄、绿灯;灯亮为1,不亮为0。
输出变量:Z--故障信号,正常工作Z 为0,发生故障Z 为1。
列出真值表②写出函数式并化简 Z R A G RAG RA G RAG RAG =++++ 经卡诺图化简得: Z R A G RA RG AG =+++ ③画出电路图(2)用3-8线译码器实现①标准与或式 03567 Z R A G RAG RA G RAG RAG m m m m m =++++=++++ ②化成与非-与非式 0356703567Z m m m m m m m m m m =++++=⋅⋅⋅⋅ ③设R =A 2、A =A 1、G =A 0 则03567Z Y Y Y Y Y =⋅⋅⋅⋅ ④画连线图(3)用4选1数据选择器实现①标准与或式 Z R A G RAG RA G RAG RAG =++++S =1时 4选1 010*********Y D A A D A A D A A D A A =+++ ②确定输入变量和地址码的对应关系令A =A 1,G = A 0 ( )()()1Z R A G R AG R AG AG =+++⋅ 则:0D R = 12D D R == 31D =4.分别用74LS153(4选1数据选择器)和74LS152(8选1)实现函数F=AB+BC+AC 。
组合逻辑电路分析与设计习题解答
A
B
C
D
F
A
B
C
D
F
0
0
0
0
0
1
0
0
0
0
0
0
0
101来自001
0
0
0
1
0
0
1
0
1
0
0
0
0
1
1
0
1
0
1
1
1
0
1
0
0
0
1
1
0
0
0
0
1
0
1
0
1
1
0
1
1
0
1
1
0
0
1
1
1
0
1
0
1
1
1
0
1
1
1
1
1
组合逻辑电路设计(1)
A
B
C
D
组合逻辑电路分析(3)
F ABCD ABC D ABCD ABC D ABCD ABC D ABCD ABC D
CD
AB
00
01 11
10
00
1
1
01
1
1
11
1
1
10
1
1
组合逻辑电路分析(3)
F ABCD ABC D ABCD ABC D ABCD ABC D ABCD ABC D
电路功能: 在ABC取值中,若1
的个数为奇数,则输出 S为1;
在ABC取值中,若1 的个数为两个或三个, 则输出C为1;
4-2(组合逻辑电路习题)
例2 某工厂有三个车间,每个车间各需要 1KW的电力,这三个车间由两台发电机 组供电,一台是1KW,另一台是2KW。 此三车间经常不同时工作,有时只有一 个车间工作,也可能有两个车间或三个 车间工作。为了节省能源,又保证电力 供应,试设计一个逻辑电路,能自动完 成配电任务。
解:确定逻辑变量并赋值
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
F
1 0 1 0 0 1 1 0 0 0 1 0 1 1 1 1
卡诺图化简
F WX Y Z W X Z X Y Z
例4 设X、Y均为4位二进制数,它们分 别为一个逻辑电路的输入和输出,要求 0≤X≤4时,Y=X,当5≤X≤9时,Y=X+4, 而且X<10。试用与非门设计此电路。 答案
n变量异或若1的个为奇数个则结果为1组合逻辑电路设计例2某工厂有三个车间每个车间各需要1kw的电力这三个车间由两台发电机组供电一台是1kw另一台是2kw
试用与非门设计一个三变量判奇电 路,若三个变量中有奇数个1,则输出为 1否则为0。
组合逻辑电路设计——例1(续)
预习
编码器 译码器 奇偶校验器
显示译码器
真值表
ABC Y
逻辑表达式
000 001 010 011 100 101 110 111
0 Y A BC AB C A B C ABC 1结论:N变量异或,若‘1’的个 1 数 0 为奇数个,则结果为1 1 直接化简 0 0 Y A BC 1
逻辑图略
组合逻辑电路设计——例2
确定逻辑变量并赋值
数字电路第4章习题课
A0 2/4 Y2
A2
译码器 Y1
Y0
EN
A1
A1 2/4(1) A0
A0 Y0Y1Y2Y3
Y0Y1Y2 Y3
EN
A1 2/4(2) A0 Y0Y1Y2Y3
EN
A1 2/4(3) A0 Y0Y1Y2Y3
Y4Y5Y6 Y7 Y8Y9Y10Y11
EN A1 2/4(4) A0 Y0Y1Y2Y3
Y12Y13Y14Y15
B4B3B2B1
A0
=
B0
A3A2A1A0 B3B2B1B0
(A>B)i (A=B)i 7485(5) (A<B)i
FA>B FA=B FA<B
A3A2A1A0 B3B2B1B0
(A>B)i (A=B)i 7485(6) (A<B)i
FA>B FA=B FA<B
FA>B FA=B FA<B
36
4.17 设A=A3A2A1A0,B=B3B2B1B0均为8421BCD码。 试用74283设计一个A、B的求和电路。(可用附加器 件)
33
CD AB 00 01 11 10
00 1 1
01 1 1
11
1
10
A0 0 1 A1
0 D0 D1
1 D2 D3
BC A 00 01 11 10
0 D D DD 1 0 0 D0
B
A
0
1
0 C⊕D C⊙D
1 0 CD
34
令A=A1 、B=A0 , 则: D0 = C⊕D, D1 =C⊙D, D2 = 0,
22
4.12 试用74138设计一个多输出组合网络,它的 输入是4位二进制码ABCD,输出为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A B
A⊕B ⊕
A⊕ B
AB
A+ B
0
2010-9-14
习题课( ) 习题课(1)
8
2010-9-14
习题课( ) 习题课(1)
9
2010-9-14
习题课( ) 习题课(1)
4
例题四
设计一个路灯的控制电路(一盏灯),要求在四个不同地方都能独立控制 设计一个路灯的控制电路(一盏灯),要求在四个不同地方都能独立控制 ), 灯的亮灭。 灯的亮灭。
2010-9-14
ห้องสมุดไป่ตู้
习题课( ) 习题课(1)
5
例题五
A、B、C、D是四位二进制数,试设计下述要求的判断电路。 是四位二进制数,试设计下述要求的判断电路。 它们中间没有1 它们中间有两个1 它们中间有奇数个1 (1)它们中间没有1(2)它们中间有两个1 (3)它们中间有奇数个1。
2010-9-14
习题课( ) 习题课(1)
7
例题七
设计一个组合逻辑电路,它有两个输入端A 三个控制端X 设计一个组合逻辑电路,它有两个输入端A、B,三个控制端X、Y、Z和一 个输出端L 要求此电路实现如下表所示的逻辑功能。 个输出端L。要求此电路实现如下表所示的逻辑功能。
X 0 0 0 0 1 1 1 1 Y 0 0 1 1 0 0 1 1 Z 0 1 0 1 0 1 0 1 L 1 A+B
3
例题三
三个工厂由甲、乙两个变电站供电。若一个工厂用电,由甲变电站供电; 三个工厂由甲、乙两个变电站供电 。若一个工厂用电,由甲变电站供电 ; 若两个工厂用电,由乙变电站供电;若三个工厂同时用电,则由甲、 若两个工厂用电,由乙变电站供电;若三个工厂同时用电,则由甲、乙两个变 电站同时供电。设计一个供电控制电路。 电站同时供电。设计一个供电控制电路。
2010-9-14
习题课( ) 习题课(1)
6
例题六
用8选1多路选择器实现下列逻辑函数 (1) F = ABCD + ABC D + ABCD + ABC D + ABC D + ABC D + ABC D (2)F=(A, B, C, D)=Σm(0, 1, 2, 3, 8, 9, 10, 11) D) 11)
组合逻辑电路 习 题 课
分析图1 例题一 分析图1 所示组合逻辑电路
图1 (b )
图1 (a )
2010-9-14
习题课( ) 习题课(1)
2
分析图 所示电路的逻辑功能,并写出简明真值表。 例题二 分析图 2 所示电路的逻辑功能,并写出简明真值表。
图2
2010-9-14
习题课( ) 习题课(1)
