Z773-山东建筑大学考研试题-P2 (2)
山东建筑大学经济学(微观、宏观)期末考试复习题

・单项选择题L有关企业的短期与长期成本的关系,以下哪种表述正确?()。
A、若SAC=SMC,则LAC=LMCB、⅛SAC=LAC.则SMC=LMCC、若SMC=LAC,则SAC=LMCD、若LAC>LMC,≡SAC>SMC答案:B2当消费者对商品的消费达到饱和点时,那么边际效用MUX为()A、正值B、负值C、零D、不确定,视具体情况而定答案:C3完全垄断市场中如果A市场的需求弹性小于B市场的需求弹性,则()A、A市场的价格高于B市场B、A市场的价格低于B市场C、A市场的价格等于B市场D、价格孰高孰低不确定答案:B4生产契约线上的点表示生产者().A、获得了最大利润B、支出了破小成本C、通过生产要素的重新配置提高了总产量D、以上均不正确答案:D5使用50个单位的劳动,一个厂商可以生产出1800单位的产量,使用60个单位的劳动,一个厂商可以生产出2100单位的产量,额外一单位劳动的边际产量是()A、32B、30C、35D、36答案:B6充分就业实现时()A、人人都有工作,没有失业者B、并不是人人都有工作,仍然有失业者C,经济中失业率高于自然失业率时的状态D、经济中失业率高「周期性失业率时的状态答案:B7当边际产量大于平均产量时,平均产量()A、递减B、不变C,递增D、先增后减答案:C8完全竞争市场中的厂商总收益曲线的斜率为()。
A,固定不变B.经常变动C、1D、O答案:A二-判断题I-用先进的机器代替工人的劳动,会使劳动的需求曲线向右移动。
A、正确B、错误答案:错误2.垄断的存在会引起市场失灵。
A、正确B、错误答案:正确3∙2013年12月31H的外汇储备量是流量。
A、正确B、错误答案:错误4∙一种物品效用的大小表明它在生产中的作用有多大。
A、正确B-错误答案:错误5∙乘数的大小取决于边际消费倾向。
A、正确B-错误答案:正确Ξ-简答题L请简述宏观经济学与微观经济学的区别与联系:答案:区别:研究的对象不同:微观经济:单个经济单位的最优化行为宏观经济:整体经济的运行规律和宏观经济政策解决的问题不同:微观经济:解决资源配置,问题宏观经济:解决资源利用何胭中心理论不同:微观经济:价格理论宏观经济:国名收入(产出)决定理论研究方法不同:微观经济:采用个量(单项数值)分析方法宏观经济:采用总量分析方法联系:相互补充,都采用了实证分析方法,微观经济是宏观经济的基础。
山东建筑大学材料力学试题
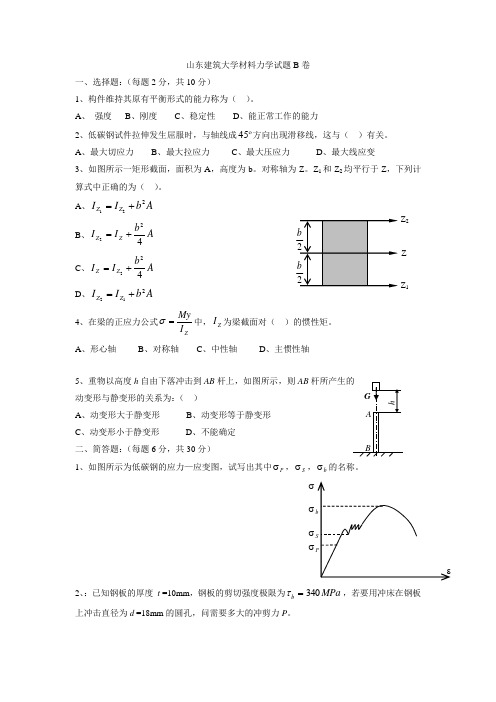
山东建筑大学材料力学试题B 卷一、选择题:(每题2分,共10分)1、构件维持其原有平衡形式的能力称为( )。
A 、 强度B 、刚度C 、稳定性D 、能正常工作的能力2、低碳钢试件拉伸发生屈服时,与轴线成45方向出现滑移线,这与( )有关。
A 、最大切应力 B 、最大拉应力 C 、最大压应力 D 、最大线应变3、如图所示一矩形截面,面积为A ,高度为b 。
对称轴为Z 。
Z 1和Z 2均平行于Z ,下列计算式中正确的为( )。
A 、A b I I Z Z 221+= B 、A bI I Z Z 422+= C 、A b I I Z Z 422+= D 、A b I I Z Z 212+= 4、在梁的正应力公式ZI My=σ中,Z I 为梁截面对( )的惯性矩。
A 、形心轴 B 、对称轴 C 、中性轴 D 、主惯性轴5、重物以高度h 自由下落冲击到AB 杆上,如图所示,则AB动变形与静变形的关系为:( )A 、动变形大于静变形B 、动变形等于静变形C 、动变形小于静变形D 、不能确定 二、简答题:(每题6分,共30分)1、如图所示为低碳钢的应力—应变图,试写出其中P σ,S σ,b σ的名称。
2、:已知钢板的厚度 t =10mm ,钢板的剪切强度极限为MPa b 340=τ,若要用冲床在钢板上冲击直径为d =18mm 的圆孔,问需要多大的冲剪力P 。
Z 2Z 1Zσσσσ3、试求图示单元体的主应力大小。
(图中应力单位:MPa )。
4时所用的边界条件和连续条件。
5、在设计图示细长压杆时,有正方形和圆形两种截面可供选择,它们的面积相同。
试判断哪种截面的稳定性好?为什么?三、计算题:(每题15分,共计60分)1、图示结构中,横梁AB 为刚性杆,设1、2杆的长度、横截面积和材料均相等。
求:在力F 作用下1、2杆的轴力。
2、一外伸工字型钢梁,工字钢的型号为22a ,梁上荷载如图所示。
已知l =6m ,F =30kN ,q =6kN/m ,材料的许用应力[σ]=170MPa ,[τ]=100MPa ,试画梁的内力图,并检查此梁是否安全。
10-11-2概率论与数理统计A卷(答案)山东建筑大学概率论与数理统计试题A期末考试试题

2010-2011-2 概率与数理统计试卷A 参考答案及评分标准一、填空题(每小题2分,共20分) 1、0.7; 2、)16,1(N ; 3、10; 4、1,1==B A; 5、44; 6、2720;7、 8、32,9、75,10、111-∑=n i i X n 。
二、选择题(每题2分,共20分)11、(B ); 12、(D ); 13、(D ); 14、(B ); 15、(C );16、(B );17、(A );18、(B ); 19、(A ); 20、(B ).三、计算题(共60分)21、(8分) 解 设A 表示事件“从剩下的产品中任取一件是正品”,i B 表示事件“已经出售的2件中有i 件次品”)2,1,0(=i ,则CC B P 210270)(=;85)/(0=B A P ---------------------------------------------------------2分CC C B P 21013171)(=;86)/(1=B A P -------------------------------------------------------4分CC B P 210232)(=;87)/(2=B A P -----------------------------------------------------------6分所以7.0878685)/()()(210232101317210272=⋅+⋅+⋅==∑=C C C C C C C i ii B A P B P A P ------------8分22、(10分)解 (1)X 的可能取值为1-,1,2,----------------------------------------------2分 且3162}1{==-=X P ,2163}1{===X P ,61}2{==X P ,------------------6分所以其概率分布为(2)()1123123≠⎪⎭⎫⎝⎛≠<=⎪⎪⎭⎫ ⎝⎛≠<X P X X P X X P 且-------------------------------------8分 322131==---------------------------------------------------------------------------------10分 23、(12分) 解 (1)由12)()(1=+=+=⎰⎰∞+∞-b adx b ax dx x f ,--------------------------2分 又85283)()(21121 21=+=+==⎭⎬⎫⎩⎨⎧>⎰⎰∞+b a dx b ax dx x f XP ,--------------------------4分所以21,1==b a ------------------------------------5分 (2)327)21()(214121412141=+==⎭⎬⎫⎩⎨⎧≤<⎰⎰dx x dx x f X P -------------------------7分(3)⎰∞-=x dt t f x F )()(当0≤x 时,00)(==⎰∞-xdt x F ;-----------------------------------------------------8分当10≤<x 时,)1(212121)21(0)(200+=+=++=⎰⎰∞-x x x x dt t dt x F x;----------10分当1>x 时,10)21(0)(1010=+++=⎰⎰⎰∞-x dt dt t dt x F ;-----------------------------11分综上, ⎪⎩⎪⎨⎧>≤<+≤=1,110,)1(210,0)(x x x x x x F ---------------------------------12分24、(10分)解 先求X e Y =的分布函数}{}{)(y e P y Y P y F X Y ≤=≤=-------------------------2分当0≤y 时,0)(=y F Y ;--------------------------------------------------------------4分当10<<y 时,00}ln {)(ln ==≤=⎰∞-yY dx y X P y F ;--------------------------------6分当1≥y 时,⎰-=≤=yx Y dx e y X P y F ln 0}ln {)(;--------------------------------------8分所以⎪⎩⎪⎨⎧≥=⋅<='=-1,111,0)()(2ln y y y e y y F y f y Y Y .----------------------------------------10分25、(10分)解),(Y X 的概率分布表为分所以Y X +的分布列为整理得Y X +的分布列为分26、(10分) 解:121122()x xE X edx θθθθθθ--+∞==+⎰---------------------------2分121222211222()2x xE X edx θθθθθθθθ--+∞==++⎰---------------------------4分令 122221122112n ii x x n θθθθθθ=⎧+=⎪⎨++=⎪⎩∑ 解得12,θθ的矩法估计为^2^1n n s x s θθ⎧==⎪⎪⎨⎪=-⎪⎩---------------------------6分似然函数12111221(,)n i i x n nL eθθθθθ=⎡⎤--⎢⎥⎢⎥⎣⎦∑=两边取对数1221121ln (,)ln n i i L n x n θθθθθ=⎡⎤=---⎢⎥⎣⎦∑ 对1θ求偏导,1212ln (,)0L nθθθθ∂=>∂,知L ln 是1θ的递增函数,1θ取到其最大的可能值使L ln 达到最大,故1θ的极大似然估计为^112min{,,}n x x x θ= 。
山东建筑大学计算机学院算法分析算法复习题(Yuconan翻译)

1.The O-notation provides an asymptotic upper bound. The Ω-notationprovides an asymptotic lower bound. The Θ-notation asymptoticallya function form above and below.2.To represent a heap as an array,the root of tree is A[1], and giventhe index i of a node, the indices of its parent Parent(i) { return ⎣i/2⎦; },left child, Left(i) { return 2*i; },right child, right(i) { return 2*i + 1; }.代表一个堆中的一个数组,树的根节点是A[1],并且给出一个节点i,那么该节点的父节点是左孩子右孩子3.Because the heap of n elements is a binary tree, the height of anynode is at most Θ(lg n).因为n个元素的堆是一个二叉树,任意节点的树高最多是4.In optimization problems, there can be many possible solutions. Eachsolution has a value, and we wish to find a solution with the optimal (minimum or maximum) value. We call such a solution an optimal solution to the problem.在最优化问题中,有很多可能的解,每个解都有一个值,我们希望找到一个最优解(最大或最小),我们称这个解为最优解问题。
考研数学三线性代数(二次型)模拟试卷2(题后含答案及解析)

考研数学三线性代数(二次型)模拟试卷2(题后含答案及解析) 题型有:1. 选择题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.设二次型f(x1,x2,x3)=XTAX,已知r(A)=2,并且A满足A2一2A=0.则下列各标准二次型(1)2y12+2y22 (2)2y12.(3)2y12+2y32.(4)2y22+2y32.中可用正交变换化为f的是( ).A.(1).B.(3),(4).C.(1),(3),(4).D.(2).正确答案:C解析:两个二次型可以用正交变换互相转化的充要条件是它们的矩阵相似,也就是特征值一样.从条件可知,A的特征值为0,2,2.(1),(3),(4)这3个标准二次型的矩阵的特征值都是0,2,2.(2)中标准二次型的矩阵的特征值是0,0,2.知识模块:线性代数2.设A.A与B既合同又相似.B.A与B合同但不相似.C.A与B不合同但相似.D.A与B既不合同又不相似.正确答案:A解析:A与B都是实对称矩阵,判断是否合同和相似只要看它们的特征值:特征值完全一样时相似,特征值正负性一样时合同.此题中A的特征值和B的特征值都是4,0,0,0,从而A与B既合同又相似.知识模块:线性代数3.A.A与B既合同又相似.B.A与B合同但不相似.C.A与B不合同但相似.D.A与B既不合同又不相似.正确答案:B 涉及知识点:线性代数4.A=.则( )中矩阵在实数域上与A合同.A.B.C.D.正确答案:D解析:用特征值看:两个实对称矩阵合同它们的特征值正负性相同.|A|=一3,对于2阶实对称矩阵,行列式小于0即两个特征值一正一负,于是只要看哪个矩阵行列式是负数就和A合同.计算得到只有(D)中的矩阵的行列式是负数.知识模块:线性代数解答题解答应写出文字说明、证明过程或演算步骤。
5.用配方法化下列二次型为标准型(1)f(x1,x2,x3)=x12+2x22+2x1x2—2x1x3+2x2x3.(2)f(x1,x2,x3) =x1x2+x1x3+x2x3.正确答案:(1)f(x1,x2,x3)=x12+2x22+2x1x2—2x1x3+2x2x3 = [x12+2x1x2—2x1x3+(x2一x3)2]一(x2一x3)2+2x22+2x23 =(x1+x2一x3)2+x22+4x2x3一x32 =(x1+x2一x3)2+x22+4x2x3+4x32一5x32=(x1+x2一x3)2+(x2+2x3)2—5x32.原二次型化为f(x1,x2,x3)=y12+y22一5y32.从上面的公式反解得变换公式:变换矩阵(2)这个二次型没有平方项,先作一次变换f(x1,x2,x3) =y12一y22+2y1y3.虽然所得新二次型还不是标准的,但是有平方项了,可以进行配方了:y12一y22+2y1y3=(y1+y3)2一y22一y32则f(x1,x2,x3)=z12一z22一z32.涉及知识点:线性代数6.已知二次型2x12+3x22+3x32+2ax2x3(a>0)可用正交变换化为y12+2y22+5y32,求a和所作正交变换.正确答案:原二次型的矩阵A和化出二次型的矩阵B相似.于是|A|=|B|=10.而|A|=2(9一a2),得a2=4,a=2.A和B的特征值相同,为1,2,5.对这3个特征值求单位特征向量.对于特征值1:得(A—E)X=0的同解方程组得属于1的一个特征向量η1=(0,1,一1)T,单位化得γ1=对于特征值2:得(A一2E)X=0的同解方程组得属于2的一个单位特征向量γ2=(1,0,0)T.对于特征值5:得(A一5E)X=0的同解方程组得属于5的一个特征向量η3=(0,1,1)T,单位化得γ3=令Q=(γ1,γ2,γ3),则正交变换X=QY把原二次型化为y12+2y22+5y32. 涉及知识点:线性代数7.设二次型f(x1,x2,x3)=XTAX=ax12+2x22-2x32+2bx1x3,(b>0)其中A的特征值之和为1,特征值之积为一12.(1)求a,b.(2)用正交变换化f(x1,x2,x3)为标准型.正确答案:由条件知,A的特征值之和为1,即a+2+(一2)=1,得a=1.特征值之积=一12,即|A|=一12,而|A|==2(一2一b2)得b=2(b>0).则(2)|λE—A|==(λ一2)2(λ+3),得A的特征值为2(二重)和一3(一重).对特征值2求两个单位正交的特征向量,即(A一2E)X=0的非零解.得(A一2E)X=0的同解方程组x1一2x3=0,求出基础解系η1=(0,1,0)T,η2=(2,0,1)T.它们正交,单位化:α1=η1,α2=方程x1一2x3=0的系数向量(1,0,一2)T和η1,η2都正交,是属于一3的一个特征向量,单位化得作正交矩阵Q=(α1,α2,α3),则作正交变换X=QY,则它把f化为Y的二次型f=2y12+2y22一3y32.涉及知识点:线性代数8.已知二次型f(x1,x2,x3)=(1一a)x12+(1一a)x22+2x32+2(1+a)x1x2的秩为2.(1)求a.(2)求作正交变换X=QY,把f(x1,x2,x3)化为标准形.(3)求方程f(x1,x2,x3)=0的解.正确答案:(1)此二次型的矩阵为则r(A)=2,|A|=0.求得|A|=-8a,得a=0.(2)|λE—A|==λ(λ一2)2,得A的特征值为2,2,0.对特征值2求两个正交的单位特征向量:得(A一2E)X=0的同解方程组x1一x2=0,求出基础解系η1=(0,0,1)T,η2=(1,1,0)T.它们正交,单位化:α1=η1,α2= 方程x1一x2=0的系数向量(1,一1,0)T和η1,η2都正交,是属于特征值0的一个特征向量,单位化得作正交矩阵Q=(α1,α2,α3),则作正交变换X=QY,则f化为Y的二次型f=2y12+2y22.(3)f(X)=x12+x22+2x32+2x1x2=(x1+x2)2+2x32于是f(x1,x2,x3)=0求得通解为:c任意.涉及知识点:线性代数9.二次型f(x1,x2,x3)=XTAX在正交变换X=QY下化为10y12一4y22一4y32,Q的第1列为(1)求A.(2)求一个满足要求的正交矩阵Q.正确答案:标准二次型10y12一4y22一4y32的矩阵为则Q-1AQ=QTAQ=B,A和B相似.于是A的特征值是10,一4,一4.(1)Q的第1列α1=是A的属于10的特征向量,其倍η1=(1,2,3)T也是属于10的特征向量.于是A的属于一4的特征向量和(1,2,3)T正交,因此就是方程x1+2x2+3x3=0的非零解.求出此方程的一个正交基础解系η2=(2,一1,0)T,η3=建立矩阵方程A(η1,η2,η3)=(10η1,一4η2,一4η3),用初等变换法解得(2)将η2,η3单位化得α3=α3=则正交矩阵Q=(α1,α2,α3)满足要求.涉及知识点:线性代数10.A=,求作一个3阶可逆矩阵P,,使得PTAP是对角矩阵.正确答案:f(x1,x2,x3)=XTAX=x12+4x22一2x32一4x1x2+4x2x3=(x1一2x2)2一2x32+4x2x3 =(x1一2x2)2一2(x2一x3)2+2x22.原二次型化为f(x1,x2,x3)=y12一2y22+2y32.从上面的公式反解得变换公式:变换矩阵涉及知识点:线性代数11.已知求作可逆矩阵P,使得(AP)TAP是对角矩阵.正确答案:涉及知识点:线性代数12.二次型f(x1,x2,x2)=x12+ax22+x32+2x1x2+2x1x3+2x2x3的正惯性指数为2,a应满足什么条件?正确答案:f(x1,x2,x3)=(x1+x2+x3)2+(a一1)x22,原二次型化为f(x1,x2,x3)=y12+(a—1)y22,则正惯性指数为2a—1>0,即a>1.涉及知识点:线性代数13.设A是一个可逆实对称矩阵,记Aij是它的代数余子式.二次型f(x1,x2,…,xn)= (1)用矩阵乘积的形式写出此二次型.(2)f(x1,x2,…,xn)的规范形和XTAX的规范形是否相同?为什么?正确答案:(1)由于A是实对称矩阵,它的代数余子式Aij=Aji,,并且A-1也是实对称矩阵,其(i,j)位的元素就是Aij/|A|,于是f(x1,x2,…,xn)=XTA-1X.(2)A-1的特征值和A的特征值互为倒数关系,因此A-1和A 的正的特征值的个数相等,负的特征值的个数也相等,于是它们的正,负惯性指数都相等,从而A-1和A合同,f(x1,x2,…,xn)和XTAX有相同的规范形.涉及知识点:线性代数14.判断A与B是否合同,其中正确答案:用惯性指数,看它们的正负惯性指数是否都一样.B的正惯性指数为2,负惯性指数为1.A的惯性指数可通过对二次型XTAX进行配方法化标准形来计算.XTAX=x12+4x22一2x32一4x1x2—4x2x3 =(x1一2x2)2—2x32一4x2x3 =(x1一2x2)2—2(x3+x2)2+2x22,则XTAX=y12一2y22+2y32,于是A的正惯性指数也为2,负惯性指数也为1.A与B合同.涉及知识点:线性代数15.二次型f(x1,x2,x3)=ax12+ax22+(a一1)x32+2x1x3—2x2x3.①求f(x1,x2,x3)的矩阵的特征值.②如果f(x1,x2,x3)的规范形为y12+y22,求a.正确答案:①f(x1,x2,x3)的矩阵为记B=则A=B+aE.求出B的特征多项式|λE一B|=λ3+λ2—2λ=λ(λ+2)(λ—1),B的特征值为一2,0,1,于是A 的特征值为a一2,a,a+1.②因为f(x1,x2,x3)的规范形为y12+y22时,所以A的正惯性指数为2,负惯性指数为0,于是A的特征值2个正,1个0,因此a=2.涉及知识点:线性代数16.a为什么数时二次型x12+3x22+2x32+2ax2x3可用可逆线性变量替换化为2y12一3y22+5y32?正确答案:就是看a为什么数时它们的矩阵合同.写出这两个二次型的矩阵B的特征值是2正1负.又看出1是A的特征值,于是A的另两个特征值应该1正1负,即|A|<0.求得|A|=6一a2,于是a满足的条件应该为:涉及知识点:线性代数17.已知A是正定矩阵,证明|A+E|>1.正确答案:此题用特征值较简单.设A的特征值为λ1,λ2,…,λn,则A+E的特征值为λ1+1,λ2+1,…,λn+1.因为A正定,所以λi>0,λi+1>1(i=1,2,…,n).于是|A+E|=(λ1+1)(λ2+1)…(λn+1)>1.涉及知识点:线性代数18.已知二次型f(x1,x2,x3)=x12+4x22+4x32+2λx1x2—2x1x3+4x2x3.当λ满足什么条件时f(x1,x2,x3)正定?正确答案:用顺序主子式.此二次型的矩阵它的顺序主子式的值依次为1,4一λ2,4(2一λ—λ2).于是,λ应满足条件4一λ2>0,2一λ—λ2>0,解出λ∈(一2,1)时二次型正定.涉及知识点:线性代数19.已知二次型f(x1,x2,…,xn)=(x1+a1x2)2+(x2+a2x3)2+…+(xn+anx1)2.a1,a2,…,an满足什么条件时f(x1,x2,…,xn)正定?正确答案:记y1=x1+a1x2,y2=x2+a2x3,…,yn=xn+anx1,则简记为Y=AX.则f(x1,x2,…,xn)=YTY=XTATAX.于是,实对称矩阵ATA就是f(x1,x2,…,xn)的矩阵.从而f正定就是ATA正定.ATA正定的充要条件是A可逆.计算出|A|=1+(一1)n-1a1a2…an.于是,f正定的充要条件为a1a2…an≠(一1)n.涉及知识点:线性代数20.设B=(A+kE)2.(1)求作对角矩阵D,使得B~D.(2)实数k满足什么条件时B正定?正确答案:(1)A是实对称矩阵,它可相似对角化,从而B也可相似对角化,并且以B的特征值为对角线上元素的对角矩阵和B相似.求B的特征值:|λE一A|=λ(λ一2)2,A的特征值为0,2,2,于是B的特征值为k2和(k+2)2,(k+2)2.则B~D.(2)当k为≠0和一2的实数时,B是实对称矩阵,并且特征值都大于0,从而此时B正定.涉及知识点:线性代数21.设A和B都是m×n实矩阵,满足r(A+B)=n,证明ATA+BTB正定.正确答案:用正定的定义证明.显然ATA,BTB都是n阶的实对称矩阵,从而ATA+BTB也是n阶实对称矩阵.由于r(A+B)=n,n元齐次线性方程组(A+B)X=0没有非零解.于是,当α是一个非零n维实的列向量时,(A+B)α≠0,因此Aα与Bα不会全是零向量,从而αT(ATA+BTB)α=αTATAα+αTBTBα=‖Aα‖2+‖Bα‖2>0.根据定义,ATA+BTB正定.涉及知识点:线性代数22.设A是m阶正定矩阵,B是m×n实矩阵,证明:BTAB正定r(B)=n.正确答案:“”BTAB是n阶正定矩阵,则r(BTAB)=n,从而r(B)=n.“”显然BTAB是实矩阵,并且(BTAB)T=BTAT(BT)T=BTAB,因此,BTAB是实对称矩阵.因为r(B)=n,所以齐次线性方程组BX=0只有零解,即若X是n维非零实列向量,则BX≠0.再由A的正定性,得到XT(BTAB)X=(BX)TA(BX)>0.由定义知,BTAB正定.涉及知识点:线性代数23.设A是3阶实对称矩阵,满足A2+2A=0,并且r(A)=2.(1)求A 的特征值.(2)当实数k满足什么条件时A+kE正定?正确答案:(1)因为A是实对称矩阵,所以A的特征值都是实数.假设λ是A的一个特征值,则λ2+2λ是A2+2A的特征值.而A2+2A=0,因此λ2+2λ=0,故λ=0或一2.又因为r(A一0E)=r(A)=2,特征值0的重数为3一r(A—0E)=1,所以一2是A的二重特征值.A的特征值为0,一2,一2.(2)A+kE 的特征值为k,k一2,k一2.于是当k>2时,实对称矩阵A+kE的特征值全大于0,从而A+kE是正定矩阵.当k≤2时,A+kE的特征值不全大于0,此时A+kE不正定.涉及知识点:线性代数24.设A,B是两个n阶实对称矩阵,并且A正定.证明:(1)存在可逆矩阵P,使得PTAP,PTBP都是对角矩阵;(2)当|ε|充分小时,A+εB仍是正定矩阵.正确答案:(1)因为A正定,所以存在实可逆矩阵P1,使得P1TAP1=E.作B1=P1TBP1,则B1仍是实对称矩阵,从而存在正交矩阵Q,使得QTB1Q是对角矩阵.令P=P1Q,则PTAP=QTP1TAP1Q=E,PTBP=QTP1TBP1Q=QTBtQ.因此P即所求.(2)设对(1)中求得的可逆矩阵P,对角矩阵PTBP对角线上的元素依次为λ1,λ3,…,λn,记M=max{|λ1|,|λ2|,…,|λn|}.则当|ε|<1/M时,E+εPTBP仍是实对角矩阵,且对角线上元素1+ελi>0,i=1,2,…,n.于是E+εPTBP正定,PT(A+εB)P=E+εPTBP,因此A+εB也正定.涉及知识点:线性代数25.设C=,其中A,B分别是m,n阶矩阵.证明C正定A,B都正定.正确答案:显然C是实对称矩阵A,B都是实对称矩阵.|λEm+n一C|==|λEm一A||λEn一B|于是A,B的特征值合起来就是C的特征值.如果C正定,则C的特征值都大于0,从而A,B的特征值都大于0,A,B都正定.反之,如果A,B都正定,则A,B的特征值都大于0,从而C的特征值都大于0,C 正定.涉及知识点:线性代数26.设D=是正定矩阵,其中A,B分别是m,n阶矩阵.记P=(1)求PTDP.(2)证明B一CTA-1C正定.正确答案:(1) (2)因为D为正定矩阵,P是实可逆矩阵,所以PTDP正定.于是由上例的结果,得B一CTA-1C正定.涉及知识点:线性代数27.二次型f(x1,x2,x3)=XTAX在正交变换X=QY下化为y12+y22,Q 的第3列为①求A.②证明A+E是正定矩阵.正确答案:①条件说明Q-1AQ=QTAQ=于是A的特征值为1,1,0,并且Q 的第3列=(1,0,1)T是A的特征值为0的特征向量.记α1=(1,0,1)T,它也是A的特征值为0的特征向量.A是实对称矩阵,它的属于特征值1的特征向量都和α1正交,即是方程式x1+x3=0的非零解.α2=(1,0,一1)T,α3=(0,1,0)T 是此方程式的基础解系,它们是A的特征值为1的两个特征向量.建立矩阵方程A(α1,α2,α3)=(0,α2,α3),两边做转置,得解此矩阵方程②A+E也是实对称矩阵,特征值为2,2,1,因此是正定矩阵.涉及知识点:线性代数28.证明对于任何m×n实矩阵A,ATA的负惯性指数为0.如果A秩为n,则ATA是正定矩阵.正确答案:设A是A的一个特征值,η是属于它的一个特征向量,即有ATA η=λη,于是ηTATAη=ληTη,即(Aη,Aη)=λ(η,η).则λ=(A η,Aη)/(η,η)≥0.如果A秩为n,则AX=0没有非零解,从而Aη≠0,(Aη,Aη)>0,因此λ=(Aη,Aη)/(η,η)>0.涉及知识点:线性代数29.如果A正定,则Ak,A-1,A*也都正定.正确答案:从特征值看.设A的特征值为λ1,λ2,…,λn.λi>0,i=1,2,…,n.则Ak的特征值为λ1k,λ2k,…,λn-1.λi-1>0,i=1,2,…,n.设A-1的特征值为λ1-1,λ2-1,…,λn-1.λi-1>0,i=1,2,…,n.设A*的特征值为|A|/λ1,|A|/λ2,…,|A|/λn.|A|/λi>0,i=1,2,…,n.涉及知识点:线性代数30.设A是正定矩阵,B是实对称矩阵,证明AB相似于对角矩阵.正确答案:A是正定矩阵,存在可逆实矩阵C,使得A=CCT,则AB=CCT B.于是C-1ABC=C-1CCTBC=CTBC.即AB相似于CTBC.而CTBC是实对称矩阵,相似于对角矩阵.由相似的传递性,AB也相似于对角矩阵.涉及知识点:线性代数31.设A,B都是n阶正定矩阵,则:AB是正定矩阵A,B乘积可交换.正确答案:“”先证明AB对称.(AB)T=BTAT=BA=AB.再证明AB的特征值全大于0.存在可逆实矩阵C,使得A=CCT.则AB=CCTB,相似于CTBC,特征值一样,而CTBC是正定的,特征值全大于0.“”AB正定,则对称.于是BA=BTAT=(AB)T=AB.涉及知识点:线性代数32.设A是一个n阶实矩阵,使得AT+A正定,证明A可逆.正确答案:设n维实列向量α满足Aα=0,要证明α=0.αT(AT+A)α=αTATα+αTAα=(Aα)Tα+αTAα=0.由AT+A的正定性得到α=0.涉及知识点:线性代数33.设A是一个n阶正定矩阵,B是一个n阶实的反对称矩阵,证明A+B 可逆.正确答案:证明(A+B)X=0没有非零解.设n维实列向量α满足(A+B)α=0,要证明α=0.注意B是反对称矩阵,αTBα=0(因为αTBα=(αTBα)T=一αTB α.) αTAα=αTAα+αTBα=αT(A+B)α=0由A的正定性得到α=0.涉及知识点:线性代数。
山东建筑大学高等数学试卷(A卷)

2006~2007-2高等数学A2试题A 卷一、填空题(每小题3分,共15分)1.函数),(y x f 在点),(y x 可微分是),(y x f 在该点连续的 条件.2.半径为a 的均匀半圆薄片(面密度为ρ)对其直径边的转动惯量为 . 3.L 为圆周222ay x =+,则()⎰+Lndsy x 22= .4.函数0,0,)(⎩⎨⎧<≤<≤--=ππx x x x x f 的傅里叶级数展开式为()()⎪⎪⎭⎫⎝⎛+++++++-=ΛΛx n n x x x x f 12cos 1215cos 513cos 31cos 42)(222ππ)(ππ≤≤-x ,则级数()ΛΛ++++++22212151311n 的和等于 ..二、选择题(每小题3分,共15分)6.函数()22,y xy x y x f +-=在点)1,1(P 处沿方向⎭⎬⎫⎩⎨⎧=41,41l ρ的方向导数( )。
(A) 最大; (B) 最小; (C) 1; (D) 0. 7.设区域D 是由0,42=-=y x y 围成,则=+=⎰⎰Ddxdy y ax I )(( )。
(A) 0>I ;(B) 0=I ;(C) 0<I ;(D) I 的符号与a 有关. 8.下列各式中正确的是( )(A)022=+-⎰Ly x ydxxdy ,其中1:22=+y x L ,沿逆时针方向; (B)⎰⎰⎰⎰∑∑⎪⎪⎭⎫ ⎝⎛++=++dS R Q P dxdy z y x R dzdx z y x Q dydz z y x P 5325253),,(),,(),,(;其中∑是平面63223=++z y x 在第一卦限的部分的上侧。
(C) ⎰⎰⎰Γ∑⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=++dz y P x Q dy x R z P dx z Q y R Rdxdy Qdzdx Pdydz 其中Γ是∑的边界曲线,且Γ的方向与∑侧符合右手法则;(D) 向量场k z y x R j z y x Q i z y x P z y x A ρρρρ),,(),,(),,(),,(++=的散度ky P x Q j x R z P i z Q y R A div ρϖρϖ⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=. 9.级数∑∞=+-12)1(n nn nb 为( )。
考研数学(一)历年真题(1990-2021)无水印
1990年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)2x t =-+(1)过点(1,21)M -且与直线34y t =-垂直的平面方程是_____________.1z t =-(2)设a 为非零常数,则lim(xx x a x a→∞+-=_____________.(3)设函数()f x =1011x x ≤>,则[()]f f x =_____________.(4)积分222e y xdx dy -⎰⎰的值等于_____________.(5)已知向量组1234(1,2,3,4),(2,3,4,5),(3,4,5,6),(4,5,6,7),====αααα则该向量组的秩是_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设()f x 是连续函数,且e ()(),xxF x f t dt -=⎰则()F x '等于(A)e (e )()xx f f x ----(B)e (e )()xx f f x ---+(C)e(e )()x x f f x ---(D)e(e )()xx f f x --+(2)已知函数()f x 具有任意阶导数,且2()[()],f x f x '=则当n 为大于2的正整数时,()f x 的n 阶导数()()n f x 是(A)1![()]n n f x +(B)1[()]n n f x +(C)2[()]nf x (D)2![()]nn f x (3)设a 为常数,则级数21sin()[n na n ∞=∑(A)绝对收敛(B)条件收敛(C)发散(D)收敛性与a 的取值有关(4)已知()f x 在0x =的某个邻域内连续,且0()(0)0,lim2,1cos x f x f x→==-则在点0x =处()f x(A)不可导(B)可导,且(0)0f '≠(C)取得极大值(D)取得极小值(5)已知1β、2β是非齐次线性方程组=AX b 的两个不同的解1,α、2α是对应其次线性方程组=AX 0的基础解析1,k 、2k 为任意常数,则方程组=AX b 的通解(一般解)必是(A)1211212()2k k -+++ββααα(B)1211212()2k k ++-+ββααα(C)1211212()2k k -+++ββαββ(D)1211212()2k k ++-+ββαββ三、(本题共3小题,每小题5分,满分15分)(1)求120ln(1).(2)x dx x +-⎰(2)设(2,sin ),z f x y y x =-其中(,)f u v 具有连续的二阶偏导数,求2.zx y∂∂∂(3)求微分方程244e xy y y -'''++=的通解(一般解).四、(本题满分6分)求幂级数(21)nn n x∞=+∑的收敛域,并求其和函数.五、(本题满分8分)求曲面积分2SI yzdzdx dxdy =+⎰⎰其中S 是球面2224x y z ++=外侧在0z ≥的部分.六、(本题满分7分)设不恒为常数的函数()f x 在闭区间[,]a b 上连续,在开区间(,)a b 内可导,且()().f a f b =证明在(,)a b 内至少存在一点,ξ使得()0.f ξ'>七、(本题满分6分)设四阶矩阵1100213401100213,0011002100010002-⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥==⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦B C 且矩阵A 满足关系式1()-''-=A E C B C E其中E 为四阶单位矩阵1,-C 表示C 的逆矩阵,'C 表示C 的转置矩阵.将上述关系式化简并求矩阵.A 八、(本题满分8分)求一个正交变换化二次型22212312132344448f x x x x x x x x x =++-+-成标准型.九、(本题满分8分)质点P 沿着以AB 为直径的半圆周,从点(1,2)A 运动到点(3,4)B 的过程中受变力F 作用(见图).F的大小等于点P 与原点O 之间的距离,其方向垂直于线段OP 且与y 轴正向的夹角小于.2π求变力F 对质点P 所作的功.十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)已知随机变量X 的概率密度函数1()e ,2xf x x -=-∞<<+∞则X 的概率分布函数()F x =____________.(2)设随机事件A 、B 及其和事件的概率分别是0.4、0.3和0.6,若B 表示B 的对立事件,那么积事件AB 的概率()P AB =____________.(3)已知离散型随机变量X 服从参数为2的泊松()Poisson 分布,即22e {},0,1,2,,!k P X k k k -=== 则随机变量32Z X =-的数学期望()E Z =____________.十一、(本题满分6分)设二维随机变量(,)X Y 在区域:01,D x y x <<<内服从均匀分布,求关于X 的边缘概率密度函数及随机变量21Z X =+的方差().D Z1991年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)设21cos x t y t=+=,则22d y dx =_____________.(2)由方程xyz +=所确定的函数(,)z z x y =在点(1,0,1)-处的全微分dz =_____________.(3)已知两条直线的方程是1212321:;:.101211x y z x y zl l ---+-====-则过1l 且平行于2l 的平面方程是_____________.(4)已知当0x →时123,(1)1ax +-与cos 1x -是等价无穷小,则常数a =_____________.(5)设4阶方阵52002100,00120011⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦A 则A 的逆阵1-A =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)曲线221e 1e x xy --+=-(A)没有渐近线(B)仅有水平渐近线(C)仅有铅直渐近线(D)既有水平渐近线又有铅直渐近线(2)若连续函数()f x 满足关系式20()()ln 2,2tf x f dt π=+⎰则()f x 等于(A)e ln 2x(B)2e ln 2x(C)e ln 2x +(D)2e ln 2x +(3)已知级数12111(1)2,5,n n n n n a a ∞∞--==-==∑∑则级数1n n a ∞=∑等于(A)3(B)7(C)8(D)9(4)设D 是平面xoy 上以(1,1)、(1,1)-和(1,1)--为顶点的三角形区域1,D 是D 在第一象限的部分,则(cos sin )Dxy x y dxdy +⎰⎰等于(A)12cos sin D x ydxdy⎰⎰(B)12D xydxdy⎰⎰(C)14(cos sin )D xy x y dxdy+⎰⎰(D)0(5)设n 阶方阵A 、B 、C 满足关系式,=ABC E 其中E 是n 阶单位阵,则必有(A)=ACB E (B)=CBA E (C)=BAC E(D)=BCA E三、(本题共3小题,每小题5分,满分15分)(1)求2lim .x π+→(2)设n是曲面222236x y z ++=在点(1,1,1)P 处的指向外侧的法向量,求函数u =在点P 处沿方向n 的方向导数.(3)22(),x y z dv Ω++⎰⎰⎰其中Ω是由曲线220y zx ==绕z 轴旋转一周而成的曲面与平面4z =所围城的立体.四、(本题满分6分)过点(0,0)O 和(,0)A π的曲线族sin (0)y a x a =>中,求一条曲线,L 使沿该曲线O 从到A 的积分3(1)(2)Ly dx x y dy +++⎰的值最小.五、(本题满分8分)将函数()2(11)f x x x =+-≤≤展开成以2为周期的傅里叶级数,并由此求级数211n n∞=∑的和.六、(本题满分7分)设函数()f x 在[0,1]上连续,(0,1)内可导,且1233()(0),f x dx f =⎰证明在(0,1)内存在一点,c 使()0.f c '=七、(本题满分8分)已知1234(1,0,2,3),(1,1,3,5),(1,1,2,1),(1,2,4,8)a a ===-+=+αααα及(1,1,3,5).b =+β(1)a 、b 为何值时,β不能表示成1234,,,αααα的线性组合?(2)a 、b 为何值时,β有1234,,,αααα的唯一的线性表示式?写出该表示式.八、(本题满分6分)设A 是n 阶正定阵,E 是n 阶单位阵,证明+A E 的行列式大于1.九、(本题满分8分)在上半平面求一条向上凹的曲线,其上任一点(,)P x y 处的曲率等于此曲线在该点的法线段PQ 长度的倒数(Q 是法线与x 轴的交点),且曲线在点(1,1)处的切线与x 轴平行.十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)若随机变量X 服从均值为2、方差为2σ的正态分布,且{24}0.3,P X <<=则{0}P X <=____________.(2)随机地向半圆0y a <<为正常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,则原点和该点的连线与x 轴的夹角小于4π的概率为____________.十一、(本题满分6分)设二维随机变量(,)X Y 的密度函数为(,)f x y =(2)2e 0,00 x y x y -+>>其它求随机变量2Z X Y =+的分布函数.1992年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)设函数()y y x =由方程e cos()0x yxy ++=确定,则dydx=_____________.(2)函数222ln()u x y z =++在点(1,2,2)M -处的梯度grad Mu=_____________.(3)设()f x =211x-+00x x ππ-<≤<≤,则其以2π为周期的傅里叶级数在点x π=处收敛于_____________.(4)微分方程tan cos y y x x '+=的通解为y =_____________.(5)设111212121212,n n n n n n a b a b a b a b a b a b a b a b a b ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A 其中0,0,(1,2,,).i ia b i n ≠≠= 则矩阵A 的秩()r A =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)当1x →时,函数1211e 1x x x ---的极限(A)等于2(B)等于0(C)为∞(D)不存在但不为∞(2)级数1(1)(1cos nn a n ∞=--∑常数0)a >(A)发散(B)条件收敛(C)绝对收敛(D)收敛性与a 有关(3)在曲线23,,x t y t z t ==-=的所有切线中,与平面24x y z ++=平行的切线(A)只有1条(B)只有2条(C)至少有3条(D)不存在(4)设32()3,f x x x x =+则使()(0)n f 存在的最高阶数n 为(A)0(B)1(C)2(D)3(5)要使12100,121⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ξξ都是线性方程组=AX 0的解,只要系数矩阵A 为(A)[]212-(B)201011-⎡⎤⎢⎥⎣⎦(C)102011-⎡⎤⎢⎥-⎣⎦(D)011422011-⎡⎤⎢⎥--⎢⎥⎢⎥⎣⎦三、(本题共3小题,每小题5分,满分15分)(1)求0x x →(2)设22(e sin ,),x z f y x y =+其中f 具有二阶连续偏导数,求2.z x y∂∂∂(3)设()f x =21ex x -+00x x ≤>,求31(2).f x dx -⎰四、(本题满分6分)求微分方程323e xy y y -'''+-=的通解.五、(本题满分8分)计算曲面积分323232()()(),x az dydz y ax dzdx z ay dxdy ∑+++++⎰⎰其中∑为上半球面z =的上侧.六、(本题满分7分)设()0,(0)0,f x f ''<=证明对任何120,0,x x >>有1212()()().f x x f x f x +<+七、(本题满分8分)在变力F yzi zxj xyk =++的作用下,质点由原点沿直线运动到椭球面2222221x y z a b c++=上第一卦限的点(,,),M ξηζ问当ξ、η、ζ取何值时,力F 所做的功W 最大?并求出W 的最大值.八、(本题满分7分)设向量组123,,ααα线性相关,向量组234,,ααα线性无关,问:(1)1α能否由23,αα线性表出?证明你的结论.(2)(2)4α能否由123,,ααα线性表出?证明你的结论.九、(本题满分7分)设3阶矩阵A 的特征值为1231,2,3,λλλ===对应的特征向量依次为1231111,2,3,149⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ξξξ又向量12.3⎛⎫⎪= ⎪ ⎪⎝⎭β(1)将β用123,,ξξξ线性表出.(2)求(nn A β为自然数).十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)已知11()()(),()0,()(),46P A P B P C P AB P AC P BC ======则事件A 、B 、C 全不发生的概率为____________.(2)设随机变量X 服从参数为1的指数分布,则数学期望2{e }XE X -+=____________.十一、(本题满分6分)设随机变量X 与Y 独立,X 服从正态分布2(,),N Y μσ服从[,]ππ-上的均匀分布,试求Z X Y =+的概率分布密度(计算结果用标准正态分布函数Φ表示,其中22()e)t xx dt --∞Φ=.1993年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)函数1()(2(0)xF x dt x =->⎰的单调减少区间为_____________.(2)由曲线223212x y z +==绕y 轴旋转一周得到的旋转面在点处的指向外侧的单位法向量为_____________.(3)设函数2()()f x x x x πππ=+-<<的傅里叶级数展开式为01(cos sin ),2n n n a a nx b nx ∞=++∑则其中系数3b 的值为_____________.(4)设数量场u =则div(grad )u =_____________.(5)设n 阶矩阵A 的各行元素之和均为零,且A 的秩为1,n -则线性方程组=AX 0的通解为_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设sin 2340()sin(),(),xf x t dtg x x x ==+⎰则当0x →时,()f x 是()g x 的(A)等价无穷小(B)同价但非等价的无穷小(C)高阶无穷小(D)低价无穷小(2)双纽线22222()x y x y +=-所围成的区域面积可用定积分表示为(A)402cos 2d πθθ⎰(B)404cos 2d πθθ⎰(C)2θ(D)2401(cos 2)2d πθθ⎰(3)设有直线1158:121x y z l --+==-与2:l 623x y y z -=+=则1l 与2l 的夹角为(A)6π(B)4π(C)3π(D)2π(4)设曲线积分[()e ]sin ()cos x Lf t ydx f x ydy --⎰与路径无关,其中()f x 具有一阶连续导数,且(0)0,f =则()f x 等于(A)e e 2x x --(B)e e 2x x --(C)e e 12x x -+-(D)e e 12x x-+-(5)已知12324,369t ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦Q P 为三阶非零矩阵,且满足0,=PQ 则(A)6t =时P 的秩必为1(B)6t =时P 的秩必为2(C)6t ≠时P 的秩必为1(D)6t ≠时P 的秩必为2三、(本题共3小题,每小题5分,满分15分)(1)求21lim(sincos ).x x x x →∞+(2)求.x dx (3)求微分方程22,x y xy y '+=满足初始条件11x y==的特解.四、(本题满分6分)计算22,xzdydz yzdzdx z dxdy ∑+-⎰⎰ 其中∑是由曲面z =与z =所围立体的表面外侧.五、(本题满分7分)求级数20(1)(1)2n nn n n ∞=--+∑的和.六、(本题共2小题,每小题5分,满分10分)(1)设在[0,)+∞上函数()f x 有连续导数,且()0,(0)0,f x k f '≥><证明()f x 在(0,)+∞内有且仅有一个零点.(2)设,b a e >>证明.baa b >七、(本题满分8分)已知二次型22212312323(,,)2332(0)f x x x x x x ax x a =+++>通过正交变换化成标准形22212325,f y y y =++求参数a 及所用的正交变换矩阵.八、(本题满分6分)设A 是n m ⨯矩阵,B 是m n ⨯矩阵,其中,n m <I 是n 阶单位矩阵,若,=AB I 证明B 的列向量组线性无关.九、(本题满分6分)设物体A 从点(0,1)出发,以速度大小为常数v 沿y 轴正向运动.物体B 从点(1,0)-与A 同时出发,其速度大小为2,v 方向始终指向,A 试建立物体B 的运动轨迹所满足的微分方程,并写出初始条件.十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)一批产品共有10个正品和2个次品,任意抽取两次,每次抽一个,抽出后不再放回,则第二次抽出的是次品的概率为____________.(2)设随机变量X 服从(0,2)上的均匀分布,则随机变量2Y X =在(0,4)内的概率分布密度()Y f y =____________.十一、(本题满分6分)设随机变量X 的概率分布密度为1()e ,.2xf x x -=-∞<<+∞(1)求X 的数学期望EX 和方差.DX (2)求X 与X 的协方差,并问X 与X 是否不相关?(3)问X 与X 是否相互独立?为什么?1994年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)011lim cot ()sin x x xπ→-=_____________.(2)曲面e 23xz xy -+=在点(1,2,0)处的切平面方程为_____________.(3)设e sin ,xxu y-=则2u x y ∂∂∂在点1(2,π处的值为_____________.(4)设区域D 为222,x y R +≤则2222()Dx y dxdy a b +⎰⎰=_____________.(5)已知11[1,2,3],[1,,23==αβ设,'=A αβ其中'α是α的转置,则n A =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设4342342222222sin cos ,(sin cos ),(sin cos ),1x M xdx N x x dx P x x x dx x ππππππ---==+=-+⎰⎰⎰则有(A)N P M<<(B)M P N <<(C)N M P <<(D)P M N<<(2)二元函数(,)f x y 在点00(,)x y 处两个偏导数00(,)x f x y '、00(,)y f x y '存在是(,)f x y 在该点连续的(A)充分条件而非必要条件(B)必要条件而非充分条件(C)充分必要条件(D)既非充分条件又非必要条件(3)设常数0,λ>且级数21nn a ∞=∑收敛,则级数1(1)nn ∞=-∑(A)发散(B)条件收敛(C)绝对收敛(D)收敛性与λ有关(4)2tan (1cos )lim2,ln(12)(1)x x a x b x c x d e-→+-=-+-其中220,a c +≠则必有(A)4b d =(B)4b d =-(C)4a c=(D)4a c=-(5)已知向量组1234,,,αααα线性无关,则向量组(A)12233441,,,++++αααααααα线性无关(B)12233441,,,----αααααααα线性无关(C)12233441,,,+++-αααααααα线性无关(D)12233441,,,++--αααααααα线性无关三、(本题共3小题,每小题5分,满分15分)(1)设2221cos()cos()t x t y t t udu ==-⎰,求dy dx 、22d y dx在t =的值.(2)将函数111()ln arctan 412x f x x x x +=+--展开成x 的幂级数.(3)求.sin(2)2sin dxx x +⎰四、(本题满分6分)计算曲面积分2222S xdydz z dxdyx y z +++⎰⎰其中S 是由曲面222x y R +=及,(0)z R z R R ==->两平面所围成立体表面的外侧.五、(本题满分9分)设()f x 具有二阶连续函数,(0)0,(0)1,f f '==且2[()()][()]0xy x y f x y dx f x x y dy '+-++=为一全微分方程,求()f x 及此全微分方程的通解.六、(本题满分8分)设()f x 在点0x =的某一邻域内具有二阶连续导数,且0()lim0,x f x x→=证明级数11()n f n∞=∑绝对收敛.七、(本题满分6分)已知点A 与B 的直角坐标分别为(1,0,0)与(0,1,1).线段AB 绕x 轴旋转一周所成的旋转曲面为.S 求由S 及两平面0,1z z ==所围成的立体体积.八、(本题满分8分)设四元线性齐次方程组(Ⅰ)为122400x x x x +=-=,又已知某线性齐次方程组(Ⅱ)的通解为12(0,1,1,0)(1,2,2,1).k k +-(1)求线性方程组(Ⅰ)的基础解析.(2)问线性方程组(Ⅰ)和(Ⅱ)是否有非零公共解?若有,则求出所有的非零公共解.若没有,则说明理由.九、(本题满分6分)设A 为n 阶非零方阵*,A 是A 的伴随矩阵,'A 是A 的转置矩阵,当*'=A A 时,证明0.≠A 十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)已知A 、B 两个事件满足条件()(),P AB P AB =且(),P A p =则()P B =____________.(2)设相互独立的两个随机变量,X Y 具有同一分布率,且X 的分布率为X 01P1212则随机变量max{,}Z X Y =的分布率为____________.十一、(本题满分6分)设随机变量X 和Y 分别服从正态分布2(1,3)N 和2(0,4),N 且X 与Y 的相关系数1,2xy ρ=-设,32X YZ =+(1)求Z 的数学期望EZ 和DZ 方差.(2)求X 与Z 的相关系数.xz ρ(3)问X 与Y 是否相互独立?为什么?1995年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)2sin 0lim(13)xx x →+=_____________.(2)202cos x d x t dt dx⎰=_____________.(3)设()2,⨯=a b c 则[()()]()+⨯++a b b c c a =_____________.(4)幂级数2112(3)n n nn n ∞-=+-∑的收敛半径R =_____________.(5)设三阶方阵,A B 满足关系式16,-=+A BA A BA 且100310,41007⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A 则B =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设有直线:L 321021030x y z x y z +++=--+=,及平面:4220,x y z π-+-=则直线L(A)平行于π(B)在π上(C)垂直于π(D)与π斜交(2)设在[0,1]上()0,f x ''>则(0),(1),(1)(0)f f f f ''-或(0)(1)f f -的大小顺序是(A)(1)(0)(1)(0)f f f f ''>>-(B)(1)(1)(0)(0)f f f f ''>->(C)(1)(0)(1)(0)f f f f ''->>(D)(1)(0)(1)(0)f f f f ''>->(3)设()f x 可导,()()(1sin ),F x f x x =+则(0)0f =是()F x 在0x =处可导的(A)充分必要条件(B)充分条件但非必要条件(C)必要条件但非充分条件(D)既非充分条件又非必要条件(4)设(1)ln(1nn u =-+则级数(A)1nn u∞=∑与21nn u∞=∑都收敛(B)1nn u∞=∑与21nn u∞=∑都发散(C)1nn u∞=∑收敛,而21nn u∞=∑发散(D)1nn u∞=∑收敛,而21nn u∞=∑发散(5)设11121311121321222321222312313233313233010100,,100,010,001101a a a a a a a a a a a a a a a a a a ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦A B P P 则必有(A)12AP P =B (B)21AP P =B (C)12P P A =B(D)21P P A =B三、(本题共2小题,每小题5分,满分10分)(1)设2(,,),(,e ,)0,sin ,yu f x y z x z y x ϕ===其中,f ϕ都具有一阶连续偏导数,且0.zϕ∂≠∂求.du dx (2)设函数()f x 在区间[0,1]上连续,并设1(),f x dx A =⎰求11()().xdx f x f y dy ⎰⎰四、(本题共2小题,每小题6分,满分12分)(1)计算曲面积分,zdS ∑⎰⎰其中∑为锥面z =在柱体222x y x +≤内的部分.(2)将函数()1(02)f x x x =-≤≤展开成周期为4的余弦函数.五、(本题满分7分)设曲线L 位于平面xOy 的第一象限内,L 上任一点M 处的切线与y 轴总相交,交点记为.A 已知,MA OA =且L 过点33(,),22求L 的方程.六、(本题满分8分)设函数(,)Q x y 在平面xOy 上具有一阶连续偏导数,曲线积分2(,)Lxydx Q x y dy +⎰与路径无关,并且对任意t 恒有(,1)(1,)(0,0)(0,0)2(,)2(,),t t xydx Q x y dy xydx Q x y dy +=+⎰⎰求(,).Q x y 七、(本题满分8分)假设函数()f x 和()g x 在[,]a b 上存在二阶导数,并且()0,()()()()0,g x f a f b g a g b ''≠====试证:(1)在开区间(,)a b 内()0.g x ≠(2)在开区间(,)a b 内至少存在一点,ξ使()().()()f fg g ξξξξ''=''八、(本题满分7分)设三阶实对称矩阵A 的特征值为1231,1,λλλ=-==对应于1λ的特征向量为101,1⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ξ求.A 九、(本题满分6分)设A 为n 阶矩阵,满足('=AA I I 是n 阶单位矩阵,'A 是A 的转置矩阵),0,<A 求.+A I 十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)设X 表示10次独立重复射击命中目标的次数,每次射中目标的概率为0.4,则2X 的数学期望2()E X =____________.(2)设X 和Y 为两个随机变量,且34{0,0},{0}{0},77P X Y P X P Y ≥≥=≥=≥=则{max(,)0}P X Y ≥=____________.十一、(本题满分6分)设随机变量X 的概率密度为()X f x =e 0x -00x x ≥<,求随机变量e XY =的概率密度().Y f y1996年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)设2lim()8,xx x a x a→∞+=-则a =_____________.(2)设一平面经过原点及点(6,3,2),-且与平面428x y z -+=垂直,则此平面方程为_____________.(3)微分方程22e xy y y '''-+=的通解为_____________.(4)函数ln(u x =在点(1,0,1)A 处沿点A 指向点(3,2,2)B -方向的方向导数为_____________.(5)设A 是43⨯矩阵,且A 的秩()2,r =A 而102020,103⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦B 则()r AB =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)已知2()()x ay dx ydyx y +++为某函数的全微分,a 则等于(A)-1(B)0(C)1(D)2(2)设()f x 具有二阶连续导数,且0()(0)0,lim1,x f x f x→'''==则(A)(0)f 是()f x 的极大值(B)(0)f 是()f x 的极小值(C)(0,(0))f 是曲线()y f x =的拐点(D)(0)f 不是()f x 的极值,(0,(0))f 也不是曲线()y f x =的拐点(3)设0(1,2,),n a n >= 且1n n a ∞=∑收敛,常数(0,2πλ∈则级数21(1)(tan nnn n a n λ∞=-∑(A)绝对收敛(B)条件收敛(C)发散(D)散敛性与λ有关(4)设有()f x 连续的导数220,(0)0,(0)0,()()(),xf f F x x t f t dt '=≠=-⎰且当0x →时,()F x '与kx 是同阶无穷小,则k 等于(A)1(B)2(C)3(D)4(5)四阶行列式112233440000000a b a b a b b a 的值等于(A)12341234a a a ab b b b -(B)12341234a a a ab b b b +(C)12123434()()a ab b a a b b --(D)23231414()()a ab b a a b b --三、(本题共2小题,每小题5分,满分10分)(1)求心形线(1cos )r a θ=+的全长,其中0a >是常数.(2)设1110,1,2,),n x x n +=== 试证数列{}n x 极限存在,并求此极限.四、(本题共2小题,每小题6分,满分12分)(1)计算曲面积分(2),Sx z dydz zdxdy ++⎰⎰其中S 为有向曲面22(01),z xy x =+≤≤其法向量与z 轴正向的夹角为锐角.(2)设变换2u x y v x ay =-=+可把方程2222260z z z x x y y ∂∂∂+-=∂∂∂∂简化为20,zu v∂=∂∂求常数.a 五、(本题满分7分)求级数211(1)2n n n ∞=-∑的和.六、(本题满分7分)设对任意0,x >曲线()y f x =上点(,())x f x 处的切线在y 轴上的截距等于01(),xf t dt x⎰求()f x 的一般表达式.七、(本题满分8分)设()f x 在[0,1]上具有二阶导数,且满足条件(),(),f x a f x b ''≤≤其中,a b 都是非负常数,c 是(0,1)内任意一点.证明()2.2bf c a '≤+八、(本题满分6分)设,TA =-I ξξ其中I 是n 阶单位矩阵,ξ是n 维非零列向量,Tξ是ξ的转置.证明(1)2=A A 的充分条件是 1.T=ξξ(2)当1T=ξξ时,A 是不可逆矩阵.九、(本题满分8分)已知二次型222123123121323(,,)55266f x x x x x cx x x x x x x =++-+-的秩为2,(1)求参数c 及此二次型对应矩阵的特征值.(2)指出方程123(,,)1f x x x =表示何种二次曲面.十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)设工厂A 和工厂B 的产品的次品率分别为1%和2%,现从由A 和B 的产品分别占60%和40%的一批产品中随机抽取一件,发现是次品,则该次品属A 生产的概率是____________.(2)设,ξη是两个相互独立且均服从正态分布2)N 的随机变量,则随机变量ξη-的数学期望()E ξη-=____________.十一、(本题满分6分)设,ξη是两个相互独立且服从同一分布的两个随机变量,已知ξ的分布率为1(),1,2,3.3P i i ξ===又设max(,),min(,).X Y ξηξη==(1)写出二维随机变量的分布率:XY123123(2)求随机变量X 的数学期望().E X1997年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)2013sin coslim(1cos )ln(1)x x x x x x →+++=_____________.(2)设幂级数1nnn a x∞=∑的收敛半径为3,则幂级数11(1)n nn na x ∞+=-∑的收敛区间为_____________.(3)对数螺线e θρ=在点2(,)(e ,)2ππρθ=处切线的直角坐标方程为_____________.(4)设12243,311t -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦A B 为三阶非零矩阵,且,=AB O 则t =_____________.(5)袋中有50个乒乓球,其中20个是黄球,30个是白球,今有两人依次随机地从袋中各取一球,取后不放回,则第二个人取得黄球的概率是_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)二元函数(,)f x y =22(,)(0,0)0(,)(0,0)xyx y x y x y ≠+=,在点(0,0)处(A)连续,偏导数存在(B)连续,偏导数不存在(C)不连续,偏导数存在(D)连续,偏导数不存在(2)设在区间[,]a b 上()0,()0,()0.f x f x f x '''><>令1231(),()(),[()()](),2ba S f x dx S fb b a S f a f b b a ==-=+-⎰则(A)123S S S <<(B)213S S S <<(C)312S S S <<(D)231S S S <<(3)设2sin ()e sin ,x t xF x tdt π+=⎰则()F x (A)为正常数(B)为负常数(C)恒为零(D)不为常数(4)设111122232333,,,a b c a b c a b c ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ααα则三条直线1112223330,0,0a x b y c a x b y c a x b y c ++=++=++=(其中220,1,2,3i i a b i +≠=)交于一点的充要条件是:(A)123,,ααα线性相关(B)123,,ααα线性无关(C)秩123(,,)r =ααα秩12(,)r αα(D)123,,ααα线性相关12,,αα线性无关(5)设两个相互独立的随机变量X 和Y 的方差分别为4和2,则随机变量32X Y -的方差是(A)8(B)16(C)28(D)44三、(本题共3小题,每小题5分,满分15分)(1)计算22(),I xy dv Ω=+⎰⎰⎰其中Ω为平面曲线220y zx ==绕z 轴旋转一周所成的曲面与平面8z =所围成的区域.(2)计算曲线积分()()(),cz y dx x z dy x y dz -+-+-⎰ 其中c 是曲线2212x y x y z +=-+=从z轴正向往z 轴负向看c 的方向是顺时针的.(3)在某一人群中推广新技术是通过其中掌握新技术的人进行的,设该人群的总人数为,N 在0t =时刻已掌握新技术的人数为0,x 在任意时刻t 已掌握新技术的人数为()(x t 将()x t 视为连续可微变量),其变化率与已掌握新技术人数和未掌握新技术人数之积成正比,比例常数0,k >求().x t 四、(本题共2小题,第(1)小题6分,第(2)小题7分,满分13分)(1)设直线:l 030x y b x ay z ++=+--=在平面π上,而平面π与曲面22z x y =+相切于点(1,2,5),-求,a b 之值.(2)设函数()f u 具有二阶连续导数,而(e sin )xz f y =满足方程22222e ,xz z z x y∂∂+=∂∂求().f u五、(本题满分6分)设()f x 连续1,()(),x f xt dt ϕ=⎰且0()lim(x f x A A x→=为常数),求()x ϕ'并讨论()x ϕ'在0x =处的连续性.六、(本题满分8分)设11110,(1,2,),2n n na a a n a +==+= 证明(1)lim n x a →∞存在.(2)级数11(1)nn n a a ∞=+-∑收敛.七、(本题共2小题,第(1)小题5分,第(2)小题6分,满分11分)(1)设B 是秩为2的54⨯矩阵123,[1,1,2,3],[1,1,4,1],[5,1,8,9]TTT==--=--ααα是齐次线性方程组x =B 0的解向量,求x =B 0的解空间的一个标准正交基.(2)已知111⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦ξ是矩阵2125312a b -⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦A 的一个特征向量.1)试确定,a b 参数及特征向量ξ所对应的特征值.2)问A 能否相似于对角阵?说明理由.八、(本题满分5分)设A 是n 阶可逆方阵,将A 的第i 行和第j 行对换后得到的矩阵记为.B (1)证明B 可逆.(2)求1.-AB 九、(本题满分7分)从学校乘汽车到火车站的途中有3个交通岗,假设再各个交通岗遇到红灯的事件是相互独立的,并且概率都是2.5设X 为途中遇到红灯的次数,求随机变量X 的分布律、分布函数和数学期望.十、(本题满分5分)设总体X 的概率密度为()f x =(1)0x θθ+01x <<其它其中1θ>-是未知参数12,,,,n X X X 是来自总体X 的一个容量为n 的简单随机样本,分别用矩估计法和极大似然估计法求θ的估计量.1998年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)2112limx x→-=_____________.(2)设1()(),,z f xy y x y f x ϕϕ=++具有二阶连续导数,则2z x y ∂∂∂=_____________.(3)设l 为椭圆221,43x y +=其周长记为,a 则22(234)Lxy x y ds ++⎰ =_____________.(4)设A 为n 阶矩阵*,0,≠A A 为A 的伴随矩阵,E 为n 阶单位矩阵.若A 有特征值,λ则*2()+A E 必有特征值_____________.(5)设平面区域D 由曲线1y x=及直线20,1,e y x x ===所围成,二维随机变量(,)X Y 在区域D 上服从均匀分布,则(,)X Y 关于X 的边缘概率密度在2x =处的值为_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设()f x 连续,则220()x d tf x t dt dx-⎰=(A)2()xf x (B)2()xf x -(C)22()xf x (D)22()xf x -(2)函数23()(2)f x x x x x =---不可导点的个数是(A)3(B)2(C)1(D)0(3)已知函数()y y x =在任意点x 处的增量2,1y xy x α∆∆=++且当0x ∆→时,α是x ∆的高阶无穷小,(0)y π=,则(1)y 等于(A)2π(B)π(C)4eπ(D)4eππ(4)设矩阵111222333a b c a b c a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦是满秩的,则直线333121212x a y b z c a a b b c c ---==---与直线111232323x a y b z c a a b b c c ---==---(A)相交于一点(B)重合(C)平行但不重合(D)异面(5)设,A B 是两个随机事件,且0()1,()0,(|)(|),P A P B P B A P B A <<>=则必有(A)(|)(|)P A B P A B =(B)(|)(|)P A B P A B ≠(C)()()()P AB P A P B =(D)()()()P AB P A P B ≠三、(本题满分5分)求直线11:111x y z l --==-在平面:210x y z π-+-=上的投影直线0l 的方程,并求0l 绕y 轴旋转一周所成曲面的方程.四、(本题满分6分)确定常数,λ使在右半平面0x >上的向量42242(,)2()()x y xy x y x x y λλ=+-+A i j 为某二元函数(,)u x y 的梯度,并求(,).u x y 五、(本题满分6分)从船上向海中沉放某种探测仪器,按探测要求,需确定仪器的下沉深度(y 从海平面算起)与下沉速度v 之间的函数关系.设仪器在重力作用下,从海平面由静止开始铅直下沉,在下沉过程中还受到阻力和浮力的作用.设仪器的质量为,m 体积为,B 海水密度为,ρ仪器所受的阻力与下沉速度成正比,比例系数为(0).k k >试建立y 与v 所满足的微分方程,并求出函数关系式().y y v =六、(本题满分7分)计算222212(),()axdydz z a dxdy x y z ∑++++⎰⎰其中∑为下半平面z =,a 为大于零的常数.七、(本题满分6分)求2sin sin sin lim .1112x n n n n n n πππ→∞⎡⎤⎢⎥+++⎢⎥+⎢⎥++⎣⎦ 八、(本题满分5分)设正向数列{}n a 单调减少,且1(1)nn n a ∞=-∑发散,试问级数11(1nn n a ∞=+∑是否收敛?并说明理由.九、(本题满分6分)设()y f x =是区间[0,1]上的任一非负连续函数.(1)试证存在0(0,1),x ∈使得在区间0[0,]x 上以0()f x 为高的矩形面积,等于在区间0[,1]x 上以()y f x =为曲边的曲边梯形面积.(2)又设()f x 在区间(0,1)内可导,且2()(),f x f x x'>-证明(1)中的0x 是唯一的.十、(本题满分6分)已知二次曲面方程2222224x ay z bxy xz yz +++++=可以经过正交变换x y z ξηζ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦P 化为椭圆柱面方程2244,ηξ+=求,a b 的值和正交矩阵.P 十一、(本题满分4分)设A 是n 阶矩阵,若存在正整数,k 使线性方程组kx =A 0有解向量,α且1.k -≠A α0证明:向量组1,,,k -αAαAα 是线性无关的.十二、(本题满分5分)已知方程组(Ⅰ)1111221,222112222,221122,22000n n n n n n n n n a x a x a x a x a x a x a x a x a x +++=+++=+++=的一个基础解析为11121,221222,212,2(,,,),(,,,),,(,,,).TTTn n n n n n b b b b b b b b b 试写出线性方程组(Ⅱ)1111221,222112222,221122,22000n n n n n n n n nb y b y b y b y b y b y b y b y b y +++=+++=+++=的通解,并说明理由.十三、(本题满分6分)设两个随机变量,X Y 相互独立,且都服从均值为0、方差为12的正态分布,求随机变量X Y -的方差.十四、(本题满分4分)从正态总体2(3.4,6)N 中抽取容量为n 的样本,如果要求其样本均值位于区间(1.4,5.4)内的概率不小于0.95,问样本容量n 至少应取多大?附:标准正态分布表22()t zx dt -Φ=⎰z1.28 1.645 1.962.33()x Φ0.9000.9500.9750.990十五、(本题满分4分)设某次考试的学生成绩服从正态分布,从中随机地抽取36位考生地成绩,算得平均成绩为66.5分,标准差为15分.问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分?并给出检验过程.附:t 分布表{()()}p P t n t n p≤=0.950.97535 1.6896 2.0301361.68832.02811999年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)2011lim(tan x x x x→-=_____________.(2)20sin()x d x t dt dx-⎰=_____________.(3)24e xy y ''-=的通解为y =_____________.(4)设n 阶矩阵A 的元素全为1,则A 的n 个特征值是_____________.(5)设两两相互独立的三事件,A B和C满足条件:1,()()(),2ABC P A P B P C =∅==<且已知9(),16P A B C =则()P A =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设()f x 是连续函数,()F x 是()f x 的原函数,则(A)当()f x 是奇函数时,()F x 必是偶函数(B)当()f x 是偶函数时,()F x 必是奇函数(C)当()f x 是周期函数时,()F x 必是周期函数(D)当()f x 是单调增函数时,()F x 必是单调增函数(2)设20()() 0x f x x g x x >=≤⎩,其中()g x 是有界函数,则()f x 在0x =处(A)极限不存在(B)极限存在,但不连续(C)连续,但不可导(D)可导(3)设 01()122 12x x f x x x ≤≤⎧⎪=⎨-<<⎪⎩,01()cos ,,2n n a S x a n x x π∞==+-∞<<+∞∑其中102()cos n a f x n xdx π=⎰(0,1,2,)n = ,则5()2S -等于(A)12(B)12-(C)34(D)34-(4)设A 是m n ⨯矩阵,B 是n m ⨯矩阵,则(A)当m n >时,必有行列式||0≠AB (B)当m n >时,必有行列式||0=AB (C)当n m >时,必有行列式||0≠AB (D)当n m >时,必有行列式||0=AB (5)设两个相互独立的随机变量X 和Y 分别服从正态分布(0,1)N 和(1,1)N ,则(A)1{0}2P X Y +≤=(B)1{1}2P X Y +≤=(C)1{0}2P X Y -≤=(D)1{1}2P X Y -≤=三、(本题满分6分)设(),()y y x z z x ==是由方程()z xf x y =+和(,,)0F x y z =所确定的函数,其中f 和F 分别具有一阶连续导数和一阶连续偏导数,求.dz dx四、(本题满分5分)求(e sin ())(e cos ),x x LI y b x y dx y ax dy =-++-⎰其中,a b 为正的常数,L 为从点(2,0)A a 沿曲线y =到点(0,0)O 的弧.五、(本题满分6分)设函数()(0)y x x ≥二阶可导且()0,(0) 1.y x y '>=过曲线()y y x =上任意一点。
(完整word版)山东建筑大学-.1线性代数试题A卷
线性代数一、单项选择题(每小题3分,共18分)1、设矩阵333223⨯⨯⨯C B A ,,,则下列运算可行的是 【 】.A AC , .B CB , .C ABC .D B A +2、设, A B 为n 阶方阵,E 为n 阶单位矩阵,则下列等式成立的是 【 】.A ()()22B A B A B A -=+- .B ()()E A E A E A -=+-2.C BA AB = .D ()E B A E B A ++=+3、设方阵A 有特征值1、2,a 是与1 对应的特征向量,b 是与2对应的特征向量,下列判断正确的是 【 】.A a 与b 线性无关 .B b a +是A 的特征向量.C a 与b 线性相关 .D a 与b 正交4、设4阶方阵A 的行列式为2,则A 的伴随矩阵*A 的行列式为 【 】(A) 2; (B) 4; (C) 8; (D) 15、112012()2, 1012a A a r A a -⎛⎫ ⎪=-= ⎪ ⎪-⎝⎭若矩阵的秩则的值为 【 】(A)0(B)0 -1(C)-1 (D) 1 1-或 或6、A 与B 为同阶方阵,如果A 与B 具有相同的特征值,则 【 】(A) A 与B 相似;(B) A 与B 合同;(C) A B =; (D) A B =二、填空题(每小题3分,共18分)7、0200003000045000D =,则_______D =. 8、设3阶矩阵A ,且矩阵行列式3=A ,则矩阵行列式=A 2 .9、设矩阵a a a a a a a a A a a a a a a a a ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,则A 的非零特征值为____________. 10、若方阵A 有一个特征值是1,则E A -= .11、n 维向量空间的子空间121220(,,,)0n n n x x x W x x x x x ⎧⎫+++=⎧⎪⎪=⎨⎨⎬++=⎩⎪⎪⎩⎭的维数是____ 12、设(,)E i j 表示由n 阶单位矩阵第i 行与第j 行互换得到的初等矩阵,则E 1[(,)]E i j -=_________.三、解答下列各题(每小题6分,共24分)13、计算行列式 7592437102102251-----=D 14、设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=200540321A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=132015001B ,求行列式AB 。
