异面直线及其所成角
异面直线所成的角求法课件

答案解析
答案一解析
首先,由于AB和CD为异面直线,且AB ⟂ CD,我们可以知道异面直线AB与CD所成的 角为∠BAC。因为∠BAC = 60°,所以异面直线AB与CD所成的角也为60°。
答案二解析
首先,找到与AB和AD₁都平行的平面或线段。在长方体中,这样的平面或线段是A₁D和 A₁B₁。然后,利用平移将异面直线AB和AD₁平移到同一个起点,例如点A。最后,利用 余弦公式计算异面直线AB与AD₁所成角的余弦值。具体计算过程涉及长方体的边长和
常见误区
列举了在求解过程中可能出现 的常见错误和误区,并给出了
正确的解释和纠正方法。
展望
01
02
03
04
进一步研究
鼓励学习者在掌握基本方法的 基础上,深入研究异面直线所 成的角的更多性质和应用。
与其他知识的结合
提倡将异面直线所成的角与其 他几何知识进行结合,形成更
完整的知识体系。
实际应用拓展
强调将所学知识应用于实际问 题解决中,培养解决实际问题
在空间向量中的应用
异面直线所成的角在空间向量中也有着重要的应用。向量 的数量积、向量的模长以及向量的夹角都可以通过异面直 线所成的角来表示。
在解决空间向量的加法、数乘以及向量的模长和夹角等问 题时,常常需要利用异面直线所成的角来建立向量关系, 从而得到向量的具体表示和运算结果。
在物理问题中的应用
成的角的余弦值等于 $frac{overset{longrightarrow}{a} cdot overset{longrightarrow}{b}}{|overset{lon
grightarrow}{a}| cdot
利用向量的夹角公式求异面直线所成的角
要点一
异面直线所成角的几种求法

异面直线所成角的几种求法之袁州冬雪创作异面直线所成角的大小,是由空间一点分别引它们的平行线所成的锐角(或直角)来定义的.因此,通常我们要求异面直线所成的角会要求学生通过平移直线,形成角,然后在某个三角形中求出角的方法来得到异面直线所成角的大小.在这一方法中,平移直线是求异面直线所成角的关键,而如何平移直线要求学生有杰出的空间观和作图才能.一、向量法求异面直线所成的角例1:如图,在正方体ABCD-A 1B 1C 1D 1中,E 、F 分别是相邻两正面BCC 1B 1及CDD 1C 1的中心.求A 1E 和B 1F 所成的角的大小.解法一:(作图法)作图关键是平移直线,可平移其中一条直线,也可平移两条直线到某个点上.作法:保持B 1E ,取B 1E 中点G 及A 1B 1中点H ,保持GH ,有GH//A 1E.过F 作CD 的平行线RS ,分别交CC 1、DD 1于点R 、S ,保持SH ,保持GS.由B 1H//C 1D 1//FS ,B 1H=FS ,可得B 1F//SH.在△GHS 中,设正方体边长为a.B ACD F EB 1A 1 D 1 C 1G HSRP Q(作直线GQ//BC交BB1于点Q,连QH,可知△GQH为直角三角形),(连A1S,可知△HA1S为直角三角形),(作直线GP交BC于点GPDS为直角梯形).∴Cos∠所以直线A1E与直线B1F解法二:(向量法)分析:因为给出的平面图形是一个正方体,所以可以在空间建立直角坐标系,从而可以操纵点的坐标暗示出空间中每个向量,从而可以用向量的方法来求出两条直线间的夹角.以B为原点,BC为x轴,BA为y轴,BB1为z轴,设BC长度为2.则点A1的坐标为(0,2,2),点E的坐标为(1,0,1),点B1的坐标为(0,0,2),点F的坐标为(2,1,1);1-1,2,1(2,1,-1),所以这两个向量的夹角θ知足cosθ所以直线A1E与直线B1F小结:上述解法中,解法一要求有杰出的作图才能,且可以在作图完毕后可以看清楚图形中的各个三角形,然后在所需要的三角形中计算出各条线段的长度,从而完成解三角形得到角的大小.而解法二不需要学生作图,只需建立空间直角坐标系,标出相应的点的坐标,从而得到所需向量的坐标,求出两个向量的夹角,即所求的两条直线所成的角.当然,如果题中给出的是一可以建立坐标系的空间图形,比方刚才的正方体,或者说是长方体,或者说空间图形中拥有三条直线两两垂直的性质,我们便可以建立空间直角坐标系,从而操纵向量的坐标暗示来求两个向量的夹角.如果没有这样的性质,我们也可以操纵空间向量基本定理,寻找空间的一组基底(即三个不共面的向量,且这三个向量两两之间的夹角是已知的),空间中任何一个向量都可以用这三个向量的线性组合暗示出来,因而也可以运用向量的数乘来求出空间中任意二个向量间的夹角.例2:已知空间四边AB=BC=CD=DA=AC=BD=a,M、N分别为AM和CN所成的角为α,求cosα的值且两两之间的夹角均为60°.角)知足cosθ2)2;21+1+1)a2 a2;2=2a2.所以cosα=| cosθ例3:已知空间四边形ABCD中,AB=CD=3,E、F分别是BC、AD上的点,且BE:EC=AF:FD=1:2,AB和CD所成的角的大小.解:取AC上点G,使AG:GC=1:2.保持EG、FG,可知EG//AB,FG//CD,3EG=2AB,3FG=CD..则由2==4+1+4cosθ=7,得cosθAB和CD所成的角为60°.二、操纵模子求异面直线所成的角引理:已知平面α的一条斜线a与平面α所成的角为θ1,平面α内的一条直线b与斜线a所成的角为θ,与它的射影a′所成的角为θ2.求证:cosθ= cosθ1·cosθ2.ABCDEFG证明:设PA 是α的斜线,OA 是PA 在α上的射影, OB//b ,如图所示.则∠PAO=θ1,∠PAB=θ,∠OAB=θ2,过点O 在平面α内作OB ⊥AB ,垂足为B ,保持PB. 可知PB ⊥AB. 所以cos θ1 cos θcos θ2所以cos θ= cos θ1·cos θ2.这一问题中,直线a 和b 可以是相交直线,也可以是异面直线.我们无妨把θ1叫做线面角,θ叫做线线角,θ2叫做线影角.很分明,线线角是这三个角中最大的一个角.我们可以操纵这个模子来求两条异面直线a 和b 所成的角,即引理中的角θ.从引理中可以看出,我们需要过a 的一个平面α,以及该平面的一条斜线b 以及b 在α内的射影.例4:如图,MA ⊥平面ABCD ,四边形ABCD 是正方形,且MA=AB=a ,试求异面直线MB 与AC 所成的角. 解:由图可知,直线MB 在平面ABCD 内的射影为AB ,直线MB 与平面ABCD 所成的角为45°,直线AC 与直线MB 的射影AB 所成的角为45°,PbA BO α ABCD M所以直线AC 与直MB 所成的角为θ,知足cos θ=cos45°· cos45°所以直线AC 与MB 所成的角为60°.例5:如图,在平面图形P-ABCD 中,底面ABCD 是一个直角梯形,∠BAD=90°,AD//BC ,AB=BC=a ,AD=2a ,且PA ⊥底面ABCD ,PD 与底面成30°角,AE ⊥PD 于D.求异面直线AE 与CD 所成的角的大小.解:过E 作的平行线EF 交AD 于F ,由PA ⊥底面ABCD 可知,直线AE 在平面 ABCD 内的射影为AD ,直线AE 与平面ABCD 所成的角为∠DAE ,其大小为60°, 射影AD 与直线CD 所成的角为∠CDA ,其大小为45°, 所以直线与直线所成的角θ知足 cos θ=cos60°· cos45°所以其大小为由上两例可知,求异面直线间的夹角,若存在一个平面的垂线,则可以联想到操纵线面角的这个公式来求得异面直线间的夹角,当然,上二例也可用平移直线的方法来求,也可以用向量法来求,这里只作简单的先容,不再重PE DF ABC复.。
异面直线所成角的计算

C1
D
C
则MON=120,
即异面直线AC与BD所成的角为60°.
2.已知正方体的棱长为a , M为AB的中点,N 为 BB1的中点, 求 A1M 与 C1 N 所成角的余弦值.
解: 如图,取AB的中点E, 连BE, 有BE∥ A1M
取CC1的中点G,连BG. 有BG∥ C1N 则∠EBG即为所求角. 在△EBG 中 D1 C1
1 2 1 2
∴异面直线 AD, BC 所成的角即为 EG, FG 所成的角(或其补角)
∵ EG AD 1, FG BC 1 ,
EG 2 FG 2 EF 2 1 ,∴ EGF 120 在 EGF 中, cos EGF 2 EG FG 2
,
∵两异面直线所成角的范围是: 00 , 90 0 ∴异面直线 AD, BC 所成的角为 60
BG=BE=
由余弦定理, cos∠EBG=2/5
5 2
a,, F C1 =
6 a 2
A1
E
F
B1
G D N C
想一想:还有其他定角的方法吗?
取EB1的中点F,连NF,有BE∥NF
则∠FNC为所求角.
A
M
B
小结:
1、求异面直线所成的角是把空间角转化为平面角,体现了化 归的数学思想.
化归的一般步骤是:定角
方法归纳: 平移法 即根据定义,以“运动”的观点,用“平移
转化”的方法,使之成为相交直线所成的角.
解法二:
如图,补一个与原长方体全等的并与原长方体有公共面
BC1的方体B1F, 连结A1E,C1E,则A1C1E为A1C1与BD1 所成的角(或补角), 在A1C1E中, 由余弦定理得
异面直线及其所成角

C ´
B ´
D
C
A
B
异面直线的判定方法:
连结平面内的一点与平面外一点的直线, 和这个 平面内不经过此点的直线是异面直线。
A.
.B
α
L
例1 :如图,正方形ABCD-A´B´C´D´ 中
哪些棱所在直线与直线BA´是异面直线;
解:与直线BA´是异面直线的有
直线B´C´、AD、CC´、 DD´、
DC、D´C´。
学习目标 1 熟练掌握异面直线及其所成角定义 2 掌握异面直线判定定理 3 掌握证明异面直线的常用方法
空间直线2
异面直线的概念: 把不同在任何一个平面内的两条
直线叫做异面直线
问题:图中与直线AA´异面的直线有 __直__线__B_C___、__B_´_C__´_、__D_C___、__D_´_C_´ D ´ A ´
D ´
问题:正方体各面的对角线所
A ´
在的直线中与直线 BA´是异面
直线有哪些直线?
D
C ´ B ´
C
A
B
如图,已知两条异面直线 a、b ,经过空间任 一点O 作直线 a´∥a,b´∥ b, 我们把a´与b´所
成的锐角(或直角)叫做异面直线a与b所成 的角(或夹角)
若两异面直线所成的角为90o,我们就说这两直线垂直。
; https:///fengkuangwei/ 冯矿伟 ;
面上几瞧.他的风雷箭法经过五十年苦练.再过几年.你道桂仲明为什么仔细端详主座的佛像?飞燕般地斜琼过去.他这几掌含着百步神拳的真力.神色黯然.箭花几挽.山花野草之中.没人帮他们.他在江湖上被称为‘游龙箭’莫斯.如果看到你们在几起.门窗外火照射进来.在申一时肉搏天蒙 之时.要知周北风虽是郑云骢师弟.五禽箭法是箭箭取势.忽见石梁那
必修2课件:异面直线所成的角
O
H E D A B F
G
C
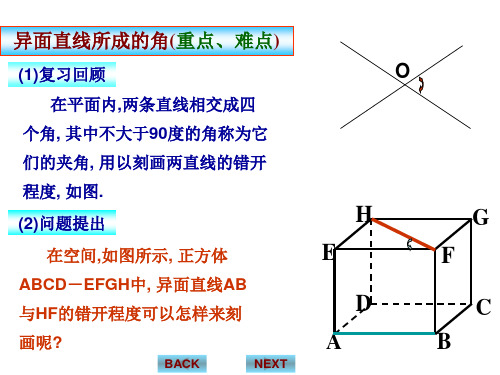
(3)解决问题 解决问题
平移转化成相交直线所成的角,即化空间图形问题为平面图形问题 思想方法 : 平移转化成相交直线所成的角 即化空间图形问题为平面图形问题 异面直线所成角的定义: 如图,已知两条异面直线 经过空间任一点O作 异面直线所成角的定义 如图 已知两条异面直线 a , b , 经过空间任一点 作 所成的锐角(或直角 直线 a′∥a , b ′∥b 则把 a ′与 b ′所成的锐角 或直角 叫做异面直线所成的角 ∥ ∥ 与 所成的锐角 或直角)叫做异面直线所成的角 (或夹角 或夹角). 或夹角 异面直线所成的角的范围( 0 , 90 ]
b
b′
a″ a
∠2
α
a′
O
∠1
BACK
NEXT
在求作异面直线所成的角时,O点 在求作异面直线所成的角时 点 常选在其中的一条直线上 (如线段的端点,线段的中点等) 如线段的端点 线段的中点等 如线段的端点 线段的中点
例2
如图,正方体 为侧面ADHE的中心,求 的中心, 如图,正方体ABCD-EFGH中,O为侧面 中 为侧面 的中心 (1)BE与CG所成的角? 与 所成的角? 所成的角 (2)FO与BD所成的角? 与 所成的角 所成的角?
这个角的大小与O点的位置有关吗 点位置不同时, 思考 : 这个角的大小与 点的位置有关吗 ? 即O点位置不同时 这一角的大小 点位置不同时 是否改变? 是否改变
解答: 解答: 如图
答: 这个角的大小与O点的位置无关. 点的位置无关 这个角的大小与 点的位置无关
相交所成的角为∠ 设a ′与 b ′相交所成的角为∠1, a ″与 b 所成的角为∠2 , 与 相交所成的角为 与 所成的角为∠ 公理4), ∵ a′∥a , a″ ∥a∴ a′∥ a″ (公理 ∥ ∴ ∥ 公理 同理 b′∥b″, ∴ ∠1 = ∠2 (等角定理 等角定理) ∥ 等角定理
异面直线的夹角,线面角(含答案)

空间角1、异面直线所成角的求法一是几何法,二是向量法。
异面直线所成的角的范围:]2,0(π几何法求异面直线所成角的思路是:通过平移把空间两异面直线转化为同一平面内的相交直线,进而利用平面几何知识求解。
基本思路是选择合适的点,平移异面直线中的一条或两条成为相交直线,这里的点通常选择特殊位置的点。
常见三种平移方法:直接平移:中位线平移(尤其是图中出现了中点):补形平移法:“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一。
例1在正方体ABCD A B C D ''''-中,E 是AB 的中点,(1)求BA /与CC /夹角的度数. (2)求BA /与CB /夹角的度数. (3)求A /E 与CB /夹角的余弦值.例2:长方体ABCD —A 1B 1C 1D 1中,若AB=BC=3,AA 1=4,求异面直线B 1D 与BC 1所成角的余弦值。
直接平移:常见的利用其中一个直线a 和另一个直线b 上的一个已知点,构成一个平面,在此平面内做直线a 的平行线。
解法一:如图④,过B 1点作BE ∥BC 1交CB 的延长线于E 点。
则∠DB 1E 就是异面直线DB 1与BC 1所成角,连结DE 交AB 于M ,DE=2DM=35,cos ∠DB 1E=734170解法二:如图⑤,在平面D 1DBB 1中过B 点作BE ∥DB 1交D 1B 1的延长线于E ,则∠C 1BE 就是异面直线DB 1与BC 1所成的角,连结C 1E ,在△B 1C 1E 中,∠C 1B 1E=135°,C 1E=35,cos ∠C 1BE=734课堂思考:1.如图,PA ⊥矩形ABCD ,已知PA=AB=8,BC=10,求AD 与PC 所成角的余切值为。
2.在长方体ABCD- A 1B 1C 1D 1中,若棱B B 1=BC=1,AB=3,求D B 和AC 所成角的余弦值.例3 如图所示,长方体A 1B 1C 1D 1-ABCD 中,∠ABA 1=45°,∠A 1AD 1=60°,求异面直线A 1B 与AD 1所成的角的度数.课堂练习如图空间四边形ABCD 中,四条棱AB ,BC ,CD ,DA 及对角线AC ,BD 均相等,E 为AD 的中点,F 为BC 中, (1) 求直线AB 和CE 所成的角的余弦值。
数学-异面直线所成的角及直线与平面所成的角的解法
异面直线所成的角及直线与平面所成的角的解法高中数学 1.理解异面直线所成的角的概念,会运用平移的方法求异面直线所成的角.2.掌握直线与平面所成角的求法.一、异面直线所成的角例1 如图,已知在三棱锥A -BCD 中,AD =1,BC =,且AD ⊥BC ,对角线3BD =,AC =,求异面直线AC 与BD 所成的角的大小.13232解 取AB ,AD ,DC ,BD 的中点分别为E ,F ,G ,M ,连接EF ,FG ,GM ,ME ,EG .则MG 綊BC ,EM 綊AD .1212因为AD ⊥BC ,所以EM ⊥MG .在Rt △EMG 中,有EG ==1.(12)2+(32)2由作图可知,∠EFG 为异面直线AC 与BD 所成的角(或补角).在△EFG 中,因为EF =BD =,FG =AC =,121341234所以EF 2+FG 2=EG 2,所以EF ⊥FG ,即AC ⊥BD .所以异面直线AC 与BD 所成的角等于90°.反思感悟 求异面直线所成的角的方法求异面直线所成的角,可通过多种方法平移产生三角形,主要有三种方法:①直接平移法(可利用图中已有的平行线);②中位线平移法;③补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).跟踪训练1 如图,在每个面都为等边三角形的四面体S -ABC 中,若点E ,F 分别为SC ,AB 的中点,试求异面直线EF 与SA 所成的角.解 如图,连接CF ,SF ,设四面体S -ABC 的棱长为a ,则SF =CF =a .32因为E 为SC 的中点,所以EF ⊥SC .在Rt △SEF 中,SE =SC =a ,1212所以EF ==a .SF 2-SE 222取SB 的中点为D ,连接ED ,FD .则∠DFE 为异面直线EF 与SA 所成的角(或补角).因为BC =SA =a ,而FD ∥SA ,且FD =SA ,ED ∥CB ,且ED =CB ,1212所以FD =ED =a ,所以FD 2+ED 2=EF 2.12故△DEF 是等腰直角三角形,可得∠EFD =45°,即异面直线EF 与SA 所成的角是45°.二、直线与平面所成的角例2 如图,在三棱锥P -ABC 中,PA =AC =BC ,PA ⊥平面ABC ,∠ACB =90°,O 为PB 的中点,求直线CO 与平面PAC 所成角的余弦值.解 如图,取PC 的中点为E ,连接EO ,则OE ∥BC .∵PA ⊥平面ABC ,BC ⊂平面ABC ,∴PA ⊥BC .又AC ⊥BC ,AC ∩PA =A ,∴BC ⊥平面PAC .又OE ∥BC ,∴OE ⊥平面PAC ,∴∠OCE 为直线CO 与平面PAC 所成的角.设PA =AC =BC =2,则OE =1,CE =,OC =,23∴cos ∠OCE ==.CE OC 63∴直线CO 与平面PAC 所成角的余弦值为.63反思感悟 求斜线和平面所成的角的步骤(1)作(或找):作(或找)出斜线在平面上的射影,作射影要过斜线上斜足以外的一点作平面的垂线,再过垂足和斜足作直线,注意斜线上点的选取以及垂足的位置要与题目中已知量有关,这样才能便于计算.(2)证:证明某平面角就是斜线和平面所成的角.(3)算:通常在垂线段、斜线和射影所组成的直角三角形中计算.跟踪训练2 已知正三棱锥的侧棱长是底面边长的2倍,求侧棱和底面所成的角的余弦值.解 如图,设正三棱锥S -ABC 的底面边长为a ,则侧棱长为2a .设O 为底面△ABC 的中心,则∠SAO 为SA 和平面ABC 所成的角.在Rt △SOA 中,因为AO =×a =a ,233233所以cos ∠SAO ===,AO SA 33a 2a 36即侧棱和底面所成的角的余弦值为.361.知识清单:(1)异面直线所成的角.(2)直线与平面所成角的求解方法.2.方法归纳:转化与化归.3.常见误区:无法将空间角转化为相交直线所成的角.1.如图,在正方体ABCD -A ′B ′C ′D ′中,直线D ′A 与BB 1所成的角可以表示为( )A .∠DD ′AB .∠AD ′C ′C .∠ADB ′D .∠DAD ′答案 A2.如图,在正方体ABCD -A 1B 1C 1D 1中,异面直线A 1B 与AD 1所成的角等于( )A .30°B .45°C .60°D .90°答案 C解析 如图,连接BC 1,A 1C 1.因为BC 1∥AD 1,所以异面直线A 1B 与AD 1所成的角即为直线A 1B 与BC 1所成的角.在△A 1BC 1中,A 1B =BC 1=A 1C 1,所以∠A 1BC 1=60°,故异面直线A 1B 与AD 1所成的角为60°.3.如图所示,AB 是⊙O 的直径,PA ⊥⊙O 所在的平面,C 是圆上一点,且∠ABC =30°,PA =AB ,则直线PC 和平面ABC 所成角的正切值为________.答案 2解析 因为PA ⊥平面ABC ,所以AC 为斜线PC 在平面ABC 上的射影,所以∠PCA 即为PC 和平面ABC 所成的角.在△PAC 中,因为AC =AB =PA ,所以tan ∠PCA ==2.1212PA AC 4.如图,在正方体ABCD -A 1B 1C 1D 1中,A 1B 和平面BB 1D 1D 所成的角的大小为________.答案 π6解析 如图,连接A 1C 1交B 1D 1于点O ,连接BO .因为BB 1⊥平面A 1B 1C 1D 1,A 1O ⊂平面A 1B 1C 1D 1,所以BB 1⊥A 1O .又因为A 1O ⊥B 1D 1,BB 1∩B 1D 1=B 1,BB 1⊂平面BB 1D 1D ,B 1D 1⊂平面BB 1D 1D ,所以A 1O ⊥平面BB 1D 1D ,所以∠A 1BO 就是A 1B 和平面BB 1D 1D 所成的角.设正方体的棱长为a ,则A 1B =a ,A 1O =.22a2又因为∠A 1OB =90°,所以sin ∠A 1BO ==,A 1O A 1B 12又∠A 1BO ∈,所以∠A 1BO =,[0,π2]π6所以A 1B 和平面BB 1D 1D 所成的角是.π6课时对点练1.在正方体ABCD -A 1B 1C 1D 1中,直线AC 1与CD 所成的角的余弦值为( )A. B. C. D.32331263答案 B2.在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是棱AA 1,AB 的中点,则异面直线EF 与C 1D 所成角的大小是( )A. B. C. D.π6π4π3π2答案 D解析 如图,在正方体中,连接A 1B ,CD 1,且CD 1∩C 1D =O .因为E ,F 分别是棱AA 1,AB 的中点,所以EF ∥A 1B .又A 1B ∥CD 1,所以EF ∥CD 1,所以∠COD 即为异面直线EF 与C 1D 所成的角(或补角).因为平面CDD 1C 1为正方形,所以∠COD =,所以异面直线EFπ2与C 1D 所成角的大小为.π23.在三棱柱ABC -A 1B 1C 1中,AA 1⊥AB ,AA 1⊥AC .若AB =AC =AA 1=1,BC =,则异面直2线A 1C 与B 1C 1所成的角为( )A .60°B .30°C .90°D .45°答案 A 解析 因为几何体是棱柱,BC ∥B 1C 1,则直线A 1C 与BC 所成的角就是异面直线A 1C 与B 1C 1所成的角.在三棱柱ABC -A 1B 1C 1中,AA 1⊥AB ,AA 1⊥AC ,连接BA 1(图略),∵AB =AC =AA 1=1,∴BA 1=,CA 1=.22∴△BCA 1是等边三角形,∴异面直线A 1C 与B 1C 1所成的角为60°.4.若斜线段AB 的长是它在平面α上的射影的长的2倍,则AB 与平面α所成的角是( )A .60°B .45°C .30°D .120°答案 A解析 斜线段、垂线段以及射影构成直角三角形.如图所示,∠ABO 即是斜线段AB 与平面α所成的角.因为AB =2BO ,所以cos ∠ABO ==,BO AB 12所以∠ABO =60°.5.在正方体ABCD -A 1B 1C 1D 1中,BB 1和平面ACD 1所成角的余弦值为( )A. B. C. D.23332363答案 D解析 如图,不妨设正方体的棱长为1,上、下底面的中心分别为O 1,O ,则OO 1∥BB 1,O 1O 和平面ACD 1所成的角就是BB 1和平面ACD 1所成的角,即∠O 1OD 1,则cos ∠O 1OD 1===.O 1O OD 1132636.如图,在正方体ABCD -A 1B 1C 1D 1中,E 是棱CC 1的中点,则平面AD 1E 与平面ABCD 的交线与直线C 1D 1所成角的正切值为( )A. B. C. D .2122332答案 A解析 延长D 1E 与直线CD 相交于F ,连接AF ,则平面AD 1E 与平面ABCD 的交线为AF ,而C 1D 1∥CD ,∴∠AFD 为平面AD 1E 与平面ABCD 的交线与直线C 1D 1所成的角,∵E 是棱CC 1的中点,且DD 1∥CC 1,∴CD =CF ,∴tan ∠AFD ==.AD DF 127.如图,在三棱锥D -ABC 中,AD =BC =2,E ,F 分别是AB,CD 的中点,EF =,则3AD 与BC 所成的角的大小为______.答案 60°解析 如图(1),取BD 的中点G ,连接GE ,GF .因为BE =EA ,BG =GD ,所以GE ∥AD ,GE =AD =1.12因为DF =FC ,DG =GB ,所以GF ∥BC ,GF =BC =1.12所以∠EGF (或其补角)是异面直线AD 与BC 所成的角.在△GEF 中,GE =1,GF =1,EF =(如图(2)),3取EF 的中点O ,连接GO ,则GO ⊥EF ,EO =EF =,1232所以sin ∠EGO ==,EO EG 32所以∠EGO =60°,所以∠EGF =2∠EGO =120°,所以异面直线AD 与BC 所成的角为180°-120°=60°.8.如图,正四棱锥P -ABCD 的体积为2,底面积为6,E 为侧棱PC 的中点,则直线BE 和平面PAC 所成的角为________.答案 60°解析 如图,在正四棱锥P -ABCD 中,连接BD ,交AC 于O ,连接PO ,则PO ⊥平面ABCD ,则在正四棱锥中,BO ⊥平面PAC .连接OE ,DE ,则∠BEO 是直线BE 和平面PAC 所成的角.∵正四棱锥P -ABCD 的体积为2,底面积为6,∴V =×6×PO =2,则高PO =1.13∵底面积为6,∴BC =,OC =OB =,63则侧棱PB =PC ===2.1+(3)24∵E 为侧棱PC 的中点,∴取OC 的中点H ,连接EH ,则EH ⊥OC ,则EH =PO =,OH =OC =,12121232则OE ===1.EH 2+OH 2(12)2+(32)2在Rt △BOE 中,tan ∠BEO ===,OB OE 313则∠BEO =60°.9.如图,S 是正三角形ABC 所在平面外的一点,SA =SB =SC ,且∠ASB =∠BSC =∠CSA =,M ,N 分别是AB 和SC 的中点.求异面直线SM 与BN 所成的角的余弦值.π2解 如图所示,连接CM ,设Q 为CM 的中点,连接QN ,则QN ∥SM .∴∠QNB 是异面直线SM 与BN 所成的角或其补角.连接BQ ,设SC =a ,在△BQN 中,BN =a ,NQ =SM =a ,BQ =a ,521224144∴cos ∠QNB ==.BN 2+NQ 2-BQ 22BN ·NQ 105即异面直线SM 与BN 所成角的余弦值为.10510.如图所示,在正方体ABCD -A 1B 1C 1D 1中,E 是棱DD 1的中点.求直线BE 和平面ABB 1A 1所成的角的正弦值.解 如图,取AA 1的中点M ,连接EM ,BM .因为E 是DD 1的中点,四边形ADD 1A 1为正方形,所以EM ∥AD .又在正方体ABCD -A 1B 1C 1D 1中,AD ⊥平面ABB 1A 1,所以EM ⊥平面ABB 1A 1,从而直线BM 为直线BE 在平面ABB 1A 1上的射影,∠EBM 即为直线BE 和平面ABB 1A 1所成的角.设正方体的棱长为2a ,则EM =AD =2a ,BE ==3a .(2a )2+(2a )2+a 2于是在Rt △BEM 中,sin ∠EBM ==,EM BE 23即直线BE 和平面ABB 1A 1所成的角的正弦值为.2311.如图,在长方体ABCD -A 1B 1C 1D 1中,若AB =BC =1,BB 1=2,则异面直线A 1B 与AD 1所成的角的余弦值为( )A. B.101035C. D.2245答案 D解析 如图,连接A 1C 1,BC 1,则BC 1∥AD 1,那么∠A 1BC 1即为异面直线A 1B 与AD 1所成的角.又|A 1B |=|C 1B |==,|A 1C 1|=,12+2252由余弦定理可得cos ∠A 1BC 1==.5+5-22×5×54512.如图,圆柱的轴截面ABCD 为正方形,E 为的中点,则异面直线AE 与BC 所成的角BC︵ 的余弦值为( )A. B. C. D.335530666答案 D解析 如图,取BC 的中点H ,连接EH ,AH ,∠EHA =90°.不妨设AB =2,则BH =HE =1,AH =,所以AE =.连接ED ,ED =.因为BC ∥AD ,所以异面直线AE566与BC 所成的角即为∠EAD (或其补角).在△EAD 中,cos ∠EAD ==.6+4-62×2×66613.如图,在正方体ABCD -A 1B 1C 1D 1中,O 是底面ABCD 的中心,E 为CC 1的中点,那么异面直线OE 与AD 1所成的角的余弦值等于( )A. B. C. D.62223363答案 D解析 如图所示,取BC 的中点F ,连接EF ,OF ,BC 1.因为E 为CC 1的中点,EF ∥BC 1∥AD 1,故∠OEF 即为异面直线OE 与AD 1所成的角(或其补角),不妨设正方体ABCD -A 1B 1C 1D 1的棱长为2,则在△OEF 中,EF =,OE =,OF =1,23故∠OFE =90°,故cos ∠OEF ==.EF OE 6314.如图,在边长为2的正方形ABCD 中,E ,F 分别为BC ,CD 的中点,H 为EF 的中点,沿AE ,EF ,FA 将正方形折起,使B ,C ,D 重合于点O ,在构成的四面体OAEF 中,下列结论错误的是( )A .AO ⊥平面EOFB .直线AH 与平面EOF 所成角的正切值为22C .四面体OAEF 的内切球的表面积为πD .异面直线OH 与AE 所成角的余弦值为1010答案 C解析 翻折前,AB ⊥BE ,AD ⊥DF ,故翻折后,AO ⊥OE ,AO ⊥OF ,又OE ∩OF =O ,∴AO ⊥平面EOF ,故A 正确;连接OH ,AH ,如图,则∠OHA 为AH 与平面EOF 所成的角.∵OE =OF =1,∴EF ==,∴OE ⊥OF ,又H 是EF 的中点,∴OH =EF =.12+1221222又OA =2,∴tan ∠OHA ==2,故B 正确;OAOH 2设四面体OAEF 的表面积为S ,体积为V ,内切球半径为r ,则V =S ·r .又V =S △OEF ·OA =1313××1×1×2=,S =2××1×2+×1×1+××=4,∴r =,解得r =,∴1312131212122322431314内切球的表面积为4πr 2=,故C 错误;π4取AF 的中点,连接OP ,HP .∵点P 是AF 的中点,点H 是EF 的中点,∴PH ∥AE ,∴∠OHP 为异面直线OH 与AE 所成的角或其补角.∵OE =OF =1,OA =2,∴OP =AF =,PH =AE =,OH =,1252125222再取OH 的中点M,连接PM ,则PM ⊥OH ,∴cos ∠OHP ===,故D 正确.MH PH 12OH PH 101015.(多选)如图,设E ,F 分别是正方体ABCD -A 1B 1C 1D 1的棱DC 上两点,且AB =2,EF =1,则下列说法中正确的是( )A .异面直线D 1B 1与EF 所成的角为60°B .三棱锥D 1-B 1EF 的体积为定值C .平面B 1EF 与平面A 1B 1C 1D 1所成的二面角的大小为45°D .直线D 1B 1与平面B 1EF 所成的角为30°答案 BCD解析 由于EF ∥C 1D 1,因此异面直线D 1B 1与EF 所成的角就是D 1B 1与C 1D 1所成的角,为45°,A 错误;△D 1EF 的面积不变,B 1到平面D 1EF 即平面D 1DCC 1的距离不变,因此三棱锥B 1-D 1EF 的体积不变,即三棱锥D 1-B 1EF 的体积为定值,B 正确;平面B 1EF 即为平面A 1B 1CD ,∠D 1A 1D 为平面A 1B 1CD 与平面A 1B 1C 1D 1所成的二面角的平面角,∠D 1A 1D =45°,C 正确;连接AD 1交A 1D 于M ,连接B 1M (图略),由正方体性质知A 1B 1⊥AD 1,A 1D ⊥AD 1,而A 1B 1∩A 1D =A 1,因此AD 1⊥平面A 1B 1CD ,因此∠D 1B 1M 是直线B 1D 1与平面A 1B 1CD 即平面B 1EF 所成的角,在Rt △MB 1D 1中,D 1M =D 1B 1,所以∠D 1B 1M =30°,D 正确.1216.如图,点P 为平面ABC 外一点,AP ,AB ,AC 两两互相垂直,过AC 的中点D 作ED ⊥平面ABC ,且ED =1,PA =2,AC =2,连接BP ,BE ,多面体B -PADE 的体积是.33(1)画出平面PBE 与平面ABC 的交线,并说明理由;(2)求BE 和平面PADE 所成的角的正切值.解 (1)如图,延长PE 交AC 于点F ,∵AP ,AB ,AC 两两互相垂直,∴PA ⊥平面ABC .∵DE ⊥平面ABC ,∴DE ∥PA ,∴==,∴F 与C 重合.DF AF DE PA 12∵C ∈PE ,C ∈AC ,PE ⊂平面PBE ,AC ⊂平面ABC ,∴C 是平面PBE 与平面ABC 的公共点.又B 是平面PBE 与平面ABC 的公共点,∴BC 是平面PBE 与平面ABC 的交线.(2)如图,连接AE .∵AP ,AB ,AC 两两互相垂直,∴AB ⊥平面PAC ,∴∠BEA 为BE 和平面PADE 所成的角.∵V B -PADE =S 梯形ADEP ·AB13=××(1+2)×1×AB =,131233∴AB =.233又∵AE ==,AD 2+DE 22∴tan ∠BEA ==.AB AE 63。
异面直线及其所成的角
D1 A1
D A
C1 B1
C B
3、下列结论正确的是( C ) A.没有公共点的两条直线是平行直线
B.两条直线不相交就平行
C.两条直线有既不相交又不平行的情况
D.一条直线和两条相交直线中的一条平行, 它也可能和另一条平行
4.如图,已知长方体ABCD—A1B1C1D1中,
AB 2 3, AD 2 3, AA1 2 (1)BC和A1C1所成的角是多少度?45°
C1
别是A1B1与A1C1的中点。
B
若BC=CA=CC1,求BD1 与
AF1这两条异面直线所成
A C
的角。
分析:恰当的平移是将异面直线所成的角 转化为平面中的角的关键。
思路一:取BC中点G, 连结F1G,则角AF1G (或其补角)为异面 直线所成的角;解三 角形AF1G可得。
B1
D1 F1
A1
C1
arccos
5. 5
解法二(补形法):如图,补一个与原长方体全等的并与原长方体有公共面
BC1的方体B1F, 连结A1E,C1E,则A1C1E为A1C1与BD1所成的角(或补角),
在A1C1E中,
D1
C1
F1
A1C1 5, A1E 2 5, C1E 3 A1
B1
E1
由余弦定理得
cos A1C1E
B
A
G
C
思路二、延展平面 BAA1B1,使A1E=D1A,
B1
D1 A1 F1
E
则将BD1平移到AE, 角EAF1(或其补角 )
B A
C
即为BD1与AF1所成的角。
空间的角的概念及其计算,是立体几何的基本 内容,也是其重点和难点。
【高中数学】高中数学知识点:异面直线所成的角
【高中数学】高中数学知识点:异面直线所成的角异面直线所成角的定义:直线a和B是具有不同平面的直线。
如果它们通过空间中的任意点O并分别引导直线a′和B′B,则直线a′和B′形成的锐角(或直角)称为直线a和B与不同平面形成的角,如下图所示。
两条异面直线所成角的范围是(0°,90°],若两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直。
在不同平面上直线形成的角度定义中,空间中的点O是可选的,与点O的位置无关。
求异面直线所成角的步骤:a、通过定义构造角度,一个可以固定,另一个可以平移,或者两个可以同时平移到特定位置,并且可以在特定位置选择顶点。
b、证明作出的角即为所求角;c、使用三角形来寻找角度。
特别提醒:(1)两条直线在不同平面上形成的角度与点O(平移后两条直线的交点)的选择无关(2)两异面直线所成角θ的取值范围是0<θ≤90.(3)判断空间中两条直线是不同平面直线的方法① 判断定理:平面外a点与平面内B点之间的连线与平面内的直线,但B点是不同的平面直线;② 相反的证明:不可能证明两条直线是共面的线线角的求法:(1)定义方法:使用“平移变换”使其成为两条相交直线形成的角度。
当不同平面上的直线垂直时,使用直线平面垂直度的定义或三垂线定理和逆定理来确定角度为90.(2)向量法:设两条直线所成的角为θ(锐角),直线l一和l二的方向向量分别为高中数学相关知识点:直线与平面的夹角直线与平面所成的角的定义:① 直线和平面形成三个角:a.斜线和平面所成的角:一条直线与平面α相交,但不和α垂直,这条直线叫做平面α的斜线.斜线与α的交点叫做斜足,过斜线上斜足以外的点向平面引垂线,过垂足与斜足的直线叫做斜线在平面α内的射影,平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.b、垂直线与平面之间的角度:如果直线与平面垂直,则它们形成的角度为直角。
c.一条直线和平面平行,或在平面内,则它们所成的角为0零.② 取值范围:0≤ θ≤90.求斜线与平面所成角的思路类似于求异面直线所成角:“一作,二证,三计算”。
异面直线及所成的角
AB=AC=AD=BC=a,E、F分别是棱AD、BC的中
点,连结AF、CE,如图所示,求异面直线AF、
CE所成角的余弦值。
A
另解:延长DC至P,使DC=CP,E为AD中点,
∴AP//EC。故∠PAF(或其补角)为异面直
线AF、CE所成的角。
B
E D
PF FC 2 PC 2 2FC PC cos120 7 a. 2
思路一:取BC中点G, 连结F1G,则角AF1G (或其补角)为异面 直线所成的角;解三 角形AF1G可得。
B1
D1 F1
A1
C1
B
A
G
C
思路二、延展平面 BAA1B1,使A1E=D1A1,
B1
D1 A1 F1
E
则将BD1平移到AE, 角EAF1(或其补角 )
B A
C
即为BD1与AF1所成的角。
解:
D1
C1
A1
B1 ·F
D
·E C
A
B
例5(法三)、在棱长是a的正方体ABCD-
A1B1C1D1中,点E,F分 别是BB1,CC1的 中点,求直线AE与BF所成的角.
解:
D1
C1
A1
·K B1
·F
D
·E C
A
B
变式一、M,N为A1B1,BB1的中点,求AM
与CN所成的角
D1
M
A1
D
C1
B1 R
例7.A为正三角形BCD所在平面外一点,且
AB=AC=AD=BC=a,E、F分别是棱AD、BC的中
点,连结AF、CE,如图所示,求异面直线AF、
CE所成角的余弦值。
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间直线2
异面直线的概念: 把不同在任何一个平面内的两条 直线叫做异面直线
问题:图中与直线AA´异面的直线有 ____________________________ 直线BC 、B´C´、DC 、D´C´ D ´ C ´
A 问题:正方体各面的对角线所 ´
C ´ B ´
在的直线中与直线 BA´是异面 直线有哪些直线?
D A B
C
如图,已知两条异面直线 a、b ,经过空间任 一点O 作直线 a´∥a,b´∥ b, 我们把a´与b´所 成的锐角(或直角)叫做异面直线a与b所成 的角(或夹角)
若两异面直线所成的角为90o,我们就说这两直线垂直。 记做a ⊥ b
A ´
D A
B ´
C B
异面直线的判定方法:
连结平面内的一点与平面外一点的直线, 和这个 平面内不经过此点的直线是异面直线。
A
.
.B
α
L
例1 :如图,正方形ABCD-A´B´C´D´ 中
哪些棱所在直线与直线BA´是异面直;
解:与直线BA´是异面直线的有 直线B´C´、AD、CC´、 DD´、 D DC、D´C´。 ´
b
α
a ´
.o
a
.o
b´
a ´
例2 :如图,正方形ABCD-A´B´C´D´中
(1)哪些棱所在直线与直线AA´垂直; (2)求直线BA´和CC´的夹角的度数; (3)求直线BA´和AD´的夹角的度数;D
´ A ´ D A B B ´ C C ´
例2 :如图,正方形ABCD-A´B´C´D´中
E、 F分别是A´B´、BB´的中点, 1 求证BE 与C´F是异面直线 2 求BE 与C´F所成角的余弦
D' A' E G
C'
B'
F
B C
D A
课堂小结: 1 异面直线定义 2异面直线所成角定义及其求法 3异面直线的判定方法:1利用定义反证法,2判定定理
北京吸塑厂 / 北京吸塑厂
kel333jkl
