2016年秋季新版浙教版七年级数学上学期3.4、实数的运算课件4
浙教版数学初一上册32《实数》课件

浙教版数学初一上册32《实数》课件一、教学内容二、教学目标1. 理解并掌握实数的概念,能区分有理数和无理数。
2. 学会实数的基本性质和运算规则,能准确进行实数的四则运算。
3. 感受数学中的无限概念,提高数学思维能力和解决问题的能力。
三、教学难点与重点教学难点:实数概念的建立,无理数的理解,无限概念的认识。
教学重点:实数的定义,实数的四则运算,实数在生活中的应用。
四、教具与学具准备教具:多媒体课件,实数教学挂图,计算器。
学具:学生用计算器,练习本,笔。
五、教学过程1. 实践情景引入:通过介绍生活中的实数实例,如长度、温度等,引出实数的概念。
2. 新课导入:讲解实数的定义,区分有理数和无理数,解释无限概念。
3. 例题讲解:讲解实数的基本性质和运算规则,通过例题演示实数四则运算的具体方法。
4. 随堂练习:让学生进行实数运算的练习,巩固所学知识。
5. 互动环节:学生分组讨论实数的性质和运算规则,分享学习心得。
六、板书设计1. 实数的定义2. 有理数与无理数3. 实数的基本性质4. 实数的四则运算规则5. 实数在生活中的应用七、作业设计1. 作业题目:(1)填空题:根据实数的性质,填空完成下列等式:3 + ___ = 5,4 × ___ = 16。
(2)选择题:下列哪个数是有理数?A. √2,B. √9,C. π,D.1.5。
2. 答案:(1)2,4(2)B(3)8,6八、课后反思及拓展延伸1. 反思:本节课学生对实数概念的理解和实数运算的掌握程度,以及教学方法的适用性。
2. 拓展延伸:引导学生探索实数的更多性质和规律,如实数的平方、立方等,提高学生的数学素养。
重点和难点解析1. 实数的定义及其分类(有理数和无理数)2. 实数的基本性质和运算规则3. 教学过程中的实践情景引入、例题讲解和随堂练习4. 板书设计中的实数性质和运算规则展示5. 作业设计中的题目类型和难度一、实数的定义及其分类实数的定义是理解后续内容的基础,应重点关注。
(浙教版)数学七年级上册课件:3.4实数的运算 (2)
B、2 3= 6
C、 2 +2 2 =3 2 D、 3 =1.732
2、一正方形的面积为10cm2,求以这个正方形 的边为直径的圆的面积。(п取3.14)
3、已知a是 5 的整数部分,b为 5的小数部分, 求a3-4b+4 5 的平方根。
1、 2│ 5 -3│的值为( ) A、2 5-6 B、2 5-3 C、6+2 5 D、6-2 5
3.分配律 a(b+c) = ab+ ac
实数的运算法则
先先算算乘乘方方,再和算开乘方除,,最再后算算乘加除减,。最如后果 算遇到加括减号。,如则果先遇进到行括括号号,里的则运先算进行括号 里的运算
有理数的运算律和运算法则在实数 范围内同样适用
典型例题 例1:计算 2×(3+ 5 )+4-2× 5
(1)你能计算下题吗?
1- 2 + 2 - 3 + 3 - 4
解:原式= 2-1+ 3- 2 + 4- 3
计算 (1) ห้องสมุดไป่ตู้ + 50 5 2 - 16
(2)
(
3)2
╳ (- 42 )
╳
(
-1
1
4
)
(3)153×( 3
1
8
-
13) ╳
3
13
(
4 5
)2
1、下列式子成立的是( )
A、 2+ 3= 5
解:原式=6+2 5 +4-2 5
=6+4+2 5 - 2 5 =6+4 =10
例2、计算下列各式的值:
(1) ( 3 + 2 ) - 2
解: 原式 = 3 + 2 - 2 = 3
(2)3 3 + 2 3
浙江省慈溪市横河初级中学七年级数学上册 3.4实数的运算课件(2) 浙教版

d (不计空气
5
好高啊
(1)计算填表:
下降高 度d 100 200 500 1000
下降时 间t
4.47
6.32
10.00 14.14
(2)如果共下降1000米,则前一个500米与 后一个500米所用的时间分别是多少?
这节课,你有什么收获,能与我们一起 分享通吗过?这节课的学习,你有那些收获,
能与我们一起分享吗?
3.4实数的运算
计算
1 2 (32 1 ) 2
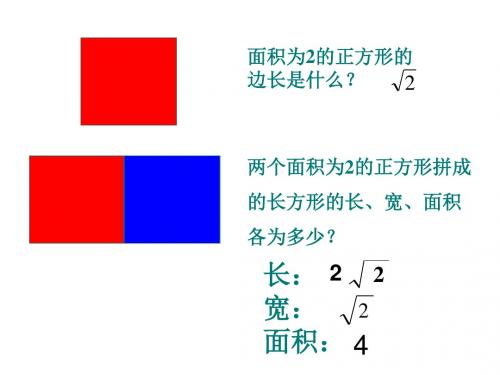
面积为2的正方形的
边长是什么? 2
面积为1的正方形的 边长又是什么?1
那么这两个正方形的边长的和是什么?
边长的差又是什么?
例1 计算
(1) 8 3 9 (精确到0.001);
解:(1)按键43301 0.748.
探究题: (1)计算: (精确到0.01)
1 2 ____, 2 1 _____
2 3 ____, 3 2 _____
gf f f f f f f h
(2)能计算下题吗?
1 2 2 3 3 4
[5-2×( 3 -2)]-3×( 2 +1)(结
果保留3个有效数字)
0.748343301
练习: (1) 4 18 (精确到0.01);
(2) 2
(结果保留3个有效数字);
(3)3 10 7 (精确到0.01).
例1 计算
(2) 9 2 (4 3)
练习:
(结果保留4个有效数字)
1. 3 7 2 7 (结果保留3个有效数字) 2. 9 2 ( 5 2) (精确到0.01)
实数运算的法则
实数运算的顺序是先算乘方和开方, 再算乘除,最后算加减. 如果遇到括号, 则先进行括号里的运算.
3.4实数的运算课时巩固课件浙教版数学七年级上册

自主练习
10.按下图所示的运算程序,能使输出的结果为5的是( D )
A.a=0,b=5 B.a=9,b=4 C.a=16,b=1 D.a=36,b=1
自主练习
11.数轴上的点 A,B 分别对应的数为 2- 2和- 2,则 A, B 之间的距离为___2___,AB 的中点表示的数是_________.
知识梳理
知识点 简单的实数运算 实数运算的顺序是:先算 乘方 和 开方 ,再算 乘除 , 最后算 加减 .如果遇到括号,那么先进行括号里的运算.
知识梳理
【例 1】计算: (1)3 -27 − 16; 解:(1)原式=-3-4=-7. (2)-22+|-1|+3 27; 解:(2)原式=-4+1+3=0.
知识梳理
【例5】将一个底面半径为10 cm的圆柱体容器里的药液倒进一个底面为 正方形的长方体容器内,如果药液在两个容器里的高度是一样的,那么 长方体容器的底面边长为多少(精确到0.1 cm)? 解:由题意得,两个容器底面积相等,即正方形的面积为π×102=100π, ∴长方体容器的底面边长为 100π≈17.7(cm). 答:长方体容器的底面边长约为 17.7 cm.
(3)3 8 − 2+( 4)2+|1- 2|;
知识梳理
【例 2】如图,数轴上 C,B 两点表示的数分别是 2, 13,且点 C 与 点 A,B 的距离相等,则点 A 表示的数是 ( C ) A. 13-4 B.3- 13 C.4- 13 D. 13-3
知识梳理
【例 3】计算:(1)
0.49 − 3 7 − 1 −
自主练习
9.计算: (1) 81-3 64. (2)4+(-3)2×2-3 27. (3)2×(3- 5)-8+2× 5. (4)2( 3-1)-| 3-2|-3 -64.
最新浙教初中数学七年级上《3.4 实数的运算》PPT课件 (7)

练习
数轴上两点A,B分别表示实数 2和 2 1 ,求A,B两点之间的距离。
3 的整数部分与小数部分的差是多 少(结果保留3个有效数字)
整数部分: 1 小数部分: 3 1
1 ( 3 1)
探究题: (1)计算: (精确到0.01)
1 2 ____, 2 1 _____
2 3 ____, 3 2 _____
(2)能计算下题吗?
1 2 2 3 3 4
这节课,你有什么收获,能与我们一起 分享通吗过?这节课的学习,你有那些收获,
能与我们一起分享吗?
1、 4 3 8 3 1 1 2 27 3
2、 1 2 8 2 2 3 1 8
计算:
面积为2的正方形的
边长是什么? 2
面积为1的正方形的 边长又是什么?1
那么这两个正方形的边长的和是什么?
边长的差又是什么?
计算
2 (3 5) 4 2 5
P81 课内练习2
例1 计算
(1) 8 3 7 (精确到0.001);
解:(1)按键顺序为
8-3 7=
0.915495942
∴ 8 3 7 0.915495942 0.915 .
实数运算的法则
实数运算的顺序是先算乘方和开方, 再算乘除,最后算加减. 如果遇到括号, 则先进行括号里的运算.
判断题
(1) 7 3 7 3 2 ×
(2) (3)2 3
×
(3)( 11)2 11
√
(4) 3 (7)3 7
√
探究学习
1、判断下列说法是否正确,并举例说明理由。 ①两个无理数的和一定是无理数; ②两个无理数的积一定是无理数; ③两个无理数的商可能是有理数.
(2)3 2 (4 3)(精确到0.01);
2024七年级数学上册第3章实数3.4实数的运算习题课件新版浙教版.pptx

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. [2023·丽水调研]已知 a , b 是两个实数,满足 a + b =0,
下列是关于 a , b 的五个结论:
① +
=0;② a2- b2=0;③
+ =0;④ a3
- b3=0;⑤| a |=| b |.则所有正确结论的序号是
浙教版 七年级上
第3章 实数
3.4 实数的运算
CONTENTS
目
录
01
夯实基础巩固练
02
整合方法提升练
03
培优探究拓展练
知识过关
实数运算的顺序:先算
最后算
加减
里的运算.
.若遇到
乘方和开方
括号
,再算
,则先进行
乘除
括号
,
实数的运算
1. 计算 − + +|-4|的结果是(
A. 8
B. -4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)上面各数有什么共同的特征?由此能得出什么结论?
【解】共同特征:它们都是两个数的算术平方根的和
的形式,而且两根号内的数的和都是13.
结论:当两根号内的数的和一定时,两根号内的数越
接近,它们的算术平方根的和越大.
1
2
3
4
5
6
7
8
9
10
11
【最新整理版】浙教版数学七年级上册3.4《实数的运算》ppt课件1.ppt
例2:用计算器计算
8 1 、
7 — 3 (精确到0.01)
2、3∏ —2×(4+ 3) (精确到0.01)
例3.跳伞运动员跳离飞机,在未打开降落
伞前,下降的高度d(米)与下降的时间t(秒)
之 阻间 力有)(精关确系到式0:.01t)
d (不计空气
5
好高啊
(1)计算填表:
下降高 度d 100 200 500 1000
(2)当a<b时, a b ____
(3)能计算下题吗?
1 2 2 3 3 4
这节课,你有什么收获,能与我们一起 分享通吗过?这节课的学习,你有那些收获,
能与我们一起分享吗?
作业:作业本3.4
3.4实数的运算
教学目标:
1回顾有理数的运算法则和运算律 2了解有理数的运算法则和运算律在 实数范围学科网 内同样适用
3掌握实数运算的法则和运算顺序 4会用计算器进行简单的实数运算, 并解决一些简单的实际问题。
教学重点和难点: 1本节教学的重点是掌握实数运算的 法则和运算顺序 2例1在实数范围内运用运算法则和 运算律较复杂,是本节教学的难点。
学情分析: 1通过自学,学生能掌握在实数范围 内有理数的运算律和运算法则仍然 成立。 2本节课要用到计算器,课前先布置 学生读懂计算器中开方键的使用说 明,所以,例2也比较简单。 3通过自学,完成81页做一做和课内 练习1.
计算
1 2 (32 1 )
Z.xx..xxk. K
2
有理数范围内的运算顺序是怎样的?
下降时 间t
47
6.32
10.00 14.14
(2)如果共下降1000米,则前一个500米与 后一个500米所用的时间分别是多少?
浙教版七年级数学上册3.4实数的运算
2 和 2 1 ,
1
3.写出两个无理数,使它们的和为6。
4.已知x, y为实数,且
则x+y的值等于
y x 3 3 x 2
。
5
拓展探究题:
(1)计算下列各数的绝对值:
(1) 3 ( 2) 2 5
(3) 3.14 (4) 9 3
(2)能计算下题吗?
1 2 2 3 3 4
看谁能口答!
1. 16 0.064 2. 16 0.064 4 0 .4 4 0 .4 4 .4 3 .6
3
3
3.
1 81
3
1 27
4. 81
3
1 1 ( ) 9 3 1 27
1 9 ( ) 3
1 27
27
合作学习
请同学们总结有理数的运算律和运算法则
思考:
2 16 (2 2 64) 44 (2 2 4) 1 (2 8) 5
2 3
先算乘方,再算乘除,最后算加减。 如有括号,先进行括号里的运算。
实数范围内的运算顺序又是怎样的呢?
先算乘方与开方,再算乘除,最后算加减。 如有括号,先进行括号里的运算。
例1:计算
3 ,则它 π的整数部分为___ 的小数部分是 π-3 ;
2 小数部分 6 的整数部分是___,
是______. 6 2
探究题:
(1)计算: (精确到0.01)
1 2 ____, 2 1 _____
2 3 ____, 3 2 _____
你有什么发现吗?利用你的发 现计算下题:
(2 ) 1
2
2 3 3 4
七年级数学上册(浙教版)课件-3.4 实数的运算
【拓展创新】 16.(10 分)【例题】设 a,b 是有理数,且满足 a+ 2×b=3-2× 2,求 a+b 的值. 解:由题意,得(a-3)+(b+2)× 2=0,
②无理数包括正无理数和负无理数;
③两个无理数的和可能是有理数;
④带根号的数都是无理数.
其中正确的有( A )
A.①②③
B.①②④
C.①③
D.②④
6.(4 分)计算-3×[6-2×( 3+1)](精确到 0.01)的结果为( B )
A.1.61
B.-1.61
C.2.39
D.-2.39
7.(6分)填空:
解:由题意,得(a-3)+(b+2)× 2=0, ∵a,b 都是有理数,∴a-3,b+2 也是有理数. 又∵ 2是无理数,∴a-3=0,b+2=0. ∴a=3,b=-2,∴a+b=3+(-2)=1. 【问题】若 x,y 都是有理数,且满足 x2-2y+ 5×y=10+3× 5,求 xy 的值. 解:根据题意,得 y=3,x2-2y=10. ∴x=4 或-4. ∴xy=64 或-64.
解:原式=10.
(5)-12-(-2)3×1-3 27×|-1|+2÷( 2)2.
解:原式=0. 8
3
10.(5 分)定义新运算“*”:对于任意两个实数 a,b,有 a*b=b2-1,例如:6*4=42-1
=15.那么当 m 为实数时,m*(m* 2 018)=(B)
A.2 0182-1
B.2 0172-1
第3章 实 数
3.4 实数的运算
浙教版·七年级上册
浙教版数学七年级上册3.4 实数的运算.docx
3.4 实数的运算一、选择题(共10小题;共50分)1. 下列二次根式中,是最简二次根式的是 ( )A. √15B. √12C. √13D. √9 2. 计算 √2×√3 的结果是 ( ) A. √5 B. √6 C. 2√3 D. 3√2 3. 若 a =√50−5,则估计 a 的值所在的范围是 ( )A. 1<a <2B. 2<a <3C. 3<a <4D. 4<a <54. 下列二次根式中,最简二次根式是 ( ) A. √8 B. √169 C. √x 2+4 D. 1x5. 化简 √18÷√2 的结果是 ( ) A. 9 B. 3 C. 3√2D. 2√3 6. 下列各式中,最简二次根式是 ( )A. √8B. √m 5C. √12D. √67. 下列运算正确的是 ( )A. a +a =a 2B. a 6÷a 3=a 2C. (π−3.14)0=0D. 2√3−√3=√3 8. 下列二次根式的运算:① √2×√6=2√3,② √18−√8=√2,③ √5=2√55,④ √(−2)2=−2.其中运算正确的有 ( )A. 1 个B. 2 个C. 3 个D. 4 个9. 下列二次根式中,不能与 √3 合并的是 ( )A. √13B. 3√3C. √23D. √1210. 按如图所示的程序计算,若开始输入的 n 值为 √2,则最后输出的结果是 ( )A. 14B. 16C. 8+5√2D. 14+√2二、填空题(共10小题;共50分)11. 计算:√3+√27= . 12. 计算 √7÷√3 的结果是 . 13. 若最简二次根式 √3a −5 和 √a +7 是同类二次根式,则 a = .14. 试举一列,说明“两个不是互为相反数的无理数的和仍是无理数”是错误的:你取的两个无理数是 ,它们的和为 .15. 已知 a =1+√2,b =1−√2,则代数式 a ⋅b 的值为 .16. 判断题:(1)√a +√b =√a +b ;(2)1−13√2=23√2 .17. 计算:a√3a +√9a −3√a√3= .18. 已知:x =√3−√2√3+√2,y =√3+√2√3−√2.那么 yx +xy = .19. 实数 a ,b 在数轴上的位置如图所示,则化简 √(−a )2+√b 2−√(a +b )2的结果为 .20. 最简二次根式 √2m −1 与 √34−3m n−1 是同类二次根式,则 mn = .三、解答题(共5小题;共65分)21. 计算:(π−3.14)0−√48−(−12)−2−∣∣−√3∣∣.22. 计算:Ⅰ √18−√8+(−√3+1)(−√3−1);Ⅱ √12×√323÷√33.23. 计算:(√12+√3)×√6−2√12.24. 计算 13√27−√6×√8+√12.25. 计算:(√2−√3)2−(√2+√3)(√2−√3).答案第一部分1. A2. B3. B4. C5. B6. D7. D8. C9. C 10. C第二部分11. 4√312. √21313. 614. 1+√3 和 1−√3(答案不唯一);215. −116. ×;×17. 3√a18. 9819. 2b20. 21第三部分21. 原式=1−4√3−4−√3=−3−5√3.22. (1) 原式=3√2−2√2+(3−1)=√2+2.(2)原式=2√3×4√233=8√2.23. 原式=(2√3+√3)×√6−2×√22=3√3×√6−√2=3×3√2−√2=9√2−√2=8√2.24. 原式=13×3√3−4√3+2√3=−√3.25. 原式=2−2√6+3−2+3=6−2√6.初中数学试卷。
