相关分析与回归分析实例

合集下载

回归分析实例PPT课件

通过各种统计检验来评估模型的拟合效果，如残差分析、R方检验、F检验等。
线性回归分析的应用
预测
使用线性回归模型来预测因变量的值，基于给定的自变量值
。
解释变量关系
通过线性回归分析来了解自变量与因变量之间的数量关系和影响程度。
控制变量效应
在实验或调查中，控制自变量的影响，以观察因变量的变化情况。
模型的建立和检验
模型的建立
首先需要收集数据，并进行数据清洗和预处理，然后选择合适的自变量和因变量，建立逻辑回归
模型。
模型的检验
通过多种检验方法对模型进行评估，包括参数估计、假设检验、模型诊断等，以确保模型的准确
性和可靠性。
模型的优化
根据检验结果对模型进行调整和优化，包括参数调整、变量筛选
详细描述
收集产品在过去一段时间的销售数据，包括销售额、销售量等，作为自变量，将未来某一段时间的产品销量作为因变量，建立回归模型。通过模型预测未来产品销量，为企业制定生产和销售计划提供依据。
实例三：疾病风险预测
总结词
基于个人健康数据和疾病历史，建立回归模型预测疾病风险。
详细描述
收集个人的健康数据和疾病历史，包括血压、血糖、胆固醇等生理指标以及家族病史等信息，作为自变量，将未来患某种疾病的风险作为因变量，建立回归模型。通过模型预测个人患某种疾病的风险，为预防和早期干预提供参考。
线性关系的假设
自变量x与因变量y之间存在线性关系，即随着x的增加（或减少），y也相应地增加（或减少）。
模型的建立和检验
01
02
03
数据收集与整理
收集相关数据，并进行必要的整理和清洗，以确保数据的质量和可靠性。

stata操作介绍之相关性分析(三)

4
用pwcorr命令实现所有变量的Pearson相关系数分析，并在显著性水平超过0.05的相关系数上打上星号，其命令为：
pwcorr , sig star(0.05)
5
2. Kendall T相关系数分析 Kendall T相关性分析是一个非参数度量变量间的相关性，其取值在一1和1之间。 Kendall T相关性分析的命令格式：
7
3. Spearman秩相关系数分析 Spearman秩相关性分析也是一种不依赖于总体分布的非参数检验，取值也在一1和1之间。 Spearman秩相关性分析的命令格式： spearman [varlist] [if] [in] [weight] [ ， spearman _ options ]
14
2.predict计算拟合值和残差指定存储类型的格式变量名
指定需要拟合值还是残差值，若为resid，则是残差
predict命令的格式: predict [type] newvar [if] [in][，single_ options]
8
用spearman命令实现所有变量的Spearman秩相关系数分析，并在显著性水平超过0.05的相关系数上打上星号，其命令为： spearman, star(0.05)
9
4.偏相关系数分析双变量相关分析是研究两个变量之间的相关关系，有时在分析两个变量之间相关关系时，往往会有其他变量的影响因素混合在里面，此时计算出来的相关系数可能并不能真正反映两个变量之间的关系。偏相关性分析的命令格式：
2
相关性分析
相关性分析主要目的是研究变量之间关系的密切程度。相关性分析的方法主要有:Pearson相关系数分析、Kendall T相关系数分析、Spearman秩相关系数分析以及偏相关系数分析。 1. Pearson相关系数分析

《2024年多元线性回归分析的实例研究》范文

《多元线性回归分析的实例研究》篇一一、引言多元线性回归分析是一种统计方法，用于研究多个变量之间的关系。

在社会科学、经济分析、医学等多个领域，这种分析方法的应用都十分重要。

本实例研究以一个具体的商业案例为例，展示了如何应用多元线性回归分析方法进行研究，以便深入理解和探索各个变量之间的潜在关系。

二、背景介绍以某电子商务公司的销售额预测为例。

电子商务公司销售量的影响因素很多，包括市场宣传、商品价格、消费者喜好等。

因此，本文通过收集多个因素的数据，使用多元线性回归分析，以期达到更准确的销售预测和因素分析。

三、数据收集与处理为了进行多元线性回归分析，我们首先需要收集相关数据。

在本例中，我们收集了以下几个关键变量的数据：销售额（因变量）、广告投入、商品价格、消费者年龄分布、消费者性别比例等。

这些数据来自电子商务公司的历史销售记录和调查问卷。

在收集到数据后，我们需要对数据进行清洗和处理。

这包括去除无效数据、处理缺失值、标准化处理等步骤。

经过处理后，我们可以得到一个干净且结构化的数据集，为后续的多元线性回归分析提供基础。

四、多元线性回归分析1. 模型建立根据所收集的数据和实际情况，我们建立了如下的多元线性回归模型：销售额= β0 + β1广告投入+ β2商品价格+ β3消费者年龄分布+ β4消费者性别比例+ ε其中，β0为常数项，β1、β2、β3和β4为回归系数，ε为误差项。

2. 模型参数估计通过使用统计软件进行多元线性回归分析，我们可以得到每个变量的回归系数和显著性水平等参数。

这些参数反映了各个变量对销售额的影响程度和方向。

3. 模型检验与优化为了检验模型的可靠性和准确性，我们需要对模型进行假设检验、R方检验和残差分析等步骤。

同时，我们还可以通过引入交互项、调整自变量等方式优化模型，提高预测精度。

五、结果分析与讨论1. 结果解读根据多元线性回归分析的结果，我们可以得到以下结论：广告投入、商品价格、消费者年龄分布和消费者性别比例均对销售额有显著影响。

简单线性相关与回归分析

临床科研设计和统计分析错误辨析与释疑简单线性相关与回归分析军事医学科学院生物医学统计咨询中心胡良平一、简单线性相关与回归分析常见错误概述两个变量之间进展简单线性相关与回归分析时，常见的错误有哪些？人们在研究两个变量之间的互相关系或依赖关系时经常运用简单线性相关分析与回归分析，然而，他们经常犯这样或那样的错误，导致结论的可信度低，有时，甚至得出绝对错误的结论来。

这方面常见的错误概括起来有如下几点：其一，脱离专业知识，盲目进展简单线性相关与回归分析；其二，对资料中因“过失误差〞造成的错误视而不见，盲目进展统计计算得出违犯专业知识的结论来；其三，将数据直接录入计算机，调用统计软件快速得出计算结果，作出结论；其四，对于仅在统计学上有意义的计算结果，盲目给出专业上的“肯定结论〞，但结论经不起理论的检验；其五，对于在专业上有联络且成对出现的变量〔X，Y〕，当二者中至少有一个为非随机变量时，也进展相关分析。

二、直线相关与回归分析常见错误案例与释疑脱离专业知识盲目进展统计分析，或者无视因过失误差造成的错误，将可能得出错误的结论。

1、脱离专业知识，盲目进展直线相关与回归分析例1：某人在北京郊区调查居民被狗咬伤的情况，结果显示：各年龄组中被狗咬伤的百分率是不同的，即：年龄由小到大，被狗咬伤的百分率依次为：很小、较小、较大、很大、较大、较小、很小、较大。

原作者的一个惊人的发现是：年龄与百分率之间的相关系数r=0.9956，P＜0.0001，因此拟合的直线回归方程也是有统计学意义的。

故原作者认为：在所调查的市郊，被狗咬者的年龄与被狗咬伤的百分率之间有很好的线性关系，可用此直线回归方程来预测该地任何一位居民被狗咬伤的概率，以便提醒人们外出时携带必要的防身器械，要倍加小心，尽可能减少被狗咬的时机。

对过失的辨析与释疑：这是一件多么荒唐可笑的事情啊！不会走的婴儿由大人抱在怀里，其被犬咬伤的发生率肯定很低；刚刚学会走路的小孩，通常都有大人在他们身边，因此，他们被犬咬伤的发生率比前者可能会高一点，但不会太高；只有那些整天到处乱跑，又没有很强抵御才能的3-6岁的孩子，被犬咬伤的时机最大；7-12岁的儿童，通常都有比拟强的抵御才能，因此，他们被犬咬伤的时机较前者会有所减少；依此类推，中青年被犬咬伤的发生率最低，上了年岁的老人，行动不便，他们被犬咬伤的发生率又会有所增大；而更老的体弱多病者整天呆在家中不出门，他们被犬咬伤的发生率几乎为零。

什么是回归分析？

03
回归分析的基本步骤
数据收集
明确研究问题
在开展回归分析前，需要明确研究的问题和目标，从而确定需要收集哪些数据。
制定数据采集计划
根据研究问题制定合理的数据采集计划，包括从何种渠道收集数据、如何收集数据等。
收集数据
根据制定的计划进行数据收集，确保数据准确、完整、可靠。
数据清洗与整理
数据清洗
选择合适的模型
根据数据的分布和特点选择合适的回归模型，例如线性回归、岭回归、Lasso回归等。
建立模型
利用所选择的模型进行拟合，生成回归方程或算法。
模型评估与优化
评估模型性能
使用适当的指标评估模型的性能，例如均方误差（MSE）、均方根误差（ RMSE）、R方值（R-squared）等。
优化模型
根据评估结果对模型进行优化，例如调整模型参数、增加变量等。
需要对自变量和因变量的关系进行合理的假设和限制，否则会导致模型失真和误导。
数据质量影响结果
回归分析的准确性取决于数据的质量和完整性。如果数据存在缺失、异常值、错误或测量误差等问题，会影响回归结果的可信度和准确性。
数据的质量和完整性也会影响回归模型的稳定性和可解释性，进而影响预测的准确性和可靠性。
删除重复、异常和缺失数据，处理不准确或不一致的数据，以减少数据中的噪声和误差。
数据整理
对数据进行必要的转换和整理，以便后续分析和建模。例如，将数据统一转换为数值型或字符型，将时间序列数据进行对齐或标准化等。
模型选择与建立
确定自变量和因变量
根据研究问题确定自变量和因变量，确保变量选取合理且具有代表性。
2023
什么是回归分析？
汇报人：
contents

(整理)回归分析应用实例讲解

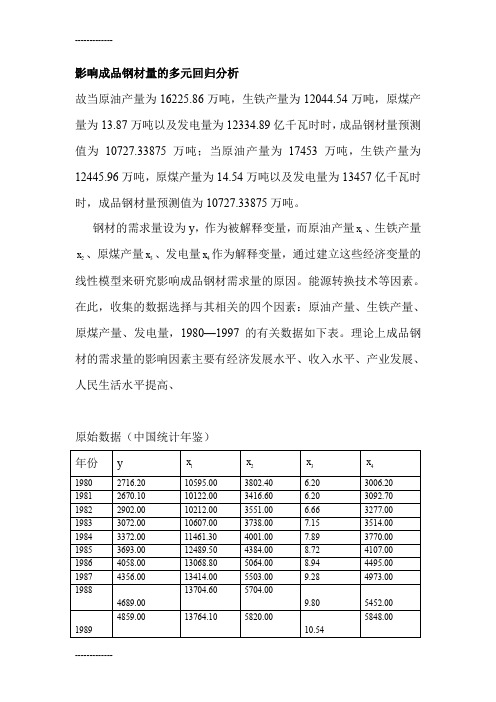
影响成品钢材量的多元回归分析故当原油产量为16225.86万吨，生铁产量为12044.54万吨，原煤产量为13.87万吨以及发电量为12334.89亿千瓦时时，成品钢材量预测值为10727.33875万吨；当原油产量为17453万吨，生铁产量为12445.96万吨，原煤产量为14.54万吨以及发电量为13457亿千瓦时时，成品钢材量预测值为10727.33875万吨。

钢材的需求量设为y，作为被解释变量，而原油产量x、生铁产量1x、原煤产量3x、发电量4x作为解释变量，通过建立这些经济变量的2线性模型来研究影响成品钢材需求量的原因。

能源转换技术等因素。

在此，收集的数据选择与其相关的四个因素：原油产量、生铁产量、原煤产量、发电量，1980—1997的有关数据如下表。

理论上成品钢材的需求量的影响因素主要有经济发展水平、收入水平、产业发展、人民生活水平提高、原始数据（中国统计年鉴）将中国成品一、模型的设定设因变量y 与自变量1x 、2x 、3x 、4x 的一般线性回归模型为:y = 0β+11223344x x x x ββββε++++ε是随机变量，通常满足()0εE =；Var(ε)=2σ二参数估计再用spss 做回归线性，根据系数表得出回归方程为：1234170.2870.0410.55417.8180.389y x x x x =-+-+ 再做回归预测，得出如下截图：故当原油产量为16225.86万吨，生铁产量为12044.54万吨，原煤产量为13.87万吨以及发电量为12334.89亿千瓦时时，成品钢材量预测值为10727.33875万吨；当原油产量为17453万吨，生铁产量为12445.96万吨，原煤产量为14.54万吨以及发电量为13457亿千瓦时时，成品钢材量预测值为10727.33875万吨。

三回归方程检验由相关系数表看出，因变量与各个自变量的相关系数都很高，都在0.9 以上，说明变量间的线性相关程度很高，适合做多元线性回归模型。

相关系数与回归系数的区别与联系

相关系数与回归系数的区别与联系一、引言在统计学中，相关系数与回归系数是两个非常重要的概念。

相关系数（r）是用来衡量两个变量之间线性关系强度的指标，而回归系数（β）则是用来表示自变量对因变量影响的程度。

尽管两者都与线性关系有关，但在实际应用中，它们有着明显的区别。

本文将阐述这两者的概念、计算方法以及它们在统计分析中的联系与区别。

二、相关系数的定义与计算1.相关系数的定义相关系数（r）是一个介于-1和1之间的数值，它反映了两个变量之间线性关系的强度和方向。

相关系数的绝对值越接近1，表示两个变量之间的线性关系越强；接近0时，表示两个变量之间几乎不存在线性关系。

2.相关系数的计算方法相关系数的计算公式为：r = ∑((x_i-平均x)*(y_i-平均y)) / (√∑(x_i-平均x)^2 * ∑(y_i-平均y)^2) 其中，x_i和y_i分别为变量X和Y的第i个观测值，平均x和平均y分别为X和Y的平均值。

三、回归系数的定义与计算1.回归系数的定义回归系数（β）是指在线性回归分析中，自变量每变动一个单位时，因变量相应变动的量。

回归系数可用于预测因变量值，从而揭示自变量与因变量之间的线性关系。

2.回归系数的计算方法回归系数的计算公式为：β= ∑((x_i-平均x)*(y_i-平均y)) / ∑(x_i-平均x)^2其中，x_i和y_i分别为变量X和Y的第i个观测值，平均x和平均y分别为X和Y的平均值。

四、相关系数与回归系数的关系1.两者在统计分析中的作用相关系数和回归系数都是在统计分析中衡量线性关系的重要指标。

相关系数用于衡量两个变量之间的线性关系强度，而回归系数则用于确定自变量对因变量的影响程度。

2.两者在实际应用中的区别与联系在实际应用中，相关系数和回归系数往往相互关联。

例如，在进行线性回归分析时，回归系数β就是相关系数r在X轴上的投影。

而相关系数r则可以看作是回归系数β的平方。

因此，在实际分析中，我们可以通过相关系数来初步判断两个变量之间的线性关系，进而利用回归系数进行更为精确的预测。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

相关分析与回归分析实例(总15页)
--本页仅作为文档封面，使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
相关与回归分析法探究实例
——上海市城市居民家庭人均可支配收入与
储蓄存款关系的统计分析
系别经济系
专业金融学
学号
姓名
指导教师
2011年1月1日
上海市城市居民家庭人均可支配收入与储蓄存款关系的统计分析
摘要：随着中国经济的迅速发展，我国居民的消费水平不断提高，居民储蓄存款作为消费支出的重要组成部分，直接关系到国家对资金的合理使用。

本文采用相关分析与回归分析方法，对上海市居民家庭人均可支配收入与储蓄存款进行了定量地分析，探求了二者之间的关系。

所得结论对研究中国居民储蓄行为的规律具有一定的参考价值。

关键词：居民家庭人均可支配收入，储蓄存款，相关分析，回归分析
自经济体制改革以后，我国国民收入分配的格局发生巨大变化。

变化之一是居民收入在国民收入中的比重迅速提高。

这使居民的消费和储蓄行为对于经济发展有越来越重要的意义。

居民储蓄存款是社会总储蓄的重要组成部分，也是推动经济增长的重要资源。

居民储蓄的快速增长，是我国经济发展的重要资金来源，是改革开放顺利进行的重要保证。

过度储蓄构成经济的一种潜在威胁甚至现实扭曲，它的负面影响也不容忽视。

为了了解我国居民储蓄的现状，认真分析影响居民储蓄变动的主要因素——居民家庭人均可支配收入，本文采用了多元统计中的相关分析及回归方法，借助于SPSS，对1997—2009年上海市城市居民家庭人均可支配收入与储蓄存款进行了分析和评价。

1.选择指标，收集数据资料
西方经济学通行的储蓄概念是，储蓄是货币收入中没有用于消费的部分。

这种储蓄不仅包括个人储蓄，还包公公司储蓄、政府储蓄。

储蓄的内容有在银行的存款、购买的有价证券及手持现金等。

在其他条件不变的情况下，个人可支配收入与居民储蓄是正比例函数关系，是居民储蓄存款增长的基本因素。

本文遵循了可比性、可操作性等原则，指标记为年份分别为a1,a2,a3,……,a11,a12,a13;人均可支配收入分别为b1,b2,b3,……,b11,b12,b13;居民储蓄存款分别为c1,c2,c3,……,c11,c12,c13。

本文研究所分析的数据资料来源于上海统计网——上海统计年鉴2010目录。

表主要年份城市居民家庭人均可支配收入
单位：元
1997 8 439 5 969 150 69 2 251
1998 8 773 6 004 98 57 2 614
1999 10 932 7 326 156 68 3 382
2000 11 718 7 832 120 65 3 701
2001 12 883 7 975 119 39 4 750
2002 13 250 7 915 436 94 4 805
2003 14 867 10 097 377 130 4 263
2004 16 683 11 422 507 215 4 539
2005 18 645 12 409 798 292 5 146
2006 20 668 13 962 959 300 5 447
2007 23 623 16 598 1 158 369 5 498
2008 26 675 18 909 1 399 369 5 998
2009 28 838 19 811 1 435 474 7 118
注：本表数据为城市居民家庭收支抽样调查资料，由国家统计局上海调查总队提供。

表居民储蓄存款（1997～2009）
年份居民储蓄存款其中人均储蓄存款（亿元）定期储蓄活期储蓄（元）
1997 2 1 14 169
1998 2 2 15 536
1999 2 2 16 572
2000 2 2 16 331
2001 3 2 19 264
2002 4 3 1 30 245
2003 6 4 1 35 385
2004 6 4 2 39 956
2005 8 6 2 47 416
2006 9 6 2 52 231
2007 9 6 3 50 194
2008 12 8 3 63 987
2009 14 9 4 75 373
注：本表数据由中国人民银行上海总部提供。

2000年起居民储蓄存款为中外资金融机构本外币存款余额。

⒉数据的分析与计算结果
（1）调用SPSS的绘制条形图功能，得到的居民储蓄存款与人均可支配收入的条形图如下
（2）调用SPSS的绘制线形图功能，得到的居民储蓄存款与人均可支配收入的线形图如下
（3）调用SPSS的绘制散点图功能，得到的居民储蓄存款与人均可支配收入的散点图如下
（4）进一步调用SPSS中的相关分析功能，得到得到的居民储蓄存款与人均可支配收入的相关系数及显著性检验输出结果如下
Correlations
居民储蓄存款人均可支配收入
居民储蓄存款Pearson Correlation1.982**
Sig. (2-tailed).000
Sum of Squares and Cross-
products
Covariance
N1313
人均可支配收入Pearson Correlation.982**1
Sig. (2-tailed).000
Sum of Squares and Cross-
products
Covariance
N1313
**. Correlation is significant at the level (2-tailed).
相关分析能够有效地揭示事物之间关系强弱程度。

当显著性水平α为时，认为两者之间存在显著的线性关系，并且呈正相关。

（5）运用SPSS的线性回归分析功能，对居民储蓄存款与人均可支配收入进行回归分析，分析结果如下
Model Summary b
Model R R Square Adjusted R
Square
Std. Error of
the Estimate Durbin-Watson
1.982a.964.961
a. Predictors: (Constant), 人均可支配收入
b. Dependent Variable: 居民储蓄存款
由模型拟合程度可知，人均可支配收入与居民存款储蓄的相关系数是R=，判决系数是R²=，修正的判决系数为，估计标准误差σ=。

可见，模型的拟合程度很理想。

由方差分析表可知，回归平方和为，自由度为1，均方差为；剩余平方和为，自由度为8，均方差为，自由度为9；F统计量的值为，单边检验概率值为P=＜α=，说明回归方程高度显著。

由表回归方程系数表可知，未标准化回归方程的常数项为，标准误差为；回归系数为，标准误差为；由此得出一元线性回归方程为Y=+。

标准化回归方程的回归系数（Beta）为，回归方程标准化后没有常数项。

回归系数检验的t统计量的值为，显著性概率p=＜α=，说明回归系数是特别显著的，也就是说，人均可支配收入与居民存款储蓄的影响特别显著。

（6）运用SPSS的指数曲线回归分析的结果为Linear
Logarithmic
Inverse
Quadratic
Cubic
Compound
Power
Growth
Exponential
Logistic
Coefficients
Unstandardized Coefficients Standardized
Coefficients
t Sig.
B Std. Error Beta
人均可支配收入.000.387.000 (Constant).001.000.000 The dependent variable is ln(1 / 居民储蓄存款).
结合各项结果来看，实际观测点与幂曲线的拟合效果最好，如图所示
3.综合结论
通过运用相关分析与回归分析方法对上海市城市居民人均可支配收入与居民存款储蓄的分析，表明了人均可支配收入与居民存款储蓄之间的正相关关系。

正是由于近年来我国居民收入的大幅度增长为居民储蓄存款的增长提供了坚实的经济基础，即居民收入的增加是我国居民储蓄增加的根本原因。

从上文可以看出1997—2009年以来我国上海城市居民可支配收入是逐年增加的。

在改革开放以前，居民的平均收入水平很低，绝大多数收入都用于基本生活品的开支需要，几乎没有储蓄。

随着经济的发展，城乡居民的人均收入增加比较快，居民收入水平的提高使居民在满足基本生活开支之后有了较多的节余，因而储蓄随之增加。

由于近年来我国居民收入的大幅度增长为居民储蓄存款的增长提供了坚实的经济基础，所以居民人均收入的增加是我国居民储蓄增加的根本原因。