2020高考数学(理)三轮复习每日一卷试题(无答案) (11)
2020高考数学 三轮冲刺 解答题专练--解三角形 三(10题含答案)

2020高考数学 三轮冲刺 解答题专练--解三角形 三1.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c.已知cosA=32,sinB=5cosC. (1)求tanC 的值;(2)若a=2,求△ABC 的面积.2.已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且满足:cos 2B -cos 2C -sin 2A=sin Asin B. (1)求角C ;(2)若c=26,△ABC 的中线CD=2,求△ABC 的面积S 的值.3.在△ABC 中,边a,b,c分别是内角A,B,C所对的边,且满足,设B的最大值为B0.(Ⅰ)求B0的值;(Ⅱ)当B=B0,a=1,c=3,D为AC的中点时,求BD的长.4.在中,内角A,B,C所对的边分别为a,b,c,.(1)若,求c的值;(2)若,求的面积.5.在△ABC中,已知.(1)求的长;(2)求的值.6.在△ABC中,a,b,c分别是角A,B,C的对边, =,且a+c=2.(1)求角B;(2)求边长b的最小值.7.在△ABC中,,.(1)求边的长;(2)求角C的大小。
8.设△ABC的内角A,B,C的对边分别为a,b,c,a=btanA,且B为钝角.(1)证明:B-A=;(2)求sin A+sin C的取值范围.9.已知函数.(I)f(x)的最小正周期;(II)求证:当时,.10.在△ABC中,a,b,c分别是角A,B,C的对边,已知3(b2+c2)=3a2+2bc.(Ⅰ)若,求tanC的大小;(Ⅱ)若a=2,△ABC的面积,且b>c,求b,c.答案解析1.解:2.解:(1)由已知得sin 2A +sin 2B -sin 2C=-sin Asin B ,由正弦定理得a 2+b 2-c 2=-ab ,由余弦定理可得cos C=a 2+b 2-c 22ab =-12.∵0<C<π,∴C=2π3.(2)法一:由|CD ―→ |=12|CA ―→+CB ―→|=2,可得CA ―→2+CB ―→ 2+2CA ―→·CB ―→=16,即a 2+b 2-ab=16,又由余弦定理得a 2+b 2+ab=24,∴ab=4.∴S=12absin ∠ACB=34ab= 3.法二:延长CD 到M ,使CD=DM ,连接AM ,易证△BCD≌△AMD,∴BC=AM=a ,∠CBD=∠MAD ,∴∠CAM=π3.由余弦定理得⎩⎪⎨⎪⎧a 2+b 2+ab =24,a 2+b 2-ab =16,∴ab=4,S=12absin ∠ACB=12×4×32= 3.3.4.5.(1)(2)6.7.8.9.10.。
2020年高考数学第三轮强化训练试卷(四)

2020年高考数学第三轮强化训练试卷(四)本试卷分第I 卷(选择题)和II 卷(非选择题)两部分,满分150分,考试时间120分钟。
一、选择题(本大题共12小题,每小题5分,共60分)下列四个选项中,只有一个是符合题目要求的。
. 1.在复平面内,复数2)1(1i i-+对应的点位于 ( )A .第一象限B . 第二象限C . 第三象限D . 第四象限2.已知:M={1,2,3},N={4,5},P={m |m ⊆M},Q={n |n ⊆N},则P ⋂Q 是( )A :{φ}B :φC :{1,2,3,4,5}D :{4,5}3.若 a 与 b -c 都是非零向量,则“a ·b=a ·c ”是“a ⊥(b -c )”的 ( )A 充分而不必要条件B 必要而不充分条件C 充分必要条件D 既不充分也不必要条件 4.已知条件p:x ≤1,条件,q :x1<1,则⌝p 是q 的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .即非充分也非必要条件5.若函数f (x )=sin ax +cos ax (a >0)的最小正周期为1,则它的图像的一个对称中心为( )A .(-8π,0) B .(0,0) C .(-81,0) D .(81,0) 6.若n xx )13(-的展开式各项系数和为64,则展开式中的常数项为 ( )A .-540B .-162C .162D .5407.已知函数f (x )=2x 的反函数f -1(x )满足f -1(a )+ f -1(b)=4,则b a 11+的最小值为 ( )A .1B .31 C .21 D .418.(文)在等比数列{}n a 中,则7a ·11a =6,4145a a +=,则2010a a = ( ) A.23 B. 23或32 C. 32 D.23-或32- (理)若{}n a 是等比数列,其中37,a a 是方程22350x kx -+=的两根,且23728()41a a a a +=+,则k 的值为 ( )A.2113-B. 23±11C. 2113D.839.已知函数32()1f x x ax =-+在区间(0,2)内单调递减,则实数a 的取值范围是( )A.3a = B. 3a ≥ C. 3a ≤ D. 03a <<10.过抛物线24y x =的焦作一条直线与抛物线相交于A 、B 两点,且5AB =,则这样的直线有 ( ) A.一条 B.两条 C.三条 D.不存在 11.设偶函数f(x)=log a |a+b|在(0,+∞)上单调递增,则f(b -2)与f(a+1)的大小关系是( ) A .f(b -2)=f(a+1) B .f(b -2)>f(a+1) C .f(b -2)<f(a+1) D .不能确定12.如图所示,在正三棱锥S —ABC 中(底面是正多边形,顶点在底面上的射影是底面的中心的棱锥为正棱锥) M 、N 分别是棱SC ,BC 的中点,且MN ⊥AM ,若侧棱SA=23,则此正三棱锥S —ABC 外接球的 表面积是( ) A .45π B .32πC .12πD .36π第Ⅱ卷(非选择题 共90分)注意事项:1.第Ⅱ卷用钢笔或圆珠笔直接答在试题卷中(除题目有特殊规定外)。
2020高考数学 三轮冲刺 解答题专练--立体几何 三(10题含答案)
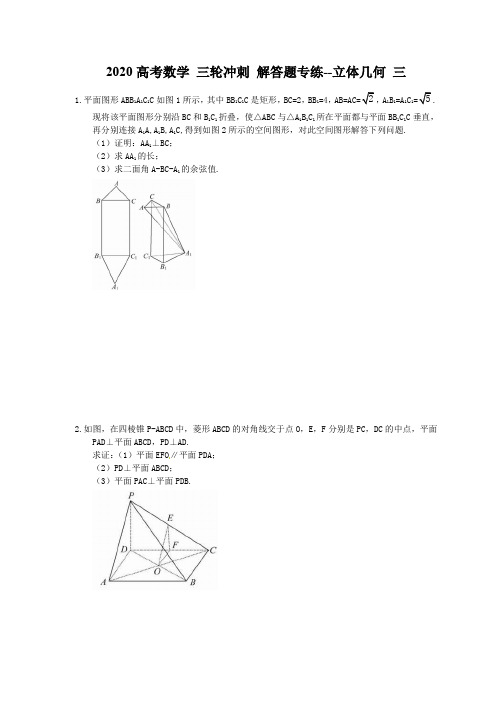
2020高考数学三轮冲刺解答题专练--立体几何三1.平面图形ABB1A1C1C如图1所示,其中BB1C1C是矩形,BC=2,BB1=4,A1B1=A1C1.现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A1A,A1B,A1C,得到如图2所示的空间图形,对此空间图形解答下列问题.(1)证明:AA1⊥BC;(2)求AA1的长;(3)求二面角A-BC-A1的余弦值.2.如图,在四棱锥P-ABCD中,菱形ABCD的对角线交于点O,E,F分别是PC,DC的中点,平面PAD⊥平面ABCD,PD⊥AD.求证:(1)平面EFO∥平面PDA;(2)PD⊥平面ABCD;(3)平面PAC⊥平面PDB.3.如图,在四棱锥中,平面,,,,,,.(I)求异面直线与所成角的余弦值;(II)求证:平面;(Ⅲ)求直线与平面所成角的正弦值.4.如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.点E是CD边的中点,点F\G分别在线段AB,BC上,且AF=2F,CG=2GB。
(1)证明:PE⊥FG;(2)求二面角P-AD-C的正切值;(3)求直线PA与直线FG所成角的余弦值.5.如图所示,在多面体AB1D1DCBA,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,1过A1,D,E的平面交CD1于F.(1)证明:EF//B1C;(2)求二面角E-A1D-B1余弦值.6.如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF//BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.(1) 求证:AO⊥BE;(2) 求二面角F-AE-B的余弦值;(3) 若BE⊥平面AOC,求a的值.7.如图,四棱锥P-ABCD中,PA⊥地面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明MN∥平面PAB;(2)求直线AN与平面PMN所成角的正弦值..8.如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF=1.25,EF交BD于点H.将△DEF沿EF折到△的位置,.(I)证明:平面ABCD;(II)求二面角的正弦值.9.如图,在已A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,,且二面角D-AF-E与二面角C-BE-F都是60°.(I)证明平面ABEF EFDC;(II)求二面角E-BC-A的余弦值.10.如图,在四棱锥P-ABCD中,AD∥BC,ADC=PAB=90°,BC=CD=AD. E为边AD的中点,异面直线PA与CD所成的角为90°.(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.答案解析1.【解题指南】(1)通过线线垂直证明线面垂直进而得到线线垂直;(2)构造Rt△AA1D,在△AA1D中求AA1;(3)先找到平面角,然后在三角形中求出.【解析】(1)取BC,B1C1的中点为点O,O1,连接AO,OO1,A1O,A1O1,则由AB=AC知AO⊥BC,由面ABC⊥面BB1C1C可知AO⊥面BB1C1C;同理,A1O1⊥面BB1C1C,由此可得AO∥A1O1,即A,O,A1,O1共面.又OO1⊥BC,OO1∩AO=O,则BC⊥面AOA1O1,所以AA1⊥BC;(2)延长A1O1到D,使O1D=OA,则O1D OA,AD OO1;OO1⊥BC,面A1B1C1⊥面BB1C1C,则OO1⊥面A1B1C1,AD⊥面A1B1C1,在Rt△AA1D中,===1AA5;(3)因为AO⊥BC,A1O⊥BC,则∠AOA1是二面角A-BC-A1的平面角.在Rt△OO1A1中,1A O===在Rt△OAA1中,2221111AO A O AAcos AOA,2AO A O5+-∠==-⨯所以二面角A-BC-A1的余弦值为5-.2.【证明】(1)∵ABCD是菱形,∴O是AC的中点.∵E,F分别是PC,DC的中点,∴EF∥PD.又EF平面PAD,PD平面PAD,∴EF∥平面PDA,同理FO∥平面PAD.而FO∩EF=F,EF,FO平面EFO,∴平面EFO∥平面PDA.(2)∵平面PAD⊥平面ABCD,PD⊥AD,平面PAD∩平面ABCD=AD,PD平面PAD,∴PD⊥平面ABCD.(3)∵PD⊥平面ABCD,AC平面ABCD,∴AC⊥PD.∵四边形ABCD是菱形,∴AC⊥BD,又PD∩DB=D,PD,DB平面PBD.∴AC⊥平面PBD.∵AC平面PAC,∴平面PAC⊥平面PDB.3.4.5.6.7.答案略;8.9.10.。
2020—2021年最新高考总复习数学(理)三轮复习模拟试题及答案解析四.docx

2018年高考数学三模试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1.设集合A={x|1≤x≤5},B={x|log2x<2},则A∪B等于()A.(﹣1,5] B.[1,4)C.(0,5] D.[﹣1,4)2.若复数z=cos θ﹣+(﹣sinθ)i(i是虚数单位)是纯虚数,则tanθ的值为()A .﹣B .C .﹣D .±3.已知函数f(x)=,则f(f(2))等于()A.0 B.4 C .﹣D .4.根据如下样本数据,得到回归方程=bx+a,则()x 3 4 5 6 7 8y 4.2.5﹣0.50.5﹣2.0﹣3.0A.a>0,b>0 B.a>0,b<0 C.a<0,b>0 D.a<0,b<0 5.若[x]表示不超过x的最大整数,执行如图所示的程序框图,则输出S的值为()A.3 B.5 C.7 D.106.某几何体的三视图如图所示.则该几何体的体积等于()A.B.2 C.D.37.在等差数列{a n}中,a3+a6=a4+5,且a2不大于1,则a8的取值范围是()A.(﹣∞,9] B.[9,+∞)C.(﹣∞,9) D.(9,+∞)8.已知sinφ=,且φ∈(,π),函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于,则f()的值为()A.B.﹣C.D.﹣9.如图,在三棱柱ABC﹣A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=CC1,则异面直线A1E与AF所成角的余弦值为()A.B.C.D.10.如图所示,已知||=1,||=,=0,点C在线段AB 上,且∠AOC=30°,设=m+n(m,n∈R),则m﹣n等于()A.B.C.﹣D.﹣11.已知双曲线C:﹣=1(a>0,b>0)的左焦点为F,若点F关于双曲线的渐近线的对称点在双曲线的右支上,则该双曲线的离心率是()A. B. C.2 D.12.若存在两个正实数x,y,使得x+a(y﹣2ex)(lny﹣lnx)=0成立,其中e为自然对数的底数,则实数a的取值范围是()A.(﹣∞,0)∪[,+∞) B.(0,] C.[,+∞)D.(﹣∞,0)二、填空题:本大题共4小题。
2020年高考数学第三轮强化训练试卷(二)

2020年高考数学第三轮强化训练试卷(二)本试卷分第I 卷(选择题)和II 卷(非选择题)两部分,满分150分,考试时间120分钟。
一、选择题(本大题共12小题,每小题5分,共60分)下列四个选项中,只有一个是符合题目要求的。
.1.如果复数2()(1)a i ai ++是实数,则实数a = ( )A .1B .-1C .2D .2-2.下列四个函数中,在(0,1)上为增函数的是 ( )A .100log y x =-B .1()100xy = C . x y sin = D .x y arccos =3.已知0>>b a ,全集=I R ,集合}2|{ba xb x M +<<=,}|{a x ab x N <<=, =P {x b x <|≤ab },则P 与N M ,的关系为 ( )A )(N C M p I I =B N MC p I I )(= C N M P I = D. N M P Y = 4.在π20≤≤x 范围内,方程|sin |(sin cos 2cos x x x x +=)的解的个数是 ( )A .1个B .2个C .3个D .4个5.在空间四边形ABCD 各边上分别取E 、F 、G 、H 四点,如果EF 和GH 能相交于点P ,那么: ( ) A 点P 必在直线AC 上 B 点P 必在直线BD 上 C 点P 必在平面ABC 内 D 点P 必在平面上ABC 外6.某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样,分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…270;使用系统抽样时,将学生统一随机编号为1,2,…270,并将整个编号依次分为10段,如果抽得号码有下列四种情况:①7,34,61,88,115,142,169,196,223,250, ②5,9,100,107,111,121,180,195,200,265; ③11,38,65,92,119,146,173,200,227,254; ④30,57,84,111,138,165,192,219,246,270; 关于上述样本的下列结论中,正确的是( )A.②、③都有不能为系统抽样B. ②、④ 都有不能为分层抽样C. ①、④可能为系统抽样D. ①、③可能为分层抽样 7.已知正数数列{a n }中,a 1=3,且对于任意大于1的整数n ,点),(1-n n a a 总在直线 2)1(lim03+=--∞→n a y x nn 上,则=( )A .0B .1C .2D .38若圆),(110122222a a C x y y x y ax y x --==+=++-+对称,过点关于直线和圆 的圆P 与y 轴相切,则圆心P 的轨迹方程是 ( )A .08442=++-y x y B .02222=+-+y x yC .08442=+-+y x yD .0122=+--y x y9.已知a x cx x x =-++→22lim 22,且函数c xb x a y ++=2ln 在1[,]e 上存在反函数,则 ( ) A .]0,(-∞∈bB ]0,(-∞∈b ∪),2[+∞eC .),2[+∞∈e bD .]2,0[e b ∈10.若)()14(*N n x n∈-的展开式中各项系数的和为729,则展开式中x 3项的系数是( ) A .-64 B .-1280 C .20 D .128011.在实数的原有运算法则中,我们补充定义新运算“⊕”如下: 当a b ≥时,a b a ⊕=; 当a b <时,a b b ⊕=2。
2020高考数学三轮冲刺抢分练仿真卷(一)

(浙江专用)2020高考数学三轮冲刺抢分练仿真卷(一)一、选择题(本大题共10小题,每小题4分,共40分)1.已知集合A={x|x2<1},集合B={x|log2x<0},则A∩B等于( ) A.(0,1) B.(-1,0) C.(-1,1)D.(-∞,1)答案A解析根据题意集合A={x|-1<x〈1},集合B={x|0<x<1},∴A∩B=(0,1).2.在平面直角坐标系中,经过点P(2错误!,-错误!),渐近线方程为y =±错误!x的双曲线的标准方程为()A。
错误!-错误!=1 B。
错误!-错误!=1C.错误!-错误!=1D.错误!-错误!=1答案B解析∵双曲线的渐近线方程为y=±错误!x,∴设所求双曲线的标准方程为2x2-y2=k.又错误!在双曲线上,则k=16-2=14,即双曲线的方程为2x2-y2=14,∴双曲线的标准方程为错误!-错误!=1。
3.设变量x,y满足约束条件错误!则目标函数z=2x+y的最大值是( )A.2 B.3 C.5 D.7答案C解析画出约束条件错误!表示的可行域,如图中阴影部分(含边界)所示,由错误!可得错误!将z=2x+y变形为y=-2x+z,平移直线y=-2x+z,由图可知当直线y=-2x+z经过点(3,-1)时,直线在y轴上的截距最大,即z最大,z的最大值为z=2×3-1=5.4.若复数z1=2+i,z2=cos α+isin α(α∈R),其中i是虚数单位,则|z1-z2|的最大值为A。
错误!-1 B。
错误! C.错误!+1 D。
错误!答案C解析方法一由题可得z1-z2=2+i-cos α-isin α=2-cos α+(1-sin α)i(α∈R),则|z1-z2|=2-cos α2+1-sin α2=错误!=错误!=错误!=6-25sinα+φ,其中tan φ=2,当sin(α+φ)=-1时,|z1-z2|有最大值,此时|z1-z2|=错误!=错误!+1。
【通用版】2020高考数学(三轮复习)冲刺专题《数列大题部分》(含答案)
专题 数列大题部分【训练目标】1、 理解并会运用数列的函数特性;2、 掌握等差数列,等比数列的通项公式,求和公式及性质;3、 掌握根据递推公式求通项公式的方法;4、 掌握常用的求和方法;5、 掌握数列中简单的放缩法证明不等式。
【温馨小提示】高考中一般有一道小题,一道大题,小题侧重于考等差数列与等比数列的性质,熟练的灵活的使用数列的性质会大大减少计算量;大题则侧重于考查根据递推公式求通项公式,求和的方法。
总之,此类题目难度中等,属于必拿分题。
【名校试题荟萃】1、(宁夏长庆高级中学2019届高三上学期第四次月考数学(理)试卷)设数列{}n a 的前n 项和,且123,1,a a a +成等差数列. (1)求数列{}n a 的通项公式;(2)记数列1{}na 的前n 项和n T ,求使得成立的n 的最小值.【答案】(1)2nn a = (2)10(2)由(1)可得112nn a ⎛⎫= ⎪⎝⎭,所以,由,即21000n>,因为,所以10n ≥,于是使得成立的n 的最小值为10.2、(宁夏长庆高级中学2019届高三上学期第四次月考数学(理)试卷)设等差数列{}n a 的公差为d ,点(,)n n a b 在函数()2x f x =的图象上(*n N ∈)。
(1)若12a =-,点87(,4)a b 在函数()f x 的图象上,求数列{}n a 的前n 项和n S ; (2)若11a =,函数()f x 的图象在点22(,)a b 处的切线在x 轴上的截距为12ln 2-,求数列{}n na b 的前n 项和n T .【答案】(1) (2)(2)由函数()f x 的图象在点22(,)a b 处的切线方程为所以切线在x 轴上的截距为21ln 2a -,从而,故22a =从而n a n =,2n n b =,2n nn a nb =所以故。
3、(辽宁省辽河油田第二高级中学2019届高三上学期期中考试数学(文)试题)设n S 为数列{}n a 的前项和,已知10a ≠,,n *∈N .(1)求1a ,2a ;(2)求数列{}n a 的通项公式; (3)求数列{}n na 的前n 项和. 【答案】(1)1,2 (2)12-=n n a (3)(3)由(2)知12-=n n n na ,记其前n 项和为n T ,于是① ②①-②得从而.4、(湖南省浏阳一中、株洲二中等湘东六校2019届高三12月联考数学(理)试题)已知数列}{n a 的前n 项和n S 满足,且11=a 。
2020版高考数学三轮复习小题专题练(一)集合、常用逻辑用语、不等式、函数与导数文苏教版(最新整理
(江苏专用)2020版高考数学三轮复习小题专题练(一)集合、常用逻辑用语、不等式、函数与导数文苏教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((江苏专用)2020版高考数学三轮复习小题专题练(一)集合、常用逻辑用语、不等式、函数与导数文苏教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(江苏专用)2020版高考数学三轮复习小题专题练(一)集合、常用逻辑用语、不等式、函数与导数文苏教版的全部内容。
小题专题练(一)集合、常用逻辑用语、不等式、函数与导数(建议用时:50分钟)1.已知集合A={x|(x+1)(x-2)〉0},B={x|-1≤x-1≤1},则A∩(∁R B)=________.2.(2019·苏州模拟)函数f(x)=错误!的定义域为________.3.已知a>0,b>0,且满足3a+b=a2+ab,则2a+b的最小值为________.4.(2019·南通调研)函数f(x)=lg x2的单调递减区间是________.5.若f(x)=ln(e3x+1)+ax是偶函数,则a=________.6.(2019·泰州期末)曲线y=2ln x在点(e,2)处的切线(e是自然对数的底数)与y轴交点的坐标为________.7.已知命题p:方程x2-2ax-1=0有两个实数根;命题q:函数f(x)=x+错误!的最小值为4.给出下列命题:①p∧q;②p∨q;③p∧(綈q);④(綈p)∨(綈q).其中是真命题的为________.(把所有正确命题的序号都填上)8.已知x,y满足约束条件错误!则z=2x+y的最大值为________.9.(2019·苏北四市联考)点P是曲线y=x2-ln x上任意一点,则P到直线y=x-2的距离的最小值是________.10.若关于x的不等式(2ax-1)ln x≥0对任意的x>0恒成立,则实数a的取值范围是________.11.设二次函数f(x)=ax2+bx+c(a,b,c为常数)的导函数为f′(x).对任意x∈R,不等式f(x)≥f′(x)恒成立,则错误!的最大值为________.12.已知定义在R上的偶函数f(x)满足f(x-4)=f(x),且在区间[0,2]上f(x)=x,若关于x的方程f(x)=log a x有三个不同的根,则a的取值范围为________.13.(2019·常州模拟)已知函数f(x)=x2e x,若f(x)在[t,t+1]上不单调,则实数t的取值范围是________.14.a为实数,函数f(x)=|x2-ax|在区间[0,1]上的最大值记为g(a).当a=________时,g(a)的值最小.小题专题练(一)1.解析:A={x|(x+1)(x-2)>0}={x|x〈-1或x〉2}.因为B={x|-1≤x-1≤1},所以B={x|0≤x≤2},所以∁R B={x|x〈0或x>2},所以A∩(∁R B)={x|x<-1或x〉2}.答案:{x|x〈-1或x>2}2.解析:若函数f(x)有意义,则错误!所以log2x>1,所以x>2.答案:(2,+∞)3.解析:因为a>0,b>0,且满足3a+b=a2+ab,所以b=错误!>0,解得1<a<3,则2a+b=2a+错误!=a-1+错误!+3≥2错误!+3=2错误!+3,当且仅当a=1+错误!,b=1时取等号.答案:3+2错误!4.解析:函数f(x)=lg x2的单调递减区间需满足x2〉0且y=x2单调递减,故x∈(-∞,0).答案:(-∞,0)5.解析:由偶函数的定义可得f(-x)=f(x),即ln (e-3x+1)-ax=ln(e3x+1)+ax,所以2ax=-ln e3x=-3x,所以a=-错误!.答案:-错误!6.解析:由曲线y=2ln x得y′=错误!,所以k=错误!,所以点(e,2)处的切线方程为y-2=错误!(x-e),令x=0得y=0,所以曲线y=2ln x在点(e,2)处的切线与y轴交点的坐标为(0,0).答案:(0,0)7.解析:因为Δ=(-2a)2-4×(-1)=4a2+4〉0,所以方程x2-2ax-1=0有两个实数根,所以命题p是真命题;当x〈0时,函数f(x)=x+错误!的取值为负值,所以命题q 为假命题,所以p∨q,p∧(綈q),(綈p)∨(綈q)是真命题.答案:②③④8.解析:x,y满足的平面区域如图阴影部分所示,根据阴影部分可得,当直线z=2x+y与圆相切于第一象限时,z取最大值,此时错误!=2,所以z的最大值为2错误!.答案:2错误!9.解析:y′=2x-1x,由y′=1,得2x-错误!=1,x=1.切点为(1,1),它到直线y=x-2的距离为错误!.答案:错误!10.解析:若x=1,则不等式成立,若x>1,则ln x>0,则不等式等价为2ax-1≥0对x>1恒成立,即2ax≥1,即a≥错误!,因为错误!<错误!,所以a≥错误!,若0<x<1,则ln x<0,则不等式等价为(2ax-1)≤0对0<x<1恒成立,即2ax≤1,即a≤12x,因为错误!>错误!,所以a≤错误!,综上a=错误!。
2020年【通用版】高考数学(三轮复习)冲刺专题《数列大题部分》(含答案)
专题 数列大题部分【训练目标】1、 理解并会运用数列的函数特性;2、 掌握等差数列,等比数列的通项公式,求和公式及性质;3、 掌握根据递推公式求通项公式的方法;4、 掌握常用的求和方法;5、 掌握数列中简单的放缩法证明不等式。
【温馨小提示】高考中一般有一道小题,一道大题,小题侧重于考等差数列与等比数列的性质,熟练的灵活的使用数列的性质会大大减少计算量;大题则侧重于考查根据递推公式求通项公式,求和的方法。
总之,此类题目难度中等,属于必拿分题。
【名校试题荟萃】1、(宁夏长庆高级中学2019届高三上学期第四次月考数学(理)试卷)设数列{}n a 的前n 项和,且123,1,a a a +成等差数列. (1)求数列{}n a 的通项公式;(2)记数列1{}na 的前n 项和n T ,求使得成立的n 的最小值.【答案】(1)2nn a = (2)10(2)由(1)可得112nn a ⎛⎫= ⎪⎝⎭,所以,由,即21000n>,因为,所以10n ≥,于是使得成立的n 的最小值为10.2、(宁夏长庆高级中学2019届高三上学期第四次月考数学(理)试卷)设等差数列{}n a 的公差为d ,点(,)n n a b 在函数()2x f x =的图象上(*n N ∈)。
(1)若12a =-,点87(,4)a b 在函数()f x 的图象上,求数列{}n a 的前n 项和n S ; (2)若11a =,函数()f x 的图象在点22(,)a b 处的切线在x 轴上的截距为12ln 2-,求数列{}n na b的前n 项和n T .【答案】(1) (2)(2)由函数()f x 的图象在点22(,)a b 处的切线方程为所以切线在x 轴上的截距为21ln 2a -,从而,故22a =从而n a n =,2n n b =,2n nn a nb =所以故。
3、(辽宁省辽河油田第二高级中学2019届高三上学期期中考试数学(文)试题)设n S 为数列{}n a 的前项和,已知10a ≠,,n *∈N .(1)求1a ,2a ;(2)求数列{}n a 的通项公式; (3)求数列{}n na 的前n 项和. 【答案】(1)1,2 (2)12-=n n a (3)(3)由(2)知12-=n n n na ,记其前n 项和为n T ,于是① ②①-②得从而.4、(湖南省浏阳一中、株洲二中等湘东六校2019届高三12月联考数学(理)试题)已知数列}{n a 的前n 项和n S 满足,且11=a 。
2020高考数学 三轮冲刺 解答题专练--数列 一(10题含答案)
2020高考数学 三轮冲刺 解答题专练--数列 一1.若数列{a n }的前n 项和为S n ,点(a n ,S n )在y=16-13x 的图象上(n ∈N *).(1)求数列{a n }的通项公式;(2)若c 1=0,且对任意正整数n 都有c n +1-c n =log 12a n .求证:对任意正整数n≥2,总有13≤1c 2+1c 3+1c 4+…+1c n <34.2.已知{a n }为等差数列,前n 项和为S n (n ∈N *),{b n }是首项为2的等比数列,且公比大于0,b 2+b 3=12,b 3=a 4-2a 1,S 11=11b 4. (1)求{a n }和{b n }的通项公式;(2)求数列{a 2n b 2n -1}的前n 项和(n ∈N *).3.设数列{a n }的各项均为正数,且a 2=4a 1,a n +1=a 2n +2a n (n ∈N *).(1)证明:数列{log 3(1+a n )}为等比数列;(2)设数列{log 3(a n +1)}的前n 项和为T n ,求使T n >520成立时n 的最小值.4. (等差数列{a n }是递增数列,前n 项和为S n ,若a 32=a 1·a 9,S 5=a 52.(1)求数列{a n }的通项公式;(2)若数列{b n }满足b n =121+⋅++n n a a n n ,求数列{b n }的前99项的和.5.已知数列{a n }中,a 1=4,a n =a n ﹣1+2n ﹣1+3(n ≥2,n ∈N *).(1)证明数列{a n ﹣2n}是等差数列,并求{a n }的通项公式;(2)设b n =,求b n 的前n 和S n .6.已知数列{21 n b }是等差数列,且b 3=-611,b 5=-713,求b 9的值.7.设数列{}的前项和为.已知=4,=2+1,.(I)求通项公式;(II)求数列{}的前项和.8.已知数列{}的首项为1,为数列{}的前n项和,,其中q>0,. (I)若成等差数列,求a n的通项公式;(ii)设双曲线的离心率为,且,证明:.9.知数列{a}的前n项和为,且满足,数列{b n}为等差数列,且满足n.(I)求数列{a n},{b n}的通项公式;(II)令,关于k的不等式的解集为M,求所有的和S.10.已知等差数列和等比数列满足a=b1=1,a2+a4=10,b2b4=a5.1(Ⅰ)求的通项公式;(Ⅱ)求和:.答案解析1.解:(1)∵S n =16-13a n ,∴当n≥2时,a n =S n -S n -1=13a n -1-13a n ,∴a n =14a n -1.又∵S 1=16-13a 1,∴a 1=18,∴a n =18×⎝ ⎛⎭⎪⎫14n -1=⎝ ⎛⎭⎪⎫122n +1.(2)证明:由c n +1-c n =log 12a n =2n +1,得当n≥2时,c n =c 1+(c 2-c 1)+(c 3-c 2)+…+(c n -c n -1)=0+3+5+…+(2n -1)=n 2-1=(n +1)(n -1). ∴1c 2+1c 3+1c 4+…+1c n =122-1+132-1+142-1+…+1n 2-1 =12×[ ⎝ ⎛⎭⎪⎫1-13+⎝ ⎛⎭⎪⎫12-14+⎝ ⎛⎭⎪⎫13-15+…+⎝ ⎛⎭⎪⎫1n -1-1n +1 ] =12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1+12-⎝ ⎛⎭⎪⎫1n +1n +1=34-12⎝ ⎛⎭⎪⎫1n +1n +1<34. 又∵1c 2+1c 3+1c 4+…+1c n ≥1c 2=13,∴原式得证. 2.解:(1)设等差数列{a n }的公差为d ,等比数列{b n }的公比为q.由已知b 2+b 3=12,得b 1(q +q 2)=12,而b 1=2,所以q 2+q -6=0. 又因为q >0,解得q=2.所以b n =2n.由b 3=a 4-2a 1,可得3d -a 1=8.① 由S 11=11b 4,可得a 1+5d=16.②由①②,解得a 1=1,d=3,由此可得a n =3n -2.所以数列{a n }的通项公式为a n =3n -2,数列{b n }的通项公式为b n =2n. (2)设数列{a 2n b 2n -1}的前n 项和为T n ,由a 2n =6n -2,b 2n -1=2×4n -1,得a 2n b 2n -1=(3n -1)×4n,故T n =2×4+5×42+8×43+…+(3n -1)×4n,4T n =2×42+5×43+8×44+…+(3n -4)×4n +(3n -1)×4n +1, 上述两式相减,得-3T n =2×4+3×42+3×43+…+3×4n -(3n -1)×4n +1=-4n 1-4-4-(3n -1)×4n +1=-(3n -2)×4n +1-8.故T n =3n -23×4n +1+83.所以数列{a 2n b 2n -1}的前n 项和为3n -23×4n +1+83.3.解:(1)证明:由已知,得a 2=a 21+2a 1=4a 1, 则a 1(a 1-2)=0,因为数列{a n }的各项均为正数,所以a 1=2.因为a n +1+1=(a n +1)2>0,所以log 3(a n +1+1)=2log 3(a n +1). 又log 3(a 1+1)=log 33=1,所以数列{log 3(1+a n )}是首项为1,公比为2的等比数列.(2)由(1)可知,log 3(1+a n )=2n -1,所以T n =1+2+22+…+2n -1=2n-1.由T n >520,得2n >521(n ∈N *),得n≥10. 则使T n >520成立时n 的最小值为10.4.解:(1)设数列{a n }公差为d(d>0),因为a 32=a 1a 9,即(a 1+2d)2=a 1(a 1+8d),有d 2=a 1d.因为d ≠0,所以a 1=d ,①因为S 5=a 52,所以5a 1+245⨯·d=(a 1+4d)2,② 由①②得,a 1=53,d=53,所以a n =53n. (2)b n =)1(535312+⋅++n n n n =925·)1(12+++n n n n =925·(1+n 1-11+n ).所以b 1+b 2+b 3+…+b 99=925[99+(1-21)+(21-31)+…+(991-1001)]=925(100-1001)=41111. 5.解:6.解:令a n =21+n b ,由题意可知{a n }成等差数列,且a 3=213+b ==6,a 5=215+b =7. 设数列{a n }的公差为d ,则a 5-a 3=2d ,∴d=21,∴a 9=a 3+6d=6+6×21=9.又219+b =a 9=9,∴b 9=-917. 7.(1);(2).8.9.10.(Ⅰ);(Ⅱ).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020高考数学三轮每日一卷
一、选择题:每小题4分,共40分
1. 已知集合1,0,2,3A,11Bxx,则=ABI( )
A.0,2 B.2,3 C.1,0,2 D.0,1,2
2. 以下哪个点在倾斜角为45且过点1,2的直线上( )
A.2,3 B.0,1 C.3,3 D.3,2
3. 某几何体的三视图如图所示,则该几何体的体积是( )
A.13 B.23 C.43 D.2
4. 若实数,xy满足020220xyxyxy,则2zxy的最大值是( )
A.0 B.1 C.2 D.3
5. 已知平面,,直线m满足m,,则“m”是“m∥”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分
也不必要条件
6. 设函数sin1xxfxe,则fx的图像大致为( )
7. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如
上图所示的弦图中,由四个全等的直角三角形和一个正方形构成.现有五种不同的颜色
可供涂色,要求相邻的区域不能用同一种颜色,则不同的涂色方案有( )
A.180 B.192 C.420
D.480
8. 甲乙两人进行乒乓球比赛,现采用三局两胜的比赛制度,规定每一局比赛都没有
平局(必须分出胜负),且每一局甲赢的概率都是p,随机变量X表示最终的比赛局数,
若103p,则( )
A.52EX B.218EX C.
1
4
DX
D.2081DX
9. 已知平面向量a,b,c满足对任意xR都有xabab,xacac成立,
=1acbc
,=3ab,则a的值为( )
A.1 B.3 C.2 D.7
10. 设实数,xy满足22413xxyyxy,则代数式2413xyyxy( )
A.有最小值631 B.有最小值413 C.有最大值1 D.有最大
值2021
二、填空题:单空题4分,多空题6分,共34分
11. 椭圆22143xy的长轴长是 ,离心率是 .
12. 已知复数z满足i112iz(i为虚数单位),则复数z的虚部为 ,模
z
.
13. 二项式62xx展开的所有项的系数和为 ,展开式中的常数项
是 .
14. 已知二次函数21fxaxbx,一次函数1gxx,不等式fxgx的解集为
1,2,则ba ;记函数fxfxgxhxgxgxfx,,,则hx
的最小值
是 .
15. 若sin211cos23,tan21,则tan .
16. 已知P为双曲线C:22221xyab0,0ab上的一点,1F,2F分别为C的左右焦点,
若12PFF△的内切圆的直径为a,则双曲线C的离心率的取值范围为 .
17. 已知数列na满足111,32a,1sin2nnaa,*Nn,记数列na的前n项和为nS,
则对任意*Nn,有①数列na单调递增;②1122nnaaS;③13144nnaa;④
2019
2020
n
a
.上述四个结论中正确的是 .(填写相应的序号)
三、解答题:4小题,共56分
18. 已知sinsin3cosfxxxx.
(1)求fx的最小正周期及最大值;
(2)在三角形ABC中,内角A,B,C所对的边分别是a,b,c,且1fB,1b,
2a
,求ABC△的面积.
19. 如图所示,四棱锥PABCD中,底面ABCD是平行四边形,PA平面ABCD,
1PAAB,2AD,F是PB中点,点E
在棱BC上移动.
(1)若ABAD,求证:PEAF;
(2)若23BAD,当点E为BC中点时,求PA与平面PDE所成角的大小.
20. 设各项均为正数的数列na的前n项和为nS,满足431nnnSaa,已知等比数
列nb,21ba,34ba,*Nn.
(1)求数列na,nb的通项公式;
(2)记nnnacb,数列nc的前n项和为nT,证明:对一切正整数n,6nT.
21. 已知抛物线2:Cxay的图像经过点2,1.
(1)求抛物线C的方程和焦点坐标;
(2)直线l交抛物线C于,AB不同的两点,且,AB位于y轴两侧,过,AB分别作抛物
线C的两条切线
交于点P,直线,APBP与x轴的交点分别记作,MN.记ABP△的面积为1S,
ANP△
的面积为2S,
BMP△
的面积为3S,试问123SSS是否为定值,若是,请求出该定值;若不是,请
说明理由.
22. 已知函数ln114fxxkxkxk,
(1)若0k,求出函数fx的单调区间及最大值;
(2)若4k且0k,求函数fx在21,14kk上的最大值gk的表达
式.
