中立法案-宁夏六盘山高级中学
宁夏回族自治区银川市六盘山高级中学高中物理人教(选修3-4)第十二章机械波第3节波长、频率和波速 课件(P

的理解
课 堂 练 习 练习7. 一列横波沿直线传播,在传播方向上 有 A 、 B 两点,相距 1.2m ,当波刚好到达 B 点时开 始计时,已知 4 秒内, A 位置的质点完成 8 次全振 动, B 位置质点完成 10 次全振动。这列波的波长 为多少?频率为多少?速度为多少?
波长λ=0.6m 频率f=2.5Hz 波速v=1.5m/s
课堂小结
1、
λ υ λf T
只是波速的定义式,
并非函数式,可与机械运动速度公
式做类比。 2、波的频率由波源决定,波
速只与介质有关。
五、板书设计
波长、频率和波速
一、复习巩固 二、新课教学 1、波长: ……
Y/cm
3、波速:…… 公式: 物理意义:……
X/cm
三、课堂练习 【例1】略 【例2】略 机动板块
2、物理意义
反映振动在介质中传播的快慢程度. 3、几点说明 (1)波速的大小由介质的性质决定,同一列波 在不同介质中传播速度不同。 (2)一列波在同一均匀介质中是匀速传播的 (3)要区分波速与质点振动速度的含义
四、波长、周期(或频率)和波速的关系
x v 或v f v t T
(1)波速等于波长和频率的乘积. (2)经过一个周期,振动在介质中传播的距离等于 一个波长 (3)波速等于波长和频率的乘积这一关系虽从机械 波得到,但对其他形式的波(如电磁波、光波) 也适用
一、波长(λ) 1、 定义: 在波动中,对平衡位置的位移总是 相等的两个相邻质点间的距离,叫做波长。 2、几点说明
(1)“位移总相等” 的含义是“每时每刻都相等” (2)位移总相等的两个质点,其速度也总是相等的 (3)每经过一个波长的距离,出现一个振动情况 完全相同的质点,因此波长描述了波传播过程中 空间上的周期性(重复性)。
宁夏回族自治区银川市六盘山高级中学高中物理人教版选修波粒二象性能量量子化习题课

宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT) 宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT)
宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT) 宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT)
宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT) 宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT)
宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT) 宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT)
Hale Waihona Puke 宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT) 宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT)
宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT) 宁夏回族自治区银川市六盘山高级中 学高中 物理人 教版( 选修3-5 )第十 七章波 粒二象 性第1 节能量 量子化 习题课(共25张PPT)
宁夏银川市六盘山高级中学2024届化学高二第一学期期中教学质量检测模拟试题含解析

宁夏银川市六盘山高级中学2024届化学高二第一学期期中教学质量检测模拟试题请考生注意:1.请用2B 铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每题只有一个选项符合题意)1、镍镉可充电电池,电极材料是Cd 和()NiO OH ,电解质是KOH ,放电时的电极反应式是()2Cd 2OH 2e Cd OH --+-=,()()222NiO OH 2H O 2e 2Ni OH 2OH --++=+。
下列说法不正确的是A .电池的总反应式是()()()222Cd 2NiO OH 2H O 2Ni OH Cd OH ++=+B .电池充电时,镉元素被还原C .电池充电时,电池的负极和电源的负极连接D .电池放电时,电池负极周围溶液的pH 不断增大 2、下列纯气体反应符合图1、图2的是( )A .X+3Y 2Z ΔH >0B .X+3Y 2Z ΔH <0C .X+2Y3Z ΔH <0D .5X+3Y4Z ΔH <03、下列各组离子在指定溶液中一定大量共存的是( ) A .含有AlO 2-的溶液中:Na + 、Al 3+、Cl -、K +B .常温下由水电离出的c(H +)·c(OH -)=10-20 mol 2·L -2的溶液中:Na +、NH 、Cl -C .常温下 c(Fe 3+)=0.1 mol·L -1的溶液中:K +、ClO -、SO 42-、SCN -D .在c(H +)=1.0×10-13 mol·L -1的溶液中:Na +、S 2-、AlO 2-、SO 32- 4、在密闭容中发生下列反应aA(g)cC(g)+dD(g),反应达到平衡后,将气体体积压缩到原来的一半,当再次达到平衡时,D 的浓度为原平衡的1.8倍,下列叙述正确的是 A .A 的转化率变大B .平衡向正反应方向移动C.D的体积分数变大D.a<c+d5、锌空气燃料电池可用作电动车电源,电解质溶液为KOH溶液,正向放电,逆向充电,总反应为:Zn+O2+4OH-+2H2O 2Zn(OH)42-,下列说法正确的是A.充电时,电解质溶液中K+向阳极移动B.充电时,电解质溶液中c(OH-)逐渐减小C.放电时,负极反应为:Zn+4OH--2e-===Zn(OH) 42-D.可用盐酸代替KOH作电解液6、已知NO和O2转化为NO2的反应机理如下:①2NO(g)N2O2(g) (快) △H1< 0,平衡常数K1②N2O2(g)+O22NO2(g) (慢) △H2< 0,平衡常数K2。
宁夏回族自治区银川市六盘山高级中学高中物理人教版(选修31)第三章第3节见种常见的磁场(导学提纲2)

磁感线及常见的磁场课堂导学提纲2课堂预期达标要求1、知道什么叫磁场的叠加,会求合磁场2、了解安培分子假说,从而解释一些磁现象3、知道磁通量的物理意义和定义式自主学习1、匀强磁场:(1)叫做匀强磁场。
(2)匀强磁场磁感线特点:是一些线。
(2)距离较近的之间,距离适中的之间和的磁场都可以看作匀强磁场。
合作探究2、磁场叠加:磁场是矢量,遵循法则例1、、如图所示,两根非常靠近且互相垂直的长直导线,当通以如图所示方向的电流时,电流所产生的磁场在导线所在平面内的哪个区域内方向是一致且向里的()A、区域ⅠB、区域ⅡC、区域ⅢD、区域Ⅳ练1、如图所示,三条长直导线都通以垂直于纸面向外的电流,且,则距三导线等距的A点的磁场方向为()A. 向上B. 向右C. 向左D. 向下3、安培分子电流假说:(1)安培分子电流假说:在原子、分子等物质微粒内部,存在着一种环形电流——,分子电流使每个物质微粒都成为微小的,它的两侧相当于两个。
(2)磁现象的电本质:磁铁的磁场和电流的磁场一样,都是由产生的。
(3)当物质受到外界磁场作用,时就会现磁性,叫磁化。
当磁铁受到,使分子电流时就会失去磁性,叫退磁。
例2、如图是铁棒甲与铁棒乙内部各分子电流取向的示意图,甲棒内部各分子电流取向是杂乱杂乱无章的,乙棒内部各分子电流取向大致相同,则下列说法中正确的是A、两棒均显磁性B、两棒均不显磁性C、甲棒不显磁性,乙棒显磁性D、甲棒显磁性,乙棒不显磁性练2、根据安培假设的思想,认为磁场是由于运动电荷产生的,这种思想如果对地磁场也适用,而目前在地球上并没有发现相对地球定向移动的电荷,那么由此判断,地球应A、带负电B、带正电C、不带电D、无法确定4、磁通量(1)定义:设在磁感应强度为B的匀强磁场中,有一个与磁场方向垂直的平面,面积为S,则B与S的乘积叫做穿过这个面积的磁通量,简称磁通。
(2)定义式:(3)单位:简称,符号。
1Wb=1T·m2(4)磁通量是标量(5)磁通密度即磁感应强度 B= 1T= 。
宁夏回族自治区银川市六盘山高级中学人教版高中物理必修2-6.3万有引力定律(共28章PPT)
【讨论】根据下列是当时可以测量的数据,如何
证明?
地表重力加速度:g = 9.8m/s2
地球半径:
R = 6400×103m
月亮周期:
T = 27.3天≈2.36×106s
月亮轨道半径: r ≈ 60R =3 .84×108m
?1
计算验证: a月360g0
计算结果: a月 4 T 22r2.7 2 1 3 0 m /s2316g0
月亮绕地球运行
地球对月球的引力、地球对地面上物 体的引力、太阳对行星的引力,也许 真的是同一种性质的力?
一、万有引力定律的发现
苹果落地、高处物体落 地、月亮绕地球运动……这 些现象引起了牛顿的沉思。
牛顿的思考: “天上的力”和“人间的力”是同一种力吗?
牛顿的猜想: 苹果与月球受到的引力可能是同一种力! 这种力可能都遵从与距离平方成反比的
关系。
重力和月球所受地球的引力是同一性 质的力,这个大胆的想法要由事实检 验。
假定设想成立,则月球与苹果的地位相当, 地球与苹果之间的引力大小和地球与月球之 间引力的大小应该同样遵从“平方反比”的 规律,已知月球轨道半径为地球半径的60倍, 根据牛顿第二定律,月球轨道处的加速度 (月球公转的向心加速度)就应该是地面附 近自由落体加速度的1/3600
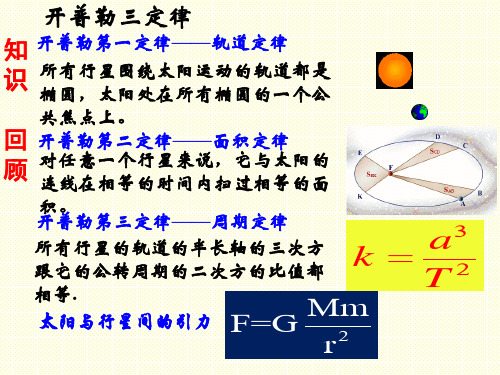
开普勒三定律
知 开普勒第一定律——轨道定律
识
所有行星围绕太阳运动的轨道都是 椭圆,太阳处在所有椭圆的一个公
共焦点上。
回 开普勒第二定律——面积定律
顾
对任意一个行星来说,它与太阳的 连线在相等的时间内扫过相等的面
积。
开普勒第三定律——周期定律
所有行星的轨道的半长轴的三次方 跟它的公转周期的二次方的比值都
宁夏回族自治区银川市六盘山高级中学高中物理人教版(选修31)第二章恒定电流第5节焦耳定律导学提纲

2.5焦耳定律课堂导学提纲课堂预期达标要求1、理解电功的概念,知道电功是指电场力对自由电荷所做的功,理解电功的公式,能进行有关的计算。
2、理解电功率的概念和公式,能进行有关的计算。
3、知道电功率和热功率的区别和联系。
能运用能量转化与守恒的观点解决简单的含电动机的非纯电阻电路问题自主学习1、电能的转化:导体内自由电荷在力作用下发生定向移动,电场力对定向移动的电荷做了,电场力做功将引起,电能转化为其他形式能,举例:电能→机械能,如电动机。
电能→内能,如电热器。
电能→化学能,如电解槽2、电功和电功率:(1)对于一段导体,两端电势差为U,把电荷q从一端搬至另一端,电场力的功W= ,若导体中形成电流为I,则q= ,所以W= 。
电场力所做的功,就是电流所做的功,简称 .(2)在相同的时间里,电流通过不同用电器所做的功一般不同。
为了描述电流做功的快慢,引入电功率的概念。
定义:做电功率;定义式:P= =;单位:瓦(W)、千瓦(kW)(3)额定功率和实际功率:叫额定电压,在这个电压下消耗的功率称额定功率。
叫实际功率。
例1、图中R1=4Ω,R2=9Ω,R3=18Ω。
通电后()A.经R1和R3的电流之比I1:I3=3:1B.R1两端的电压和R3两端的电压之比U1:U3=4:9C.三个电阻消耗的电功率之比P1:P2:P3=2:1:2D.三个电阻消耗的电功率之比P1:P2:P3=2: 2:1练1、不考虑温度对电阻的影响,对一个“220V,40W”的灯泡,下列说法正确的是A.接在110 V的电路上时的功率为20 WB.接在110 V的电路上时的功率为10 WC.接在440 V的电路上时的功率为160WD.接在220 V的电路上时的功率为40 W合作探究3、焦耳定律(1)内容:电流通过导体产生的热量,由、导体和通电成正比。
表达式:Q= 。
(2)热功率:。
即P= = 。
4、纯电阻电路和非纯电阻电路:(1)纯电阻电路:电路消耗的电功率转化为内能(只含白炽灯、电炉等电热器的电路)。
宁夏回族自治区银川市六盘山高级中学2019-2020学年高一语文下学期期中试题(含解析)不分版本
宁夏回族自治区银川市六盘山高级中学2019-2020学年高一语文下学期期中试题(含解析)不分版本宁夏回族自治区银川市六盘山高级中学2019-2020学年高一语文下学期期中试题〔含解析〕一、根底选择题1.以下加点字中,读音无误一项为哪一项A. 敕.造〔là〕逡.巡〔quān〕合从.缔交〔zòng〕跂.而望矣〔qĭ〕B. 句读.〔dòu〕崤.函〔xiáo〕瓮.牖绳枢〔wèng〕六艺经传.〔zhuàn〕C. 狗彘.〔zhì〕庠.序〔yáng〕陈抟.老祖〔chuán〕养生丧.死〔sānɡ〕D. 筋.骨〔jīn〕藩.篱〔pān〕锲.而不舍〔qì〕其曲.中规〔qū〕【答案】B【解析】【详解】此题考查学生识记现代汉语普通话常用字的字音的能力。
解答此类题目,首先要明确题干的要求,如此题“以下加点字中,读音无误的一项〞,然后依据字形和字义辨析字音正误。
A项,“敕.造〔là〕〞应为“敕.造〔chì〕〞;C项,“庠.序〔yáng〕〞应为“庠.序〔xiáng〕〞,“陈抟.老祖〔chuán〕〞应为“陈抟.老祖〔tuán〕〞;D项,“藩篱〔pān〕〞应为“藩篱〔fān〕〞,“锲.而不舍〔qì〕〞应为“锲.而不舍〔qiè〕〞。
应选B【点睛】对多音字的把握,掌握音随意转的原那么。
吃不准的情况下,可多考虑从词语具体意义的角度入手解决问题。
常见多音字标次读音正确的可能性大,标常读音正确的可能性小。
善用排除法。
如果题干是全部不相同的,就把有两项相同的去掉;如果题干是与所给字的读音全部相同的,那么去掉一个不同的一项;如果题干是读音全都正确,就去掉有一个错误的一项;如果题干是读音有错误的一组,就排除肯定无误的一项;总之,用排除法是一种比拟好的方法。
当然也需要一定的知识积累的。
宁夏银川市六盘山高级中学2025届数学高一上期末学业质量监测模拟试题含解析
cos x
9 cos x
6 ,当且仅当 cos x
如下: ①平移:平移异面直线中的一条或两条,作出异面直线所成的角; ②认定:证明作出的角就是所求异面直线所成的角; ③计算:求该角的值,常利用解三角形;
④取舍:由异面直线所成的角的取值范围是 (0, ] ,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.求 2
异面直线所成的角要特别注意异面直线之间所成角的范围 7、B
【详解】设经过 n 次提炼后,水中的杂质不超过原来的 4%,
由题意得 1 50%n 4% ,
得n
log 1
2
1 25
2 log2
5
2lg 5 lg 2
21 lg 2
lg 2
4.7 ,
所以至少需要 5 次提炼,
故选:A.
2、A 【解析】
g x 存在两个零点,等价于 y x m 与 f x 的图像有两个交点,数形结合求解.
达到能求向量数量积的目的 8、A
【解析】根据题意,确定角 的终边上点的坐标,再利用三角函数定义,即可求解,得到答案
【详解】由题意,点
P
sin
π 3
,
cos
π 3
在角
α
的终边上,即
P
3 2
,
1 2
,则 r
OP
1,
由三角函数的定义,可得 sin y 1 r2
故选 A
【点睛】本题主要考查了三角函数的定义的应用,其中解答中确定出角的终边上点的坐标,利用三角函数的定义求解
故选:A 6、C
【解析】如图所示,补成直四棱柱 ABCD A1B1C1D1 ,
则所求角为 BC1D, BC1 2, BD 22 1 2 21cos 60 3,C1D AB1 5 ,
宁夏六盘山高级中学2020-2021学年高二上学期期中数学(理)试题
宁夏六盘山高级中学2020-2021学年高二上学期期中数学(理)试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知数列{}n a 满足:10a >,112n n a a +=,则数列{}n a 是( ) A .递增数列 B .递减数列C .摆动数列D .不确定 2.已知ABC中,60,3,A BC AB ︒∠===B ∠=( ) A .45° B .75° C .135° D .45°或135° 3.已知等差数列{a n }中,a 7+a 9=16,a 4=1,则a 12的值是( )A .15B .30C .31D .644.若正实数,a b 满足1a b +=,则( ) A .11a b +有最大值4 B .ab 有最小值14CD .22a b +有最小值2 5.在等差数列{}n a 中,已知69131620a a a a +++=,则S 21等于( )A .100B .105C .200D .06.已知实数x y 、满足约束条件238044010,x y x y x y -+≥⎧⎪--≤⎨⎪+-≥⎩则z x y =-的最大值及最小值的和为( )A .3﹣B .2﹣C .1D .27.在三角形ABC 中,,,a b c 是角,,A B C 所对的边,满足222a ab b c ++=,则C 的大小是( )A .30°B .60°C .90°D .120° 8.已知数列{a n }中,a 1=1,a n =3a n ﹣1+4(n∈N *且n≥2),,则数列{a n }通项公式a n 为( ) A .3n ﹣1 B .3n+1﹣8 C .3n ﹣2 D .3n9.若数列{}n a 满足*111(,n nd n N d a a +-=∈为常数),则称数列{}n a 为“调和数列”, 若正项数列1{}n b 为“调和数列”,且12990b b b +++=,则46b b ⋅的最大值是( ) A .10 B .100 C .200 D .40010.设102m <<,若(12)m m k -恒成立,则k 的最小值为( ) A .1 B .12 C .14 D .1811.已知函数())24f παα=-+,在锐角三角形ABC 中,()6f A =,且cos2cos2B C =,则tan B 的值为( )A .1 B1 C.2 D112.已知,a b 为正实常数,实数,x y 且满足22221a b x y+=,则22x y +的最小值是( ) A .+a bB)+a b C .2()a b + D .22a b +二、填空题13.命题P :若x ∈R12x ≥+,该命题是________命题(指真假)14.等比数列{}n a 的前n 项和为n S ,已知3339,22a S ==,则公比q =________. 15.三角形ABC 中, 3B π=,三边长,,a b c 成等差数列,且6ac =,则b 的值是_______16.设数列1,2,2,3,3,3,4,4,4,4,……的前n 项和为n S ,则51S =___________三、解答题17.求下列不等式的解集(1)2320x x -+≤(2)()(1)0,()x a ax a R +->∈18.在三角形ABC 中,,AD BC E ⊥为BC 的中点,::2:1:,BAC 135BD AD DC m ︒=∠=(1)求m 的值;(2)若AE =,求三角形ABC 的面积.19.已知非常数列的等差数列{}n a 中,45a =,它的第一,三,七项依次成等比数列 (1)求数列{}n a 的通项公式.(2)设数列12n n a a +⎧⎫⎨⎬⎩⎭的前n 项的和为n T ,求n T . 20.在ABC 中,角,,A B C 的对边分别为,,,a b c 且ccos B 与cos b C的等差中项为cos A .(1)求cos A 的值;(2)若ABCAB CA ⋅的值.21.一个生产公司投资A 生产线500万元,每万元可创造利润1.5万元,该公司通过引进先进技术,在生产线A 投资减少了x 万元,且每万元的利润提高了0.5%x ;若将少用的x 万元全部投入B 生产线,每万元创造的利润为131.51000a x ⎛⎫- ⎪⎝⎭万元,其中0a >. ()1若技术改进后A 生产线的利润不低于原来A 生产线的利润,求x 的取值范围; ()2若生产线B 的利润始终不高于技术改进后生产线A 的利润,求a 的最大值. 22.设等差数列{}n a 的前n 项和为n S ,且12n n n S na a c =+-(c 是常数,n +∈N ),26a =.(1)求c 的值及数列{}n a 的通项公式;(2)设122n n n a b +-=,求数列{}n b 的前n 项和为n T .参考答案1.B【解析】【分析】{}n a 是公比为12的正项等比数列,单调递减,得到答案. 【详解】 10a >,112n n a a +=,故{}n a 是公比为12的正项等比数列,单调递减. 故选:B .【点睛】本题考查了数列的单调性,属于简单题.2.B【分析】根据正弦定理得到45C =︒,计算得到答案.【详解】 根据正弦定理:sin sin a c A C =,故2sin 32C ==, c a <,故C A ∠<∠,故45C =︒,故75B ∠=︒.故选:B .【点睛】本题考查了正弦定理解三角形,多解是容易发生的错误.3.A【分析】根据等差数列性质解得8a ,再根据等差数列性质得结果.【详解】因为79881284162168216115a a a a a a a +=∴=∴=∴=-=-=故选:A【点睛】本题考查等差数列性质,考查基本分析求解能力,属基础题.4.C【解析】试题分析:因为正实数,满足,所以112224a b a b b a a b a b a b +++=+=++≥+=,故11a b+有最小值4,故A 不正确;由基本不等式可得112,4a b ab ab +=≥∴≤,故有最大值14,故B 不正确;由于()22122,2a b a b ab ab a b +=++=+≤∴+≤,故+a b 由最大值为2,故C 正确;()22211212122a b a b ab ab +=+-=-≥-=,故22a b +由最小值12,故D 不正确. 考点:基本不等式5.B【解析】试题分析:()121691316121212120101052a a a a a a a a S ++++=∴+=∴==考点:等差数列性质及求和6.B【分析】画出可行域和目标函数,根据平移得到最大值和最小值,得到答案.【详解】如图所示:画出可行域和目标函数, 根据平移得到:当1,0x y ==时,z 有最大值为1;当1,2x y =-=时,z 有最小值为3-; 故选:B .【点睛】本题考查了线性规划求最值问题,画出函数图像是解题的关键.7.D【分析】根据余弦定理直接计算得到答案.【详解】根据余弦定理:2222cos a ab C b c -+=,即1cos 2C =-,即120C ∠=︒. 故选:D【点睛】本题考查了余弦定理求角度,属于简单题.8.C【解析】在a n =3a n ﹣1+4两边同时加上2,得a n +2=3a n −1+6=3(a n −1+2),根据等比数列的定义,数列{a n +2}是等比数列,且公比为3.以a 1+2=3为首项.等比数列{a n +2}的通项a n +2=3⋅3n −1=3n ,移向得an =3n −2.故选C.9.B【解析】试题分析:由于正项数列1{}n b 为“调和数列”,,为等差数列, ,.的最大值为100.考点:等差数列的性质和基本不等式的应用.10.D【分析】设函数()()12f m m m =-,求函数的最大值得到答案.【详解】设函数()()2211122248f m m m m m m ⎛⎫=-=-+=--+ ⎪⎝⎭,故()max 1148f m f ⎛⎫== ⎪⎝⎭. 故18k ≥. 故选:D .【点睛】本题考查了不等式恒成立问题,转化函数的最值问题是解题的关键.11.D【分析】根据()6f A =得到4A π∠=,根据cos2cos2B C =得到38B C π∠=∠=,利用二倍角公式计算得到答案.【详解】())264f A A π=-+=,即sin(2)4A π-=. 锐角三角形ABC ,故32,444A πππ⎛⎫-∈- ⎪⎝⎭,故244A ππ-=,4A π∠=.()2,20,B C π∈,cos2cos2B C =,故38B C π∠=∠=.22tan 3tan 2tan 11tan 4B B B π===--,故tan 1B =或tan 1B =(舍去). 故选:D .【点睛】本题考查了三角恒等变换,意在考查学生的计算能力.12.C【分析】变换得到()22222222a b x y x y x y ⎛⎫+++ ⎪⎝⎭=,展开利用均值不等式计算得到答案. 【详解】()()2222222222222222222a b a y b x x y x y a b a b a b x y x y ⎛⎫+++=+++≥+=+ ⎝⎭=⎪. 当222222a y b x x y=,即22ay bx =时等号成立. 故选:C .【点睛】本题考查了均值不等式求最值,变换()22222222a b x y x y x y ⎛⎫+++ ⎪⎝⎭=是解题的关键. 13.假【分析】举出反例得到答案.【详解】当1x =32x =+=12x ≥+不成立.故答案为:假.【点睛】本题考查了命题的真假判断,属于简单题.14.1或12-【解析】∵3339,22a S ==, ①当1q =时,393322S ==⨯,满足条件. ②当1q ≠时,可得()2113231912a q a q q ⎧=⎪⎪⎨-⎪=⎪-⎩.解得1612a q =⎧⎪⎨=-⎪⎩. 综上可知:1q =或12-. 点睛:等比数列求和公式中当1q ≠和1q =时,公式不一样,切勿用错. 当1q =时,1n S na =;当1q ≠时,()111n n a q S q -=-. 15【分析】根据等差数列得到2a c b +=,利用余弦定理计算得到答案.【详解】边长,,a b c 成等差数列,故2a c b +=,根据余弦定理:()22222cos 3b a c ac B a c ac =+-=+-,即22418b b =-,解得b ..【点睛】本题考查了等差中项,余弦定理,意在考查学生的综合应用能力.16.345【分析】数列等于m 的项共有m 项,计算()1512m m +≤得到9m ≤,故()2225112...9514510S =++++-⨯,得到答案.【详解】根据题意知:数列等于m 的项共有m 项,故()1512m m +≤,解得9m ≤. 当9m =时,()1452m m +=,故()2225112...9514510345S =++++-⨯=. 故答案为:345.【点睛】本题考查了数列求和,意在考查学生对于数列公式方法的灵活运用.17.(1)[]1,2;(2)答案不唯一,见解析【分析】(1)直接解不等式得到答案.(2)讨论0a >,0a =,0a <三种情况,分别计算得到答案.【详解】(1)2320x x -+≤,即()()120x x --≤,故12x ≤≤,即[]1,2x ∈.(2)()(1)0x a ax +->当0a =时,0x ->,即0x <;当0a >时,1()()0x a x a +->,故1x a >或x a <-; 当0a <时,1()()0x a x a +-<,故1x a a<<-; 综上所述:0a =时,(),0x ∈-∞;0a >时,()1,,x a a ⎛⎫∈-∞-+∞ ⎪⎝⎭,0a <时,1,x a a ⎛⎫∈- ⎪⎝⎭; 【点睛】本题考查了解不等式,分类讨论是常用的数学方法,需要熟练掌握.18.(1)3m =;(2)10S =【分析】(1)根据和差公式()tan tan 135CAD BAD ∠=︒-∠,计算得到答案.(2)设2BD t =,AD t =,3CD t =,根据勾股定理得到2t =,计算面积得到答案.【详解】(1):2:1BD AD =,故tan 2BAD ∠=,()tan135tan tan tan 13531tan135tan BAD CAD BAD BAD ︒-∠∠=︒-∠==+︒⋅∠,故tan 31m CAD ∠==, 故3m =. (2)::2:1:3BD AD DC =,设2BD t =,AD t =,3CD t =,0t >.在ADE ∆中,根据勾股定理:2252t t ⎛⎫=+ ⎪⎝⎭,解得2t =,故1102102S =⨯⨯=. 【点睛】本题考查了和差公式,三角形面积,意在考查学生的计算能力.19.(1) 1n a n =+;(2) 2nn T n =+ 【分析】(1)根据题意得到()()211126a d a a d +=+,4135a a d =+=,计算得到答案. (2)1211212n n a a n n +⎛⎫=- ⎪++⎝⎭,利用裂项求和得到答案. 【详解】(1)根据题意:2317a a a =⋅,即()()211126a d a a d +=+,4135a a d =+=, 解得12,1a d ==,故1n a n =+.(2)()()1221121212n n a a n n n n +⎛⎫==- ⎪++++⎝⎭, 故111111112...2233412222n n T n n n n ⎛⎫⎛⎫=-+-++-=-=⎪ ⎪++++⎝⎭⎝⎭. 【点睛】本题考查了等差数列的通项公式,裂项求和,意在考查学生对于数列公式方法的灵活运用. 20.(1)4;(2)- 【分析】(1)变换得到cos cos cos A c B b C =+,利用正弦定理计算得到答案.(2)根据面积公式到8bc =,再计算数量积得到答案.【详解】(1)2cos a A 是cos c B 与cos b C 的等差中项,cos cos cos A c B b C ∴=+,由正弦定理,sin sin cos cos sin sin()sin A A C B C B C B A =+=+=.故cos A =.(2)cos A =sin A =1sin 2S bc A ==,故8bc =,故cos AB CA bc A ⋅=-=-【点睛】本题考查了正弦定理,面积公式,向量的数量积,意在考查学生的计算能力和综合应用能力. 21.(1)0300x <≤ (2)5.5【分析】(1)分别列出技术改造前后利润根据题意列出不等关系求解即可.(2)中不高于可转化为式子之间的恒成立问题,通过参变分离求最值从而得参数范围.【详解】(1)由题意得:()()1.550010.5% 1.5500x x -+≥⨯,整理得:23000x x -≤故0300x <≤.(2)由题意知,生产线B 的利润为131.51000a x x ⎛⎫- ⎪⎝⎭万元,技术改进后,生产生A 的利润为()()1.550010.5%x x -+万元,则()()131.5 1.550010.5%1000a x x x x ⎛⎫-≤-+ ⎪⎝⎭恒成立,235001252x ax x ∴≤+-,且0x >,50031252x a x ∴≤+-.又5004125x x +≥,当且仅当250x =时等号成立,0 5.5a ∴<≤,a ∴的最大值为5.5.【点睛】本题主要考查了函数的实际应用问题,第二问实际问题中的不高于转化为恒成立问题是本题解题的关键步骤,利用基本不等式求最值要注意变量的取值范围.22.(1) 2c =;22n a n =+ (2) 222n nn T +=-【分析】 (1)先令1n =得出12a c =,再令2n =,利用作差法得出23a c =,于此得出2c =,可由1a 和2a 的值求出等差数列{}n a 的公差,于此可求出等差数列{}n a 的通项公式; (2)先求出数列{}n b 的通项公式,再利用错位相减法求出数列{}n b 的前n 项和n T .【详解】(1)因为12n n n S na a c =+-,所以当1n =时,11112S a a c =+-,解得12a c =. 当2n =时,222s a a c =+-,即1222a a a a c +=+-.解得23a c =,所以36c =,解得2c =,则14a =.数列{}n a 的公差212d a a =-=.所以1(1)22n a a n d n =+-=+;(2)因为112222222n n n n n a n n b ++-+-===, 所以231232222n n n T =+++⋯+,① 2341112322222n n n T +=+++⋯+,② 由①-②可得23411111111112112222222222n n n n n n n n n T ++++=++++⋯+-=--=-, 所以222n n n T +=-. 【点睛】本题考查等差数列通项的求解,考查错位相减法求和,解题时要注意错位相减求和法所适用数列通项的结构类型,要熟练错位相减法求和的基本步骤,难点在于计算量较大,属于中等题.。
