贵州省贵师大附中周林高级中学2016-2017学年高一下学
2016-2017学年贵州省贵阳市高一(上)期末数学试卷与解析word

2016-2017学年贵州省贵阳市高一(上)期末数学试卷一、选择题(共10小题,每小题4分,满分40分)1.(4分)已知集合A={0,1,2},B={2,3},则集合A∪B=()A.{1,2,3}B.{0,1,2,3}C.{2}D.{0,1,3}2.(4分)化简÷(b)(a>0,b>0)结果为()A.a B.b C.D.3.(4分)正弦函数f(x)=sinx图象的一条对称轴是()A.x=0 B.C.D.x=π4.(4分)下列函数中,既是偶函数又存在零点的是()A.f(x)=sinx B.f(x)=x2+1 C.f(x)=lnx D.f(x)=cosx5.(4分)设y1=log0.70.8,y2=log1.10.9,y3=1.10.9,则有()A.y3>y1>y2B.y2>y1>y3C.y1>y2>y3D.y1>y3>y26.(4分)已知正方形ABCD的边长为1,则•=()A.1 B.C.D.27.(4分)如果cos(π+A)=﹣,那么sin(+A)的值是()A.B.C.D.8.(4分)要得到函数y=sin(2x+)的图象,只需将函数y=sin2x的图象()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位9.(4分)函数y=f(x)在区间上的简图如图所示,则函数y=f(x)的解析式可以是()A.f(x)=sin(2x+)B.f(x)=sin(2x﹣)C.f(x)=sin(x+)D.f(x)=sin(x﹣)10.(4分)对于函数f(x),如果存在非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,已知函数y=f (x)(x∈R)满足f(x+2)=f(x),且x∈[﹣1,1]时,f(x)=x2,则y=f(x)与y=log5x的图象的交点个数为()A.3 B.4 C.5 D.6二、填空题(共5小题,每小题4分,满分20分)11.(4分)学校先举办了一次田径运动会,某班有8名同学参赛,又举办了一次球类运动会,该班有12名同学参赛,两次运动会都参赛的有3人.两次运动会中,这个班共有名同学参赛.12.(4分)溶液酸碱度是通过pH值刻画的,pH值的计算公式为pH=﹣lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升,纯净水中氢离子的浓度为[H+]=10﹣7摩尔/升,则纯净水的pH=.13.(4分)已知,那么=.14.(4分)计算(lg2)2+lg2•lg50+lg25=.15.(4分)设A,B是非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合中B都有唯一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射,设f:x→是从集合A到集合B的一个映射.①若A={0,1,2},则A∩B=;②若B={1,2},则A ∩B=.三、解答题(共4小题,满分32分)16.(8分)已知向量=(1,0),=(1,1),=(﹣1,1).(Ⅰ)λ为何值时,+λ与垂直?(Ⅱ)若(m+n)∥,求的值.17.(8分)已知函数f(x)=x﹣.(Ⅰ)判断f(x)的奇偶性;(Ⅱ)用函数单调性的定义证明:f(x)在(0,+∞)上是增函数.18.(8分)已知函数f(x)=sin2+sin cos.(Ⅰ)求f(x)的最小正周期;(Ⅱ)若x∈[,π],求f(x)的最大值与最小值.19.(8分)已知函数f(x)=1﹣(a>0且a≠1)是定义在R上的奇函数.(Ⅰ)求a的值;(Ⅱ)若关于x的方程|f(x)•(2x+1)|=m有1个实根,求实数m的取值范围.四、阅读与探究(共1小题,满分8分)20.(8分)阅读下面材料,尝试类比探究函数y=x2﹣的图象,写出图象特征,并根据你得到的结论,尝试猜测作出函数对应的图象.阅读材料:我国著名数学家华罗庚先生曾说:数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征.我们来看一个应用函数的特征研究对应图象形状的例子.对于函数y=,我们可以通过表达式来研究它的图象和性质,如:(1)在函数y=中,由x≠0,可以推测出,对应的图象不经过y轴,即图象与y轴不相交;由y≠0,可以推测出,对应的图象不经过x轴,即图象与x轴不相交.(2)在函数y=中,当x>0时y>0;当x<0时y<0,可以推测出,对应的图象只能在第一、三象限;(3)在函数y=中,若x∈(0,+∞)则y>0,且当x逐渐增大时y逐渐减小,可以推测出,对应的图象越向右越靠近x轴;若x∈(﹣∞,0),则y<0,且当x逐渐减小时y逐渐增大,可以推测出,对应的图象越向左越靠近x轴;(4)由函数y=可知f(﹣x)=﹣f(x),即y=是奇函数,可以推测出,对应的图象关于原点对称.结合以上性质,逐步才想出函数y=对应的图象,如图所示,在这样的研究中,我们既用到了从特殊到一般的思想,由用到了分类讨论的思想,既进行了静态(特殊点)的研究,又进行了动态(趋势性)的思考.让我们享受数学研究的过程,传播研究数学的成果.2016-2017学年贵州省贵阳市高一(上)期末数学试卷参考答案与试题解析一、选择题(共10小题,每小题4分,满分40分)1.(4分)已知集合A={0,1,2},B={2,3},则集合A∪B=()A.{1,2,3}B.{0,1,2,3}C.{2}D.{0,1,3}【解答】解:∵集合A={0,1,2},B={2,3},则集合A∪B={0,1,2,3},故选:B.2.(4分)化简÷(b)(a>0,b>0)结果为()A.a B.b C.D.【解答】解:原式==a,故选:A3.(4分)正弦函数f(x)=sinx图象的一条对称轴是()A.x=0 B.C.D.x=π【解答】解:f(x)=sinx图象的一条对称轴为+kπ,k∈Z,∴当k=0时,函数的对称轴为,故选:C.4.(4分)下列函数中,既是偶函数又存在零点的是()A.f(x)=sinx B.f(x)=x2+1 C.f(x)=lnx D.f(x)=cosx【解答】解:对于A,是奇函数;对于B,是偶函数,不存在零点;对于C,非奇非偶函数;对于D,既是偶函数又存在零点.故选:D.5.(4分)设y1=log0.70.8,y2=log1.10.9,y3=1.10.9,则有()A.y3>y1>y2B.y2>y1>y3C.y1>y2>y3D.y1>y3>y2【解答】解:y1=log0.70.8∈(0,1);y2=log1.10.9<0;y3=1.10.9>1,可得y3>y1>y2.故选:A.6.(4分)已知正方形ABCD的边长为1,则•=()A.1 B.C.D.2【解答】解:.故选A.7.(4分)如果cos(π+A)=﹣,那么sin(+A)的值是()A.B.C.D.【解答】解:由题意可得:,根据诱导公式可得cosA=,所以=cosA=,故选B.8.(4分)要得到函数y=sin(2x+)的图象,只需将函数y=sin2x的图象()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位【解答】解:由于函数y=sin(2x+)=sin2(x+),∴将函数y=sin2x的图象向左平移个单位长度,可得函数y=sin(2x+)的图象,故选:B9.(4分)函数y=f(x)在区间上的简图如图所示,则函数y=f(x)的解析式可以是()A.f(x)=sin(2x+)B.f(x)=sin(2x﹣)C.f(x)=sin(x+)D.f(x)=sin(x﹣)【解答】解:由图象知A=1,∵=,∴T=π,∴ω=2,∴函数的解析式是y=sin(2x+φ)∵函数的图象过()∴0=sin(2×+φ)∴φ=kπ﹣,∴φ=﹣∴函数的解析式是y=sin(2x﹣)故选B.10.(4分)对于函数f(x),如果存在非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,已知函数y=f (x)(x∈R)满足f(x+2)=f(x),且x∈[﹣1,1]时,f(x)=x2,则y=f(x)与y=log5x的图象的交点个数为()A.3 B.4 C.5 D.6【解答】解:∵函数y=f(x)(x∈R)满足f(x+2)=f(x),∴f(x)是周期为2的周期性函数,又x∈[﹣1,1]时,f(x)=x2.根据函数的周期性画出图形,如图,由图可得y=f(x)与y=log5x的图象有4个交点故选:B.二、填空题(共5小题,每小题4分,满分20分)11.(4分)学校先举办了一次田径运动会,某班有8名同学参赛,又举办了一次球类运动会,该班有12名同学参赛,两次运动会都参赛的有3人.两次运动会中,这个班共有17名同学参赛.【解答】解:设A={x|x是参加田径运动会比赛的学生},B={x|x是参加球类运动会比赛的学生},A∩B={x|x是两次运动会都参加比赛的学生},A∪B={x|x是参加所有比赛的学生}.因此card(A∪B)=card(A)+card(B)﹣card(A∩B)=8+12﹣3=17.故两次运动会中,这个班共有17名同学参赛.故答案为:17.12.(4分)溶液酸碱度是通过pH值刻画的,pH值的计算公式为pH=﹣lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升,纯净水中氢离子的浓度为[H+]=10﹣7摩尔/升,则纯净水的pH=7.【解答】解:由题意可得:该溶液的PH值为﹣lg10﹣7=7故答案为:713.(4分)已知,那么=.【解答】解:因为,所以||=.故答案为.14.(4分)计算(lg2)2+lg2•lg50+lg25=2.【解答】解:原式=2 lg5+lg2•(1+lg5)+(lg2)2=2 lg5+lg2(1+lg5+lg2)=2 lg5+2 lg2=2;故答案为2.15.(4分)设A,B是非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合中B都有唯一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射,设f:x→是从集合A到集合B的一个映射.①若A={0,1,2},则A∩B={0,1} ;②若B={1,2},则A∩B={1}或∅.【解答】解:①根据题意,A={0,1,2},通过对应关系f:x→,B={0,1,},所以A∩B={0,1};②根据题意,B={1,2}时,过对应关系f:x→,得A={1}或{4}或{1,4};所以A∩B={1}或∅.故答案为:{0,1},{1}或∅.三、解答题(共4小题,满分32分)16.(8分)已知向量=(1,0),=(1,1),=(﹣1,1).(Ⅰ)λ为何值时,+λ与垂直?(Ⅱ)若(m+n)∥,求的值.【解答】解:(Ⅰ)∵向量=(1,0),=(1,1),=(﹣1,1).∴=(1+λ,λ),∵+λ与垂直,∴()•=1+λ+0=0,解得λ=﹣1,∴λ=1时,+λ与垂直.(Ⅱ)∵=(m,0)+(n,n)=(m+n,n),又(m+n)∥,∴(m+n)×1﹣(﹣1×n)=0,∴=﹣2.∴若(m+n)∥,则=﹣2.17.(8分)已知函数f(x)=x﹣.(Ⅰ)判断f(x)的奇偶性;(Ⅱ)用函数单调性的定义证明:f(x)在(0,+∞)上是增函数.【解答】解:(Ⅰ)函数f(x)=x﹣的定义域是D=(﹣∞,0)∪(0,+∞),任取x∈D,则﹣x∈D,且f(﹣x)=﹣x﹣=﹣(x﹣)=﹣f(x),∴f(x)是定义域上的奇函数;(Ⅱ)证明:设x1,x2∈(0,+∞),且x1<x2,则f(x1)﹣f(x2)=(x1﹣)﹣(x2﹣)=(x1﹣x2)+(﹣)=;∵0<x1<x2,∴x1x2>0,x1﹣x2<0,x1x2+1>0,∴<0,即f(x1)<f(x2),∴f(x)在(0,+∞)上是增函数.18.(8分)已知函数f(x)=sin2+sin cos.(Ⅰ)求f(x)的最小正周期;(Ⅱ)若x∈[,π],求f(x)的最大值与最小值.【解答】解:(Ⅰ)函数f(x)=sin2+sin cos=+sinx=sinx﹣cosx+=sin(x﹣)+,由T==2π,知f(x)的最小正周期是2π;(Ⅱ)由f(x)=sin(x﹣)+,且x∈[,π],∴≤x﹣≤,∴≤sin(x﹣)≤1,∴1≤sin(x﹣)+≤,∴当x=时,f(x)取得最大值,x=π时,f(x)取得最小值1.19.(8分)已知函数f(x)=1﹣(a>0且a≠1)是定义在R上的奇函数.(Ⅰ)求a的值;(Ⅱ)若关于x的方程|f(x)•(2x+1)|=m有1个实根,求实数m的取值范围.【解答】解:(Ⅰ)∵f(x)=1﹣(a>0且a≠1)是定义在R上的奇函数,∴f(0)=0,即1﹣=0,∴a=2;(Ⅱ)设h(x)=|f(x)•(2x+1)|,g(x)=m,如图所示,m=0或m≥1,两函数图象有一个交点,∴关于x的方程|f(x)•(2x+1)|=m有1个实根时,实数m的取值范围是m=0或m≥1.四、阅读与探究(共1小题,满分8分)20.(8分)阅读下面材料,尝试类比探究函数y=x2﹣的图象,写出图象特征,并根据你得到的结论,尝试猜测作出函数对应的图象.阅读材料:我国著名数学家华罗庚先生曾说:数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征.我们来看一个应用函数的特征研究对应图象形状的例子.对于函数y=,我们可以通过表达式来研究它的图象和性质,如:(1)在函数y=中,由x≠0,可以推测出,对应的图象不经过y轴,即图象与y轴不相交;由y≠0,可以推测出,对应的图象不经过x轴,即图象与x轴不相交.(2)在函数y=中,当x>0时y>0;当x<0时y<0,可以推测出,对应的图象只能在第一、三象限;(3)在函数y=中,若x∈(0,+∞)则y>0,且当x逐渐增大时y逐渐减小,可以推测出,对应的图象越向右越靠近x轴;若x∈(﹣∞,0),则y<0,且当x逐渐减小时y逐渐增大,可以推测出,对应的图象越向左越靠近x轴;(4)由函数y=可知f(﹣x)=﹣f(x),即y=是奇函数,可以推测出,对应的图象关于原点对称.结合以上性质,逐步才想出函数y=对应的图象,如图所示,在这样的研究中,我们既用到了从特殊到一般的思想,由用到了分类讨论的思想,既进行了静态(特殊点)的研究,又进行了动态(趋势性)的思考.让我们享受数学研究的过程,传播研究数学的成果.【解答】解:(1)在y=x2﹣中,x≠0,可以推测出:对应的图象不经过y轴,即与y轴不相交,(2)令y=0,即x2﹣=0,解得x=±1,可以推测出,对应的图象与x相交,交点坐标为(1,0)和(﹣1,0),(3)在y=x2﹣中,当0<x<1时,>1>x2,则y<0,当x>1时,<1<x2,则y>0,可以推测出:对应的图象在区间(0,1)上图象在x轴的下方,在区间(1,+∞)上图象在x轴的上方,(4)在y=x2﹣中,若x∈(0,+∞),则当x逐渐增大时逐渐减小,x2﹣,逐渐增大,即y逐渐增大,所以原函数在(0,+∞)是增函数,可以推测出:对应的图象越向右逐渐升高,是单调递增的趋势,(5)由函数y=x2﹣可知f(﹣x)=f(x),即函数为偶函数,可以推测出:对应的图象关于y轴对称赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.O DAB CEAOD CB2.如图,已知四边形ABCD内接于⊙O,对角线AC⊥BD于P,设⊙O的半径是2。
贵州省遵义市南白中学2016-2017学年高一下学期期中数学试卷(Word版含答案)

2016-2017学年贵州省遵义市南白中学高一(下)期中数学试卷一.选择题(本题共12小题,每小题5分,共60分;每个小题只有一个正确选项)1.设集合M={x|4≤2x≤16},N={x|x(x﹣3)<0},则M∩N=()A.(0,3)B. C. C.;x(x﹣3)<0⇒0<x<3,则N={x|x(x﹣3)<0}=(0,3);则M∩N=,∴α=.故选:A.3.已知△ABC中,a=,b=,B=60°,那么角A等于()A.45° B.60° C.120°或60°D.135°或45°【考点】HP:正弦定理.【分析】根据正弦定理,即可求出A的大小.【解答】解:∵△ABC中,a=,b=,∴a<b,且A<B,又B=60°,即A<60°,由正弦定理得sinA==,则A=45°或135°(舍去),故选:A.4.数列{a n}满足a n=4a n﹣1+3,且a1=0,则此数列的第5项是()A.15 B.255 C.16 D.36【考点】8H:数列递推式.【分析】分别令n=2,3,4,5代入递推公式计算即可.【解答】解:a2=4a1+3=3a3=4a2+3=4×3+3=15a4=4a3+3=4×15+3=63a5=4a4+3=4×63+3=255故选B.5.在△ABC中,若acosA=bsinB,则sinAcosA+cos2B=()A.1 B.C.﹣1 D.【考点】HP:正弦定理.【分析】利用三角形中的正弦定理,将已知等式中的边用三角形的角的正弦表示,代入要求的式子,利用三角函数的平方关系求出值.【解答】解:∵acosA=bsinB,∴由正弦定理得sinAcosA=sinBsinB,∴sinAcosA+cos2B=sin2B+cos2B=1.故选:A.6.在等比数列{a n}中,a n>0,a2=1﹣a1,a4=9﹣a3,则a4+a5=()A.16 B.27 C.36 D.81【考点】8G:等比数列的性质.【分析】首先根据等比数列的性质求出q=3和a1=的值,然后代入a4+a5=a1q3+a1q4=即可求出结果.【解答】解:∵a2=1﹣a1,a4=9﹣a3∴a1q+a1=1 ①a1q3+a1q2=9 ②两式相除得,q=±3∵a n>0∴q=3 a1=∴a4+a5=a1q3+a1q4=27故选B.7.若△ABC的内角A满足,则sinA﹣cosA=()A.B.C.D.【考点】GS:二倍角的正弦.【分析】A是三角形的内角,可得sinA>cosA.再利用(sinA﹣cosA)2=1﹣2sinAcosA=1﹣sin2A 即可得出.【解答】解:∵A是三角形的内角,∴sinA>cosA.∵(sinA﹣cosA)2=1﹣2sinAcosA=1﹣sin2A=1﹣=.∴.故选:A.8.在等差数列{a n}中,若a3+a4+a5+a6+a7=15,a9+a10+a11=39,则公差d等于()A.1 B.2 C.3 D.4【考点】84:等差数列的通项公式.【分析】利用等差数列的性质及其通项公式即可得出.【解答】解:由等差数列{a n}的性质,a3+a4+a5+a6+a7=15,a9+a10+a11=39,∴5a5=15,3a10=39.即a5=3,a10=13,∴3+5d=13,解得d=2.故选:B.9.设等比数列{a n}的前n项和为S n.若S2=3,S4=15,则S6=()A.31 B.32 C.63 D.64【考点】89:等比数列的前n项和.【分析】由等比数列的性质可得S2,S4﹣S2,S6﹣S4成等比数列,代入数据计算可得.【解答】解:S2=a1+a2,S4﹣S2=a3+a4=(a1+a2)q2,S6﹣S4=a5+a6=(a1+a2)q4,所以S2,S4﹣S2,S6﹣S4成等比数列,即3,12,S6﹣15成等比数列,可得122=3(S6﹣15),解得S6=63故选:C10.△ABC的内角A、B、C的对边分别是a、b、c,若B=2A,a=1,b=,则c=()A.B.2 C.D.1【考点】HP:正弦定理;GS:二倍角的正弦.【分析】利用正弦定理列出关系式,将B=2A,a,b的值代入,利用二倍角的正弦函数公式化简,整理求出cosA的值,再由a,b及cosA的值,利用余弦定理即可求出c的值.【解答】解:∵B=2A,a=1,b=,∴由正弦定理=得:===,∴cosA=,由余弦定理得:a2=b2+c2﹣2bccosA,即1=3+c2﹣3c,解得:c=2或c=1(经检验不合题意,舍去),则c=2.故选B11.已知函数,其图象相邻的两条对称轴方程为x=0与,则()A.f(x)的最小正周期为2π,且在(0,π)上为单调递增函数B.f(x)的最小正周期为2π,且在(0,π)上为单调递减函数C.f(x)的最小正周期为π,且在上为单调递增函数D.f(x)的最小正周期为π,且在上为单调递减函数【考点】GQ:两角和与差的正弦函数;H1:三角函数的周期性及其求法;H5:正弦函数的单调性.【分析】利用两角和差的正弦公式化简函数的解析式为f(x)=2sin(ωx﹣),由题意可得=,解得ω的值,即可确定函数的解析式为f(x)=2sin(2x﹣),由此求得周期,由2kπ﹣≤2x﹣≤2kπ+,k∈z,求得x 的范围,即可得到函数的增区间,从而得出结论.【解答】解:∵函数=2[sin(ωx﹣cosωx]=2sin(ωx﹣),∴函数的周期为.再由函数图象相邻的两条对称轴方程为x=0与,可得=,解得ω=2,故f(x)=2sin(2x﹣).故f(x)=2sin(2x﹣)的周期为=π.由 2kπ﹣≤2x﹣≤2kπ+,k∈z,可得kπ﹣≤x≤kπ+,故函数的增区间为,k∈z,故函数在上为单调递增函数,故选C.12.设等差数列{a n}的前n项和为S n,且S2015>0,S2016<0.则数列{}的最大的项的n 的值为()A.1007 B.1008 C.1009 D.1010【考点】85:等差数列的前n项和.【分析】等差数列{a n}的前n项和为S n,且S2015>0,S2016<0.可得S2015=2015a1008>0,S2016=1008(a1008+a1009)<0.可得a1008>0,a1009<0,公差d<0.可知:S1008最大,而a1008是正值中的最小值.即可得出.【解答】解:等差数列{a n}的前n项和为S n,且S2015>0,S2016<0.∴S2015==2015a1008>0,S2016==1008(a1008+a1009)<0.∴a1008>0,a1009<0,公差d<0.可知:S1008最大,而a1008是正值中的最小值.则数列{}的最大的项的n的值是1008.故选:B.二.填空题(本题共4小题,每小题5分,共20分;将正确答案填写在相应的横线上)13.已知△ABC得三边长成公比为的等比数列,则其最大角的余弦值为.【考点】HR:余弦定理;8G:等比数列的性质.【分析】根据三角形三边长成公比为的等比数列,根据等比数列的性质设出三角形的三边为a, a,2a,根据2a为最大边,利用大边对大角可得出2a所对的角最大,设为θ,利用余弦定理表示出cosθ,将设出的三边长代入,即可求出cosθ的值.【解答】解:根据题意设三角形的三边长分别为a, a,2a,∵2a>a>a,∴2a所对的角为最大角,设为θ,则根据余弦定理得:cosθ==﹣.故答案为:﹣14.设函数,则f=f(5×400+4)=f(4),从而可得答案.【解答】解:∵,∴f=f(4)=42+1=17,故答案为:17.15.已知正项等比数列{a n}中,a5a2n﹣5=102n(n≥3,n∈N*),则当n≥1,n∈N*时表达式lga1+lga2+lga3+…+lga n的值为.【考点】88:等比数列的通项公式.【分析】由正项等比数列{a n}中,a5a2n﹣5=102n(n≥3,n∈N*),得到,由此能求出lga1+lga2+lga3+…+lga n的值.【解答】解:∵正项等比数列{a n}中,a5a2n﹣5=102n(n≥3,n∈N*),∴=102n,∴,∴当n≥1,n∈N*时,lga1+lga2+lga3+…+lga n=lg(a1×a2×…×a n)=lg=.故答案为:.16.已知数列{a n}的通项公式a n=nsin,其前n项和为S n,则S2016= ﹣1008 .【考点】8E:数列的求和.【分析】结合三角函数的周期性可知a4k﹣3=4k﹣3、a4k﹣2=0、a4k﹣1=﹣(4k﹣1)、a4k=0,进而可知a4k﹣3+a4k﹣2+a4k﹣1+a4k=﹣2,计算即得结论.【解答】解:因为a n=nsin,所以a4k﹣3=4k﹣3,a4k﹣2=0,a4k﹣1=﹣(4k﹣1),a4k=0,所以a4k﹣3+a4k﹣2+a4k﹣1+a4k=﹣2,又因为504×4=2016,所以S2016=504×(﹣2)=﹣1008,故答案为:﹣1008.三.解答题(本题共6小题,共70分;作答应写出必要的文字说明、证明过程或演算步骤)17.已知直线l1上的点满足ax+4y+6=0,直线l2上的点满足(a+1)x+ay﹣=0.试求:(Ⅰ)a为何值时l1∥l2(Ⅱ)a为何值时l1⊥l2.【考点】IJ:直线的一般式方程与直线的垂直关系;II:直线的一般式方程与直线的平行关系.【分析】(Ⅰ)根据直线的平行关系得到关于a的方程,解出即可;(Ⅱ)根据直线的垂直关系得到关于a的方程,解出即可.【解答】解:(Ⅰ)∵l1∥l2,∴a2﹣4(a+1)=0,且4×(﹣)﹣6a≠0,解得:a=4;(Ⅱ)∵l1⊥l2,a(a+1)+4a=0,解得:a=0或a=﹣.18.设数列{a n}的前n项和为S n,且满足a1=1,2S n=(n+1)a n.(Ⅰ)求{a n}的通项公式;(Ⅱ)设T n=++…+,求T n.【考点】8E:数列的求和;8H:数列递推式.(Ⅰ)由a1=1,2S n=(n+1)a n,得n≥2时,2S n﹣1=na n﹣1,两式相减得,【分析】n≥2,由此利用累乘法和能求出a n=n.(Ⅱ)由==,利用裂项求能求出T n=++…+的值.【解答】解:(Ⅰ)∵数列{a n}的前n项和为S n,且满足a1=1,2S n=(n+1)a n,①∴n≥2时,2S n﹣1=na n﹣1,②①﹣②,得2a n=(n+1)a n﹣na n﹣1,n≥2,整理,得,n≥2,∴=1×=n,n=1时,上式成立,∴a n=n.(Ⅱ)∵==,∴T n=++…+=1﹣=1﹣=.19.在锐角△ABC中,角A,B,C所对的边分别为a,b,c,且=(,2sinA),=(c,a)若(Ⅰ)求角C的大小;(Ⅱ)若c=,且△ABC的面积为,求a+b的值.【考点】HT:三角形中的几何计算.【分析】(Ⅰ)根据向量的数量积以及正弦定理可得sinC=,即可求出C;(Ⅱ)根据三角形的面积公式和余弦定理即可求出.【解答】解:(Ⅰ)由∥得a=2csinA,及正弦定理得sinA=2sinCsinA,∵A∈(0,π),∴sinA≠0,∴sinC=,∵△ABC中是锐角三角形,∴C=;(Ⅱ)∵S△ABC=absinC=,∴ab=6,由余弦定理得c2=a2+b2﹣2abcosC,∴7=a2+b2﹣ab=(a+b)2﹣3ab═(a+b)2﹣18,解得a+b=5或a+b=﹣5(舍),∴a+b=5.20.设数列{a n}满足a1+3a2+32a3+…+3n﹣1a n=(n∈N*).(1)求数列{a n}的通项公式;(2)设b n=,求数列{b n}的前n项和S n.【考点】8E:数列的求和;8H:数列递推式.【分析】(1)由a1+3a2+32a3+…+3n﹣1a n=⇒当n≥2时,a1+3a2+32a3+…+3n﹣2a n﹣1=,两式作差求出数列{a n}的通项.(2)由(1)的结论可知数列{b n}的通项.再用错位相减法求和即可.【解答】解:(1)∵a1+3a2+32a3+…+3n﹣1a n=,①∴当n≥2时,a1+3a2+32a3+…+3n﹣2a n﹣1=.②①﹣②,得3n﹣1a n=,所以(n≥2),在①中,令n=1,得也满足上式.∴.(2)∵,∴b n=n•3n.∴S n=3+2×32+3×33+…+n•3n.③∴3S n=32+2×33+3×34+…+n•3n+1.④④﹣③,得2S n=n•3n+1﹣(3+32+33+…+3n),即2S n=n•3n+1﹣.∴.21.在海岸A处,发现北偏东45°方向,距离A为海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜(Ⅰ)问C船与B船相距多少海里?C船在B船的什么方向?(Ⅱ)问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.【考点】HU:解三角形的实际应用.【分析】(I)在△ABC中根据余弦定理计算BC,再利用正弦定理计算∠ABC即可得出方位;(II)在△BCD中,利用正弦定理计算∠BCD,再计算BD得出追击时间.【解答】解:(I)由题意可知AB=﹣1,AC=2,∠BAC=120°,在△ABC中,由余弦定理得:BC2=AB2+AC2﹣2AB•AC•cos120°=6,∴BC=.由正弦定理得:,即,解得sin∠ABC=,∴∠ABC=45°,∴C船在B船的正西方向.(II)由(1)知BC=,∠DBC=120°,设t小时后缉私艇在D处追上走私船,则BD=10t,CD=10t,在△BCD中,由正弦定理得:,解得sin∠BCD=,∴∠BC D=30°,∴△BCD是等腰三角形,∴10t=,即t=.∴缉私艇沿东偏北30°方向行驶小时才能最快追上走私船.22.设△ABC的内角A,B,C所对的边分别为a,b,c且acosC+,则角A的大小为60°;若a=1,则△ABC的周长l的取值范围为(2,3] .【考点】HP:正弦定理.【分析】将已知的等式左右两边都乘以2变形后,利用正弦定理化简,再利用诱导公式及两角和与差的正弦函数公式变形,根据sinC不为0,得出cosA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;由A的度数求出sinA的值,及B+C的度数,用B 表示出C,由正弦定理表示出b与c,而三角形ABC的周长l=a+b+c,将表示出的b与c,及a 的值代入,利用两角和与差的正弦函数公式化简,整理后再利用特殊角的三角函数值及两角和与差的正弦函数公式化为一个角的正弦函数,由B的范围求出这个角的范围,利用正弦函数的图象与性质得出此时正弦函数的值域,即可得到l的范围.【解答】解:acosC+c=b变形得:2acosC+c=2b,利用正弦定理得:2sinAcosC+sinC=2sinB=2sin(A+C)=2sinAcosC+2cosAsinC,∴sinC=2cosAsinC,即sinC(2cosA﹣1)=0,由sinC≠0,得到cosA=,又A为三角形的内角,则A=60°;∵a=1,sinA=,B+C=120°,即C=120°﹣B,∴===,即b=sinB,c=sin,则△ABC的周长l=a+b+c=1+sinB+sin=1+(sinB+cosB)=1+2(sinB+cosB)=1+2sin(B+30°),∵0<B<120°,∴30°<B+30°<150°,∴<sin(B+30°)≤1,即2<1+2sin(B+30°)≤3,则l范围为(2,3].故答案为:60°;(2,3]2017年6月13日。
贵州省遵义市南白中学2016-2017学年高一下学期期中考试数学试题(word版含答案)

遵义市南白中学2016-2017-2高一半期考试试卷数 学注意事项:1.本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分;考试时间120分钟,满分150分2. 所有试题均在答题卡上作答,在试卷上作答无效........,考试结束后,请将答题卡交回 第Ⅰ卷(选择题 共60分)一.选择题(本题共12小题,每小题5分,共60分;每个小题只有一个正确选项) 1. 设集合{}1624≤≤=x x M ,{}0)3(<-=x x x N ,则=N MA .()3,0B .[]3,2C .[)3,2D .()4,32. 若直线过点(1,2),(4,2+3)则此直线的倾斜角是A .6πB .4πC .3πD .2π3. 已知△ABC 中,,︒===60,3,2B b a 那么角A 等于A .135°或45°B .30°C .135°D . 45° 4. 已知数列{}n a 的通项公式143n n a a -=+,且10a =,则此数列的第5项是A. 15B. 255C. 16D. 36 5. 在△ABC 中,若,sin cos B b A a =则=+B A A 2cos cos sinA .1B .21C .1-D .21-6. 在等比数列{}n a 中,若n a >0,且a 2=1-a 1,a 4=9-a 3,则a 4+a 5的值A .16B .81C .36D .277. 若ABC ∆的内角A 满足2sin 23A =-,则sin cos A A -=A. B.C .53D .53- 8. 在等差数列{}n a 中,若3456715a a a a a ++++=,9101139a a a ++=,则公差d 等于A .1B .2C .3D .49. 设等比数列{}n a 的前n 项和为n S ,若23S =,415S =,则6S =A. 31B. 32C. 63D. 6410. △ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若B =2A ,a =1,b =3,则c =A .2 3B .1 C. 2D . 211.已知函数()sin())(0,||)2f x x x πωφωφωφ=++><,其图象相邻的两条对称轴方程为0x =与2x π=,则A .()f x 的最小正周期为2π,且在(0,)π上为单调递增函数B .()f x 的最小正周期为2π,且在(0,)π上为单调递减函数C .()f x 的最小正周期为π,且在(0,)2π上为单调递增函数 D .()f x 的最小正周期为π,且在(0,)2π上为单调递减函数 12. 设等差数列}{n a 的前n 项和为n S ,且20150S >,20160S <.则数列{}nn S a 的最大的项的n的值为 A .1007 B .1008 C .1009 D.1010第Ⅱ卷(非选择题 共90分)二.填空题(本题共4小题,每小题5分,共20分;将正确答案填写在相应的横线上) 13. 已知△ABC 的三边长成公比为2的等比数列,则其最大角的余弦值为________.14. 设函数⎩⎨⎧-<≤+=),5(,50,1)(2x f x x x f 则=)2014(f ________. 15. 已知正项等比数列{}n a 中,252510(3,)nn a a n n N -+=≥∈,则当1,n n N +≥∈时 表达式123lg lg lg lg n a a a a ++++ 的值为=________.16. 已知数列{}n a 的通项公式sin2n n a n π=,其前n 项和为n S ,则2016S =_______.三.解答题(本题共6小题,共70分;作答应写出必要的文字说明、证明过程或演算步骤) 17(本题满分10分)已知直线1l 上的点满足460ax y ++=,直线2l 上的点满足33(1)042a x ay ++-=试求:(Ⅰ)a 为何值时1l ∥2l ; (Ⅱ)a 为何值时1l⊥2l.18(本题满分12分) 设数列}{n a 的前n 项和为n S ,且满足11a =,2(1)n n S n a =+.(Ⅰ)求{n a }的通项公式;(Ⅱ)求和T n =1211123(1)n a a n a ++++19(本题满分12分)在锐角ABC △中,角C B A ,,所对的边分别为c b a ,,,且()A m s i n 2,3=→,()a c n ,=→若→m //→n(Ⅰ)求角C 的大小;(Ⅱ)若c = ABC的面积为,求a b +的值..20(本题满分12分)已知:数列}{n a 满足*-∈=++++N a na a a a n n ,333313221 .(Ⅰ)求数列}{n a 的通项;(Ⅱ)设,n n a nb =求数列}{n b 的前n 项和S n .21(本题满分12分)在海岸A 处,发现北偏东45方向,距离A 为)13(- 海里的B 处有一艘走私船,在A 处北偏西75方向,距离A 为2 海里的C 处有一艘缉私艇奉命以310海里 /时的速度追截走私船,此时,走私船正以10 海里 /时的速度从B 处向北偏东30方向逃窜(Ⅰ)问C 船与B 船相距多少海里?C 船在B 船的什么方向?(Ⅱ)问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间。
贵州省遵义市2016-2017学年高一下学期期末考试地理试题版含解析
遵义市2016~2017学年度第二学期期末统考试卷高一地理第Ⅰ卷本卷共有30个小题,每小题2分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的。
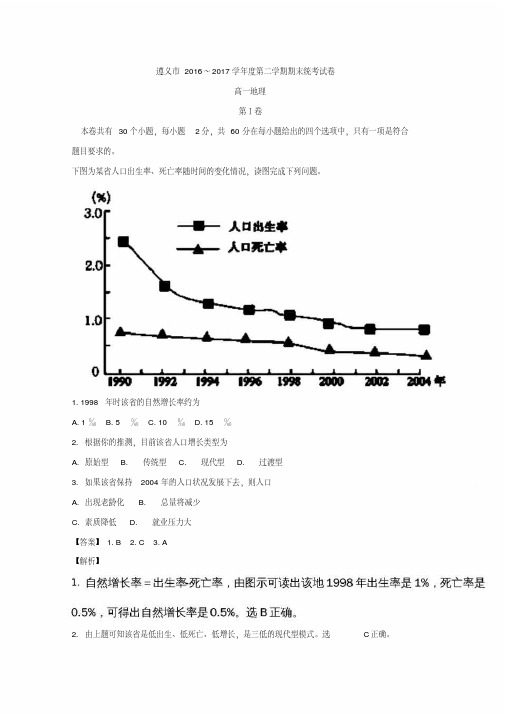
下图为某省人口出生率、死亡率随时间的变化情况,读图完成下列问题。
1. 1998年时该省的自然增长率约为A. 1‰B. 5‰C. 10‰D. 15‰2. 根据你的推测,目前该省人口增长类型为A. 原始型B. 传统型C. 现代型D. 过渡型3. 如果该省保持2004年的人口状况发展下去,则人口A. 出现老龄化B. 总量将减少C. 素质降低D. 就业压力大【答案】1. B 2. C 3. A【解析】2. 由上题可知该省是低出生、低死亡、低增长,是三低的现代型模式。
选C正确。
3. 2004年,该省人口的自然增长率维持较低水平,出生率持续下降,照此下去,该省将出现老龄化现象。
选A正确。
下图为示意人口容量值与要素之间的关系,横轴表示各制约因素的影响程度,读图完成下列问题。
4. 环境人口容量是指A. -个恒定不变的数量B. 环境最适宜的人口数量C. 环境能持续供养的人口数量D. 环境能供养人口的最佳数量5. 对图中相关原理说法正确的是A. 甲为人口合理容量B. 乙为环境人口容量C. 人口容量与消费水平呈正相关D. 人口容量与资源、科技等呈正相关【答案】4. C 5. D【解析】4. 环境人口容量是指一个国家或地区的环境人口容量,是在可预见到的时期内,利用本地资源及其他资源和智力、技术等条件,在保证符合社会文化准则的物质生活水平条件下,该国家或地区所能持续供养的人口数量。
它会随着生产力水平的变化而变化,并不是一恒定数;环境最适宜的人口数是环境的合理人口容量。
选C正确。
5. 图中甲值大于乙值,甲表示环境人口容量,乙表示环境合理人口容量;人口容量与消费水平呈负相关,与资源、科技呈正相关。
选D正确。
【点晴】环境人口容量的大小受到资源因素、科学技术因素、综合生活水平等因素的影响。
贵州省遵义航天高级中学2016-2017学年高一下学期第一次月考理科综合试题含答案
2016~2017学年第二学期第一次月考高一理科综合试题可能用到的相对原子质量:H:1 O:16 C:12 N:14 Na:23 Fe:56一、单项选择题(共18题,每小题6分,共108分)1.下图所示为真核生物细胞呼吸的部分过程,可在细胞质基质中发生的是A.①②③ B.②③④C.①③④D.①②④2.细胞呼吸原理广泛应用于生产实践中。
下表中有关措施与对应的的是目的不恰当...选应用措施目的项A种子贮存晒干降低自由水含量,降低细胞3.下图为某同学对植物叶绿体中色素分离的结果,其中所标记的色素名称或颜色正确的是()4.下列是关于光合作用的实验,叙述不正确的是选项实验内容实验结论A 萨克斯的实验证明绿色植物叶片在光下能产生淀粉B恩吉尔曼的水绵实验证明水绵在光下能产生氧气呼吸B水果保鲜零上低温降低酶的活性,降低细胞呼吸C乳酸菌制作酸奶通气促进乳酸菌的有氧呼吸D栽种庄稼疏松土壤促进根有氧呼吸,有利于吸收矿质离子C 卡尔文的实验证明了CO2被用于合成糖类等有机物D 鲁宾和卡门的同位素标记实验证明光合作用释放的氧气都来自反应物CO25.光合作用可分为光反应和暗反应两个阶段,下列叙述正确的是( )A.光反应消耗水,暗反应消耗ATP B..光反应不需要酶,暗反应需要多种酶C.光反应储存能量,暗反应消耗能量D.光反应固定二氧化碳,暗反应还原二氧化碳6.染色单体形成、染色体出现和消失分别发生在细胞周期的()A.前期、中期、后期B.间期、前期、末期C.。
间期、前期、后期D.前期、后期、末期7.化学与人类生活、生产和社会可持续发展密切相关,下列说法正确的是()A.为了防止富脂食品氧化变质,延长食品的保质期,在包装袋中常放入生石灰B.用活性炭为糖浆脱色和用次氯酸盐漂白纸浆的原理相同C。
小苏打是发酵粉的主要成分D.淀粉遇碘变蓝,故在厨房里可用米汤检验加碘食盐中的碘8.设N A为阿伏加德罗常数的值,下列说法不正确的是()A.用带孔的铝箔包裹的4.6g钠与足量的水反应放出的气体大于0。
2016-2017年贵州省遵义市航天高中高一(下)期中数学试卷和答案

【解答】解:根据题意,依次分析选项: 对于 A、函数 y=sinx,有 f(﹣x)=sin(﹣x)=﹣sinx=﹣f(x) ,为奇函数,且当 x=kπ,k 为整数时,y=sinx=0,y=sinx 存在零点,符合题意; 对于 B、y=lnx,为对数函数,是非奇非偶函数,不符合题意; 对于 C、y=x2,为二次函数,是偶函数,不符合题意; 对于 D、y= ,为反比例函数,是奇函数,但不存在零点,不符合题意; 故选:A. 4. (5 分)在△ABC 中, A. + B. =
5. (5 分)已知 a= A.b<c<a
B.a<b<c
C.b<a<c
6. (5 分)为了得到函数 y=sin(3x﹣ 上所有点( ) 个单位长度 个单位长 个单位长度 个单位长度
)的图象,只需要把函数 y=sin3x 的图象
A.向左平行移动 B.向右平行移动 C.向左平行移动 D.向右平行移动 7. (5 分) A.﹣sin3﹣cos3
,求证:数列{bn}为等差数列; .
第 3 页(共 13 页)
2016-2017 学年贵州省遵义市航天高中高一(下)期中数 学试卷
参考答案与试题解析
一、选择题:本题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有 一项是符合题目要求. 1. (5 分)已知集合 A={0,1,2,3},B={y|y=2x,x∈A},则 A⋂ B=( A.{0,1} B.{0,2} C.{1,2} D.{1,3} )
=( B.sin3﹣cos3
) D.cos3﹣sin3
C.sin3+cos3
8. (5 分)已经等差数列{an}的前 n 项和为 Sn,S9>0,S8<0,则使得 Sn 取得最 小值的 n 为( A.3 9. (5 分)已知 ) B.4 C.5 D.6 =( )
贵州黔东南州凯里一中2016-2017学年高一下学期期中数学试卷 含解析
2016—2017学年贵州省黔东南州凯里一中高一(下)期中数学试卷一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的).1.如图所示,U是全集,A、B是U的子集,则阴影部分所表示的集合是()A.A∩B B.B∩(∁U A) C.A∪B D.A∩(∁U B)2.已知a,b∈R,且a>b,则下列不等式中成立的是( )A. B.a2>b2C.lg(a﹣b)>0 D.3.已知函数f(x)=,则f(5)=( )A.32 B.16 C. D.4.要得到函数y=sin(2x+)的图象,只需将函数y=sin2x的图象()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位5.在△ABC 中,已知a=2,b=2,A=30°,则B=()A.60°或120°B.30°或150°C.60°D.30°6.等差数列{a n}中,a3,a7是函数f(x)=x2﹣4x+3的两个零点,则{a n}的前9项和等于()A.﹣18 B.9 C.18 D.367.已知0<a<1,则a2、2a、log2a的大小关系是()A.a2>2a>log2a B.2a>a2>log2a C.log2a>a2>2a D.2a>log2a>a2 8.已知向量、满足||=1,||=2,且(4+)⊥,则与的夹角为()A.30°B.60°C.120°D.150°9.若函数是奇函数,且在区间是减函数,则ϕ的值可以是( )A.B.C.D.10.设f(x)是定义在R上的恒不为零的函数,对任意实数x,y∈R,都有f(x)•f(y)=f(x+y),若a1=,a n=f(n)(n∈N*),则数列{a n}的前n项和S n的取值范围是( )A.[,2)B.[,2] C.[,1) D.[,1]11.已知α为第四象限的角,且=,则tanα=()A.﹣ B.﹣ C.﹣D.﹣312.若函数y=f(x)对x∈R满足f(x+2)=f(x),且x∈时,f(x)=1﹣x2.设g(x)=,则函数h(x)=f(x)﹣g(x)在区间内零点的个数为()A.8 B.10 C.12 D.14二、填空题(本大题共4小题,每小题5分,共20分)13.已知tanα=3,则的值为.14.设a>0,b>0,若3a与3b的等比中项是,则+的最小值为.15.如图,在正方形ABCD中,AD=4,E为DC上一点,且=3,F为BC的中点,则•= .16.设表示不超过x的最大整数,如,对于给定的n∈N*,定义,则当时,函数的值域为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.已知集合A={x|x2﹣4x﹣5≤0},函数y=ln(x2﹣4)的定义域为B.(Ⅰ)求A∩B;(Ⅱ)若C={x|x≤a﹣1},且A∪(∁R B)⊆C,求实数a的取值范围.18.设A,B,C,D为平面内的四点,且A(1,3),B(2,﹣2),C (4,1)(Ⅰ)若=,求D点的坐标及||;(Ⅱ)设向量=,=,若k﹣与+3平行,求实数k的值.19.在△ABC中,内角A,B,C的对边分别为a,b,c,且=.(Ⅰ)求角B的大小;(Ⅱ)若b=2,△ABC的面积为2,求△ABC的周长.20.某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米.已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元.(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;(总开发费用=总建筑费用+购地费用)(2)要使整幢写字楼每平方米开发费用最低,该写字楼应建为多少层?21.已知函数f(x)=sinxcosx﹣cos2x﹣m.(Ⅰ)求函数f(x)的最小正周期与单调递增区间;(Ⅱ)若x∈时,方程f(x)=0有实数解,求实数m的取值范围.22.已知数列{a n}的前n项和为S n,a1=1且a n+1=2S n+1(n∈N*);数列{b n}中,b1=3且对n∈N*,点(b n,b n+1)都在函数y=x+2的图象上.(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)是否存在正整数n,使得a1b1+a2b2+…+a n b n>100n?若存在,求n的最小值;若不存在,请说明理由.2016-2017学年贵州省黔东南州凯里一中高一(下)期中数学试卷参考答案与试题解析一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的).1.如图所示,U是全集,A、B是U的子集,则阴影部分所表示的集合是()A.A∩B B.B∩(∁U A) C.A∪B D.A∩(∁U B)【考点】1J:Venn图表达集合的关系及运算.【分析】集合韦恩图,判断出阴影部分中的元素在B中但不在A中即在B与A的补集的交集中.【解答】解:由图知,阴影部分中的元素在集合B中但不在集合A中,所以阴影部分所表示的集合是B∩(∁U A)故选B2.已知a,b∈R,且a>b,则下列不等式中成立的是()A. B.a2>b2C.lg(a﹣b)>0 D.【考点】71:不等关系与不等式.【分析】此题要结合指数函数的图象,利用指数函数的单调性解决.【解答】解:由指数函数x图象与性质得,此指数函数在R是减函数,又a>b,∴故选D.3.已知函数f(x)=,则f(5)=()A.32 B.16 C. D.【考点】3T:函数的值;3B:分段函数的解析式求法及其图象的作法.【分析】根据题设条件知f(5)=f(2)=f(﹣1)=2﹣1=.【解答】解:f(5)=f(2)=f(﹣1)=2﹣1=.故选C.4.要得到函数y=sin(2x+)的图象,只需将函数y=sin2x的图象( )A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【分析】由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.【解答】解:由于函数y=sin(2x+)=sin2(x+),∴将函数y=sin2x的图象向左平移个单位长度,可得函数y=sin (2x+)的图象,故选:B5.在△ABC 中,已知a=2,b=2,A=30°,则B=()A.60°或120°B.30°或150°C.60°D.30°【考点】HP:正弦定理.【分析】由已知结合正弦定理可得sinB=,结合范围B∈(30°,180°),可求B的值.【解答】解:∵a=2,b=2,A=30°,∴由正弦定理可得sinB===,又∵B∈(30°,180°),∴B=60°或120°.故选:A.6.等差数列{a n}中,a3,a7是函数f(x)=x2﹣4x+3的两个零点,则{a n}的前9项和等于()A.﹣18 B.9 C.18 D.36【考点】85:等差数列的前n项和.【分析】由韦达定理得a3+a7=4,从而{a n}的前9项和S9==,由此能求出结果.【解答】解:∵等差数列{a n}中,a3,a7是函数f(x)=x2﹣4x+3的两个零点,∴a3+a7=4,∴{a n}的前9项和S9===.故选:C.7.已知0<a<1,则a2、2a、log2a的大小关系是()A.a2>2a>log2a B.2a>a2>log2a C.log2a>a2>2a D.2a>log2a>a2【考点】4M:对数值大小的比较.【分析】根据指数函数,幂函数,对数函数的性质分别判断取值范围即可得到结论.【解答】解:∵0<a<1,∴0<a2<1,1<2a<2,log2a<0,∴2a>a2>log2a,故选:B.8.已知向量、满足||=1,||=2,且(4+)⊥,则与的夹角为()A.30°B.60°C.120°D.150°【考点】9R:平面向量数量积的运算.【分析】根据(4+)•=0得出=﹣1,从而得出cos<>.【解答】解:∵(4+)⊥,∴(4+)•=4+=0,∴=﹣b2=﹣1.∴cos<>===﹣,∴<>=120°.故选C.9.若函数是奇函数,且在区间是减函数,则ϕ的值可以是() A.B.C.D.【考点】H2:正弦函数的图象.【分析】根据正弦函数的奇偶性可得ϕ+=kπ,k∈Z,故可取ϕ=,检验满足条件,可得结论.【解答】解:∵函数是奇函数,∴ϕ+=kπ,k∈Z,故可取ϕ=,此时,f(x)=2sin(2x+π)=﹣2sin2x,在区间上,2x∈,y=sin2x单调递增,故f(x)=﹣2sin2x,满足f(x)在区间是减函数,故选:B.10.设f(x)是定义在R上的恒不为零的函数,对任意实数x,y∈R,都有f(x)•f(y)=f(x+y),若a1=,a n=f(n)(n∈N*),则数列{a n}的前n项和S n的取值范围是()A.[,2)B.[,2] C.[,1) D.[,1]【考点】3P:抽象函数及其应用.【分析】根据f(x)•f(y)=f(x+y),令x=n,y=1,可得数列{a n}是以为首项,以为等比的等比数列,进而可以求得S n,进而S n的取值范围.【解答】解:∵对任意x,y∈R,都有f(x)•f(y)=f(x+y),∴令x=n,y=1,得f(n)•f(1)=f(n+1),即==f(1)=,∴数列{a n}是以为首项,以为等比的等比数列,∴a n=f(n)=()n,∴S n==1﹣()n∈[,1).故选C.11.已知α为第四象限的角,且=,则tanα=()A.﹣B.﹣C.﹣ D.﹣3【考点】GI:三角函数的化简求值.【分析】由已知利用三倍角公式及诱导公式化简求得sinα,进一步得到cosα,再由商的关系求得tanα.【解答】解:由=,得,即,得sinα=±.∵α为第四象限的角,∴sinα=﹣,则cosα=.∴tanα=.故选:A.12.若函数y=f(x)对x∈R满足f(x+2)=f(x),且x∈时,f(x)=1﹣x2.设g(x)=,则函数h(x)=f(x)﹣g (x)在区间内零点的个数为()A.8 B.10 C.12 D.14【考点】52:函数零点的判定定理.【分析】由已知可得函数f(x)是周期为2的周期函数,作出函数f(x)与g(x)的图象,数形结合得答案.【解答】解:函数h(x)=f(x)﹣g(x)的零点,即方程函数f(x)﹣g(x)=0的根,也就是两个函数y=f(x)与y=g(x)图象交点的横坐标,由f(x+2)=f(x),可得f(x)是周期为2的周期函数,又g(x)=,作出两函数的图象如图:∴函数h(x)=f(x)﹣g(x)在区间内零点的个数为14.故选:D.二、填空题(本大题共4小题,每小题5分,共20分)13.已知tanα=3,则的值为.【考点】GH:同角三角函数基本关系的运用.【分析】利用同角三角函数的基本关系,求得要求式子的值.【解答】解:∵tanα=3,则==,故答案为:.14.设a>0,b>0,若3a与3b的等比中项是,则+的最小值为9 .【考点】7F:基本不等式;88:等比数列的通项公式.【分析】由条件可得3a•3b =3,故a+b=1,利用基本不等式求出它的最小值.【解答】解:∵a>0,b>0,是3a与3b的等比中项,∴3a•3b =3,故a+b=1.∴+=+=1+4++≥5+2 =9,当且仅当=时,等号成立,故+的最小值为9,故答案为:9.15.如图,在正方形ABCD中,AD=4,E为DC上一点,且=3,F为BC的中点,则•= 20 .【考点】9R:平面向量数量积的运算.【分析】利用向量的加法法则与共线向量基本定理把用基向量表示,展开数量积得答案.【解答】解:如图,在正方形ABCD中,AD=4.∵=3,∴,又F为BC的中点,∴.∴•====.故答案为:20.16.设表示不超过x的最大整数,如,对于给定的n∈N*,定义,则当时,函数的值域为.【考点】34:函数的值域.【分析】将区间分为、=1,所以==4当=2,∴==,故函数C8x的值域是故答案为:三、解答题(本大题共6小题,共70分。
贵州省贵阳市第六中学2016-2017学年高一下学期第一次测试化学试题缺答案
1。
答卷前,考生务必在答题卡上指定位置填写自己的姓名、考号、并粘贴条形码。
2.选择题的作答:毎小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号.3。
非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内.4。
考试结束后,只上交答题卡,学生自己保存好试卷以备讲评使用。
第Ⅰ卷(共64分)可能用到的相对原子质量:C-12 H-1 O—16 N—14 S-32 Mn—55 K—39 Cl-35。
5一、选择题(共16小题,每小题4分,每题只有一个正确选项)1.如图是元素周期表的轮廓图,图中给出了四个不同的区域。
人们寻找催化剂和耐高温、耐腐蚀的合金材料的区域应是2。
在元素周期表中,第3、4、5、6周期所含元素的数目分别是A.8、18、32、32 B.8、18、18、32C。
8、18、18、18 D.8、8、18、183。
下列物质中酸性最强的是A. H2SiO3B。
H3PO4 C. H2SO4D。
HClO44。
下列微粒中,与氩原子具有相同电子层结构的是A。
Na+ B.Cl—C。
D.Ne5.简单原子的原子结构可用下图的表示方法来形象表示,其中●表示质子或电子,〇表示中子,则下列有关①②③的叙述中正确的是A。
①、②、③互为同位素B.①、②、③互为同素异性体C。
①、②、③是三种化学性质不同的粒子D.①、②、③具有相同的质量数6。
下列关于元素周期表和元素周期律的说法不正确的是A。
从F到I,其氢化物的稳定性逐渐减弱B.因为Al原子比Na原子失去电子数目多,所以Al比Na的还原性强C.第三周期从Na到Cl,最高价氧化物对应的水化物碱性逐渐减弱,酸性逐渐增强D。
O与S为同主族元素,O比S的原子半径小,O比S的非金属性强7. 己知在周期表中第118号元素位于周期表的第七周期0族,预测第114号元素的下列叙述中,错误的是A。
位于周期表的第七周期第ⅣA族B。
原子的最外层有4个电子C。
20162017学年贵州省贵阳市高一(上)期末数学试卷
2016-2017学年贵州省贵阳市高一(上)期末数学试卷一、选择题(共10小题,每小题4分,满分40分)1.(4分)已知集合A={0,1,2},B={2,3},则集合A∪B=()A.{1,2,3}B.{0,1,2,3}C.{2}D.{0,1,3}2.(4分)化简÷(b)(a>0,b>0)结果为()A.a B.b C.D.3.(4分)正弦函数f(x)=sinx图象的一条对称轴是()A.x=0 B.C.D.x=π4.(4分)下列函数中,既是偶函数又存在零点的是()A.f(x)=sinx B.f(x)=x2+1 C.f(x)=lnx D.f(x)=cosx5.(4分)设y1=log0.70.8,y2=log1.10.9,y3=1.10.9,则有()A.y3>y1>y2B.y2>y1>y3C.y1>y2>y3D.y1>y3>y26.(4分)已知正方形ABCD的边长为1,则•=()A.1 B.C.D.27.(4分)如果cos(π+A)=﹣,那么sin(+A)的值是()A.B.C.D.8.(4分)要得到函数y=sin(2x+)的图象,只需将函数y=sin2x的图象()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位9.(4分)函数y=f(x)在区间上的简图如图所示,则函数y=f(x)的解析式可以是()A.f(x)=sin(2x+)B.f(x)=sin(2x﹣)C.f(x)=sin(x+)D.f(x)=sin(x﹣)10.(4分)对于函数f(x),如果存在非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,已知函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[﹣1,1]时,f(x)=x2,则y=f(x)与y=log5x的图象的交点个数为()A.3 B.4 C.5 D.6二、填空题(共5小题,每小题4分,满分20分)11.(4分)学校先举办了一次田径运动会,某班有8名同学参赛,又举办了一次球类运动会,该班有12名同学参赛,两次运动会都参赛的有3人.两次运动会中,这个班共有名同学参赛.12.(4分)溶液酸碱度是通过pH值刻画的,pH值的计算公式为pH=﹣lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升,纯净水中氢离子的浓度为[H+]=10﹣7摩尔/升,则纯净水的pH=.13.(4分)已知,那么=.14.(4分)计算(lg2)2+lg2•lg50+lg25=.15.(4分)设A,B是非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合中B都有唯一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射,设f:x→是从集合A到集合B的一个映射.①若A={0,1,2},则A∩B=;②若B={1,2},则A ∩B=.三、解答题(共4小题,满分32分)16.(8分)已知向量=(1,0),=(1,1),=(﹣1,1).(Ⅰ)λ为何值时,+λ与垂直?(Ⅱ)若(m+n)∥,求的值.17.(8分)已知函数f(x)=x﹣.(Ⅰ)判断f(x)的奇偶性;(Ⅱ)用函数单调性的定义证明:f(x)在(0,+∞)上是增函数.18.(8分)已知函数f(x)=sin2+sin cos.(Ⅰ)求f(x)的最小正周期;(Ⅱ)若x∈[,π],求f(x)的最大值与最小值.19.(8分)已知函数f(x)=1﹣(a>0且a≠1)是定义在R上的奇函数.(Ⅰ)求a的值;(Ⅱ)若关于x的方程|f(x)•(2x+1)|=m有1个实根,求实数m的取值范围.四、阅读与探究(共1小题,满分8分)20.(8分)阅读下面材料,尝试类比探究函数y=x2﹣的图象,写出图象特征,并根据你得到的结论,尝试猜测作出函数对应的图象.阅读材料:我国著名数学家华罗庚先生曾说:数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征.我们来看一个应用函数的特征研究对应图象形状的例子.对于函数y=,我们可以通过表达式来研究它的图象和性质,如:(1)在函数y=中,由x≠0,可以推测出,对应的图象不经过y轴,即图象与y轴不相交;由y≠0,可以推测出,对应的图象不经过x轴,即图象与x轴不相交.(2)在函数y=中,当x>0时y>0;当x<0时y<0,可以推测出,对应的图象只能在第一、三象限;(3)在函数y=中,若x∈(0,+∞)则y>0,且当x逐渐增大时y逐渐减小,可以推测出,对应的图象越向右越靠近x轴;若x∈(﹣∞,0),则y<0,且当x逐渐减小时y逐渐增大,可以推测出,对应的图象越向左越靠近x轴;(4)由函数y=可知f(﹣x)=﹣f(x),即y=是奇函数,可以推测出,对应的图象关于原点对称.结合以上性质,逐步才想出函数y=对应的图象,如图所示,在这样的研究中,我们既用到了从特殊到一般的思想,由用到了分类讨论的思想,既进行了静态(特殊点)的研究,又进行了动态(趋势性)的思考.让我们享受数学研究的过程,传播研究数学的成果.2016-2017学年贵州省贵阳市高一(上)期末数学试卷参考答案与试题解析一、选择题(共10小题,每小题4分,满分40分)1.(4分)已知集合A={0,1,2},B={2,3},则集合A∪B=()A.{1,2,3}B.{0,1,2,3}C.{2}D.{0,1,3}【解答】解:∵集合A={0,1,2},B={2,3},则集合A∪B={0,1,2,3},故选:B.2.(4分)化简÷(b)(a>0,b>0)结果为()A.a B.b C.D.【解答】解:原式==a,故选:A3.(4分)正弦函数f(x)=sinx图象的一条对称轴是()A.x=0 B.C.D.x=π【解答】解:f(x)=sinx图象的一条对称轴为+kπ,k∈Z,∴当k=0时,函数的对称轴为,故选:C.4.(4分)下列函数中,既是偶函数又存在零点的是()A.f(x)=sinx B.f(x)=x2+1 C.f(x)=lnx D.f(x)=cosx【解答】解:对于A,是奇函数;对于B,是偶函数,不存在零点;对于C,非奇非偶函数;对于D,既是偶函数又存在零点.故选:D.5.(4分)设y1=log0.70.8,y2=log1.10.9,y3=1.10.9,则有()A.y3>y1>y2B.y2>y1>y3C.y1>y2>y3D.y1>y3>y2【解答】解:y1=,1);y2=;y3=,可得y3>y1>y2.故选:A.6.(4分)已知正方形ABCD的边长为1,则•=()A.1 B.C.D.2【解答】解:.故选A.7.(4分)如果cos(π+A)=﹣,那么sin(+A)的值是()A.B.C.D.【解答】解:由题意可得:,根据诱导公式可得cosA=,所以=cosA=,故选B.8.(4分)要得到函数y=sin(2x+)的图象,只需将函数y=sin2x的图象()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位【解答】解:由于函数y=sin(2x+)=sin2(x+),∴将函数y=sin2x的图象向左平移个单位长度,可得函数y=sin(2x+)的图象,故选:B9.(4分)函数y=f(x)在区间上的简图如图所示,则函数y=f(x)的解析式可以是()A.f(x)=sin(2x+)B.f(x)=sin(2x﹣)C.f(x)=sin(x+)D.f(x)=sin(x﹣)【解答】解:由图象知A=1,∵=,∴T=π,∴ω=2,∴函数的解析式是y=sin(2x+φ)∵函数的图象过()∴0=sin(2×+φ)∴φ=kπ﹣,∴φ=﹣∴函数的解析式是y=sin(2x﹣)故选B.10.(4分)对于函数f(x),如果存在非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,已知函数y=f (x)(x∈R)满足f(x+2)=f(x),且x∈[﹣1,1]时,f(x)=x2,则y=f(x)与y=log5x的图象的交点个数为()A.3 B.4 C.5 D.6【解答】解:∵函数y=f(x)(x∈R)满足f(x+2)=f(x),∴f(x)是周期为2的周期性函数,又x∈[﹣1,1]时,f(x)=x2.根据函数的周期性画出图形,如图,由图可得y=f(x)与y=log5x的图象有4个交点故选:B.二、填空题(共5小题,每小题4分,满分20分)11.(4分)学校先举办了一次田径运动会,某班有8名同学参赛,又举办了一次球类运动会,该班有12名同学参赛,两次运动会都参赛的有3人.两次运动会中,这个班共有17名同学参赛.【解答】解:设A={x|x是参加田径运动会比赛的学生},B={x|x是参加球类运动会比赛的学生},A∩B={x|x是两次运动会都参加比赛的学生},A∪B={x|x是参加所有比赛的学生}.因此card(A∪B)=card(A)+card(B)﹣card(A∩B)=8+12﹣3=17.故两次运动会中,这个班共有17名同学参赛.故答案为:17.12.(4分)溶液酸碱度是通过pH值刻画的,pH值的计算公式为pH=﹣lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升,纯净水中氢离子的浓度为[H+]=10﹣7摩尔/升,则纯净水的pH=7.【解答】解:由题意可得:该溶液的PH值为﹣lg10﹣7=7故答案为:713.(4分)已知,那么=.【解答】解:因为,所以||=.故答案为.14.(4分)计算(lg2)2+lg2•lg50+lg25=2.【解答】解:原式=2 lg5+lg2•(1+lg5)+(lg2)2=2 lg5+lg2(1+lg5+lg2)=2 lg5+2 lg2=2;故答案为2.15.(4分)设A,B是非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合中B都有唯一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射,设f:x→是从集合A到集合B的一个映射.①若A={0,1,2},则A∩B={0,1} ;②若B={1,2},则A∩B={1}或∅.【解答】解:①根据题意,A={0,1,2},通过对应关系f:x→,B={0,1,},所以A∩B={0,1};②根据题意,B={1,2}时,过对应关系f:x→,得A={1}或{4}或{1,4};所以A∩B={1}或∅.故答案为:{0,1},{1}或∅.三、解答题(共4小题,满分32分)16.(8分)已知向量=(1,0),=(1,1),=(﹣1,1).(Ⅰ)λ为何值时,+λ与垂直?(Ⅱ)若(m+n)∥,求的值.【解答】解:(Ⅰ)∵向量=(1,0),=(1,1),=(﹣1,1).∴=(1+λ,λ),∵+λ与垂直,∴()•=1+λ+0=0,解得λ=﹣1,∴λ=1时,+λ与垂直.(Ⅱ)∵=(m,0)+(n,n)=(m+n,n),又(m+n)∥,∴(m+n)×1﹣(﹣1×n)=0,∴=﹣2.∴若(m+n)∥,则=﹣2.17.(8分)已知函数f(x)=x﹣.(Ⅰ)判断f(x)的奇偶性;(Ⅱ)用函数单调性的定义证明:f(x)在(0,+∞)上是增函数.【解答】解:(Ⅰ)函数f(x)=x﹣的定义域是D=(﹣∞,0)∪(0,+∞),任取x∈D,则﹣x∈D,且f(﹣x)=﹣x﹣=﹣(x﹣)=﹣f(x),∴f(x)是定义域上的奇函数;(Ⅱ)证明:设x1,x2∈(0,+∞),且x1<x2,则f(x1)﹣f(x2)=(x1﹣)﹣(x2﹣)=(x1﹣x2)+(﹣)=;∵0<x1<x2,∴x1x2>0,x1﹣x2<0,x1x2+1>0,∴<0,即f(x1)<f(x2),∴f(x)在(0,+∞)上是增函数.18.(8分)已知函数f(x)=sin2+sin cos.(Ⅰ)求f(x)的最小正周期;(Ⅱ)若x∈[,π],求f(x)的最大值与最小值.【解答】解:(Ⅰ)函数f(x)=sin2+sin cos=+sinx=sinx﹣cosx+=sin(x﹣)+,由T==2π,知f(x)的最小正周期是2π;(Ⅱ)由f(x)=sin(x﹣)+,且x∈[,π],∴≤x﹣≤,∴≤sin(x﹣)≤1,∴1≤sin(x﹣)+≤,∴当x=时,f(x)取得最大值,x=π时,f(x)取得最小值1.19.(8分)已知函数f(x)=1﹣(a>0且a≠1)是定义在R上的奇函数.(Ⅰ)求a的值;(Ⅱ)若关于x的方程|f(x)•(2x+1)|=m有1个实根,求实数m的取值范围.【解答】解:(Ⅰ)∵f(x)=1﹣(a>0且a≠1)是定义在R上的奇函数,∴f(0)=0,即1﹣=0,∴a=2;(Ⅱ)设h(x)=|f(x)•(2x+1)|,g(x)=m,如图所示,m=0或m≥1,两函数图象有一个交点,∴关于x的方程|f(x)•(2x+1)|=m有1个实根时,实数m的取值范围是m=0或m≥1.四、阅读与探究(共1小题,满分8分)20.(8分)阅读下面材料,尝试类比探究函数y=x2﹣的图象,写出图象特征,并根据你得到的结论,尝试猜测作出函数对应的图象.阅读材料:我国著名数学家华罗庚先生曾说:数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征.我们来看一个应用函数的特征研究对应图象形状的例子.对于函数y=,我们可以通过表达式来研究它的图象和性质,如:(1)在函数y=中,由x≠0,可以推测出,对应的图象不经过y轴,即图象与y轴不相交;由y≠0,可以推测出,对应的图象不经过x轴,即图象与x轴不相交.(2)在函数y=中,当x>0时y>0;当x<0时y<0,可以推测出,对应的图象只能在第一、三象限;(3)在函数y=中,若x∈(0,+∞)则y>0,且当x逐渐增大时y逐渐减小,可以推测出,对应的图象越向右越靠近x轴;若x∈(﹣∞,0),则y<0,且当x逐渐减小时y逐渐增大,可以推测出,对应的图象越向左越靠近x轴;百度文库- 让每个人平等地提升自我!(4)由函数y=可知f(﹣x )=﹣f(x),即y=是奇函数,可以推测出,对应的图象关于原点对称.结合以上性质,逐步才想出函数y=对应的图象,如图所示,在这样的研究中,我们既用到了从特殊到一般的思想,由用到了分类讨论的思想,既进行了静态(特殊点)的研究,又进行了动态(趋势性)的思考.让我们享受数学研究的过程,传播研究数学的成果.【解答】解:(1)在y=x2﹣中,x≠0,可以推测出:对应的图象不经过y轴,即与y轴不相交,(2)令y=0,即x2﹣=0,解得x=±1,可以推测出,对应的图象与x相交,交点坐标为(1,0)和(﹣1,0),(3)在y=x2﹣中,当0<x<1时,>1>x2,则y<0,当x>1时,<1<x2,则y>0,可以推测出:对应的图象在区间(0,1)上图象在x轴的下方,在区间(1,+∞)上图象在x 轴的上方,(4)在y=x2﹣中,若x∈(0,+∞),则当x逐渐增大时逐渐减小,x2﹣,逐渐增大,即y逐渐增大,所以原函数在(0,+∞)是增函数,可以推测出:对应的图象越向右逐渐升高,是单调递增的趋势,(5)由函数y=x2﹣可知f(﹣x)=f(x),即函数为偶函数,可以推测出:对应的图象关于y轴对称11。
贵州省铜仁一中2016-2017学年高一下学期期中数学试卷(Word版含答案)
2016-2017学年贵州省铜仁一中高一(下)期中数学试卷一、选择题:(本大题共12题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.不等式(3x+1)(1﹣2x)>0的解集是()A.B. C.D.2.在△ABC中,角A,B,C的对边分别为a,b,c,且A=30°,B=15°,a=3,则c的值为()A.6 B.C.3 D.33.设M=2a(a﹣2)+4,N=(a﹣1)(a﹣3),则M,N的大小关系为()A.M>N B.M<N C.M=N D.不能确定4.已知f(x)=log2(x2+7),a n=f(n),则{a n}的第五项为()A.3 B.4 C.5 D.65.在△ABC中,角A,B,C的对边分别为a,b,c,且c2﹣a2﹣b2=ab,则角C=()A.B.C. D.6.如果等差数列{a n}中,a3+a4+a5=12,那么a1+a2+…+a7=()A.14 B.21 C.28 D.357.下列不等式一定成立的是()A.lg(x2+)>lgx(x>0)B.sinx+≥2(x≠kx,k∈Z)C.x2+1≥2|x|(x∈R)D.(x∈R)8.在△ABC中,A,B,C成等差数列,且b2=ac,则△ABC的形状是()A.直角三角形B.等腰直角三角形C.等腰三角形D.等边三角形9.在数列{a n}中,a1=1,a n﹣a n﹣1=,则a n=()A.B.C.D.10.不等式(a﹣2)x2+2(a﹣2)x﹣4<0对x∈R恒成立,则实数a的取值范围是()A.(﹣∞,2)B. C.(﹣2,2] D.(﹣∞,﹣2)11.在等比数列{a n}中,S4=1,S8=3,则a17+a18+a19+a20的值是()A.14 B.16 C.18 D.2012.已知m,n是满足m+n=1,且使取得最小值的正实数,若函数y=x a过点 P(m,n),则α的值为()A.3 B.2 C.D.﹣1二、填空题:(本大题共4小题,每小题5分,共20分)13.设数列{a n}的前n项和S n=n2,则a8= .14.在△ABC中,若∠A=120°,AB=5,BC=7,则△ABC的面积S= .15.若实数x,y满足不等式组,目标函数z=x+2y,则z的取值范围为.16.两等差数列{a n}和{b n},前n项和分别为S n,T n,且,则等于.三、解答题:(本大题共5小题,共70分,解答应写出文字说明,证明过程,或演算步骤)17.已知a,b,c分别为△ABC三个内角A,B,C的对边,.(1)求角A;(2)若a=2,△ABC的面积为,求b,c.18.已知关于x的一元二次不等式ax2+x+b>0的解集为(﹣∞,﹣2)∪(1,+∞).(Ⅰ)求a和b的值;(Ⅱ)求不等式ax2﹣(c+b)x+bc<0的解集.19.设数列{b n}的前n项和为S n,且b n=2﹣2S n;数列{a n}为等差数列,且a5=10,a7=14.(1)求数列{a n}、{b n}的通项公式;(2)若c n=a n b n,T n为数列{c n}的前n项和.求T n.20.如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6海里,渔船乙以5 海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.(1)求渔船甲的速度;(2)求sinα的值.21.等比数列{a n}的各项均为正数,且.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=|10+2log3a n|,求数列{b n}的前n项和S n;(Ⅲ)设,求证:.22.(1)解不等式|2x+1|﹣|x﹣4|>2;(2)已知:a>0,b>0,求证:.2016-2017学年贵州省铜仁一中高一(下)期中数学试卷参考答案与试题解析一、选择题:(本大题共12题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.不等式(3x+1)(1﹣2x)>0的解集是()A.B.C.D.【考点】74:一元二次不等式的解法.【分析】把不等式化为(3x+1)(2x﹣1)<0,求出解集即可.【解答】解:不等式(3x+1)(1﹣2x)>0可化为(3x+1)(2x﹣1)<0,解得﹣<x<,∴不等式的解集是{x|﹣<x<}.故选:B.2.在△ABC中,角A,B,C的对边分别为a,b,c,且A=30°,B=15°,a=3,则c的值为()A.6 B.C.3D.3【考点】HP:正弦定理.【分析】利用正弦定理和内角和定理即可求解c的值.【解答】解:由题意,A=30°,B=15°,∴C=180°﹣45°=135°a=3,由正弦定理:,可得解得:c=3.故选:D.3.设M=2a(a﹣2)+4,N=(a﹣1)(a﹣3),则M,N的大小关系为()A.M>N B.M<N C.M=N D.不能确定【考点】15:集合的表示法.【分析】把M,N代入M﹣N作差后,判断差的符号,即可比较出大小关系.【解答】解:∵M﹣N=2a(a﹣2)+4﹣(a﹣1)(a﹣3)=2a2﹣4a+4﹣(a2﹣4a+3)=a2+1>0,∴M>N.故选:A.4.已知f(x)=log2(x2+7),a n=f(n),则{a n}的第五项为()A.3 B.4 C.5 D.6【考点】8I:数列与函数的综合.【分析】利用数列与函数的关系式,直接求解即可.【解答】解:f(x)=log2(x2+7),a n=f(n),则{a n}的第五项为a5=log2(52+7)=log232=5,故选:C.5.在△ABC中,角A,B,C的对边分别为a,b,c,且c2﹣a2﹣b2=ab,则角C=()A.B.C. D.【考点】HR:余弦定理.【分析】根据题意,利用余弦定理求出cosC,即可得出角C的大小.【解答】解:△ABC中,c2﹣a2﹣b2=ab,∴a2+b2﹣c2=﹣ab,∴cosC===﹣,又C∈(0,π),∴角C=.故选:D.6.如果等差数列{a n}中,a3+a4+a5=12,那么a1+a2+…+a7=()A.14 B.21 C.28 D.35【考点】8F:等差数列的性质;85:等差数列的前n项和.【分析】由等差数列的性质求解.【解答】解:a3+a4+a5=3a4=12,a4=4,∴a1+a2+…+a7==7a4=28故选C7.下列不等式一定成立的是()A.lg(x2+)>lgx(x>0)B.sinx+≥2(x≠kx,k∈Z)C.x2+1≥2|x|(x∈R)D.(x∈R)【考点】72:不等式比较大小.【分析】由题意,可对四个选项逐一验证,其中C选项用配方法验证,A,B,D三个选项代入特殊值排除即可【解答】解:A选项不成立,当x=时,不等式两边相等;B选项不成立,这是因为正弦值可以是负的,故不一定能得出sinx+≥2;C选项是正确的,这是因为x2+1≥2|x|(x∈R)⇔(|x|﹣1)2≥0;D选项不正确,令x=0,则不等式左右两边都为1,不等式不成立.综上,C选项是正确的.故选:C.8.在△ABC中,A,B,C成等差数列,且b2=ac,则△ABC的形状是()A.直角三角形B.等腰直角三角形C.等腰三角形D.等边三角形【考点】HR:余弦定理.【分析】先根据A,B,C成等差数列和三角形内角和,求B的值,进而根据b2=ac代入余弦定理求得a2+c2﹣ac=ac,整理求得a=c,判断出A=C,最后判断三角形的形状.【解答】解:由A,B,C成等差数列,有2B=A+C,因为A,B,C为△ABC的内角,所以A+B+C=π,可得B=.由a,b,c成等比数列,有b2=ac,根据b2=ac代入余弦定理求得a2+c2﹣ac=ac,即(a﹣c)2=0,因此a=c,从而A=C,所以△ABC为等边三角形.故选:D.9.在数列{a n}中,a1=1,a n﹣a n﹣1=,则a n=()A.B.C.D.【考点】8E:数列的求和.【分析】累加法:先变形得,a n﹣a n﹣1==,由a n=a1+(a2﹣a1)+(a3﹣a2)+…+(a n﹣a n﹣1),可得a n(n≥2),注意检验a1是否适合.【解答】解:a n﹣a n﹣1==,则,,,…,以上各式相加得,,所以(n≥2),又a1=1,所以,故选A.10.不等式(a﹣2)x2+2(a﹣2)x﹣4<0对x∈R恒成立,则实数a的取值范围是()A.(﹣∞,2)B. C.(﹣2,2] D.(﹣∞,﹣2)【考点】3R:函数恒成立问题.【分析】这是一道类似二次不等式在x∈R恒成立求参数的问题,应首先考虑a﹣2是否为零.【解答】解:①当a=2时,不等式恒成立.故a=2成立②当a≠2时,要求解得:a∈(﹣2,2)综合①②可知:a∈(﹣2,2]故选C.11.在等比数列{a n}中,S4=1,S8=3,则a17+a18+a19+a20的值是()A.14 B.16 C.18 D.20【考点】8G:等比数列的性质.【分析】根据等比数列的性质可知,从第1到第4项的和,以后每四项的和都成等比数列,由前8项的和减前4项的和得到第5项加到第8项的和为2,然后利用第5项到第8项的和除以前4项的和即可得到此等比数列的公比为2,首项为前4项的和即为1,而所求的式子(a17+a18+a19+a20)为此数列的第5项,根据等比数列的通项公式即可求出值.【解答】解:∵S4=1,S8=3,∴S8﹣S4=2,而等比数列依次K项和为等比数列,则a17+a18+a19+a20=(a1+a2+a3+a4)•25﹣1=16.故选B.12.已知m,n是满足m+n=1,且使取得最小值的正实数,若函数y=x a过点 P(m,n),则α的值为()A.3 B.2 C.D.﹣1【考点】7F:基本不等式.【分析】根据题意,由基本不等式的性质分析可得m=、n=时,取到最小值,可得P的坐标,将p的坐标代入函数解析式计算可得答案.【解答】解:根据题意, =()(m+n)=10+(+)≥10+2=16,分析可得:当=,即n=3m时,取到最小值16,又由m+n=1,即m=、n=时,取到最小值16,则P(,),则有()α=,解可得α=;故选:C.二、填空题:(本大题共4小题,每小题5分,共20分)13.设数列{a n}的前n项和S n=n2,则a8= 15 .【考点】84:等差数列的通项公式.【分析】根据数列前n项和的定义可得a8=S8﹣s7再代入计算即可.【解答】解:∵a n=S n﹣S n﹣1(n≥2),S n=n2∴a8=S8﹣S7=64﹣49=15故答案为1514.在△ABC中,若∠A=120°,AB=5,BC=7,则△ABC的面积S= .【考点】HP:正弦定理.【分析】用余弦定理求出边AC的值,再用面积公式求面积即可.【解答】解:据题设条件由余弦定理得|BC|2=|AB|2+|AC|2﹣2|AB||AC|cosA即49=25+|AC|2﹣2×5×|AC|×(﹣),即AC|2+5×|AC|﹣24=0解得|AC|=3故△ABC的面积S=×5×3×sin120°=故应填15.若实数x,y满足不等式组,目标函数z=x+2y,则z的取值范围为.【考点】7C:简单线性规划.【分析】由约束条件作出可行域,数形结合得到最优解,把最优解的坐标代入目标函数即可求得k值.【解答】解:由不等式组,约束条件作出可行域如图:B(,﹣1),A(2,2),由z=x+2y得:y=﹣x+z,显然直线过B(,﹣1)时,z最小,z的最小值是﹣,直线过A(2,2)时,z最大,z的最大值是6,故答案为:.16.两等差数列{a n}和{b n},前n项和分别为S n,T n,且,则等于.【考点】8F:等差数列的性质.【分析】利用==,即可得出结论.【解答】解:====.故答案为:.三、解答题:(本大题共5小题,共70分,解答应写出文字说明,证明过程,或演算步骤)17.已知a,b,c分别为△ABC三个内角A,B,C的对边,.(1)求角A;(2)若a=2,△ABC的面积为,求b,c.【考点】HR:余弦定理;HP:正弦定理.【分析】(1)运用正弦定理,以及同角的商数关系,结合特殊角的三角函数值,即可得到A;(2)由余弦定理和面积公式,联立方程,即可解得b,c.【解答】解:(1)sinAsinC﹣sinCcosA=0,∵C为三角形的内角,∴sinC≠0,∴sinA﹣cosA=0,整理得:tanA=,则A=;(2)∵a=2,sinA=,cosA=,△ABC的面积为,∴bcsinA=bc=,即bc①;∴由余弦定理a2=b2+c2﹣2bccosA得:4=b2+c2﹣bc=(b+c)2﹣3bc=(b+c)2﹣12,整理得:b+c②,联立①②解得:b=c=2.18.已知关于x的一元二次不等式ax2+x+b>0的解集为(﹣∞,﹣2)∪(1,+∞).(Ⅰ)求a和b的值;(Ⅱ)求不等式ax2﹣(c+b)x+bc<0的解集.【考点】74:一元二次不等式的解法.【分析】(Ⅰ)由一元二次不等式与对应方程的关系,利用根与系数的关系,即可求出a、b 的值;(Ⅱ)把a、b的值代入化简不等式,讨论c的值,求出对应不等式的解集.【解答】解:(Ⅰ)由题意知﹣2和1是方程ax2+x+b=0的两个根,由根与系数的关系,得,解得;…(Ⅱ)由a=1、b=﹣2,不等式可化为x2﹣(c﹣2)x﹣2c<0,即(x+2)(x﹣c)<0;…则该不等式对应方程的实数根为﹣2和c;所以,①当c=﹣2时,不等式为(x+2)2<0,它的解集为∅;…②当c>﹣2时,不等式的解集为(﹣2,c);…②当c<﹣2时,不等式的解集为(c,﹣2).…19.设数列{b n}的前n项和为S n,且b n=2﹣2S n;数列{a n}为等差数列,且a5=10,a7=14.(1)求数列{a n}、{b n}的通项公式;(2)若c n=a n b n,T n为数列{c n}的前n项和.求T n.【考点】8E:数列的求和;8H:数列递推式.【分析】(1)根据等差数列的性质求出公差d,代入通项公式得出a n,利用b n=证明{b n}为等比数列,从而得出b n;(2)利用错位相减法求出T n.【解答】解:(1)设数列{a n}的公差为d,则,∴a n=a5+(n﹣5)d=2n,∵b n=2﹣2S n,当n=1,则b1=2﹣2b1,解得.当n≥2时,由b n=2﹣2S n,∴b n﹣1=2﹣2S n﹣1,∴b n﹣b n﹣1=﹣2(S n﹣S n﹣1)=﹣2b n.∴.∴{b n}是以为首项,为公比的等比数列,∴.(2),∴,①∴,②①﹣②得:=,∴.20.如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6海里,渔船乙以5 海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.(1)求渔船甲的速度;(2)求sinα的值.【考点】HU:解三角形的实际应用.【分析】(1)在△ABC中使用余弦定理计算BC,从而得出渔船甲的速度;(2)在△ABC中,使用正弦定理计算∠BCA,从而得出sinα.【解答】解:(1)依题意,∠BAC=120°,AB=6,AC=5×2=10,∠BCA=α.在△ABC中,由余弦定理,得BC2=AB2+AC2﹣2AB×AC×cos∠BAC=62+102﹣2×6×10×cos120°=196.解得BC=14,所以渔船甲的速度为海里/小时.答:渔船甲的速度为7海里/小时.(2)在△ABC中,因为AB=6,∠BAC=120°,BC=14,∠BCA=α,由正弦定理,得.即.答:sinα的值为.21.等比数列{a n}的各项均为正数,且.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=|10+2log3a n|,求数列{b n}的前n项和S n;(Ⅲ)设,求证:.【考点】8E:数列的求和;88:等比数列的通项公式.【分析】(Ⅰ)设公比是q,根据等比数列的通项公式和题意求出q和a1,再求出a n;(Ⅱ)由(Ⅰ)和对数的运算化简b n=|10+2log3a n|,对n进行分类讨论,分别利用等差数列的前n项和公式求出S n;(Ⅲ)由(Ⅰ)和对数的运算化简,代入结合结论进行放缩,利用裂项相消法证明成立.【解答】解:(Ⅰ)设数列{a n}的公比为q,由得,,所以.由条件可知a n>0,则.由2a1+3a2=1得,2a1+3a2q=1,所以.所以数列{a n}的通项式为a n=;(Ⅱ)由(Ⅰ)得,b n=|10+2log3a n|=|10﹣2n|,则当n≤5时,10﹣2n≥0,当n>5时,10﹣2n<0,(1)当n≤5时,b n=10﹣2n, =﹣n2+9n,(2)当n>5时,b n=2n﹣10,则S n=8+6+…+0+(2+4+6+…+2n﹣10)=20+=n2﹣9n+40,综上可得,;…(Ⅲ)由(Ⅰ)得,,因为当n≥2时,所以<=,所以,故.…22.(1)解不等式|2x+1|﹣|x﹣4|>2;(2)已知:a>0,b>0,求证:.【考点】R6:不等式的证明;R5:绝对值不等式的解法.【分析】(1)对x的范围进行讨论,去绝对值符号解出;(2)使用作差法证明.【解答】(1)解:①若x≤﹣,则不等式为﹣2x﹣1﹣(4﹣x)>2,解得x<﹣7,②若﹣<x≤4,则不等式为2x+1﹣(4﹣x)>2,解得<x≤4,③若x>4,则不等式为2x+1﹣(x﹣4)>2,解得x>4,综上,原不等式的解集为 {x|x<﹣7或x>}.(2)证明:∵a>0,b>0∴===.∴.2017年6月13日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
周林高中2016—2017学年度第二学期入学考试
高一理科综合能力测试化学试卷
7. 铝对生物有毒害作用,尤其对人体的毒害更加严重。下列不正确的是( )
A. 杜绝铝制品在生产生活中的应用
B. 不能用铝制器皿长期存放酸性或碱性食品
C. 不吃或少吃使用了含铝食品添加剂的食物
D. 氢氧化铝可用于药物治疗胃酸过多
8. 用N A表示阿伏伽德罗常数值,下列说法正确的是( )
A. 物质的量浓度为0.5 mol/L的MgCl 2溶液中,共含有Cl - 个数为 N
A
B. 1mol任何气体的体积都为 22.4L
C. 7.8gNa 2O 2中所含阴离子的数目是0.1N A
D. 标准状况下, 2.24L水中含有的分子数为0.1N A
9.下列说法正确的是 ( )
A、摩尔是七个基本物理量之一
B、硫酸钠和水分别属于非电解质和弱电解质
C、硫酸、纯碱、醋酸钠和生石灰分别属于酸、碱、盐和氧化物
D、分散系中分散质粒子的直径:Fe(OH)3浊液>Fe(OH)3胶体>FeCl3溶液
10.现在NaOH、Na2CO3、Ba(OH)2三种无色溶液,选用一种试剂就能把它们鉴别出来,这种试
剂是( )
A.HCl B.Ca(OH)2 C.H2SO4 D NaHCO3
11. 下列离子方程式正确的是
A. 铁与盐酸的反应: 2Fe + 6H + = 2Fe 3 + + 3 H 2↑
B. 碳酸钙溶于醋酸中:CaCO 3+2H +=Ca 2 ++2H 2O+CO 2↑
C. 铜片插入硝酸银溶液 :Cu + Ag + = Cu 2+ + Ag
D. 钠与水反应: :2Na+2H 2O = 2OH - +2Na + + H 2 ↑
12. 在下列转化发生还原反应的是 ( )
A. HCl→Cl 2 B. CaCO 3 → CO 2 C. PbSO 4→Pb D. C→CO
2
13. 将30ml 0.5mol/L NaOH 溶液加水稀释到500ml ,稀释后溶液中NaOH的物质的量
浓度为( )
A. 0.3 mol/L B. 0.03 mol/L C . 0.05 mol/L D .
0.04 mol/L
26. (16分) 实验室用NaOH固体 配制250mL 1.00mol/LNaOH溶液,填空回答下列问题:
(1)配制该溶液时使用的仪器除托盘天平、烧杯、玻璃棒外,还必须用到的仪器
有 。
(2). 配制250mL 1.00mol·L -1的NaOH溶液的步骤如下,完成下列填空:
①计算:所需NaOH固体的质量为___________;
②称量
③溶解:将称量好的NaOH固体放入烧杯中,然后用适量蒸馏水溶解,该步操作用到的另一
仪器的作用______________;
(3)其余步骤正确的操作顺序是(每个字母限用一次) ________________
A、用30mL水洗涤烧杯和玻璃棒2—3次,洗涤液均注入容量瓶,振荡
B、将已冷却的NaOH溶液沿玻璃棒注入250mL的容量瓶中
C、将容量瓶盖紧,颠倒摇匀
D、改用胶头滴管加水,使溶液凹面恰好与刻度相切
E、继续往容量瓶内小心加水,直到液面接近刻度1—2cm处
(4)若实验中出现下列现象对所配溶液浓度有什么影响?(填偏高、偏低、无影响)
①氢氧化钠溶解后未冷却至室温即进行转移
②定容时俯视刻度线
(5)若定容时液面高于刻度线应采取的措施是
(6)在进行操作③时,不慎将液体溅到皮肤上,则处理的方法是 。
27. (14分)钠的化合物在自然界中分布广,钠及其化合物具有广泛的用途。
(1)钠的化学性质很活泼,可用于冶炼金属,如钠与氯化钾在熔融条件下可冶炼钾,是利用
了钾的沸点比钠低,钾变成了气体,离开了反应体系,使得Na把K置换出来了.写出该反应的化
学方程式:
_________________________________________________________________。
但钠与不活泼金属盐溶液反应并不能置换出金属单质,如将钠投入CuSO4溶液中反应方程式
为2Na+2H2O+CuSO4===Na2SO4+Cu(OH)2↓+H2↑,该反应的氧化剂是____________(填化
学式)。
(2)过氧化钠(Na2O2)可用作呼吸面具的供氧剂,Na2O2与人体呼出的CO2反应可生成O2,该反
应原理为2Na2O2+2CO2===2Na2CO3+O2,Na2O2中氧元素的化合价为____________,该反应
____________氧化还原反应(填“是”或“不是”)。Na2O2也可与水反应生成NaOH和O2,将Na2O
2
加入FeCl2溶液中,可观察到的现象是
__________________________________________________________。
(3)钠元素在海水中的储量极为丰富,主要以NaCl形式存在,取适量的海水于试管中,加入
AgNO3溶液会产生白色沉淀,写出该反应的离子方程式:
_______________________________________________________。
(4)现有一块金属钠露置于空气中一段时间,该固体可能部分变质为Na2CO3,请设计合理的
实验方案验证是否有Na2CO3生成?
_______________________________________________________________________________
______
___________________ (写出简要的实验步骤、现象及结论)。
28. (14分) 某河道两旁有甲、乙两工厂,排放的废水中,共含K +、Ag +、Fe 3 +、C1 -、
OH -、NO 3 -六种离子。
(1)甲厂的废水明显呈碱性,故甲厂废水中一定含有的离子是__________、还含有的离子是
________和________ ,利用离子共存条件及电中性原理解释原
因 。
(2)乙厂的废水中含有另外三种离子。如果加一定量铁粉,可以回收其中的 (填
写元素符号)。
(3)另一种设想是将甲厂和乙厂的废水按适当的比例混合,可以使废水中的________(填写
离子符号)转化为沉淀。经过滤后的废水主要含________,可用来浇灌农田。
34(化学)、(14分)某混合物A,含有KAl(SO4)2、Al2O3和Fe2O3,在一定条件下可实现下图
所示的物质之间的转化:
据此判断:
(1)固体B的化学式为________;固体E所含物质的化学式为________。
(2)反应①的离子方程式为
________ 。
(3)沉淀Ⅰ与氢氧化钠反应的离子方程式
___ ___。
(4)由溶液D得到固体E所需的瓷质仪器名称 :
。
(5)沉淀Ⅱ的主要成分是: ,将其溶于少量稀盐酸所得的溶液
中阳离
子的检验最好的试剂是 。
