人教版九年级数学下册第二十八章 《锐角三角函数 复习》
人教版九年级数学下册28章 锐角三角函数 复习与小结优质课件.ppt

3. sin 2 40 cos2 40= 1
广东省怀集县诗洞镇初级中学 陈超洁
一、基础知识
上,BD=4,AD=BC,cos∠ADC=
3 5
求:(1)DC的长;
(2)sinB的值.
二、强化训练
解:
(1)设DC=3x,则AD=5x
由BD+DC=AD 解得:x=2
得:4+3x=5x
所以DC=3x=6
(2)由(1)知 DC=6 AD=10
由勾股定理的AC=8,AB=2
二、强化训练
8.如图,某数学兴趣小组想测量一棵树CD的 高度,他们先在点A处测得树顶C的仰角为 30°,然后沿AD方向前行10m,到达B点,在 B处测得树顶C的仰角高度为60°(A、B、D 三点在同一直线上).请你根据他们测量数 据计算这棵树CD的高度(结果精确到0.1m).
B . sinA =13
C . tanA=13
D. cosA= 5
2.如图12,在Rt△ABC中,∠ACB1=2 90°,
CD⊥AB,垂足为D.若AC= 5 ,BC=2,则 sin∠ACD的值为___3_5_
二、强化训练
3.如图,在Rt△ABC中,CD是斜边AB 上B的的值中是线_,_43_已__知_C.D=2,AC=3,则sin
1 4.若∠α的余角是30°,则cosα的值是_2___. 5 .某水坝的坡度i=1: ,坡长AB=20米则 坝的高度为_1_0_米___
二、强化训练
6.计算:2sin30°-2cos60°+tan45°
最新人教版初中九年级《数学》下册第二十八28章全章总复习知识点考点重难要点整理复习完整完美精品打印版

第二十八章总复习
知识点考点重难点要点整理复习汇总 最新精品完整完美必备复习资料
第二十八章 锐角三角函数
一.知识框架
二.知识概念
1.Rt△ABC 中
∠A的对边 (1)∠A 的对边与斜边的比值是∠A 的正弦,记作 sinA= 斜边
∠A的邻边 (2)∠A 的邻边与斜边的比值是∠A 的余弦,记作 cos邻边的比值是∠A 的正切,记作 tanA= ∠A的邻边
∠A的邻边 (4)∠A 的邻边与对边的比值是∠A 的余切,记作 cota= ∠A的对边
2.特殊值的三角函数:
a
sin cos tan cot aa a a
30 1 3 3
°22 3
3
45 °
22 22
1
1
60 3 1 °2 2
3 33
本章内容使学生了解在直角三角形中,锐角的对边与斜边、邻边与斜边、对边与邻边、邻边与对边的 比值是固定的;通过实例认识正弦、余弦、正切、余切四个三角函数的定义。并能应用这些概念解决一些 实际问题。
【三角函数是数学中属于初等函数中的超越函数的一类函数。它们的本质是任何角的集合与一个比值 的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。其定义城为整个实数域。另一 种定义是在直角三角形中,但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解,将其定 义扩展到复数系。】
人教版九年级数学下册第28章《锐角三角函数知识点总结、典型例题、练习(精选)
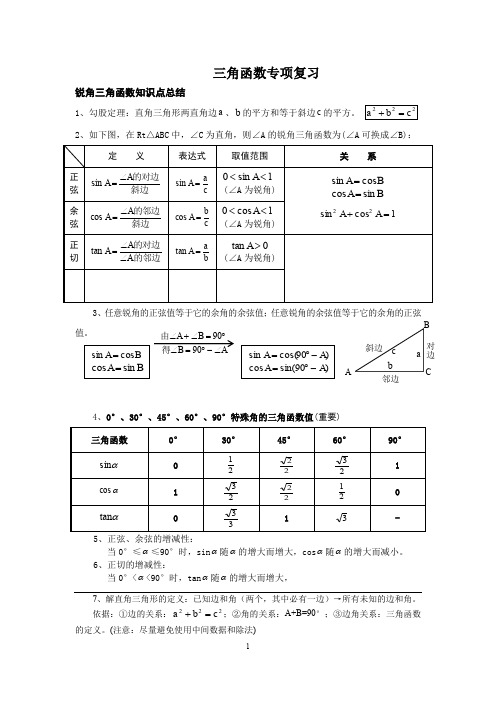
三角函数专项复习锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
6、正切的增减性:当0°<α<90°时,tan α随α的增大而增大,7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)BA cos sin =BA sin cos =)90cos(sin A A -︒=)90sin(cos A A -︒=A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba c8、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
九年级数学下册 第28章锐角三角函数复习教案 人教新课标版 教案

第28章 锐角三角函数复习教案锐角三角函数(第一课时) 教学三维目标:一.知识目标:初步了解正弦、余弦、正切概念;能较正确地用siaA 、cosA 、tanA 表示直角三角形中两边的比;熟记功30°、45°、60°角的三角函数,并能根据这些值说出对应的锐角度数。
二.能力目标:逐步培养学生观察、比较、分析,概括的思维能力。
三.情感目标:提高学生对几何图形美的认识。
教材分析:1.教学重点: 正弦,余弦,正切概念2.教学难点:用含有几个字母的符号组siaA 、cosA 、tanA 表示正弦,余弦,正切 教学程序: 一.探究活动1.课本引入问题,再结合特殊角30°、45°、60°的直角三角形探究直角三角形的边角关系。
2.归纳三角函数定义。
siaA=斜边的对边A ∠,cosA=斜边的邻边A ∠,tanA=的邻边的对边A A ∠∠3例1.求如图所示的Rt ⊿ABC 中的siaA,cosA,tanA 的值。
4.学生练习P21练习1,2,3 二.探究活动二1.让学生画30°45°60°的直角三角形,分别求sia 30°cos45° tan60° 归纳结果2. 求下列各式的值(1)sia 30°+cos30°(2)2sia 45°-21cos30°(3)004530cos sia +ta60°-tan30°三.拓展提高P82例4.(略) 1. 如图在⊿ABC 中,∠A=30°,tanB=23,AC=23,求AB 四.小结 五.作业课本解直角三角形应用(一) 一.教学三维目标 (一)知识目标使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.(二)能力训练点通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.(三)情感目标渗透数形结合的数学思想,培养学生良好的学习习惯. 二、教学重点、难点和疑点 1.重点:直角三角形的解法.2.难点:三角函数在解直角三角形中的灵活运用.3.疑点:学生可能不理解在已知的两个元素中,为什么至少有一个是边. 三、教学过程 (一)知识回顾1.在三角形中共有几个元素?2.直角三角形ABC 中,∠C=90°,a 、b 、c 、∠A 、∠B 这五个元素间有哪些等量关系呢? (1)边角之间关系 sinA=c a cosA=c b tanA=ba(2)三边之间关系a 2+b 2=c 2(勾股定理) (3)锐角之间关系∠A+∠B=90°.以上三点正是解直角三角形的依据,通过复习,使学生便于应用. (二) 探究活动1.我们已掌握Rt △ABC 的边角关系、三边关系、角角关系,利用这些关系,在知道其中的两个元素(至少有一个是边)后,就可求出其余的元素.这样的导语既可以使学生大概了解解直角三角形的概念,同时又陷入思考,为什么两个已知元素中必有一条边呢?激发了学生的学习热情.2.教师在学生思考后,继续引导“为什么两个已知元素中至少有一条边?”让全体学生的思维目标一致,在作出准确回答后,教师请学生概括什么是解直角三角形?(由直角三角形中除直角外的两个已知元素,求出所有未知元素的过程,叫做解直角三角形).3.例题评析例 1在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别为a 、b 、c ,且b= 2 a=6,解这个三角形.例2在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别为a 、b 、c ,且b= 20 B ∠=350,解这个三角形(精确到0.1).解直角三角形的方法很多,灵活多样,学生完全可以自己解决,但例题具有示范作用.因此,此题在处理时,首先,应让学生独立完成,培养其分析问题、解决问题能力,同时渗透数形结合的思想.其次,教师组织学生比较各种方法中哪些较好,选一种板演.完成之后引导学生小结“已知一边一角,如何解直角三角形?”答:先求另外一角,然后选取恰当的函数关系式求另两边.计算时,利用所求的量如不比原始数据简便的话,最好用题中原始数据计算,这样误差小些,也比较可靠,防止第一步错导致一错到底.例 3在Rt △ABC 中,a=104.0,b=20.49,解这个三角形. (三) 巩固练习在△ABC 中,∠C 为直角,AC=6,BAC ∠的平分线AD=43,解此直角三角形。
下册第28章第7课时《锐角三角函数》单元复习-2020秋人教版九年级数学全一册课件(共19张PPT)

(1)求楼房 OB 的高度; (2)求小红在山坡上走过的距离 AC(不取近似值).
(1)200 3 m
(2)200
15- 3
5
m
小结:解决此类题型的关键是借助仰角构造直角三角形并解 直角三角形,注意数形结合思想的应用以及辅助线的作法.
★13.日照间距系数反映了房屋的日照情况,如图 1,当前后 房屋都朝向正南时,日照间距系数=L∶H-H1,其中 L 为楼 间水平距离,H 为南侧楼房高度,H1 为北侧楼房底层窗台至 地面高度.如图 2,山坡 EF 朝北,EF 长为 15 m,坡度 i=1∶ 0.75,山坡顶部平地 EM 上有一高为 22.5 m 的楼房 AB,底部 A 到点 E 的距离为 4 m.
800 C.sin α m D.ta8n00α m
精典范例
6.【例 1】在△ABC 中,∠C=90°,sin A=54,则 tan B=( B )
A.34
B.3义是解决此类问题的关键.
变式练习
10.如图,在边长均为 1 的小正方形网格中,点 A,B,C, D 都在这些小正方形的顶点上,AB,CD 相交于点 O,则 tan∠AOD= 2 .
4.如图,在△ABC 中,AB=10,∠A=30°,∠C=45°,△ABC
的面积是
225+25 2
3 .
知识点四:解直角三角形的应用 (1)与圆相关; (2)与仰角、俯角相关; (3)与方位角相关; (4)与坡度、坡角相关.
5.如图,某地修建高速公路,要从 A 地向 B 地修一条隧道(点 A,B 在同一水平面上).为了测量 A,B 两地之间的距离,一 架直升飞机从 A 地出发,垂直上升 800 m 到达 C 处,在 C 处 观察 B 地的俯角为 α,则 A,B 两地之间的距离为( D ) A.800sin α m B.800tan α m
人教版 九年级下册数学第二十八章 锐角三角函数 锐角三角函数单元复习和巩固

锐角三角函数单元复习与巩固一、目标与策略明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!学习目标:●了解锐角三角函数的概念,能够正确应用sinA 、cosA、tanA表示直角三角形中两边的比;记忆30°、45°、60°的正弦、余弦和正切的函数值,并会由一个特殊角的三角函数值说出这个角;●能够正确地使用计算器,由已知锐角求出它的三角函数值,由已知三角函数值求出相应的锐角;●理解直角三角形中边与边的关系,角与角的关系和边与角的关系,会运用勾股定理、直角三角形的两个锐角互余、以及锐角三角函数解直角三角形,并会用解直角三角形的有关知识解决简单的实际问题;●通过锐角三角函数的学习,进一步认识函数,体会函数的变化与对应的思想,通过解直角三角的学习,体会数学在解决实际问题中的作用,并结合实际问题对微积分的思想有所感受.重点难点:●重点:锐角三角函数的概念和直角三角形的解法.●难点:锐角三角函数的概念.复习策略:●本章由锐角三角函数和解直角三角形两节构成。
锐角三角函数以相似三角形为基础进行学习,解直角三角形以锐角三角函数和勾股定理为基础进行学习,在学习的过程中不断地综合直角三角形的有关知识。
二、学习与应用知识框图通过知识框图,先对本单元知识要点有一个总体认识。
“凡事预则立,不预则废”。
科学地预习才能使我们上课听讲更有目的性和针对性。
A B C c b a 知识点一:锐角三角函数(一)正弦、余弦、正切的定义如右图、在Rt △ABC 中,∠C=900,如果锐角A 确定: (1)sinA= ,这个比叫做∠A 的 . (2)cosA= ,这个比叫做∠A 的 .(3)tanA= ,这个比叫做∠A 的 .要点诠释:(1)正弦、余弦、正切是在一个直角三角形中定义的,其本质是两条线段的 ,它只是一个 ,其大小只与锐角的 有关,而与所在直角三角形的大小无关.(2)sinA 、cosA 、tanA 是一个整体符号,即表示∠A 四个三角函数值,书写时习惯上省略符号“∠”,但不能写成sin·A ,对于用三个大写字母表示一个角时,其三角函数中符号“∠”不能省略,应写成sin ∠BAC ,而不能写出sinBAC .(3)sin 2A 表示(sinA)2,而不能写成sinA 2.(4)三角函数有时还可以表示成sin ,cos αβ等.(二)锐角三角函数的定义锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数.要点诠释:对于锐角A 的每一个确定的值,sinA 有唯一确定的值与它对应,所以sinA 是∠A 的函数.同样,cosA 、tanA 也是∠A 的函数,其中∠A 是自变量,sinA 、cosA 、tanA 分别是对应的函数.其中自变量∠A 的取值范围是 °<∠A< °,函数值的取值范围是 <sinA< , <cosA< ,tanA> .(三)锐角三角函数之间的关系:余角三角函数关系:“正余互化公式”如∠A+∠B=90°, 那么:sinA=cos ;cosA=sin ;同角三角函数关系:sin 2A +cos 2A= ; =sin cos AA(四)30︒、45︒、60︒角的三角函数值 知识要点梳理认真阅读、理解教材,尝试把下列知识要点内容补充完整,若有其它补充可填在右栏空白处。
第28章+锐角三角函数知识点总结及思维导图+2023—2024学年人教版数学九年级下册
第28章锐角三角函数【思维导图】28.1锐角三角函数【知识点】1.Rt△ABC中,∠C=90°.(1)∠A的对边与斜边比,叫做∠A的正弦,记为sinA,即sinA=∠A的对边斜边=aa(2)∠A的邻边与斜边比,叫做∠A的余弦,记为cosA,即cosA=∠A的邻边斜边=aa(3)∠A的对边与邻边比,叫做∠A的正切,记为tanA,即tanA=∠A的对边∠A的邻边=aa∠A的正弦、余弦、正切统称为∠A的锐角三角函数.提示:sin A 不是sin与A的乘积,而是一个整体,cosA和tanA同理;锐角三角函数的三种表示方法:sin A,sin 56°,sin∠DEF.2.一个锐角的三角函数值是一个比值,它与三角形的大小无关,它没有单位.在Rt△ABC中,当锐角A的度数一定时,无论这个直角三角形大小如何,∠A的锐角三角函数值为定值.锐角三角函数锐角α30°45°60°sin α12√22√32cos α√32√2212tan α√331√3(1)正弦值、正切值随角度的增大而增大,余弦值随角度的增大而减小.(2)sin α=cos(90°-α)cos α=sin(90°-α)tan α·tan(90°-α)=1(3)锐角A 的正弦、余弦的取值范围分别为:0<sin A<1,0<cos A<1, (4)cos 2A+sin 2A=1 sin 2A+sin 2(90°-α)=1(5)tan A=sin A cos A4.锐角三角函数值是个常数值,它只与角的度数有关,将来离开了直角三角形也存在.5.若α=45°,则sin α=cos α; 若α<45°,则sin α<cos α; 若α>45°,则sin α>cos α;28.2解直角三角形及其应用 28.2.1 解直角三角形【知识点】1.在直角三角形中,由已知元素求出其余未知元素的过程就是解直角三角形.2.在直角三角形中,三边之间的关系是a 2+b 2=c 2(勾股定理); 两锐角之间的关系是∠A+∠B=90° 边角之间的关系有sinA=∠A 的对边斜边,cosA=∠A 的邻边斜边,tanA=∠A 的对边∠A 的邻边3.在直角三角形的六个元素中,除直角外的五个元素只要知道其中的两个元素,就可以求出其余三个元素,其中至少有一个是边.4.在Rt △ABC 中,∠C=90°,若已知∠A=α,AB=c ,较简便的方法是用正弦求出BC ,用余弦求出AC ,也可用勾股定理求出AC ,根据直角三角形的两锐角互余求出∠B.单元练习一、选择题1.已知∠α为锐角,且sin a=12,则∠α=( )A.30°B.45°C.60°D.90°2.sin 60°的相反数是( )A.-12B.−√33C.−√32D.−√223.如图,在∠ABC中,∠B=90°,BC=2AB,则cosA的值为( )A.52B.12C.255D.554.如图,在4×5 的正方形网格中,每个小正方形的边长都是1,∠ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB 的值为( )A.3√55B.√175C. 35D. 455.在∠ABC中,∠A,∠B均为锐角,且|2sin A-1|与(cos a-√22)2互为相反数,则∠C的度数是( )A.45°B.75°C.105°D.120°6.如图,在∠ABC中,∠C=90°,AB=15,sinB=35,则AC的长为( )A.3 B.9 C.4 D.127.如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪的高A D为1.5米,则铁塔的高BC为( )A.(1.5+150tanα)米a.(1.5+150tan a)米C.(1.5+150sinα)米a.(1.5+150sin a)米8.在Rt∠ABC 中,∠C=90°,AB=2BC,则cos A 的值为 ( ) A.√32 B .12 C .√33 D .√229.如图,在∠ABC 中,CA =CB =4,cosC =14 ,则sinB 的值为( )A.102 B .153 C .64 D .10410.如图,电线杆CD 的高度为h ,两根拉线 AC 与BC 相互垂直,∠CAB=α,则拉线 BC 的长度为(点 A,D,B 在同一条直线上)( ) a .asin a a .acos a a .atan a D. h·cosα11.定义一种运算:cos(α+β)=cos αcos β-sin αsin β,cos(α-β)=cos αcos β+sin αsin β.例如:当α=60°,β=45°时,cos(60°-45°)=12×√22+√32×√22=√2+√64,则cos 75°的值为 ( )A.√6+√24 B .√6-√24C.√6-√22 D .√6+√2212.如图,由边长为1的小正方形构成的网格中,点A ,B ,C 都在格点上,以AB 为直径的圆经过点C ,D ,则cos∠ADC 的值为( )A .21313B .31313C .23D .53 二、填空题,则cos B=_______.13.在∠ABC中, aa=90°,tan a=√3314.已知α为锐角,当无意义时,cos α的值是_______.√3tan a-115.如图,在Rt∠ABC中,∠ACB=90°,CD∠AB,垂足为D,若AC= 5 ,BC =2,则sin∠ACD的值为_________.16.某物体沿着坡比为4:3的坡面上升了8米,那么在坡面上移动了_______米.17.如图,已知正方形ABCD和正方形BEFG,点G在AD上,GF与CD交于点,正方形ABCD的边长为8,则BH的长为_______.H,tan∠ABG=1218.如图,在平面直角坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C是第一象限内一点,且AC=2,设tan∠BOC=m,则m的取值范围是_________.三、解答题19.图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图,经测量,钢条AB=AC=50 cm,∠AB C=47°.(1)求车位锁的底盒BC的长;(2)若一辆汽车的底盘高度为30cm,当车位锁上锁时,问这辆汽车能否进入该车位? (参考数据:aaa47°≈0.73,aaa47°≈0.68,aaa47°≈1.07)20.某景区为给游客提供更好的游览体验,拟在如图∠所示的景区内修建观光索道.其设计示意图如图∠所示,以山脚A为起点,沿途修建AB、CD两段长度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC,BC长为50 m.索道AB与AF的夹角为15°,CD与水平线的夹角为45°,A、B两处的水平距离AE为576 m,DF∠AF,垂足为点F.(图∠中所有点都在同一平面内,点A、E、F 在同一水平线上)(1)求索道AB的长(结果精确到1 m);(2)求AF的长(结果精确到1 m).(参考数据:sin 15°≈0.25,cos 15°≈0.96,tan 15°≈0.26,√2≈1.41)21.八年级二班学生到某劳动教育实践基地开展实践活动,当天,他们先从基地门口A处向正北方向走了450米,到达菜园B处锄草,再从B处沿正西方向到达果园C处采摘水果,再向南偏东37°方向走了300米,到达手工坊D处进行手工制作,最后从D处回到门口A处,手工坊在基地门口北偏西65°方向上,求菜园与果园之间的距离.(结果保留整数.参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)。
人教版-数学-九年级下册--第二十八章 锐角三角函数全章小结与复习测试(含答案)
小结与复习知识结构基础知识1.直角三角形的边角关系:在Rt△ABC中,∠A+∠B=90°,a2+b2=c2,sinA=cosB=ac, cosA=sinB=bc,tanA=cotB=ab, cosA=tanB=ba.2.互余两角三角函数间的关系:如∠A+∠B=90°,那么sinA=cosB,cosA=sinB. 3.同角三角函数间的关系:sin2A+cos2A=1,tanA·cotA=1,tanA=sin cos,cotcos sinA AAA A.4.特殊角的三角函数三角函数0°30°45°60°90°sinα 0 1222321cosα 1 322212tanα 0 321 3不存在cotα不存在3 1 33解直角三角形的基本类型解直角三角形的基本类型及其解法如下表:类型已知条件解法解直角三角形注意点1.尽量使用原始数据,使计算更加准确.2.有的问题不能直接利用直角三角形内部关系解题,•但可以添加合适的辅助线转化为解直角三角形的问题.3.一些较复杂的解直角三角形的问题可以通过列方程或方程组的方法解题.4.解直角三角形的方法可概括为“有弦(斜边)用弦(正弦、余弦),无弦有切(正切、余切),宁乘毋除,取原避中”其意指:当已知或求解中有斜边时,可用正弦或余弦;无斜边时,就用正切或余切;当所求元素既可用乘法又可用除法时,则用乘法,不用除法;既可由已知数据又可用中间数据求解时,则取原始数据,忌用中间数据.5.必要时按照要求画出图形,注明已知和所求,•然后研究它们置于哪个直角三角形中,应当选用什么关系式来进行计算.6.要把添加辅助线的过程准确地写在解题过程之中.7.解含有非基本元素的直角三角形(即直角三角形中中线、高、角平分线、•周长、面积等),一般将非基本元素转化为基本元素,或转化为元素间的关系式,再通过解方程组来解.应用题解题步骤度量工具、工程建筑、测量距离等方面应用题的解题步骤可概括为如下几步:第一步,审清题意,要弄清仰角、俯角、坡度、坡角、水平距离、垂直距离、水平等概念的意义.第二步,构造出要求解的直角三角形,对于非直角三角形的图形可作适当的辅助线把它们分割成一些直角三角形和矩形(包括正方形).第三步,选择合适的边角关系式,使运算尽可能简便,不易出错.第四步,按照题目中已知数的精确度进行近似计算,并按照题目要求的精确度确定答案及注明单位. 思想方法总结 1.转化思想转化思想贯穿于本章的始终.例如,利用三角函数定义可以实现边与角的转化,利用互余两角三角函数关系可以实现“正”与“余”的互化;利用同角三角函数关系可以实现“异名”三角函数之间的互化.此外,利用解直角三角形的知识解决实际问题时,首先要把实际问题转化为数学问题. 2.数形结合思想本章从概念的引出到公式的推导及直角三角形的解法和应用,无一不体现数形结合的思想方法.例如,在解直角三角形的问题时,常常先画出图形,使已知元素和未知元素更直观,有助于问题的顺利解决. 3.函数思想锐角的正弦、余弦、正切、余切都是三角函数,其中都蕴含着函数的思想.例如,任意锐角a 与它的正弦值是一一对应的关系.也就是说,对于锐角a 任意确定的一个度数,sina 都有惟一确定的值与之对应;反之,对于sina 在(01)之间任意确定的一个值,锐角a 都有惟一确定的一个度数与之对应. 4.方程思想在解直角三角形时,若某个元素无法直接求出,往往设未知数,根据三角形中的边角关系列出方程,通过解方程求出所求的元素. 中考新题型 例1 计算:(1)sin 230°-cos45°·tan60°(223tan 30︒+分析:把特殊角的三角函数值代入计算即可.解:(1)sin30°-cos45°·tan60°=14-2=14(2)原式+1-3×(3)2+1-1+2(1-2)=2 说明:熟记30°、45°、60°角的三角函数值,是解决这类问题的关键,•这类题也是中考考查的重点,在选择题和填空题中出现的更多.例 2 如右图,已知缆车行驶线与水平线间的夹角α=30°,β=45°.•小明乘缆车上山,从A到B,再从B到D都走了200米(即AB=BD=200米),•请根据所给的数据计算缆车垂直上升的距离.(计算结果保留整数,以下数据供选用:sin47°≈0.7314,cos47•°≈0.6820,tan47°≈1.0724)分析:缆车垂直上升的距离分成两段:BC与DF.分别在Rt△ABC和Rt△DBF•中求出BC 与DF,两者之和即为所求.解:在Rt△ABC中,AB=200米,∠BAC=α=30°,∴BC=AB·sinα=200sin30°=100(米).在Rt△BDF中,BD=200米,∠DBF=β47°,∴DF=BD·sinβ=200·sin47°≈200×0.7314=146.28(米).∴BC+DF=100+146.28=246.28(米).答:缆车垂直上升了246.28米.说明:解直角三角形在实际生活中的应用,是中考考查的重点,也是考查的热点.要解决好这类问题:一是要合理地构造合适的直角三角形;•二是要熟记特殊角的三角函数值;三是要有很好的运算能力和分析问题的能力.课时作业设计本章单元测试.单元测试一、选择题.1.在△ABC中,∠C=90°,AB=15,sinA=13,则BC等于().A.45 B.5 C.15D.1452.在Rt△ABC中,∠ACB=90°,若cotA=34,则cosA等于().A.45B.35C.43D.343.如图,为测一河两岸相对两电线杆A、B间的距离,在距A点15米的C处(AC⊥AB)测得∠ACB=50°,则A、B之间的距离应为().A .15sin50°米B .15cos50°米;C .15tan50°米D .15cot50°米CBAaADC(第3题) (第6题) (第7题) 4.如果si n 2a+sin 230°=1,那么锐角a 的度数是( ). A .15° B .30° C .45° D .60° 5.在Rt △ABC 中,∠C=90°,若2,则cosB 的值为( ). A .12B .22C . 32D .16.如图,为了测量河两岸A 、B 两点的距离,在与AB 垂直的方向上取点C ,•测得AC=a ,∠ACB=a ,那么AB 等于( ).A .a ·sinaB .a ·cosaC .a ·tanaD .a ·cota7.如图Rt △ABC 中,∠ACB=90°,CD ⊥AB ,D 为垂足.若AC=4,BC=3,则sin ∠ACD 的值为( ). A .43 B .34 C .45 D .358.已知直角三角形中30°角所对的直角边长是2cm ,则斜边的长是( ). A .2cm B .4cm C .6cm D .8cm 9.在△ABC 中,sinB=cos (90°-C )=12,那么△ABC 是( ). A .等腰三角形 B .等边三角形 C .直角三角形 D .等腰直角三角形10.在Rt △ABC 中,∠C=90°,AB=13,AC=12,BC=5,则下列各式中正确的是( ). A .sinA=125 B .cosA=1213 C .tanA=125 D .cotA=121311.如图,为测楼房BC 的高,在距离房30米的A 处测得楼顶的仰角为α,则楼高BC•的高为( ).A.30tanα米B.3030.30sin.tan30sinC Dααα米米BAαCBADC(第11题) (第12题)12.如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=15,则AD的长为().A.2 B.2 C.1 D.22二、填空题.13.如图,如果△APB绕点B按逆时针方向旋转30°后得到△A′P′B′,且BP=2,•那么PP′的长为________.(不取近似值,以下数据供解题使用:sin15°=6262,cos1544-+︒=)(第13题) (第14题) (第21题)14.如图,沿倾斜角为33°的山坡植树,要求相邻两棵树的水平距离AC为2m,那么相邻两棵树的斜坡距离AB约为________m.(精确到0.01m)15.sin30°=________.1635°=________.(精确到0.01)17.若圆周角α所对弦长为sinα,则此圆的半径r为_______.18.锐角A满足2sin(A-15°)3A=________.19.计算:3tan30°+cot45°-2tan45°-2cos60°=_________.20.已知A是锐角,且sinA=13,则cos(90°-A)=________.21.为了测量一个圆形铁环的半径(如图),某同学采用了如下办法:•将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若测得PA=5cm,则铁环的半径是______cm.三、计算题.22°-).23.计算:cos60°-1.24.计算:(1)sin30°+cos45°+tan60°-cot30°.(2cot303tan30 cos27sin30cos45︒-︒︒+︒-︒25.若方程2x2+(4sinθ)x+1=0(0<θ<90°)有两个相等的实数根,求θ的值.四、解答题.26.如图,为申办2010年冬奥会,需改变哈尔滨市的交通状况.在大道拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形区域为危险区,现在某工人站在离B点3米处的D处测得树的顶端A点的仰角为60°,树的底部B•点的俯角为30°,问距离B点8 1.73)27.我边防战士在海拔高度(即CD 的长)为50米的小岛顶部D 处执行任务,上午8时发现在海面上的A 处有一艘船,此时测得该船的俯角为30°,该船沿着AC•方向航行一段时间后到达B 处,又测得该船的俯角为45°,求该船在这一段时间内的航程.(•计算结果保留根号)28.如图,在离地面高度5米处引拉线固定电线杆,拉线和地面成58°,•求拉线下端点A 与杆底D 的距离AD .(精确到0.01米)58B A4mD C答案:一、1.B 2.B 3.C 4.D 5.B 6.C 7.C 8.B 9.A 10.B 11.A 12.B二、13 14.2.38 15.12 16.1.10 17.1218.75° 1920.1321.三、22°-)0.23.解:原式=12-12.24.(1)12(2)1 25.θ=45°. 四、26.过点C 作CE ⊥AB 于E ,Rt △CBE 中,tan30°=BE CE,∴BE=CE ·tan30° Rt △CAE 中,tan60°=AEEC,∴AE=CE ·tan60°∴4×1.73=6.92<8. ∴保护物不在危险区.27.解:根据题意,∠ADC=60°,∠BDC=∠DBC=45°,∴BC=DC=50.在Rt △ADC 中,AC=CD ×tan ∠AB=AC-BC=50-1)(米).答:该船在这段时间内的航程为50)米. 28.解:在Rt △ACD 中,∠ADC=90°,∠CAD=58°,CD=5米.∵tan ∠CAD=CDAD , ∴AD=5tan tan 58CD CAD =∠︒≈3.12(米).答:拉线下端点A 与杆底D 的距离AD 约为3.12米.。
人教版九年级数学下册 第28章《锐角三角函数》小结与复习课件)(共20张PPT)
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成 。21.8.1021.8.1019:14:4419:14:44August 10, 2021
•
14、谁要是自己还没有发展培养和教 育好, 他就不 能发展 培养和 教育别 人。2021年8月 10日星 期二下 午7时14分44秒19:14:4421.8.10
•
10、阅读一切好书如同和过去最杰出 的人谈 话。19:14:4419:14:4419:148/10/2021 7:14:44 PM
•
11、一个好的教师,是一个懂得心理 学和教 育学的 人。21.8.1019:14:4419:14Aug-2110- Aug-21
•
12、要记住,你不仅是教课的教师, 也是学 生的教 育者, 生活的 导师和 道德的 引路人 。19:14:4419:14:4419:14Tues day, August 10, 2021
特殊角的三角函数值
重点知识
特殊角的三角函数值:
锐角α 30o
45o
三角函数
sinα
cosα
tanα
60o 增减性 递增 递减 递增
•
9、要学生做的事,教职员躬亲共做; 要学生 学的知 识,教 职员躬 亲共学 ;要学 生守的 规则, 教职员 躬亲共 守。21.8.1021.8.10T uesday, August 10, 2021
•
4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为,半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19
☆人教版九年级数学下册第28章 锐角三角函数知识点及典型例题
人教版九年级数学下册第28章 锐角三角函数知识点及典型例题知识点一:锐角三角函数的定义: 一、 锐角三角函数定义:在Rt △ABC 中,∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c , 则∠A 的正弦可表示为:sinA= , ∠A 的余弦可表示为cosA=∠A 的正切:tanA= ,它们弦称为∠A 的锐角三角函数 例1.如图所示,在Rt △ABC 中,∠C =90°.第1题图①斜边)(sin =A =______, 斜边)(sin =B =______; ②斜边)(cos =A =______,斜边)(cos =B =______;③的邻边A A ∠=)(tan =______,)(tan 的对边B B ∠==______. 例2. 锐角三角函数求值:在Rt △ABC 中,∠C =90°,若a =9,b =12,则c =______,sin A =______,cos A =______,tan A =______, sin B =______,cos B =______,tan B =______.例3.已知:如图,Rt △TNM 中,∠TMN =90°,MR ⊥TN 于R 点,TN =4,MN =3.求:sin ∠TMR 、cos ∠TMR 、tan ∠TMR .典型例题:类型一:直角三角形求值1.已知Rt △ABC 中,,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B .2.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,⋅=∠43sin AOC求:AB 及OC 的长.3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,⋅=∠53sin AOC (1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC .4. 已知A ∠是锐角,178sin =A ,求A cos ,A tan 的值对应训练:(西城北)3.在Rt △ABC 中,∠ C =90°,若BC =1,AB =5,则tan A 的值为A .55 B .255 C .12D .2 (房山)5.在△ABC 中,∠C =90°,sin A=53,那么tan A 的值等于( ).A .35B . 45C . 34D . 43类型二. 利用角度转化求值:1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点.DE ∶AE =1∶2.求:sin B 、cos B 、tan B .2. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与x 轴的正半轴交于点D ,B 是y 轴右侧圆弧上一点,则cos ∠OBC 的值为( ) A .12 B .32C .35D .453.(孝感中考)如图,角α的顶点为O ,它的一边在x 轴的正半轴上,另一边OA 上有一点P (3,4),则 sin α= .D C B A Oyx第8题图4.(庆阳中考)如图,菱形ABCD 的边长为10cm ,DE ⊥AB ,3sin 5A =,则这个菱形的面积= cm 2.5.(齐齐哈尔中考)如图,O ⊙是ABC △的外接圆,AD 是O ⊙的直径,若O ⊙的半径为32,2AC =,则sin B 的值是( )A .23 B .32 C .34 D .436. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =,AB=8,则tan EFC ∠的值为 ( )A.34 B.43C.35D.45A D EC B F7. 如图6,在等腰直角三角形ABC ∆中,90C ∠=︒,6AC =,D 为AC 上一点,若1tan 5DBA ∠= ,则AD 的长为( )A .2B .2C .1D .228. 如图6,在Rt △ABC 中,∠C =90°,AC =8,∠A 的平分线AD =3316求 ∠B 的度数及边BC 、AB 的长.DABC图6类型三. 化斜三角形为直角三角形例1 (安徽)如图,在△ABC 中,∠A=30°,∠B=45°,AC=23,求AB 的长.例2.已知:如图,△ABC 中,AC =12cm ,AB =16cm ,⋅=31sin A(1)求AB 边上的高CD ; (2)求△ABC 的面积S ; (3)求tan B .例3.已知:如图,在△ABC 中,∠BAC =120°,AB =10,AC =5.求:sin ∠ABC 的值.对应训练1.(重庆)如图,在Rt △ABC 中,∠BAC=90°,点D 在BC 边上,且△ABD 是等边三角形.若AB=2,求△ABC 的周长.(结果保留根号)2.已知:如图,△ABC 中,AB =9,BC =6,△ABC 的面积等于9,求sin B .3. ABC 中,∠A =60°,AB =6 cm ,AC =4 cm ,则△ABC 的面积是A.23 cm 2B.43 cm 2C.63 cm 2D.12 cm 2类型四:利用网格构造直角三角形例1 (内江)如图所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为( )A .12B .55C .1010D .255对应练习:1.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_______.CBA2.如图,A 、B 、C 三点在正方形网络线的交点处,若将ABC ∆绕着点A 逆时针旋转得到''B AC ∆,则't a nB 的值为 A.41 B. 31 C.21D. 13.正方形网格中,AOB ∠如图放置,则tan AOB ∠的值是( )A . 5 5 B. 2 5 5 C.12 D. 2特殊角的三角函数值当 时,正弦和正切值随着角度的增大而 余弦值随着角度的增大而例1.求下列各式的值.(昌平)1).计算:︒-︒+︒60tan 45sin 230cos 2.(朝阳)2)计算:︒-︒+︒30cos 245sin 60tan 2.锐角α 30° 45° 60° sin αcos αtan αA BO(黄石中考)计算:3-1+(2π-1)0-33tan30°-tan45°(石景山)4.计算:030tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+.(通县)5.计算:tan 45sin 301cos 60︒+︒-︒;例2.求适合下列条件的锐角α .(1)21cos =α(2)33tan =α(3)222sin =α (4)33)16cos(6=- α(5)已知α 为锐角,且3)30tan(0=+α,求αtan 的值(6)在AB C ∆中,若0)22(sin 21cos 2=-+-B A ,B A ∠∠,都是锐角,求C ∠的度数.例3. 三角函数的增减性 1.已知∠A 为锐角,且sin A <21,那么∠A 的取值范围是 A. 0°< A < 30° B. 30°< A <60° C. 60°< A < 90° D. 30°< A < 90° 2. 已知A 为锐角,且030sin cos <A ,则 ( )A. 0°< A < 60°B. 30°< A < 60°C. 60°< A < 90°D. 30°< A < 90° 例4. 三角函数在几何中的应用1.已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.2.已知:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求:(1)∠BAD ;(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD .3. 已知:如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD .4. 如图,在Rt △ABC 中,∠C=90°,53sin =B ,点D 在BC 边上,DC= AC = 6,求tan ∠BAD 的值.DCBA5.如图,△ABC 中,∠A=30°,3tan 2B =,43AC =.求AB 的长.解直角三角形:1.在解直角三角形的过程中,一般要用的主要关系如下(如图所示): 在Rt △ABC 中,∠C =90°,AC =b ,BC =a ,AB =c ,①三边之间的等量关系:________________________________.②两锐角之间的关系:__________________________________. ③边与角之间的关系:==B A cos sin ______;==B A sin cos _______;==BA tan 1tan _____;==B A tan tan 1______.④直角三角形中成比例的线段(如图所示).在Rt △ABC 中,∠C =90°,CD ⊥AB 于D .CD 2=_________;AC 2=_________; BC 2=_________;AC ·BC =_________.类型一例1.在Rt △ABC 中,∠C =90°.(1)已知:a =35,235=c ,求∠A 、∠B ,b ;(2)已知:32=a ,2=b ,求∠A 、∠B ,c ;ACB(3)已知:32sin =A ,6=c ,求a 、b ;(4)已知:,9,23tan ==b B 求a 、c ;(5)已知:∠A =60°,△ABC 的面积,312=S 求a 、b 、c 及∠B .例2.已知:如图,△ABC 中,∠A =30°,∠B =60°,AC =10cm .求AB 及BC 的长.例3.已知:如图,Rt △ABC 中,∠D =90°,∠B =45°,∠ACD =60°.BC =10cm .求AD 的长.例4.已知:如图,△ABC中,∠A=30°,∠B=135°,AC=10cm.求AB及BC的长.类型二:解直角三角形的实际应用仰角与俯角:例1.(福州)如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB 两点的距离是()A.200米B.200米C.220米D.100()米例2.已知:如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离mDE,求点B到地=32面的垂直距离BC.例3(昌平)19.如图,一风力发电装置竖立在小山顶上,小山的高BD=30m.从水平面上一点C测得风力发电装置的顶端A的仰角∠DCA=60°,测得山顶B的仰角∠DCB=30°,求风力发电装置的高AB的长.例4 .如图,小聪用一块有一个锐角为30︒的直角三角板C测量树高,已知小聪和树都与地面垂直,且相距33米,小聪身高AB为1.7米,求这棵树的高度.例5.已知:如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50m.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求山的高度及缆绳AC的长(答案可带根号).例5.(泰安)如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB 的高度为()A.10米B.10米C.20米D.米例6.益阳)超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A 处,离益阳大道的距离(AC )为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B 处行驶到C 处所用的时间为8秒,∠BAC=75°. (1)求B 、C 两点的距离;(2)请判断此车是否超过了益阳大道60千米/小时的限制速度? (计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732,3≈1.732,60千米/小时≈16.7米/秒)类型四. 坡度与坡角例.(广安)如图,某水库堤坝横断面迎水坡AB 的坡比是1:3,堤坝高BC=50m ,则应水坡面AB 的长度是( )A .100mB .1003mC .150mD .503m类型五. 方位角 1.已知:如图,一艘货轮向正北方向航行,在点A 处测得灯塔M 在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B 处,测得灯塔M 在北偏西45°,问该货轮继续向北航行时,与灯塔M 之间的最短距离是多少?(精确到0.1海里,732.13 )2.(恩施州)新闻链接,据[侨报网讯]外国炮艇在南海追袭中国渔船被中国渔政逼退2012年5月18日,某国3艘炮艇追袭5条中国渔船.刚刚完成黄岩岛护渔任务的“中国渔政310”船人船未歇立即追往北纬11度22分、东经110度45分附近海域护渔,保护100多名中国渔民免受财产损失和人身伤害.某国炮艇发现中国目前最先进的渔政船正在疾速驰救中国渔船,立即掉头离去.(见图1)解决问题如图2,已知“中国渔政310”船(A)接到陆地指挥中心(B)命令时,渔船(C)位于陆地指挥中心正南方向,位于“中国渔政310”船西南方向,“中国渔政310”船位于陆地指挥中心南偏东60°方向,AB=海里,“中国渔政310”船最大航速20海里/时.根据以上信息,请你求出“中国渔政310”船赶往出事地点需要多少时间.综合题:三角函数与四边形:(西城二模)1.如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=2,tan∠BDC=6 3.(1) 求BD 的长; (2) 求AD 的长.18.如图,在平行四边形ABCD 中,过点A 分别作AE ⊥BC 于点E ,AF ⊥CD 于点F .(1)求证:∠BAE =∠DAF ; (2)若AE =4,AF =245,3sin 5BAE ∠=,求CF 的长.三角函数与圆:1. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与x 轴的正半轴交于点D ,B 是y 轴右侧圆弧上一点,则cos ∠OBC 的值为( ) A .12 B .32C .35D .45(延庆)19. 已知:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接AC 与⊙O交于点D,(1) 求证:∠AOD=2∠C(2) 若AD=8,tanC=34,求⊙O 的半径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
┃习题讲练 图7
┃习题讲练
ห้องสมุดไป่ตู้
解:过点 A 作 AD⊥BC 交 BC 延长线于点 D.
由题意,BC=600×5.5=3300(米).
在直角△ACD 中,
∵∠DCA=45°,
∴∠CAD=∠DCA=45°,
∴AD=CD.
图8
设 AD=x 米,在直角△ABD 中,tanB=ABDD,
∴(3300+x)·tan15°=x,
∴x= 3-1≈1.732-1=0.732>0.7.
答:计划修筑的这条公路不会穿越公园.
┃ 习题讲练
15.一艘轮船自南向北航行,在 A 处测得北偏东 21.3°方向有一 座小岛 C,继续向北航行 60 海里到达 B 处,测得小岛 C 此时在轮 船的北偏东 63.5°方向上.之后,轮船继续向北航行约多少海里,距 离小岛 C 最近?
图 16
┃ 习题讲练
解:∵AB∥DC,∴CADB=DBOO. ∵△AOB 的面积等于 9,△AOD 的面积等于 6,∴SS△△AAOODB=DBOO =23,∴CADB=DBOO=32. ∵AB=7,∴C7D=23,∴CD=134.
┃ 习题讲练
14.去年某省将地处 A、B 两地的两所大学合并成一所综合大学, 为了方便 A、B 两地师生的交往,学校准备在相距 2 千米的 A、B 两地之间修筑一条笔直的公路(如图 17 中的线段 AB),经测量,在 A 地的北偏东 60°方向和 B 地的北偏西 45°方向的 C 处有一个半径为 0.7 千米的公园,问计划修筑的这条公路会不会穿越公园?为什么?
图3
┃ 考点攻略 ► 考点二 特殊角的三角函数值的考查 例 2 计算: 2(2cos45°-sin60°)+ 424-tan230°.
解:原式= 22× 22- 23+24 6- 332=2- 26+ 26-13=35.
┃ 考点攻略 ► 考点三 解直角三角形
例 3 已知:如图 4 所示,在 Rt△ABC 中,∠C=90°,AC = 3.点 D 为 BC 边上一点,且 BD=2AD,∠ADC=60°.求△ABC 的周长.(结果保留根号)
.
(2)直角三角形可解的条件和解法
条件:解直角三角形时知道其中的2个元素(至少有一个是边), 就可以求出其余的3个未知元素.
┃ 知识归纳
解法:①一边一锐角,先由锐角关系求出另一锐角;知斜边, 再用正弦(或余弦)求另两边;知直角边用正切求另一直角边,再 用正弦或勾股定理求斜边.②知两边:先用勾股定理求另一边, 再用边角关系求锐角.③斜三角形问题可通过添加适当的辅助线 转化为直角三角形问题.
a =b .
┃ 知识归纳
[易错点] 忽视用边的比表示锐角的正弦、余弦和正切的前 提是在直角三角形中.
2.30°,45°,60°角的三角函数值
sin30°=
1 2
,sin45°=
2 2
3
,sin60°= 2
;
cos30°=
3 2
2
,cos45°= 2
,cos60°=
1 2
;
tan30°=
3 3
,tan45°= 1
解得 x≈1208.2
答:飞机距地面的飞行高度约为 1208.2 米.
┃ 习题讲练
5.如图9,小刚同学在綦江南州广场上观测新华书店楼房墙 上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角 为30°,然后他正对屏幕方向前进了6米到达B处,又测得该屏幕 上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE =21米,请你帮小刚求出该屏幕上端与下端之间的距离CD.(结果 保留根号)
┃ 习题讲练
(2)由(1)得,BC=AC=5 2 2(米), 在直角三角形 ADC 中, CD=taAn3C0°=25 6(米). 所以 BD=CD-BC=52( 6- 2)≈2.5875≈2.59(米), 因为 6-2.59=3.41>3, 所以这样改造是可行的.
┃ 习题讲练
7.如图 11,在梯形 ABCD 中,AD∥BC,AC⊥AB,AD=CD,
┃ 考点攻略
方法技巧 解直角三角形的一般思路是:有斜(斜边)用弦(正弦、余弦), 无斜用切(正切),宁乘勿除,取原避中.对于较复杂的图形,要 善于将其分解成简单的图形,并借助桥梁(相等的边、公共边、相 等的角等)的作用将两个图形有机地联系在一起,从而达到解题的 目的.
┃ 考点攻略
► 考点四 解直角三角形在实际中的应用 例4 [2010·广州] 目前世界上最高的电视塔是广州新电视
=45,则 AC=____5____.
图12
┃ 习题讲练
10.如图 13,在平行四边形 ABCD 中,E 为 AD 的中点,△DEF
的面积为 1,则△BCF 的面积为( D )
A.1 B.2 C.3 D.4
图13
┃ 习题讲练 11.已知如图 14,在△ABC 中,DE∥BC,△ADE 与梯形 BDEC
┃ 考点攻略
方法技巧 解应用题时,先要将实际问题转化为数学问题,找出直角三 角形并寻找联系已知条件和未知量的桥梁,从而利用解直角三角 形的知识得到数学问题的答案,最后得到符合实际情况的答案.
┃ 习题讲练 1. 12+2sin60°=___3__3___.
┃ 习题讲练
2.计算1+2sitnan304°5°-3cot60°的值为_2_-___3___.
参考数据:sin21.3°≈295,tan21.3°≈25,sin63.5°≈190,tan63.5°≈2
┃ 习题讲练
图19
┃ 习题讲练
解:过点 C 作 AB 的垂线,垂足为点 D. 设 BD=x,在 Rt△BCD 中,tan∠CBD=tan63.5°=CBDD,∴CD= x·tan63.5°. 在 Rt△ACD 中,tanA=tan21.3°=ACDD, ∵AD=AB+BD=60+x, ∴CD=(60+x)·tan21.3°. ∴x·tan63.5°=(60+x)·tan21.3°, ∵tan21.3°≈25,tan63.5°≈2, 解得 x≈15. 答:轮船继续向北航行约 15 海里,距离小岛 C 最近.
复习 ┃ 知识归纳
┃知识归纳┃
1.锐角三角函数的定义 如图 1 所示:在 Rt△ABC 中,∠C=90°,a,b,c 分别是∠A, ∠B,∠C 的对边.
图1
┃ 知识归纳
(1)∠A 的正弦:sinA=∠A斜的边对边=ac;
∠A的邻边 (2)∠A的余弦:cosA= 斜边
b =c;
∠A的对边 (3)∠A的正切:tanA= ∠A的邻边
1
的面积之比是 1∶8,则 AD 与 DB 的比值为____2____.
图 14
┃ 习题讲练
12.如图 15,已知△ABC∽△DBE,AB=6,DB=8,则SS△△ADBBCE
9
=___1_6____.
图 15
┃ 习题讲练
13.如图 16,已知梯形 ABCD 中,AB∥DC,△AOB 的面积 等于 9,△AOD 的面积等于 6,AB=7,求 CD 的长.
┃ 习题讲练
【典型思想方法分析 】
转化思想 在解直角三角形和利用解直角三角形的边角关系解决实际问题 时,常常寻找已知量和未知量的关系建立方程,将几何问题转化为 代数问题求解,体现了数学的转化思想.
┃ 习题讲练
【针对训练 】
6.如图 10 所示,某幼儿园为了加强安全管理,决定将园内的滑 滑板的倾角由 45°降为 30°,已知原滑滑板 AB 的长为 5 米,点 D、 B、C 在同一水平地面上.
┃ 习题讲练
3.如图 6,以直角坐标系的原点 O 为圆心,以 1 为半径作圆,若 P 是该圆上第一象限内的点,且 OP 与 x 轴正方向组成的角为 α,则
点 P 的坐标是___(_c_o_s_α__,__s_in__α_)___.
图6
┃ 习题讲练
4.歼 10 战斗机是我国自主研制的第三代战斗机.在某次军事 演习中,某飞行员驾驶一架歼 10 战斗机,沿水平方向向地面目标 A 的正上方匀速飞行.如图 7 所示,在空中 B 点测得目标 A 的俯角为 15°.经过 5.5 秒到达 C 点,在 C 点测得目标 A 的俯角为 45°,已知歼 10 战斗机的飞行速度为 600 米/秒.求飞机距地面飞行的高度.(结 果精确到 0.1 米,参考数据:sin15°≈0.017,tan15°≈0.268)
(1)改善后滑滑板会加长多少(精确到 0.01 米)? (2)若滑滑板的正前方能有 3 米长的空地就能保证安全,原滑滑 板的前方有 6 米长的空地,像这样改造是否可行?说明理由.(参考 数据: 2≈1.414, 3≈1.732, 6≈2.449)
┃ 习题讲练 图10
┃ 习题讲练
解:(1)在直角三角形 ABC 中,sin45°=AACB, 所以 AC=AB·sin45°=522(米). 在直角三角形 ADC 中, 因为∠ADC=30°, 所以 AD=2AC=5 2≈5×1.414(米)=7.070(米)≈7.07(米), 所以改善后滑滑板会加长 7.07-5=2.07(米).
图4
┃ 考点攻略
[解析] 要求△ABC的周长,先通过解Rt△ADC求出CD和AD 的长,然后根据勾股定理求出AB的长.
┃ 考点攻略
解:在 Rt△ADC 中, ∵sin∠ADC=AACD, ∴AD=sin∠ACADC=sin630°=2. ∴BD=2AD=4. ∵tan∠ADC=ADCC, ∴DC=tan∠ACADC=tan630°=1. ∴BC=BD+DC=5. 在 Rt△ABC 中,AB= AC2+BC2=2 7. ∴△ABC 的周长=AB+BC+AC=2 7+5+ 3.
cos∠DCA=45,BC=10,则 AB 的值是( ) B
A.3 B.6 C.8 D.9
图11
┃ 习题讲练 8.在 Rt△ABC 中,∠C=90°,AC=9,sinB=35,则 AB=( A )
