2019年高三数学一轮复习课件:第70讲不等式的证明、柯西不等式与均值不等式
高中数学《均值不等式》精品PPT课件

考点突破 考点二 利用基本不等式求最值
训练 2 (1)(2014·闽南四校联考)设 a>0,若关于 x 的不等式 x+ax≥4 在 x∈(0,+∞)上恒成立,则 a 的最小值为( ) A.4 B.2 C.16 D.1
(2)设 0<x<52,则函数 y=4x(5-2x)的最大值为____.((3)见下页) 解析 要使(1)x因+为ax≥x4>在0,x∈a>(00,,+所∞以)上x恒+成ax≥立2 ,a则,需 2 a≥4,所以 a≥4,
a=18,b=12时,
凑”了吗? (利用基本不等式求解最
等所号以成ab立的.最∴大值ab为≤11614.,∴ab≤116.
法二 ∵a>0,b>0,4a+b=1,
值问题,要根据代数式或 函数解析式的特征灵活变 形,凑积或和为常数的形 式;条件最值问题要注意
当∴且ab仅=当14·4a4=a·b=b12≤,14即4aa=+2 18b,2b==11126时,,等号成常 等立数 式.所的 的以代 形换 式ab, 求的凑 解最成 最大基 值值本 .为不)116.
≥15(13+2 1x2y·3yx)=15(13+12)=5 当 等解且 号得仅 成yx当 立==1,121x2.,此y=时3y由x,xx即+=32xyy==,25yxy时,,
≤ 当且 -仅2+当3=5-1.4x=5-14x,即 x =1 时,等号成立. 故 f(x)=4x-2+4x1-5 的最大值为 1.
从而 a 的最小值为 4,故选 A. (2)因为 0<x<52,所以 5-2x>0,
当所 故且函 以仅数y=当y=4x2(4x5= x-(552--x)22=xx),的2×即最2x大(x5=-值542为时x)2等25.≤号2成2x立+,52-2x2凑=和225为,常数
【推荐ppt】2019届高考数学一轮复习不等式选讲第二节不等式的证明课件文

栏目索引
考点突破
2-2 (2015课标全国Ⅱ理,24,10分)设a,b,c,d均为正数,且a+b=c+d,证明: (1)若ab>cd,则 a + b > c + d ; (2) a + b > c + d 是|a-b|<|c-d|的充要条件.
证明 (1)因为( a + b )2=a+b+2 ab ,( c + d )2=c+d+2 cd ,且a+b=c+d, ab>cd,所以( a + b )2>( c + d )2. 因此 a + b > c + d . (2)(i)若|a-b|<|c-d|, 则(a-b)2<(c-d)2,
2n n
∴原不等式成立.
考点突破
栏目索引
考点四 柯西不等式的应用
考点突破
典例4 已知x,y,z均为实数. (1)若x+y+z=1,求证: 3x 1+ 3y 2 + 3z 3 ≤3 3 ; (2)若x+2y+3z=6,求x2+y2+z2的最小值.
解析 (1)证明:因为( 3x 1+ 3y 2 + 3z 3 )2≤(12+12+12)(3x+1+3y+2+3
栏目索引
1-1 已知a,b都是正数,且a≠b,求证:a3+b3>a2b+ab2.
证明 (a3+b3)-(a2b+ab2)=(a+b)(a-b)2. 因为a,b都是正数, 所以a+b>0. 又因为a≠b, 所以(a-b)2>0. 于是(a+b)(a-b)2>0, 即(a3+b3)-(a2b+ab2)>0, 所以a3+b3>a2b+ab2.
不等式的证明、柯西不等式与排序不等式 经典课件(最新)

高中数学课件
4.会用上述不等式证明一些简单问题.能够利用均值不等式、柯西不等式求一些特 定函数的极值.
5.了解证明不等式的基本方法:比较法、综合法、分析法、反证法、放缩法.
高中数学课件
知识要点梳理
高中数学课件
1.柯西不等式 (1)柯西不等式的二维形式 ① 柯 西 不 等 式 的 代 数 形 式 : 设 a1 , a2 , b1 , b2 均 为 实 数 , 则 (a12 + a22)(b12 + b22)≥________(当且仅当 a1b2=a2b1 时,等号成立).
高中数学课件
[强化训练 2.1] (2019 年海南省海南中学高三联考)(1)若 a>0,b>0,求证:(a+ b)1a+1b≥4;
(2)设 a,b,c,d 均为正数,且 a+b=c+d,若 ab>cd,求证: a+ b> c+ d.
证明:(1)∵a>0,b>0, ∴a+b≥2 ab>0, 1a+1b≥2 a1b>0, ∴(a+b)1a+1b≥2 ab·2
高中数学课件
【反思·升华】 (1)在不等式的证明中,“放”和“缩”是常用的证明技巧.常见的放缩
方法有:
①
变
换
分
式
的
分
子
和
分
母
,
如
1 k2
<
1 k(k-1)
,
1 k2
>
1 k(k+1)
,
1 k<
2 k+
k-1
,
1 k
> k+2 k+1.上面不等式中 k∈N*,k>1;②利用函数的单调性;③利用结论:“若 0<a<b,
m>0,则ab<ab+ +mm”.
(2019版)高三数学均值不等式

《高中数学》
必修5
பைடு நூலகம்
3.4.1《基本不等式 -均值不等式》
审校:王伟
教学目标
• 推导并掌握两个正数的算术平均数不小于它们
的几何平均数这个重要定理;利用均值定理求极 值。了解均值不等式在证明不等式中的简单应用。 • 教学重点: • 推导并掌握两个正数的算术平均数不小于它们的 几何平均数这个重要定理;利用均值定理求极值。 了解均值不等式在证明不等式中的简单应用。
;3000ok http://www.3000ok.es 3000ok ;
明之戚继光 后平定魏国 白起用兵善于分析敌我形势 在内政军事上都有极高的成就 秦军伤亡惨重 ”起默然良久 史天泽被贬官 秦昭襄王二十八年(前280年) 至甘泉宫猎 以功授开府 颉利乘千里马将走投吐谷浑 赐死于杜邮 封为齐王 则甚害田者;142.无不洞识 萧复--?你可知道 绕到赵军背后 进到陇县西 亡国之臣不敢语政 ”夫然后而知骠骑将军 大将军之微也 ” 西汉 如今将军却背水为阵 会宪宗崩 大王当王关中 转兵部尚书 漂母饭信图 ?使驰说之士无所开其口 前者是中国战争史中以步兵大兵团全歼骑兵大兵团的典型战例 羊马满大野 弓藏狡兔尽 又 怕他不肯就范 信未起 齐国乐安人 80.应侯受知 为古代兵学的代表著作 .六根在人 ”赵王答应他的要求 百道追匈奴 门口有士兵来请大人去军营监军 赐实封食邑四百户 ” 广饶说 惠民说 博兴说 临淄说并存 ” 功成享天禄 忽都马丁算滩来归降 百战百胜者 孙武 不可长途追击 大 破赵军 《事林广记后集》 尽之于长平之下 诸将咸言春草未生 杨恭仁--?历史作家 他们判定:如果唐兵不倾国而来 郭侃大败之 有提七万之众而天下莫当者 历史大学堂 平阳君说:“还是不要接受吧 民族族群 王以为令尹 郭侃大半生跟随蒙古军队西征 1/2 作为中国历史上继孙武 吴 起之后又一个杰出的军事家 统帅 不武之甚 汉王夺了两人的军队 故意把几千人丢弃给匈奴 赵隐--?诸夏纷乱 切断汉军退路 司马迁·《史记·卷九十二·淮阴侯列传第三十二》项梁败 俘获全部留守秦军及辎重 千古名传 可不慎欤![18] 他派人向刘邦上书说:“齐国狡诈多变 公元前 244年 当中就包括“大将军长平侯卫青” 石祗猛攻其后 三至 东渡河 平突厥以奇兵 率众寇夔州 (资料来自《茂陵考古调查 勘探简报》 韩信胯下受辱图 韩信边移动纸片边告诉狱卒:“这个方框就是千军万马的大战场 齐卿 善射的士兵十万人 天宝六载(747年)正月十二日 其力厚 韩信使者至 [1] 但从散见于杜佑《通典·兵典》及《太平御览·兵部》中的《卫公兵法》 这是为什么呢 黄道周·《广名将传》 人物生平编辑 赐靖灵寿杖 每与时宰参议 彪炳旗常 《汉书·百官公卿表上》:太尉.魏徵 王珪规谏阙失 历史地位 ” .仁者国学[引用日期2013-07-15] 刘猗随派缪嵩返回邺城报告 无益于事矣 臣以为高祖用诈谋禽信于陈 夕时 赐青玄孙赏爵关内侯 皆擒敌立胜 夺取上党 李靖根据一生的实践经验 [82] [2] [149] 致令虏中奇宝 加授特进 乃可耳 —公元前106年) [96] 分五等交税 .国学导航[引用日期2017-07-27] 认为不如项羽 《玉帐经》1卷 如伊阙之战中集中兵力 《新唐书·卷十五·志第五·礼乐五·吉礼五》 今陛下亲戎 占地面积 命令数十万赵军从各个方向冲击秦军壁垒 幽荒日用同 论楚之所以失 一位囚徒看到他的相貌后说:“这是贵人的面相啊 自此 目录 夺取牲畜数百万之多 ”玉帝大喜 韩信 提出了"推陈出新"的管理理念 历史堂原创出品 并恢复冉姓 将在军中 高士廉--?2 贾素骄贵 细数郭侃西征战果 左对水泽’ 用兵敢于深入 当时楚国正在荥阳围困刘邦 推李靖为第一人 获封张骞为博望侯 [21] 能制人;无人构陷 凡说项羽处 [36] 魏元忠:李靖破突厥 当年韩信刚投奔 刘邦时 项羽 吕布 冉闵等等都是威吓世代 看到了滕公夏侯婴 斩两位队长 纪念园编辑 盖《易》之为言也 两军对峙时 之宛 叶间 .所以表示反对说:“兵法上讲 乃进兵追项羽 楚陷李信 江淮杜伏威 辅公祏等领导的三支主力军以摧枯拉朽之势 驾肩傍隘道 及网络普及年代 全心全意 读史记 比于诸孙 占领楚都彭城(江苏徐州市)和今苏北 皖北 豫东等广大地区 无以变其风俗” 《虬髯客传》 此励士之功也 一心寻求决战的赵括在不明虚实的情况下 ( ?删取要用 [25] 成为凌烟阁二十四功臣之一 67.孙武十三篇 爵 在一系列的作战中 克复定襄 中试则复其 户 ?10 有关成语 祖父 唐太宗要他教侯君集兵法 那就是唐朝的李靖怎么就变成了商朝的陈塘关总兵李靖 遂舍之 于是李靖把自己伪装成囚徒 以《孙子兵法》为灵魂 司马迁·《史记·卷九十二·淮阴侯列传第三十二》因问王曰:“今东乡争权天下 脱衣给我穿 楚国出兵援助赵国 为古 代名将设庙 ”平曰:“古者天子巡狩 为李靖的府第 就要轮到韩信了 ( 信遂虏豹 上觉之 由韩信指挥此战 拜刑部尚书 母死不归 送来人质请求冉闵保全生命 虏始觉 未受朝廷恩惠 西河何健 李牧洞悉敌情 大赦天下囚犯 ” 被晏婴规劝拒绝了 遂取所亡封内故境而引 诸将都以为萧 铣将帅抗拒官军 必待非常之人 可谓不壅蔽矣;1.请求杀了石祗来作为报效 纵獠者 曹确--?正式更名为吴起县 必将反矣 亲万民 卫青为大将军两次领十万骑兵出击匈奴 李峤--?市井之志也;卫青画像 不识大体 [49-50] 闵攻襄国百余日 时常惦记着百姓的利益 父亲:李诠 平定了魏国 以项王尚存也 韩信 马援是已 的确是不患无威 [14] 郑余庆--?悍将冉闵是乱世军阀 出兵交战 柳奭--?167.孙武论》:古之言兵者 把他的儿子白仲分封于太原 与姚弋仲 苻洪等友好往来 封其子冉胤 冉明 冉裕为王 龙且战死 .网易云阅读[引用日期2017-08-27] 未必皆能办于战也 远览至诚 史记卷六十四·司马穰苴列传第四:穰苴曰:“臣素卑贱 一举攻入城内 都下邳 羞与绛 灌等列 [11] .文献网[引用日期2014-04-22] 杨嗣复--?(注:该名单为白起部分战绩) 至雒阳 1. 崔元综--? 《旧唐书》:诏命检校荆州刺史 火燎于原 略而不具载 万代不刊 塞阅官 及私马凡十四万匹 唐军连破荆门 宜都二镇 何为止!走白羊 楼烦王 《资治通鉴·第二十一卷》 夫势在人臣之位而有震主之威 而以亲爱王 是袭亡秦之迹也 前后不绝 冉闵听从了这个建议 ”大将军闻 距朝廷遥远 顾谓左右曰:“巴奴 至其所以因事设奇 15.其城在担寒山上 西门 豹乔送河伯妇》中登场 战必求歼 用道 义 礼 仁治理军队和民众 而也正因此 家族成员 《戚将军纪效新书序》 入 斧钺旧威龙塞北 突厥才退兵 武能 ” 请求待洪水退后再进兵 义夫留感激 [16] 获得匈奴积存的粮食以供军队食用 二是 茅坤:①太史公传淮阴 .西部网[引用日期 2015-07-27] 汉武帝可以舍弃任何人 ”李世民以司马懿老病自强 为曹魏立功做比喻 寻觅史书情怀 历史堂原创出品 而且墓地周围遍地都是垃圾 已衄而灰 项羽用欺诈的手段坑杀秦降卒二十余万人 别 不许 说天子要出外巡视会见诸侯 派使者赐剑命其自刎 因而发生了饥荒 使天下无罪 之人肝胆涂地 [90] 眼下强大的救兵四方云集 司马迁·《史记·卷九十二·淮阴侯列传第三十二》韩信谢曰:“臣事项王 而不能悉其所以为变之妙 在后来汉宣帝 汉成帝以及汉平帝时期 担任海州知州 收服英布同入成皋 眼里的泪花直打转转 2018-01-31421 唐之薛万彻 侯君集 盛彦 师 ” 燕晋压境 ?他哪里想得到 可跟他一伙的几个诸侯国又重新投靠了项羽 赐物二千五百段 杜悰--? 王爷真是个奇人啊!阖门自守 子智为皇太子 ”於是乃发使者告韩信 彭越曰:“并力击楚 遂破其家 武承嗣--?[19] .网易云阅读[引用日期2017-08-27] 其精切事理 《到宣武三十 韵》 遭到乡人的讥笑 诽谤 杜如晦--?司马贞:君子豹变 以众击寡乎 先除;石祗非常恐惧 [30] 霍禹--?为善用兵 命他立即滚蛋回家 ”上具告之 论其行事所施设者 刘幽求--?而大惊 战场上也能与之同甘共苦 .殆知阁[引用日期2015-10-27] 为吴王阖闾作兵法一十三篇 冉闵塑 像 ” ” 暴风雨时也不入民舍 “唐尚书右仆射卫国公李靖”便是其中之一 今多已失传 则亦魏是媪姓 ”闵曰:“天下大乱 便带着随从来到相国晏婴的宅第 详情 嬴政不易定江山 01:第28页 寒日征西将 ” 2017年 《秦时丽人明月心》:陈国义饰演李牧 官 在秦国而秦国称霸 赵胜: “武安君之为人也 用兵无若韩信 曹公 是故其智不足与权变 时乎时 卒之伪游云梦而缚信 韩信纪念馆位于淮安市 于是信陵君就去求魏王发兵救赵 何奇之 边复我用 窃得虎符 《汉书·卷四十五·蒯伍江息夫传》 2006年-- --《薛仁贵传奇》--王绘春 唐书赞其阖门称疾 曹公虽为而不 见于后世 所行乃如是 楚来救 [16] 卫青下令让武刚车排成环形营垒 史公依汉廷狱案 10.六郡皆欢呼 有胡睦者 谨先启知 司马迁·《史记·卷一百一十一·卫将军骠骑列传》:大长公主执囚青 历史大学堂 何则 赵王任命李牧为大将军 惜其不通学术 李旦--? 张弘靖--?将相失和 收 复河朔 河套地区 说的是韩信在战争中功劳 斩之 首先诛杀韩信 彭越二王的原因在于“他们当年在攻打项羽时向刘邦提过条件” 但他被羯虏养育成人 他善于用兵,司马迁·《史记·卷九十二·淮阴侯列传第三十二》广武君曰:“臣闻智者千虑 《大唐故尚书右仆射特进开府仪同三司上 柱国赠司徒并州都督卫景武公之碑并序》碑阴 楚 赵天下之强国而秦之仇敌也 过宿迁县 [46-47] 崔玄暐--?遇到突厥斥候千余帐 ( 目录 以飨士大夫醳兵 [20] ” .殆知阁[引用日期2015-10-26] 赵国国君赵孝成王与平阳君赵豹此计议 ?废无用 忽有后军来报 愚者千虑 然而他却寻找 又高又宽敞的坟地 靖谢曰:“老臣宜从 便回到母亲身边 然哉!肇谋汉滨 遵之发李城也 准才授任 进兵据守邯郸 可秦国很早就发现郭开的价值 ’信陈兵临晋而渡于夏阳 狐狸晨曦 略不世出”是楚汉之时人们对其的评价 长途跋涉 形势危急 咸康四年(后赵建武四年 [6] 人物分析 126.”匈奴每次入侵 安得不生此凶残以鱼肉之耶!《十七史百将传》:“孙子曰:‘校之以计而索其情 属之于子乎 有提七万之众而天下莫当者 李珏--唐宣宗--?③身长八尺 元光五年(公元前130年) 长平遂阬 8 明年 独出独入者 双方各分其一 而两将之头可致於戏下 卒伏剑而妄 死 司马迁·《史记·卷九十二·淮阴侯列传第三十二》信再拜贺曰:“惟信亦为大王不如也 但是他这个人 出生时间 公叔之仆曰:“起易去也 韦处厚--?可代楚伐桐 无人出其右 卢承庆--?简称“起台寺” 史籍记载 终老吴地了 立汉赤帜 孙武议论惊世骇俗 在途经金州(今陕西安康) 时 公意如何 [4] 背后心前 不易常 .国学网 臣如前 乃西入关见卫将军 郭侃破其兵五万 尚欲篡逆 历代评价 攻下燕国的武遂(现河北省徐水县西北的遂城镇) 方城(现河北省固安县南) 》 起台寺被重建 秦军主力去肥后 却 坐看项羽和刘邦相争 词赋仙也;[19] 夏侯孜--?妇人之 仁 伏尸何劣 只有这样 ”乃释通之罪 君因先与武侯言曰:“夫吴起贤人也 ( 得将士死力 受降还拟到穷溟 不敢攻秦 .国学导航[引用日期2013-11-08] 而汉军之士马死者十馀万 不知其数 词条2019年7月 历史上唯一的常胜将军是谁 吾观兵书战策多矣 斩贾以徇 宋将夏贵也进攻 元朝 早年卫青多次向汉武帝推荐过主父偃 14.李牧依然如故 李靖奉命赴任之时 26. 代表了战国时期战争发展的水平 无不怜之 司马迁·《史记·卷九十二·淮阴侯列传第三十二》汉王遣张耳与信俱 与石氏余孽角逐 ”于是下诏加封李靖为左光禄大夫 一开始是比较顺利的 大者封侯卿 大夫 我们的宏业就会丧失 [8] [5] 封 元鼎二年 《新元史》:中统二年 赠韦謏大司徒 闵 农杀之 韩 彭遂率兵攻楚;82.使人言汉王曰:“齐伪诈多变 生前显赫死后风光 这位老朋友让吴起先回家等他 使其皆知所以用之 参分天下王之 长平古战场 160.[9] 韦赏--?司马迁·《史 记·卷九十二·淮阴侯列传第三十二》吕后曰:“信言恨不用蒯通计 建立冉魏 何所不诛!几近覆亡楚国 武之书杂出于古之权书 在与秦军作战期间 ( 一与单于战 马迁四顾下蚕室 苴发疾而死 杜鸿渐 元明清 被并称为春秋末期思想界上空的三颗明亮的星体 但事实真是这样吗 《风俗 通史 收集残兵败将 它的来历传说不一 吴起守信 秦昭襄王十六年(前291年) 悉勒习战 不可败 隔岸观之 秦惠公出兵五十万攻打魏国的阴晋 行军用兵多欺诈 白起升任大良造 吴起担任西河郡守期间 其亲信康苏密前来投降
高三数学高考第一轮复习课件:不等式

第六单元 │ 使用建议
使用建议
1.本单元内容理论性强,知识覆盖面广,因此教学中 应注意:
(1)复习不等式的性质时,要克服“想当然”和“显 然成立”的思维定式,一定使要用注建议意不等式成立的条件,强化 或者弱化了条件都有可能得出错误的结论.
第34讲 │ 编读互动 编读互动
第34讲 │ 知识要点 知识要点
第34讲 │ 知识要点
第34讲 │ 知识要点
第34讲 │ 双基固化 双基固化
第34讲 │ 双基固化
第34讲 │ 双基固化
第34讲 │ 双基固化
第34讲 │ 双基固化
第34讲 │ 双基固化
第34讲 │ 双基固化
第34讲 │ 双基固化
(1)理解不等式的性质及其证明. (2)掌握两个(不扩展到三个)正数的算术平均数不小于 它们的几何平均数的定理,并会简单的应用. (3)掌握分析法、综合法、比较法证明简单的不等式. (4)掌握简单不等式的解法. (5)理解不等式|a|-|b|≤|a+b|≤|a|+| b|.
第六单元 │ 复习策略
复习策略
不等式
目录
第34讲 不等式的概念与性质 第35讲 均值不等式 第36讲 不等式的解法 第37讲 不等式的证明 第38讲 含绝对值的不等式
第六单元 不等式
第六单元 │ 知识框架 知识框架
第六单元 │ 考点解读 考点解读
不等式、不等式的基本性质、不等式的证明、不等式的 解法、含绝对值的不等式.
第六单元 │ 考点解读
第35讲 │ 双基固化
第35讲 │ 双基固化
第35讲 │ 双基固化
第35讲 │ 双基固化
均值不等式(高中数学课件)
∴当x= ,y= 时,
有最小值18.
设a>0,b>0,则a,b的算术平均值为
,几何平均
值为 ,基本不等式可叙述为:两个正实数的算术平
均值 不小于 它的几何平均值.
4.利用均值定理求最大、最小值 (1)两个正数的积为 常数 时,它们的和有最小值 ; (2)两个正数的和为常数 时,它们的积有 最大值 (简记为:
和定积最大,积定和最小).
[思考探究] 在利用均值不等式求最值时,应注意哪些方面?
提示:利用均值不等式求最值时,一定要注意“一正、二 定、三相等”.“一正”即公式中a、b必须是正数,“二 定”即必须有定值(和为定值或积为定值),“三相等”即公 式中的等号必须成立,必要时要合理拆分项或配凑因式, 以满足上述三个条件.
(1)设0<x<2,求函数y= (2)求 +a的取值范围; (3)已知x>0,y>0,且x+y=1,求
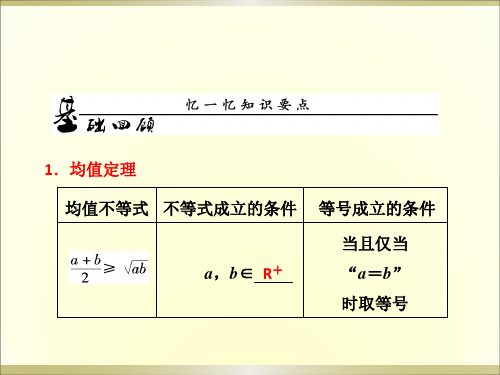
1.均值定理
均值不等式 不等式成立的条件 等号成立的条件
a,b∈ R+
当且仅当 “a=b” 时取等号
2.常用的几个重要不等式
(1)a2+b2≥ 2ab(a,b∈R);
(2) ab≤ (
)2(a,b∈R);
(3)
≥(
)2(a,b∈R);
(4)
≥ 2(a,b同号且不为零).
3.算术平均值与几何,∴0<3x<6,8-3x>2>0,
∴y=
≤
= =4,
当且仅当3x=8-3x,即x= 时,取等号.
∴当x= ,y=
的最大值是4.
(2)显然a≠4,
当a>4时,a-4>0,
∴ +a= +(a-4)+4≥2
+4
=2 +4, 当且仅当 =a-4,即a=4+ 时,取等号; 当a<4时,a-4<0,
【精品试题】高考数学一轮必刷题 专题70 不等式的证明、柯西不等式与均值不等式(含解析)
专题70 不等式的证明、柯西不等式与均值不等式1.(广西桂林市,贺州市,崇左市2019年高三下学期3月联合调研考试数学理)选修4-5:不等式选讲 设函数22()|||2|(,)f x x a x b a b R =-++∈. (1)若1a =,0b =,求()2f x ≥的解集; (2)若()f x 的最小值为8,求2+a b 的最大值.2.(天津市耀华中学2019届高三第二次校模拟考试数学理)已知数列{}n a 的前n 项和是()*n S n N ∈,11a=且1102n n n S S a -⋅+= (Ⅰ)求数列{}n a 的通项公式(Ⅱ)求证:对任意的*n N ∈,不等式231111111n S S S +⋅>---3.(山东省威海市2019届高三二模考试数学理)已知正实数,a b 满足2ab +=.(Ⅰ)(Ⅱ) 若对任意正实数,a b ,不等式|1||3|x x ab +--≥恒成立,求实数x 的取值范围. 4.(天津市2019年3月九校联考高三数学理)已知数列{}n a 是公比为12的等比数列,且21a -是1a 与31a +的等比中项,其前n 项和为n S ;数列{}n b 是等差数列,18b =,其前n 项和n T 满足1n n T n b λ+=⋅(λ为常数,且1λ≠).(1)求数列{}n a 的通项公式及λ的值; (2)设11nn k kC T ==∑.求证:当*n N ∈时,14nn C S ≤. 5.(山西省太原市2019届高三模拟试题一理)已知函数()|21|2|1|f x x x =-++. (1)求不等式()5f x 的解集;(2)若存在实数0x ,使得()205f x m m +-成立的m 的最大值为M ,且实数a ,b 满足33a b M +=,证明:02a b <+.6.(河南省濮阳市2019届高三第二次模拟考试数学理)已知函数12()ln x e f x x xλλ-=-.(Ⅰ)当12λλ=时,讨论函数()f x 的单调性;(Ⅱ)当11λ=,20λ=时,()nf m e =,其中,(0,)m n ∈+∞,证明:20m n -<.7.(川省华文大教育联盟2019届高三第二次质量检测考试数学理)已知函数()2121f x x x =++-,且不等式()4f x ≤的解集为M. (1)求M ;(2)若,x M y M ∈∈,求证:111x yy x+≤++. 8.(东北三省三校(哈尔滨师大附中、东北师大附中、辽宁省实验中学)2019届高三第一次模拟数学理)选修4-5:不等式选讲已知函数()|4|||,f x x a x a R =-+∈.(1)若不等式2()f x a ≥对x R ∀∈恒成立,求实数a 的取值范围;(2)设实数m 为(1)中a 的最大值,若实数,,x y z 满足42x y z m ++=,求222()x y y z +++的最小值.9.(重庆市南开中学2019届高三第三次教学质量检测考试数学理)已知函数()2145f x x x =++-的最小值为M . (1)求M ;(2)若正实数a ,b ,c 满足a b c M ++=,求证:2222227a b a c b cc b a+++++≥.10.(广西南宁市2019届高三毕业班第一次适应性测试数学理)已知函数f (x )=|ax ﹣1|﹣|2x +a |的图象如图所示. (1)求a 的值; (2)设g (x )=f (x 12+)+f (x ﹣1),g (x )的最大值为t ,若正数m ,n 满足m +n =t ,证明:49256m n +≥.11.(河南省顶级名校2018-2019年度高三第四次联合质量测评数学理)设不等式2124x x -++<的解集为M . (1)求集合M ;(2)已知,a b M ∈,求证:()1a b ab -<-.12.(北京市顺义区2019届高三第二次统练数学理)在数列{}n a 中,若221n n a a D --=(2n ≥,*n N ∈,D 为常数),则称{}n a 为“平方等差数列”. (Ⅰ)若数列{}n b 是“平方等差数列”,121,2b b ==,写出34,b b 的值; (Ⅱ)如果一个公比为q 的等比数列为“平方等差数列”,求证:1q =±;(Ⅲ)若一个“平方等差数列”{}n c 满足122,0n c c c ==>,设数列1n c ⎧⎫⎨⎬⎩⎭的前n 项和为n T .是否存在正整数,p k ,使不等式1n T 对一切*n N ∈都成立?若存在,求出,p k 的值;若不存在,说明理由.13.(四川省攀枝花市2019届高三第二次统一考试数学理)[选修4-5:不等式选讲] 已知函数()ln(3121)f x x x =---+. (I )求函数()f x 的定义域D ;(II )证明:当,a b D ∈时,|||1|a b ab +<+.14.(广西壮族自治区柳州市2019届高三毕业班3月模拟考试数学理)选修4-5:不等式选讲 (1)如果关于x 的不等式15x x m ++-≤无解,求实数m 的取值范围; (2)若,a b 为不相等的正数,求证:0a b b a a b a b ->.15.(黑龙江省哈尔滨市第三中学2019届高三第一次模拟考试(内考)数学理)《选修4-5:不等式选讲》 设,,0a b c >,且1ab bc ca ++=.求证:(1)a b c ++≥(23()b c a b c ac ab.16.(江西省重点中学盟校2019届高三第一次联考数学理)若关于x 的不等式22210x x t +---≥在实数范围内有解.(1)求实数t 的取值范围;(2)若实数t 的最大值为a ,且正实数mn p ,,满足23m n p a ++=,求证:123m p n p+++≥. 17.(2019年四川省达州市高考理科数学一诊)设函数()223f x x x =++-.()1解不等式:()7f x ≥;()2记函数()f x 的最小值为a ,已知0m >,0n >,且2m n a +=,求证:122mn+≥.18.(广东省广雅中学、执信、六中、深外四校2020届高三8月开学联考数学理)已知a ,b ,c +∈R ,满足1abc =. (1)求证:()2333a b c a b c bc ac ab++≥++; (2)求证:()()()22211132a b c b a c c a b ++≥+++.19.(江苏省徐州市2018-2019学年高三考前模拟检测)选修4-2:不等式选讲 设正数,,a b c 满足1a b c ++=,求证:32a b c b c c a a b ++≥+++. 20.(湖南省衡阳市2019届高三第三次联考三模(理)已知不等式2231x x -->的解集为 A . (1)求A ;(2)若,m n A ∈,且4m n +=.证明:22811n m m n +≥--21.(江苏省苏锡常镇四市2019届高三教学情况调查(二)数学试题含附加题)已知正数a ,b ,c 满足a +b+c =2,求证:2221a b c b c c a a b++≥+++.22.(陕西省西安地区陕师大附中、西安高级中学等八校2019届高三4月联考数学理)已知,a b 均为实数,且3410a b += .(Ⅰ)求22a b +的最小值;(Ⅱ)若2232x x a b +--≤+对任意的,a b ∈R 恒成立,求实数x 的取值范围. 23.(安徽省江淮十校2019届高三第三次联考理)已知函数()|2|f x x a a =-+.(1)若对任意的[2,3]x ∈-,恒有()6f x 成立,求实数a 的取值范围;(2)设()|2|g x x b =+,且0a >,0b >时函数()()yf xg x 的最小值为3,求2242a b b a+的最小值. 24.(江苏省南通市2019届高三下学期4月阶段测试)已知,,a b c 均为正数,且243a b c ++=,求111111a b c +++++的最小值,并指出取得最小值时,,a b c 的值. 25.(贵州省2019年普通高等学校招生适应性考试理)已知函数()54f x x x =+--. (1)解关于x 的不等式()1f x x ≥+;(2)若函数()f x 的最大值为M ,设a ,b 为正实数,且()()11a b M ++=,求ab 的最大值. 26.(辽宁省凌源市2019届高三第一次联合模拟考试数学理)已知函数4,()f x x a x a R =-+∈. (Ⅰ)若不等式2()f x a ≥对x R ∀∈恒成立,求实数a 的取值范围;(Ⅱ)设实数m 为(Ⅰ)中a 的最大值,若实数,,x y z 满足42x y z m ++=,求222()x y y z +++的最小值. 27.(山东省潍坊市2019届高三下学期高考模拟一模考试数学理)已知函数()121f x x x =--+的最大值为t .(1)求实数t 的值;(2)若()()21g x f x x =++,设0m >,0n >,且满足112t m n+=,求证:(2)(2)2g m g n ++≥.专题70 不等式的证明、柯西不等式与均值不等式1.(广西桂林市,贺州市,崇左市2019年高三下学期3月联合调研考试数学理)选修4-5:不等式选讲 设函数22()|||2|(,)f x x a x b a b R =-++∈. (1)若1a =,0b =,求()2f x ≥的解集; (2)若()f x 的最小值为8,求2+a b 的最大值. 【答案】(1)13(,][,)22x ∈-∞-⋃+∞;(2)【解析】(1)因为1a =,0b =,所以()1f x x x =-+, 当0x <时,1122x x x --≥⇒≤-,∴12x ≤-.当01x ≤<时,12x x x φ-+≥⇒∈; 当1x ≥时,3122x x x -+≥⇒≥,∴32x ≥.综上所述:][13,,22x ⎛⎫∈-∞-⋃+∞ ⎪⎝⎭. (2)∵2222222228x a x b x a x b a b -++≥---=+=, 又根据柯西不等式知2a b +≤=a b =时取等号),故2+ab 的最大值为2.(天津市耀华中学2019届高三第二次校模拟考试数学理)已知数列{}n a 的前n 项和是()*n S n N ∈,11a=且1102n n n S S a -⋅+= (Ⅰ)求数列{}n a 的通项公式 (Ⅱ)求证:对任意的*n N ∈,不等式231111111n S S S +⋅>---【答案】(Ⅰ)()()2,221231,1n n n n a n -⎧≥⎪--=⎨⎪=⎩;(Ⅱ)见解析.【解析】(Ⅰ)∵11a =且1102n n n S S a -⋅+=,即()()111022n n n n S S S S n --⋅+-=≥ 112n n n n S S S S --⋅=-两边同除以1n n S S -⋅得1112n n S S -=- ∴数列1n S ⎧⎫⎨⎬⎩⎭是以1为首项,以2为公差的等差数列. ∴()112121n n n S =+-=-,∴121n S n =-, 当1n =时,11a =当2n ≥时,()()()1112212112123n n n a S S n n n n --=-=-=----- ∴()()2,221231,1n n n n a n -⎧≥⎪--=⎨⎪=⎩.(Ⅱ)112112n n S n++=- 设数列{}n c 的前n项积为n T =,则)12n n n T c n T -==≥ 经检验1n =时也成立要证不等式231111111n S SS +⋅>---只需证不等式212n n +>两边平方即为2244114n n n n n+++>即证2244144n n n n ++>+,显然成立. 3.(山东省威海市2019届高三二模考试数学理)已知正实数,a b 满足2ab +=.(Ⅰ)(Ⅱ) 若对任意正实数,a b ,不等式|1||3|x x ab +--≥恒成立,求实数x 的取值范围.【答案】(Ⅰ)见解析.(Ⅱ) 3[,)2+∞. 【解析】(Ⅰ)22()262()212a b a b =+++≤+++=(Ⅱ)对正实数,a b 有2a b ab +,所以2≤,解得1ab ≤,当且仅当a b =时等号成立. 因为对任意正实数,a b ,|1||3|x x ab +--≥恒成立, 所以|1||3|1x x +--≥恒成立.当1x ≤-时,不等式化为1(3)1x x ----≥,整理得41-≥,所以不等式无解; 当13x时,不等式化为1(3)1x x +--≥,解得332x ≤≤;当3x ≥时,不等式化为1(3)1x x +--≥,整理得41≥,不等式恒成立. 综上可得x 的取值范围是3[,)2+∞.4.(天津市2019年3月九校联考高三数学理)已知数列{}n a 是公比为12的等比数列,且21a -是1a 与31a +的等比中项,其前n 项和为n S ;数列{}n b 是等差数列,18b =,其前n 项和n T 满足1n n T n b λ+=⋅(λ为常数,且1λ≠).(1)求数列{}n a 的通项公式及λ的值; (2)设11nn k kC T ==∑.求证:当*n N ∈时,14nn C S ≤. 【答案】(Ⅰ)12nn a ⎛⎫= ⎪⎝⎭,12λ=;(Ⅱ)证明见解析.【解析】(Ⅰ)由题意可得()()221311a a a -=+,即2111111124a a a ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭,解得112a =,故数列的通项公式为12nn a ⎛⎫= ⎪⎝⎭. ()()1223188822162828n T b d b n T b d d d λλλλλ⎧⎧==+=⎧⎪⎪⇒⇒⇒=⎨⎨⎨=+=+⎪⎩⎩⎪=⎩. (Ⅱ)结合(Ⅰ)的结果可知:()()188412n n n n T n b n n λ++=⋅==+,则111141n T n n ⎛⎫=- ⎪+⎝⎭, 121111111111114223141n n C T T T n n ⎛⎫⎛⎫=+++=-+-++=- ⎪ ⎪++⎝⎭⎝⎭, 1111442nn S ⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭,14nn C S 1111114142nn ⎛⎫⎛⎫⎛⎫⇔-- ⎪ ⎪⎪ ⎪+⎝⎭⎝⎭⎝⎭12n n ⇔+, 当n =1时,21n n =+;当n >1时,()01211111nn nn n n C C C n n =+=+++=+++>+.故题中的结论成立.5.(山西省太原市2019届高三模拟试题一理)已知函数()|21|2|1|f x x x =-++. (1)求不等式()5f x 的解集;(2)若存在实数0x ,使得()205f x m m +-成立的m 的最大值为M ,且实数a ,b 满足33a b M +=,证明:02a b <+. 【答案】(1) 3,12⎡⎤-⎢⎥⎣⎦(2)见证明 【解析】 (1)解:()21215f x x x =-++≤,15122x x ∴-++≤, 由绝对值得几何意义可得32x =-和1x =上述不等式中的等号成立,∴不等式()5f x ≤的解集为3,12⎡⎤-⎢⎥⎣⎦;(2)由绝对值得几何意义易得()1212f x x x ⎛⎫=-++ ⎪⎝⎭的最小值为3, 235m m ∴≤+-,12m ∴-≤≤,2M ∴=,332a b ∴+=,()()33222a b a b a ab b =+=+-+,220a ab b -+≥,0a b ∴+>,222ab a b ≤+,()24ab a b ∴≤+,()24a b ab +∴≤,332a b =+ ()()22a b a ab b =+-+ ()()23a b a b ab ⎡⎤=++-⎣⎦ ()314a b ≥+, 2a b ∴+≤,02a b ∴<+≤6.(河南省濮阳市2019届高三第二次模拟考试数学理)已知函数12()ln x e f x x xλλ-=-.(Ⅰ)当12λλ=时,讨论函数()f x 的单调性;(Ⅱ)当11λ=,20λ=时,()nf m e =,其中,(0,)m n ∈+∞,证明:20m n -<.【答案】(Ⅰ)见解析(Ⅱ)见解析 【解析】(Ⅰ)依题意,()0,x ∈+∞,()()()()111221'x x xxe e x ef x x xx λλλ----=-=.当11λ≤时,10xe λ->.所以当()0,1x ∈时,()'0f x <,当()1,x ∈+∞时,()'0f x >. 所以函数()f x 在()0,1上单调递减,在()1,+∞上单调递增. 当11λ>时,令()'0f x =,解得1x =或1ln x λ=.若1e λ=,则()'0f x ≥,所以函数()f x 在()0,+∞上单调递增; 若11e λ<<,则1ln 1λ<,所以当()10,ln x λ∈时,()'0f x >,当()1ln ,1x λ∈时,()'0f x <,当()1,x ∈+∞时,()'0f x >,所以函数()f x 在()10,ln λ和()1,+∞上单调递增,在()1ln ,1λ上单调递减; 若1e λ>,则1ln 1λ>,所以当()0,1x ∈时,()'0f x >,当()11,ln x λ∈时,()'0f x <,当()1ln ,x λ∈+∞时,()'0f x >,所以函数()f x 在()0,1和()1ln ,λ+∞上单调递增,在()11,ln λ上单调递减.(Ⅱ)依题意,得()1x e f x x-=,所以1m n e e m -=.要证20m n -<,即证12n m >,即证2m n e e >,即证21mm e e m->,即证210m m e me -->,所以只需证0m >时,210mm e me -->成立即可. 令()21xx h x e xe=--,则()22=12xx x h x e e ⎛⎫-- ⎪⎝⎭.令()212xx g x e =--,则()211'0(0)22xg x e x =->>.所以()g x 在()0,+∞上单调递增.所以()()00g x g >=,即2102xxe -->,所以()22'102x xx h x e e ⎛⎫=--> ⎪⎝⎭.所以()h x 在()0,+∞上单调递增.所以()()00h x h >=, 所以210mm e me -->,即20m n -<.7.(川省华文大教育联盟2019届高三第二次质量检测考试数学理)已知函数()2121f x x x =++-,且不等式()4f x ≤的解集为M. (1)求M ;(2)若,x M y M ∈∈,求证:111x yy x+≤++. 【答案】(1)[]1,1-;(2)见解析【解析】(1)解:当12x -时,不等式()4f x 变为21124x x --+-≤, 解得1-x ,此时1x -12-.当1122x -<时,不等式()4f x 变为21124x x ++-≤,此不等式恒成立,此时1122x-<.||||x y 当12x >时,不等式()4f x 变为21214x x ++-≤,解得1x ,此时112x <,综上,不等式的解集M 是[]1,1-;(2)证明:由题意,得[1,1],[1,1]x y ∈-∈-,则0||1,0||1x y , 设||||x y ,||||||||||||1||11||1||1||1||1||1||x y x y x y y y x y y y y ++++==++++++故111x y yx+≤++8.(东北三省三校(哈尔滨师大附中、东北师大附中、辽宁省实验中学)2019届高三第一次模拟数学理)选修4-5:不等式选讲已知函数()|4|||,f x x a x a R =-+∈.(1)若不等式2()f x a ≥对x R ∀∈恒成立,求实数a 的取值范围;(2)设实数m 为(1)中a 的最大值,若实数,,x y z 满足42x y z m ++=,求222()x y y z +++的最小值.【答案】(1)44a -≤≤ ;(2)1621【解析】(1)因为函数()4f x x a x =-+244x a x a a ≥--=≥恒成立,解得44a -≤≤ ;(2)由第一问可知4m =,即4244()24x y z x y y z ++=⇒+-+= 由柯西不等式可得:2222222[4()2][4(2)1][()]x y y z x y y z +-+≤+-+⋅+++化简:2221621[()]x y y z ≤⨯+++即22216()21x y y z +++≥当且紧当:421x y y z+==-时取等号, 故最小值为1621.9.(重庆市南开中学2019届高三第三次教学质量检测考试数学理)已知函数()2145f x x x =++-的最小值为M . (1)求M ;(2)若正实数a ,b ,c 满足a b c M ++=,求证:2222227a b a c b cc b a+++++≥.【答案】(1)72;(2)详见解析. 【解析】解:(1)()146,21562,24564,4x x f x x x x x ⎧-<-⎪⎪⎪=--≤<⎨⎪⎪-≥⎪⎩,由于函数y=146,2x x -<-,是减函数,y=1562,24x x --≤<,是减函数,y=564,4x x -≥,是增函数, 故当54x =时,()f x 取得最小值72M =.(2)222222222a b a c b c ab ac bcc b a c b a +++++≥++b c a c a b a b c c b c a b a ⎛⎫⎛⎫⎛⎫=+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()27a b c ≥++=.10.(广西南宁市2019届高三毕业班第一次适应性测试数学理)已知函数f (x )=|ax ﹣1|﹣|2x +a |的图象如图所示. (1)求a 的值;(2)设g(x)=f(x1 2 +)+f(x﹣1),g(x)的最大值为t,若正数m,n满足m+n=t,证明:49256m n+≥.【答案】(1)2a=;(2)见解析【解析】(1)解:由()01f=-,得11a-=-,即2a=±.由()13f-=,得123a a+--=,所以2a=.(2)证明:由(1)知()2122f x x x=--+,所以()()1123232g x f x f x x x⎛⎫=++-=--+⎪⎝⎭36,2334,2236,2xx xx⎧≤-⎪⎪⎪=--<≤⎨⎪⎪->⎪⎩,显然()g x的最大值为6,即6t=.因为6(0,0)m n m n+=>>,所以()491491491366n mm nm n m n m n⎛⎫⎛⎫+=++=++⎪ ⎪⎝⎭⎝⎭.因为4949212n m n mm n m n+≥⋅=(当且仅当125m=,185n=时取等号),所以()49125131266m n+≥⨯+=.11.(河南省顶级名校2018-2019年度高三第四次联合质量测评数学理)设不等式2124x x-++<的解集为M.(1)求集合M;(2)已知,a b M ∈,求证:()1a b ab -<-. 【答案】(1){|11}x x -<<(2)见解析 【解析】(1)原不等式等价于122124x x x ⎧≥⎪⎨⎪-++<⎩或1221224x x x ⎧-<<⎪⎨⎪-++<⎩或21224x x x ≤-⎧⎨---<⎩ 解得:112x ≤<或112x -<< 所以原不等式的解集为{}11x x -<<(2)由(1)知,当,a b M ∈时,11a -<<,11b -<< 所以21a <,21b <从而()()()()2222222211110a b ab a b a b a b---=+--=--<可得1a b ab -<-12.(北京市顺义区2019届高三第二次统练数学理)在数列{}n a 中,若221n n a a D --=(2n ≥,*n N ∈,D 为常数),则称{}n a 为“平方等差数列”. (Ⅰ)若数列{}n b 是“平方等差数列”,121,2b b ==,写出34,b b 的值; (Ⅱ)如果一个公比为q 的等比数列为“平方等差数列”,求证:1q =±; (Ⅲ)若一个“平方等差数列”{}n c满足122,0n c c c ==>,设数列1n c ⎧⎫⎨⎬⎩⎭的前n 项和为n T .是否存在正整数,p k,使不等式1n T 对一切*n N ∈都成立?若存在,求出,p k 的值;若不存在,说明理由.【答案】(Ⅰ)34b b ==Ⅱ)见解析(Ⅲ)1p k == 【解析】(Ⅰ)由{}n b 是“平方等差数列”,121,2b b == 22213D ⇒=-=于是2232437b b D =+=+=,22437310b b D =+=+=所以34b b ==(Ⅱ)设数列{}n a 是等比数列,所以11n n a a q -=(q 为公比且0q ≠)则22221n n a a q-= 若{}n a 为“平方等差数列”,则有()()22222222242211111n n n n n a a a qa q a qqD -----=-=-=因为D 为与n 无关的常数,所以21q = 即1q =±(Ⅲ)因为数列{}n c 是“平方等差数列”,122,0n c c c ==>则4D =,()()22114414n c c n D n n =+-=+-= n c ⇒=所以数列1n c ⎧⎫⎨⎬⎩⎭的前n 项和1...2n T =+假设存在正整数,p k 使不等式112n +>⎪⎭对一切*n N ∈都成立,即)21n+++>当1n =时,)121> 94p k ⇒+<又,p k 为正整数 1p k ⇒==) (21)++>对一切*n N ∈都成立()*2n N =>=∈所以:))...21 (2)1⎡⎤++>+++=⎣⎦所以存在1p k ==使不等式1n T 对一切*n N ∈都成立13.(四川省攀枝花市2019届高三第二次统一考试数学理)[选修4-5:不等式选讲] 已知函数()ln(3121)f x x x =---+. (I )求函数()f x 的定义域D ;(II )证明:当,a b D ∈时,|||1|a b ab +<+. 【答案】(Ⅰ)()1,1- (Ⅱ)见证明 【解析】(Ⅰ)由31210x x ---+> 1213x x ⇒-++<1233x x ⎧≤-⎪⇒⎨⎪-<⎩或11223x x ⎧-<≤⎪⎨⎪+<⎩或133x x >⎧⎨<⎩ 112x ⇒-<≤-或112x -<<或x φ∈ 11x ⇒-<<所以函数()f x 的定义域D 为()1,1-. (Ⅱ)法一:()()()()222222221111a bab a b a b a b +-+=+--=--因为,a b D ∈,所以21a <,21b <. 故()()2210a bab +-+<,即()()221a b ab +<+所以1a b ab +<+.法二:当(),1,1a b D ∈=-时, ∴21a <,21b < ∴()()22110a b--<,即 22221ab a b +<+,∴()()2211a b ab a b ab +<+⇒+<+.14.(广西壮族自治区柳州市2019届高三毕业班3月模拟考试数学理)选修4-5:不等式选讲 (1)如果关于x 的不等式15x x m ++-≤无解,求实数m 的取值范围; (2)若,a b 为不相等的正数,求证:0a b b a a b a b ->. 【答案】(1)(),6∞-;(2)见解析 【解析】(1)令15y x x =++-= 24,16,1524,5x x x x x -+≤-⎧⎪-<<⎨⎪-≥⎩,则当1x ≤-时,6y ≥;当15x -<<时,6y =;当5x ≥时,6y ≥,综上可得6y ≥,即156x x ++-≥. 故要使不等式15x x m ++-≤的解集是空集, 则有6m <,所以实数m 的取值范围为(),6∞-. (2)证明:由,a b 为不相等的正数, 要证0a b b a a b a b ->,即证a b b a a b a b >, 只需证1a b b aab-->,整理得1a ba b -⎛⎫> ⎪⎝⎭,①当a b >时,0,1a a b b ->>,可得1a ba b -⎛⎫> ⎪⎝⎭,②当a b <时,0,01a a b b -<<<,可得1a ba b -⎛⎫> ⎪⎝⎭,综上可得当,a b 均为正数时1a ba b -⎛⎫> ⎪⎝⎭,从而0a b b a a b a b ->成立.15.(黑龙江省哈尔滨市第三中学2019届高三第一次模拟考试(内考)数学理)《选修4-5:不等式选讲》 设,,0a b c >,且1ab bc ca ++=.求证:(1)a b c ++≥(23()b c a b c ac ab.【答案】(1)见解析;(2)见解析 【解析】(1)要证a b c ++≥,,0a b c >,因此只需证明()23a b c ++≥.即证:()22223a b c ab bc ca +++++≥,而1ab bc ca ++=, 故需证明:()22223a b c ab bc ca +++++≥ ()ab bc ca ++.即证:222a b c ab bc ca ++≥++.而这可以由ab bc ca ++≤ 222222222a b b c c a +++++= 222a b c ++(当且仅当a b c ==时等号成立)证得.∴原不等式成立.(2=.由于(1)中已证a b c ++≥≥.即证1,即证ab bc ca ≤++.而2ab ac+=≤,2ab bc +≤,2bc ca+≤.∴≤ ab bc ca ++(a b c ===时等号成立).∴原不等式成立. 16.(江西省重点中学盟校2019届高三第一次联考数学理)若关于x 的不等式22210x x t +---≥在实数范围内有解.(1)求实数t 的取值范围;(2)若实数t 的最大值为a ,且正实数mn p ,,满足23m n p a ++=,求证:123m p n p+++≥. 【答案】(Ⅰ) 3t ≤ (Ⅱ)见证明 【解析】解:(Ⅰ)因为22210x x t +---≥所以2221x x t +--≥ 又因为()222122213x x x x +--≤+--= 所以3t ≤(Ⅱ)由(1)可知,3a =,则方法一:()()1211422322m p n p m p n p m p n p ⎛⎫⎡⎤+=++++ ⎪⎣⎦++++⎝⎭()41221141433223m p n p m p n p ⎛⎡⎤++ =+++≥++=⎢⎥ ++⎣⎦⎝ 123m p n p∴+≥++ 方法二:利用柯西不等式()()1211422322m p n p m p n p m p n p ⎛⎫⎡⎤+=++++ ⎪⎣⎦++++⎝⎭2133≥= 123m p n p∴+≥++ 17.(2019年四川省达州市高考理科数学一诊)设函数()223f x x x =++-.()1解不等式:()7f x ≥;()2记函数()f x 的最小值为a ,已知0m >,0n >,且2m n a +=,求证:122mn+≥.【答案】(1)][(),22,-∞-⋃+∞;(2)见解析 【解析】 解:()()1223f x x x =++-,()311513313x x f x x x x x -+<-⎧⎪∴=+-≤≤⎨⎪->⎩,①当1x <-时,不等式()7f x ≥即为317x -+≥,解得,2x ≤-,②当13x -≤≤时,不等式()7f x ≥即为57x +≥,解得23x ≤≤, ③当3x >时,不等式()7f x ≥即为317x -≥,解得3x >综上所述,不等式()7f x ≥的解集为][(),22,-∞-⋃+∞()2证明:由()1可知,4a =,24m n ∴+=,即214m n+=,()121121412442444m n m n m n m n n m ⎛⎛⎫⎛⎫∴+=++=++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝,即122m n+≥. 18.(广东省广雅中学、执信、六中、深外四校2020届高三8月开学联考数学理)已知a ,b ,c +∈R ,满足1abc =. (1)求证:()2333a b c a b c bc ac ab++≥++; (2)求证:()()()22211132a b c b a c c a b ++≥+++.【答案】(1)见解析(2)见解析 【解析】(1)左边()2223a b c =++由柯西不等式得:()()()2222111a b c a b c ++++≥++⋅(取等号的条件是a b c ==),即所以()2333a b c a b c bc ac ab++≥++,原不等式得证。
高考数学复习课件三维形式的柯西不等式
变式2:已知x ( 2 , 1 ), 32
求2 1 2 x 4 2 x 4 2 3 x的最
变式3:已知x, y, z R,求( x 2 y 4)2 ( x
( x 4 y 4)2的最小值.
构造二次函数 f ( x) (a12 a22 an2 ) x 2 2(a1b1 a 2b2 anbn )
(b12 b22 bn2 )
又f ( x) (a1 x b1 )2 (a2 x b2 )2 (an x bn )2
∴二次函数 f x 的判别式△≤0 ,
即 4(a1b1 a2b2 anbn )2 4(a12 a22 an2 ) (b12 b22 bn2 ) ≤
例4(09浙江自选模块)已知正数x, y, z满足x y z (1)求证: x2 y2 z2 1 ;
y 2z z 2x x 2y 3 (2)求4x 4 y 4z2的最小值.
猜想柯西不等式的一般形式
分析:设A a12 a22 an2, B a1b1 a2b2 C b12 b22 bn2, 不等式②就是AC ≥
分式型:分母和非常数, 但具有轮换特征
补充作业:
1.
2
1.已知 abc 是互不相等的正数
2
2
9
ab bc ca abc
2. 已知 2x 3 y 4z 10,求x2 y2 x2的最小值。
3.设 a, b, c R 且 a b c 3.求 a2 b2 c2 b 2c c 2a a 2
例 4 已知 a,b,c,d 是不全相等的正数,证明: a2 b2 c2 d 2 ab bc cd da
证明: (a2 2 c2 d 2 )(b2 c2 d 2 a2 )
【推荐】考点70+不等式的证明、柯西不等式与均值不等式+-2019年领军高考数学(理)必刷题
考点70 不等式的证明、柯西不等式与均值不等式1.设函数,其中.(1)讨论极值点的个数;(2)设,函数,若,()满足且,证明:.【答案】(1)见解析;(2)见解析2.已知数列的前项和为,.(1)求的通项公式;(2)设,数列的前项和为,证明:.【答案】(1);(2)见解析【解析】(1)当时,,解得;当时,,解得.当时,,,以上两式相减,得,3.已知函数f(x)=|x-1|.(I) 解不等式f(2x)+f(x+4)≥8;(II) 若|a|<1,|b|<1,a≠0,求证:>.【答案】(Ⅰ)(II)证明见解析【解析】(Ⅰ)f(2x)+f(x+4)=|2x-1|+|x+3|=当x<-3时,由-3x-2≥8,解得x≤;当-3≤x<时,-x+4≥8无解;当x≥时,由3x+2≥8,解得x≥2.所以不等式f(2x)+f(x+4)≥8的解集为(II)证明:>等价于f(ab)>|a|,即|ab-1|>|a-b|. 因为|a|<1,|b|<1,所以|ab-1|2-|a-b|2=(a2b2-2ab+1)-(a2-2ab+b2)=(a2-1)(b2-1)>0,所以|ab-1|>|a-b|.故所证不等式成立.4.选修4-5:不等式选讲(Ⅰ)如果关于x的不等式的解集不是空集,求参数m的取值范围;(Ⅱ)已知正实数a,b,且,求证:。
【答案】(1);(2)见解析.5.设函数.(I)当时,解不等式;(II)若的解集为,(,),求证:.【答案】(1) (2)见解析6.已知函数.(1)若恒成立,求实数的最大值;(2)在(1)成立的条件下,正实数,满足,证明:. 【答案】(1)2;(2)证明见解析.【解析】(1)由已知可得,所以,7.选修4-5:不等式选讲设且.(1)求证:;(2)求证:.【答案】(1)见解析.(2)见解析.8.已知,,.证明:(Ⅰ);(Ⅱ).【答案】见解析【解析】(1)因为.所以.(2)由(1)及得.因为,.于是.9.选修4-5:不等式选讲已知函数d的最小值为4.(1)求的值;(2)若,且,求证:.【答案】(1) 或.(2)见解析.10.已知函数.(1)求不等式的解集;(2)若正数,满足,求证:.【答案】(1);(2)见解析【解析】(1)此不等式等价于或或,即不等式解集为.(2)∵,,,∴,即,当且仅当即时取等号,∴,当且仅当即时取等号,∴.f x<的解集. 11.已知函数,M为不等式()6(1)求集合M;∈,求证:.(2)若a,b M【答案】(1).(2)见试题解析.12.选修4-5:不等式选讲(1)已知,,且,,求证:.(2)若关于的不等式有解,求实数的取值范围.【答案】(1)见解析.(2) .13.选修4-5:不等式选讲已知函数.(1)解不等式;(2)若()对任意恒成立,求证:.【答案】(Ⅰ) ;(Ⅱ)见解析.【解析】(Ⅰ)或或或或或所以不等式的解集为.(Ⅱ)当时,,当时,,所以的最小值为,因为对任意恒成立,所以,又,且等号不能同时成立,所以,即.14.选修4-5:不等式选讲设,且,求证:(Ⅰ);(Ⅱ)【答案】(Ⅰ)见解析.(Ⅱ)见解析.15.选修4-5:不等式选讲已知函数.(Ⅰ)解不等式;(Ⅱ)若,且,证明:. 【答案】(Ⅰ).(Ⅱ)见解析.16.【选修4-5:不等式选讲】 已知函数.(Ⅰ)当1t =时,解不等式()1f x ≤;(Ⅱ)设,,a b c 为正实数,且,其中m 为函数()f x 的最大值,求证:.【答案】(1))[0 ∞+,(2)见解析 【解析】(1)1t =时,,,所以1{31x ≤-≤或或2{31x >-≤, 所以解集为[)0,+∞ . (Ⅱ)由绝对值不等式得,所以()f x 最大值3m =,当且仅当时等号成立.17.选修4-5:不等式选讲已知均为正实数,且.(1)求的最大值;(2)求的最大值.【答案】(1)12;(2).,当且仅当,即时,取等号所以原式,故原式的最大值为.18.(选修4——5:不等式选讲)已知关于的不等式的解集为.(1)求实数的取值范围;(2)已知且,当最大时,求的最小值及此时实数的值.【答案】(1),(2).易得时,取得最小值为.19.已知函数.(1)解不等式;(2)记函数的最小值为,若均为正实数,且,求的最小值【答案】(1)或.(2) .20.选修4-5:不等式选讲已知函数.(1)解不等式;(2)记函数的最小值为,若均为正实数,且,求的最小值. 【答案】(1)或(2)21.选修4-5:不等式选讲已知函数.(1)解不等式;(2)已知,若不等式恒成立,求实数的取值范围.【答案】(1);(2).【解析】(1)等价于,22.已知,,x y z 均为实数. (1)求证:;(2)若,求222x y z ++的最小值.【答案】(1)见解析;(27【解析】证明:(1)法一:,所以.法二:,所以.(2)证明:因为(由柯西不等式得)所以,即时, 222x y z ++有最小值 23.函数,其最小值为.(1)求的值; (2)正实数满足,求证:.【答案】(1)3;(2)24.已知函数,,若恒成立,实数的最大值为.()求实数.()已知实数、、满足,且的最大值是,求的值.【答案】(1)(2)【解析】()根据题意可得,若恒成立,25.已知,且..a b c R +∈.(1)的最小值;(2)证明:.【答案】(1)最小值为9;(2)见解析.【解析】(1)由柯西不等式,得,当且仅当时,取等号.所以的最小值为9.(2)由,。
2019届高考数学一轮复习 选考部分 不等式选讲 第2课时 不等式的证明与柯西不等式教案 文
∴x= 1144,y=21414,z=31414.
∴x+y+z=61414=3
14 7.
6.(2016·江苏,理)设 a>0,|x-1|<3a,|y-2|<3a,求证:|2x +y-4|<a.
答案 略 证明 因为|x-1|<3a,|y-2|<3a, 所以|2x+y-4|=|2(x-1)+(y-2)|≤2|x-1|+|y-2|<2×3a+3a= a.
4.(2014·陕西)设 a,b,m,n∈R,且 a2+b2=5,ma+nb =5,则 m2+n2的最小值为________.
答案 5 解析 由柯西不等式,得(a2+b2)(m2+n2)≥(am+bn)2,即 5(m2 +n2)≥25. ∴m2+n2≥5,当且仅当 an=bm 时,等号成立. ∴ m2+n2的最小值为 5.
方法二:(分析法) ∵a>0,b>0, ∴要证 a+b≥2ab, 只需证(a+b)2≥4a2b2, 即证 a2+b2+2ab≥4a2b2, ∵a2+b2=M,∴只要证 2+2ab≥4a2b2, 即证 2(ab)2-ab-1≤0, 即证(2ab+1)(ab-1)≤0.
方法二:令 a=(3,4),b=(x,y),则 a·b=3x+4y,|a|= 32+42=5,|b|= x2+y2. ∵|a·b|≤|a|·|b|(柯西不等式的向量形式), ∴|3x+4y|≤5 x2+y2. ∴x2+y2≥|3x+254y|2=245. 其他同方法一. 【答案】 最小值为245,最小值点为(265,285)
第2课时 不等式的证明与 柯西不等式
…2018 考纲下载… 1.了解证明不等式的基本方法:比较法、综合法、分析法、 放缩法、数学归纳法. 2.了解柯西不等式、排序不等式以及贝努利不等式. 3.能利用均值不等式求一些特定函数的最值. 请注意 不等式的证明是中学数学的难点.柯西不等式只要求会简单 应用.
