柱压弯抗震验算
钢筋混凝土柱抗震性能设计规范

钢筋混凝土柱抗震性能设计规范一、前言随着城市化进程的不断加速,钢筋混凝土结构的建筑越来越普遍。
而地震是一种不可预测的自然灾害,对建筑物的抗震性能要求也越来越高。
因此,本文旨在对钢筋混凝土柱的抗震性能设计规范进行详细介绍,以提高建筑物的抗震能力。
二、基本原则1. 安全性原则在进行钢筋混凝土柱的抗震性能设计时,必须始终以安全性为第一原则。
设计应满足国家相关规定和标准,合理选用结构材料和构造形式,确保建筑物的抗震能力。
2. 经济性原则在保证安全的前提下,应尽可能降低建筑物的成本。
在设计过程中,应选用经济性良好的构造形式和材料,提高结构的抗震能力,同时减少材料的浪费和使用成本。
3. 实用性原则在设计过程中,应根据建筑物的实际情况进行设计。
建筑物的抗震设计应结合其所处的地理位置、地形地貌、建筑用途和结构形式等因素,充分考虑实际情况。
三、设计要求1. 抗震设计水平钢筋混凝土柱的抗震设计应满足国家相关规定和标准,其中,地震烈度为六级以上的地区,建筑物应采用抗震设防烈度不低于八度的设计标准。
2. 断面尺寸的确定钢筋混凝土柱的断面尺寸应满足以下要求:(1)柱的截面应满足受力要求,弯矩和剪力的设计值应不大于截面的承载能力。
(2)柱的高宽比应控制在一定范围内,一般为不超过15:1,以保证柱的稳定性。
(3)柱的截面应尽可能保持规则,避免出现尖角、圆角等不规则形状。
3. 钢筋的选用在钢筋混凝土柱的设计中,应选用合适的钢筋。
钢筋的应力应满足以下要求:(1)钢筋抗拉强度应符合国家标准。
(2)钢筋的抗拉性能应符合设计要求。
(3)钢筋的强度应适当大于混凝土的强度。
4. 混凝土的选用在钢筋混凝土柱的设计中,应选用合适的混凝土。
混凝土的强度应满足以下要求:(1)混凝土的强度应符合国家标准。
(2)混凝土的强度应适当大于钢筋的强度。
(3)混凝土的配合比应满足设计要求。
5. 抗震构造形式在钢筋混凝土柱的设计中,应选用合适的抗震构造形式。
常见的抗震构造形式有框架结构、剪力墙结构、框剪结构等。
附录J 单层钢筋混凝土柱厂房纵向抗震验算

附录J 单层钢筋混凝土柱厂房纵向抗震验算J.1 厂房纵向抗震计算的修正刚度法J.1.1 纵向基本自振周期的计算按本附录计算单跨或等高多跨的钢筋混凝土柱厂房纵向地震作用时,在柱顶标高不大于15m且平均跨度不大于30m时,纵向基本周期可按下列公式确定:1 砖围护墙厂房可按下式计算:式中Ψ1-屋盖类型系数,大型屋面板钢筋混凝土屋架可采用1.0,钢屋架采用0.85;l-厂房跨度(m),多跨厂房可取各跨的平均值;H-基础顶面至柱顶的高度(m)。
2 敞开、半敞开或墙板与柱子柔性连接的厂房,可按第1款式(J.1.1-1)进行计算并乘以下列围护墙影响系数:式中Ψ2-围护墙影响系数,小于1.0时应采用1.0。
J.1.2 柱列地震作用的计算1 等高多跨钢筋混凝土屋盖的厂房,各纵向柱列的柱顶标高处的地震作用标准值,可按下列公式确定:式中Fi-i柱列柱顶标高处的纵向地震作用标准值;α1-相应于厂房纵向基本自振周期的水平地震影响系数,应按本规范第5.1.5条确定;Geq-厂房单元柱列总等效重力荷载代表值应包括按本规范第5.1.3条确定的屋盖重力荷载代表值、70%纵墙自重、50%横墙与山墙自重及折算的柱自重(有吊车时采用10%柱自重,无吊车时采用50%柱自重);Ki-i柱列柱顶的总侧移刚度,应包括i柱列内柱子和上、下柱间支撑的侧移刚度及纵墙的折减侧移刚度的总和,贴砌的砖围护墙侧移刚度的折减系数,可根据柱列侧移值的大小,采用0.2~0.6;Kai-i柱列柱顶的调整侧移刚度;Ψ3-柱列侧移刚度的围护墙影响系数,可按表J.1.21采用;有纵向砖围护墙的四跨或五跨厂房,由边柱列数起的第三柱列,可按表内相应数值的1.15倍采用;Ψ4-柱列侧移刚度的柱间支撑影响系数,纵向为砖围护墙时,边柱列可采用1.0,中柱列可按表J.1.2-2采用。
2 等高多跨钢筋混凝土屋盖厂房,柱列各吊车梁顶标高处的纵向地震作用标准边柱列值,可按下式确定:式中Fci-i柱列在吊车梁顶标高处的纵向地震作用标准值;Gci-集中于i柱列吊车梁顶标高处的等效重力荷载代表值,应包括按本规范第5.1.3条确定的吊车梁与悬吊物的重力荷载代表值和40%柱子自重;Hci-i柱列吊车梁顶高度;Hi-i柱列柱顶高度。
建筑结构抗震:第三章 地震作用和结构抗震验算

u p
7
up p ue
弹塑性位移增大系数
同一结构,同样的地震作用 存在比较稳定的关系
(2)影响楼层弹塑性变形的主要因素 楼层受剪的承载力分布
Vy y Ve
按构件的实际配筋和材料强度标准值 计算的层间受剪承载力
罕遇地震作用下按弹性理论求得的层间剪力
楼层间屈服承载力系数
y 小 p 大
这个系数对弹塑性变形影响很大
1/550
钢筋混凝土框架-抗震墙、柱板-抗震墙、框架-核心筒 1/800
钢筋混凝土抗震墙、筒中筒 钢筋混凝土框支层 多、高层钢结构
1/1000 1/1000 1/300
2021/7/2
5
二、罕遇地震作用下结构的抗震变形验算
目的:大震不倒
第一阶段设计已经具有很大的变形储备,一般可以不验算罕遇 地震作用下的变形。但以下结构必须进行弹塑性变形验算 :
目的:保证非结构构件(围护墙、填充墙、装饰物等)不破坏
验算层间位移(按弹性理论)
小震不坏
ue
Ve K
[e ]H
Ve 用反应谱法求得的层间剪力 K 层间侧移刚度,计算方法以后要讲到(高层)
[e ] 层间弹性位移限角 见表3—13
4
弹性层间位移限角 表3-13
结构类型
钢筋混凝土框架
[θe]
高烈度区的高大单层钢筋混凝土排架结构,楼层屈服承载力系 数小于0.5的结构,高度大于150m的钢结构,甲乙类建筑物,采用隔 震和减震消能设计的结构等
以下结构宜进行弹塑性变形验算:
高度较大,规范要求须按时程分析进行多遇地震下补充计算的 高层建筑结构,当其属不规则类型时;
7度时Ⅲ、Ⅳ类场地和8度时乙类建筑中钢筋混凝土结构和钢结 构;
柱截面设计
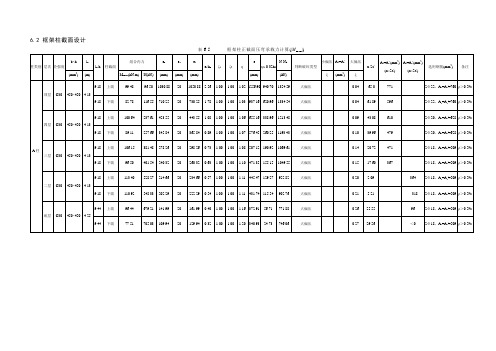
6.2 框架柱截面设计表6-5框架柱正截面压弯承载力计算(|M续表6-5框架柱正截面压弯承载力计算(|M表6-6框架柱正截面压弯承载力计算(N续表6-6 框架柱正截面压弯承载力计算(N表6-7 框架柱正截面压弯承载力计算(N续表 6-7 框架柱正截面压弯承载力计算(N为了满足和提高框架结构“强柱弱梁”程度,在抗震设计设计中采用增大柱端弯矩设计值的方法,一、二、三级框架的梁柱节点处,除框架顶层和柱轴压比小于0.15者及框支梁与框支柱的节点外,柱端组合的弯矩设计值应符合下式要求:cc b MM η=∑∑例如二层A 柱下端和底层A 柱上端弯矩,计算过程如下: 考虑地震组合时二层横梁AD 左端弯矩最大值为357.41 kN m ⋅,cc b MM η=∑∑=1.1×357.41=393.15kN m ⋅ 上下柱端的弯矩设计值按柱线刚度分配,二层A 柱下端弯矩M c =10.36/(10.36+8.04)×393.15=221.36kN m ⋅,底层A 柱上端弯矩M c =8.04/(10.36+8.04)×393.15=171.79kN m ⋅。
表6-8 框架柱正截面压弯抗震验算(|M注:按柱实际配筋(A s+A s’+ A s侧)计算的总配筋率ρ=(12×314.2)/(450×450)=1.86%,0.7%<ρ<5%,所以满足要求。
续表6-8 框架柱正截面压弯抗震验算(|M注:按柱实际配筋(A s+A s’+ A s侧)计算的总配筋率ρ=(12×314.2)/(450×450)=1.86%,0.7%<ρ<5%,所以满足要求。
表6-9框架柱正截面压弯抗震验算(N注:按柱实际配筋(A s+A s’+ A s侧)计算的总配筋率ρ=(12×314.2)/(450×450)=1.86%,0.7%<ρ<5%,所以满足要求。
5.4 框架柱的抗震设计解析

解:2.斜截面受剪承载力
(1)剪力设计值
u l V 1.2(M c Mc ) / Hn
1.2
770 730 521.74kN 4.2 0.75
(2)剪压比应满足
V 1 1
RE
(0.2 f c bh0 )
RE
(0.2 f c bh0 )
1 521.74kN (0.2 15 500 565 ) 997kN 0.85
解:3.轴压比验算
N / bhf c 2710000 0.63 0.80 (可) 14.3 500 600
4.体积配筋率验算
由轴压比 N 0.63, 根据表v 0.136,采用井字复合箍筋(见教材P150) 配箍率为:sv n1 As1l1 n2 As 2l2 4 78.5 450 4 78.5 550 1.27% Acor s 450 550 100
为了不使框架底层柱过早出现塑性铰,规范规定:一、二、三级框 架底层柱底截面组合的弯矩设计值应分别乘以增大系数1.5、1.25、1.15。
(2)在弯曲破坏前不发生剪切破坏
(a)柱剪力设计值的调整
t b V Vc (M c Mc ) / Hn
9度时和一级框架尚应符合
t b V 1.2(M cua M cua ) / Hn
V---柱端组合剪力设计值;
Hn
---柱的净高;
t b Mc 、M c --分别为柱上下端顺时针或逆时针方向截面组合的弯 矩设计值; t b M cua 、M cua ---分别为偏心受压柱上下端顺时针或逆时针方向根 据实配钢筋面积和材料强度标准值和轴压力等计算的 抗震承载力所对应的弯矩值;
Vc ---柱的剪力增大系数,一级为1.4,二级为1.2,三级为1.1。
圆形墩柱抗弯计算公式

圆形墩柱抗弯计算公式圆形墩柱是建筑结构中常见的一种构件,它承受着来自上部结构和外部荷载的弯曲力。
为了确保圆形墩柱的稳定性和安全性,需要进行抗弯计算,以确定其承载能力和设计参数。
本文将介绍圆形墩柱抗弯计算的相关公式和方法。
圆形墩柱的抗弯计算需要考虑其受力情况、材料特性和几何形状等因素。
在进行抗弯计算时,需要确定墩柱的截面特性、受力情况和材料特性,然后应用相关的公式和方法进行计算。
下面将介绍圆形墩柱抗弯计算的相关公式和方法。
首先,我们需要确定圆形墩柱的截面特性。
圆形墩柱的截面特性主要包括截面面积、截面惯性矩和截面模量。
截面面积可以根据墩柱的直径和高度计算得出,截面惯性矩和截面模量可以根据墩柱的几何形状和材料特性计算得出。
这些截面特性将在后续的抗弯计算中起到重要作用。
其次,我们需要确定圆形墩柱的受力情况。
圆形墩柱在受到弯曲力作用时,会产生弯曲应力和弯曲变形。
为了确定墩柱的抗弯承载能力,需要计算墩柱在弯曲状态下的应力和变形。
弯曲应力可以根据墩柱的受力情况和截面特性计算得出,而弯曲变形可以根据墩柱的受力情况和材料特性计算得出。
最后,我们需要应用相关的公式和方法进行抗弯计算。
圆形墩柱的抗弯计算可以采用弹性理论和塑性理论进行分析。
在弹性理论中,可以采用梁的弯曲理论和截面受拉受压的平衡条件进行计算;在塑性理论中,可以考虑墩柱的屈服和破坏状态进行计算。
根据墩柱的具体情况和设计要求,可以选择合适的计算方法进行抗弯计算。
综上所述,圆形墩柱的抗弯计算涉及到截面特性、受力情况和计算方法等多个方面。
在进行抗弯计算时,需要综合考虑这些因素,并应用相关的公式和方法进行计算。
通过合理的抗弯计算,可以确保圆形墩柱具有足够的承载能力和稳定性,从而保障建筑结构的安全性和可靠性。
柱验算
基础J-1(编号14)地基承载力特征值fak承载力修正系数ηb承载力修正系数ηd基底以下土的重度γ基底以上土的加权平均重度γm 基础埋深d(用于承载力修正)基础根部高度H 基础端部高度h1柱宽bc'注意啦:柱高hc'轴心荷载pk 通过Y向双柱形心距离cy X向pkmaxX通过X向双柱形心距离cxX向pkminX >0可以覆土厚度 ds(用于计算基础自重)Y向pkmaxY 通过永久荷载控制的荷载组合分项系数γz Y向pkminY >0可以混凝土强度等级X方向冲切验算通过钢筋强度fy Y方向冲切验算通过保护层厚度as X方向剪切验算通过柱1竖向力Fk1Y方向剪切验算通过柱1基础顶面弯矩Mkx1'柱下局部受压通过柱1基础顶面弯矩Mky1'AsI=741mm^2/M 柱1基础顶面剪力Vkx1As Ⅱ=760mm^2/M柱1基础顶面剪力Vky1Φ12@153基础长宽比(L/B)向轴力点=Fk2*cx/(Fk1+Fk2)=0mm Φ12@149h0=460mm Y 向轴力点=Fk2*cy/(Fk1+Fk2)=0mm (双柱)柱根宽度bc 400mm X向轴力偏心距ex0=0mm (双柱)柱根长度hc 400mmY向轴力偏心距ey0=0mmFk=1139.00kN fc=14.3N/mm^2竖向力F=γz*Fk=1537.65kN ft=1.43N/mm^2fa=fak+ηb*γ*(b-3)+ηd*γm*(d-0.5)=306.2kpa 轴心受压基底面积=(Fk+Gk)/(fa-γg*ds) 3.79M^2(注:γg 取20.0kN/M^3)计算基础长度b=1948mm 取基础长度b=计算基础宽度L=1948mm取基础宽度L=Mx=γz*{(Mkx1'+Mkx2')-(Vky1+Vky2)*H+Fk*ey0}=18.3kN·M My=γz*{(Mky1'+Mky2')+(Vkx1+Vky2)*H+Fk*ex0}=0.1kN·MY 轴方向截面面积 Acb 0.81M^2X 轴方向截面面积 AcL 0.81M^2X 轴基础顶面坡度20.56°Y 轴基础顶面坡度20.56°基础底面积A 4.41M^2X向Wx =l * b * b / 6 1.54M^3Y 向Wy = b * l * l / 61.54M^3基础及土自重标准值Gk=γg*A*ds=26.46kN 基础及的土重设计值G=γz*Gk=35.721kN 轴心荷载作用下pk = (Fk + Gk) / A 264.28<fa=306.2kpa 通过X 向pkmaxX =(Fk+Gk)/A+|Mky|/Wx=264.34< 1.2*fa=367.4kpa 通过X 向pkminX =(Fk+Gk)/A -|Mky|/Wx=264.21>0.00kpa >0可以X 向偏心矩ex=Mky/(Fk+Gk)=0.000<b/6=0.35m Y 向pkmaxY =(Fk+Gk)/A+|Mkx|/Wy=273.06< 1.2*fa=367.4kpa 通过Y 向pkminY =(Fk+Gk)/A -|Mkx|/Wy=255.50>0.00kpa >0可以Y 向偏心矩ey=Mkx/(Fk+Gk)=0.012<L/6=0.350m 中间结果pmaxX=γz*PkmaxX=356.86kpa pjmaxX=pmaxX-G/A=348.8kpa Alx=0.5*(L+bc+2*Ho)*(L-bc-2*Ho)/2+L*(b-hc-L+bc)/2=pmaxY=γz*PkmaxY=368.62kpapjmaxY=pmaxY-G/A=360.5kpaAlx=L*[0.5*(b-hc)-h0]=X方向冲切验算Alx=0.5*(b-hc+2*bc+2*Ho)*[(b-hc)/2-Ho]=因b - hc=1700=L - bc=1700mm b=2100>hc+2*Ho=1320mm L=2100>b c+2*Ho=1320mm Aly=0.5*(b+hc+2*Ho)*(b-hc-2*Ho)/2+b*(L-bc-b+hc)/2=Alx=0.5*(b-hc+2*bc+2*Ho)*[(b-hc)/2-Ho]=666900mm^2Aly=b*[0.5*(L-bc)-h0]=ab = Min{bc + 2 * Ho,l} =1320mm Aly=0.5*(l-bc+2*hc+2*Ho)*[(l-bc)/2-Ho]=amx = (bc + ab) / 2 =860mm0.7 * βhp * ft * amx * Ho =356.40>Flx=pjmaxX*Alx=232.59通过Y方向冲切验算Aly=0.5*(l-bc+2*hc+2*Ho)*[(l-bc)/2-Ho]=666900m m^2ab = Min{hc + 2 * Ho,b}1320mm amy = (hc + ab) / 2860mm0.7 * βhp * ft * amY * Ho =356.40>Fly=pjmaxY*Aly=240.43通过X 方向(b 方向)剪切验算计算宽度Lo={1.0-0.5*[1.0-(bc+2*50)/L]*(Ho-h1)/Ho}*L=1647.83mm回目录Vx=pj*Ax=pj*(b-hc)*L/2=622.54<0.7*βh*ft*Lo*Ho=758.76通过Y 方向(l 方向)剪切验算计算宽度bo={1.0-0.5*[1.0-(hc+2*50)/b]*(Ho-h1)/Ho}*b=1647.83mm Vy=pj*Ay=pj*(l-bc)*b/2=622.54<0.7*βh*ft*bo*Ho=758.76通过X 方向(b 方向)柱边(绕 Y 轴)抗弯计算pmaxX=γz*PkmaxX=356.86kpapminX=γz*PkminX=356.69kpapX=pminX+(pmaxX-pminX)*(b+hc)/b/2=356.79kpaMIx=(b-hc)^2*[(2*L+bc)*(pmaxX+pX-2*G/A)+(pmaxX-pX)*L]/48=193.2kN·MMⅡx=(L-bc)^2*(2*b+hc)*(pmaxX+pminX-2*G/A)/48=193.1kN·MY 方向(l 方向)柱边(绕 X 轴)抗弯计算pmaxY=γz*PkmaxY=368.62kpapminY=γz*PkminY=344.92kpapY=pminY+(pmaxY-pminY)*(L+bc)/L/2=359.03kpaMIy=(b-hc)^2*[(2*L+bc)*(pmaxY+pY-2*G/A)+(pmaxY-pY)*L]/48=198.3kN·MMⅡy=(L-bc)^2*(2*b+hc)*(pmaxY+pminY-2*G/A)/48=193.1kN·MMⅠ= Max{MⅠx,MⅡy} =193.17kN·MAsⅠ=MⅠ/0.9*h0*fy*L=741mm^2/MΦ12@153MⅡ= Max{MⅡx,MⅠy} =198.26kN·MAsⅡ=MⅡ/0.9*h0*fy*B=760mm^2/MΦ12@149柱下局部受压承载力计算混凝土局部受压面积 Al = bc * hc =160000mm^2Ab = (bx + 2 * c) * (by + 2 * c)=250000mm^2βl = Sqr(Ab / Al)= 1.251.35 * βc * βl * fc * Al =3861.00> F =1537.7kN通过回目录L*(b-hc-L+bc)/2=666900819000 (b-hc)/2-Ho]=6669002*Ho)/2+b*(L-bc-b+hc)/2=666900819000 (l-bc)/2-Ho]=666900。
结构抗震验算
结构抗震验算的内容
2 下列结构宜进行弹塑性变形验算: 下列结构宜进行弹塑性变形验算: 1) 表5.1.2-1所列高度范围且属于表 所列高度范围且属于表3.4.2-2所列竖向 所列高度范围且属于表 所列竖向 不规则类型的高层建筑结构; 不规则类型的高层建筑结构;
表5.1.2-1 5.1.2烈度、 烈度、场地类别 类场地及7 8度Ⅰ、Ⅱ类场地及7度 8度Ⅲ、Ⅳ类场地 9度 房屋高度范围(m) 房屋高度范围(m) >100 >80 >60
ψW
结构抗震验算的内容
多遇地震下结构承载力验算
S ≤ R/ γ RE
多遇地震下结构弹性变形验算
∆ue ≤[θe ]h
或
∆ue ≤[θe ] h
结构抗震验算的内容
弹性层间位移角限值 结构类型 钢筋混凝土框架 钢筋混凝土框架-抗震墙、板柱-抗震墙、框架- 钢筋混凝土框架-抗震墙、板柱-抗震墙、框架-核心筒 钢筋混凝土抗震墙、 钢筋混凝土抗震墙、筒中筒 钢筋混凝土框支层 多、高层钢结构
γ Eh、Eh、 Ev γγ Ev γ
1.3 0.0 1.3
0.0 1.3 0.5
结构抗震验算的内容
S = γGSGE +γ EhSEhk +γ EvSEvk +ψWγW SWk
γG ——重力荷载分项系数,一般取 ,当重力荷载效 重力荷载分项系数, 重力荷载分项系数 一般取1.2,
应对构件承载能力有利时,不应大于 应对构件承载能力有利时,不应大于1.0
表5.1.2-1 5.1.2采用时程分析的房屋高度范围 房屋高度范围(m) 房屋高度范围(m) >100 >80 >60
烈度、 烈度、场地类别 类场地及7 8度Ⅰ、Ⅱ类场地及7度 8度Ⅲ、Ⅳ类场地 9度
砌体女儿墙构造柱抗风抗震验算
1.计算模型带构造柱女儿墙,由构造柱完全承担女儿墙的风载及地震荷载,构造柱按悬臂梁考虑2.计算资料2.1 女儿墙参数高度 L=1.50m墙顶标高 H=16.50m(墙顶距室外地面高度)墙体容重 γW =2.2 构造柱参数构造柱间距 S=3.0m 钢筋保护层厚度20mm 截面宽度 b=240mm 截面高度 h=300mm 混凝土强度等级C20抗压强度 f c =纵向钢筋牌号:HRB400抗拉强度 f y =箍筋钢筋牌号:HPB300抗拉强度 f yv =3.荷载标准值计算3.1 风荷载基本风压 ω0=0.60kPa 地面粗糙度:D 阵风系数 βgz =1.651高度变化系数μz =0.510体形系数 μsl =1.625标准风压 W k =βgz μsl μz ω0=0.82kPa 剪力标准值 V w,k =SL ωk =3.69kN弯矩标准值 M w,k =0.5V w,k L=2.8kN·m3.2 水平地震荷载地震加速度: 0.40g 影响系数 αmax =0.32功能系数 γ=0.9类别系数 ε=1.4状态系数 δ1=2.0位置系数 δ2=2.0剪力标准值 V E,k = γεδ1δ2 αmax G=34.8kN弯矩标准值M w,k =0.5V w,k L=26.1kN·m4.荷载组合4.1 风荷载控制剪力 V W =1.4V w,k =5.17kN 弯矩 M W =1.4M w,k =4.2 地震荷载控制剪力V E =1.3V E,k +0.2×1.4×V w,k =46.3kN 弯矩M E =1.3M E,k +0.2×1.4×M w,k =5.构造柱配筋计算5.1 配筋纵筋:2Φ12As=226mm²箍筋:Φ6@200肢数:2Asv=57mm²5.2 纵筋验算(按单筋悬挑梁计算)(γRE =0.75)钢筋合力点边距 a=32mm相对界限受压区高度 ξb =0.518受压区高度 x=f y As/α1f c b=35mm最大容许弯矩 [M]=α1f c bx(h 0-0.5x)=21.36kN (《混规》6.2.10)[M] ≥ M W [M] < γRE M E纵筋不满足5.3 箍筋验算αcv =0.7f t = 5.3.1 风压控制下最大容许剪力[V W ]=αcv f t bh 0+f yv A sv h 0/s=73.1kN≥Vw (《混规》6.3.1)箍筋满足 5.3.2 地震荷载控制下最大容许剪力 (γRE =0.85)[V E ]=[0.6αcv f t bh 0+f yv A sv h 0/s]/γRE =61.7kN ≥VE (《混规》11.3.4)箍筋满足5.4 配筋验算结论:配筋不满足3.9kN·m34.7kN·m 1.10N/mm²带构造柱砌体女儿墙计算20.0kN/m³9.60N/mm²360N/mm²270N/mm²。
柱子钢筋弯折长度计算公式
柱子钢筋弯折长度计算公式在建筑工程中,柱子是承受和传递楼板和梁的重量的重要结构元素。
为了确保柱子的稳定性和承载能力,钢筋的设计和施工是至关重要的。
在柱子的设计和施工过程中,钢筋的弯折长度是一个重要的参数,它决定了柱子的抗弯能力和承载能力。
本文将介绍柱子钢筋弯折长度的计算公式以及相关的理论知识。
柱子钢筋弯折长度的计算公式可以用来确定柱子在受压状态下的钢筋的弯折长度,从而确定钢筋的受力状态和受力能力。
柱子的弯折长度取决于柱子的截面尺寸、混凝土和钢筋的强度、受力状态等因素。
在建筑工程中,一般采用以下的柱子钢筋弯折长度计算公式:Lb = k λ d。
其中,Lb为钢筋的弯折长度,k为系数,λ为受压区高度与截面尺寸的比值,d为柱子的截面尺寸。
在实际工程中,系数k的取值一般根据国家标准或者设计规范来确定。
在中国,一般采用GB 50010-2010《混凝土结构设计规范》中的规定来确定系数k的取值。
根据该规范,系数k的取值与混凝土的强度等级、受压区钢筋的强度等级等因素有关。
在设计和施工中,需要根据具体的情况来确定系数k的取值。
受压区高度与截面尺寸的比值λ是另一个影响柱子钢筋弯折长度的重要因素。
λ的取值一般由设计规范或者理论计算来确定。
在实际工程中,需要根据柱子的具体情况来确定λ的取值。
通常情况下,λ的取值范围在0.5到0.8之间。
柱子的截面尺寸d是柱子钢筋弯折长度计算公式中的另一个重要参数。
柱子的截面尺寸取决于柱子的设计要求和施工工艺。
在设计和施工中,需要根据柱子的具体情况来确定d的取值。
柱子钢筋弯折长度计算公式的应用可以帮助工程师和施工人员确定柱子的钢筋布置方式和数量,从而保证柱子的抗弯能力和承载能力。
在实际工程中,需要根据具体的情况来确定柱子钢筋弯折长度,从而保证柱子的安全可靠。
除了柱子钢筋弯折长度计算公式,还有一些其他的计算公式和方法可以用来确定柱子的钢筋布置方式和数量。
例如,可以采用受压区钢筋配筋率、受压区混凝土偏心受压等方法来确定柱子的钢筋布置方式和数量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.25上端82.48183.17
11.25下端69.95200.45
11.25上端104.85557.95
11.25端下108.37575.23
13.75上端126.17761.19
13.75下端141.59787.59
11.25上端80.47213.35
11.25下端66.67230.63
11.25上端107.72644.99
11.25下端109.17662.27
13.75上端129.29861.39
13.75下端147.66887.79
5.5l0/h柱截面Mmax(kN·m)N(kN)400×400400×400400×400400×400l0(m)4.54.55.54.54.5二层底层混凝土强度C30C30C30C30C30C30
柱类别A柱B柱层次
顶层二层底层顶层组合内力b×h(mm2)400×400
400×400
0.080.7511.070.9483.31455
0.090.7511.090.9472.00359
0.240.7511.170.97118.85213
0.250.7511.170.97122.80213
0.330.7511.280.85137.47181
0.340.7511.260.85151.89193
0.090.7511.090.9482.32386
0.100.7511.110.9469.78303
0.280.7511.190.98125.35194
0.290.7511.190.98127.27192
0.380.7511.310.85143.72167
0.390.7511.280.85160.78181
ξcηnsCmM'eo(mm)轴压比
框架柱正截面压弯抗震验算(│Mmax│)
γ
RE
204751.32635367-949.39大偏压
203791.05539271-932.11大偏压
202330.65393125-574.61大偏压
202330.65393125-557.33大偏压
202010.5636193-371.37大偏压
202130.59373105-344.97大偏压
204061.13566298-919.21大偏压
203230.90483215-901.93大偏压
202140.60374106-487.57大偏压
202120.59372104-470.29大偏压
201870.5234779-271.17大偏压
202010.5636193-244.77大偏压
ei(mm)ei/he(mm)ei-0.3hoN-Nb(kN)判断破坏类型e
a
(mm)
32.0230.089-48.0501
35.0440.097-45.0381
97.5440.27117.5
100.5650.27920.6
133.0750.37053.1
137.6910.38257.7
37.2990.104-42.7455
40.3200.112-39.7325
112.7600.31332.8
115.7810.32235.8
150.5930.41870.6
155.2080.43175.2
x小偏压ξAs=As'(mm2)大偏压ξx-2a'
As=As'
(mm2)
(X<2a')
ρ>0.2%ρ>0.2%396ρ>0.2%418ρ>0.2%444ρ>0.2%559ρ>0.2%ρ>0.2%ρ>0.2%396ρ>0.2%403ρ>0.2%465ρ>0.2%607ρ>0.2%As=As'(mm2)(X>2a')备注选用钢筋(mm2) 3 ϕ18.As=A's=763 3 ϕ18.As=A's=763 3 ϕ18.As=A's=763 3 ϕ18.As=A's=763 3 ϕ18.As=A's=763 3 ϕ18.As=A's=763 3 ϕ18.As=A's=763 3 ϕ18.As=A's=763 3 ϕ18.As=A's=763
3 ϕ18.As=A's=763
3 ϕ18.As=A's=763
3 ϕ18.As=A's=763
