12-13上概率统计(3学时)A卷答案

合集下载

上海大学12-13(冬)概率统计B试题(A卷)答案和评分参考

四、计算题:（共 60 分） 15、（本题共 10 分）设有两罐，其中第一个罐中黑球 6 个，白球 4 个；第二个罐中白球和黑球各 5 个。现在随机选取一罐，并从该罐中随机抽取一球。计算， 1）抽到的球是黑球的概率； 2）如果发现抽到的是白球，该球是从第一个罐中抽取的概率是多大？
11、随机变量 X 的概率密度和分布函数分别为 f ( x ) 和 F ( x ) ，则一定有
1 ； F1 (n, m)
C
。
(B) F (m, n) 1 F1 (n, m) ； (D) F (m, n)
1 。 F1 (m, n)
1） P( A) P( A | B) P( B) P( A | B) P( B) 0.55 （2+1 分） 2） P( B | A)
1 的均值为 d ，方差为 c 2 。（错） 3
2、任意多个互不相容事件并的概率一定等于这些事件概率之和。 3、如果 X1 , 样本均值 X
, X n 是来自于服从正态分布 N (, 2 ) 的总体 X 的简单样本，那么
1 n 1 n 2 和样本方差 X S ( X i X )2 是独立的。 i n 1 i 1 n i 1
编号服药前服药后
1 134
2 122
3 132
4 130
5 128
6 140
7 118
8 127
9 125
10 142
1）计算 Z1 X Y 的分布律；2）计算 Z2 max{X ,Y } 的分布律； 3）计算协方差 cov( X , Y ) ；4）计算相关系数 XY 。解 1） Z1
（对）
9、设随机变量 X 与 Y 相互独立，且都服从相同指数分布，密度函数为

概率统计A1 答案

f
(x,
y)
8e(2x4 y) ,
x 0, y 0
0,
其它
故
P( X
Y)
8e2 xe4 y dxdy
0x
8 e2x
0
( e4y 4
)x dx
1 3
9、解:（1）由分布函数的性质
F (, )
lim
A(B
arctan
x)(C
arctan
y)
A(B
)(C
)
1
x y
2
2
F (,
YX
0.9.
18、解: 由随机变量 ( X ,Y ) 服从 G (x, y) 0 x y 1上的均匀分布，
此时 SG
1 ，从而随机变量 ( X ,Y ) 的概率密度为 2
1
f
(
x,
y)
SG
2, (x, y) G 0, 其它
（1） fX (x)
f
(x, y)dy
1
2dy
x
2(1 x), 0
PX
k
C
k 3
0.7
k
0.33k
,
k
0,1, 2, 3
所以
PX
1
P X
0 P X
1 0.3 3 C 310.3 2 0.7
27 125
2、解: 随机变量 X 1, 2,3
P{X 1} F (1) F (1 ) 9 0 9 19 19
P{X 2} F (2) F (2 ) 15 9 6 19 19 19
P{X
3}
C31
C32 43
C33
7 43
； P{X

(完整版)12-13-1概率统计期中试卷(理工)答案

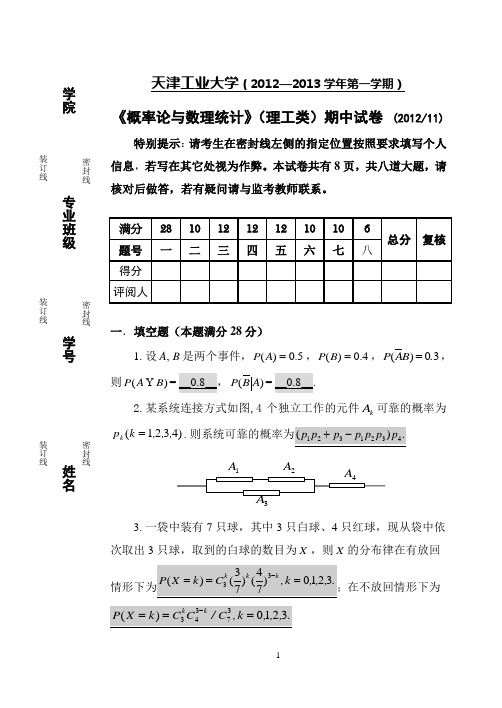
1天津工业大学（2012—2013学年第一学期）《概率论与数理统计》（理工类）期中试卷 (2012/11)特别提示：请考生在密封线左侧的指定位置按照要求填写个人信息，若写在其它处视为作弊。

本试卷共有8页，共八道大题，请核对后做答，若有疑问请与监考教师联系。

一．填空题（本题满分28分）1.设B A ,是两个事件，5.0)(=A P ，4.0)(=B P ，30)(.B A P =，则)(B A P Y )(A B P2.某系统连接方式如图,4个独立工作的元件k A 可靠的概率为)4321(,,,k p k =.3.一袋中装有7只球，其中3只白球、4只红球，现从袋中依次取出3只球，取到的白球的数目为X ，则X 的分布律在有放回在不放回情形下为 -----------------------密封线----------------------------------------密封线---------------------------------------密封线----------------------------------------------学院专业班级学号姓名----------------------装订线----------------------------------------装订线----------------------------------------装订线---------------------------------------------24.设随机变量X 的概率密度⎩⎨⎧<<=0 10 )(其它,x ,Ax x f X ，则常数A13+=X Y 的概率密度=)(y f Y5．设随机变量X 的分布律为则X 的分布函数为=)(x F X．6．设随机变量)(λ~X π（泊松分布），且20)(-==e X P ，则常数λ≤)2(X P7．设随机变量)61(,U ~X （均匀分布），则X的概率密度函数为t 的二次方程012=+-Xt t 有实根的概率为8．设随机变量X 的概率密度函数为2(3)4(),x f xx +-=-∞<<+∞则23+=X Y ；而概率)2(->Y P 知9772.0)2(=Φ）．3二．（本题满分10分）设某厂有甲乙丙三条流水线生产同一种产品，产量分别占15%，80%，5%；次品率分别为0.02，0.01和0.03；三条流水线的产品混放在同一库房。

高三第1章概率与统计单元AB卷及答案

高三第1章《概率与统计》单元AB 卷及答案浙江省诸暨市学勉中学（311811）郭天平概率与统计单元测试题A一、选择题（每题5分，共40分）1.有下列问题：①某路口一天经过的车辆数ξ；②某无线寻呼台一天内收到寻呼的次数ξ；③一天之内的温度ξ；④某人一生中的身高ξ；⑤射击运动员对某目标进行射击，击中目标得1分，未击中目标得0分，则运动员得到的分数ξ；上述问题中的变量为离散型随机变量的是（） A ．①②③⑤ B ．①②④ C ．① D ．①②⑤2. 某市为抽查控制汽车尾气排放的执行情况, 选择了抽取汽车车牌号的末位数字是6的汽车进行检查,这样的抽样方式是( ).A.抽签法B.简单随机抽样C.分层抽样D.系统抽样 3. 已知随机变量ξ的分布列为:又变量32+=ξη, 则η的期望是( ). A.37B. 4C.－1D. 14.有N 件产品,其中有M 件次品,从中有放回地抽n 件产品,抽到的次品数的数学期望值是( ) A. n B. (1)M n N- C. M nND. (1)M n N+5. 设ξ是随机变量,且()4010=ξD ,则()ξD 等于 ( )A. 0.4B. 4C. 40D. 4006．在某餐厅内抽取100人,其中有30人在15岁以下,35人在16至25岁,25人在26至45岁,10人在46岁以上,则数 0.35 是16到25岁人员占总体分布的 ( ) A.概率 B.频率 C.累计频率 D.频数7. 已知随机变量ξ服从二项分布⎪⎭⎫⎝⎛31,6~B ξ,则()==2ξP ( )A.163 B.2434 C.24316 D.243808. 甲、乙两台自动车床生产同种标准件，表示甲机床生产1000件产品中的次品数，表示乙机床生产1000件产品中的次品数，经过一段时间的考察，的分布列分别为（）据上两表判定（）A ．甲比乙质量好B ．乙比甲质量好C ．甲比乙质量相同D ．无法判定二、填空题（每题5分，共20分）9. 一个容量为20的样本数据,分组后,组距与频数如下: (]2,20,10； (]3,30,20； (]4,40,30；(]5,50,40；(]4,60,50； (]2,70,60，则样本在区间 (],50-∞上的频率为________________10. 一射手对靶射击,直到第一次中靶为止.他每次射击中靶的概率是 0.6 ,他有4颗弹子,射击结束后尚余子弹数目ξ的数学期望E ξ=______________11．一本1000页的书共有100个错别字，假设每个错别字出现在每一页上都是等可能的，则任一页上错字个数的期望是_____________12．一次数学测验有25道选择题构成，每个选择题有4个选择项，其中有且只有一个选项正确，每选一个正确答案得4分，不作出选择或选错的不得分，满分100分，某学生选对任一题的概率是0.8，则此学生在这一次测试中的成绩的=ηE __________;=ηD ____________.三、解答题（每题10分，共40分）13.一个出租车司机从饭店到火车站途中有六个交通岗，假设他在各交通岗到红灯这一事件是相互独立的，并且概率都是.31（1）求这位司机遇到红灯前，已经通过了两个交通岗的概率；（2）求这位司机在途中遇到红灯数ξ的期望和方差14.摇奖器有10个小球，其中8个小球上标有数字2，2个小球上标有数字5，现摇出3个小球，规定所得奖金（元）为这3个小球上记号之和，求此次摇奖获得奖金数额的数学期望15．甲、乙两名射手各打10发子弹，每发击中环数如下：甲：10，6，7，10，8，9，9，10，5，10；乙：8，7，9，10，9，8，7，9，8，9。

12年A卷及答案

n 1 m ( X k ) 2 X k 2 ~ 2 (n m 1) ； m k 1 k m 1
5、
1 ； n 1
0, y 1 y 1 3 6、 FY ( y ) ( ) 2 ,1 y 3 ； 2 1, y 3
；
7、 DX
设随机过程 X (t ) a sin(t ) ,其中 a 和是非零常数, 是在 (0,2 ) 上服从均匀分布的随机变量。试求： (1)写出的概率密度 f ( ) ； (3)求 E[ X (t ) X (t )] ；（2）求 E[ X (t )] ; (4)判断 X (t ) 是否为平稳过程？ )
北京航空航天大学
BEIHANG UNIVERSITY
2011－2012 学年第一学期期末
考试统一用答题册
考试课程概率统计 A （A09B204A）概率统计 B（A09B204B）
A
（试卷共 6 页，五道题）
班级_____________ 姓名______________ 考场教室_________
题号一二三
学号 _____________ 成绩 _________ 任课教师_________
四[四] 五[五] 总分
分数
阅卷人校对人
2012 年元月 10 日(10:30-12:30)
一、单项选择题（每小题 4 分，满分 36 分）
1、设连续型随机变量 X 的概率密度为 f ( x) ,分布函数为 F ( x) ，则一定有( )成立。 (B) F ( x) 是连续函数； (D) 对任意实数 x ，成立 F ( x) f ( x) 。
X
k 1
15

概率统计12-13试卷和答案

1 x 1
其他
，
1 y 1
其他
。
4分
(2) 因 f ( x, y ) f X ( x) fY ( y ) ，故 X 与 Y 不独立。 (3) P{ X Y } 即是 ( X , Y ) 落入区域 G {( x, y ) | x y, x y 1} 的概率，有
3 (1 ) 2 其中 (0 1) 是未知参数，利用总体 X 的如下样本值： x1 1, x2 2, x3 1 ，求参数的矩估计值和最大似然估计值．．．．．．．．．．．．
1
2
2 2 (1 )
7. 设某次考试的成绩服从正态分布，随机抽取了 36 位考生的成绩，算得平均分为 66.5 分，标准差为 s 15 ，问：在显著性水平 0.05 下，是否可以认为这次考试的平均成绩为 70 t0.05 (35) 1.6869 ， t0.05 (36) 1.6833 ) 分？ (已知 t0.025 (35) 2.0301 ， t0.025 (36) 2.0281 ，
三、计算题（本大题共 7 小题，每题 10 分，共 70 分）
1 4 1. 某地气象预报表明，在一年中有 5 的日子预报下雨，有 5 的日子预报不下雨. 某位王先生， 1 若预报下雨必带伞；若预报不下雨带伞的概率为 8 ，求： (1)这位王先生带伞的概率；(2) 某日发现这位王先生带伞，则这天预报下雨的概率是多少？
( A) 1 n Xi ；
i 1
n
( B)
1 Xi ； n1 i 1
n
(C )
1 X i2 ； n1 i 1
n
( D)
1 X2 n i
i 1

概率统计答案(详解)

第一章随机事件与概率1. 用集合的形式写出下列随机试验的样本空间与随机事件A ：(1) 抛一枚硬币两次，观察出现的面，事件{=A 两次出现的面相同}；(2) 记录某电话总机一分钟内接到的呼叫次数，事件{=A 一分钟内呼叫次数不超过3次}；(3) 从一批灯泡中随机抽取一只，测试其寿命，事件{=A 寿命在2000到2500小时之间}。

解 (1) 用+表示出现正面，-表示出现反面。

)},(),,(),,(),,{(--+--+++=Ω， )},(),,{(--++=A . (2) 012{,,,,}kΩωωωω=，0123{,,,}A ωωωω=.其中k ω 表示1分钟内接到k 次呼唤，0,1,2,k =(3) 记x 为抽到的灯泡的寿命（单位：小时），则{|0}x x Ω=≥， {|20005000}A x x =≤≤.2. 在区间]2,0[上任取一数，记⎭⎬⎫⎩⎨⎧≤<=121x x A ，⎭⎬⎫⎩⎨⎧≤≤=2341x x B ，求下列事件的表达式：(1)B A ；(2)B A ；(3)B A ；(4)B A . 解 (1) 1342AB x x B ⎧⎫=≤≤=⎨⎬⎩⎭; (2) 10122AB x x x B ⎧⎫=≤≤<≤⎨⎬⎩⎭或1131422x x x x ⎧⎫⎧⎫=≤≤<≤⎨⎬⎨⎬⎩⎭⎩⎭; (3) 因为B A ⊂，所以ΦAB =；(4)130242AB A x x x ⎧⎫=≤<<≤⎨⎬⎩⎭或=⎭⎬⎫⎩⎨⎧≤<≤<<≤223121410x x x x 或或 3. 用事件C B A ,,的运算关系式表示下列事件：(1) A 出现，C B ,都不出现（记为1E ）； (2) B A ,都出现，C 不出现（记为2E ）； (3) 所有三个事件都出现（记为3E ）； (4) 三个事件中至少有一个出现（记为4E ）； (5) 三个事件都不出现（记为5E ）； (6) 不多于一个事件出现（记为6E ）；(7) 不多于两个事件出现（记为7E ）； (8) 三个事件中至少有两个出现（记为8E ）。

2012-2013(1)概率统计(A)(定稿)(答案)

2012 — 2013 学年第一学期课程名称概率统计试卷类型 A 答案考试形式闭卷考试时间 100 分钟1. 21；2. npq 或)1(p np -；3. 43； 4. 9.37； 5. )69.40,31.39(. 二、选择题（共5 小题，每题3 分，共计15分） 1. D ； 2. C ； 3. B ； 4. D ； 5. A . 三、（本题10 分）解：设i A （i =1、2）表示“第i 次取得正品”，则i A 表示“第i 次取得次品” .（1）12211121()()()91045P A A P A A P A ==⨯=； …………4分（2）21212()()()P A P A A P A A =+211211()()()()P A A P A P A A P A =+281219109105=⨯+⨯=. …………6分四、（本题12 分）解：（1）由()1F +∞=，得lim ()1x x k e k -→+∞-==； …………4分（2）3113{13}(3)(1)(1)(1)P X F F e e e e ----<<=-=---=-； …………4分（3）由在()f x 的连续点处有()()F x f x '=，得00(),0x x f x e x -<⎧=⎨≥⎩，. …………4分五、（本题16 分）解：（1）1{1}(,)X Y P X Y f x y dxdy +≤+≤=⎰⎰1120164x x dx xdy -==⎰⎰； …………6分(2) 16(1),016,01()(,)=0,0,x X x x x xdy x f x f x y dy +∞-∞⎧-<<<<⎧⎪==⎨⎨⎩⎪⎩⎰⎰其他其他. …………4分 206,013,01()(,)=0,0,yY xdx y y y f x f x y dx +∞-∞⎧⎧<<<<⎪==⎨⎨⎩⎪⎩⎰⎰其他其他； …………4分 (3)因为(,)()()X Y f x y f x f y ≠，所以X 和Y 不是相互独立的. …………2分六、（本题12 分）解：（1）12()(,)12x E X xf x y dxdy dx xy dy +∞+∞-∞-∞==⎰⎰⎰⎰140445x dx ==⎰； …………6分（2）13()(,)12x E XY xyf x y dxdy dx xy dy +∞+∞-∞-∞==⎰⎰⎰⎰150132x dx ==⎰. …………6分七、（本题10 分）解：似然函数 11()(1)(1)()nnni i i i L x x θθθθθ===+=+∏∏，对数似然函数 1l n ()l n (1)l n nii L n x θθθ==++∑， …………4分令 1l n ()l n 01ni i d n L x d θθθ==+=+∑，得θ的最大似然估计值为 1ˆ1ln nii n x θ==--∑， …………4分 θ的最大似然估计量为 1ˆ1ln nii nXθ==--∑. …………2分八、（本题10分）解：检验假设222201:0.048:0.048H H σσ=≠ …………2分拒绝域为222102(1)(4)n s αχσ--≤或22202(1)(4)n s αχσ-≥， …………3分0.1α=，20.00778s =，5n =，0.950.0522(4)0.71,(4)9.49χχ==，观察值220.0522(1)40.0077813.51(4)9.490.048n s χσ-⨯=≈>=， …………3分故拒绝0H ，喷洒该种农药后小麦叶片宽度的方差不正常. …………2分。

概率统计习题12答案

概率统计习题12答案概率统计习题1、2答案习题12.设a,b,c都就是事件,先行通过对a,b,c,a,b,c中的一些事件的房俐并的运算式则表示以下事件:1)a,b,c中仅有a发生.2)a,b,c中至少有两个发生.3)a,b,c中至多两个发生.4)a,b,c 中恰有两个发生.5)a,b,c中至多有一个发生.答案1)abc;2)ab5)abc3.袋中存有四个球,其中存有两个红球,一个黄球和一个白球.存有送回地扣三次,谋发生以下情况的概率:a?“三次都是红的”,b?“三次颜色全同”,c?“三次颜色全不同”,d?“三次颜色不全同”,e?“三次中无红”,f?“三次中无红或无黄”.求解每次抽球都可以抽到4个球中的任一一个，存有4钟可能将，3次抽球共计43?64种可能将，因此样本空间所含64个样本点。

每次抽球都可以抽到2个红球中的任意一个，有2种可能，3次抽球都抽到t球共有23?8种可能，因此事件a含有8个样本点。

abcabcacbc;3)abc(或abc);4)abcabcabc;abc.3次抽球都抽到t球共计23?8种可能将，3次抽球都抽到黄球共计13?1种可能将，3次抽球都抽到白球共计13?1种可能将，因此事件b所含8?1?1?10个样本点。

3?3!?6种，对应于每一种排列，抽到的球有2?1?1?2种可能，3种颜色的排列有a3因此事件c含有6?2?12个样本点。

因为事件b所含10个样本点，故事件d?b所含64?10?54个样本点。

每次抽球都可以抽到黄球和白球中的任一个，有2种可能，3次抽球都抽不到t球共有23?8种可能，因此事件e含有8个样本点。

3次都扣没红球存有8种可能将，3次都扣没黄球存有33?27中可能将，3次都扣没红球和黄球存有13?1中可能将，因此事件f所含8?27?1?34个样本点。

1由上只须p(a)?8/64?1/8，p(b)?10/64?5/32，p(c)?12/64?3/16，p(d)?54/64?27/32，p(e)?8/64?1/8p(f)?34/64?17/32。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

莆田学院期末考试参考答案及评分标准
2012 — 2013 学年第一学期 (A)卷
课程名称：概率论与数理统计A 年级/专业： 11级计算机、计教、通信、电信试卷类别开卷（）闭卷（√）学历层次本科考试用时 120 分钟一、填空题（每空3分，共15分）
1、① 1/3
2、① 0.9544
3、① 21
4、① 1
5、①()()
/2/21,1X n X n αα⎛
⎫-- ⎪⎝⎭
二、单项选择题（每小题3分，共15分）
三、计算题（共70分） 1、（10分）设A 为事件“产品合格”，B 为事件“机器调整良好”。

已知()0.98P A B =,()
0.55P A B =,()0.95P B =,()
0.05P B =,
所需求的概率为()P B A . （4分）由贝叶斯公式：
()()()()()()()
P A B P B P B A P A B P B P A B P B
=
=
0.98*0.95
0.98*0.950.55*0.05
+=0.97
答：机器调整良好的概率是97%。

（6分）
2、（15分）解：(1) 由于B A x B x Ax x x f +=
+==⎰⎰⎰
+∞
∞-2
3
d d d )(13
221,
又因为3}X {22}X {1<<=<<P P ，则⎰⎰=3221d d x B x Ax ，即B A =2
3。

解得2
1
,31==B A 。

(8分)
(2) ⎪⎪⎪⎩
⎪⎪⎪⎨⎧≤<≤-<<-≤=⎪⎪⎪⎩⎪⎪⎪
⎨⎧
≤+<≤+<<≤==⎰⎰⎰⎰⎰⎰
∞
x x x x x x x t t t x t t t x t t x x x f x F x x x
3,13
2),1(2121),1(6
11,03,d 21
d 3
132,d 21d 3121,d 311,0d )()(221322121- (7分) 3、（15分）解：
(1)()11
2
001,166
f x y dxdy dx Cxy dy C C +∞+∞-∞-∞===⇒=⎰
⎰⎰⎰ （5分） (2)()()1
202,01
6,01,0,0,X x x xy dy x f x f x y dy +∞-∞⎧<<<<⎧⎪===⎨⎨
⎩⎪⎩
⎰⎰其他其他 ()()1
2206,013,01
,0,0,Y xy dx y y x f x f x y dx +∞-∞⎧⎧<<<<⎪===⎨⎨
⎩⎪⎩
⎰⎰其他其他（5分） (3)由(2)得()()(),X Y f x y f x f x =,(),x y -∞<<+∞-∞<<+∞
所以X Y 与相互独立. （5分） 4、（10分）解：
(1) 由已知得1)(=X E ，9)(=X D ,0)(=Y E ,16)(=Y D ，得3
1
)(21)(31)23(
)(=+=+=Y E X E Y X E Z E 。

()(
)()2(,)3232111
()()(,)943111
()()9431423
XY X Y X Y
D Z D D Cov D X D Y Cov X Y D X D Y ρ=++=++=++=+-= （5分） (2) )2
3,
(),(Y X X Cov Z X Cov += ),(21
),(31Y X Cov X X Cov +=
)()(2
1
)(31Y D X D X D XY ρ+=
033=-=
故0)
()()
,(==
Z D X D Z X Cov XZ ρ。

（5分）
5、（10分）解：由已知，θθσθθ22)1(2)1(210)(22-=-⨯+-⨯+⨯=X E ，
令X X E =)(，即X =-θ22，解得θ的矩估计量21ˆX -=θ。

（6分）
且注意到θθθ=-⨯-=-=)22(2
11)(211)ˆ(X E E ，故θˆ是θ的无偏估计量。

（4分）
6、（10分）0:190H μ≤ 1:190H μ> （2分）
2.5
x t =
== （5分） 0.05(15) 1.75 2.5t =<，所以拒绝0H ，说明平均工作温度比制造商所说的要高。

（3分）。