进制转换ppt
合集下载
进制转换ppt

2.非十进制数转换成十进制数
2)八进制数转换成十进制数 方法同二进制转换成十进制完全一样,仅仅 基数有所不同。
例:将(24.6)8转换成十进制 (24.6)8=(2×81+4×80+6×8-1)10 =(20.75)10
2.非十进制数转换成十进制数
3)十六进制数转换成十进制数 说明:十六进制数共有 16个不同的符号: 0、1、2、3 、 4 、 5 、 6 、 7 、 8 、 9 、 A 、 B 、 C 、 D 、 E 、 F ,其中 A 表 示 10 , B 表示 11 , C 表示 12 , D 表示 13 , E 表示 14 , F 表 示15,转换方法同前,仅仅基数为16。
1.2计算机中信息的表示
进位计数制的概念
计算机中常用的几种进制
不同进位制之间的转换 总结 布置作业
一、进位计数制的概念
1. 进位计数制 Introduction ☞
进位计数制也称数制,就是人们利用数字符号按进 位原则进行数据大小计算的方法。通常人们在日常生活 中是以十进制来表达数值并进行计算的。另外还有二进 3. Challengers Forwad 制、八进制和十六进制等。
说明:通常采用按位展开、按权相乘法
三、不同进位制数之间的转换
1、十进制转非十进制
二进制
八进制
十六进制
1、十进制转非十进制
方法: 整数部分除基取余
小数部分乘基取整
1、十进制转非十进制
1)十进制整数转换成二进制整数
说明:通常采用“除2取余法,商为零止,倒排列”
例:将(57)10转换成二进制数
1、十进制转非十进制
1、十进制转非十进制
说明:对一个既有整数又有小数部分的十进制数, 只要分别把整数部分和小数部分转换成二进制,然后 用小数点连接起来即可。 练习:将(215.25)10转换成二进制数
进位制之间的转换课件

数据的混淆和加密。
工程技术中的应用
01
02
03
电子工程
在电子工程中,进位制转 换用于数字电路设计和分 析,如逻辑电路、微处理 器等。
通信工程
通信工程中的信号处理和 编码解码过程常常涉及到 进位制转换,如调制解调 、信道编码等。
自动化系统
在自动化控制系统中,进 位制转换用于数字化传感 器的信号处理和控制系统 的数据传输。
二进制转八进制
从右往左每三位一组,不足三位补0,然后每组中的二进制数对应 一个八进制数。
二进制转十六进制
从右往左每四位一组,不足四位补0,然后每组中的二进制数对应 一个十六进制数。
八进制、十六进制转二进制
将每位八进制或十六进制数转换为对应的二进制数,然后按照顺序 拼接起来即可。
03
进位制转换方法
整数部分的转换方法
整体转换法
将混合数看作一个整体,使用整数部分转换方法进行转换, 注意小数点的位置,得到转换结果。
04
进位制转换实例解析
二进制与十进制转换实例
01
02
03
04
转换方法
将二进制数按权展开求和即可 得到相应的十进制数。
例子
二进制数 1011 转换为十进制 数。
• 计算
1×2³ + 0×2² + 1×2¹ + 1×2⁰ = 8 + 0 + 2 + 1 = 11
常见进位制类型
十进制(Decimal)
使用0-9这10个数字符号,基 数为10。
二进制(Binary)
使用0和1两个数字符号,基数 为2。
八进制(Octal)
使用0-7这8个数字符号,基数 为8。
最新总结进制数转换-二进制-八进制-十进制-十六进制--之间转换方法课件PPT

位(bit,比特):计算机内部最小的数据单位,即二进制的一位数 0或1.
字节(byte,拜特,用“B”表示): 1B=8bit ;(1B=1个英文字母=1个数字; 1个汉字=2B)
1KB=1024B; 1MB=1024KB; 1GB=1024MB; 1TB=1024GB.
计算机内部电路只有两种状态,内部数据只能采用二进制表 示,外部输入的其它进制数需通过编译器转化为二进制数.
制”
制”
关键点(技巧):因为2的4次方等于16,所以 4位二进制数等于1位十六进制数。
(101111) 2=(0010 1111) 2
前面补 0成4位
一组
=( 2
F ) 16
注意不能 写成15
( A F ) 16 =( 1010 1111) 2 =( 10101111) 2
返回
*八进制数与十六进制数间的转换
三.十进制→十六进制 (整数部分除16取余, 小数部分乘16取整)
四.十六进制→二进制 (每一位十六进制数表示 四位二进制数)
五.八进制→二进制 (每一位八进制数表示 三位二进制数)
返回
八进制数、十六进制数和十进制数的转换
这三者转换时:
➢可把二进制数作为媒介, ➢先把待转换的数转换成二进制数, ➢然后将二进制数转换成相应数制形式
A 20 B21 C 22 D 23 2、字符“a”的ASCII码值是1100001,转换成十
进制是( ),字符“c”的ASCII码值是是( )
二.八进制→十进制 (按位权乘8的N-1次方)
三.十六进制→十进制 (按位权乘16的N-1次方)
四.二进制→十六进制 (每四位二进制数表示 一位十六进制数)
五.二进制→八进制 (每三位二进制数表示 一位八进制数)
字节(byte,拜特,用“B”表示): 1B=8bit ;(1B=1个英文字母=1个数字; 1个汉字=2B)
1KB=1024B; 1MB=1024KB; 1GB=1024MB; 1TB=1024GB.
计算机内部电路只有两种状态,内部数据只能采用二进制表 示,外部输入的其它进制数需通过编译器转化为二进制数.
制”
制”
关键点(技巧):因为2的4次方等于16,所以 4位二进制数等于1位十六进制数。
(101111) 2=(0010 1111) 2
前面补 0成4位
一组
=( 2
F ) 16
注意不能 写成15
( A F ) 16 =( 1010 1111) 2 =( 10101111) 2
返回
*八进制数与十六进制数间的转换
三.十进制→十六进制 (整数部分除16取余, 小数部分乘16取整)
四.十六进制→二进制 (每一位十六进制数表示 四位二进制数)
五.八进制→二进制 (每一位八进制数表示 三位二进制数)
返回
八进制数、十六进制数和十进制数的转换
这三者转换时:
➢可把二进制数作为媒介, ➢先把待转换的数转换成二进制数, ➢然后将二进制数转换成相应数制形式
A 20 B21 C 22 D 23 2、字符“a”的ASCII码值是1100001,转换成十
进制是( ),字符“c”的ASCII码值是是( )
二.八进制→十进制 (按位权乘8的N-1次方)
三.十六进制→十进制 (按位权乘16的N-1次方)
四.二进制→十六进制 (每四位二进制数表示 一位十六进制数)
五.二进制→八进制 (每三位二进制数表示 一位八进制数)
课件二进制.ppt

10
1010
12
11
1011
13
12
1100
14
13
1101
15
14
1110
16
15
1111
17
9
A
B
C
D
E
F
4
➢各种进制之间的转换
二进制、八进制、十六进制转换成十进制
-方法:按权相加
(10101.11)2 =12(34510)823 122 021 120 12-1 12-2 =16 + 0 + 4 + 0 + 1 + 0.5 + 0.25
表示形式: ➢十进制小数形式:(必须有小数点) 如 0.123, .123, 123.0, 0.0, 123. ➢指数形式:(e或E之前必须有数字;指 数必须为整数)如12.3e3 ,123E2, 1.23e4, e-5, 1.2E-3.5
实型常量的类型 ➢默认double型 ➢在实型常量后加字母f或F,认为是float 型
64
-1.7e308 ~ 1.7e308
128
-1.2e4932 ~ 1.2e4932
8
-128 ~ 127
8
0 ~ 255
13
➢ VC6.0 基本数据类型
14
3.2 常量和变量
➢常量
定义:程序运行时其值不能改变的量(即常数)
分类:
➢符号常量:用标识符代表常量
定义格式: #define 符号常量 常量
第3章 数据类型、运算符与表达式
▪ 计算机中数的表示 ▪ C语言的基本数据类型 ▪ 常量和变量 ▪ 数据类型转换 ▪ 运算符与表达式
八、十六转换成十进制 PPT

拓展
• 二进制转十进制的方法:“按权展开求和 ”
• 例: (1011.01)2
拓展
• 二进制转十进制的方法:“按权展开求和 ”
• 例: (1011.01)2
带小数的十进制数按位权展开式例如:
123.4=1×102+2×101+3×100+4×10-1
拓展
• 二进制转十进制的方法:“按权展开求和 ”
• 方法:“按位权展开求和” • 例:(F5)16 • = 15×161+5×160 • = 240+5 • = 245
小试牛刀
• 1、将十六进制数A8H转换成十进制数。
课堂小结
数制 十进制 数码 0,1,2,3,4,5,6,7
,8,9
二进制
0,1
八进制 十六进制
0,1,2,3,4,5,6,7 0,1,2,3,4,5,6,7,8,9,A, B,C,D,E,F
二进制转十进制
• 方法:“按位权展开求和” • 例: (1011)2
= ( 1×23+0×22+1×21+1×20 )10 =(8+0+2+1)10 =(11)10
• 规律:个位上的数字的次数是0,十位上的 数字的次数是1,......,依次递增。
小试牛刀
• 1、将二进制数(110)2转换成十进制数。 • 2、将二进制数( 11011001 )2转换成十进
点击添加文本
添加文本
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
点击添加文本
点击添加文本
点击添加文本
十六进制数码: 0,1,2,3,4,5,6,7,8,9,
有趣的进制转换

有趣的进制转换
实验中学新校区 杨惠芳 2018-7-12
授课流程
进位计数制的概念
计算机中常用的几种进制
不同进位制之间的转换 中考链接 小结
讨论
除了十进制,你还能说出生活中的其他进制吗
六十进制 (1分钟为60秒) 十二进制 (12个月为1年)
一、进位计数制的概念
☞进位计数制
1. Introduction 人们使用有限个数码来表示数据,按进位的方法进 行记数,称为进位记数制,也称数制。 通常人们在日常生活中是以十进制来表达数值并进 行计算的。
1、十进制转非十进制
二进制
八进制
十六进制
1、十进制转非十进制
方法: 整数部分除基取余
小数部分乘基取整
1、十进制转非十进制
1)十进制整数转换成二进制整数
说明:通常采用“除2取余法,商为零止,倒排列”
例:将(57)10转换成二进制数
1、十进制转非十进制
2)十进制小数转换成二进制小数 说明:采用“乘以2顺向取整法”。即把给定 的十进制小数不断乘以2,取乘积的整数部分作为二 进制小数的最高位,然后把乘积小数部分再乘以 2, 取乘积的整数部分,得到二进制小数的第二位,如 此不断重复,得到二进制小数的其他位。 例:将(0.875)10转换成二进制小数: 0.875×2=1.75 整数部分=1 (高位) 0.75×2=1.5 整数部分=1 0.5×2=1 整数部分=1 (低位) 所以,(0.875)10=(0.111)2
2)十六进制数转换成二进制数 方法:由于十六进制的一位相当于二进制的四位 ,只需把每一个十六进制数字改写成等值的四位 二进制数,并保持高低位的次序不变即可。
例:将(4C.2E)16转换成二进制数: (4C.2E)16 =(0100 1100.0010 1110)2 =(1001100.0010111)2
十进制数转换二进制数课件
小数转换
将(0.125)10转换为二进制数 (0.125)10=( 0.001 )2
直到积中小数部分为0或达到 所要求的精度为止,再把各次整 数顺排。
乘2取整
0.125
×
2 ……取整0
0.250
0.25 ×2
0.50
……取整0 顺 序
× 0.25 1.0
……取整1
小结
十进制数转换为二进制数时,由于整数和小数的转 换方法不同,所以先将十进制数的整数部分和小数部分 分别转换后,小数点的位置不变,再加以合并。
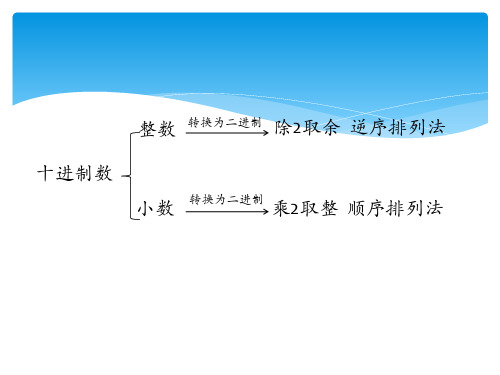
整数 转换为二进制 除2取余 逆序排列法
十进制数 小数 转换为二进制 乘2取整 顺序排列法
整数转换
将(57)10转换为二进制数 (57)10=( 111001 )2 除到商为0时为止,再把
各次余数倒排。
除2取余
2 57 ……余1
∟∟ 2 28 ……余0
2 14 ……余0
∟∟ 2 7 ……余1 ∟ 2 3 ……余1 ∟ 2 1 ……余1
谢谢,再见
计算机一级PPT03进制转换 [自动保存的]
![计算机一级PPT03进制转换 [自动保存的]](https://img.taocdn.com/s3/m/ea6fc32e78563c1ec5da50e2524de518964bd3a9.png)
结论:若R进制小数点向右移动n位,那么这个数扩 大为原来的Rn倍。
若R进制小数点向左移动n位,那么这个数缩 小为原来的Rn倍。(如何证明?)
进制转换练习
312D=________B=________O 10110110B=_________D 55D=_______O 59D=_______H 78H=_______D 34D=_______B 1537O=_______H 48AH=________O 256D=________B
个字节的存储空间。 它有三套编码方式,分别是:utf-8、utf-16、utf-32
练一练
2.6 进制的四则运算
方法:满R进一,借一当R
八进制加法:16+5= 23 二进制加法:1011+11=1110 二进制减法:1011-111=100
进制四则运算练习
十六进制:AC9H+1234H=_______H 七进制:1234+5412=_________。 八进制:453-257=_______。 二进制:101011+101101=_______。 六进制:452-353=_______。 八进制:574+666=______。
03信息编码
序 进制及其转换
信
息
有符号数的表示
表
信息编码
示
1 有符号数和无符号数
无符号数:直接转换成二进制进行表示。 例如:3表示为11, 5表示为101
有符号数:规定首位为符号位,用0表示正, 用1表示负,其余位为数值位。
例如:+3表示为0000 0011 -5表示为1000 0101
2 数的范围
2.1 R进制→十进制
• 方法:按位权展开,并逐项相加 • 例:101100B、56O、2BH转换为十进制 • 2BH= 2×161 + 11×160
若R进制小数点向左移动n位,那么这个数缩 小为原来的Rn倍。(如何证明?)
进制转换练习
312D=________B=________O 10110110B=_________D 55D=_______O 59D=_______H 78H=_______D 34D=_______B 1537O=_______H 48AH=________O 256D=________B
个字节的存储空间。 它有三套编码方式,分别是:utf-8、utf-16、utf-32
练一练
2.6 进制的四则运算
方法:满R进一,借一当R
八进制加法:16+5= 23 二进制加法:1011+11=1110 二进制减法:1011-111=100
进制四则运算练习
十六进制:AC9H+1234H=_______H 七进制:1234+5412=_________。 八进制:453-257=_______。 二进制:101011+101101=_______。 六进制:452-353=_______。 八进制:574+666=______。
03信息编码
序 进制及其转换
信
息
有符号数的表示
表
信息编码
示
1 有符号数和无符号数
无符号数:直接转换成二进制进行表示。 例如:3表示为11, 5表示为101
有符号数:规定首位为符号位,用0表示正, 用1表示负,其余位为数值位。
例如:+3表示为0000 0011 -5表示为1000 0101
2 数的范围
2.1 R进制→十进制
• 方法:按位权展开,并逐项相加 • 例:101100B、56O、2BH转换为十进制 • 2BH= 2×161 + 11×160
