2016中考数学试题和答案
中考2016数学试题及答案

中考2016数学试题及答案第一部分选择题1. 当x=3时,下列各式中必然成立的是()A. 2x + 1 = 8B. x - 5 = 2xC. 3x + 2 = 2x + 3D. 4x - 3 = 3 - x答案: B2. 下列各点坐标中,纵坐标是负数的点是()A. (3, 4)B. (-2, -5)C. (-1, 3)D. (0, 1)答案: B3. 如果a:b = 4:5, b:c = 3:2,那么a:c的值为()A. 12:10B. 20:27C. 8:15D. 16:9答案: C4. 在矩形ABCD中,AB = 3cm, BC = 4cm,如图所示。
若点A沿着矩形与圆心重合的圆弧BC移动,点A所走过的弧长为()(图略)A. 4π cmB. 6π cmC. 8π cmD. 12π cm答案: C5. 若图中所示的“AxB”表示包含x个正方形的正方形,那么当x=3时,共有的小正方形数量是()A. 64B. 63C. 57D. 56答案: C第二部分解答题1. 完整准确地用两个自然数的乘法结果表示小写字母“a”的值。
答案: "a"的值为ab或ba,其中a, b为两个自然数。
2. 设数a, b满足2a + b = 10,a - 2b = 1,求a和b的值。
答案: 将第一个等式的a用第二个等式表示出来,得到a = 2b + 1;将该式代入第一个等式,得到2(2b + 1) + b = 10,解得b = 2,代入第二个等式得到a = 5。
因此,a = 5,b = 2。
3. 在数轴上,点A表示数a, B表示数b,若a < b,则点A与B的位置关系是()A. A在B的左边B. A在B的右边C. A、B在同一点上D. 无法确定答案: A4. 如图,正方形ABCD的边长为6cm,点P, Q分别在AB, CD边上,且AP : PB = DQ : QC = 1:3,那么线段PQ的长度是多少?(图略)答案: 可以设AP的长度为x,因此PB的长度为6 - x。
2016年中考数学真题试题及答案(word版)
(2)共12种情况,有6种情况两次摸到相同颜色棋子,所以概率为 . 24. 解:(1)设第一批购进水果x千克,则第二批购进水果2.5千克,依
据题意得: ,解得x=200,经检验x=200是原方程的解,∴x+2.5x=700, 答:这两批水果功够进700千克; (2)设售价为每千克a元,则: , 630a≥7500×1.26,∴ ,∴a≥15,答:售价至少为每千克15元. 25. (1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD, ∠EAB=90°+∠EAD, ∴∠GAD=∠EAB,又∵AG=AE,AB=AD,∴△GAD≌△EAB, ∴EB=GD; (2)EB⊥GD,理由如下:连接BD,由(1)得:∠ADG=∠ABE,则 在△BDH中, ∠DHB=180°-(∠HDB+∠HBD)=180°-90°=90°,∴EB⊥GD; (3)设BD与AC交于点O,∵AB=AD=2在Rt△ABD中,DB= , ∴EB=GD= . 26. 解:(1)由y=0得,ax2-2ax-3a=0,∵a≠0,∴x2-2x-3=0,解得 x1=-1,x2=3, ∴点A的坐标(-1,0),点B的坐标(3,0); (2)由y=ax2-2ax-3a,令x=0,得y=-3a,∴C(0,-3a),又 ∵y=ax2-2ax-3a=a(x-1)2-4a,得D(1,-4a),∴DH=1,CH=-4a(-3a)=-a,∴-a=1,∴a=-1,∴C(0,3),D(1,4), 设直线CD的解析式为y=kx+b,把C、D两点的坐标代入得, ,解得 , ∴直线CD的解析式为y=x+3; (3)存在.由(2)得,E(-3,0),N(-
保密 ★ 启用前
2016年中考真题数学试卷
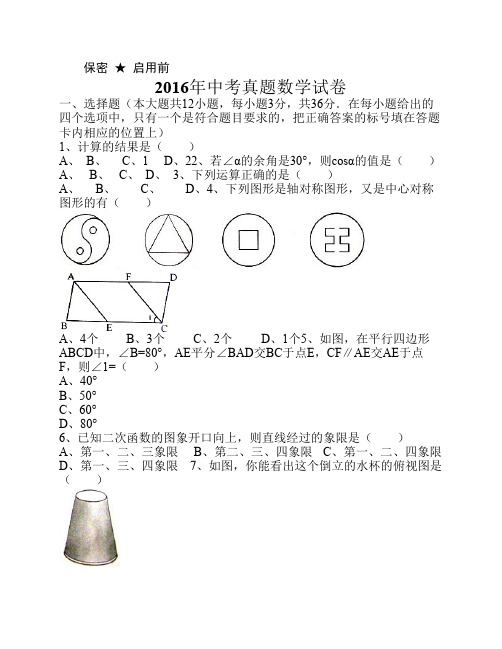
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的 四个选项中,只有一个是符合题目要求的,把正确答案的标号填在答题 卡内相应的位置上) 1、计算的结果是( ) A、 B、 C、1 D、22、若∠α的余角是30°,则cosα的值是( ) A、 B、 C、 D、 3、下列运算正确的是( ) A、 B、 C、 D、4、下列图形是轴对称图形,又是中心对称 图形的有( )
2016年河南省中考数学试卷-答案

、、、,画树状图如图:【解析】设四个小组分别记作A B C D36033332πn R25111111x x x x xx x x x ++=-=-+--.51x -≤<.(2)频数分布直方图如下图所示:所以ODE △,DEM △都是等边三角形,所以OD OE EM DM ===,所以四边形OEMD 是菱形。
tan379CD ︒≈2.2513.5=(米)(3)由函数图象知:①函数22||y x x -=的图象关于y 轴对称;②当1x >时,y 随x 的增大而增大.(4)①由函数图象知:函数图象与x 轴有3个交点,所以对应的方程22||0x x -=有3个实数根.②由函数图象知:因为22||y x x -=的图象与直线2y =有两个交点,所以22||2x x -=有2个实数根.③由函数图象知:因为关于x 的方程22||x x a -=有4个实数根,所以a 的取值范围是10a -<<.【提示】本题正确的识别图象是解题的关键。
(1)根据函数的对称性即可得到结论; (2)描点、连线即可得到函数的图象;(3)根据函数图象得到函数22||y x x -=的图象关于y 轴对称;当1x >时,y 随x 的增大而增大; (4)①根据函数图象与x 轴的交点个数,即可得到结论;②如图,根据22y x =-的图象与直线2y =的交点个数,即可得到结论;③根据函数的图象即可得到a 的取值范围是10a ﹣<< . 【考点】二次函数的图象,根的判别式22.【答案】(1)因为点A 为线段BC 外一动点,且BC a =,AB b =,所以当点A 位于CB 的延长线上时,线段AC 的长取得最大值,且最大值为BC AB a b +=+, (2)①CD BE =,理由:因为ABD △与ACE △是等边三角形,所以AD AB =,AC AE =,60BAD CAE ∠=∠=︒, 所以BAD BAC CAE BAC ∠+∠=∠+∠,即CAD EAB ∠=∠.在CAD △与EAB △中,AD ABCAD EAB AC AE =⎧⎪∠=∠⎨⎪=⎩,所以CAD EAB △≌△,所以CD BE =.②因为线段BE 长的最大值=线段CD 的最大值,由(1)知,当线段CD 的长取得最大值时,点D 在CB 的延长线上,所以最大值为4BD BC AB BC +=+=.(3)如下图1,连接BM ,将APM △绕着点P 顺时针旋转90°得到PBN △,连接AN ,33832。
2016年天津市中考数学试卷及解析答案

2016年天津市中考数学试卷及解析答案2016年天津市中考数学试卷一、选择题:共12小题,每小题3分,共36分1.计算 (-2)-5 的结果等于()。
A。
-7 B。
-3 C。
3 D。
72.sin60°的值等于()。
A。
√2/2 B。
√3/2 C。
1/2 D。
1/√23.下列图形中,可以看作是中心对称图形的是()。
A。
B。
C。
D。
4.2016年5月24日《XXX》报道,2015年天津外环线内新栽植树木xxxxxxx株,将xxxxxxx用科学记数法表示应为()。
A。
0.612×10^7 B。
6.12×10^6 C。
61.2×10^5 D。
612×10^45.如图是一个由4个相同的正方体组成的立体图形,它的主视图是()。
A。
B。
C。
D。
6.估计的值在()。
A。
2和3之间 B。
3和4之间 C。
4和5之间 D。
5和6之间7.计算。
的结果为()。
A。
1 B。
x C。
D。
8.方程 x^2+x-12=0 的两个根为()。
A。
x1=-2,x2=6 B。
x1=-6,x2=2 C。
x1=-3,x2=4 D。
x1=-4,x2=39.实数a,b在数轴上的对应点的位置如图所示,把 -a,-b,按照从小到大的顺序排列,正确的是()。
A。
-a << -b B。
<<-a<<-b C。
-b << -a D。
<<-b<<-a10.如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是()。
A。
∠DAB′=∠CAB′ B。
∠ACD=∠B′CD C。
AD=AE D。
AE=CE11.若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是()。
A。
y1<y3<y2 B。
y1<y2<y3 C。
2016中考数学试题及答案解析

2016中考数学试题及答案解析2016年中考数学已经结束,本文将对本次考试试题出现的知识点进行解析,帮助考生对数学考点更加清晰明确。
2016年中考数学试题及答案解析一、单项选择题1.斐波那契数列(第n项满足公式 Fn=Fn-1+Fn-2)中,第25项的值为(A. 1250B. 1280C. 1290D. 1300答案:D,解析:F1=1,F2=1,F3=2,那么F25=F24+F23=750+550=1300。
2.若复数z=(6-3i)*(2+i),z的共轭复数为(A. 8-3iB. 8+3iC. 6-iD. 6+i答案: B. 8+3i,解析:z的共轭复数即为z的根号共轭复数,即(6-3i)(2+i)的根号共轭复数为(6+3i)(2-i),得到结果8+3i。
3.下列函数中的值正确的连续12点的解析式是(A. y=x^2-3x+7B. y=3x^2+2x-1C. y=(x-2)^2-5x+7D. y=x^2+7答案: C,解析:根据函数y=(x-2)^2-5x+7,它的x取值为0,1,2,3,4,5,6,7,8,9,10,11,且y均为正数,因此其值正确。
二、解答题4.一家公司把罐装蜂蜜装入木箱,每个木箱里装有六个罐装蜂蜜,每罐蜂蜜重1.5Kg,请计算出20个木箱装蜂蜜重量是多少答案:20*6*1.5kg=180kg。
解析:每个木箱里装6个罐装蜂蜜,每个蜂蜜罐重1.5Kg,20个木箱装蜂蜜重量计算为:20*6*1.5kg=180kg。
5.若△ABC的面积为40,AB=4,BC=6,则BC角度数是(答案:60°. 解析:△ABC的面积为40,AB=4,BC=6,则AB:BC=2:3,可利用海伦公式求出其BC角α,即:α=arccos(2/3)=60°。
2016年山东省菏泽市中考数学试卷(含答案解析)

2016年山东省菏泽市中考数学试卷一、选择题(本大题共8个小题,每小题3分,共24分,在每小题给出的四个选项A、B、C、D中,只有一个选项是正确的,请把正确的选项涂在答题卡相应位置)1.(3分)下列各对数是互为倒数的是()A.4和﹣4 B.﹣3和C.﹣2和 D.0和02.(3分)以下微信图标不是轴对称图形的是()A.B.C.D.3.(3分)如图所示,该几何体的俯视图是()A.B.C.D.4.(3分)当1<a<2时,代数式|a﹣2|+|1﹣a|的值是()A.﹣1 B.1 C.3 D.﹣35.(3分)如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为()A.2 B.3 C.4 D.56.(3分)在▱ABCD中,AB=3,BC=4,当▱ABCD的面积最大时,下列结论正确的有()①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.A.①②③B.①②④C.②③④D.①③④7.(3分)如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为()A.25:9 B.5:3 C.:D.5:38.(3分)如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为()A.36 B.12 C.6 D.3二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内)9.(3分)2016年春节期间,在网络上用“百度”搜索引擎搜索“开放二孩”,能搜索到与之相关的结果个数约为45100000,这个数用科学记数法表示为.10.(3分)如图,将一副三角板和一张对边平行的纸条按如图方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是.11.(3分)某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是岁.12.(3分)已知m是关于x的方程x2﹣2x﹣3=0的一个根,则2m2﹣4m=.13.(3分)如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=.14.(3分)如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x 轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=.三、解答题(本题共78分,把解答和证明过程写在答题卡的相应区域内)15.(6分)计算:2﹣2﹣2cos60°+|﹣|+(π﹣3.14)0.16.(6分)已知4x=3y,求代数式(x﹣2y)2﹣(x﹣y)(x+y)﹣2y2的值.17.(6分)南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C 之间的距离.18.(6分)列方程或方程组解应用题:为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克,已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)19.(7分)如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.(1)求证:四边形DEFG是平行四边形;(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.20.(7分)如图,在平面直角坐标系xOy中,双曲线y=与直线y=﹣2x+2交于点A(﹣1,a).(1)求a,m的值;(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.21.(10分)如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.(1)求证:PC是⊙O的切线;(2)若PC=3,PF=1,求AB的长.22.(10分)锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是.(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是.(3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.23.(10分)如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°①求证:AD=BE;②求∠AEB的度数.(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=2CM+BN.24.(10分)在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.(1)试求抛物线的解析式;(2)记抛物线顶点为D,求△BCD的面积;(3)若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.2016年山东省菏泽市中考数学试卷参考答案与试题解析一、选择题(本大题共8个小题,每小题3分,共24分,在每小题给出的四个选项A、B、C、D中,只有一个选项是正确的,请把正确的选项涂在答题卡相应位置)1.(3分)下列各对数是互为倒数的是()A.4和﹣4 B.﹣3和C.﹣2和 D.0和0【分析】根据倒数的定义可知,乘积是1的两个数互为倒数,据此求解即可.【解答】解:A、4×(﹣4)≠1,选项错误;B、﹣3×≠1,选项错误;C、﹣2×(﹣)=1,选项正确;D、0×0≠1,选项错误.故选C.【点评】主要考查了倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.要求掌握并熟练运用.2.(3分)以下微信图标不是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的概念求解,看图形是不是关于直线对称.【解答】解:A、是轴对称图形;B、是轴对称图形;C、是轴对称图形;D、不是轴对称图形.故选D.【点评】本题主要考查了轴对称的概念,轴对称的关键是寻找对称轴,两边图象折叠后可重合.3.(3分)如图所示,该几何体的俯视图是()A.B.C.D.【分析】根据俯视图是从物体的上面看得到的视图进行解答即可.【解答】解:从上往下看,可以看到选项C所示的图形.故选:C.【点评】本题考查了三视图的知识,掌握俯视图是从物体的上面看得到的视图是解题的关键.4.(3分)当1<a<2时,代数式|a﹣2|+|1﹣a|的值是()A.﹣1 B.1 C.3 D.﹣3【分析】根据a的取值范围,先去绝对值符号,再计算求值.【解答】解:当1<a<2时,|a﹣2|+|1﹣a|=2﹣a+a﹣1=1.故选:B.【点评】此题考查的知识点是代数式求值及绝对值,关键是根据a的取值,先去绝对值符号.5.(3分)如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为()A.2 B.3 C.4 D.5【分析】直接利用平移中点的变化规律求解即可.【解答】解:由B点平移前后的纵坐标分别为1、2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2、3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A、B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2.故选:A.【点评】本题考查了坐标系中点、线段的平移规律,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.6.(3分)在▱ABCD中,AB=3,BC=4,当▱ABCD的面积最大时,下列结论正确的有()①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.A.①②③B.①②④C.②③④D.①③④【分析】当▱ABCD的面积最大时,四边形ABCD为矩形,得出∠A=∠B=∠C=∠D=90°,AC=BD,根据勾股定理求出AC,即可得出结论.【解答】解:根据题意得:当▱ABCD的面积最大时,四边形ABCD为矩形,∴∠A=∠B=∠C=∠D=90°,AC=BD,∴AC==5,①正确,②正确,④正确;③不正确;故选:B.【点评】本题考查了平行四边形的性质、矩形的性质以及勾股定理;得出▱ABCD的面积最大时,四边形ABCD为矩形是解决问题的关键.7.(3分)如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为()A.25:9 B.5:3 C.:D.5:3【分析】先根据等腰三角形的性质得到∠B=∠C,∠B′=∠C′,根据三角函数的定义得到AD=AB•sinB,A′D′=A′B′•sinB′,BC=2BD=2AB•cosB,B′C′=2B′D′=2A′B′•cosB′,然后根据三角形面积公式即可得到结论.【解答】解:过A 作AD⊥BC于D,过A′作A′D′⊥B′C′于D′,∵△ABC与△A′B′C′都是等腰三角形,∴∠B=∠C,∠B′=∠C′,BC=2BD,B′C′=2B′D′,∴AD=AB•sinB,A′D′=A′B′•sinB′,BC=2BD=2AB•cosB,B′C′=2B′D′=2A′B′•cosB′,∵∠B+∠B′=90°,∴sinB=cosB′,sinB′=cosB,∵S△BAC=AD•BC=AB•sinB•2AB•cosB=25sinB•cosB,S△A′B′C′=A′D′•B′C′=A′B′•cosB′•2A′B′•sinB′=9sinB′•cosB′,∴S△BAC :S△A′B′C′=25:9.故选A.【点评】本题考查了互余两角的关系,解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了等腰三角形的性质和三角形面积公式.8.(3分)如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为()A.36 B.12 C.6 D.3【分析】设△OAC和△BAD的直角边长分别为a、b,结合等腰直角三角形的性质及图象可得出点B的坐标,根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论.【解答】解:设△OAC和△BAD的直角边长分别为a、b,则点B的坐标为(a+b,a﹣b).∵点B在反比例函数y=的第一象限图象上,∴(a+b)×(a﹣b)=a2﹣b2=6.∴S△OAC ﹣S△BAD=a2﹣b2=(a2﹣b2)=×6=3.故选D.【点评】本题考查了反比例函数系数k的几何意义、等腰三角形的性质以及面积公式,解题的关键是找出a2﹣b2的值.本题属于基础题,难度不大,解决该题型题目时,设出等腰直角三角形的直角边,用其表示出反比例函数上点的坐标是关键.二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内)9.(3分)2016年春节期间,在网络上用“百度”搜索引擎搜索“开放二孩”,能搜索到与之相关的结果个数约为45100000,这个数用科学记数法表示为 4.51×107.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于45100000有8位,所以可以确定n=8﹣1=7.【解答】解:45100000这个数用科学记数法表示为4.51×107.故答案为:4.51×107.【点评】此题考查科学记数法表示较大的数的方法,准确确定a与n值是关键.10.(3分)如图,将一副三角板和一张对边平行的纸条按如图方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是15°.【分析】过A点作AB∥a,利用平行线的性质得AB∥b,所以∠1=∠2,∠3=∠4=30°,加上∠2+∠3=45°,易得∠1=15°.【解答】解:如图,过A点作AB∥a,∴∠1=∠2,∵a∥b,∴AB∥b,∴∠3=∠4=30°,而∠2+∠3=45°,∴∠2=15°,∴∠1=15°.故答案为15°.【点评】本题考查了平行线的性质:两直线平行,内错角相等.11.(3分)某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是15岁.【分析】根据中位数的定义找出第20和21个数的平均数,即可得出答案.【解答】解:∵该班有40名同学,∴这个班同学年龄的中位数是第20和21个数的平均数,∵15岁的有21人,∴这个班同学年龄的中位数是15岁;故答案为:15.【点评】此题考查了中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),熟练掌握中位数的定义是本题的关键.12.(3分)已知m是关于x的方程x2﹣2x﹣3=0的一个根,则2m2﹣4m= 6.【分析】根据m是关于x的方程x2﹣2x﹣3=0的一个根,通过变形可以得到2m2﹣4m值,本题得以解决.【解答】解:∵m是关于x的方程x2﹣2x﹣3=0的一个根,∴m2﹣2m﹣3=0,∴m2﹣2m=3,∴2m2﹣4m=6,故答案为:6.【点评】本题考查一元二次方程的解,解题的关键是明确题意,找出所求问题需要的条件.13.(3分)如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=.【分析】作EF⊥BC于F,如图,设DE=CE=a,根据等腰直角三角形的性质得CD=CE=a,∠DCE=45°,再利用正方形的性质得CB=CD=a,∠BCD=90°,接着判断△CEF为等腰直角三角形得到CF=EF=CE=a,然后在Rt△BEF中根据正切的定义求解.【解答】解:作EF⊥BC于F,如图,设DE=CE=a,∵△CDE为等腰直角三角形,∴CD=CE=a,∠DCE=45°,∵四边形ABCD为正方形,∴CB=CD=a,∠BCD=90°,∴∠ECF=45°,∴△CEF为等腰直角三角形,∴CF=EF=CE=a,在Rt△BEF中,tan∠EBF===,即tan∠EBC=.故答案为.【点评】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了等腰直角三角形的性质.14.(3分)如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x 轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=﹣1.【分析】将这段抛物线C1通过配方法求出顶点坐标及抛物线与x轴的交点,由旋转的性质可以知道C1与C2的顶点到x轴的距离相等,且OA1=A1A2,照此类推可以推导知道点P(11,m)为抛物线C6的顶点,从而得到结果.【解答】解:∵y=﹣x(x﹣2)(0≤x≤2),∴配方可得y=﹣(x﹣1)2+1(0≤x≤2),∴顶点坐标为(1,1),∴A1坐标为(2,0)∵C2由C1旋转得到,∴OA1=A1A2,即C2顶点坐标为(3,﹣1),A2(4,0);照此类推可得,C3顶点坐标为(5,1),A3(6,0);C4顶点坐标为(7,﹣1),A4(8,0);C5顶点坐标为(9,1),A5(10,0);C6顶点坐标为(11,﹣1),A6(12,0);∴m=﹣1.故答案为:﹣1.【点评】本题考查了二次函数的性质及旋转的性质,解题的关键是求出抛物线的顶点坐标.三、解答题(本题共78分,把解答和证明过程写在答题卡的相应区域内)15.(6分)计算:2﹣2﹣2cos60°+|﹣|+(π﹣3.14)0.【分析】原式利用负整数指数幂法则,特殊角的三角函数值,绝对值的代数意义,以及零指数幂法则计算即可得到结果.【解答】解:原式=﹣2×+2+1=+2.【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.16.(6分)已知4x=3y,求代数式(x﹣2y)2﹣(x﹣y)(x+y)﹣2y2的值.【分析】首先利用平方差公式和完全平方公式计算,进一步合并,最后代入求得答案即可.【解答】解:(x﹣2y)2﹣(x﹣y)(x+y)﹣2y2=x2﹣4xy+4y2﹣(x2﹣y2)﹣2y2=﹣4xy+3y2=﹣y(4x﹣3y).∵4x=3y,∴原式=0.【点评】此题考查整式的化简求值,注意先化简,再代入求得数值即可.17.(6分)南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C 之间的距离.【分析】作AD⊥BC,垂足为D,设CD=x,利用解直角三角形的知识,可得出AD,继而可得出BD,结合题意BC=CD+BD可得出方程,解出x的值后即可得出答案.【解答】解:如图,作AD⊥BC,垂足为D,由题意得,∠ACD=45°,∠ABD=30°.设CD=x,在Rt△ACD中,可得AD=x,在Rt△ABD中,可得BD=x,又∵BC=20(1+),CD+BD=BC,即x+x=20(1+),解得:x=20,∴AC=x=20(海里).答:A、C之间的距离为20海里.【点评】此题考查了解直角三角形的应用,解答本题的关键是根据题意构造直角三角形,将实际问题转化为数学模型进行求解,难度一般.18.(6分)列方程或方程组解应用题:为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克,已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)【分析】设A4薄型纸每页的质量为x克,则A4厚型纸每页的质量为(x+0.8)克,然后根据“双面打印,用纸将减少一半”列方程,然后解方程即可.【解答】解:设A4薄型纸每页的质量为x克,则A4厚型纸每页的质量为(x+0.8)克,根据题意,得:=2×,解得:x=3.2,经检验:x=3.2是原分式方程的解,且符合题意,答:A4薄型纸每页的质量为3.2克.【点评】本题主要考查分式方程的应用,根据题意准确找到相等关系并据此列出方程是解题的关键.19.(7分)如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.(1)求证:四边形DEFG是平行四边形;(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.【分析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC,DG∥BC且DG=BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;(2)先判断出∠BOC=90°,再利用直角三角形斜边的中线等于斜边的一半,求出EF即可.【解答】解:(1)∵D、G分别是AB、AC的中点,∴DG∥BC,DG=BC,∵E、F分别是OB、OC的中点,∴EF∥BC,EF=BC,∴DG=EF,DG∥EF,∴四边形DEFG是平行四边形;(2)∵∠OBC和∠OCB互余,∴∠OBC+∠OCB=90°,∴∠BOC=90°,∵M为EF的中点,OM=3,∴EF=2OM=6.由(1)有四边形DEFG是平行四边形,∴DG=EF=6.【点评】此题是平行四边形的判定与性质题,主要考查了平行四边形的判定和性质,三角形的中位线,直角三角形的性质,解本题的关键是判定四边形DEFG 是平行四边形.20.(7分)如图,在平面直角坐标系xOy中,双曲线y=与直线y=﹣2x+2交于点A(﹣1,a).(1)求a,m的值;(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.【分析】(1)将A坐标代入一次函数解析式中即可求得a的值,将A(﹣1,4)坐标代入反比例解析式中即可求得m的值;(2)解方程组,即可解答.【解答】解:(1)∵点A的坐标是(﹣1,a),在直线y=﹣2x+2上,∴a=﹣2×(﹣1)+2=4,∴点A的坐标是(﹣1,4),代入反比例函数y=,∴m=﹣4.(2)解方程组解得:或,∴该双曲线与直线y=﹣2x+2另一个交点B的坐标为(2,﹣2).【点评】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:反比例函数的图象上点的坐标特征,待定系数法确定函数解析式,熟练掌握待定系数法是解本题的关键.21.(10分)如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.(1)求证:PC是⊙O的切线;(2)若PC=3,PF=1,求AB的长.【分析】(1)连接OC,欲证明PC是⊙O的切线,只要证明PC⊥OC即可.(2)延长PO交圆于G点,由切割线定理求出PG即可解决问题.【解答】解:(1)如图,连接OC,∵PD⊥AB,∴∠ADE=90°,∵∠ECP=∠AED,又∵∠EAD=∠ACO,∴∠PCO=∠ECP+∠ACO=∠AED+∠EAD=90°,∴PC⊥OC,∴PC是⊙O切线.(2)解法一:延长PO交圆于G点,∵PF×PG=PC2,PC=3,PF=1,∴PG=9,∴FG=9﹣1=8,∴AB=FG=8.解法二:设⊙O的半径为x,则OC=x,OP=1+x∵PC=3,且OC⊥PC∴32+x2=(1+x)2解得x=4∴AB=2x=8【点评】本题考查切线的判定、切割线定理、等角的余角相等等知识,解题的关键是熟练运用这些知识解决问题,学会添加常用辅助线,属于中考常考题型.22.(10分)锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是.(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是.(3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.【分析】(1)锐锐两次“求助”都在第一道题中使用,第一道肯定能对,第二道对的概率为,即可得出结果;(2)由题意得出第一道题对的概率为,第二道题对的概率为,即可得出结果;(3)用树状图得出共有6种等可能的结果,锐锐顺利通关的只有1种情况,即可得出结果.【解答】解:(1)第一道肯定能对,第二道对的概率为,所以锐锐通关的概率为;故答案为:;(2)锐锐两次“求助”都在第二道题中使用,则第一道题对的概率为,第二道题对的概率为,所以锐锐能通关的概率为×=;故答案为:;(3)锐锐将每道题各用一次“求助”,分别用A,B表示剩下的第一道单选题的2个选项,a,b,c表示剩下的第二道单选题的3个选项,树状图如图所示:共有6种等可能的结果,锐锐顺利通关的只有1种情况,∴锐锐顺利通关的概率为:.【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.23.(10分)如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°①求证:AD=BE;②求∠AEB的度数.(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=2CM+BN.【分析】(1)①通过角的计算找出∠ACD=∠BCE,再结合△ACB和△DCE均为等腰三角形可得出“AC=BC,DC=EC”,利用全等三角形的判定(SAS)即可证出△ACD≌△BCE,由此即可得出结论AD=BE;②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC,再通过角的计算即可算出∠AEB的度数;(2)根据等腰三角形的性质结合顶角的度数,即可得出底角的度数,利用(1)的结论,通过解直角三角形即可求出线段AD、DE的长度,二者相加即可证出结论.【解答】(1)①证明:∵∠CAB=∠CBA=∠CDE=∠CED=50°,∴∠ACB=∠DCE=180°﹣2×50°=80°.∵∠ACB=∠ACD+∠DCB,∠DCE=∠DCB+∠BCE,∴∠ACD=∠BCE.∵△ACB和△DCE均为等腰三角形,∴AC=BC,DC=EC.在△ACD和△BCE中,有,∴△ACD≌△BCE(SAS),∴AD=BE.②解:∵△ACD≌△BCE,∴∠ADC=∠BEC.∵点A,D,E在同一直线上,且∠CDE=50°,∴∠ADC=180°﹣∠CDE=130°,∴∠BEC=130°.∵∠BEC=∠CED+∠AEB,且∠CED=50°,∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°.(2)证明:∵△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=120°,∴∠CDM=∠CEM=×(180°﹣120°)=30°.∵CM⊥DE,∴∠CMD=90°,DM=EM.在Rt△CMD中,∠CMD=90°,∠CDM=30°,∴DE=2DM=2×=2CM.∵∠BEC=∠ADC=180°﹣30°=150°,∠BEC=∠CEM+∠AEB,∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°,∴∠BEN=180°﹣120°=60°.在Rt△BNE中,∠BNE=90°,∠BEN=60°,∴BE==BN.∵AD=BE,AE=AD+DE,∴AE=BE+DE=BN+2CM.【点评】本题考查了等腰三角形的性质、全等三角形的判定及性质、解直角三角形以及角的计算,解题的关键是:(1)通过角的计算结合等腰三角形的性质证出△ACD≌△BCE;(2)找出线段AD、DE的长.本题属于中档题,难度不大,但稍显繁琐,解决该题型题目时,利用角的计算找出相等的角,再利用等腰三角形的性质找出相等的边或角,最后根据全等三角形的判定定理证出三角形全是关键.24.(10分)在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.(1)试求抛物线的解析式;(2)记抛物线顶点为D,求△BCD的面积;(3)若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.【分析】(1)根据待定系数法即可解决问题.(2)求出直线BC与对称轴的交点H,根据S△BDC =S△BDH+S△DHC即可解决问题.(3)由,当方程组只有一组解时求出b的值,当直线y=﹣x+b 经过点C时,求出b的值,当直线y=﹣x+b经过点B时,求出b的值,由此即可解决问题.【解答】解:(1)由题意解得,∴抛物线解析式为y=x2﹣x+2.(2)∵y=x2﹣x+2=(x﹣1)2+.∴顶点坐标(1,),∵直线BC为y=﹣x+4,∴对称轴与BC的交点H(1,3),∴S△BDC =S△BDH+S△DHC=•3+•1=3.(3)由消去y得到x2﹣x+4﹣2b=0,当△=0时,直线与抛物线相切,1﹣4(4﹣2b)=0,∴b=,当直线y=﹣x+b经过点C时,b=3,当直线y=﹣x+b经过点B时,b=5,∵直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,∴<b≤3.【点评】本题考查待定系数法确定二次函数解析式、二次函数性质等知识,解题的关键是求出对称轴与直线BC交点H坐标,学会利用判别式确定两个函数图象的交点问题,属于中考常考题型.。
2016年江西省中考数学试卷-答案

23=24 x x x故选C.OAB S S =【提示】由反比例函数的图象过第一象限可得出-+x x 3)(3)(x16.【答案】(1)补全条形统计图如图:补全条形统计图如图:+46(2)用样本中关心孩子“情感品质”方面的家长数占被调查人数的比例乘以总人数3600可得答案; (3)无确切答案,结合自身情况或条形统计图,言之有理即可. 【考点】条形统计图,用样本估计总体17.【答案】(1)如图(画法有两种,正确画出其中一种即可)(2)如图:(画出其中一种即可)【解析】(1)如图所示,45ABC ∠=︒.(AB 、AC 是小长方形的对角线)(2)线段AB 的垂直平分线如图所示【提示】(1)根据等腰直角三角形的性质即可解决问题;(2)根据正方形、长方形的性质对角线相等且互相平分,即可解决问题. 【考点】应用与设计作图 18.【答案】(1)证明:连接OC ,∵OAC ACO ∠=∠,PE OE ⊥,OC CD ⊥,∴APE PCD ∠=∠, ∵APE DPC ∠=∠,∴DPC PCD ∠=∠,∴DC DP =; (2)解:以A ,O ,C ,F 为顶点的四边形是菱形;∴四边形OACF为菱形.++-14)9(2)解法一:他们的“最终稿点数”如下表所示:5解法二:5OB︒≈⨯sin92即所作圆的半径约为3.13cm;AB︒≈⨯sin92【提示】(1)根据题意作辅助线OC AB ⊥于点C ,根据10OA OB cm ==,90OCB ∠=︒,18AOB ∠=︒,可以求得∠BOC 的度数,从而可以求得AB 的长;(2)由题意可知,作出的圆与(1)中所作圆的大小相等,则AE AB =,然后作出相应的辅助线,画出图形,从而可以求得BE 的长,本题得以解决. 【考点】解直角三角形的应用 22.【答案】(1)如图1,∵四边形ABCD 是正方形,由旋转知:'AD AD =,'90D D ∠=∠=︒,'60DAD OAP ∠=∠=︒,∴'DAP D AO ∠=∠,∴'()APD AOD ASA △≌△∴AP AO =,∵60OAP ∠=︒,∴△AOP 是等边三角形;(2)如图2,作AM DE ⊥于M ,作AN CB ⊥于N .∵五边形ABCDE 是正五边形,由旋转知:'AE AE =,'108E E ∠=∠=︒,'60EAE OAP ∠=∠=︒ ∴'EAP E AO ∠=∠∴'()APE AOE ASA △≌△∴'OAE PAE ∠=∠.在Rt △AEM 和Rt △ABN 中,72AEM ABN ∠=∠=︒,AE AB =∴Rt Rt ()AEM ABN AAS △≌△, ∴EAM BAN ∠=∠,AM AN =.在Rt △APM 和Rt △AON 中,AP AO =,AM AN =∴Rt Rt ()APM AON HL △≌△ ∴PAM OAN ∠=∠,∴PAE OAB ∠=∠,∴'OAE OAB ∠=∠(等量代换)故答案为:是.所以:存在Rt△A k B k B k+1与Rt△A m B m B m+1相似,其相似比为64:1或8:1.。
2016河南中考数学试题及答案

2016河南中考数学试题及答案一、选择题(共40题,每题2分)1. 【解析】选C。
已知矩形的长和宽比为5:3,设长为5x,宽为3x,根据题意得到以下等式:5x + 3x = 40,解得x = 4,则长为20,宽为12。
所以周长为2(20 + 12) = 64(单位:cm)。
2. 【解析】选A。
解方程x^2 - 9 = 0,得到x = ±3,所以x的值为3或-3,选项A符合题意。
3. 【解析】选B。
已知等腰直角三角形,那么两个直角边的长度一样,设为x,则斜边长为x√2,根据勾股定理得到以下等式:x^2 + x^2 = (x√2)^2,整理得到x = (2 - √2)x,即1 = (2 - √2),解得x = √2 - 1,所以选项B符合题意。
4. 【解析】选A。
已知a:b = 2:3,c:b = 3:5,将c的值代入第一个等式中,得到a:b:c = 2:3:9,所以选项A符合题意。
5. 【解析】选C。
根据题意,1个女生的译文是1个字,1个男生的译文是2个字,设男生人数为x,则女生人数为x + 4。
根据总字数等于总人数的2倍得到以下等式:1(x + 4) + 2x = 1300,解得x = 436,所以男生人数为436人,女生人数为440人,所以选项C符合题意。
...二、解答题6. 【解析】答案:分式为1/7。
题目描述:某商店原价为42元的商品打8折,之后的价格再降低20%。
求最终的价格是原价的几分之几?解答步骤:原价打折后的价格为42 * 0.8 = 33.6元;价格再降低20%后的价格为33.6 * 0.8 = 26.88元;最终价格与原价的比值为26.88 / 42 = 0.64,约为4/7,所以最终的价格是原价的4/7。
7. 【解析】答案:3时17分。
题目描述:某地有两个水库,甲水库每小时汇入1000立方米水,乙水库每小时排出800立方米水。
初始时,两个水库都是空的。
如果同时打开两个水库,经过多长时间两个水库的水位相等?解答步骤:甲水库每小时净汇入1000 - 800 = 200立方米水;设经过t小时后,两个水库的水位相等,则甲水库汇入水的总量为200t;乙水库排出的总水量为800t;由于两个水库最终的水位相等,所以200t = 800t,解得t = 1/3,即1小时20分钟,所以经过1小时20分钟后两个水库的水位相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年中考数学试题(考试时间:120分钟 满分:150分)说明:1.答卷前,考生务必将本人的姓名、考试证号、科目填涂在答题卡相应的位置上,同时在试卷的密封线内也务必将本人的准考证号、考试证号、姓名、学校填写好,在第2页的右下角填写好座位号.2.第Ⅰ卷上选择题答案必须填涂在答题卡上相应的答题栏内,在第Ⅰ卷上答题无效. 3.非选择题部分用钢笔或圆珠笔直接在第Ⅱ卷相应的位置上作答. 4.考试结束,试卷与答题卡一并上交.第Ⅰ卷(选择题 共24分)一、选择题(本大题共8题,每题3分,共24分.每题的四个选项中,只有一个选项是符合要求的.) 1.在平面直角坐标系中,点(12)P -,的位置在( )A .第一象限B .第二象限C .第三象限D .第四象限 2.估计68的立方根的大小在( )A .2与3之间B .3与4之间C .4与5之间D .5与6之间3.如图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是( )A .7个B .6个C .5个D .4个4.在平面直角坐标系中,将点A (1,2)的横坐标乘以1-,纵坐标不变,得到点A ',则点A 与A '的关系是( )A .关于x 轴对称B .关于y 轴对称C .关于原点对称D .将点A 向x 轴负方向平移一个单位得点A ' 5.如图,已知四边形ABCD 是平行四边形,下列结论中不正确的是( ) A .当AB BC =时,它是菱形 B .当AC BD ⊥时,它是菱形C .当90ABC ∠=时,它是矩形D .当AC BD =时,它是正方形 6.如图,已知四边形ABCD 中,R 、P 分别是BC 、CD 上的点,E 、F 分别是AP 、RP 的中点,当点P 在CD 上从C 向D 移动而点R 不动时,那么下列结论成立的是( ) A .线段EF 的长逐渐增大 B .线段EF 的长逐渐减小(第5题图)D CBA R P DC B AE F(第6题图)主视图左视图俯视图(第3题图)C .线段EF 的长不变D .线段EF 的长与点P 的位置有关7、函数1ky x-=的图象与直线y x =没有交点,那么k 的取值范围是( ) A .1k > B .1k < C .1k >- D .1k <-8.若关于x 的一元二次方程2250ax x +-=的两根中有且仅有一根在0与1之间(不含0和1),则a 的取值范围是( )A .3a <B .3a >C .3a <-D .3a >-第Ⅱ卷(非选择题 共126分)二.填空题(本大题共10题,每题3分,共30分.把答案填在题中的横线上.) 9.如果□+2=0,那么“□”内应填的实数是______________.10.2008年5月26日下午,奥运圣火扬州站的传递在一路“中国加油”声中胜利结束,全程11.8千米,11.8千米用科学记数法表示是___________米. 11.函数y =x 的取值范围是_______________.12.已知63x y xy +==-,,则22x y xy +=______________.13.我们扬州的旅游宣传口号是“诗画瘦西湖,人文古扬州.给你宁静,还你活力”.为了了解广大市民对这一旅游宣传口号的知晓率,应采用的合适的调查方式为___________.(选填“普查”或“抽样调查”)14.小红将考试时自勉的话“细心·规范·勤思”写在一个正方体的六个面上,其平面展开图如图所示,那么在该正方体中,和“细”相对的字是__________.15.一副三角板如图所示叠放在一起,则图中α∠的度数是_________. 16.如图,在菱形ABCD 中,DE ⊥AB ,垂足为E ,DE =6cm ,3sin 5A =,则菱形ABCD 的面积是__________2cm .17.如图△ABC 是等腰直角三角形,BC 是斜边,P 为△ABC 内一点,将△ABP 绕点A 逆时针旋转后与△ACP ´重合,如果AP =3,那么线段PP '的长等于____________.细 心 规 范 勤 思 (第14题图) (第15题图) 30 45 α (第16题图) D CB E A A P CB P ' (第17题图)18.按如图所示的程序计算,若开始输入的x 的值为48,我们发现第一次得到的结果为24,第2次得到的结果为12,……,请你探索第2009次得到的结果为___________.三、解答题(本大题共8题,共96分.解答应写出文字说明、证明过程或演算步骤) 19.(本题满分14分,每(1)题6分,每(2)题8分) (1)计算:220081(1)cos602-⎛⎫-- ⎪⎝⎭. (2)课堂上,李老师出了这样一道题:已知2008x =-22213111x x x x x -+-⎛⎫÷+ ⎪-+⎝⎭的值. 小明觉得直接代入计算太繁了,请你来帮他解决,并写出具体过程.20.(本题满分10分)星期天上午,茱萸湾动物园熊猫馆来了甲、乙两队游客,两队游客的年龄如下表所示: 甲队:乙队:(2)根据前面的统计分析,回答下列问题:①能代表甲队游客一般年龄的统计量是_____________________________; ②平均数能较好地反映乙队游客的年龄特征吗?为什么?(第18题图)如图,在△ABD 和ACE 中,AB =AD ,AC =AE ,∠BAD =∠CAE ,连接BC 、DE 相交于点F ,BC 与AD 相交于点G .(1)试判断线段BC 、DE 的数量关系,并说明理由; (2)如果∠ABC =∠CBD ,那么线段FD 是线段F G 和 FB 的比例中项吗?为什么?22.(本题满分12分)一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外都相同.(1)小明认为,搅均后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球是等可能的.你同意他的说法吗?为什么?(2)搅均后从中一把摸出两个球,请通过列表或画树状图求两个球都是白球的概率; (3)搅均后从中任意摸出一个球,要使摸出红球的概率为32,应如何添加红球? 23.(本题满分12分)某校师生积极为汶川地震灾区捐款,在得知灾区急需帐篷后,立即到当地的一家帐篷厂采购,帐篷有两种规格:可供3人居住的小帐篷,价格每顶160元;可供10人居住的大帐篷,价格每顶400元.学校花去捐款96000元,正好可供2300人临时居住. (1)求该校采购了多少顶3人小帐篷,多少顶10人大帐篷;(2)学校现计划租用甲、乙两种型号的卡车共20辆将这批帐篷紧急运往灾区,已知甲型卡车每辆可同时装运4顶小帐篷和11顶大帐篷,乙型卡车每辆可同时装运12顶小帐篷和7顶大帐篷.如何安排甲、乙两种卡车可一次性地将这批帐篷运往灾区?有哪几种方案? 24.(本题满分12分)如图,在以O 为圆心的两个同心圆中,AB 经过圆心O ,且与小圆相交于点A 、与大圆相交于点B .小圆的切线AC 与大圆相交于点D ,且CO 平分∠ACB . (1)试判断BC 所在直线与小圆的位置关系,并说明理由; (2)试判断线段AC 、AD 、BC 之间的数量关系,并说明理由;(3)若8cm 10cm AB BC ==,,求大圆与小圆围成的圆环的面积.(结果保留π)B DC A GE F红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来未来40天内,前20天每天的价格1y (元/件)与时间t (天)的函数关系式为1254y t =-(120t ≤≤且t 为整数),后20天每天的价格2y (元/件)与时间t (天)的函数关系式为21402y t =-+(2140t ≤≤且t 为整数).下面我们就来研究销售这种商品的有关问题: (1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m (件)与t (天)之间的关系式;(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a 元利润(4a <)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t (天)的增大而增大,求a 的取值范围. 26.(本题满分14分)已知:矩形ABCD 中,1AB =,点M 在对角线AC 上,直线l 过点M 且与AC 垂直,与AD 相交于点E .(1)如果直线l 与边BC 相交于点H (如图1),AM =31AC 且AD =a ,求AE 的长;(用含a 的代数式表示)(2)在(1)中,又直线l 把矩形分成的两部分面积比为2∶5,求a 的值;(3)若AM =41AC ,且直线l 经过点B (如图2),求AD 的长; (4)如果直线l 分别与边AD 、AB 相交于点E 、F ,AM =41AC .设AD 长为x ,△AEF 的面积为y ,求y 与x 的函数关系式,并指出x 的取值范围.(求x 的取值范围可不写过程)扬州市2008年初中毕业、升学统一考试数学试题参考答案及评分标准说明:若有本参考答案没有提及的解法,只要解答正确,请参照给分.ADCBE HM l图1 ADCBE M图2 l第I 卷(选择题 共24分)一、选择题(本大题共8题,每题3分,共24分)1.B 2.C 3.C 4.B 5.D 6.C 7.A 8.B第II 卷(非选择题 共126分)二、填空题:(每题3分,共30分)9.2-; 10.41.1810⨯; 11.3x -≥; 12.18-; 13.抽样调查14.范; 15.75; 16.60; 17. 18.8说明:第11题若答案是3x >-不给分;第172分. 三、解答题:(本大题共8题,共96分) 19.(1)解:原式11442=-+-12=. 说明:第一步中每对一个运算给1分,第二步2分.(2)解:原式2(1)13(1)(1)11x x x x x x x -+-⎛⎫=÷+ ⎪+--+⎝⎭12(1)11x x x x --=÷++ 1112(1)x x x x -+=+-12=. 20.解:(1)15 5.5 6 1.8 . (2)①平均数或中位数或众数;②平均数不能较好地反映乙队游客的年龄特征.因为乙队游客年龄中含有两个极端值,受两个极端值的影响,导致乙队游客年龄方差较大,平均数高于大部分成员的年龄.说明:第(1)题中平均数、中位数、众数各1分,方差2分,第(2)题中学生说理只要说出受“极端值影响”的大意即可给分. 21.解:(1)BC DE ,的数量关系是BC DE =. 理由如下:BAD CAE BAC DAE ∠=∠∴∠=∠,. 又AB AD AC AE ==,,ABC ADE ∴△≌△(SAS ). BC DE ∴=.(2)线段FD 是线段FG 和FB 的比例中项.理由如下:ABC ADE △≌△,ABC ADE ∴∠=∠. ABC CBD ADE CBD ∠=∠∴∠=∠,. 又BFD DFG ∠=∠, BFD DFG ∴△∽△.2BF DFFD FG FB DF GF∴=∴=,. 即线段FD 是线段FG 和FB 的比例中项.说明:若第(1)、(2)题中结论已证出,但在证明前未作判断的不扣分. 22.解:(1)不同意小明的说法. 因为摸出白球的概率是23,摸出红球的概率是13, 因此摸出白球和摸出红球不是等可能的.(2)树状图如图(列表略)P ∴(两个球都是白球)2163== (3)(法一)设应添加x 个红球,由题意得1233x x +=+ 解得3x =(经检验是原方程的解)答:应添加3个红球. (法二)添加后P (摸出红球)23=∴添加后P (摸出白球)21133=-= ∴添加后球的总个数1263=+=. ∴应添加633-=个红球. 23.解:(1)设该校采购了x 顶小帐篷,y 顶大帐篷.根据题意,得310230016040096000x y x y +=⎧⎨+=⎩,.解这个方程组,得100200x y =⎧⎨=⎩,.(2)设甲型卡车安排了a 辆,则乙型卡车安排了(20)a -辆.根据题意,得412(20)100117(20)200a a a a +-⎧⎨+-⎩≥,≥.白2红白1 白1红白2 白1白2 红解这个不等式组,得1517.5a ≤≤.车辆数a 为正整数,∴15a =或16或17. 205a ∴-=或4或3. 答:(1)该校采购了100顶小帐篷,200顶大帐篷.(2)安排方案有:①甲型卡车15辆,乙型卡车5辆;②甲型卡车16辆,乙型卡车4辆;③甲型卡车17辆,乙型卡车3辆. 24.解:(1)BC 所在直线与小圆相切,理由如下:过圆心O 作OE BC ⊥,垂足为E , AC 是小圆的切线,AB 经过圆心O ,OA AC ∴⊥,又CO 平分ACB OE BC ∠⊥,.OE OA ∴=.BC ∴所在直线是小圆的切线. (2)AC BD BC +=理由如下:连接OD .AC 切小圆O 于点A ,BC 切小圆O 于点E , CE CA ∴=.在Rt OAD △与Rt OEB △中,90OA OE OD OB OAD OEB ==∠=∠=,,,Rt Rt OAD OEB ∴△≌△(HL ) EB AD ∴=. BC CE EB =+,BC AC AD ∴=+.(3)90BAC ∠=,8106AB BC AC ==∴=,,.BC AC AD =+,4AD BC AC ∴=-=.圆环的面积2222πππ()S OD OA OD OA =-=- 又222OD OA AD -=, 224π16πcm S ∴==.说明:若第(1)、(2)题中结论已证出,但在证明前未作判断的不扣分. 25.解:(1)将194t m =⎧⎨=⎩,和390t m =⎧⎨=⎩,代入一次函数m kt b =+中,有94903k b k b =+⎧⎨=+⎩,.296k b =-⎧∴⎨=⎩,. 296m t ∴=-+. 经检验,其它点的坐标均适合以上解析式, 故所求函数解析式为296m t =-+.(2)设前20天日销售利润为1p 元,后20天日销售利润为2p 元. 由221111(296)514480(14)578422p t t t t t ⎛⎫=-++=-++=--+⎪⎝⎭,120t ≤≤,∴当14t =时,1p 有最大值578(元).由2221(296)20881920(44)162p t t t t t ⎛⎫=-+-+=-+=-- ⎪⎝⎭. 2140t ≤≤且对称轴为44t =,∴函数2p 在2140t ≤≤上随t 的增大而减小.∴当21t =时,2p 有最大值为2(2144)1652916513--=-=(元).578513>,故第14天时,销售利润最大,为578元.(3)2111(296)5(142)4809642p t t a t a t a ⎛⎫=-++-=-+++-⎪⎝⎭对称轴为(142)142122a t a -+==+⎛⎫⨯- ⎪⎝⎭.120t ≤≤,∴当14220a +≥即3a ≥时,1p 随t 的增大而增大.又4a <,34a ∴<≤.26.解:(1)在矩形ABCD 中,901D AB AD a ∠===,,,13AC AM AC ∴===90AME D MAE DAC ∠=∠=∠=∠,,Rt Rt AME ADC ∴△∽△,AE ACAM AD∴=. 222111133a AC AMa AE ADa a++∴===. (2)(法一)AD BC ∥,易得AME CMH △∽△,2HC MCAE AM∴==. 2222(1)2(1)22333a a a HC AE BH a a a a ++-∴==∴=-=,.∴梯形面积222112212336ABHEa a a S a a a⎛⎫+--=+= ⎪⎝⎭. 2222125767ABNE AHNE ABCD EHCD S a S S aS a -=∴=∴=,,. 227(21)12a a ∴-=,2a ∴=(负值舍去,经检验是原方程的解)(法二)由(1)得2221121333a a a AE DE a a a a++-=∴=-=,. AD BC ∥,易得AME CMH △∽△,2CH MCAE AM∴==. 22(1)23a HC AC a +∴==,222(1)233a a BH a a a +-∴=-=,25ABHENHCDS S =,2222122332221533a a a a a a a a+-+∴=+-+272a a ∴=∴=,.(负值舍去,经检验是原方程的解)(3)(法一)与(1)、(2)同理得2213(1)3344a HC a AE HC AE a AE a ++==∴==,,, 223(1)344a a BH a a a +-∴=-=.直线l 过点B .2304a BH a-∴==.230a a ∴-=∴=,(负值舍去,经检验是原方程的解)(法二)连接BD 交AC 于点O ,则12AO CO AC ==. 又14AM AC =,12AM MO AO ∴==. BE AO ⊥,AB BO AO ∴==.ABO ∴△是等边三角形,12AB BD AD =∴=∴=,,(4)(法一)在Rt ACD △中,1AD x CD ==,,AC ∴AM =由AME ADC △∽△有:AE ACAM AD=,214x AE x +∴=.90FAE AME ∠=∠=,90AFE FAM FAM MAE ∴∠+∠=∠+∠=.AFE MAE ∴∠=∠,又90FAE ADC ∠=∠=,Rt Rt AFE DAC ∴△∽△. 2AFE DAC S AE S DC ⎛⎫∴= ⎪⎝⎭△△2016中考数学试题和答案11 / 11 221142y x x x ⎛⎫+∴= ⎪⎝⎭,2224(1)123232x x x y x x +++∴== y ∴与x 的函数关系式是241232x x y x++=x (法二)在Rt ACD △中,1AD x CD AC AM ==∴==,, 由AME ADC △∽△,有214AE AC x AE AM AD x+=∴=,. 90FAE AME ∠=∠=,90AFE FAM FAM MAE ∴∠+∠=∠+∠=,AFE MAE ∴∠=∠,又90Rt Rt FAE ADC AFE DAC ∠=∠=∴,△∽△. AF AD x AE DC∴==,214x AF x AE +∴==, 2222241111(1)1222443232x x x x x y AE AF x x x+++++∴====. y ∴与x 的函数关系式是241232x x y x++=x 说明:写出3x ≥和x 各得1分.。
