北京市东城区2015届高三第二学期综合练习(一)数学文
北京市东城区2015届高三二模考试语文试题(含答案)

北京市东城区2014—2015学年度第二学期高三综合练习(二)语文本试卷共10页,共150分。
考试时长150分钟。
考生务必将答案写在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、本大题共10小题,共31分。
阅读下面的文字,按要求完成1-10题。
【材料一】中药命名的文化意蕴?厚朴?是一味中药。
中医药书称其因?本质朴而皮厚?得名。
但这看似简单的药名却实在不简单。
厚,是淳厚的厚;朴,是质朴的朴。
淳厚与质朴是中国人一向赞美的品德,巧妙地落在了一味药草上。
在数千种中草药中,有很多这样粗看自然质朴,细品却韵味十足的药名。
“百合”的意趣医圣张仲景的经典著作《金匮要略》中记录了这样一种病:患病者精神、饮食、行动皆异于常人,沉默少言,欲睡难眠,不思饮食,此为?百合病?。
中医认为这个病多由心神失养,或情致不调等引起。
治疗这个病常用?百合?为主药,以百合地黄汤为主方,在此基础上再根据病情及时调整。
那么,?百合?究竟是什么样子呢?说来没什么稀奇,罗大佑歌中的?野百合?和近年被阿宝唱响的?山丹丹?就是这味百合良药。
娇艳的百合花在山野蓬蒿.中亭亭玉立,其生于地下的鳞茎由近百块鳞瓣抱合而成,古人将其视为?百年好合?的吉兆,花也因此得名。
不过,治疗百合病的不是美丽的花朵,而是那抱合的鳞茎。
百合具有滋阴润肺、镇静安神之功效,在中医看来,精神、情绪上的问题,就要用?百合?去治。
因此,就有了百合病是?因以百合为主药才得名?的说法,百合也有了?因治百合病才叫百合?的另一种得名原因。
中草药中,像百合一样拥有美妙、独特的名字的还有很多。
比如《神农本草经》一书中将一种主治时疾寒热、内补不足的?玉竹?列为上品,但此草并非竹类,它还有个名字叫?葳蕤..?,有华美之意。
不过,?玉竹?之名更雅。
李时珍说?其叶光莹像竹,其根长而多节?,故名玉竹。
药名的诗情比起西药以化学分析为起点命名的科学和理性,中药本草的命名则大都感性。
有的药名本身就极富诗意,成为可以寄喻.情思的对象。
东城区2022-2023第二学期高三一模数学试题答案终稿

- 北京市东城区2022—2023学年度第二学期高三综合练习(一)数学参考答案及评分标准 2023.3一、选择题(共10小题,每小题4分,共40分) (1)B (2)A (3)D (4)B (5)C (6)B(7)A(8)D(9)B (10)C 二、填空题(共5小题,每小题5分,共25分)(11)(0,1] (12)2±(13)2214y x -= (答案不唯一) (14)111424n -(15 ② ③三、解答题(共6小题,共85分) (16)(共13分)解:(Ⅰ)因为()sin sin()3f x x x π=++=1sin sin 2x x x ++=3sin 2x x +6x π+()所以()f x 的最小正周期为2π ………………6分(Ⅱ)由题设,()()))66y f x f x x x ϕϕππ=-+=+++,由6x π=是该函数零点可知,sin()sin(+)06666ϕππππ+-+=,即sin()32ϕπ+=. 故+=+2,33k k ϕπππ∈Z 或+=+2,33k k ϕπ2ππ∈Z , 解得2,k k ϕ=π∈Z 或23k ϕπ=+π,k ∈Z . 因为0ϕ>,所以ϕ的最小值为3π. ………13分 (17)(共13分)解:(Ⅰ)从甲、乙两名同学共进行的13次测试中随机选取一次,有13种等可能的情形,其中有4次成绩超过90分.则从甲、乙两名同学共进行的13次测试中随机选取一次,该次成绩超过90分的概率为413. …3分(Ⅱ)随机变量X 的所有可能取值为1,2,3.133346C C 1(1)5C P X ===; 223346C C 3(2)5C P X ===; 313346C C 1(3).5C P X === 则随机变量X 的分布列为:X 1 2 3 P153515故随机变量X 的数学期望1311232555EX =⨯+⨯+⨯=. ………11分(Ⅲ)EX EY >. ………13分(18)(共15分)解:(Ⅰ)连接1AD ,11B D ,BD .因为长方体1111ABCD A B C D -中,1BB ∥1DD 且11BB DD =, 所以四边形11BB D D 为平行四边形. 所以E 为1BD 的中点,在△1ABD 中,因为E ,F 分别为1BD 和AB 的中点, 所以1EFAD .因为EF ⊄平面11ADD A ,1AD ⊂平面11ADD A , 所以EF平面11ADD A . ………………6分(II )选条件①:1CE B D ⊥.(ⅰ)连接1B C .因为长方体中12AA AD ==,所以122B C =在△1CBD 中,因为E 为1B D 的中点,1CE B D ⊥,xyz所以122CD B C ==如图建立空间直角坐标系D xyz -,因为长方体中12A A AD ==,22CD =,则(0,0,0)D ,(2,0,0)A ,(0,22,0)C ,(2,22,0)B ,2,0)F ,12,2)B ,2,1)E . 所以(1,2,1)CE =-,(2,2,0)CF =-,(2,0,0)CB =. 设平面CEF 的法向量为111(,,)x y z =m ,则0,0,CE CF ⎧⋅=⎪⎨⋅=⎪⎩m m 即1111120,220.x z x ⎧+=⎪⎨=⎪⎩ 令11x =,则12y =11z =,可得2,1)=m .设平面BCE 的法向量为222(,,)x y z =n , 则0,0,CE CB ⎧⋅=⎪⎨⋅=⎪⎩n n 即222220,20.x y z x ⎧+=⎪⎨=⎪⎩令21y =,则20x =,22z =,所以2)=n .设平面CEF 与平面BCE 的夹角为θ , 则||6cos |cos ,|.||||3θ⋅=<>==m n m n m n所以平面CEF 与平面BCE 的夹角的余弦值为63. (ⅱ)因为(0,2,0)AF =, 所以点A 到平面CEF 的距离为||1||AF d ⋅==m m . ………………15分选条件②:1B D 与平面11BCC B 所成角为4π. 连接1B C .因为长方体1111ABCD A B C D -中,CD ⊥平面11BCC B ,1B C ⊂平面11BCC B , 所以1CD B C ⊥.所以1DB C ∠为直线1B D 与平面11BCC B 所成角,即14DB C π∠=.所以△1DB C 为等腰直角三角形.因为长方体中12AA AD ==,所以1B C =所以1CD B C == 以下同选条件① .(19)(共15分)解:(Ⅰ)当0a =时,()ln f x x x =-,定义域为(0,)+∞.()ln 1f x x '=--,令()0f x '=,得1ex =, 当1(0,)e x ∈时,()0f x '>,当1(,+)ex ∈∞时,()0f x '<,所以()f x 的单调递增区间为1(0,)e. ………………5分(Ⅱ)令()()2ln 1h x f x ax x '==--,则121()2ax h x a x x-'=-=. 当e 2a ≥时,令()0h x '=,得12x a =. 当1(0,)2x a ∈时,()0h x '<,()h x 单调递减;当1(,)2x a∈+∞时,()0h x '>,()h x 单调递增;所以当12x a=时,()h x 最小值为()g a =1()ln(2)2h a a =.当e2a ≥时,ln(2)a 的最小值为1,所以()g a 的最小值为1. ………………11分(III )由(Ⅱ)知()f x '在11[,]42a a 上单调递减,在13[,]24a a上单调递增, 又313()ln 424f a a'=-,111()ln 424f a a '=--,所以13(ln(2),ln )24M a a =-,11(ln(2),ln )24N a a=--,111331(ln )(ln )ln ln 1ln 310242444a a a a----=--=->, 所以M ⫋N . ………………15分(20)(共14分)解:(Ⅰ)由题设,得2221,.b ca abc =⎧⎪⎪=⎨⎪⎪=+⎩解得a 所以椭圆E 的方程为2213x y +=. ………………5分(Ⅱ)直线BC的方程为1(y k x -=.由221( 33y k x x y ⎧-=+⎪⎨+=⎪⎩得2222(31)6)90k x k x k +++++=.由22226)4(31)(9)0k k k ∆=+-⨯+⨯+>,得0k <.设1122(,),(,)B x y C x y,则12x x +=,12x x =.直线AB 的方程为1111y y x x -=+.令0y =,得点M的横坐标为111M x x y =-=-.同理可得点N的横坐标为221N x x y =-=-.1M N x x k +=-+1k =-1k =-1k =-=-.因为点D坐标为(,则点D 为线段MN 的中点,所以12MD MN=. ………………14分 (21)(共15分)解:(Ⅰ)满足条件的数表22A 为141424233231⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,,所以1112a a +的值分别为5,5,6. …………5分(Ⅰ)若当11121n a a a +++取最大值时,存在1j n ≤≤,使得22j a n =.由数表2n A 具有性质P 可得j 为奇数, 不妨设此时数表为1112122222n n n aa a A n a a ⎛⎫= ⎪⎝⎭. ①若存在1(1)k a k k n ≤≤为偶数,,使得111k a a >,交换1k a 和2n 的位置,所得到的新数表也具有性质P , 调整后数表第一行和大于原数表第一行和,与题设矛盾,所以存在1i n ≤≤,使得12i a n =.②若对任意的1(1)k a k k n ≤≤为偶数,,都有111k a a <,交换12a 和11a 的位置,所得到的新数表也具有性质P ,此时转化为①的情况.综上可知,存在正整数(1)k k n ≤≤,使得12k a n =. ………………10分 (Ⅲ)当n 为偶数时,令2n k =,对任意具有性质P 数表11121221222n n n a a a A a a a ⎛⎫= ⎪⎝⎭, 一方面,122214241,22,2()()()(41)(43)(21)k k a a a a a a k k k -+-++--+-+++≤,因此212141,222242,2()()3k k a a a a a a k +++++++≤.①另一方面,211(1351)i i a a i n -=-,,,,≥, 因此11131,2121232,21()()k k a a a a a a k --++++++-≤. ② 记111121,2221222,2,n n S a a a S a a a =+++=+++.由①+②得2123S S k k +-≤.又21282S S k k +=+,可得21112k kS +≤.构造数表2143415427433231312142638413n k kk k k k k k k k k A k k k k k k k ++-+-+-+-+⎛⎫=⎪++++-⎝⎭可知数表2n A 具有性质P ,且2211111228k k n nS ++==. 综上可知,当n 为偶数时,11121n a a a +++的最大值为21128n n+. ………………15分。
北京市朝阳区2015届高三第二次综合练习数学【理】试题(含答案)
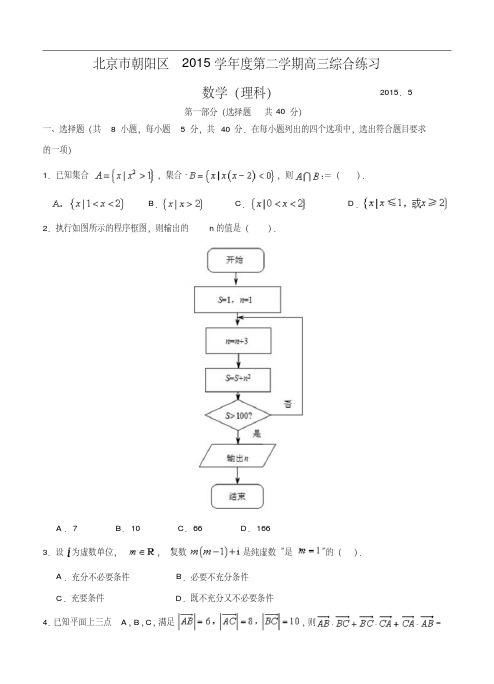
北京市朝阳区2015学年度第二学期高三综合练习数学(理科)2015.5第一部分(选择题共40 分)一、选择题(共8 小题,每小题 5 分,共40 分.在每小题列出的四个选项中,选出符合题目要求的一项)1.已知集合,集合,则=().B.C.D.2.执行如图所示的程序框图,则输出的n的值是().A.7 B.10 C.66 D.1663.设为虚数单位,,“复数是纯虚数”是“”的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件4.已知平面上三点A,B,C,满足,则=().A.48 B.-48 C.100 D.-1005.已知函数,若对任意的实数x,总有,则的最小值是().A.2 B.4 C.D.26.已知双曲线与抛物线有一个公共的焦点F,且两曲线的一个交点为P.若,则双曲线的渐近线方程为().7.已知函数,若对任意,都有成立,则实数m的取值范围是().8.如图,将一张边长为1的正方形纸ABCD折叠,使得点B始终落在边AD上,则折起部分面积的最小值为().第Ⅱ卷(非选择题共110 分)二、填空题:本小题共 6 小题,每小题 5 分,共30 分.9.展开式中含项的系数是__________.10.已知圆C的圆心在直线x-y=0上,且圆C与两条直线x+y=0和x+y-12=0都相切,则圆C 的标准方程是__________.11.如图,已知圆B的半径为5,直线AMN与直线ADC为圆B的两条割线,且割线AMN过圆心B.若AM=2,,则AD=__________.12.某四棱锥的三视图如图所示,则该四棱锥的侧面积为__________.13.已知点在函数的图像上,则数列的通项公式为__________;设O为坐标原点,点,则,中,面积的最大值是__________.14.设集合,集合A中所有元素的个数为__________;集合 A 中满足条件“”的元素个数为__________.三、解答题:本大题共 6 小题,共80 分.解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题共13分)在梯形ABCD中,(Ⅰ)求AC的长;(Ⅱ)求梯形ABCD的高.16.(本小题共13分)某学科测试中要求考生从A,B,C三道题中任选一题作答,考试结束后,统计数据显示共有600名学生参加测试,选择A,B,C三题答卷数如下表:(Ⅰ)某教师为了解参加测试的学生答卷情况,现用分层抽样的方法从600份答案中抽出若干份答卷,其中从选择A题作答的答卷中抽出了3份,则应分别从选择B,C题作答的答卷中各抽出多少份?(Ⅱ)若在(Ⅰ)问中被抽出的答卷中,A,B,C三题答卷得优的份数都是2,从被抽出的A,B,C三题答卷中再各抽出1份,求这3份答卷中恰有1份得优的概率;(Ⅲ)测试后的统计数据显示,B题的答卷得优的有100份,若以频率作为概率,在(Ⅰ)问中被抽出的选择B题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望EX.17.(本小题共14分)如图,在直角梯形ABCD中,.直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面平面ABCD.(Ⅰ)求证:;(Ⅱ)求直线BD和平面BCE所成角的正弦值;(Ⅲ)设H为BD的中点,M,N分别为线段FD,AD上的点(都不与点D重合).若直线平面MNH,求MH的长.18.(本小题共13分)已知点M为椭圆的右顶点,点A,B是椭圆C上不同的两点(均异于点M),且满足直线MA与直线MB斜率之积为14.(Ⅰ)求椭圆C的离心率及焦点坐标;(Ⅱ)试判断直线AB是否过定点:若是,求出定点坐标;若否,说明理由.19.(本小题共14分)已知函数.(Ⅰ)当时,求函数的单调区间;(Ⅱ)若在区间(1,2)上存在不相等的实数成立,求的取值范围;(Ⅲ)若函数有两个不同的极值点,,求证:.。
2022-2023学年北京市东城区高三下学期综合练习(一)数学试卷(PDF版)

北京市东城区2022-2023学年度第二学期高三综合练习(一)数 学 2023.3本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合22{|}0A x x -=<,且a A ∈,则a 可以为(A )2- (B )1-(C )32(D (2)在复平面内,复数iz对应的点的坐标是(3,1)-,则z = (A )13i + (B )3i + (C )3i -+ (D )13i -- (3)抛物线24x y =的准线方程为(A )1x = (B )1x =- (C )1y = (D )1y =- (4)已知0x >,则44x x-+的最小值为 (A )2- (B )0(C )1 (D )(5)在△ABC 中,a =2b c =,1cos 4A =-,则ABC S =△(A )(B )4(C ) (D )(6)设,m n 是两条不同的直线,αβ,是两个不同的平面,且m α⊂,αβ ,则“m n ⊥”是“n β⊥”的(A )充分而不必要条件 (B )必要而不充分条件(C )充分必要条件 (D )既不充分也不必要条件 (7)过坐标原点作曲线2e1x y -=+的切线,则切线方程为(A )y x = (B )2y x = (C )21e y x = (D )e y x =(8)已知正方形ABCD 的边长为 2,P 为正方形ABCD 内部(不含边界)的动点,且满足0PA PB ⋅=,则CP D P ⋅的取值范围是(A )(0,8] (B )[0,8) (C )(0,4] (D )[0,4)(9)已知1a ,2a ,3a ,4a ,5a 成等比数列,且1和4为其中的两项,则5a 的最小值为(A )64- (B )8- (C )164 (D )18(10)恩格斯曾经把对数的发明、解析几何的创始和微积分的建立称为十七世纪数学的三大成就.其中对数的发明,曾被十八世纪法国大数学家拉普拉斯评价为“用缩短计算时间延长了天文学家的寿命”.已知正整数N 的70次方是一个83位数,由下面表格中部分对数的近似值(精确到0.001),可得N 的值为(A )13 (B )14 (C )15 (D )16第二部分(非选择题 共110分)二、填空题 共5小题,每小题5分,共25分。
2015年高考模拟试题三模试题_北京市东城区2015年高考第三次模拟考试数学文科试题
2.下列函数在其定义域内为偶函数的是 (A) y 3
x
(B) y sin 2 x
2
(C) y
x
(D) y cos 2 x
3.命题“ x0 N , x0 x0 2 ”的否定是 (A) x0 N , x0 x0 2
2
(B) x0 N , x0 x0 2
2 2
ABC 面积的最大值是
(A) 2 (B) 4 (C) 3 (D) 2 3
9.某物流公司运费计算框图如图所示,其中 d 为按运送里程给运费打的折扣,n 为运送 物品的件数.现有顾客办理 A、B 两件物品递送,其中 A 物品运送单价为 p1=0.02 元/ 千克•千米,重量为 w1=5 千克,运送里程为 s1=250 千米;B 物品运送单价为 p2=0.03 元/ 千克•千米,重量为 w2=6 千克,运送里程为 s2=500 千米.则按运费计算框图算出该顾客 应付运费 sum= (A) 94.5 元 (C) 103.5 元 (B) 97 元 (D) 106 元
[30,35) 内的概率。
19. 如 图 , 在 四 棱 锥 P ABCD 中 , 底 面 ABCD 是 正 方 形 , 平 面 PAD 平 面 ABCD ,
2
(C) x0 N , x0 x0 2
2
(D) x0 N , x0 x0 2
2
4.设 a log 0.6 0.5, b log 2 (log 3 8) ,则 (A) a 1 b (B) a b 1 (C) b 1 a (D) 1 b a
2
则椭圆 C 的长轴长的最小值为
·2·
15. 某学科考试共有 100 道单项选择题,有甲、乙两种计分法。若某学生有道题答对,道题答错,道 题未作答,则甲计分法的得分为 X a 科考试,现有如下结论: ①同一学生的 X 分数不可能大于 Y 分数; ②任意两个学生 X 分数之差的绝对值不可能大于 Y 分数之 差的绝对值;③用 X 分数将全班排名次的结果与用 Y 分数将全班排次的结果是完全相同的;④ X 分 数与 Y 分数是正相关的。 其中正确的有 (写出所有正确的结论的序号) 三、解答题 16.已知向量 m (cos x,sin(
北京市东城区届高三月综合练习理科数学试题二含答案

北京市东城区2015-2016学年度第二学期高三综合练习(二)数学参考答案及评分标准 (理科)第Ⅰ卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分)1.B2.C3.A4.D5.A6.C7.A8.D第Ⅱ卷(共110分)二、填空题(本大题共6小题,每小题5分,共30分) 9. 122a -<< 10. 5 11. 52 12. 0.4;13. 13. 31,22⎛⎤+ ⎥⎝⎦14. ①②④ 三、解答题(本大题共6小题,共80分)15.(本小题共13分)解:(Ⅰ)因为()3sin cos 12sin()+16f x x x x πωωω=++=+, 又()f x 的最小正周期为π,所以π2πω=,即ω=2. --------------------------------------------------------------------6分(Ⅱ)由(Ⅰ)可知()2sin(2)+16f x x π=+, 因为02x π≤≤, 所以72666x πππ≤+≤. 由正弦函数的性质可知,当262x ππ+=,即6x π=时,函数()f x 取得最大值,最大值为f (6π)=3; 当7266x ππ+=时,即2=x π时,函数()f x 取得最小值,最小值为f (2π)=0. ------13分16.(本小题共14分)证明:(Ⅰ)因为ABC ∆是等腰直角三角形90CAB ∠=o ,E F ,分别为AC BC ,的中点, GD F EC 'CB A所以EF AE ⊥,EF C E '⊥.又因为AE C E E '⋂=,所以EF AEC '⊥平面.由于EF AB P ,所以有AB AEC '⊥平面. -------------------------4分 解:(Ⅱ)(i)取AC '中点D ,连接,,,DE EF FG GD ,由于GD 为ABC '∆中位线,以及EF 为ABC ∆中位线,所以四边形DEFG 为平行四边形.直线GF 与AC '所成角就是DE 与AC '所成角.所以四棱锥C ABFE '-体积取最大值时,C E '垂直于底面ABFE .此时AEC '∆为等腰直角三角形,ED 为中线,所以直线ED AC '⊥.又因为ED GF P ,所以直线GF 与AC '所成角为π2. -------------------------------------------------------10分 (ii) 因为四棱锥C ABFE '-体积取最大值,分别以EA EF EC '、、所在直线为x 轴、y 轴、z 轴,建立空间直角坐标系如图,则(0,0,)C a ',(,2,0)B a a ,(0,,0)F a ,(,2,)C B a a a '-,(0,,)C F a a '-.设平面C B F '的一个法向量为n =(x,y,z),由0,0C B C F ⎧⎪⎨⎪⎩'⋅='⋅=n n uuu r uuu r 得⎩⎨⎧=-=-+002az ay az ay ax , 取y =1,得x =-1,z =1.由此得到n =(-1,1,1). zy x F E C 'CB A同理,可求得平面C AE '的一个法向量m =(0,1,0). 所以 13cos 33⋅==n m .故平面C'AE 与平面C'BF 的平面角的夹角的余弦值为33.--------------------------------------14分17.(本小题共13分)解:(Ⅰ)根据投篮统计数据,在10场比赛中,甲球员投篮命中率超过0.5的场次有5场, 分别是4,5,6,7,10,所以在随机选择的一场比赛中,甲球员的投篮命中率超过0.5的概率是12. 在10场比赛中,乙球员投篮命中率超过0.5的场次有4场,分别是3,6,8,10, 所以在随机选择的一场比赛中,甲球员的投篮命中率超过0.5的概率是25. ---------------------------------------3分(Ⅱ)设在一场比赛中,甲、乙两名运动员恰有一人命中率超过0.5为事件A ,甲队员命中率超过0.5且乙队员命中率不超过0.5为事件1B ,乙队员命中率超过0.5且甲队员命中率不超过0.5为事件2B .则1213121()()()25252P A P B P B =+=⨯+⨯=.------------------------------------------------7分 (Ⅲ)X 的可能取值为0,1,2,3.00332327(0)()()55125P X C ===; 11232354(1)()()55125P X C ===; 22132336(2)()()55125P X C ===; 33328(3)()5125P X C ===; X 的分布列如下表: X0 1 2 3 P27125 54125 36125 812526355EX np ==⨯=. --------------------------------------------------------13分 18.(本小题共14分)解:(Ⅰ)222(31)()2(1)(2)22x x f x x x x x -++'=-+=>-++ , 当()0f x '>时,所以 2310x x ++<.解得 3522x -+-<<. 当()0f x '>时, 解得 352x -+>. 所以 ()f x 单调增区间为35(2,)2-+-,单调减区间为35(,)2-++∞.------------4分 (Ⅱ) 设2()()()2ln(2)(1)(1)(1)h x f x g x x x k x x =-=+-+-+>-, 当2k =时,由题意,当(1,)x ∈-+∞时,()0h x <恒成立.22(31)2(3)(1)()222x x x x h x x x -++-++'=-=++, 当1x >-时,()0h x '<恒成立,()h x 单调递减. 又(1)0h -=,当(1,)x ∈-+∞时,()(1)0h x h <-=恒成立,即()()0f x g x -<. 对于1x ∀>-,()()f x g x <恒成立. ---------------------------------8分(Ⅲ) 因为 222(31)2(6)22()22x x x k x k h x k x x -++++++'=-=-++.由(II)知,当k = 2时,f (x) < g (x)恒成立, 即对于x > –1,2 ln (x + 2) – (x + 1)2 < 2 (x + 1),不存在满足条件的x 0;当k > 2时,对于x > –1,x + 1 > 0,此时2 (x + 1) < k (x + 1).2 ln (x + 2) – (x + 1)2 < 2 (x + 1) < k (x + 1),即f (x) < g (x)恒成立, 不存在满足条件的x 0;当k < 2时,令t (x) = –2x 2 – (k + 6)x – (2k + 2),可知t (x)与h (x)符号相同,当x (x 0 , +)时,t (x) < 0,h (x) < 0,h (x)单调递减.当x (–1 , x 0)时,h (x) > h (–1) = 0,即f (x) – g (x) > 0恒成立.综上,k 的取值范围为(–, 2). -------------------------------------------------------14分 19.(本小题共13分)解:(Ⅰ)由题意,以椭圆短轴的两个端点和一个焦点为顶点的三角形是等腰直角三角形,所以 b c =, 222b a =, 则椭圆C 的方程为122222=+b y b x . 又因为椭圆C:过点A(2,1),所以112222=+bb ,故a=2,b=.2 所以 椭圆的的标准方程为12422=+y x . --------------------------------------------------------4分 (Ⅱ)222)(y p x MP +-=. 因为 M(x,y)是椭圆C 上的动点,所以12422=+y x , 故 22)41(2222x x y -=-=. 所以 222222211()222(2) 2.222x MP x p x px p x p p =-+-=-++=--+ 因为M(x,y)是椭圆C 上的动点,所以 2≤x .(1) 若22≤p 即1≤p ,则当2x p =时MP 取最小值22p -,此时M 2(2,22)p p ±-.(2)若1p >,则当2x =时,MP 取最小值2-p ,此时M )0,2(.(3)若1p <-,则当2x =-时,MP 取最小值2+p ,此时M )0,2(-. -------13分20.(本小题共13分)(Ⅰ)由212(1)n n n n d a a a n ++=+-≥以及n n d a =可得: 2120(1)n n a a n ++-=≥所以从第二项起为等比数列. 经过验证{}n a 为等比数列12n n a -=. -------------------2分(Ⅱ)由于1n d ≥所以有2121n n n a a a +++-≥.令1n n n c a a +=-则有11n n c c +-≥叠加得:4n c n ≥-所以有14n n a a n +-≥-,叠加可得:29102n n n a -+≥,所以最小值为-5. --------------------------------------------------------6分(Ⅲ)由于1n d =,11a =, 21a =若11d =可得32a =,若11d =-可得30a =同理,若21d =可得44a =或42a =,若21d =-可得40a =或42a =-具体如下表所示7452321111010325⎧⎧⎧⎪⎨⎪⎪⎩⎪⎨⎪⎧⎪⎪⎨⎪⎪⎩⎪⎩⎨⎧⎧⎪⎨⎪⎪-⎪⎩⎪⎨⎪-⎧⎪-⎪⎨⎪-⎩⎪⎩⎩所以{}n a 可以为112211221122L L或110011001100L L此时相应的{}n d 为 11111111----L L或11111111----L L------------------------------------------------------13分。
2023.5北京东城区 高三二模数学 答案
北京市东城区2022—2023学年度第二学期高三综合练习(二)数学参考答案及评分标准2023.5一、选择题(共10小题,每小题4分,共40分)(1)A (2)C (3)B (4)A (5)D (6)C(7)B(8)C(9)C(10)A二、填空题(共5小题,每小题5分,共25分)(11)12(12)π12(13)0m =(答案不唯一)(14)717(15)①③④三、解答题(共6小题,共85分)(16)(共13分)解:(Ⅰ)由正弦定理得sin sin b A a B =,由题设得sin cos02Ba B a -=,2sincos cos 0222B B Ba a -=,因为022B π<<,所以cos 0.2Ba ≠所以1sin22B =.26B π=,3B π=.………………6分(Ⅱ)选条件①:sin sin 2sin .A CB +=因为3,3b B π==,sin sin 2sin .A C B +=由正弦定理得26a c b +==,由余弦定理得2229()3a c ac a c ac =+-=+-,解得9ac =.所以1sin 24ABC S ac B ==△.由9,6,ac a c =⎧⎨+=⎩解得3a =.………13分选条件②:c =已知,3,3,3B b c π===由正弦定理得1sin sin 2c C B b ==,因为c b <,所以6C π=,2A π=.223.a b c =+=所以13322ABC S bc ==△.(17)(共14分)解:(I )由题设知.AB AC ⊥因为平面ABC ⊥平面ABD ,平面ABC 平面ABD AB =,,所以AC ⊥平面ABD .因为BE ⊂平面ABD ,所以AC ⊥BE .因为ABD △为等边三角形,E 是AD 的中点,所以AD ⊥BE .因为AC AD A =,所以BE ⊥平面ACD .所以BE CD ⊥.………………6分(II )设AEADλ=,[0,1]λ∈.取AB 的中点O ,BC 的中点F ,连接OD ,OF ,则OD ⊥AB ,OF AC .由(I )知AC ⊥平面ABD ,所以OF ⊥平面ABD ,所以OF ⊥AB ,OF ⊥OD .如图建立空间直角坐标系O xyz -,则(1,0,0)A -,(1,0,0)B ,(1,2,0)C -,3)D .所以(2,0,0)BA =- ,3)AD = ,(2,2,0)BC =- ,(1,3)CD =-,(3)BE BA AE BA AD λλλ=+=+=-.设平面BCE 的法向量为(,,)x y z =n ,则0,0,BC BE ⎧⋅=⎪⎨⋅=⎪⎩ n n 即220,(2)30.x y x z λλ-+=⎧⎪⎨-+=⎪⎩令3x λ=,则3y λ=,2z λ=-.于是(33,2)λλλ=-n .因为直线CD 和平面BCE所成角的正弦值为10,所以||10|cos ,|10||||CD CD CD ⋅<>==n n n ,整理得2826110λλ-+=,解得12λ=或114λ=.因为[0,1]λ∈,所以12λ=,即12AE AD =.………………14分(18)(共13分)解:(Ⅰ)根据表中数据,可知这7名学生中有4名学生的第二次考试成绩高于第一次考试成绩,分别是学生1,学生2,学生4,学生5,则从数学学习小组7名学生中随机选取1名,该名学生第二次考试成绩高于第一次考试成绩的概率为4.7………3分(Ⅱ)(i)随机变量X 可能的取值为0,1,2.这7名学生第二次考试成绩与第一次考试成绩的差分别为1,1,3-,3,1,4-,5-.2793(0)7C P X ===;2762(1)7C P X ===;2762(2)7C P X ===.则随机变量X 的分布列为:X 012P372727X 的数学期望32260127777EX =⨯+⨯+⨯=.………11分(ii)DX DY <.………13分(19)(共15分)解:(Ⅰ)因为抛物线22(0)y px p =>过点(1,2),所以24p =,即2p =.故抛物线C 的方程为24y x =,焦点(1,0)F ,准线方程为1x =-.所以112 1.2OFM S =⨯⨯=△………………6分(Ⅱ)设直线l 的方程为(0)y kx m k =+≠.由24, y x y kx m⎧=⎪⎨=+⎪⎩得222(24)0k x km x m +-+=.由0∆>有10km ->.设1111(,),(,),A x yB x y 则12242km x x k -+=,2122m x x k =.设AB 的中点为00(,)N x y ,则120222x x kmx k+-==.N 到准线的距离20221k km d x k -+=+=,12AB x =-==依题意有2ABd =,222k km k -+=,整理得2220k km m ++=,解得0k m +=,满足0∆>.所以直线(0)y kx m k =+≠过定点(1,0).………………15分(20)(共15分)解:(Ⅰ)()e (sin cos )2x f x x x '=+-,(0)1f '=-,(0)0f =.所以曲线()y f x =在点(0,(0))f 处的切线方程为y x =-.………………5分(Ⅱ)令()()e (sin cos )2x g x f x x x '==+-,则()2e cos x g x x '=,当[1,1]x ∈-时,()0g x '>,()g x 在[1,1]-上单调递增.因为(0)10g =-<,(1)e(sin1cos1)20g =+->,所以0(0,1)x ∃∈,使得0()0g x =.所以当0(1,)x x ∈-时,()0f x '<,()f x 单调递减;当0(,1)x x ∈时,()0f x '>,()f x 单调递增.()1esin12e 21f =-<-<,()sin1121ef -=->,所以()()max sin112ef x f =-=-.………………11分(Ⅲ)满足条件的a 的最大整数值为2-.理由如下:不等式()e xf x x a +>恒成立等价于sin ex xa x <-恒成立.令()sin e xx x x ϕ=-,当0x ≤时,0e xx-≥,所以()1x ϕ>-恒成立.当0x >时,令()e x x h x =-,()0h x <,1()e x x h x -'=,()h x '与()h x 的情况如下:x (0,1)1(1,)+∞()h x '-0+()h x 1e-所以min 1()(1).eh x h ==-当x 趋近正无穷大时,()0h x <,且()h x 无限趋近于0,所以()h x 的值域为1[,0)e-.因为sin [1,1]x ∈-,所以()x ϕ的最小值小于1-且大于2-.所以a 的最大整数值为2-.………………15分(21)(共15分)解:(Ⅰ)由题设知(5){478}A =,,,(5)=3s .………………4分(Ⅱ)依题意()1(12)i s a i n ≥=,,, ,则有11.()i s a ≤因此12111.()()()n n s a s a s a +++≤ 又因为12111()()()n n s a s a s a +++=,所以() 1.i s a =所以12,,,n a a a 互不相同.………………9分(Ⅲ)依题意12,.a a ab ==由()i i j A a +∈或()j i j A a +∈,知i j i a a +=或i j j a a +=.令1j =,可得1i i a a +=或11i a a +=,对于2,3,...1i n =-成立,故32a a =或31a a =.①当a b =时,34n a a a a ==== ,所以12n a a a na +++= .②当a b ≠时,3a a =或3a b =.当3a a =时,由43a a =或41a a =,有4a a =,.同理56n a a a a ==== ,所以12(1)n a a a n a b +++=-+ .当3a b =时,此时有23a a b ==,令13i j ==,,可得4()A a ∈或4()A b ∈,即4a a =或4a b =.令14i j ==,,可得5()A a ∈或5()A b ∈.令23i j ==,,可得5()A b ∈.所以5a b =.若4a a =,则令14i j ==,,可得5a a =,与5a b =矛盾.所以有4a b =.不妨设23(5)k a a a b k ====≥ ,令1(2,3,,1)i t j k t t k ==+-=-, ,可得1()k A b +∈,因此1k a b +=.令1,i j k ==,则1k a a +=或1k a b +=.故1k a b +=.所以12(1)n a a a n b a +++=-+ .综上,a b =时,12n a a a na +++= .3a a b =≠时,12(1)n a a a n a b +++=-+ .3a b a =≠时,12(1)n a a a n b a +++=-+ .………………15分。
北京市2015届高三综合能力测试(二)数学(理)试题含答案
A.充分不必要条件 C.充要条件
6、已知数列 an 满足 a1 1 ,且 an an 1 2n ,则数列 an 的前 20 项的和为( A. 3 211 3 B. 3 211 1 C. 3 210 2
7、已知向量 a , b 是夹角为 60 的单位向量.当实数 1 时,向量 a 与向量 a b 的夹角范围是( ) A. B. 0 , 60 60 ,120
3 210 3
-1-
C. 120 ,180
D. 60 ,180
8、某几何体的三视图如图所示,该几何体的各面中互相垂直的面的对数是 ( A. 2 D. 8 二、填空题(本大题共 6 小题,每小题 5 分,共 30 分. ) 9、双曲线 C : x 2
5
若直线 y x b 与 f x 在 x 1 处相切,求实数 a , b 的值;
-3-
若 a 0 ,求证: f x 存在唯一极小值.
2 19、 (本小题满分 14 分)已知椭圆 C1 过点 2 ,1 ,且其右顶点与椭圆 C2 : 2 2 x 2 y 4 的右焦点重合.
求证:平面 1AC 底面 AC ; 求 1C 与平面 A1A1 所成角的正弦值; 若 , F 分别是线段 A1C1 , C1C 的中点,问在线段 1F 上是否存在点 ,使
得 // 平面 A1A1 .
18、 (本小题满分 13 分)已知函数 f x x a ln x .
7 ,求边 C 的长.
-2-
16、 (本小题满分 13 分)在某地区的足球比赛中,记甲、乙、丙、丁为同一小组 的四支队伍,比赛采用单循环制(每两个队比赛一场) ,并规定小组积分前两名 的队出线,其中胜一场积 3 分,平一场积 1 分,负一场积 0 分.由于某些特殊原 因,在经过三场比赛后,目前的积分状况如下:甲队积 7 分,乙队积 1 分,丙和丁 1 队各积 0 分.根据以往的比赛情况统计,乙队胜或平丙队的概率均为 ,乙队 4 1 胜、平、负丁队的概率均为 ,且四个队之间比赛结果相互独立. 3 求在整个小组赛中,乙队最后积 4 分的概率;
北京市2015届高三模拟考试数学(文)专题08圆锥曲线(无答案)
圆锥曲线1.【北京市西城区2014年高三二模试卷】直线2y x =为双曲线2222 1(0,0)x y C a b a b -=>>:的一条渐近线,则双曲线C 的离心率是( )(A B )2(C D )23.【丰台区2014年高三年级第二学期统一练习(二)】已知A 1,A 2双曲线2222:1x y C a b -=(0,0)a b >>的顶点,B 为双曲线C 的虚轴一个端点.若△A 1BA 2是等边三角形,则双曲线C 的离心率e 等于 .4.【北京市东城区2013—2014学年度第二学期高三综合练习(一)】若双曲线2214x y m -=的,则m=(A (B )3 (C (D )5. 【北京市顺义区2014届高三4月第二次统练(二模)】已知点A 在抛物线24y x =上,且点A 到直线10x y --=A 的个数为 ( )A .1B . 2C . 3D . 46.【北京市东城区2013—2014学年度第二学期高三综合练习(一)】设抛物线的顶点在原点,准线方程为x=2,则抛物线的方程为 .7. 【北京市顺义区2014届高三4月第二次统练(二模)】双曲线2214y x -=的渐近线方程为____________.8. 【北京市海淀区2014届高三下学期期末练习(二模)】若抛物线22y px =(0)p >的准线经过双曲线221x y -=的左顶点,则p =_____.9.【北京市昌平区2014届高三4月第二次统练(二模)】 已知双曲线22221,(0,0)x y a b a b-=>>的焦距为10,一条渐近线的斜率为34,则此双曲线的标准方程为______,焦点到渐近线的距离为_____ .10. 【北京市东城区2014届高三下学期综合练习(二)】在棱长为1的正方体1111ABCD A BC D -中,点P 是正方体棱上一点(不包括棱的端点),1PA PC m +=, ①若2m =,则满足条件的点P 的个数为________; ②若满足1PA PC m +=的点P 的个数为6,则m 的取值范围是________.11.【北京市西城区2014年高三二模试卷】设抛物线24C y x =:的焦点为F ,M 为抛物线C 上一点,且点M 的横坐标为2,则||MF = .12. 【北京市顺义区2014届高三4月第二次统练(二模)】(本小题共14分)已知椭圆E 的两个焦点分别为(1,0)-和(1,0),离心率2e =. (Ⅰ)求椭圆E 的方程;(Ⅱ)若直线:l y kx m =+(0k ≠)与椭圆E 交于不同的两点A 、B ,且线段AB 的垂直平分线过定点1(,0)2P ,求实数k 的取值范围.13. 【北京市朝阳区高三年级第二次综合练习】(本小题满分14分)已知椭圆C 的中心在原点O ,焦点在x 轴上,离心率为12,右焦点到右顶点的距离为1. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)若直线:l 10mx y ++=与椭圆C 交于,A B 两点,是否存在实数m ,使O A O B O A O B +=-成立?若存在,求m 的值;若不存在,请说明理由.14. 【北京市海淀区2014届高三下学期期末练习(二模)】(本小题满分14分)已知椭圆G 短轴端点分别为(0,1),(0,1)A B -. (Ⅰ)求椭圆G 的标准方程;(Ⅱ)若C ,D 是椭圆G 上关于y 轴对称的两个不同点,直线BC 与x 轴交于点M ,判断以线段MD 为直径的圆是否过点A ,并说明理由.15. 【北京市东城区2014届高三下学期综合练习(二)】(本小题共13分)已知椭圆22221x y a b +=的一个焦点为(2,0)F (Ⅰ)求椭圆方程;(Ⅱ)过点(3,0)M 且斜率为k 的直线与椭圆交于B A ,两点,点A 关于x 轴的对称点为C ,求△MBC 面积的最大值.16.【北京市西城区2014年高三二模试卷】(本小题满分14分)设12,F F 分别为椭圆22: 12x W y +=的左、右焦点,斜率为k 的直线l 经过右焦点2F ,且与椭圆W 相交于,A B 两点.(Ⅰ)求1ABF ∆的周长;(Ⅱ)如果1ABF ∆为直角三角形,求直线l 的斜率k .17.【北京市昌平区2014届高三4月第二次统练(二模)】 (本小题满分14分) 已知椭圆2222:1(0)x y C a b a b+=>>的焦点为12(1,0),(1,0)F F -,点P 是椭圆C 上的一点,1PF 与y 轴的交点Q 恰为1PF 的中点,34OQ =. (Ⅰ)求椭圆C 的方程; (Ⅱ)若点A 为椭圆的右顶点,过焦点1F 的直线与椭圆C 交于不同的两点,M N ,求AMN ∆面积的取值范围.。
北京市2015届高三模拟考试数学(文)专题03导数(无答案)
导数1. 【北京市朝阳区高三年级第二次综合练习】(本小题满分13分) 已知函数e ()xa f x x⋅=(a ∈R ,0a ≠). (Ⅰ)当1a =时,求曲线()y f x =在点()1,(1)f 处切线的方程;(Ⅱ)求函数()f x 的单调区间;(Ⅲ)当()0,x ∈+∞时,()f x 1≥恒成立,求a 的取值范围.2. 【北京市顺义区2014届高三4月第二次统练(二模)】(本小题共13分) 已知函数321()23f x x x ax b =-++的图象在点(3,(3))P f 处的切线方程为 35y x =-.(Ⅰ)求实数,a b 的值; (Ⅱ)设()()2m g x f x x =+-. ①若()g x 是[3,)+∞上的增函数,求实数m 的最大值;②是否存在点Q ,使得过点Q 的直线若能与曲线()y g x =围成两个封闭图形,则这两个封闭图形的面积总相等. 若存在,求出点Q 坐标;若不存在,说明理由.4. 【北京市东城区2014届高三下学期综合练习(二)】(本小题共13分)已知a ∈R ,函数3211()(2)62f x x a x b =+-+,()2lng x a x =. (Ⅰ)若曲线()y f x =与曲线()y g x =在它们的交点(1,)c 处的切线互相垂直,求a ,b 的值;(Ⅱ)设()'()()F x f x g x =-,若对任意的12,(0,)x x ∈+∞,且12x x ≠,都有2121()()()F x F x a x x ->-,求a 的取值范围.5.【北京市西城区2014年高三二模试卷】(本小题满分13分) 已知函数2e ()1xf x ax x =++,其中a ∈R . (Ⅰ)若0a =,求函数()f x 的定义域和极值;(Ⅱ)当1a =时,试确定函数()()1g x f x =-的零点个数,并证明.6.【北京市昌平区2014届高三4月第二次统练(二模)】 (本小题满分13分) 已知函数32()213a f x x x ax =+--,'(1)0-=f . (Ⅰ)求函数()f x 的单调区间;(Ⅱ)如果对于任意的[2,0)x ∈-,都有()3f x bx ≤+,求b 的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市东城区2014-2015学年度第二学期综合练习(一)
高三数学 (文科)
本试卷共5页,共150分。考试时长120分钟。考生务必将答案答在答题卡上,在试卷
上作答无效。考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)
一、选择题(共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出符合题
目要求的一项)
(1)在复平面内,复数12iz对应的点的坐标为
(A)(1,2) (B)(2,1)
(C) (1,2) (D)(2,1)
(2)双曲线2214xy的渐近线方程为
(A)12yx (B)3yx
(C)2yx (D)5yx
(3)记函数)(xf的导函数为)(xf,若()fx对应的曲线在点))(,(00xfx处的切线方程为
1yx
,则
(A)0()=2fx (B)0()=1fx
(C)0)(0xf (D)0()=1fx
(4)已知命题p:直线a,b不相交,命题q:直线a,b为异面直线,则p是q的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(5)在区间[0,2]上随机取一个实数x,则事件“310x”发生的概率为
(A)12 (B)13
(C)14 (D)16
(6)执行如图所示的程序框图,若输出的b的值为4,
则图中判断框内①处应填
(A)2 (B)3
(C)4 (D)5
(7)设集合1,(,)1.xyDxyxy,则下列命题中正确的是
(A)(,)xyD,20xy (B)(,)xyD,22xy
(C)(,)xyD,2x (D)(,)xyD,1y
(8)某学校餐厅每天供应500名学生用餐,每星期一有A,B两种菜可供选择.调查资料
表明,凡是在星期一选A种菜的学生,下星期一会有20%改选B种菜;而选B种菜的学
生,下星期一会有30%改选A种菜.用na,nb分别表示在第n个星期的星期一选A种菜
和选B种菜的学生人数,若1300a,则+1na与na的关系可以表示为
(A)111502nnaa (B)112003nnaa
(C)113005nnaa (D)
121805nnaa
第Ⅱ卷
(非选择题 共110分)
二、填空题共6小题,每小题5分,共30分。
(9)已知集合1A,1,21Bm,若AB,则实数m的值为 .
(10)将函数()sin(2)3fxx的图象向右平移6个单位后所得图象对应的解析式
为 .
(11)在矩形ABCD中,AB(1,3),(,2)ACk,则实数k .
(12)已知函数()fx的对应关系如下表所示,数列na满足13a,1()nnafa,则
4
a
,
2015
a
.
x
1 2
3
()fx
3
2 1
(13)函数()fx是定义在R上的偶函数,且满足(2)()fxfx.当[0x,1]时,
()2fxx.若在区间[2,3]上方程+2()0axafx
恰有四个不相等的实数根,
则实数a的取值范围是________.
(14)C是曲线21(10)yxx上一点,CD垂直于y轴,D是垂足,点A的坐
标是1,0().设CAO(其中O表示原点),将ACCD表示成关于的函数
()f,则()f= ,()f
的最大值为 .
三、解答题(共6小题,共80分。解答应写出文字说明,演算步骤或证明过程)
(15)(本小题共13分)
下面的茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).
甲组 乙组
9 0 9
x
2 1
5 y 8
7
4 2 4
已知甲组数据的中位数为13,乙组数据的平均数是16.8.
(Ⅰ)求x,y的值;
(Ⅱ)从成绩不低于10分且不超过20分的学生中任意抽取3名,求恰有2名学生在乙
组的概率.
(16)(本小题共13分)
在△ABC中,sin3cos2AA.
(Ⅰ)求A的大小;
(Ⅱ)现给出三个条件:①2a; ②45B;③3cb.
试从中选出两个可以确定△ABC的条件,写出你的选择并以此为依据求△ABC的面
积 (只需写出一个选定方案即可,选多种方案以第一种方案记分) .
(17)(本小题共14分)
如图甲,⊙O的直径2AB,圆上两点,CD在直径AB的两侧,且
CBA3DAB.沿直径AB将半圆ACB
所在平面折起,使两个半圆所在的平面互
相垂直(如图乙).F为BC的中点,E为AO的中点.
(Ⅰ)求证 :CBDE;
(Ⅱ)求三棱锥CBOD的体积;
(Ⅲ)在劣弧BD上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位
置;
若不存在,请说明理由.
(18)(本小题共14分)
已知1x是函数()2lnbfxxxx的一个极
值点
.
(Ⅰ)求实数b的值;
(Ⅱ)求()fx的单调递减区间;
(Ⅲ)
设函数3()()gxfxx,试问过点2(,5)可作多少条直线与曲线()ygx相
切?请说明理由
.
(19)(本小题共13分)
已知椭圆C:222210xyabab的左、右焦点分别为1F,2F,离心率为12,
M
为椭圆上任意一点且△12MFF的周长等于6.
(Ⅰ)求椭圆C的方程;
(Ⅱ)以M为圆心,1MF为半径作圆M,当圆M与直线 l4x:有公共点时,求
△12MFF面积的最大值.
(20)(本小题共13分)
已知等差数列na中,15a,2474aa,数列nb前n项和为nS,且
2(1)nnSb
nN()
.
(Ⅰ)求数列na和nb的通项公式;
(Ⅱ)设数列,,nnnancbn为奇数为偶数,,求nc的前n项和nT;
(Ⅲ)把数列na和nb的公共项从小到大排成新数列nd,试写出1d,2d,并证明
n
d
为等比数列.
