2018年中考数学复习课时37圆的有关概念与性质导学案无答案20180429157

合集下载

《圆》整理和复习(导学案)

4.培养学生的数据分析能力，通过对圆的周长、面积等计算，提高数据处理和计算能力；
5.培养学生的团队协作能力，通过小组讨论、合作探究，加深对圆的知识点的理解和应用。
三、教学难点与重点
1.教学重点
-圆的基本概念：圆心、半径、直径、周长、面积的定义及其相互关系；
-圆的性质：半径相等、直径垂直、弧相等、圆心角相等的特点及其应用；
《圆》整理和复习（导学案）
一、教学内容
《圆》整理和复习（导学案）
1.圆的基本概念：圆心、半径、直径、周长、面积；
2.圆的性质：半径相等、直径垂直、弧相等、圆心角相等；
3.圆的方程：圆的相交、相离；
5.圆与圆的关系：相切、相交、相离；
6.圆的切线、割线；
7.圆的扇形、圆心角、圆周角；
举例解释：
-通过实际测量和计算，让学生掌握圆的周长和面积的计算方法，并理解其在生活中的应用，如计算车轮的行驶距离；
-通过几何作图，让学生直观感受圆的性质，如半径相等、圆心角相等，并应用于解决实际问题，如设计等分圆的图形。
2.教学难点
-圆的方程推导：理解圆的标准方程和一般方程的推导过程，尤其是从标准方程到一般方程的转换；
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解圆的基本概念。圆是由一组等距离于圆心的点组成的几何图形。它是平面几何中最重要的图形之一，具有许多独特的性质和应用。
2.案例分析：接下来，我们来看一个具体的案例。这个案例展示了圆在实际中的应用，以及它如何帮助我们解决问题，如计算车轮的周长和面积。
-在计算扇形、圆心角、圆周角时，通过实际案例和公式推导，使学生能够熟练掌握计算方法，并应用于实际测量和设计问题。
四、教学流程
（一）导入新课（用时5分钟）

2018年中考数学复习课时37圆的有关概念与性质导学案无答案2

课时37．圆的有关概念与性质【课前热身】1.(如图，AB 是⊙O 的直径，点C 在⊙O 上，则ACB ∠的度数为（）A ．30oB ．45oC ．60oD ．90o2.如图，已知圆心角78BOC ∠=o，则圆周角BAC ∠的度数是（） A ．156oB ．78oC ．39oD ．12o3.如图所示，圆O 的弦AB 垂直平分半径OC ．则四边形OACB 是（）A ．正方形 B.长方形 C ．菱形 D ．以上答案都不对4.如图，AB 是⊙O 的弦，OC AB ⊥于点C ，若8cm AB =，3cm OC =，则⊙O 的半径为 cm ．5. (荆门)如图，半圆的直径AB ＝___ ．【考点链接】1. 圆上各点到圆心的距离都等于 .2. 圆是对称图形，任何一条直径所在的直线都是它的；圆又是对称图形，是它的对称中心.3. 垂直于弦的直径平分，并且平分；平分弦（不是直径）的垂直于弦，并且平分 .4. 在同圆或等圆中，如果两个圆心角，两条弧，两条弦，两条弦心距，两个圆周角中有一组量，那么它们所对应的其余各组量都分别 .5. 同弧或等弧所对的圆周角，都等于它所对的圆心角的 .AC BO 第4题第5题 012-11 A 第2题第3题第1题6. 直径所对的圆周角是，90°所对的弦是 . 【典例精析】例1 (呼伦贝尔）如图：AC⌒ =CB ⌒ ，D E ，分别是半径OA 和OB 的中点，CD 与CE 的大小有什么关系？为什么？例2已知：如图，30PAC ∠=︒，在射线AC 上顺次截取AD =3cm ，DB =10cm ，以DB 为直径作⊙O 交射线AP 于E 、F 两点，求圆心O 到AP 的距离及EF 的长．【中考演练】1.下列命题中，正确的是（）① 顶点在圆周上的角是圆周角； ② 圆周角的度数等于圆心角度数的一半； ③ 90o的圆周角所对的弦是直径； ④ 不在同一条直线上的三个点确定一个圆； ⑤ 同弧所对的圆周角相等 A ．①②③B ．③④⑤C ．①②⑤D ．②④⑤2.兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示，已知AB ＝16m ，半径 OA ＝10 m ，高度CD 为_ ____m ．CBOEDAOADBE FPＣＥＡＯＤＢ3.如图，⊙O 中OA BC ⊥，25CDA ∠=o，则AOB ∠的度数为．4.如图，射线AM 交一圆于点B 、C ，射线AN 交该圆于BC ⌒ =DE ⌒ ．点D 、E ，且（1）求证：AC = AE ；（2）利用尺规作图，分别作线段CE 的垂直平分线与∠MCE 的平分线，两线交于点F （保留作图痕迹，不写作法），求证：EF 平分∠CEN ．﹡5.如图，ABC △是⊙O 的内接三角形，AC BC =，D 为⊙O 的AB ⌒ 上一点，延长DA 至点E ，使CE CD =．（1）求证：AE BD =；（2）若AC BC ⊥，求证：2AD BD CD +=．ABC DEMNBAO CD第2题第3题。

新课标人教版《数学》九年级上册圆的概念和性质的复习导学案

圆的概念和性质的复习导学案一、圆的有关概念和性质考点一圆的有关概念和性质1.圆的定义动态：在同一平面内,一条线段OA绕着它固定的一个端点O旋转____,另一个端点A所形成的封闭图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径.静态：圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点的集合.2.圆的有关的概念3.圆的性质(1)圆的对称性:圆既是轴对称图形,又是中心对称图形,任意一条____所在的直线都是它的对称轴,圆心是它的对称中心.(2)圆的确定:不在同一直线上的____个点确定一个圆.三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心就是三角形三边的垂直平分线的交点,叫做三角形的______.（3）圆的旋转不变性：圆绕圆心任意旋转一个角度都和自身重合.考点二垂径定理及其推论(高频)考点三圆心角、弧、弦之间的关系1.圆心角:顶点在圆心的角叫做圆心角.2.定理:在同圆或等圆中,相等的圆心角所对的____相等,所对的____相等. 推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中,有一组量相等,那么其余的各组量也都____ .考点四圆周角定理及其推论(高频)考点五圆与多边形1.圆的内接多边形(1)如果一个多边形的每一个顶点都在同一个圆上,这个多边形叫做这个圆的__________,这个圆叫做这个多边形的__________.(2)圆内接四边形的性质:圆的内接四边形的对角_____.2.正多边形与圆(见第24课时)二、例题教学命题点1圆周角定理及其推论例1.(2019·安徽,10,4分)如图,Rt△ABC中,AB⊥BC,AB=6,BC=4.P是△ABC内部的一个动点,且满足∠P AB=∠PBC.则线段CP长的最小值为( ) A.32B.2C.81313D.121313例2.(2019·安徽,19,10分)如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.例3.(2019·安徽,13,5分)如图,点A,B,C,D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=_____°.命题点4圆的性质例4.(2019·安徽,20,10分)在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.(1)如图1,当PQ∥AB时,求PQ的长度;(2)如图2,当点P在BC上移动时,求PQ长的最大值.三、巩固练习考法1圆周角定理及其推论1.(2019·四川乐山)如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=()A.10°B.20°C.30°D.40°考法2垂径定理及其推论2.（1）(2019·湖南长沙)如图,在⊙O中,弦AB=6,圆心O到AB的距离OC=2,则⊙O的半径长为____.（2）(2019·江苏宿迁)如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为____.考法3圆心角、弧、弦之间的关系3.(2019·山东济宁)如图,在⊙O中, 弧AB=弧AC,∠AOB=40°,则∠ADC的度数是( )A.40°B.30°C.20°D.15°考法4圆内接四边形4.(2019·宁夏)已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.(1)求证:AB=AC;课后作业：1.(2019·海南)如图,AB是⊙O的直径,AC,BC是⊙O的弦,直径DE⊥AC于点P,若点D在优弧ABC上,AB=8,BC=3,则DP=_____.2.(2019·广西南宁)如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )A.140°B.70°C.60°D.40°3.(2019·浙江舟山改编)把一张圆形纸片按照如图所示的方式折叠两次后展开,图中的虚线表示折痕,则∠BOC的度数是( )A.120°B.135°C.150°D.165°4.(2019·甘肃兰州)如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC=()A.45°B.50°C.60°D.75°∠ABC=105°,∠BAC=25°,则∠E的度数为( )A.45°B.50°C.55°D.60°6.(2019·湖南岳阳)如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD=____°.。

圆的相关概念导学案

圆的相关概念导学案第页姓名：一、圆的定义定义1：定义2：表示：半径：，圆心：确定圆的条件：什么是等圆？二、相关概念1、弧：表示：优弧：劣弧：等弧：弧的度数：；弧的长度：2、半圆：3、弦：4、直径：5、过圆上一点最短的弦：过圆上一点最长的弦：6、弦心距:7、圆周角：8、圆心角：9、点与圆的位置关系10、过圆内一点最长的弦：过圆内一点最短的弦：11、过圆内外一点最长的线段：过圆外一点最短的线段：3、下列图形能称为圆周角的为：A、B、C、D、一．选择题（共32小题）1．下列说法错误的是（）A．直径是圆中最长的弦B．长度相等的两条弧是等弧C．面积相等的两个圆是等圆D．半径相等的两个半圆是等弧2．如图，在⊙O中，弦的条数是（）2题11题12题3．下列说法错误的是（）A．圆上的点到圆心的距离相等B．过圆心的线段是直径C．直径是圆中最长的弦D．半径相等的圆是等圆4．下列说法：（1）长度相等的弧是等弧，（2）半径相等的圆是等圆，（3）等弧能够重合，（4）半径是圆中最长的弦，其中正确的有（）个5．下列结论正确的是（）A．长度相等的两条弧是等弧B．半圆是弧C．半径是弦D．弧是半圆6．下列说法正确的是（）A．长度相等的弧是等弧B．相等的圆心角所对的弧相等C．面积相等的圆是等圆D．劣弧一定比优弧短7．下列判断结论正确的有（）个（1）直径是圆中最大的弦．（2）长度相等的两条弧一定是等弧．（3）面积相等的两个圆是等圆．（4）同一条弦所对的两条弧一定是等弧．（5）圆上任意两点间的部分是圆的弦．8．下列说法错误的是（）A．直径是圆中最长的弦B．半径相等的两个半圆是等弧C．面积相等的两个圆是等圆D．长度相等的两条弧是等弧9．由所有到已知点O的距离大于或等于3，并且小于或等于5的点组成的图形的面积为（）10．下列说法错误的是（）A．圆有无数条直径B．连接圆上任意两点之间的线段叫弦C．过圆心的线段是直径D．能够重合的圆叫做等圆11．如图所示，MN为⊙O的弦，∠N=50°，则∠MON的度数为（）12．如图，在△ABC中，∠ACB=90°，∠A=40°，以C为圆心，CB为半径的圆交AB于点D，连接CD，则∠ACD=（）13．有下列四个说法：①半径确定了，圆就确定了；②直径是弦；③弦是直径；④半圆是弧，但弧不一定是半圆．其中错误说法的个数是（）14．如图，一枚半径为r的硬币沿着直线滚动一圈，圆心经过的距离是（）A．4πr B．2πr C．πr D．2r15．下列说法正确的是（）A．劣弧一定比优弧短B．面积相等的圆是等圆C．长度相等的弧是等弧D．如果两个圆心角相等，那么它们所对的弧也相等16．已知，在同圆中有两条互相平分的弦，那么下列结论中正确的是（）A．这两条弦都是直径B．这两条弦最多有一条是直径C．这两条弦都不是直径D．这两条弦至少有一条是直径17．下列语句中，不正确的有（）A．①③④B．②③C．②D．②④①直径是弦；②弧是半圆；③经过圆内一定点可以作无数条弦；④长度相等的弧是等弧．18．到圆心的距离不大于半径的点的集合是（）A．圆的外部B．圆的内部C．圆D．圆的内部和圆19．下列说法错误的是（）A．面积相等的两个圆是等圆B．半径相等的两个半圆是等弧C．直径是圆中最长的弦D．长度相等的两条弧是等弧20．下面说法正确的是（）（1）直径是弦；（2）弦是直径；（3）半圆是弧；（4）弧是半圆．A．（1）（2）B．（2）（3）C．（3）（4）D．（1）（3）21．下列语句正确的有（）个①直径是弦；②半圆是弧；③长度相等的弧是等弧；④经过圆内一定点可以作无数条弦；⑤经过圆内一定点可以作无数条直径．22．下列说法中正确的是（）A．弦是直径B．弧是半圆C．半圆是圆中最长的弧D．直径是圆中最长的弦23．下列说法中，正确的是（）A．弦是直径B．半圆是弧C．过圆心的线段是直径D．圆心相同半径相同的两个圆是同心圆24．如图，在⊙O中，点A，O，D在一条直线上，点B，O，C在一条直线上，那么图中有弦（）条25．下列说法正确的是（）A．半圆是弧，弧也是半圆B．过圆上任意一点只能做一条弦，且这条弦是直径C．弦是直径D．直径是同一圆中最长的弦26．下列说法：①弧分为优弧和劣弧；②半径相等的圆是等圆；③过圆心的线段是直径；④长度相等的弧是等弧；⑤半径是弦，其中错误的个数为（）个27．给出下列说法：①直径是弦；②优弧是半圆；③半径是圆的组成部分；④两个半径不相等的圆中，大的半圆的弧长小于小的半圆的周长．其中正确的有（）个28．下列说法正确的是（）A．长度相等的两条弧是等弧B．优弧一定大于劣弧C．不同的圆中不可能有相等的弦D．直径是弦且同一个圆中最长的弦29．下列说法错误的是（）A．直径相等的两个圆是等圆B．圆中最长的弦是直径C．半圆是弧D．连接圆上两点，所得到的线段叫做直径30．下列说法：①直径是弦；②弦是直径；③过圆上任意一点有无数条弦，且这些弦都相等；④直径是圆中最长的弦．其中正确的是（）个31．下列说法正确的有（）个①半径相等的两个圆是等圆；②半径相等的两个半圆是等弧；③过圆心的线段是直径；④分别在两个等圆上的两条弧是等弧．32．下列说法正确的个数是（）个①直径是圆中最长的弦；②弧是半圆；③过圆心的直线是直径；④半圆不是弧；⑤长度相等的弧是等弧．二．填空题（共9小题）33．线段AB=10cm，在以AB为直径的圆上，到点A的距离为5cm的点有个．34．如图，CD是⊙O的直径，∠EOD=84°，AE交⊙O于点B，且AB=OC，则∠A的度数是．35．如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于点E，已知AB=2DE，若△COD为直角三角形，则∠E的度数为°．36．如图，若点O为⊙O的圆心，则线段是圆O的半径；线段是圆O的弦，其中最长的弦是；是劣弧；是半圆．37．半径为5的⊙O中最大的弦长为．38．下列说法：①弦是直径；②直径是弦；③过圆心的线段是直径；④一个圆的直径只有一条．其中正确的是（填序号）．39．若⊙O的半径为6cm，则⊙O中最长的弦为厘米．40．已知⊙O中最长的弦为16cm，则⊙O的半径为cm．41．半径为1的圆中最长的弦长等于．。

人教版九年级上册圆的概念及性质教学案(无答案)

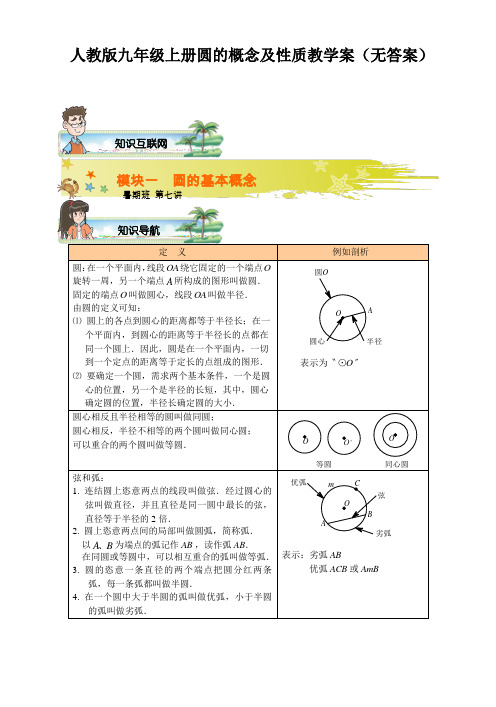
人教版九年级上册圆的概念及性质教学案（无答案）定义例如剖析圆：在一个平面内，线段OA绕它固定的一个端点O 旋转一周，另一个端点A所构成的图形叫做圆．固定的端点O叫做圆心，线段OA叫做半径．由圆的定义可知：⑴ 圆上的各点到圆心的距离都等于半径长；在一个平面内，到圆心的距离等于半径长的点都在同一个圆上．因此，圆是在一个平面内，一切到一个定点的距离等于定长的点组成的图形．⑵ 要确定一个圆，需求两个基本条件，一个是圆心的位置，另一个是半径的长短，其中，圆心确定圆的位置，半径长确定圆的大小．圆O半径圆心AO表示为〝O⊙〞圆心相反且半径相等的圆叫做同圆；圆心相反，半径不相等的两个圆叫做同心圆；可以重合的两个圆叫做等圆．等圆O‘O同心圆O弦和弧：1. 连结圆上恣意两点的线段叫做弦．经过圆心的弦叫做直径，并且直径是同一圆中最长的弦，直径等于半径的2倍．2. 圆上恣意两点间的局部叫做圆弧，简称弧．以A B、为端点的弧记作AB，读作弧AB．在同圆或等圆中，可以相互重合的弧叫做等弧．3. 圆的恣意一条直径的两个端点把圆分红两条弧，每一条弧都叫做半圆．4. 在一个圆中大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧．Cm劣弧优弧弦BAO表示：劣弧AB优弧ACB或AmB知识互联网模块一圆的基本概念知识导航暑期班第七讲OEDCB A 圆心角和圆周角：1. 顶点在圆心的角叫做圆心角．2. 顶点在圆上，并且两边都和圆相交的角叫做圆周角．O DC BA 圆周角圆心角下面这些都不是圆周角：【例1】如图，假定点O 为O ⊙的圆心，那么线段_________________是圆O的半径；线段___________是圆O 的弦，其中最长的弦是________；________是劣弧；___________是半圆．假定40A ∠=︒，那么ABO ∠=_________，C ∠=_______，ABC ∠=_______．【例2】如图，AB 为O ⊙的直径，CD 是O ⊙的弦，AB CD 、的延伸线交于点E ，假定2AB DE =，18E ∠=︒，求AOC ∠的度数．定理例如剖析1. 垂直于弦的直径平分弦，并且平分弦所对的两条弧．2. 平分弦〔不是直径〕的直径垂直于弦，并且平分弦所对的两条弧.如图，AB 是O ⊙的直径，CD 是弦E DCBAO1. 假定AB CD ⊥于E ，那么CE DE =；才干提升夯实基础知识导航模块二垂直于弦的直径OCBADCBA NM OAC AD =；BC BD =．2. 假定CE DE =，那么AB CD ⊥； AC AD =；BC BD =．【例3】 1．如图，M N 、区分是O ⊙中长度相等但不平行的两条弦AB CD 、的中点．求证：AMN CNM ∠=∠．2．如图，∠P AC =30°，在射线AC 上依次截取AD =3cm ，DB =10cm ，以DB 为直径作⊙O 交射线AP 于E 、F 两点，那么线段EF 的长是cm ．3．如图，⊙O 的半径为2，弦32=AB ，点C 在弦AB 上，AB AC 41=，那么OC 的长为〔〕A ．2 B ．3 C ．23 D ． 7【例4】 ⊙O 的半径为5cm ，弦AB ∥CD ，且AB =8 cm ，CD =6cm ，求AB 与CD 之间的距离．定理例如剖析弧、弦、圆心角之间的关系：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．推论：在同圆或等圆中，假设两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其他各组量区分相等． O D CB A如图，由定理可知：假定AOB COD ∠=∠，那么AB CD =、AB CD =；假定AB CD =，那么AOB COD ∠=∠、AB CD =；假定AB CD =，那么AB CD =、AOB COD ∠=∠．才干提升知识导航模块三弧、弦、圆心角和圆周角E O BDFCA【例5】 ⑴ 如图，△ACD 和△ABE 都内接于同一个圆，那么∠ADC +∠AEB +∠BAC =⑵ 在⊙O 中，直径AB ⊥CD 于点E ，衔接CO 并延伸交AD 于点F ，且CF ⊥AD ．那么∠D = ． ⑶ 如图，点A 、B 、C 、D 在⊙O 上，O 点在∠D 的外部，四边形OABC 为平行四边形，那么∠OAD +∠OCD = °．⑷ 如图，A B C D 、、、是O ⊙上的点，直径AB 交CD 于点E ， 57C ∠=︒，45D ∠=︒，那么CEB ∠=________． ⑸ 如以下图OA =OB =OC 且∠ACB =30°，那么∠AOB 的大小是． ⑹ O ⊙的弦AB 长等于圆的半径，那么该弦所对的圆周角为．【例6】如图，AB ，CD 是⊙O 的弦，AB ⊥CD ，BE 是⊙O 的直径，AC =3，求线段DE 的长度．判别正误⑴ 半圆是弧⑵ 半径相等的两个圆是等圆⑶ 过圆心的线段是直径⑷ 两个端点可以重合的弧是等弧⑸ 圆的恣意一条弦把圆分红优弧和劣弧两局部 ⑹ 长度相等的弧是等弧 ⑺ 直径是最大的弦 ⑻ 半圆所对的弦是直径 ⑼ 两个劣弧的和是半圆⑽ 圆的半径是R ，那么弦长的取值范围是大于0且不大于2R知识模块一圆的基本概念课后演练【演练1】：如图，在同心圆中，大圆的弦AB 交小圆于C D ，两点．⑴ 求证：AOC BOD ∠=∠；⑵ 试确定AC 与BD 两线段之间的大小关系，并证明你的结论．知识模块二垂直于弦的直径课后演练【演练2】如图，O ⊙的弦AB 垂直于弦CD ，E 为垂足，3AE =，7BE =，且AB CD =，那么圆心O 到CD 的距离是__________．【演练3】如下图，在Rt ABC △中，90C ∠=︒，2AC =，1BC =，假定以C 为圆心、CB 的长为半径的圆交AB 于P ，那么AP = .才干提升实战演练DCAOCB EDA【演练4】在半径为1的O∠的度数为⊙中，弦AB AC、的长区分为和，那么BAC ___________．知识模块三弧、弦、圆心角和圆周角课后演练【演练5】如图，在O⊙的直径，AC、BC区分交O⊙于E、D，D是BE⊙中，AB是O的中点，40∠的大小．A∠=︒，求C。

圆的概念导学案

24.1.1 圆班级___________姓名___________学习目标：1.让学生在探索过程中认识圆，理解圆的本质属性. 2.了解弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等有关的概念，理解概念之间的区别与联系。

活动一，情景引入圆是生活中常见的图形，许多物体都给我们以圆的形象.1.你还能举例说明我们生活中哪些物体是圆形的吗？2.为什么人们把车轮都做成圆形的呢？从本节课开始，我们将会更清楚地了解圆以及一些相关的概念和性质. 活动二，探究新知（一）探索圆的概念1.请你用圆规画一个半径为2cm 的圆.2.你能利用棉线和铅笔试着画一个半径为2cm 的圆吗？试试看。

于是由上面两种画圆的过程，我能说出圆的形成过程。

即：运动论（动态的圆） ___________ ______________________________________________________________3.在你画的圆中量一量，圆上任意一点到圆心（定点）的距离相等吗？为什么？反过来，平面到点O 的距离半径（定长）的长的点都在圆上吗？我经过测量，得出如下结论：________________ __________________________________________________________________________ 于是我进一步理解了圆的概念：集合论（静态的圆）_____________________________________ _________________________________________________________________________________. 以O 为圆心的圆，记做“——————”，读做“——————”.(二)探究圆的相关概念我通过对课件的观察与理解。

知道了如下的相关概念：（1）弦和直径：叫做弦，叫做直径.如图 1，、是弦；是直径.（2）弧：叫做弧，叫做优弧，叫做劣弧.用符号表示图1中各条弧._____ ________ ______ (3)———————————叫做半圆；_________________________————————————叫做等弧；活动三，运用新知矩形ABCD 的对角线AC,BD 相交于点O.求证：A,B,C,D 四个点在以点O 为圆心的同一个圆上。

新课标人教版《数学》九年级上册圆的概念和性质的复习导学案(无答案)

2018年北师大版九年级数学下册第三章圆圆的基本性质复习课教案

ABC DE例1图圆的基本性质复习课教案考纲要求：1．理解圆、弧、弦、圆心角、圆周角的概念，了解等圆、等弧的概念。

2．探索圆周角、弧、弦之间的关系，了解并证明圆周角定理及其推论，圆周角的度数等于它所对弧上的圆心角度数的一半，直径所对的圆周角是直角，90°的圆周角所对的弦是直径，圆内接四边形的对角互补。

教学重点：掌握圆的基本性质教学难点：圆的基本性质的应用教学过程：一、引入师：大家请看老师黑板上所画的图形圆。

这是我们这节课要复习的主要内容，请大家回顾，什么是圆？生：平面内到定点的距离等于定长的所有点组成的图形。

师：根据定义，确定圆必须有几个条件？生：圆心和半径。

师：和圆有关的两种角是圆心角和圆周角，请同学们回顾它们的定义。

生：顶点在圆心的角是圆心角。

顶点在圆上、两边和圆相交的角是圆周角。

师：今天，老师带来了一个圆形纸片，但圆心找不到了，你们能通过折纸的方法帮老师找到这个圆的圆心吗？生：对折两次，两条折痕的交点就是圆心。

师：非常好，这两条折痕其实是圆的什么？对折后能完全重合，说明圆具有什么性质？生：折痕是直径，说明圆具有轴对称性。

师：圆是一个轴对称图形，从它的轴对称性我们可以得到垂径定理及其逆定理。

下面，我们回顾一下垂径定理及其逆定理的内容。

生：垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

逆定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧。

师：刚才，我们通过折纸的方法找到了圆的两条直径，如图，两条直径与的交点O 就是圆心。

那么，图中与、与相等吗？为什么？生：相等。

因为它们所对的圆心角相等。

师：在一个圆中，只要圆心角相等，它们所对的弧一定相等，这是因为圆具有旋转不变性。

这种旋转不变性，使得圆的三种基本量圆心角、弧、弦之间具有特殊的关系。

接下来我们就来复习这些内容。

二、知识回顾 1．圆心角定理及其推论。

定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等。

人教版九年级数学 24.1.1圆及圆有关的概念导学案(无答案)

§24.1.1 圆及与圆有关的概念导学案一.学习目标1、理解、掌握圆及与圆有关的概念.2、经历探索点与圆的位置关系的过程，以及如何确定点和圆的三种位置关系.3、初步渗透数形结合和转化的数学思想，并逐步学会用运动、集合的观点去认识世界、解决问题.二.学习重点：理解、掌握圆及圆有关的概念.三.学习难点：会确定点和圆的位置关系.教学过程一、情境引入：思考：生活中,我们会看到哪些物体,它们给我们以圆的形象？二、探究学习：1．尝试：怎样画圆（1）利用圆规画一个⊙O ，使⊙O 的半径r=3cm.① 圆的画法、半径、圆心，记法、读法；②圆的定义（概念）在一个平面内，线段OA 绕着它固定的一个端点旋转一周，另一个端点所形成的图形叫做圆；③要确定一个圆，需要确定两个元素即：_________和___________;其中____________确定圆的位置；_______________确定圆的大小；④在平面内任意取一点P ，点与圆有哪几种位置关系？若⊙O 的半径为r ，点P 到圆心O 的距离为d ，那么：d > r 点P 在圆______d = r 点P 在圆______d < r 点P 在圆______ ⑤ 概括总结．圆是到定点（圆心）距离定长（半径）的点的集合.也就是说如果有几个点，它们到某一点的距离都相等，那么这几个点都在同一个圆上；数量关系位置关系如果有几个点都在圆上，那么它们到圆心的距离都相等（等于半径长）位置关系数量关系⇔⇔⇔⇔⇔2.与圆有关的概念①弦和直径弦：直径：（特殊的弦）弦和直径的关系：②⎧⎪⎨⎪⎩优弧圆弧半圆劣弧直径把圆分成两部分（两条弧），其中每条弧都叫做半圆。

弧：圆上任意两点间的部分叫做弧。

大于半圆的弧叫优弧，小于半圆的弧叫做劣弧；记法：读法；③等圆和等弧（在同圆或等圆中）等圆：重叠、或比较半径得到；等弧：重叠得到;等弧是全等的图形；等弧一定弧长相等；相等的弧长不一定是等弧；4.典型例题：例1、已知线段AB、CD是圆O的直径，顺次连接点A、C、B、D，得到四边形ACBD；观察所得四边形，这个四边形是什么特殊四边形？请证明你的猜想。

河北省2018年中考数学总复习第一编教材知识梳理篇第7章圆第1节圆的有关概念及性质精练试题

第七章　圆第一节　圆的有关概念及性质1．(2017庆阳中考)如图，△ABC 内接于⊙O ，若∠OAB ＝32°，则∠C ＝(　A )A ．58° B ．32° C ．64° D ．72°(第1题图) (第2题图)2．(2017兰州中考)如图，在⊙O 中，＝，点D 在⊙O 上，∠CDB ＝25°，则∠AOB ＝(　B )AB ︵ BC︵ A ．45° B ．50° C ．55° D ．60°3．(乐山中考)如图，C ，D 是以线段AB 为直径的⊙O 上两点，若CA ＝CD ，则∠ACD ＝40°，则∠CAB ＝(　B )A ．10°B ．20°C ．30°D ．40°,(第3题图)) ,(第4题图))4．(2017泸州中考)如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E.若AB ＝8，AE ＝1，则弦CD 的长是(　B )A .B ．2C ．6D ．8775．(2017新疆建设兵团中考)如图，⊙O 的半径OD 垂直于弦AB ，垂足为点C ，连接AO 并延长交⊙O 于点E ，连接BE ，CE.若AB ＝8，CD ＝2，则△BCE 的面积为(　A )A ．12B ．15C ．16D ．18,(第5题图)) ,(第6题图))6．(2016唐山友谊中学一模)如图，一个宽为2cm 的刻度尺(单位：cm )，放在圆形玻璃杯的杯口上，刻度尺的一边与杯口外沿相切，另一边与杯口外沿两个交点处的读数恰好是3和9，那么玻璃杯的杯口外沿半径为____cm .1347．(黑龙江中考)直径为10 cm 的⊙O 中，弦AB ＝5 cm ，则弦AB 所对的圆周角是__30°或150°__．8．(巴中中考)如图所示，∠A 是⊙O 的圆周角，∠OBC ＝55°，则∠A ＝__35°__．,(第8题图)) ,(第9题图))9．(2016唐山友谊中学一模)如图，⊙O 是△ABC 的外接圆，直径AD ＝4，∠ABC ＝∠DAC ，则AC 长为__2__．210．如图，边长为1的小正方形构成的网格中，半径为1的⊙O 的圆心O 在格点上，则∠AED 的正切值为____.1211．(安徽中考)在⊙O 中，直径AB ＝6，BC 是弦，∠ABC ＝30°，点P 在BC 上，点Q 在⊙O 上，且OP ⊥PQ.(1)如图①，当PQ ∥AB 时，求PQ 的长度；(2)如图②，当点P 在BC 上移动时，求PQ 长的最大值．解：(1)连接OQ.∵PQ ∥AB ，OP ⊥PQ ，∴OP ⊥AB ，在Rt △OBP 中，∵tan B ＝，∴OP ＝3ta n 30°＝OPOB ，在Rt △OPQ 中，∵OP ＝，OQ ＝3，∴PQ ＝＝；33OQ2－OP26(2)连接OQ.在Rt △OPQ 中，PQ ＝＝，当OP 的长最小时，PQ 的长最大，此时OP ⊥OQ2－OP29－OP2BC ，则OP ＝OB ＝，∴PQ 长的最大值为＝.12329－(32)2 33212．(2018中考预测)已知⊙O 的半径为13 cm ，弦AB ∥CD ，AB ＝24 cm ，CD ＝10cm ，则AB ，CD 之间的距离为(　D )A ．17 cmB ．7 cmC ．12 cmD ．17 cm 或7 cm13．(聊城中考)如图，四边形ABCD 内接于⊙O ，F 是上一点，且＝，连接CF 并延长交AD 的CD ︵ DF ︵ BC︵延长线于点E, 连接AC.若∠ABC ＝105°，∠BAC ＝25°，则∠E 的度数为(　B )A ．45°B ．50°C ．55°D ．60°,(第13题图)) ,(第14题图))14．(杭州中考)如图，已知AC 是⊙O 的直径，点B 在圆周上(不与A ，C 重合)，点D 在AC 的延长线上，连接BD 交⊙O 于点E ，若∠AOB ＝3∠ADB ，则(　D )A ．DE ＝EB B .DE ＝EB2C .DE ＝DO D ．DE ＝OB315．(2017盐城中考)如图，将⊙O 沿弦AB 折叠，点C 在上，点D 在上，若∠ACB ＝70°，则∠A AmB ︵ AB︵ DB ＝__110°__．,(第15题图)) ,(第16题图))16．(2017宜宾中考)如图，等腰△ABC 内接于⊙O ，已知AB ＝AC ，∠ABC ＝30°，BD 是⊙O 的直径，如果CD ＝，则AD ＝__4__．43317．(龙东中考)如图，MN 是⊙O 的直径，MN ＝4，∠AMN ＝40°，点B 为弧AN 的中点，点P 是直径M N 上的一个动点，则PA ＋PB 的最小值为__2__．318．(河南中考)如图，在Rt △ABC 中，∠ABC ＝90°，点M 是AC 的中点，以AB 为直径作⊙O 分别交AC ，BM 于点D ，E.(1)求证：MD ＝ME;(2)填空：①若AB ＝6，当AD ＝2DM 时，DE ＝________；②连接OD ，OE ，当∠A 的度数为________时，四边形ODME 是菱形．解：(1)如图所示，连接AE ，BD ，DE.在Rt △ABC 中，点M 是AC 的中点， ∴MA ＝MB ，∴∠MAB ＝∠MBA.∵四边形ABED 是圆内接四边形， ∴∠ADE ＋∠ABE ＝180°，又∠ADE ＋∠MDE ＝180°，∴∠MDE ＝∠MBA.同理可证：∠MED ＝∠MAB ，∴∠MDE ＝∠MED ，∴MD ＝ME ；(2)①2；②60°19．(德州中考)如图，⊙O 的半径为1，A ，P ，B ，C 是⊙O 上的四个点，∠APC ＝∠CPB ＝60°. (1)判断△ABC 的形状：________；(2)试探究线段PA ，PB ，PC 之间的数量关系，并证明你的结论；(3)当点P 位于的什么位置时，四边形APBC 的面积最大？求出最大面积．AB︵解：(1)等边三角形；(2)PA ＋PB ＝PC.证明：如图，在PC 上截取PD ＝PA ，连接AD.∵∠APC ＝60°，∴△PAD 是等边三角形，∴PA ＝AD ，∠PAD ＝60°.又∵∠BAC ＝60°，则∠BAC ＝∠DAB ＋∠DAC ＝60°，∴∠PAB ＝∠DAC. ∵AB ＝AC, ∴△PAB ≌△DAC ，∴PB ＝DC.∵PD ＋DC ＝PC, ∴PA ＋PB ＝PC ；(3)当点P 为的中点时，四边形APBC 面积最大．理由如下：如图，过点P 作PE ⊥AB ，垂足为E, AB︵过点C 作CF ⊥AB ，垂足为F ，连接BO.∵S △PAB ＝AB·PE ，S △ABC ＝AB·CF ，1212∴S 四边形APBC ＝AB(PE ＋CF )．∵当点P 为的中点时，PE ＋CF ＝PC,PC 为⊙O 直径，12AB︵ ∴四边形APBC 面积最大.∵△ABC 为圆内接正三角形，∴∠BOF ＝60°.又∵⊙O 的半径为1，∴在Rt △BOF 中，BF ＝OB sin 60°＝，32∴AB ＝2BF ＝，∴S 四边形A PBC ＝×2×＝.31233。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

课时 37．圆的有关概念与性质
【课前热身】
1.(如图， AB 是⊙O 的直径，点C 在⊙O 上，则
ACB 的度数为（
）
A ．30
B ． 45
C ． 60
D ．90
2.如图，已知圆心角 BOC 78 ，则圆周角 BAC 的度数是（
）
A ．156
B ． 78
C ．39
D ．12
3.如图所示，圆 O 的弦 AB 垂直平分半径 OC ．则四边形 OACB 是（）
A ．正方形 B.长方形
C ．菱形
D ．以上答案都不对
A C
B
O
第 3题
第 4题
第 1题
第 2题
4.如图， AB 是⊙O 的弦，OC AB 于点C ，若 AB
8cm ，
OC 3cm ，则⊙O 的半径为
cm ．
1
-2
B
-1
1 A 2
5. (荆门)如图，半圆的直径 AB ＝___ ．第 5 题
【考点链接】
1. 圆上各点到圆心的距离都等于 .
2. 圆是对称图形，任何一条直径所在的直线都是它的；圆又
是
对称图形，
是它的对称中心.
3. 垂直于弦的直径平分，并且平分
；平分弦（不是直径）的
垂直于弦，并且平分
.
4. 在同圆或等圆中，如果两个圆心角，两条弧，两条弦，两条弦心距，两个圆周角中有一组
量
，那么它们所对应的其余各组量都分别
.
5. 同弧或等弧所对的圆周角，都等于它所对的圆心角的
.
1
6. 直径所对的圆周角是，90°所对的弦是.
【典例精析】
⌒⌒
例1 (呼伦贝尔）如图：AC= ，D，E分别是半径OA和OB的中点，CD与CE的大小有什么关
CB
C
系？为什么？
B
A
D E
O
例2已知：如图，PAC30，在射线AC上顺次截取AD =3cm，DB =10cm，以DB为直径作⊙O交射线AP于E、F两点，求圆心O到AP的距离及EF 的长．
P
F
E
A D
B C
O
【中考演练】
1.下列命题中，正确的是（）
①顶点在圆周上的角是圆周角；②圆周角的度数等于圆心角度数的一半；
③90的圆周角所对的弦是直径；④不在同一条直线上的三个点确定一个圆；
⑤同弧所对的圆周角相等
A．①②③B．③④⑤C．①②⑤D．②④⑤
2.兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示，已知AB＝16m，
半径OA＝10 m，高度CD为_ ____m．
2
3.如图，⊙O中OA BC，CDA25，则AOB的度数为．
C
A B
D
4.如图，射线AM交一圆于点B、C，射线AN交该圆于点D、E，且⌒B C=⌒D E．
第2题第3题
（1）求证：AC = AE；
（2）利用尺规作图，分别作线段CE的垂直平分线与∠MCE的平分线，两线交于点F（保留作图痕迹，不写作法），求证：EF平分∠CEN．
A
B
D
C E
M N
⌒
﹡5.如图，△ABC是⊙O的内接三角形，AC BC，D为⊙O的AB上一点，延长DA至点E，使CE CD．
（1）求证：AE BD；
（2）若AC BC，求证：AD BD2CD．
Ｃ
Ｅ
Ｏ
Ｂ
Ａ
Ｄ
3。