必修5--基本不等式几种解题技巧及典型例题
北师版数学高二-必修5课件基本不等式与最大(小)值

+
9yx≥2
y x
·9yx=6,当且仅当yx
=
9yx,即
y=3x
时,取等号.
又1
x
+
9y=1,∴x=4,y=12.
∴当 x=4,y=12 时,x+y 取得最小值 16.
解法二:由1x + 9y=1,得 x=yy-9.∵x>0,y>0,∴y>9.
x+y=yy-9+y=y+y-y9-+9 9=y+y9-9+1=y-9+y9-9+10.∵y>9,∴y-9>0.
会得出错误答案,就会陷入困境.例如,当 x>1 时,函数 f(x)=x+x1-1≥2 xx-1,所以
函数 f(x)的最小值是 2
xx-1.由于 2
x 是一个与
x-1
x
有关的代数式,很明显这
是一个错误的答案.在出现这种情况时,可以通过对所求代数式的合理配凑,
转化为“和式”或“积式”是定值的形式后再进行求解.例如当 x>1
时,f(x)=x+x1-1=(x-1)+x1-1+1≥2 (x-1)·x1-1+1=3,即该函数的最小值为 3.
-4-
3.2 基本不等式与最大(小)值
首页
J 基础知识 ICHU ZHISHI
Z 重点难点 HONGDIAN NANDIAN
S 随堂练习 UITANG LIANXI
(3)“三相等”,即等号能够成立,即存在正数 x,y 使基本不等式两边相等, 也就是存在正数 x,y 使得 xy = x+2y.如果忽视这一点,就会得出错误答案.
例如,y= x2 + 2 + x21+2,满足“正”和“定值”的条件,但要取等号必须 x2 + 2 = x21+2,即 x2+2=1,这是不可能的,所以其最小值不是 2.
人教版必修五数学《基本不等式》PPT课件

·人教版必修五数学PPT课件·
目 录
1
重要不等式
2
基本不等式
3
有关常用理论4Biblioteka 例题学习1 重要不等式
1. 重要不等式
当a,b是任意实数时,有a2+b2≥2ab,当且仅当a=b时,等号成立.
2 基本不等式
2. 基本不等式
2. 基本不等式
2. 基本不等式
从数列的角度看,a,b的算术平均数是a,b的等差中项,几何平均 数是a,b的正的等比中项,则基本不等式可表示为:a与b的正的等比中 项不大于它们的等差中项.
【做一做2】 已知ab=16,a>0,b>0,则a+b的最小值为
.
答案:8
2. 基本不等式
2. 基本不等式
2. 基本不等式
2. 基本不等式
3 有关常用理论
3. 有关常用理论
3. 有关常用理论
4 例题学习
4. 例题学习
题型一
比较大小
4. 例题学习
4. 例题学习
题型二 利用基本不等式求最值
4. 例题学习
4. 例题学习
4. 例题学习
4. 例题学习
同学们!下课啦!
·人教版必修五数学PPT课件· 千图老师
必修五基本不等式题型分类(绝对经典)学习资料

最新必修五基本不等式题型分类(绝对经典)基本不等式复习知识要点梳理知识点:基本不等式1 •如果a,bRab2・ab (当且仅当_A_厂时取="号)・22•如果a,bRab ab(当且仅当匸一时取」’号)2在用基本不等式求函数的最值时,应具备三个条件:一正二定三取等。
①一正:函数的解析式中,各项均为正数;②二定:函数的解析式中,含变数的各项的和或积必须有一个为定值;③三取等:函数的解析式中,含变数的各项均相等,取得最值。
类型一:利用(配凑法)求最值a「求下列函数的最大(或最小)1(1)求火一一(X 0)的最小值;X 1(2)若x 0,y 0,2x y 4,求xy的最大值(3)已知“〕/ ,且■••求•二|的最大值及相应的’匸的值5变式1:已知x ■,求函数y=4x2 1的最大值4 4x5X类型二:含“ 1 ”的式子求最值02 •已知「」”求:「的最小值.2 3变式1:若x 0, y 0, x y=1,求——的最小值xy变式2 :2 3x 0, y 0, x y=2,求的最小值变式求函数y= 2 2 (0 X )的最小值类型三:求分式的最值问题X?X 13•已知x0,的最小值变式1求函数y x1 2 X3(X $的值域变式2:求函数y X2 44J的最小值类型四:求负数范围的最值问题、1 曰4. xO,求x ■的最大值X4X变式1:求f (x) x (x 0)的值域Xx12 2x 1变式2:求f (x) 亠的值域x类型五:利用转化思想和方程消元思想求最值例5•若正数a,b满足abab 3,则(1) ab的取值范围是(2) a+b的取值范围是变式1:若x,y>0满足2x+y+6 xy,则xy的最小值是变式2:已知x ‘ y>0满足x+2y+2xy 8,则x+2y的最小值是课堂练习:1 :已知a,b R,下列不等式中不正确的是()(A) a1 2 3 b 2ab ( B) ■■- ab (C) a24n 4 b2 b222:在下列函数中最小值为2的函数是()1(A)y x-X(B) y 3X3X1 1(C)y lg x (1 x 10) (D)y sin x (Oxla x sin x 214:若x3,求yx —的最小值x33:若x0,求y3x*的最小值X1 1 6: x 0, y 0, x+3y=1求 --- 的最小值xy作业(共80分,限时40分钟)1、(5 分)1 4设x,y 为正数, 3.4.5.A. 6B.9C.12则(xy )(丄4)的最小值为()xyD.15A. (5分) 若a,b 为实数,且a(A ) 18(B ) 6(5分)设正数x 、y 满足2x y(A) 50 (B) 20 2,则歹3b 的最小值是((C ) 23 (D )24320 ,贝U lg x lg y 的最大值是((C) 11g5(D)1(5分)已知a,b 为正实数,且a1[的最小值为(2b 1,则 ---- 、ab )4,2B. 6C.3 ・ 2 2D. 3+2 2 (5分)设a 、b 2,2(A) 1 ab abR,且 a b, a b(B)ab 12,则必有() a 2b 2 6.( 5分)F 列结论正确的是22,2 1A.翁XabClik 文 1 时,Igx(D)丄 ? l g xa 2b 22B.ab 0时,C.当x 2时,x —的最小值为xD.7. ( 5 分)若ab 1、P Igalgb、Q 12(lga|gb),R ©笃,则下列不等式成立的是()(A) R PQ (B) P Q R (C)Q P R (D)P RQ8. (5分)函数vx1—(x1)的最小值是X 19. (5分)已知两个正实数x・y满足尖系式x 4y 40,则Igx lg y的最大值是110・(5分)已知0 x-JIJx (1 2x)的最大值是211. (5分)已知x,v R,且x 4y 1,则x y的最大值为____________12. (5分)若正数a,b满足abab3,,则ab的取值范围是13. (10分)已知abc是3个不全等的正数。
高中必修5:基本不等式综合ppt课件

即 z2 4 0 0 0 07 2 0 21 6 0 0
z297当60x0=y,即x=y=40时,等号成立 所以,将水池的地面设计成边长为40m的正方形 时总造价最低,最低总造价为297600元.
.
设计一副宣传画,要求画面面积为4840cm2,画面 的宽与高的比为a(a<1),画面的上下各留出8cm的 空白,左右各留5cm的空白,怎样确定画面的高与 宽的尺寸,能使宣传画所用纸张面积最小?
.
【应用练习】
(1)把36写成两个正数的积,当这两个正数取什么值时,它们的和最小? ∵ ab2 ab ab=36 ∴当a=b=6时,和a+b最小为12
(2)把18写成两个正数的和,当这两个正数取什么值时,它们的积最大?
∵ ab ( a b)2
2
a+b=18
∴当a=b=9时,积ab最大为81
不等式 ab a b 是一个基本不等式,它在解决实际问题中由广泛的应用,
解: 设矩形菜园的长为xm,宽为ym,则 xy=100 篱笆的长为2(x+y)m
100 m 2
由 x y xy
2
可得 xy2 xy20
∴2(x+y)≥40
当且仅当x=y时等号成立,此时x=y=10
∴这个矩形的长、宽都为10m时,所用篱笆最短,最短篱笆是40m
练习:已知三角形的面积等于50,两条直角边各为多少时,两条直角边的和最小?
号).
.
基础知识
重要变形2
若 a0,b0,则2ab abab a2b2,
ab
2
2
当 且 仅 当 ab时 取 等 号 。(由小到大)
.
应用基本不等式求最值的条件:ab ab ( a>0,b>0)
【精品专区】必修5不等式复习
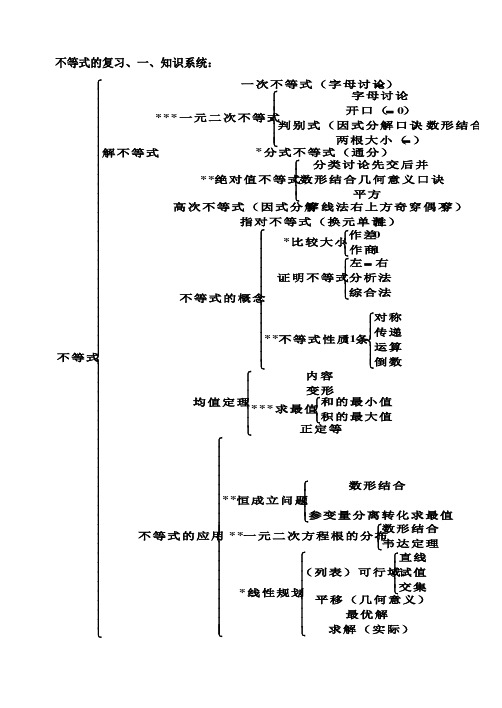
不等式的复习、一、知识系统:⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧=⎩⎨⎧⎪⎩⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧===求解(实际)最优解平移(几何意义)交集试值直线(列表)可行域线性规划韦达定理数形结合一元二次方程根的分布参变量分离转化求最值数形结合恒成立问题不等式的应用正定等积的最大值和的最小值求最值变形内容均值定理倒数运算传递对称条不等式性质综合法分析法右左证明不等式作商作差比较大小不等式的概念性)指对不等式(换元单调穿)穿线法右上方奇穿偶不高次不等式(因式分解平方数形结合几何意义口诀分类讨论先交后并绝对值不等式分式不等式(通分))两根大小()数形结合判别式(因式分解口诀)开口(字母讨论一元二次不等式)一次不等式(字母讨论解不等式不等式********11**10****0***表6.《不等式的概念》知识总结典型例题: 例1、 ax>b例2、1)XTZP25 –42)XTZP26 –14 例3、1128≥--x x例4、1)XTZP27 –72)x x -<-31 3)231>-+-x x例5、1)0)5)(4)(2)(1(>+-+-x x x x例6、1)01lg )(lg 22>--x x 2)0224>--xx例7、1)XTZP21 –11 2)XTZP21 –10 3)XTZP21 –8 4)XTZP21 –9例8、1)XTZP23–7 2)XTZP23–8 3)XTZP23–4 4)XTZP32–8 5)XTZP33–12 6)x>0,y>0, x+y=1求yx 41+的最小值例9、1)XTZP27 –62)XTZP27 –83)XTZP28 –11 例10、例11、1)XTZP36 –132)XTZP30–13表7.《均值定理》知识总结表8.《解不等式》知识总结表9.《解不等式》知识总结。
人教A版高中数学必修5《三章 不等式 3.4 基本不等式:√ab≤(a+b)%2》示范课课件_4

3. 基本不等式变形公式
a b 2 ab
ab (a b)2 4
作业
1.预习课本第99页例1和例2 2.思考:基本不等式有什么作用?在利用基本 不等式时需要满足什么条件?
3.4基本不等式: ab a b
2
这是2002年在北京召开的第24届国际数学 家大会会标.会标根据中国古代数学家赵爽的 弦图设计的,颜色的明暗使它看上去象一个风 车,代表中国人民热情好客.
D
a2 b2
b
G
F
A
a HE
探究1:
1、正方形ABCD的
面积S=_a_2___b 2
C 2.四个直角三角形的
当 a 0,b 0 时, a b≥ ab , 当且仅当
a = b时,等号成立.
2
基本不等式的几何解释是什么?
如图, AB是圆的直径, O为圆心,
点C是AB上一点, AC=a, BC=b. 过
点C作垂直于AB的弦DE,连接AD、 BD、OD.
A
ab ①如何用a, b表示OD? OD=___2___
x
等号成立的条件.
2.已知 0 x 1,求证:x(1 x) 1 ,并推导出式中等
4
号成立的条件.
小结:
1. 重要不等式
当 a, b R时,a2 b2 2ab,当且仅当 a b 时等号成立.
2. 基本不等式
当 a, b R时,a b ab ,当且仅当 a b 时等号成立.
面积和 S=_2a_b
3、S与 S有什么
样的不等关系?
B
S>S′ 即 a2 b2 2ab
问:那么它们有相等的情况吗?
D
高中数学必修五第三章不等式复习知识点与例题

一对一个性化辅导教案例1:解下列不等式题型2:简单的无理不等式的解法例1 :解下列不等式(2) x 2x 2 1题型3 :指数、对数不等式2例1 :若log a 1,则a 的取值范围是()3A. a 1B . 0 a —C - — a 133练习:1 2x 1 .x 1 ;(1) x 3 4x 0 ;2 2(2) (x 1) (x 5x 6) 0 ;(3)2x 2 x 1 2x 1练习: 解不等式(1)3x 5 x 2 2x 3(2) (2x 1)2(x 7)3(3 2x)(x 4)6D. 0 a -或 a 131、不等式2x 3 4x的解集是__________________ 。
2、不等式log1(x 2) 0的解集是_____________ 。
22e x 1x 23、设f(x)=‘1则不等式f(x) 2的解集为( )log3(x2 1),x 2,A. (1,2) (3, ) B . (710, ) C. (1,2) ) D . (1,2)题型4 :不等式恒成立问题1 2例1:若关于x的不等式一X 2x mx的解集是{x |0 x 2},则m的值是2练习:2 1 1一元二次不等式ax bx 2 0的解集是(一,—),贝U a b的值是( )2 3A. 10 B . 10 C. 14 D . 14例2:已知不等式x2 (a 1)x a 0,(1)若不等式的解集为(1,3),则实数a的值是_________________ 。
(2) __________________________________________________________ 若不等式在(1,3)上有解,则实数a 的取值范围是 _______________________________________________________ 。
(3) ____________________________________________________________ 若不等式在(1,3)上恒成立,则实数a的取值范围是 _____________________________________________________ 。
2019年人教版高中数学必修五考点练习:基本不等式的配凑技巧(含答案解析)

6a 2b 当且仅当 b = a 且2a+b-1=0,即a=2- 3,b=2 3-3时取等号.
32 故b+a的最小值为7+4 3. 答案:7+4 3
10. 【解析】选D. log4 (3a 4b) log2 ab, 可得 3a 4b ab, 且 a 0,b 0
3a 4b 1, 即 3 4 1,
5
10
A.3
B. 3
3
C. 2
D.3
9. 已知x>y>0,求
的最小值及取最小值时的x、y的值.
2 10. 若b>a>1,且3logab+6logba=11,则a3+b-1的最小值为________.
二、“1”的变换
14 1. 已知a>0,b>0,a+b=2,则y=a+b的最小值是
7
A. 2
B.4
9
C. 2
4. 已知 x , y , z 0 , 1 且 x y z 2 ,求 xy yz zx 的最大值.
5. 已知实数x,y满足x2+y2-xy=1 ,则x+y的最大值为________. 6. 设x,y为实数,若4x2+y2+xy=1,则2x+y的最大值是________.
12 7. 若实数a,b满足a+b= ab,则ab的最小值为( )
3y 4x
31
+ x+y
·
∴x+y= x y 3 =2+2+ x +3y≥4+2 x 3y=8,当且仅当x=4,y=2时取等号,
32 故x+y的最小值是8.
16 1 8. 解析:已知x>0,y>0,且x+16y=xy. 即 x +y=1.
( ) 16 1
16y x
+
则x+y=(x+y) x y =16+1 + x +y≥17+2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
均值不等式应用(技巧)
技巧一:凑项
1、 求y = 2x + 1x - 3 (x > 3)的最小值
2、已知x > 32 ,求y = 22x - 3 的最小值
3、已知x < 54 ,求函数y = 4x – 2 + 14x - 5 的最大值。
技巧二:凑系数
4、当0 < x < 4时,求y = x(8 - 2x)的最大值。
5、设0 < x < 32 时,求y = 4x(3 - 2x)的最大值,并求此时x的值。
6、已知0 < x < 1时,求y = 2x(1 - x) 的最大值。
7、设0 < x < 23 时,求y = x(2 - 3x) 的最大值
技巧三:分离
8、求y = x2 + 7x + 10x + 1 (x > -1)的值域; 9、求y = x2 + 3x + 1x (x > 0)的值域
10、已知x > 2,求y = x2 - 3x + 6x - 2 的最小值
11、已知a > b > c,求y = a - ca - b + a - cb - c 的最小值
12、已知x > -1,求y = x + 1x2 + 5x + 8 的最大值
技巧四:应用最值定理取不到等号时利用函数单调性
13、求函数y = x2 + 5x2 + 4 的值域。
14、若实数满足a + b = 2,则3a + 3b的最小值是 。
15、若 + = 2,求 1x + 1y 的最小值,并求x、y的值。
技巧六:整体代换
16、已知x > 0,y > 0,且 1x + 9y = 1,求x + y的最小值。
17、若x、y∈R+且2x + y = 1,求 1x + 1y 的最小值
18、已知a,b,x,y∈R+ 且 ax + by = 1,求x + y的最小值。
19、已知正实数x,y满足2x + y = 1,求 1x + 2y 的最小值
20、已知正实数x,y,z满足x + y + z = 1,求 1x + 4y + 9z 的最小值
技巧七:取平方
21、已知x,y为正实数,且x2 + y22 = 1,求x1 + y2 的最大值。
22、已知x,y为正实数,3x + 2y = 10,求函数y = 3x + 2y 的最值。
23、求函数y = 2x - 1 + 5 - 2x (12 < x < 52 )的最大值。
技巧八:已知条件既有和又有积,放缩后解不等式
24、已知a,b为正实数,2b + ab + a = 30,求函数y = 1ab 的最小值。
25、已知a>0,b>0,ab - (a + b ) = 1,求a + b的最小值。
26、若直角三角形周长为1,求它的面积最大值。
27、已知正数a,b满足ab = a + b + 3,求ab的取值范围。
课后练习
1、已知x > 0,y > 0,满足x + 2y = 1,求 1x + 1y 的最值
2、若x > 0,y > 0,且 2x + 8y = 1,求xy的最值
3、若-4 < x < 1,求 x2 - 2x + 22x - 2 的最大值
4、函数f (x) = x2x4 + 2 (x ≠ 0)的最大值是 ;此时的x值为 。
5、若对任意x > 0,xx2 + 3x + 1 ≤ a恒成立,则a的取值范围是 。
6、若点A(-2,-1)在直线mx + ny + 1 = 0上,其中mn > 0,则 1m + 2n 的最小
值为
7、已知x + 3y – 2 = 0,则3x + 27y + 1的最小值为
8、若x,y∈(0,+?)且2x + 8y – xy = 0,求x + y的最小值
9、已知两个正数a,b满足a + b = 4,求使 2a + 8b ≥ m恒成立的m的范围
10、函数y = - 1(a>0,a≠1)的图像恒过定点A,若点A在直线mx +
ny + 1 = 0上,其中mn > 0,求则 1m + 1n 的最小值为
11、已知x1·x2·…·x2009·x2010 = 1,且x1、x2…x2009、x2010都是正数,则(1 + x1)(1
+ x2)…(1 + x2009)(1 + x2010)的最小值是
12、已知直线l过点P(2,1),且与x轴、y轴的正半轴分别交于A、B两点,O
为坐标原点,则三角形OAB面积的最小值为
13、若x、y、z∈R+,x - 2y + 3z = 0,求 y2xz 的最小值
14、已知A(0,9)、B(0,16)两点,C(x,0)是x轴上任意一点,求当点C
在何位置时,∠ACB最大?
15、已知不等式(x + y)( 1x + ay ) ≥ 9对任意正实数x,y恒成立,则正实数a的最
小值为
