相平衡主要三元相图阅读与解析
合集下载
第五章三元相图-PPT精品.ppt
3 等温界面（水平截面） （1）做法：某一温度下的水平面与相图中各面的交线。 （2）截面图分析 3个相区：L, α, L+α; 2条相线：L1L2, S1S2（共轭曲线）; 若干连接线：可作为计算相对量的杠杆（偏向低熔
点组元；可用合金成分点与顶点的连线近似代替，过给定合 金成分点，只能有唯一的共轭连线。）
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （1）相图分析
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （2）等温截面 应用：可确定平衡相及其成分；可运用杠杆定律和重心定律。
是直边三角形 三相平衡区 两相区与之线接 （水平截面与棱柱面交线）
单相区与之点接 （水平截面与棱边的交点，表 示三个平衡相成分。）
类型： 包共晶转变 包晶转变
与4个单相区点接触； 相区邻接（四相平衡面） 与6个两相区线接触；
与4个三相区面接触。
第四节 三元相图总结
二 组元在固态有限溶解的共晶相图 3 四相平衡
两相共晶线 液相面交线 线：EnE 两相共晶面交线 液相单变量线 液相区与两相共晶面交线 固相单变量线
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （1）相图分析
液相面 固相面(组成) 面： 二相共晶面 三相共晶面 溶解度曲面：6个 两相区：6个 区： 单相区：4个 三相区：4个 四相区：1个
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图
（4）投影图 律）
定律）
合金结晶过程分析； 相组成物相对量计算（杠杆定律、重心定
组织组成物相对量计算（杠杆定律、重心
第四节 三元相图总结
二 组元在固态有限溶解的共晶相图
1 两相平衡
立体图：共轭曲面。 等温图：两条曲线。
点组元；可用合金成分点与顶点的连线近似代替，过给定合 金成分点，只能有唯一的共轭连线。）
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （1）相图分析
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （2）等温截面 应用：可确定平衡相及其成分；可运用杠杆定律和重心定律。
是直边三角形 三相平衡区 两相区与之线接 （水平截面与棱柱面交线）
单相区与之点接 （水平截面与棱边的交点，表 示三个平衡相成分。）
类型： 包共晶转变 包晶转变
与4个单相区点接触； 相区邻接（四相平衡面） 与6个两相区线接触；
与4个三相区面接触。
第四节 三元相图总结
二 组元在固态有限溶解的共晶相图 3 四相平衡
两相共晶线 液相面交线 线：EnE 两相共晶面交线 液相单变量线 液相区与两相共晶面交线 固相单变量线
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （1）相图分析
液相面 固相面(组成) 面： 二相共晶面 三相共晶面 溶解度曲面：6个 两相区：6个 区： 单相区：4个 三相区：4个 四相区：1个
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图
（4）投影图 律）
定律）
合金结晶过程分析； 相组成物相对量计算（杠杆定律、重心定
组织组成物相对量计算（杠杆定律、重心
第四节 三元相图总结
二 组元在固态有限溶解的共晶相图
1 两相平衡
立体图：共轭曲面。 等温图：两条曲线。
三元相图
© meg/aol ‘02
例如，三角形ABC内S点所代表的成分可通过下述方法求出：
设等边三角形各边长为100％，AB，BC，CA顺序分别代表B，C，A三 组元的含量。由 S点出发，分别向A，B，C顶角对应边BC，CA，AB
引平行线，相交于三边的c，a，b点。根据 等边三角形的性质，可得
Sa十Sb十Sc＝AB＝BC＝CA＝100％， 其中，Sc＝Ca=ω A/（%），Sa=Ab=ω B /（%）， Sb=Bc= ω C /（%）。
© meg/aol ‘02
C. 局部图形表示法
如果只需要研究三元系
中一定成分范围内的材
料，就可以在浓度三 角
形中取出有用的局部(见 图8.5)加以放大，这样会 表现得更加清晰。
外侧，且在另二条边的延长线范 围内。这需要从物质M1＋M2中 取出一定量的M3才能得到混合物 M，此规则称为交叉位置规则。
A
M1
C
M2 M
P M3
B
由杠杆规则：M1＋M2＝P M+M3＝P
M1＋M2＝M＋M3
从M1＋M2中取出M3愈多，则M点离M3愈远。
© meg/aol ‘02
9)共轭位置规则
在三元系统中，物质组成点M
M
A
B
© meg/aol ‘02
5)直线定律——在一确定的温度下，当某三元合金处于两相平衡时， 合金的成分点和两平衡相的成分点必定位于成分三角形中的同一条直
线上。该规则称为直线定律。
B
g’ f’ e’ s (α) e f g P
q
(β)
A
C
© meg/aol ‘02
证明如下：设合金P在某一温度下处于α 相（s点）和β 相（q点）两相平衡， α 相和β 相中的B组元含量分别为Ae’和Ag’。两相中C、B两组元的质量之和
第五章 三元相图
B
B%
C%
A
← A% C% →
C
b c
a
图 部分浓度三角形
§5.1.2 浓度三角形中具有特定意义的线
1）与某一边平行的直线
C
含对角组元浓度相等
A% d C% c
Bc C% 100% BC
A
B B% 图 平行于浓度三角形某一条边的直线
确定O点的成分 1）过O作A角对边的平行线 2）求平行线与A坐标的截距 得组元A的含量 3）同理求组元B、C的含量
三元系中如果任意两个组 元都可以无限互溶,那么它们 所组成的三元合金也可以形 成无限固溶体,这样的三元合 金相图,叫三元匀晶相图。
相图概况
[1] 特征点： ta, tb, tc- 三个纯组 元的熔点； [2]特征面：液相面、固相面； [3]相区：L, α, L+α。
图 三元匀晶相图
§5.3.1 相图分析
( A B )
Ax nE nA Ee
( A B C )
Ax ne nA Ee
§5.4.2 组元在固态下有限溶解，具有共晶转变的三 元相图
1.相图分析
从占有空间的角度看,固态有限互溶三元共晶相图比固态 完全不互溶三元共晶相图要多三个单相区(α、 β、 γ)和三个 固态两相区(α+β、 β+ γ、 α+ γ)。
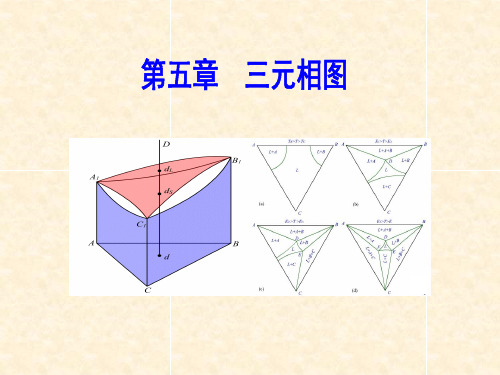
图 过成分三角形顶点的变温截面图
图 平行于成分三角形一边的变温截面图
用垂直截面图可以分析合金的平衡结晶过程，了解合金在 平衡冷却过程中发生相变的临界温度，以及可以了解合金在 一定温度下所处的平衡状态。 但是，用垂直截面图不能了解合金在一定温度下的平衡相 成分和平衡相的重量。
图 变温截面图的应用
第六章 三元相图
来计算。
如右图中的合金o，其中的
A
C
相与 相的相对量分别为：
% mo 100%
mn
三元相图中的杠杆定律
% on 100%
mn
6-1 三元相图基础
3. 重心法则：当三元系合金
B
处于三相平衡时，研究它们之间
的成分和相对量的关系，则须用
重心法则。如右图中，O为合金
( )
的成分点，P、Q、S分别为三个
三条三相共晶转变线相交于 a
E点。成分为 E 的液相在该点温
l
度下发生四相平衡共晶转变： f
LE TE A B C
E点称为三元共晶点，其所对应 m
的温度成为四相共晶转变温度。 A
c
e3 k
j
e1
b
e2
p g Eh
C
三元共晶点 E与三个固相的 成分点m、n、p 组成的水平面称 为四相平衡共晶转变平面。
由于第三组元的加入，三个
二元共晶点在三元系中均演化成
为三相共晶转变线 e1E、e2E 和 e3E。当液相成分沿着这三条曲 线变化时，则分别发生三相共晶
转变： e1 E e2E e3E
L AB L BC L AC
a c
e3
l
k
f j
e1
b
e2
m
p
g
A
Eh C
n
B
固态互不溶解的三元共晶相图
6-2 固态互不溶解的三元共晶相图
6-1 三元相图基础
三、三元相图中的杠杆定律及重心法则
1. 直线法则：一定温度下，三元系材料处于两相平衡 时，材料的成分点和其两个平衡相的成分点必然位于同一条 直线上，该规律称为直线法则或三点共线原则。
第八章 三元相图
L+A+ B + C
C
TA E1
TB E1 E3 E TA A3 A2 A1 TC E E2 E2
LA
L B
E3
L C
E
TB
B3 B2 E2 B1
E1
E3 TC E C3 C2
A
B
C1
C
液 相 面
初 生 相 开 始 析 出
——
TA A3 A2 A1 TB E1 E3 TC E B3 B2
E2
三元匀晶相图及合金的凝固（a）相图（b）冷却曲线。
2、平衡结晶过程分析
见图 三元固溶体在结晶过 程中液、固相成分的变化
任一合金O，由L缓冷, 当 冷到L面t1时开始凝固, 结晶 出成分为S1的固溶体，这 时L的成分=合金O的成分。 随T↓，固相沿固相面变化 ， 而对应的L沿液相面变化, 分别形成两条空间曲线， 冷到t4 时固相成分=合金O 的成分，与固相面相交， 凝固结束。
第八章 三元合金相图
工程实用材料多是三组元或三组元以上的，三组元的合 金可举例如下：轴承钢中的Fe-C-Cr合金；高锰耐磨钢中的 Fe-C-Mn合金；不锈钢中的Fe-Cr-Ni合金；铸铁中的Fe-C-Si 合金；铝合金中的Al-Mg-Si合金，Al-Cu-Mg合金等等。 当第三组元量大或量少影响大时，以三元研究，以掌握 成分、组织与性能的关系及合理应用。
B1
A
B
C3 C2
C1
C
固 相 面
A1
LA+ B LA+ B + C
B1
LA+ C
TA C1 A3 A2 A1
E
L B +C
四三 相相 平平 衡衡 共共 晶晶 转 变 结 束
C
TA E1
TB E1 E3 E TA A3 A2 A1 TC E E2 E2
LA
L B
E3
L C
E
TB
B3 B2 E2 B1
E1
E3 TC E C3 C2
A
B
C1
C
液 相 面
初 生 相 开 始 析 出
——
TA A3 A2 A1 TB E1 E3 TC E B3 B2
E2
三元匀晶相图及合金的凝固（a）相图（b）冷却曲线。
2、平衡结晶过程分析
见图 三元固溶体在结晶过 程中液、固相成分的变化
任一合金O，由L缓冷, 当 冷到L面t1时开始凝固, 结晶 出成分为S1的固溶体，这 时L的成分=合金O的成分。 随T↓，固相沿固相面变化 ， 而对应的L沿液相面变化, 分别形成两条空间曲线， 冷到t4 时固相成分=合金O 的成分，与固相面相交， 凝固结束。
第八章 三元合金相图
工程实用材料多是三组元或三组元以上的，三组元的合 金可举例如下：轴承钢中的Fe-C-Cr合金；高锰耐磨钢中的 Fe-C-Mn合金；不锈钢中的Fe-Cr-Ni合金；铸铁中的Fe-C-Si 合金；铝合金中的Al-Mg-Si合金，Al-Cu-Mg合金等等。 当第三组元量大或量少影响大时，以三元研究，以掌握 成分、组织与性能的关系及合理应用。
B1
A
B
C3 C2
C1
C
固 相 面
A1
LA+ B LA+ B + C
B1
LA+ C
TA C1 A3 A2 A1
E
L B +C
四三 相相 平平 衡衡 共共 晶晶 转 变 结 束
第八章三元相图
●结晶速度足够慢，液、固 相均能充分扩散，固相成分 由S1→ S2 →S3 →S4变化， 液相成分由L1 →L2 →L3 →L4 ，直至液相耗尽。 最后得到与合金组成完 全相同、成分均匀的三元固 溶体。
4. 变温截面图 (垂直截面) ●三元系变温截面截取三 维相图中液相面及固相 面所得的两条曲线并非 固相及液相的成分变化 迹线，它们之间不存在 相平衡关系，因此，只 可以根据这些线判断合 金凝固的临界温度点， 而不能根据这些线确定 两平衡相的成分及相对 量(即，不能应用杠杆 定律)。
2. 等温截面图(水平截面) ●在等温截面上， l1l2为等温截面与液相面的交线，s1s2为等温截 面与固相面的交线，它们称为共轭曲线。 ●在等温截面上，根据直线法则，合金的成分点一定位于两平 衡相L相和α相对应成分点的共轭连线上。 ●通过给定的合金成分点， 只能有唯一但不定的共 轭连线。根据相率，一 个平衡相的成分可以独 立改变，而另一平衡相 的成分必定随之变化。 因此，在一定温度下， 欲确定两个平衡相的成 分，必须先用实验方法 确定其中一相的成分， 然后利用直线法则来确 定另一相的相应成分。
8.1.1 三元相图成分表示方法 一般用成分三角形或浓度三角形表示。三元系的成分常用的 成分三角形是等边三角形，另外，也采用等腰三角形和直角三角 形） 1. 等边成分三角形 ●三角形的三个顶点A、B、 C分别表示三个组元； ●三角形的三条边分别表示 3 个二元系的成分坐标； ●三角形内的任一点表示三 元系的某一成分。
练习
C2
g+e
C1+C2
C1
C2+e
a+ g a+ g
●液相面投影图特点
三 进
两进一出
一进两出
●截面：面→线；线→点 垂直截面
三元相图
• 1.立体图 • f=c-p+1 fmax=4 单相区
两相区
三相区 四相区
同析三角台
单相区(1个液相区，固溶体相、、的单相区)
液相面
相单相区为afmk与Aa之间的区域
a1aa0a0’a1为B 组元在相中的固溶度面 b1bb0b0’b1为A 组元在相中的固溶度面
两相区
三元共晶转变前 三元共晶转变后
4）三个固相平衡三棱台 A）三条棱为三条单变量线；也称同析线，即有一相同时析 出另两相，从而由单相区直接进入三相区； B) 顶面与四相平衡面重合，底面与成分三角形重合； C) 三个侧面是三相区和两相区（均为固相）的分界面； D）合金进入该相区后，随温度的下降，三相的相对量随之 发生改变（由重心定理可知）。 (
8.3 固态有限互 溶的三元共晶相 图
1. 空间模型
组元在固态有限互 溶的三元共晶相图的
空间模型，如图8．17 所示。
1）液相面和固相面
图中每个液、固两相平衡区和单相固溶体区之间都存 在一个和液相面共扼的固相面，即
固相面afmla和液相面ae1Ee3a共扼；
固相面bgnhb和液相面be1Ee2b共扼;
3)三元共晶转变面
成分为E的液相在水平面mnp（三元共晶转变面）发
生四相平衡的共晶转变：
Le1 ~ E f ~ m g ~ n Le2 ~ E h~ n i ~ p LE m n p Le3 ~ E k ~ p i ~ m
2.
投影图
图8.19 为三元共晶相图的 投影图。
从图中可清楚看到3条共晶转变线的投影e1E，e2E 和e3E把浓 度三角形划分成3个区域Ae1Ee3A ， Be1Ee2B和C e2Ee3 C， 这是3个液相面的投影。 投影图中间的三角形mnp为四相平衡共晶平 面。
两相区
三相区 四相区
同析三角台
单相区(1个液相区，固溶体相、、的单相区)
液相面
相单相区为afmk与Aa之间的区域
a1aa0a0’a1为B 组元在相中的固溶度面 b1bb0b0’b1为A 组元在相中的固溶度面
两相区
三元共晶转变前 三元共晶转变后
4）三个固相平衡三棱台 A）三条棱为三条单变量线；也称同析线，即有一相同时析 出另两相，从而由单相区直接进入三相区； B) 顶面与四相平衡面重合，底面与成分三角形重合； C) 三个侧面是三相区和两相区（均为固相）的分界面； D）合金进入该相区后，随温度的下降，三相的相对量随之 发生改变（由重心定理可知）。 (
8.3 固态有限互 溶的三元共晶相 图
1. 空间模型
组元在固态有限互 溶的三元共晶相图的
空间模型，如图8．17 所示。
1）液相面和固相面
图中每个液、固两相平衡区和单相固溶体区之间都存 在一个和液相面共扼的固相面，即
固相面afmla和液相面ae1Ee3a共扼；
固相面bgnhb和液相面be1Ee2b共扼;
3)三元共晶转变面
成分为E的液相在水平面mnp（三元共晶转变面）发
生四相平衡的共晶转变：
Le1 ~ E f ~ m g ~ n Le2 ~ E h~ n i ~ p LE m n p Le3 ~ E k ~ p i ~ m
2.
投影图
图8.19 为三元共晶相图的 投影图。
从图中可清楚看到3条共晶转变线的投影e1E，e2E 和e3E把浓 度三角形划分成3个区域Ae1Ee3A ， Be1Ee2B和C e2Ee3 C， 这是3个液相面的投影。 投影图中间的三角形mnp为四相平衡共晶平 面。
8.7包晶相图
三元相图
❖ 具有三相平衡的三元共晶相图 ❖ 具有三相平衡的三元包晶相图 ❖ 具有四相平衡的三元包共晶相图 ❖ 具有四相平衡的三元包晶相图 ❖ 三元相图举例
三相平衡的三元相图
❖ 由相律可知三元合金在三相平衡时，其自由度为1，所以温 度和三个平衡相的成分只有一个可以独立改变，即在温度一 定时三个平衡相的成分是一定的，温度改变时三个平衡相的 成分也随之改变，当一个相的成分被确定后，则温度和另外 两个相的成分就随之而定了。
可见合金应发生四相平衡包晶转变
在发生这一转变的前后，应发生 共晶转变
及
包晶转变
O点位于初晶的 液相面内，其初生相应为 。
综上所述，合金O的平衡凝固过程为：
由于O点位于L、 单变量线之间 转变结束后，L、 两相平衡
然后发生
转变
合金凝固后的组织应为单一的 相。
但因O点位于三角形a1b1c1内，所以在进行
包晶转变的L、 单变量线之间
,
,
初晶 的液相面内，同时还位于三角形
,
a1b1c1内，由此可以推断，此合金的凝
固顺序应为：
室温组织为初晶 ＋次生 ＋次生 。
总结：如何区分四相平衡的类型
1.四相平衡共晶转变平面
（1）四相平衡共晶转变的反应式为：L→α+β+γ。 （2）在立体图中四相平衡平面，其上面与三个三相平衡棱 柱衔接，下面与一个三相平衡棱柱衔接。图中带箭头的线分 别为平衡相的单变量线，也就是三棱柱的棱边。
而成分位于 bpc中的合金在
L r 反应后， 进入 L r 三相区
而成为位于ap线上的三元合金在凝固时 不发生三相平衡包晶转变。
(L , L r)
在匀晶转变 L 后
在Tp温度发生四相平衡包共晶转变
❖ 具有三相平衡的三元共晶相图 ❖ 具有三相平衡的三元包晶相图 ❖ 具有四相平衡的三元包共晶相图 ❖ 具有四相平衡的三元包晶相图 ❖ 三元相图举例
三相平衡的三元相图
❖ 由相律可知三元合金在三相平衡时，其自由度为1，所以温 度和三个平衡相的成分只有一个可以独立改变，即在温度一 定时三个平衡相的成分是一定的，温度改变时三个平衡相的 成分也随之改变，当一个相的成分被确定后，则温度和另外 两个相的成分就随之而定了。
可见合金应发生四相平衡包晶转变
在发生这一转变的前后，应发生 共晶转变
及
包晶转变
O点位于初晶的 液相面内，其初生相应为 。
综上所述，合金O的平衡凝固过程为：
由于O点位于L、 单变量线之间 转变结束后，L、 两相平衡
然后发生
转变
合金凝固后的组织应为单一的 相。
但因O点位于三角形a1b1c1内，所以在进行
包晶转变的L、 单变量线之间
,
,
初晶 的液相面内，同时还位于三角形
,
a1b1c1内，由此可以推断，此合金的凝
固顺序应为：
室温组织为初晶 ＋次生 ＋次生 。
总结：如何区分四相平衡的类型
1.四相平衡共晶转变平面
（1）四相平衡共晶转变的反应式为：L→α+β+γ。 （2）在立体图中四相平衡平面，其上面与三个三相平衡棱 柱衔接，下面与一个三相平衡棱柱衔接。图中带箭头的线分 别为平衡相的单变量线，也就是三棱柱的棱边。
而成分位于 bpc中的合金在
L r 反应后， 进入 L r 三相区
而成为位于ap线上的三元合金在凝固时 不发生三相平衡包晶转变。
(L , L r)
在匀晶转变 L 后
在Tp温度发生四相平衡包共晶转变
第5章-2---三元相图1
5.13 四相平衡共晶系
5.13.4 综合投影图
冷却过程中有 四相反应
L-a+b+
5.13 四相平衡共晶系
5.13.4 综合投影图
5.13 四相平衡共晶系 L
L－a
合金 o
L－a+b
L－a+b+
a+a + b+a+b++b+
L
合金 o’
L－b
L－a+b
a+b
b+a+b+a+
5.13.4 综合投影图
5.13 四相平衡共晶系
5.13.3、垂直截面
5.13 四相平衡共晶系
5.13.4 综合投影图
1、作法：将立体图中 各空间曲面、曲线投 影到成分三角形
2、用途： a、可得到各个面的投影 b、可得到各相区的投影 c、各种成分的平衡冷却
过程 d、组织分区图
5.13 四相平衡共晶系
5.13.4 综合投影图
5.13 四相平衡共晶系
5.13.4 综合投影图
5.13 四相平衡共晶系
I a; II a + bII ; III a + bII + II ; IV a + (a + b ) + bII ; V a + (a + b ) + bII + II ; VI a + (a + b ) + (a + b + ) + bII + II
用杠杆定理
5.12 三相平衡三元
5.12.2 几种典型的三相平衡三元系
5.12 三相平衡三元系
三元相图
浓度三角形的基本性质①等含量规则：平行于一边的直线上所有点，表示这个边对应顶点的组元含量均相等；②等比例规则：过一顶点的直线上所有点，表示另两个顶点代表的两组元的含量比为一定值。
③背向规则：过一组元的直线上所有的点，离该组元越远，该组元越少，而其他两组元成分比例不变。
直线法则、杠杆定律及重心法则（1）杠杆定律及直线法则：当两个组成已知的相转变成一个新相时，则新相的组成点必在两个原始相组成点的连线上，且位于两点之间，两个原始相的质量之比与它们的组成点到新相组成点之间的距离成反比，称为三元系统的杠杆规则；反之，一个相在一定温度下转变为两个相时也成立。
推论当给定合金在一定温度下处于两相平衡时，若其中一相的成分给定，另一相的成分点必在已知相成分点与合金成分点连线的延长线上；若两平衡相的成分点已知，合金的成分点必然位于两个已知成分点的连线上。
(2) 重心法则把M、N、Q三相混合，要得到新相点P，可采用下述方法：根据杠杆规则先将M和N混合成S，S相的组成点必定在MN连线上，且在M和N之间，具体位置要根据M、N的相对含量而定；接着把S和Q混合得到P相。
即M＋N＝S，S＋Q＝P。
综合两式，所以M＋N＋Q＝P表明P相可以通过M、N、Q三相合成而得。
反之，从P相可以分解出M、N、Q三相。
P 点所处的这种位置称为重心位置。
重心法则外推组元在固态互不相溶的共晶相图（1）相图分析面：液相面：3个两元共晶面：6个三元共晶面：1个区：单相区：4个两相区：3个三相区：4个四相区：1个三相共晶平衡区的三元相相图分析：线：三条单变量曲线液相面交线两相共晶线面：2个液相面3个固相面2个固溶面2个三相共晶面区：3个单相区3个两相区1个三相区a：A+C为溶剂B为溶质的固溶体；b：B为溶剂A+C为溶质的固溶体投影图分析各线、面、区在投影图中的位置相图分析：线：三条单变量曲线液相面交线两相共晶线面：2个液相面3个固相面2个固溶面2个三相共晶面区：3个单相区3个两相区1个三相区共晶型与包晶型反应两类三相区的比较共晶型反应三相区 包晶型反应三相区 水平截面图直边三角形 倒立 正立垂直截面图曲边三角形 正立倒立上或下顶点与液相区相连接侧顶点与液相区相连接相区接触法则相数差接触类型 实例 1面接触 2or0线接触 3点接触从占有空间的角度看,固态有限互溶三元共晶相图比固态完全不互溶三元共晶相图要多三个单相区(a,b,g)和三个固态两相区(a+b,b+g,g+a),请见下表:相图分析：线：3条两相共晶线面：3个液相面3个固相面6个两相共晶开始面3个两相共晶结束面3个两相共析面（两相固溶面）相图分析：线：3条两相共晶线Ee1 、Ee2 、Ee3面：3个液相面ae1Ee3a 、be2Ee2b 、ce3Ee2c3个固相面almfa 、bgnhb 、ckpic6个两相共晶开始面（α+β）feEmf 、ge1Eng （β+γ）he2Enh、ie2Epi（γ+α）le3Eml、ke3Epk3个两相共晶结束面fmngf 、hnpih 、qmpli3个两相共析面（两相固溶面）mm'n'nm 、nn'p'pn 、mm'p'pm6个单相析出面（单相固溶面）（α→γII ) ll'm'ml (α→βII ) ff'm'mf(β→αII ) gg'nn'g (β→γII ) hnn'h'h(γ→αII ) kk'p'pk (γ→βII ) ii'p'pi1个3相共晶面以材料O为例,冷却到液相面,开始凝固出初晶a,其成分点位于与液相面Ae1Ee3共轭的固相面Afml上,但需用连相线来确定。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
L +B C p=3 f=1
I (B消失)[S ，S]
LS p=2 f=2
E[S ，S+(C+A)]
L S+C+A p=4 f=0
E(L消失)[5 ，A+S+C]
总结 C
1、无变量点性质 P点：L+B S+C
E点： L A＋S+C
ቤተ መጻሕፍቲ ባይዱ
2、界线性质PQ是转熔线 L+B S
C
其它为共熔线。
e4
E Pm
(1) 点的性质：
P 单转熔点 L＋A S＋C ；
E 共熔点 L S＋C＋B
R 过渡点，双降点 L＋A＋B S
B
(L起介质作用)
(2) 用切线规则判断界线性质。
PR ： L＋A S
b (3) 分析1点的析晶路程
a
C
C
P FE
NS
.1 D R
AO
B
A
S
e3
B
熔体1 L
1 [A , (A)] L A
连线的延长线上，则表示界线上该处具有转熔性质，其
中远离交点的晶相被回吸。
共熔性质 分界点
界线上任一点的切线与 相应连线的交点实际上 表示了该点液相的瞬时 析晶组成
瞬时析晶组成是指液 相冷却到该点温度， 从该点组成的液相中 所析出的晶相组成
转熔性质
区别于系统固相的总组成 = 该点析出的晶体 + 冷却到 该点之前析出的所有晶体
生成一个固相分解的二元化合物的三元相图
R点：没有相应的副三角形 R点是一个双转熔点
LRAB S
过渡点 不是析晶的结束点
生成一个固相分解的二元化合物的三元系统
C
C
PE
A A S+A S
S
.1
S+B
R B
e3
A+B
L+A
L+B e3/
特点：三个无变量点，但只能划分两个 副三角形，即可能的析晶终点是P点或E 点。
(2) 不同组成的结晶路程分析 A、划分副三角形， 确定组成点的位置；
B、 分析析晶产物和析晶终点； C、分析析晶路线，正确书写其结晶路
程； D、利用规则检验其正确性。
C
分析：1点在S的初晶区内，
开始析出晶相为S，
C
e4
E Pm
e3
AD
1
.
S
B
D
A
e1 F
QS
B
组成点在ASC内， 析晶终点为E点， 析出晶相为A、S、C；
A
e1
QS
B
熔体2 L
2 [B , (B)] L B
p=1 f=3
p=2 f=2
L C +B Q[B , B＋(C)]
p=3 f=1
P [O ，B+(S)+C]
L+B S+C p=4 f=0
P(L消失)[2 ，B＋S+C]
C
D
F
C .G
e4
3 E Pm
e3
分析：3点在C的初晶区内， 开始析出的晶相为C，
熔体1 L
LS
1 [S , (S)]
p=1 f=3
p=2 f=2
L A +S D[S , S＋(A)]
p=3 f=1
E [ F，A+S+(C)]
L A +S+C E(L消失)[1,A＋S+C]
p=4 f=0
C
2点在B的初晶区，
开始析出的晶相为B，
C
e4
E
P
Q m
e3
2. O
A
S
B
组成点在BSC内， 析晶终点为P点，析 出晶相为B、S、C。
在ASC内，析晶终 点在E点，结晶终产物是A、 S、C。途中经过P点，P点
A
S
A
e1
熔体3 L p=1 f=3
B
QS
B
3 [C , (C)] L C
p=2 f=2
是转熔点，同时也是过渡 点。 L+B S+C
L C +B m[C , C＋(B)]
p=3 f=1
P [D ，B+(S)+C]
L+B S+C p=4 f=0
相平衡
(三元系统图) 主要相图解析
生成一个一致熔二元化合物的三元相图
相当于2个简 单三元相图 的组合
• 在三元系统 中某二个组分 间生成的化合 物称为二元化 合物
• 二元化合物的 组成点在浓度 三角形的一条 边上
• 一致熔化合物 的组成点在其 初晶区内
生成一个不一致熔二元化合物的三元相图
转熔线
冷 却 时 pP 界 线 上 的液相回吸晶体B 而析出晶体S
p=1 f=3
p=2 f=2
L +A S D[A , A＋(S)]
p=3 f=1
LS N (A消失)[S ，S]
p=2 f=2
F[S ，S+(C)]
L S+C p=3 f=1
E[O ，(B)+S+C]
L B+S+C E(L消失)[1 ，B+S+C] p=4 f=0
具有一个一致熔三元化合物的三元相图
e3
3、组成点
在 ASC内，E点是析晶终点，
A
S
B
在 BSC内，P点是析晶终点。A
e1
在连线SC上，P点是析晶终点。
QS
B
4、 P点:在多边形PCSQ范围内，经过P点时发生转熔， 晶相B先消失， 液相沿PE移动，在E点液相消失； 在 SPQ内存在穿晶区； 在 BSC内，在P点液相先消失； 在连线SC上，B和液相同时消失。
3. 重心规则
判断无变量点的性质
• 如无变量点处于其相应的副三角形的重心位，则该无变 量点为低共熔点；如无变量点处于其相应的副三角形的 交叉位，则为单转熔点；如无变量点处于其相应的副三 角形的共轭位，则为双转熔点。
双降点
共轭位
4. 三角形规则
判断结晶产物和结晶终 点
• 原始熔体组成点所在副三角形的三个顶点表示的物质即 为其结晶产物；与这三个物质相应的初晶区所包围的三 元无变量点是其结晶结束点。
三元化合物，一致熔
具有一个不一致熔三元化合物的三元相图
具有不一致熔融三元化合物的三元系统相图
(1) 特点：组成点不在初晶区内；
(2) 划分三个副三角形；
(3) 用重心规则或温降变化方向判断点的性质，
无变量点所处位置有两种可能，交叉位或共轭位， C
相应的性质为单转熔点或双转熔点；
(4)用切线规则判断界线性质。有时某一界线具
有两种性质， 即共熔线和转熔线。
e1 E1
C E2 e2
E1：低共熔点 LA＋S＋C E2： 低共熔点 LB＋S＋C
界线pP由二元相图的 转熔点p’发展而得：
不一致熔二元化合物 组成点不在其初晶区
判读三元相图的规则
1. 连线规则
判断界线的温度走向
• 将一条界线（或其延长线）与相应的连线（或其延长线） 相交，其交点是该界线上的温度最高点。
2. 切线规则
判断界线的性质
• 将界线上某一点所作的切线与相应的连线相交，如交点 在连线上，则表示界线上该处具有共熔性质；如交点在
L S+C P(B消失)[F ，S+C]
p=3 f=1
E [G ，S+(A)+C] L A+S+C E(L消失)[3 ，A+S+C] p=4 f=0
C
注：5点在ES的连线上
C
e4
E Pm
e3
I
A
S H
.5
B
A
e1
Q
熔体5 L
5 [B , (B)] L B
p=1 f=3
p=2 f=2
S
B
H[B , B＋(S)]