2017年第十届“认证杯”数学建模网络挑战赛
2017年数学建模竞赛的策略与实践

数学建模竞赛的策略与实践
2.参加数学建模竞赛的基本原则
1-2-3-4-5-6原则:
一个中心:目标; 二个基本点:队员能力,优势互补; 三个要素:方法、模型、摘要; 四个精神:主人、拼搏、合作、忍让; 五个环节:识题、假设、建模、求解、写作; 六个意识:参与、竞争、攻关、创新、特色、
自圆。
3
数学建模竞赛的策略与实践
2017年数学建模竞赛 的策略与实践
数学建模竞赛的策略与实践
1.参加数学建模竞赛的策略 模型假设要选取必要条件; 模型分析要选取充分条件; 模型建立要选取充分必要条件; 模型检验要做误差和灵敏度分析; 模型评价要做多因素的综合评价。 论文摘要要做聚类分析; 论文结构要做整数规划; 论文内容要做动态规划; 文中模型要用好线性规划与非线性规划。
3.问题的分析与假设
根据评阅原则,基本假设的合理性很重要 (1)根据题目中条件和要求作出假设 (2)关键性(本质性)假设不能缺
(3)假设要切合问题本身 (4)假设要规范、精练(3-5条),有些假设可以在正文中给出
4.符号说明
公式符号在Mathtype中输入,注意符号的选取【通用、简洁、易记,避免过于复杂的记号】
平台,计算过程中,中间结果呈现要适当(一定要突出重点)
• 题目中要求回答的问题、数值结果、结论,需一一列出 • 结果表示:要集中、直观、凸显,便于比较分析 (表现形式可以多样化) • 必要时对问题解答,作定性或定量分析和讨论,最后结论要明确 • 最终数值结果的正确性或合理性
7.模型与算法的优缺点分析及改进
携手共进,齐创精品工程
Thank You
世界触手可及
▲ 表述:通顺、规范、准确、精练、大气【避免出现:说话象书面语,写作象口头语】 ▲ 重点突出:一定要突出模型、算法、结论、创新点、特色 ▲ 表述层次清晰:让人一看就知道这篇论文研究什么问题,做了什么工作,用的什么方法,得到什么结果,
2017数学建模国赛题目

2017数学建模国赛题目(实用版)目录一、2017 年数学建模国赛简介二、2017 年数学建模国赛题目概述三、题目 A:基于无人机的森林防火系统四、题目 B:城市交通信号灯控制优化五、题目 C:无人机航拍图像处理及应用六、题目 D:新型城镇化背景下的乡村规划正文一、2017 年数学建模国赛简介2017 年数学建模国赛,即 2017 年全国大学生数学建模竞赛,是中国工业与应用数学学会主办的面向全国大学生的群众性科技活动,目的在于激励学生学习数学的积极性,提高学生建立数学模型和运用计算机技术解决实际问题的综合能力,鼓励广大学生踊跃参加课外科技活动,开拓知识面,培养创造精神及合作意识,推动大学数学教学体系、教学内容和方法的改革。
二、2017 年数学建模国赛题目概述2017 年数学建模国赛共有四个题目,分别是:基于无人机的森林防火系统、城市交通信号灯控制优化、无人机航拍图像处理及应用、新型城镇化背景下的乡村规划。
这四个题目分别涉及到林业、交通、航空、城乡规划等领域,旨在考查学生运用数学知识解决实际问题的能力。
三、题目 A:基于无人机的森林防火系统题目 A 要求参赛选手针对森林防火问题,建立无人机监测森林火情的数学模型,并结合实际数据,分析火情发生的可能性,为森林防火工作提供科学依据。
此题考查了学生对无人机技术、遥感技术、数据挖掘等领域的综合运用能力。
四、题目 B:城市交通信号灯控制优化题目 B 要求参赛选手针对城市交通信号灯控制问题,建立数学模型,分析交通流量、拥堵状况等数据,优化信号灯控制策略,提高道路通行能力。
此题考查了学生对交通工程、数据分析、优化算法等领域的综合运用能力。
五、题目 C:无人机航拍图像处理及应用题目 C 要求参赛选手针对无人机航拍图像处理问题,研究图像去噪、增强、拼接等技术,并结合实际场景,分析航拍图像在农业、地质、环保等领域的应用价值。
此题考查了学生对图像处理、计算机视觉、遥感技术等领域的综合运用能力。
2017年全国大学生数学建模竞赛优秀论文

2017年全国大学生数学建模竞赛优秀论文数学是知识的工具,亦是其它知识工具的泉源。
所有研究顺序和度量的科学均和数学有关,数学建模是培养学生运用数学工具解决实际问题的最好表现。
下文是店铺为大家搜集整理的关于2017年全国大学生数学建模竞赛优秀论文的内容,欢迎大家阅读参考!2017年全国大学生数学建模竞赛优秀论文篇1浅析数学建模课程改革及其教学方法论文关键词:数学课程;数学建模;课程设置;课程改革论文摘要:数学建模教学和竞赛的开展,是培养学生创新能力的重要途径。
对数学建模竞赛中出现的问题进行分析,找出问题产生的根源与必修课和专业课设置不合理有关,应对高校数学课程的设置、教学方式等进行改革,并提出具体改革建议。
1. 前言数学建模,从宏观上讲是人们借助数学改造自然、征服自然的过程,从微观上讲是把数学作为一种工具并应用它解决实际问题的教学活动方式。
数学建模教育本身是一种素质教育,数学建模的教学与竞赛是实施素质教育的有效途径,它既增强了学生的数学应用意识,又提高了学生运用数学知识和计算机技术分析和解决问题的能力。
因而加强数学建模教育,培养学生的数学应用意识与能力已成为我国高校数学建模课程改革的重要目标之一。
虽然目前我国许多高校在数学建模方面取得了一些成绩,但大学生们在竞赛中也暴露出了许多问题,引发出对传统的课程设置和教学方法的思考。
2. 数学建模的现状和所存在问题与原因分析2.1 建模竞赛的现状根据竞赛时间(九月中下旬),我国大部分高校每年一般在七月中旬便开始组织学生的报名培训工作。
培训内容分为两个部分:首先集中讲解一些基础知识,主要包括常微分方程、概率与数理统计、运筹学、数学实验、建模基础等课程;然后进行建模的模拟训练,以往届国内外普通组和大专组的部分竞赛题为选题,让学生自愿结组,在规定时间内完成,并自愿为同学讲解各自的解题思路和方法。
参赛学生首先要参加培训,他们一般是先关注校园网上的通知,再到各院系自愿报名而组成,经培训后选拔出参赛队员。
2017年数模国赛B题优秀论文(省一等奖)

二、问题分析
2.1 问题的总分析 本文首先要求我们研究已完成项目的定价规律,分析部分任务未完成的原因,其次 针对部分任务未完成的原因,重新设计任务的定价方案,再次在问题二的基础上考虑任 务打包的情况,修改问题二的定价模型,并分析对最终的任务完成情况的影响,最后针 对新项目的任务位置信息设计任务定价方案,并评价此方案的实施效果。
基于任务吸引度的众包平台定价方案优化
摘要
本文对自助式劳务平台的运营模式及运营效果进行了分析, 建立多目标规划模型对 定价方案进行了优化,并加入任务打包情况对此方案进行了修改,最终应用在新项目的 任务定价中。 对问题一,该项目任务点分布于四个不同城市。在分析定价规律时,考虑数据的宏 观分布情况,分别以各任务点与市中心距离、各任务点处会员分布密度为回归变量,以 定价为响应变量,通过回归分析研究变量间的定量关系,确定回归系数后,以会员分布 密度与定价的回归方程作为定价规律判定。回归方程表明:定价在宏观上与会员分布密 度呈反比例函数关系。其次,在分析任务未完成原因时,分别定义任务的距离吸引度、 标价吸引度来量化距离、 标价对任务完成情况的影响, 将任务未完成原因归结为四方面: 标价吸引度低、距离吸引度低、会员分布密度低、其它因素。 对问题二,将设计定价方案的过程视为定价方与任务完成方进行博弈的过程,在博 弈论的视角下对众包任务定价方案进行了设计。首先定义了定价基准值的概念,来量化 任务本身的价值。根据问题一的分析结果,任务未完成原因主要是距离吸引度、标价吸 引度过低,因此在定价时,从权衡各任务点距离吸引度、标价吸引度入手,分析了任务 完成过程中个体的行为规律。针对任务完成方,分析了会员预定各任务的概率;针对定 价方,分析了任务被预定概率、任务被完成概率,其中任务被完成概率与由会员信誉值 决定的概率修正因子有关。以任务被完成概率、定价为目标,建立了无约束多目标规划 模型,利用遗传算法确定了每个任务的最优定价。最后,比较了所设计方案与原方案下 任务完成比例和任务标价,很好地表现出了新方案优化效果。其中新方案的任务完成率 为:0.7122,标价总额为:34112.7356。 对问题三, 要求修改问题二中定价模型, 从而导出适用于含任务包的任务定价方案。 任务打包后,对定价方案造成的影响主要是:任务包中任务个数与会员预定限额之间的 矛盾。首先,在考虑会员预定限额的基础上,确定了任务包的基准价、标价吸引度及距 离吸引度。受到物流配送区域划分方法的启发,建立了基于点密度的任务聚类模型对任 务进行打包处理。进而类比问题二,建立了含任务包的目标规划模型,确定最优定价, 并得出此定价下的任务完成概率。与问题二中任务完成率、标价总额进行对比,结果表 明,将任务打包后任务完成率提高。其中打包后的任务完成率为:0.8059,标价总额为: 36371.4592。 对问题四,针对新项目任务分布高度集中的特点,需要结合实际,对任务包内任务 个数进行限制。基于任务个数上限,对问题三打包方案进行了改进,运用改进后的打包 方案对任务打包后,通过建立含任务包的目标规划定价模型,确定了每项任务的定价。 结果分析表明,在此方案下任务完成率为:0.5042。最后,加入任务开始预定时间指标, 对众包任务的下发、预定、完成过程进行仿真分析,作为模型的改进。
数学建模2017b题范文

数学建模2017b题范文嘿,朋友!你知道数学建模吗?那可不是一般的厉害!想想看,数学建模就像是给复杂的现实世界搭建了一座清晰明了的桥梁。
它可不是单纯的数字游戏,而是解决实际问题的神奇法宝。
就拿 2017b 题来说吧,那简直就是一场充满挑战和惊喜的冒险!它就像一个迷宫,一开始你觉得自己迷失其中,找不到方向。
可当你一点点运用数学知识,一点点分析问题,你会发现,那些看似无解的难题,其实都隐藏着线索。
比如说,题目中涉及到的数据,那可不是随便给你的。
它们就像一颗颗珍贵的宝石,等着你去挖掘、去打磨,最终变成璀璨的项链。
你得仔细琢磨每个数据背后的含义,为什么是这个数值,而不是别的?这难道不是很有趣吗?在解决问题的过程中,你得像个超级侦探,不放过任何一个细节。
一点点的偏差,可能就会让你的结果谬之千里。
这难道不紧张刺激吗?而且,数学建模还需要团队合作。
这就像一场接力赛,每个人都要发挥自己的优势,跑得快的冲在前头,耐力好的在后面稳住阵脚。
大家相互配合,相互支持,共同朝着目标前进。
如果有人掉链子,整个团队都可能受到影响。
这难道不考验大家的默契吗?还有啊,数学建模能让你充分发挥自己的创造力。
你可以尝试不同的方法,不同的思路,就像在画布上自由挥洒颜料,创造出属于自己的独特作品。
谁说一定要按照常规来?只要能解决问题,一切皆有可能!这难道不让人兴奋吗?当你终于得出结论,那种成就感,简直无法用言语来形容!就好像你爬上了一座高山,俯瞰着脚下的美景,心中充满了自豪和满足。
所以说,数学建模 2017b 题,它不仅仅是一道题目,更是一次成长的机会,一次挑战自我的冒险。
它让我们看到了数学的魅力,感受到了团队的力量,体验到了创造的快乐。
难道你不想也来试试,感受一下这种无与伦比的美妙吗?总之,数学建模 2017b 题是一次令人难忘的经历,它让我们在数学的海洋中畅游,发现了无数的宝藏。
让我们一起勇敢地面对挑战,用数学的力量去改变世界吧!。
2017“认证杯”数学中国数学建模网络挑战赛高中组个人赛赛题

地震监测台站的合理布局问题(高中组个人赛赛题)2017年8月8日21时19分46秒,四川省北部阿坝州九寨沟县发生了7.0级地震,震中位于北纬33.20度,东经103.82度的九寨沟核心景区西部5公里处的比芒村,震中东距九寨沟县城永乐镇39公里、南距松潘县66公里、东北距舟曲县83公里、东南距文县85公里、西北距若尔盖县90公里,东偏北距陇南市105公里,南距成都市285公里。
九寨沟地震致使九寨沟县经济社会遭到重创,所有在建项目和新建项目全面停工或延期开工,全县预估直接经济损失达224.5亿元。
地震监测台站可以对地震时和地震前的各类自然现象进行监测,其对地震发生时的灾情掌握和地震发生前的预报具有重要的意义,是一个国家抗灾减灾综合实力的体现。
基于地震监测设施观测内容、原理的不同,其一般可以分为测震监测设施、强震监测设施与前兆监测设施三类。
测震、强震监测设施主要用于地震发生时对地震运动状态的观测,测震监测设施精度较高,可观测1.0级强度的地震;强震监测设施精度较低,用于观测4.0以上级别的地震。
前兆监测设施主要通过对多类物理和化学场量的持续观测,研究了解地震发生机理并做出地震预报。
根据观测的对象,将前兆观测分为三类,即形变(含重力)观测、电磁观测和地下流体观测。
地震监测台站的布局原则如下:1、均衡全面原则:各类地震监测设施基本做到均衡分布、全面覆盖。
2、新技术原则:结合地震台预报技术发展特点,大力增加技术更加先进、对城市建设干扰较小的地震监测设施,如GPS卫星观测设施,确保地震监测水平不断提升。
3、城乡建设协调原则:新建、迁建的地震监测设施尽量避开对其有影响的干扰要素,如三级公路,高压输电线路,工厂等。
4、经济原则:如果在半径100公里的范围内台站数少于20的,应以增建新的台站为主,如果在25-30之间的,应以改建原有台站提高台站的观测质量为主。
5、精度原则:达到全县1.0级以上的地震监测能够在3分钟内给出,4.0级以上地震的初步测定结果,能够在20分钟内完成,对有显著影响的地震在震后1小时内能够锁定震中位置。
2017数学建模国赛B题

我们看到,价格定的越高,任务完成的概率就越大,������1增大,反映了任务完在于增加成本,此时������2也增加,因此,衡量定价绩效
的总体指标ω是这两者经过调整之后的差值:
ω = ������1 − ������2
此外,我们给出一个辅助的定价绩效的指标:区域会员参与度δ:
1
一、问题重述
“拍照赚钱”是移动互联网下的一种自助式服务模式。用户下载 APP,注册成为 APP 的 会员,然后从 APP 上领取需要拍照的任务(比如上超市去检查某种商品的上架情况),赚取 APP 对任务所标定的酬金。这种基于移动互联网的自助式劳务众包平台,为企业提供各种商 业检查和信息搜集,相比传统的市场调查方式可以大大节省调查成本,而且有效地保证了调 查数据真实性,缩短了调查的周期。因此 APP 成为该平台运行的核心,而 APP 中的任务定价 又是其核心要素。如果定价不合理,有的任务就会无人问津,而导致商品检查的失败。
不同价格区间执行率不同的问题,此时会员得到的报酬各处平均,因此不同位置定价的不同
将会导致相同的执行率。
6
10
8
6
4
2
0
60-65.5
65.5
65.5-70 70-75
75-80
>80
已完成项目数与未完成项目数之比
图 3 会员执行率与定价之间的关系 下面分析 APP 定价的因素:
图 4 未完成任务价格与分布情况
价格越高,放弃该任务的动机越低,由于价格已经远远高于平均成本,因此会员执行率大大
提高。因此存在一个较高的价格,高于此价格,会员基本都愿意执行。因此对于会员的选择
问题,可以看作一个随机变量,该变量由会员的位置与任务位置的相互关系来决定,同时受
2017年全国大学生数学建模竞赛(吉林赛区)评审结果-1
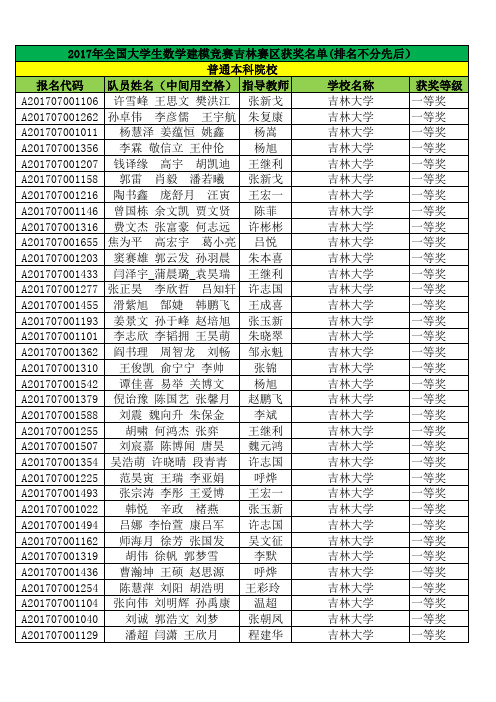
一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖 一等奖
A201707001453 A201707001528 A201707001105 A201707001518 A201707001218 A201707001261 A201707001513 A201707001349 A201707001463 A201707001630 A201707001302 A201707001321 A201707001457 A201707001313 A201707001536 A201707001459 A201707001056 A201707001116 A201707001408 A201707001131 A201707001418 A201707001292 A201707001259 A201707001439 A201707001208 A201707001305 A201707001293 A201707001241 A201707001148 A201707001426 A201707001568 A201707001565 A201707001010 A201707001283 A201707001124 A201707001529 A201707001108 A201707001221
王昕 丁雪 朱晓翠 王继利 曹阳 邹永魁 王彩玲 杜新伟 杨泰山 孙维鹏 王成喜 张富 韩玉柱 黄庆道 李国发 王德辉 王皓 于新 吴文征 温超 梁树青 王敏 李春光 曹春玲 孙鹏 刘思远 于新 张宝玉 李立明 张新戈 徐明旭 任长宇 孙晓松 王敏 王德辉 李国发 李聪 徐明旭
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十届“认证杯”数学中国数学建模网络挑战赛承诺书我们仔细阅读了第十届“认证杯”数学中国数学建模网络挑战赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题.我们知道,抄袭别人的成果是违反竞赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出.我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性.如有违反竞赛规则的行为,我们接受相应处理结果.我们允许数学中国网站()公布论文,以供网友之间学习交流,数学中国网站以非商业目的的论文交流不需要提前取得我们的同意.我们的参赛队号为:3345参赛队员(签名):队员1:队员2:队员3:参赛队教练员(签名):参赛队伍组别(例如本科组):本科组第十届“认证杯”数学中国数学建模网络挑战赛编号专用页参赛队伍的参赛队号:(请各个参赛队提前填写好):3345竞赛统一编号(由竞赛组委会送至评委团前编号):竞赛评阅编号(由竞赛评委团评阅前进行编号):2017年第十届“认证杯”数学中国数学建模网络挑战赛第一阶段论文题目移动端考研产品的春天真的到来了吗?关键词移动端SPSS动态定价马尔科夫链层次分析法摘要:本文针对移动端考研产品的未来发展问题,使用主成分分析、Logistic回归分析、动态定价原理分析、灵敏度分析、层次分析法等,分别构建标准化模型、回归模型、动态定价模型、马尔科夫预测模型、层次分析模型等模型,运用了Excel,SPSS,Matlab,Visio等软件,最后,结合实际调查数据,做出了确定可行性的层次分析模型.针对问题一,首先对附件2中的调查数据进行预处理,将问卷的23个问题转化为数据,然后定性分析这23个问题,排除与调查目标关联不大的6个问题.接着对其余问题的调查数据进行探索性分析,将之可视化,并分别通过主成分分析、Logistic回归分析,得出影响移动端考研产品发展的主要因素是移动端考研产品自身的特点和相对于其他考验渠道的优势.针对问题二,依据移动端考研产品的独特服务特性,建立服务产品的动态定价与销售关系.并利用运筹学中的灵敏度分析,考虑影响商品盈利的主要因素,最终得到最大获利的价格区间估计在(1054.18,1205.74)的范围内.再利用现有的市场数据,采用马尔科夫链模型,预测移动端考研产品的潜在市场占有率可达28.7%以上,并将逐年增长.针对问题三,结合调查问卷数据,选择武汉市作为研究对象,分别从经济、社会、技术等方面考虑移动端考研产品在该市推广投放的可行性.建立层次分析模型,从经济上的人力投入,软硬件,系统维护,产品生命周期;社会上的宣传,影响力,线下竞争;考研上的关注,认可度等,将这些因素结合权重得出考点类产品、录播课程类产品适合主要投入,而题库/练习类产品、直播类课程产品、单词/词典类产品较次之.本文最大的亮点,处理庞大错杂的数据,合理优化,使数据成分清晰,图标鲜明,逻辑严谨,对产品价格的因素逐个定性分析,利用时间连续函数,动态调整每个阶段价格,统筹兼顾.因为新兴移动端考研产品特性,马尔科夫可以避免过去数据影响,合理预测潜在市场.考研产品的投入,利用不同产品数据,构建多种方案,更加接近现实,模型解决实际问题更加准确恰当,适用范围广.参赛队号:3345所选题目:C题英文摘要(选填)AbstractIn?this?paper,?we?focus?on?the?future?development?of?mobile?research?produc ts,?using?principal?component?analysis,?Logistic?regression?analysis,?dynam ic?pricing?principle?analysis,?sensitivity?analysis,?analytic?hierarchy?pro cess,?etc.,?respectively,?to?build?a?standardized?model,?regression?model,? dynamic?pricing?model,?Markov?prediction?model?,?AHP,?Matlab,?Visio?and?oth er?software,?and?finally,?the?model?results?and?the?actual?survey?data?comb ined?to?determine?the?feasibility?of?the?hierarchy?analysis?model.To?question?1,?the?survey?data?in?Annex?2?is?processed?first,?resulting?in? a?collating?table.?And?then?analyze?the?23?questions?in?Annex?2,?and?ultima tely?determine?some?of?the?problems?excluded.?According?to?the?rest?of?the? data,?the?statistical?analysis,?linear?regression?analysis,?principal?compo nent?analysis?and?Logistic?regression?analysis?show?that?the?main?factors?i nfluencing?the?development?of?mobile?research?products?are?the?characterist ics?of?the?mobile?research?and?development?products?and?the?advantages?of?o ther?test?channels.In?view?of?the?problem?2,?according?to?the?unique?characteristics?of?mobile ?research?products,?the?establishment?of?service?products,?dynamic?pricing? and?sales?relationship.?And?use?the?sensitivity?analysis?in?operational?res earch?to?consider?the?main?factors?that?affect?the?profitability?of?the?com modity,?and?finally?the?maximum?profit?price?range?is?estimated?in?the?rang e?of?(1054.18,1205.74)?.For?the?product?market?forecast,?the?use?of?existin g?market?data,?Markov?chain?model,?a?reasonable?forecast?of?market?share?re ached?the?theoretical?28.7%,?and?will?grow?year?by?year.In?view?of?the?problem3,?we?choose?Wuhan?cityas?the?object,?consider?the?fe a s i b i l i t y?o f?t h e? city's?economic,?social?and?college?entrance?examination?education,?establi sh?the?level?analysis?model,?from?the?economic?human?input,?hardware?and?so ftware,?system?maintenance,?product?life?cycle;?social?propaganda,?Influenc e,?the?line?of?competition;?PubMed?on?the?attention,?recognition,?etc.,?the se?factors?combined?with?the?weight?of?test?sites,?recording?and?recording? courses?for?the?main?input,?and?the?question?bank?/?practice?products,?live ?course?products,?Dictionary?category?is?second.The?biggest?bright?spot?of?this?paper,?dealing?with?huge?and?wrong?data,?re asonable?optimization,?make?the?data?composition?clear,?icon?clear,?logical ?rigor,?the?product?price?factor?qualitative?analysis,?the?use?of?time?continuous?function,?dynamic?adjustment?of?each?stage?of?the?price,?Malcolm?can ?avoid?the?impact?of?the?past?data,?a?reasonable?forecast?of?potential?mark et.Application?of?research?products,?the?use?of?different?product?data,?bui ld?a?variety?of?programs,?closer?to?reality,?the?model?to?solve?practical?p roblems?more?accurate?and?appropriate,?itwillhavewiderangeofapplication.C题移动端考研产品的春天真的到来了吗?一、问题的重述1.1背景知识随着近年来考研人数的大幅度增长,以及移动互联网时代的来到,使许多考研活动转移到了手机等互联网平台.移动互联网产品的实用性和便捷性,对现有考研市场产生巨大变化.移动端考研产品相比于PC端使用人数更多,使用时长更长.对影响移动端考研产品发展的主要因素,以及考研产品的价格区间和潜在市场占有率的研究,有助于未来移动端考研产品的推广与使用.1.2问题重述在移动端考研产品的发展中,需要考虑众多影响因素,如开发成本,市场潜力,产品优缺点以及大学生对移动客户端的使用意愿.结合大量论文及相关要求,建立数学模型分析一下问题:问题一根据一万份调查问卷的数据,对数据进行处理,求出对移动端考研发展的主要因素.问题二为了尽量满足大学生的学习成本更低和开发商的利润最大化,对移动端考研产品进行定价分析.对于考研辅导行业市场(PC端辅导,线下辅导班培训),估测移动端考研产品在这一市场的潜在占有率.问题三对于一般高校相对较多的城市,拥有相对多有考研意愿和条件的人.从经济、社会情况、考研特点三方面,研究移动端考研产品投放到该城市的可行性.二、问题的分析2.1问题的总分析问题的总体分析方法有三种:(1)对论文的标题进行分析,找出建模的相关资料,得出应用的方法.(2)对问题的总体进行整体分析,可以提出应当用到的方法.(3)画出整体分析框图如图1所示.图1整体流程图2.2对各个问题的分析(1)对问题一的分析考虑到问题一的数据来源于问卷调查,所以应当先对数据进行预处理(将数据不全或不正确答卷数据进行处理).将表格中的数据进行量化分析,将多因子中提取部分主要因子进行分析.在SPSS中进行因子分析,主成分分析,回归分析.通过分析的显着性结果对比分析出影响移动端考研产品发展的主要因素.(2)对问题二的分析首先要对信息类产品(即移动端考研产品)的定价理论进行分析,以及移动端考研产品的特殊因素对定价的影响,建立出移动端考研产品的动态定价模型.同时要与线下培训的价格和PC端考研辅导价格进行对比.对于市场的分析,通过附件二中问题16的数据统计,得出线下端和线上端的使用人数的比列,其使用概率可与马尔科夫的初始概率相同.(3)对问题三的分析问题要求建立数学模型,评价移动端考研产品投放的可靠性.首先,对目标进行层次分析,将移动端考研产品投放情况分解为各个组成因素,并将这些因素按分组关系分组,形成一个有序的递阶层次结构,通过两两比较的方式确定层次中诸因素的相对重要性,然后综合人的判断以确定决策诸因素相对重要性的总排序.三、模型的假设1.假设从附件二中所筛选出的数据都是真实可靠的.2.假设处理数据时不会出现错误删除的情况.3.不考虑其他突变因素对移动端产品发展的影响,如部分地区不能进行考研、移动端产品遭到新技术的淘汰等.四、符号说明五、 模型的建立与求解5. 1问题一的分析与求解:问题1要求根据已筛选过的附件2(C 题使用)中汇总调查的有关数据对移动端考研产品发展的影响因素,进行描述性统计分析[2],线性回归分析,主成分分析,Logistic 回归分析[3].首先我们将附件2里的数据进行量化分析,录入SPSS 时对多选题定义多重响应集,并删去无效数据.然后对数据进行描述性统计分析和逐步法线性回归分析,得出问题2、5、6、8、17、23与我们所分析的移动端考研产品发展的影响因素关联不大,所以我们将这六个问题在这一问题中排除.对剩余数据进行进一步分析.接下来以第16题为依据,将被调查者分为两类,一类为线下端和PC 端的考研生,一类为移动端的考研生.分别进行主成分分析和Logistic 回归分析,最终确定对移动端考研产品发展的主要影响因素.对数据的初步分析可得,其中男生3417人,女生6358,来自一线城市的有1065人,二线城市的有4520人,三线城市的有3492人,其他地方有698人,年龄段在18~20岁的有603人、20~23岁7567人、23~25岁1276人、25岁以上329人,并且6207人选择线下渠道进行考研学习,1255人选择线上PC 端进行考研学习,2313人选择线上移动端学习.图2数据量化分析饼图(1) 主成分分析由于选取的变量较多,因此我们对数据进行“降维”,所以运用软件SPSS 对数据进行主成分分析.设()12,,,i i i ip x x x x =为总体x 的样本,每个i x 有p 个指标,()12,,,i i i ip x x x x =即原始数据矩阵为111212919p p p x x x x x x x ⎛⎫ ⎪= ⎪ ⎪ ⎪⎝⎭,(5-1) 根据前述分析,主成分分析的步骤如下:(1) 将原始数据标准化:1,2,,i x i p *==,(5-2)(2)建立相关系数矩阵:()ij p p R r ⨯=,(5-3)其中ij r 为i x *与j x *的相关系数;(3)计算R 的特征值i λ;由主成分的总方差解释表可看出,主成分的累积贡献率到达70%~90%.图3选择移动端的碎石图图4总碎石图图3和4为碎石图,由两张碎石图做比较,可看出在第四个特征根处变得比较平缓,可以表明提取三个个主成分.表二:成分得分系数矩阵组件1 23 X1 -.036 .083.755 X2 .276 -.089-.301 X3 .010 -.353.136 X4 .022 .523-.002 X5 -.447 -.039.156 X6 .333 .099.191 X7 .279 -.035.122 X8 .023 -.159.429 X9 .079 .502.160 X10 -.405 -.046.002提取方法:主成份分析. 表2为主成分得分系数矩阵,根据该矩阵,可以写出标准化的原始变量表示的主成分的表达式.若记标准化的原始变量为123456789zx zx zx zx zx zx zx zx zx 、、、、、、、、,两主成分记为12f f 、,则表达式为:因此由表三和表四,得出对移动端考研产品发展的主要影响因素有3个,分别为x 2、49x x 和.图5旋转后的空间组件图(2)Logistic 回归分析对主成分分析出的主要因素进行进一步的标准化Logistic 回归分析,剔除显着性不高的因素,再次进行分析得到上表五,由图可拟合模型:综合两种分析,得出影响移动端考研产品发展的主要因素是移动端考研产品自身的特点和相对于其他考验渠道的优势.5. 2问题二的分析与求解:5.2.1问题二的分析:移动端考研产品由于其特殊的使用特性与对象,具有很强的时效性.其可定义为易逝商品.由于阶段性的时间差异,商品价格会有很大的变化.运用易逝产品动态价格模型,设置一个合理价格区间显得尤为重要.由于线上考研产品的刚刚起步,与线下竞争存在很大的差别.运用马尔科夫预测模型,对潜在市场占有率进行合理有效的预测. 5.2.2问题二的求解:(1) 建模思路:在传统的消费市场中,更改价格会需要企业投入大量的人力物力,大大的增加了成本,故大多企业采取固定价格.而在新兴互联网经济下,网络服务性商品可以建立数据库,随市场变化调整价格.(2)模型的建立模型假设:在线考研商品的发售量假设为X ,在发售期内[0,L ]内价格需要进行几次调整.假定顾客取消率是时间t 的减函数,即(),[0,1]t θηη=∈,t 表示从预售期开始所经历的时间.由于研究生考试的接近,假设取消率随时间的增加而减少.假设顾客取消产品惩罚费用是价格的线性函数,即,(0,1)i i r p λλ=∈.在实际线上辅导班中,由于某些原因,会存在退班的学生.而退换的费用也是价格的百分比.将销售期的长度L 划分为n 个相等的时间段,假设每段间隔时间后,服务产品价格就会被重新调整一次.价格集合P i ={p 1,p 2,p 3,…,p n }.假设预售期内价格设定的次数n 是外生的.一般模型的建立用需求函数的一般形式d (p i )建立上述背景销售商的动态定价及订货策略模型[4].任意i 阶段预定速率为:()()()()i i i dI t d p t I t dt θ=-,1i T t T -≤≤,i =1,2,3……n ,(5-4) 又()t t θη=,所以,任意阶段t 时刻的预定水平为:()()11i i i t I t td p b ηηη+-⎡⎤=+⎢⎥+⎣⎦,1i i T t T -≤≤,i =1,2,3……n ,(5-5) 其中b i 为第i 阶段的常数.由于预售期初产品预定量为0,即有边界条件I 1(0)=0,所以c 1=0,所以任意i 阶段t 时刻的预定水平的表达式为:()111(), 1,2,3......1(), , 1,2,3......1n i i i i td p i n I t t t d p b T t T i nηηη+--⎧=⎪+⎪=⎨⎡⎤⎪+≤≤=⎢⎥⎪+⎣⎦⎩,(5-6) 1.销售收益已知第i 阶段的需求速率d (p i )和取消速率θ(t ),所以有[]111110()()()()1T T S d p t I t dt d p θη=-=+⎰,(5-7) []1111()()()()()(), 2,3,4 (1)ii i T i i i i i i i i T S d p t I t dt T T d p b T T i n ηηθη-----=-=-+-=+⎰,(5-8) 注:由于式(5-8)中存在1ni T --,所以i S 中i 须从2开始,因此,式(5-7)1S 需要单独写出.同下面取消费用收益的建模. 则整个预售期总的销售收益为:1111121()()()(),2,3,4......11ni i i i i i i i i T p d p T T p d p T T p b i n ηηηη--+-=⎡⎤=+-+-=⎢⎥++⎣⎦∑,(5-9) 由于式(5-9)中2n ≥,所以n=1时(单阶段)的销售收益函数如下:1111111()() , 111s T LR S p p d p pd p n ηη====++(5-10) 2.取消费用收益()1111()()1T i c t I t dt T d p ηθη==+⎰,(5-11) ()111()()()(),2,3,4 (1)i Tii i i i i i i i T c t I t dt T T d p b T T i n ηηηθη-----==---=+⎰,(5-12) 则整个预售期因取消惩罚而获得的取消费用收益为:1nc i i i R c r ==∑,(5-13)由于,(0,1)i i r p λλ=∈,所以取消费用收益如下:112nc i ii R c r c r ==+∑()()()111112(),2,3,4 (11)ni i i i i i i i i T p d p T T p d p T T p b i n ηηληληληη-----=⎡⎤=+--=⎢⎥++⎣⎦∑,(5-14) 当n=1时取消费用收益函数为:11111()()11c LR c r T p d p pd p ληληηη===++,(5-15) (1)订货成本D Na =,(5-16)(2)目标函数根据面前的分析可得利润函数表达式如下:11112(,,)(1)() , 11(1)(1)()()()11 (1)(i s c n i i i i i i R X p n R R DLpd p Xa n T p d p T T p d p T ληηληληηηλ-==+-+-=+++=+-+++-∑12) 2ni i i i T p b Xa i n ηη---=⎧⎪⎪⎪⎪⎨⎪⎪⎪--≤≤⎪⎩∑,(5-17) 上面(5-17)式所含的变量n ,p ,X 都是未知的,需要通过优化计算后才能确定的,因此销售商的利润R 实际上是关于(n ,p ,X )的函数.但是注意到预售期末,销售商需要将所有的服务产品预售完毕,因此在初始时要使销售商预定的产品数量与销售的数量一致,所以有()n n X I T =,所以目标函数(5-17)就转变为寻找最优的n ,p i 使得目标函数R (n ,p i )最大化.(3)模型的求解假定移动端考研产品将在六月份开始,L =30天之后使用,此服务产品的成本为a =1.教育机构在未来30天预售此产品.产品需求函数为d (p i )=10-p i ,即b =10,k =1;顾客取消率是时间减函数,顾客取消惩罚费用i i r p λ=,λ为常数.(1)假设max n =6,企业获得最大利润的价格调整次数n .给出利润R 和预期订货量X 随价格调整为情况;表六:X 为未知结果的算例结果n1 2 3 4 5 6 R 1065.78 1066.10 1066.14 1054.78 1066.01 1065.95 X 323.00 323.11 323.97 324.64 325.14 325.44从表中我们可以看出,随着价格设定次数n 的增加,收益R 会先增大后减小.n =4的时候,销售获得最大利益为1054.78对应购买最多为324.64.(2)假定n =4时,对模型中的参数进行灵敏度分析.研究各参数对对企业总利润和订货量的影响.保持其它参数不变,下面依次对参数L ,a ,λ进行灵敏度分析.表七:参数L 的灵敏度分析L30 32 34 36 38 40 R 1054.78 1105.10 1155.42 1205.74 1256.06 1306.40 X 324.64 332.95 341.26 349.57 357.88 366.19上表反应了,随着预售期的增长,企业初期总的利润和订货量会随之增加.因为当需求函数确定,销售时间越长,销量自然会越高.企业利润越高.表八:参数a 的灵敏度测定c 1 2 34 5 6R 1054.78 899.44 761.97 642.35 540.60 390.69 X 324.64 311.38 298.11 284.86 271.59 245.07从表中数据可以看出,随着成本的增加,企业获得总利润会减少,当其它因素不变,当企业的成本增加是,为了不亏损,企业一般会提高售价,相应的市场会减少,总利润降低.表九:参数λ的灵敏度分析0.1 0.15 0.2 0.25 0.3 0.35 R 1045.96 1050.37 1054.78 1059.21 1063.75 1068.09 X324.71 324.68 324.64 324.60 324.56 324.52从上表可以看出,随着顾客取消订单而收取惩罚费用的增加,产品总的利润增加,而订货数减少.这是因为λ的增加,顾客会慎重购买需求降低,从而产品的销量会下降.所以当其它因素不变的时候,前者带来的收入增加量大于后者收入减少量时,会呈现上表的情况.综上所述:移动端考研产品的合理价格区间设置条件参数,a =1,d (p i )=10-p i ,k =10,b =1,0.2i i r p =,n =4.即为移动端考研产品在预售初期的时间范围类,进行4次价格调整.适当增加售价,考虑影响商品盈利的主要因素,价格区间估计在(1054.18,1205.74)的范围内,得到最大的盈利销售. 5.2.3对市场占有率预测[5]的分析考虑到市场占有率的特殊性,我们对这组变量采用马尔科夫预测模型[1],即: 马尔科夫链是一个离散时间随机过程,这个过程中的每一步都需要做一个随机选择,一个马尔科夫链包括N 个状态,在市场占有率的统计时,对每款产品的选择就是一种状态,当选择另一款产品时,就转移到了另一种状态.因此,在有N 款网络产品的情况下,就存在着N N ⨯的转移概率矩阵,其中每个元素的值在[0,1]之间,并且中的每一行的元素之和为1,马尔科夫链的下一个状态的分布仅仅依赖于当前状态,且与如何到达当前状态无关.因此,一段时间后产品使用的概率向量S (1)可以表示为:=000101000000101()()()()()()[()()()]()()()k k k k kk p t p t p t p t p t p t n t n t n t p t p t p t ⎛⎫⎪ ⎪⋅⋅⋅⨯ ⎪⎪⎝⎭,(5-18)其中i 为产品的提供企业,i =0时则表示不使用任何产品;n i (t )为t 时刻(初始时刻)使用i 产品的概率,0()1i n t ≤≤,且所有概率之和为样本容量1,即:()1Ni i n t ==∑,(5-19)p ij (t )表示在[,]t t t +∆时期内由选择i 产品转移到j 产品的概率,0,1,,0i k j ==,1,,k t ∆可以是一个任意一个时间段.p ij (t )满足:1)()kij j p t =∑=1,0,1,i k =;2) 0≤p ij (t )≤1,i ,j =0…,k (1) 转移概率矩阵的确定:在转移概率矩阵P 中,含有2(1)k +个未知元素p ij (t ),可以根据统计选择每一款产品的数量()i l N t 来推导,()i l N t 中i =0,1,2,,k +2.11001111121002112210011()()()()()()()() ()()()()l l l k l k l l l k l k k l l k l k k l kkN t N t p N t p N t p N t N t p N t p N t p N t N t p N t p N t p +++=+++=+++=+++,(5-20)这样,只需要在k +2个时间点测出每款产品的使用数量N i (t 1),即可通过k (k +1)线性方程组解出p ij (t ),从而转移到转移概率矩阵P . (2)产品市场占有率的预测:可以预测k 个时间段后产品i 的市场占有率为:()(0)k k S S P =⋅,(5-21)当市场处于平衡时,()()k k S P S ⋅=,(5-22)由()01[()()()]k k S n t k t n t k t n t k t =+⋅∆+⋅∆+⋅∆结合公式(5-22),有()1Ni i n t k t =+⋅∆=∑,(5-23)因此可以预测出平衡状态下的市场占有率. (3)对问题运用模型进行求解:通过Excle 软件对问题16进行条形统计可知首先我们将使用倾向与市场的占有率成正比,所以近似可得出市场占有率=使用倾向率.图6三种产品使用人数条形图即可确定初始概率分布为i =0,i =1,i =2 S (2016)=S (0)=[0.23,0.77],即统计周期开始的时候选择线下培训的比列为64%,选择线上PC 端的比例为13%,而线上PC 端的比例为23%,当需对线上移动端的市场做预测分析时,根据下列公式可以得出转移矩阵P ;从线下到线下的概率001{00}n n p P X X +===, 从线下到线上PC 的概率011{10}n n p P X X +===, 从线上PC 端到线下的概率101{01}n n p P X X +===, 从线上PC 端到线上PC 端的概率111{11}n n p P X X +===, 通过对目前市场占有情况的调查可以得到下列表格:p 0p 1 p 0 0.98 0.02 p 10.080.92由表可以得到市场转移矩阵0.980.020.080.92⎡⎤=⎢⎥⎣⎦P , 这时将模型代入,将时间差为一年,即一次以概率矩阵P 间隔一年,根据(4)可以预测一年后的市场占有率:i =0,i =1,S (k )=S (0). S(2016)=[0.23,0.77];S(2017)=S(2016)*P 1=[0.287,0.713]; S(2018)=S(2016)*P 2=[0.3383,0.6617]; S(n)=S(2016)*P n ,当市场继续沿这一趋势发展下去,则马尔科夫链到达平衡,设线上线下的占有率分别为[x ,1-x ]; 按计算公式可得;[]0.980.02,10.080.92x x ⎡⎤-⎢⎥⎣⎦, 可解得x =0.8,1-x =0.2,可见,如果就目前情况发展下去,2017年线上移动端的市场占有率已达到28.7% 在没有外界因素的干扰下,最终在移动端达到市场占有率的80%. 5. 3问题三的分析与求解: 5.3.1模型建立:(1) 建立层次模型[6]结构图7层次分析图(2) 构造判断(成对比较)矩阵在准则层的对应条件下,我们将方案层与之相对的重要性赋予A 1,…,A n 的相应权重.为了使定性的结果,易于使人接受,我们使用成对比较矩阵A=(a ij )n×n .并采用1~9标度方法.(3) 层次单排序及其一致性检验一致矩阵:对于,,i j k ∀均有ij jk ik C C C •=的正反矩阵,根据矩阵理论,Ax x λλ=代表特征值,对所有的11nii i i a n λ===∑有.当矩阵完全一致时,1max =λλ,其余特征值为0;而矩阵A 不具有完全一致性时,1max =,n λλ>其余的特征值有以下关系:max 2ni i n λλ==-∑.上述结论知道,当判断矩阵不完全一致时,相应的判断矩阵的特征值也发生变化,因此我们引入判断矩阵最大特征值以外的其余特征根的负平均值,作为衡量判断矩阵偏离一致性的指标,即用max =1nCI n λ--,(5-24)1. CI 值越大,表明判断矩阵偏离完全一致性的程度越大;CI 越小,表明判断矩阵一致性越好.2. 当矩阵具有满意一致性时,max λ稍大于n ,其余特征值也接近于0,下面对满意度一致性给出一个度量.R.I 是多次重复进行的随机判断矩阵特征值的计算后取得算术平均数得到的.下标是1~9维矩阵重复1000次取得的平均随机一致指标.表十三:平均一致性指标(RI)维数 1 2 3 4 5 6 7 8 9 R.I 0 0 0.52 0.90 1.12 1.26 1.36 1.41 1.46当阶数大于2时,判断矩阵的一致性指标CI 与同阶平均一致性指标RI 之比成为随机一致性比率,记为CR .当0.10CICR RI=<,(5-25) 时,即认为判断矩阵具有满意的一致性,否则就需要调整判断矩阵,使之具有满意性满意的一致性.(4) 层次总排序及其一致性检验计算出某层次因素相对于上一层次中某因素的相对重要性,这种排序方式方式称为单层次排序.具体说就是根据判断矩阵计算对于上一层某元素而言本层次与之有联系元素的重要性次序的权值.1.计算判断矩阵每一行元素的乘积i M()11,2,,ni ij j M a i n ===∏,(5-26)2.计算的i M n 次方根i Wi W =3.对向量12,,,Tn W W W W ⎡⎤=⎣⎦正交化1ii njj W W W ==∑,(5-28)则12,,,Tn W W W W ⎡⎤=⎣⎦即为所求得特征向量.4.计算判断矩阵的最大特征根max λ()max 1niii AW nW λ==∑,(5-29)其中i AW 表示AW 中第i 个元素.5.3.2模型求解:(1)依据层次结构模型,我们以武汉市为例,经过数据调研分析,我们假设对于移动端产品的投放的主要影响是:首先是考研教育情况,其次是社会情况,最后是经济情况.可以构造判断矩阵为 求解为:0.1050.6370.258W ⎛⎫⎪= ⎪ ⎪⎝⎭λmax =3.308,C.I =0.019,R.I=0.58,C.R =0.033<0.1,将矩阵输入Matlab 运算(详细见附录).(2)第三层相对于第二层元素矩阵判断11234711325=113112114122131********B ⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭, 求解为:0.4910.2320.0920.1380.046W ⎛⎫⎪ ⎪⎪= ⎪ ⎪ ⎪⎝⎭λmax =5.126,C.I =0.032,R.I=1.12,C.R =0.028<0.1.(3)计算单一准则下元素的相对重要性21171157153=3111351231B ⎛⎫⎪⎪ ⎪ ⎪⎝⎭, 求解为:0.550.5640.1180.263W ⎛⎫⎪⎪= ⎪ ⎪⎝⎭λmax =4.117,C.I =0.039,R.I=0.90,C.R =0.043<0.1, 311331133=1131111311B ⎛⎫⎪⎪⎪⎪⎝⎭,求解为:0.4060.4060.0940.094W ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭max4λ=,C.I =0,R.I=0.9,C.R =0, 表十六:方案总权重分布表0.1580.1640.3930.1130.172W ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭C.I =0.028,R.I=0.923,C.R =0.03<0.1, 该计算结果表明,对于武汉市移动端考研产品的投放情况为:考虑该市的经济、社会、考研教育可行性,建立层次分析模型,从经济上的人力投入,软硬件,系统维护,产品生命周期;社会上的宣传,影响力,线下竞争;考研上的关注,认可度等,将这些因素结合权重得出考点类产品、录播课程类产品适合主要投入,而题库/练习类产品、直播类课程产品、单词/词典类产品较次之.六、模型的评价与推广一、模型的评价1.优点(1)本文巧妙运用思路流程图,将建模思路完整清晰的展现出来;(2)利用Excel 软件对数据进行处理并作出各种图表,简便,直观,快捷;(3)利用Spss 软件对挑选出的数据进行各种分析,并作出分析图表,鲜明,清晰;(4)运用多种数学软件(如Matlab 、Excel),取长补短,使计算结果更加准确、明晰;(5)本文建立的模型与实际紧密联系,充分考虑影响产品投放的不同因素,从而使模型更贴近实际,通用性强.2.缺点(1)对于一些数据,对其进行了一些必要处理,会带来一些误差;(2)第一个模型为使计算简便,使所得结果更理想化,忽略了一些次要影响因素;(3)在马尔科夫预测模型中,由于数据不够充分,因此预测存在误差.二、模型的推广(1)层次分析法被广泛应用于安全科学研究,诸如煤矿安全研究、危险化学品评价、油库安全性评价、城市灾害应急能力、交通安全评价等诸多方面;在于气象相关的环境科学研究中,层次分析法已在大气环境研究、水环境研究、生态环境研究等领域得到了应用.(2)动态定价模型是一种允许企业根据产品要求改变价格的模型,诸如汽车共乘平台优步、美国职业棒球大联盟球票销售、Uber等方面得到了应用.七、参考文献[1]司守奎、孙兆,数学建模算法与应用[M],北京:国防工业出版社,2016.[2]汪东华,多元统计分析与SPSS应用[M],上海:华东理工大学出版社,2010.[3]何晓群、闵素芹,实用回归分析[M],北京:高等教育出版社,2014.[4]王海娟,网络环境下两类易逝品动态定价模型研究[D],华南理工大学硕士学位论文,2014.[5]张西祥、李陶深,基于云计算的软件网络市场占有率统计与预测模型[J],第31卷增刊2,2011.[6]AHP方法及其应用,.八、附录A=[1,1/5,1/3;5,1,3;3,1/3,1]%A矩阵运算A=1.00000.20000.33335.00001.00003.00003.00000.33331.0000>>[V,D]=eig(A);>>C=max(diag(D))%最大特征根位置C=3.0385>>f=find(diag(D)==max(diag(D)));%求lamda位置,其中diag为矩阵对角线上的元素>>W=V(:,f)/sum(V(:,f))%归一特征向量W=0.10470.63700.2583>>B=A/sum(V(:,f))%计算权向量B=0.69530.13910.2318。
