土木工程《分层法》例题详解
混凝土-分层法-弯矩分配法计算题

分层法与弯矩分配法的优缺点比较
可以考虑杆件之间的相互作用; 可以方便地进行优化设计和调整。 弯矩分配法的缺点
分层法与弯矩分配法的优缺点比较
计算过程相对复杂;
需要对杆件进行编号和线刚度计算。
05 计算题解析
计算题一:简支梁的弯矩计算
总结词
简支梁的弯矩计算是混凝土结构分析中的基础问题,主要涉及到均布荷载和集 中荷载的作用。
弯矩分配法的应用范围
01
弯矩分配法适用于各种类型的结构,包括梁、板、 壳等。
02
弯矩分配法可以用于计算结构的静力弯矩和动力弯 矩,也可以用于分析结构的稳定性。
03
弯矩分配法可以用于单层结构和多层结构的设计计 算,也可以用于大型复杂结构的分析和设计。
03 混凝土结构分析
混凝土结构的分类
01
02
03
01
分层法的优点
02
可以单独对每一层进行分析,计算简单明了;
03
可以考虑每一层的材料和尺寸差异;
分层法与弯矩分配法的优缺点比较
需要将结构分层,可能会 影响计算的精度;
分Байду номын сангаас法的缺点
可以适用于各种水平结构 的计算。
01
03 02
分层法与弯矩分配法的优缺点比较
对于复杂结构,分层可能会比较困难。 弯矩分配法的优点 可以适用于各种竖向结构的计算;
感谢您的观看
将各层的内力进行汇总,得到整个结 构的内力。
分层法与弯矩分配法的计算步骤
弯矩分配法
1
2
确定结构的杆件和节点,并对其进行编号;
计算各杆件的线刚度;
3
分层法与弯矩分配法的计算步骤
进行弯矩分配,将各杆件的弯矩按照一定的规则进行分配;
《分层法》例题详解

例:如图1所示一个二层框架,忽略其在竖向荷载作用下的框架侧移,用分层法计算框架的弯矩图,括号内的数字,表示各梁、柱杆件的线刚度值(EIil)。
图1解:1、图1所示的二层框架,可简化为两个如图2、图3所示的,只带一层横梁的框架进行分析。
图2 二层计算简图图3 底层计算简图2、计算修正后的梁、柱线刚度与弯矩传递系数采用分层法计算时,假定上、下柱的远端为固定,则与实际情况有出入。
因此,除底层外,其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为12,其余各层柱的弯矩传递系数为13。
各层梁的弯矩传递系数,均为12。
图4 修正后的梁柱线刚度图5 各梁柱弯矩传递系数3、计算各节点处的力矩分配系数计算各节点处的力矩分配系数时,梁、柱的线刚度值均采用修正后的结果进行计算,如:G节点处:7.630.6687.63 3.79GH GHGHGH GDGjGi ii iiμ====++∑GD3.790.3327.63 3.79GD GDGH GDGjGi ii iiμ====++∑H节点处:7.630.3537.63 3.7910.21HG HGHGHG HE HIHjHi ii i iiμ====++++∑3.790.1757.63 3.7910.21HI HIHIHG HE HIHjHi ii i iiμ====++++∑10.210.4727.63 3.7910.21HE HEHEHG HE HIHjHi ii i iiμ====++++∑同理,可计算其余各节点的力矩分配系数,计算结果见图6、图7。
图6 二层节点处力矩分配系数图7 底层节点处力矩分配系数4、采用力矩分配法计算各梁、柱杆端弯矩(1)第二层:①计算各梁杆端弯矩。
先在G、H、I节点上加上约束,详见图8图8 二层计算简图计算由荷载产生的、各梁的固端弯矩(顺时针转向为正号),写在各梁杆端下方,见图9:213.13kN m 12F GHql M =-=-⋅213.13kN m 12F HGql M ==⋅ 27.32kN m 12F HI ql M=-=-⋅27.32kN m 12F IHql M==⋅ 在节点G 处,各梁杆端弯矩总与为:13.13kN m FG GH M M ==-⋅在节点H 处,各梁杆端弯矩总与为:13.137.32 5.81kN m F F H HG HI M M M =+=-=⋅在节点I 处,各梁杆端弯矩总与为:7.32kN m F I IH M M ==⋅②各梁端节点进行弯矩分配,各两次,详见图9 第一次弯矩分配过程:放松节点G,即节点G 处施加力矩13.13kN m ⋅,乘以相应分配系数0、668与0、332,得到梁端+8.76kN m ⋅与柱端+4.37kN m ⋅,+8.76kN m ⋅按12传到GH 梁H 端;放松节点I,即在节点I 处施加力矩7.32kN m -⋅,乘以相应分配系数0、935与0、065,得到梁端 6.32kN m -⋅与柱端+1.00kN m ⋅, 6.32kN m -⋅按12传到IH 梁H 端;放松节点H,相应的在节点H 处新加一个外力偶矩,其中包括GH 梁右端弯矩、IH 梁左端弯矩、GH 梁与IH 梁传来的弯矩。
分层法和D值法

(2)影响反弯点高度的具体因素:
a) 侧向外荷载的形式 b) 梁柱线刚度比 c) 结构总层数及该柱所在的层数 d) 柱上下横梁线刚度比 e) 上、下层层高的变化
(3)计算方法 <a> 梁柱线刚度比、层数、层次对反弯点高度的影响 标准反弯点高度比: y0 (反弯点到柱下端距离与柱全高的比值) 条件:框架横梁的线刚度、柱的线刚度和层高沿框架高度保持不变。
2)分配系数——杆AB在结点A的分配系数等于杆AB的转动刚度与交于
A点的各杆的转动刚度之和的比值。以 表示。
Aj
S Aj S
均为固端
Aj
iAj i
A
A
3)固端弯矩 方向 +
4)传递系数——当近端有转角时,远端弯矩与近端弯矩的比值。用C表 示。
M BA CABM AB
3. 计算步骤
解:
边柱:( i1 i3 0 或 i3 i4 0 )
k i2 i4 2ic
梁柱刚度比K和α的关系
楼 层
简图
一 般 柱
边 柱
底 层 柱
固 结
K
k i1 i2 i3 i4 2ic
k
2k
k i1 i2 ic
0.5 k
2k
2. 计算各柱的剪力
➢ 计算方法同反弯点法。 ➢ 则第j层、第k柱的剪力:
M 1上 V1h1 / 3 M 1下 V1 2h1 / 3
5. 根据节点平衡计算梁端弯矩
6. 由梁两端的弯矩,根据梁的平衡条件,可求出梁的剪力。 7. 由梁的剪力,根据结点的平衡条件,可求出柱的轴力。
例题:作下图所示框架的弯矩图,图中括号内数字为各杆的线刚度
解: 当同层各柱h相等时,可直接用柱线刚度计算它们的分配 系数。这里只有第3层中柱与同层其他柱高不同,做如下 变换,即可采用折算线刚度计算分配系数。
混凝土分层法弯矩分配法计算题课件

题目五:高速公路桥的弯矩分配
要点一
总结词
要点二
详细描述
高速公路桥的弯矩分配需要综合考虑桥梁的结构形式、荷 载情况以及墩台刚度等因素。
在进行高速公路桥的弯矩分配时,我们需要全面考虑桥梁 的结构形式、荷载情况以及墩台刚度等因素。具体来说, 对于连续梁桥,一般采用刚度等效原则进行弯矩分配;对 于简支梁桥,则需考虑支座弹性变形对弯矩分配的影响。 此外,还要根据实际荷载情况,对墩台进行合理的刚度设 计,以确保弯矩分配的合理性。
总结词
简单梁的弯矩分配是混凝土结构 中常见的计算问题。
详细描述
简单梁是指跨度较小的梁,其弯 矩分配可以通过集中力或弯矩作 用进行计算。根据梁的跨度、荷 载和截面尺寸等因素,可以得出
弯矩分配的数值解。
公式展示
对于简单梁,弯矩分配可以通过 查表或计算得出,常用的弯矩分 配系数可以根据经验或规范得出。
题目二:连续梁的弯矩分配
弯矩分配法的应用范围
弯矩分配法适用于计算梁和柱的弯矩分布和传递,特别适用于复杂的结 构和多层的结构。
弯矩分配法也可以用于计算板的弯矩分布和传递,但需要采用其他的方 法来考虑板的剪切变形和翘曲变形。
需要注意的是,弯矩分配法是一种近似计算方法,其精度取决于节点的 类型、受力情况和支承条件等因素,因此在进行结构设计时,还需要进 行详细的力学分析和计算。
题目三:刚构桥的弯矩分配
总结词
刚构桥的弯矩分配是混凝土结构中常见的计算问题之一。
详细描述
刚构桥是指主要承受弯矩作用的桥梁结构,其弯矩分配需要考虑主梁、墩柱等不同构件的 弯矩作用。根据刚构桥的类型、跨度、荷载和截面尺寸等因素,可以得出弯矩分配的数值 解。
公式展示
对于刚构桥,弯矩分配可以通过有限元法、分层法或经验公式进行计算。常用的弯矩分配 系数可以根据经验或规范得出。同时还需要考虑不同构件之间的弯矩传递与平衡,以确定 最终的弯矩分配情况。
分层法题目解答
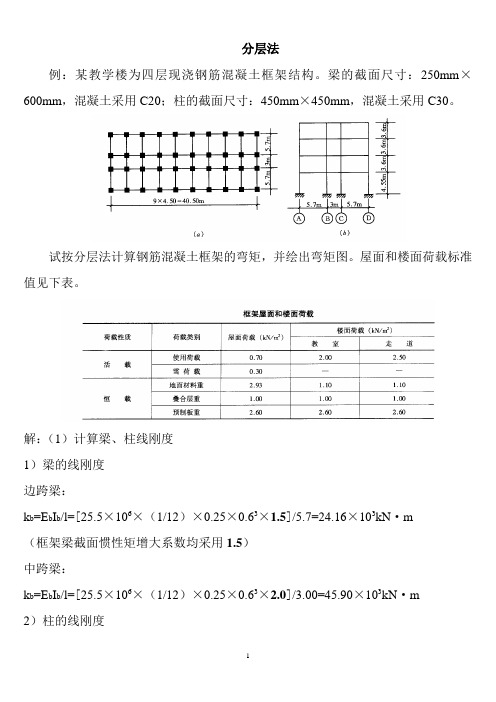
分层法例:某教学楼为四层现浇钢筋混凝土框架结构。
梁的截面尺寸:250mm×600mm,混凝土采用C20;柱的截面尺寸:450mm×450mm,混凝土采用C30。
试按分层法计算钢筋混凝土框架的弯矩,并绘出弯矩图。
屋面和楼面荷载标准值见下表。
解:(1)计算梁、柱线刚度1)梁的线刚度边跨梁:k b=E b I b/l=[25.5×106×(1/12)×0.25×0.63×1.5]/5.7=24.16×103kN·m(框架梁截面惯性矩增大系数均采用1.5)中跨梁:k b=E b I b/l=[25.5×106×(1/12)×0.25×0.63×2.0]/3.00=45.90×103kN·m2)柱的线刚度底层柱:k c=E c I c/h=[30×106×(1/12)×0.45×0.453]/4.55=22.53×103kN·m 其他层柱:k c=E c I c/h=[30×106×(1/12)×0.45×0.453]/3.60=28.48×103kN·m(2)计算分配系数除底层外,各层柱的线刚度应乘以0.9。
(3)荷载分析1)屋面梁上线荷载设计值恒载:1.2[(2.93+1.00+2.60)×4.5+0.25×0.60×25×1.2]=40.67kN/m 活载: 1.4×0.7×4.5=4.41kN/m (系数1.2为考虑梁挑檐及抹灰重的系数)q1=45.08kN/m 2)楼面梁上线荷载设计值教室恒载:1.2[(1.10+1.00+2.60)×4.5+0.25×0.60×25×1.2]=30.78kN/m活载: 1.4×2.00×4.5×0.9=11.34kN/m (系数0.9为屋面及楼面活荷载折减系数)q2=42.12kN/m 走道恒载:30.78kN/m 活载: 1.4×2.50×4.5×0.9=14.18kN/mq3=44.96kN/m(4)梁端固端弯矩M F顶层边跨梁(教室):M F=q1l12/12=45.08×5.72/12=122.05kN·m中跨梁(走道):M F=q1l22/3=45.08×(3/2)2/3=33.81kN·m其他层边跨梁(教室):M F=q2l12/12=41.12×5.72/12=114.04kN·m中跨梁(走道):M F=q3l22/3=44.96×(3/2)2/3=33.72kN·m(5)弯矩分配与传递(用弯矩分配法计算)1)屋面层列表计算,如表1。
竖向荷载计算--分层法例题详解-推荐下载
MH
M
F HG
M
在节点 I 处,各梁杆端弯矩总和为:
MI
M
F IH
F HI
7.32kN m
13.13 7.32
②各梁端节点进行弯矩分配,各两次,详见图 9
第一次弯矩分配过程:
M
F HG
M
5.81kN m
放松节点 G,即节点 G 处施加力矩13.13kN m ,乘以相应分配系数 0.668 和 0.332,得到梁端 +8.76kN m 和柱端 +4.37kN m , +8.76kN m 按 1 传到 GH 梁 H 端;
见图 9:
图 8 二层计算简图
计算由荷载产生的、各梁的固端弯矩(顺时针转向为正号),写在各梁杆端下方,
M
M
F GH
F HI
ql 2 12
ql 2 12
13.13kN m
7.32kN m
在节点 G 处,各梁杆端弯矩总和为:
MG
M
F GH
13.13kN m
在节点 H 处,各梁杆端弯矩总和为:
例:如图 1 所示一个二层框架,忽略其在竖向荷载作用下的框架侧移,用分层 法计算框架的弯矩图,括号内的数字,表示各梁、柱杆件的线刚度值( i EI )。
l
图1 解:1、图 1 所示的二层框架,可简化为两个如图 2、图 3 所示的,只带一层横梁的 框架进行分析。
图 2 二层计算简图
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
分层法——精选推荐
第5章 框架结构设计5.1 结构布置框架结构布置主要是确定柱在平面上的排列方式(柱网布置)和选择结构承重方案,这些均必须满足建筑平面及使用要求,同时也须使结构受力合理,施工简单。
5.1.1 柱网和层高工业建筑柱网尺寸和层高根据生产工艺要求确定。
常用的柱网有内廊式和等跨式两种。
内廊式[图2.1.1(a)]的边跨跨度一般为6~8m ,中间跨跨度为2~4m 。
等跨式的跨度一般为6~12m 。
柱距通常为6m ,层高为3.6m~5.4m 。
民用建筑柱网和层高根据建筑使用功能确定。
目前,住宅、宾馆和办公楼柱网可划分为小柱网和大柱网两类。
小柱网指一个开间为一个柱距[图5.1.1(a,b)],柱距一般为3.3m ,3.6m ,4.0m 等;大柱网指两个开间为一个柱距[图5.1.1(c)],柱距通常为6.0m ,6.6m ,7.2m ,7.5m 等。
常用的跨度(房屋进深)有:4.8m ,5.4m ,6.0m ,6.6m ,7.2m ,7.5m 等。
宾馆建筑多采用三跨框架。
有两种跨度布置方式:一种是边跨大、中跨小,可将卧室和卫生间一并设在边跨,中间跨仅作走道用;另一种则是边跨小、中跨大,将两边客房的卫生间与走道合并设于中跨内,边跨仅作卧室,如北京长城饭店[图5.1.1(b)]和广州东方宾馆[图5.1.1(c)]。
办公楼常采用三跨内廊式、两跨不等跨或多跨等跨框架,如图2.1.1(a),(b),(c)。
采用不等跨时,大跨内宜布置一道纵梁,以承托走道纵墙。
近年来,由于建筑体型的多样化,出现了一些非矩形的平面形状,如图2.1.1(d),(e),(f)所示。
这使柱网布置更复杂一些。
5.1.2 框架结构的承重方案(1)横向框架承重。
主梁沿房屋横向布置,板和连系梁沿房屋纵向布置[图5.1.2(a)]。
由于竖向荷载主要由横向框架承受,横梁截面高度较大,因而有利于增加房屋的横向刚度。
这种承重方案在实际结构中应用较多。
(2)纵向框架承重。
分层法例题详解
例:如图1所示一个二层框架,忽略其在竖向荷载作用下的框架侧移,用分层法计算框架的弯矩图,括号内的数字,表示各梁、柱杆件的线刚度值(EIil)。
图1解:1、图1所示的二层框架,可简化为两个如图2、图3所示的,只带一层横梁的框架进行分析。
图2 二层计算简图图3 底层计算简图2、计算修正后的梁、柱线刚度与弯矩传递系数采用分层法计算时,假定上、下柱的远端为固定,则与实际情况有出入。
因此,除底层外,其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为12,其余各层柱的弯矩传递系数为13。
各层梁的弯矩传递系数,均为12。
图4 修正后的梁柱线刚度图5 各梁柱弯矩传递系数3、计算各节点处的力矩分配系数计算各节点处的力矩分配系数时,梁、柱的线刚度值均采用修正后的结果进行计算,如:G节点处:7.630.6687.63 3.79GH GHGHGH GDGjGi ii iiμ====++∑GD3.790.3327.63 3.79GD GDGH GDGjGi ii iiμ====++∑H节点处:7.630.3537.63 3.7910.21HG HGHGHG HE HIHjHi ii i iiμ====++++∑3.790.1757.63 3.7910.21HI HIHIHG HE HIHjHi ii i iiμ====++++∑10.210.4727.63 3.7910.21HE HEHEHG HE HIHjHi ii i iiμ====++++∑同理,可计算其余各节点的力矩分配系数,计算结果见图6、图7。
图6 二层节点处力矩分配系数图7 底层节点处力矩分配系数4、采用力矩分配法计算各梁、柱杆端弯矩(1)第二层:①计算各梁杆端弯矩。
先在G、H、I节点上加上约束,详见图8图8 二层计算简图计算由荷载产生的、各梁的固端弯矩(顺时针转向为正号),写在各梁杆端下方,见图9:213.13kN m 12F GHql M =-=-⋅213.13kN m 12F HGql M ==⋅ 27.32kN m 12F HI ql M=-=-⋅27.32kN m 12F IHql M==⋅ 在节点G 处,各梁杆端弯矩总与为:13.13kN m FG GH M M ==-⋅在节点H 处,各梁杆端弯矩总与为:13.137.32 5.81kN m F F H HG HI M M M =+=-=⋅在节点I 处,各梁杆端弯矩总与为:7.32kN m F I IH M M ==⋅②各梁端节点进行弯矩分配,各两次,详见图9 第一次弯矩分配过程:放松节点G,即节点G 处施加力矩13.13kN m ⋅,乘以相应分配系数0、668与0、332,得到梁端+8.76kN m ⋅与柱端+4.37kN m ⋅,+8.76kN m ⋅按12传到GH 梁H 端;放松节点I,即在节点I处施加力矩7.32kN m-⋅,乘以相应分配系数0、935与0、065,得到梁端 6.32kN m-⋅与柱端+1.00kN m⋅, 6.32kN m-⋅按12传到IH梁H端;放松节点H,相应的在节点H处新加一个外力偶矩,其中包括GH梁右端弯矩、IH梁左端弯矩、GH梁与IH梁传来的弯矩。
一级建造师复习指导:1Z204051分层法
1Z204050 熟悉常见的⼯程质量统计分析⽅法的应⽤1Z204051 分层法(1)由于⼯程质量形成的影响因素多,因此,对⼯程质量状况的调查和质量问题的分析,必须分门别类地进⾏,以便准确有效地找出问题及其原因,这就是分层法的基本思想。
例题:()是分层法的基本思想。
A.⼯程质量形成的影响因素多,必须分门别类地进⾏B.了解⼯程质量问题形成的统计规律就⾏了。
C.寻求解决⼯程质量问题最有效的⽅法。
D.所有质量问题都是相关的。
答案:A。
(2)调查分析的层次划分,根据管理需要和统计⽬的,通常可按照以下分层⽅法取得原始数据。
●按时间分:⽉、⽇、上午、下午、⽩天、晚间、季节。
●按地点分:地域、城市、乡村、楼层、外墙、内墙。
●按材料分:产地、⼚商、规格、品种。
●按测定分:⽅法、仪器、测定⼈、取样⽅式。
●按作业分:⼯法、班组、⼯长、⼯⼈、分包商。
●按⼯程分:住宅、办公楼、道路、桥梁、隧道。
●按合同分:总承包、专业分包、劳务分包。
例题:商品混凝⼟搅拌⼚,最近专供某⼯程的混凝⼟,为分析质量不稳定情况的原因,宜按()分层⽅法取得原始质量数据。
A.按时间分;B.按地点分;C.按作业分;D.按⼯程分;E.按合同分。
答案:AC。
例题:22.调查分析按合同类型的层次划分不包括( )。
A.总承包层次 B.联合体承包层次C.专业分包层次 D.劳务分包层次答案:B.例题:9.常见的⼯程质量统计分析中,调查分析的层次划分可以采⽤( )等划分⽅法。
A.按企业⾪属关系划分 B.按时间划分C.按施⼯企业所有制划分 D.按⼯程划分 E.按合同划分答案:BDE.1Z204052 因果分析图法(1)因果分析图法,也称为质量特性要因分析法,其基本原理是对每⼀个质量特性或问题,采⽤如图1Z204052所⽰的⽅法,逐层深⼊排查可能原因。
然后确定其中最主要原因,进⾏有的放⽮的处置和管理。
图1Z204052表⽰混凝⼟强度不合格的原因分析,其中,第⼀层⾯从⼈、机械、材料、施⼯⽅法和施⼯环境进⾏分析;第⼆层⾯、第三层⾯,依此类推。
1《分层法》例题详解
例:如图1所示一个二层框架,忽略其在竖向荷载作用下的框架侧移,用分层法计算框架的弯矩图,括号内的数字,表示各
1/3。
各层梁的弯矩传递系数,均为1/2.
图4 修正后的梁柱线刚度
图5 各梁柱弯矩传递系数
3、计算各节点处的力矩分配系数 如:G 节点处:
7.630.6687.63 3.79GH
GH GH GH GD Gj
G
i i i i i
μ=
===++∑
将各杆变成单跨梁,刚节点看成是固定端。
图8 二层计算简图
计算由荷载产生的、各梁的固端弯矩(顺时针转向为正号左负右正),
②各梁端节点进行负弯矩分配和传递,各两次,
图9 二层弯矩分配传递过程(2)第一层:
①计算各梁杆端弯矩。
图10 底层计算简图
计算由荷载产生的、各梁的固端弯矩(顺时针转向为正号),写在各梁杆端下
递,
13
89
图11 底层弯矩分配传递过程
5、将二层与底层各梁、柱杆端弯矩的计算结果叠加,就得到各梁、柱的最后
弯矩图,详见图12。
图12 弯矩图(单位:kN m )
6、力矩再分配
由以上各梁、柱的杆端弯矩图可知,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例:如图1所示一个二层框架,忽略其在竖向荷载作用下的框架侧移,用分层法计算框架的弯矩图,括号内的数字,表示各梁、柱杆件的。
图1
解:1、简化为两个图:图2、图3所示
图2 第二层计算简图
图3 底层计算简图
2、计算修正后的梁、柱线刚度与弯矩传递
系数
除底层外,其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为1/2,其余各层柱的弯矩传递系数为1/3。
各层梁的弯矩传递系数,均为1/2.
图4 修正后的梁柱线刚度
图5 各梁柱弯矩传递系数 3、计算各节点处的力矩分配系数 如:G 节点处:
7.630.6687.63 3.79GH
GH GH GH GD Gj
G
i i i i i
μ=
===++∑ GD 3.790.3327.63 3.79GD
GD GH GD Gj
G
i i i i i
μ=
===++∑
H 节点处:
7.63
0.353
7.63 3.7910.21
HG
HG HG HG HE HI Hj
H
i i i i i i
μ=
=
==++++∑
3.790.1757.63 3.7910.21HI
HI HI HG HE HI Hj
H
i i i i i i
μ=
===++++∑
10.210.4727.63 3.7910.21HE
HE HE HG HE HI Hj
H
i i i i i i
μ=
===++++∑
其余各节点的力矩分配系数见图6、图7。
图6 二层节点处力矩分配系数
图7 底层节点处力矩分配系数
4、采用力矩分配法计算各梁、柱杆端弯矩(1)第二层:
①计算各梁杆端弯矩。
将各杆变成单跨梁,刚节点看成是固定端。
图8 二层计算简图
计算由荷载产生的、各梁的固端弯矩(顺时针转向为正号左负右正),
213.13kN m 12
F
GH
ql M =-=-⋅ 2
13.13kN m 12
F HG
ql M
==⋅ 2
7.32kN m 12F HI
ql M
=-=-⋅ 2
7.32kN m
12
F IH ql M ==⋅ ②各梁端节点进行负弯矩分配和传递,各两次,
第一次负弯矩分配与传递后再进行 第二次负弯矩分配与传递: ③计算各柱的杆端弯矩。
下柱GH HG HI下柱 IH下柱
图9 二层弯矩分配传递过程
(2)第一层:
①计算各梁杆端弯矩。
图10 底层计算简图
计算由荷载产生的、各梁的固端弯矩(顺时针转向为正号),写在各梁杆端下方:
2
17.81kN m
12
F
DE
ql
M=-=-⋅
2
17.81kN m
12
F
ED
ql
M==⋅
2
8.89kN m
12
F
EF
ql
M=-=-⋅
2
8.89kN m
12
F
FE
ql
M==⋅
②各梁端节点进行负弯矩分配与传递,③计算各柱的杆端弯矩。
二层柱的远端弯矩为各柱的近端弯矩的1/3(即传递系数为1/3),底层柱的远端弯矩为近端弯矩的1/2.
02
图11 底层弯矩分配传递过程
5、将二层与底层各梁、柱杆端弯矩的计算结果叠加,就得到各梁、柱的最后弯矩图,详见图12。
图12 弯矩图(单位:kN m )
6、力矩再分配
由以上各梁、柱的杆端弯矩图可知,节点处有不平衡力矩,可以将不平衡力矩再在节点处进行一次分配,此次分配只在节点处进行,
并且在各杆件上不再传递。
在本题中,由于不平衡力矩相对较小,力矩可不再分配。
