2015年黑龙江省哈尔滨三中高考一模数学试卷(理科)【解析版】
2020年黑龙江省哈尔滨三中高考数学一模试卷(文科)(有解析)

2020年黑龙江省哈尔滨三中高考数学一模试卷(文科)一、单项选择题(本大题共12小题,共60.0分)1.已知集合A={0,1,2,3},B={x|−1≤x<3}则A∩B=()A. {1,2}B. {0,1,2}C. {0,1,2,3}D. ⌀2.若复数z=1+i3−4i,则|z−|=()A. 25B. √25C. √105D. 2253.已知a⃗=(3,4),|b⃗ |=2,两向量夹角θ=60°,则a⃗·b⃗ 的值是()A. 7B. 12C. 5D. 254.函数f(x)=(x+1)ln(|x−1|)的图象大致为()A. B.C. D.5.已知双曲线x2a2−y2b2=1(a>0,b>0)的离心率为√52,过右焦点F的直线与两条渐近线分别交于点A,B,且与其中一条渐近线垂直,若△OAB的面积为163,其中O为坐标原点,则双曲线的焦距为()A. 2√3B. 2√5C. 2√10D. 2√156.甲、乙、丙三位同学获得某项竞赛活动的前三名,但具体名次未知,3人作出如下预测:甲说:我不是第三名;乙说:我是第三名;丙说:我不是第一名.若甲、乙、丙3人的预测结果有且只有一个正确,由此判断获得第三名的是A. 甲B. 乙C. 丙D. 无法预测7.某一算法框图如图,输出的S值为()A. √32B. −√32C. √3D. 08. 函数f(x)=3sin(ωx −π6)(ω>0)在区间[0,π]上恰有2个零点,则ω的取值范围为( )A. (76,136]B. [76,136)C. (56,116]D. [56,116)9. 若函数f(x)={1+1gx,x >a(a −1)x −88,x ≤a,在R 上是单调函数,则a 的取值范围为( )A. (1,10]B. (1,+∞)C. (0,10]D. [10,+∞)10. 在三棱锥A −BCD 中,ΔBCD 是等边三角形,平面ABC ⊥平面BCD ,若该三棱锥外接球的表面积为60π,且球心到平面BCD 的距离为√3,则三棱锥A −BCD 的体积的最大值为( )A. 3√3B. 9√3C. 27D. 8111. 已知定义在R 上的奇函数f(x),当x >0时,f(x)=log 2(2x +1),则f(−12)等于( ).A. log 23B. log 25C. 1D. −112. 如图,抛物线C :y 2=4x 的焦点为F ,过点F 的直线与抛物线C和y 轴分别交于点A ,B ,E 为准线l 上一点,且|AF|=|AB|=|AE|,则△BEF 的面积为( )A. 2√3B. 3√22C. 3√2D. 2√33二、填空题(本大题共4小题,共20.0分)13.已知tanα=−34,则cos2α=______.14.设x,y满足约束条件{x−y≥1x+y≤4x≥0y≥0,则z=x−3y的取值范围为_________.15.在锐角△ABC中,a,b,c分别为角A,B,C所对的边,且满足b=2asinB,则∠A=______.16.设函数f(x)=e x(2x−3)−a2x2+ax,若函数f(x)在(−∞,1)内有两个极值点,则实数a的取值范围是______.三、解答题(本大题共7小题,共82.0分)17.设各项均为正数的数列{a n}满足4S n=(a n+1)2(n∈N∗).(Ⅰ)求a n的通项公式;(Ⅱ)设b n=1a n⋅a n+1,n∈N∗,求b n的前n项和T n.18.某学校共有1500名学生,为调查该校学生每周使用手机上网时间的情况,采用分层抽样的方法,收集100名学生每周上网时间的样本数据(单位:小时).根据这100个样本数据,得到学生每周上网时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].(1)估计该校学生每周平均使用手机上网时间(每组数据以组中值为代表);(2)估计该校学生每周使用手机上网时间超过4个小时的概率;(3)将每周使用手机上网时间在(4,12]内的定义为“长时间使用手机上网”;每周使用手机上网时间在(0,4]内的定义为“不长时间使用手机上网”.在样本数据中,有25名学生不近视.请完成每周使用手机上网的时间与近视程度的2×2列联表,并判断是否有95%的把握认为“该校学生的每周使用手机上网时间与近视程度有关”.近视不近视合计长时间使用手机不长时间使用手机15合计25.附:K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)P(K2≥k0)0.10.050.0100.005k0 2.7063.8416.6357.87919.如图,在四棱锥S−ABCD中,SA⊥底面ABCD,底面ABCD是正方形,点M是SD的中点,AN⊥SC,且交SC于点N,SA=AD.(1)求证:SC⊥MN;(2)若SA=2,求三棱锥M−ANC的体积.20. 椭圆mx 2+ny 2=1与直线x +y =1相交于A 、B 两点,C 为AB 中点,若|AB|=2√2,O 为坐标原点,OC 的斜率为√22,求m ,n 的值.21. 已知函数f(x)=x −lnx −a(a ∈R ).(1)讨论f(x)的零点个数;(2)若g(x)=e x−a −xlnx +(1−a)x ,a ∈(1,e −1],求g(x)的极小值ℎ(a)的值域.22. 已知在直角坐标系xOy 中,圆锥曲线C 的参数方程为{x =2cosθy =√3sinθ(θ为参数),定点A(0,−√3),F 1、F 2是圆锥曲线C 的左、右焦点.(Ⅰ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求经过点F1且平行于直线AF2的直线l的极坐标方程;(Ⅱ)设(Ⅰ)中直线l与圆锥曲线C交于M,N两点,求|F1M|⋅|F1N|.23.已知函数f(x)=|ax−3|,不等式f(x)≤2的解集为{x|1≤x≤5}.(1)解不等式f(x)<2f(x+1)−1;(2)若m≥3,n≥3,f(m)+f(n)=3,求证:1m +4n≥1.【答案与解析】1.答案:B解析:本题考查交集的求法,考查交集定义等基础知识,是基础题,利用交集定义直接求解. 解:∵集合A ={0,1,2,3},B ={x|−1≤x <3}, ∴A ∩B ={0,1,2}. 故选:B .2.答案:B解析:解:z =1+i3−4i =(1+i)(3+4i)(3−4i)(3+4i)=−1+7i 25=−125+725i ,|z|=√(−125)2+(725)2=√225=√25, 故选:B .根据复数代数形式的乘除运算以及复数的模即可求出.本题考查复数代数形式的乘除运算,考查了复数的模,是基础题.3.答案:C解析:本题考查了数量积的定义,属于基础题. 利用数量积的定义即可得出. 解:∵a⃗ =(3,4),∴|a ⃗ |=5. 又|b ⃗ |=2,两向量夹角θ=60°,则a⃗ ⋅b ⃗ =|a ⃗ ||b ⃗ |cos60°=5×2×12=5. 故选C .4.答案:B解析:本题主要考查利用函数的解析式研究函数的图象,属于基础题.可从对数的运算性质和函数的单调性取特值(或范围)入手用排除法解此题.解:当x>2时,x+1>3,ln(x−1)>0,则f(x)=(x+1)ln(|x−1|)=(x+1)ln(x−1)>0,且随着x→+∞时,f(x)→+∞,故排除A、C;当x<−1时,,x+1<0,|x−1|>2,ln|x−1|>0,则f(x)=(x+1)ln(|x−1|)<0,故排除D.故选B.5.答案:C解析:本题考查双曲线的焦距的求法,注意运用双曲线的渐近线方程和离心率公式,以及点到直线的距离公式,考查化简整理的运算能力,属于中档题.【解得】解:由题意可得e=ca =√52,a2+b2=c2,双曲线x2a2−y2b2=1(a>0,b>0)的渐近线方程为y=±bax,设两条渐近线的夹角为θ,则tanθ=tan∠AOB=2aba2−b2,设FB⊥OB,则F到渐近线y=bax的距离为d=b,即有|OB|=a,则△OAB的面积可以表示为12⋅a⋅atanθ=a3ba2−b2=163,解得a=2√2,b=√2,c=√10,则2c=2√10,故选C.6.答案:A解析:本题考查了简易逻辑推理,属于基础题.分别假设甲,乙,丙预测正确,再根据其他人预测错误逐个判断各人的名次.解:(1)若只有甲预测正确,则甲为第一名或第二名,由于乙预测不正确,故乙是第一名或第二名,于是丙为第三名,故丙预测正确,矛盾;(2)若乙预测正确,则甲预测也正确,矛盾;故而只有丙预测正确,即丙为第二或第三名,由于甲预测不正确,故而甲为第三名,于是丙为第二名,乙为第一名.故选A.7.答案:D解析:解:由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S=sinπ3+sin2π3+sinπ+⋯+sin2016π3的值,由于y=sin nπ3的周期为6,且同一周期内各函数值的累加和为0,由于2016÷6=336,故S=sinπ3+sin2π3+sinπ+⋯+sin2016π3=336×0=0,故选:D.由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答,属于基础题.8.答案:B解析:本题考查函数的零点存在性问题,涉及三角函数的图像及性质的应用,属于中档题目.解:∵x∈[0,π],ω>0,,∵函数f(x)在区间[0,π]上恰有2个零点, ∴π≤ωπ−π6<2π,解得76≤ω<136.故选B .9.答案:A解析:解:若函数f(x)={1+1gx,x >a(a −1)x −88,x ≤a ,在R 上是单调函数,由y =lgx ,x >a 是增函数, 所以{a −1>01+lga ≥(a −1)a −88,当a >1时,lga −a 2+a +89>0,画出函数y =1+lga , 以及y =a 2−a −88的图象如图: 可得,a ∈(1,10]. 故选:A .判断函数的单调性,利用函数的单调性的性质,列出不等式,即得所求.本题主要求函数的单调性的性质,分段函数的应用,属于中档题.10.答案:C解析:本题考查球内接多面体体积的求法,考查空间想象能力与思维能力,属于中档题.由题意画出图形,再由已知求出底面三角形的边长,数形结合可知,当△ABC 为等边三角形时,三棱锥A −BCD 的体积取最大值,则答案可求. 解:如图,取等边三角形BCD的中心G,过G作三角形BCD的垂线GO,截去GO=√3.则O为三棱锥外接球的球心,设外接球半径为R,由4πR2=60π,得R2=15.即OD=√15,∴DG=√15−3=2√3.则DE=3√3,可得BC=6,过O作OF⊥平面ABC,则F为三角形ABC的外心,连接DG并延长,角BC于E,则E为BC的中点,要使三棱锥A−BCD的体积最大,则AFE共线,即△ABC为等边三角形,此时三棱锥A−BCD的高为3√3.∴三棱锥A−BCD的体积的最大值为V=13×12×6×3√3×3√3=27.故选C.11.答案:D解析:解:∵由f(x)是定义在R上的奇函数可得f(−x)=−f(x),∴f(−12)=−f(12)=−log2(2×12+1)=−1.故选:D.由f(x)是定义在R上的奇函数可得f(−12)=−f(12),由此可解得f(−12)的值.本题主要考察函数奇偶性的性质,属于基础题.12.答案:B解析:本题考查了抛物线的性质,三角形的面积计算,属于中档题.根据抛物线的性质,求出a值,即可计算三角形的面积.解:抛物线的焦点为F(1,0),准线方程为x =−1.设E(−1,2a),则A(a 2,2a),由中点公式可得B(0,4a),故2a 2=1,解得a =√22, 故E (−1,√2),B(0,2√2), ∴直线BF :2√2x +y −2√2=0,故可得点E 到直线BF 的距离d =√2+√2−2√2|√(−2√2)2+1=√2,又|AB|=√(0−1)2+(2√2−0)2=3,∴△BFE 的面积为12×3×√2=3√22. 故选B . 13.答案:725解析:解:∵tanα=−34,∴cos2α=cos 2α−sin 2αcos 2α+sin 2α=1−tan 2α1+tan 2α=1−9161+916=725, 故答案为:725.利用同角三角函数的基本关系、二倍角公式化简要求的式子,可得结果.本题主要考查同角三角函数的基本关系、二倍角公式的应用,属于基础题.14.答案:[−2,4]解析:本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.由约束条件作出可行域,联立方程组求出最优解的坐标,代入目标函数得答案.解:由约束条件{x −y ≥1x +y ≤4x ≥0y ≥0作出可行域如图,联立{x +y =4x −y =1,解得A(52,32), 联立{y =0x +y =4,解得B(4,0), 由图可知,当目标函数z =x −3y 过A 时,z 有最小值为−2;当目标函数z =x −3y 过B 时,z 有最大值为:4.故答案为:[−2,4].15.答案:π6解析:解:∵b =2asinB ,∴sinB =2sinAsinB ,∵sinB ≠0,∴sinA =12,∵A 为锐角,∴A =π6, 故答案为:π6根据正弦定理即可求出.本题考查了正弦定理,以及解三角形,属于基础题. 16.答案:(0,1)解析:解:函数f(x)=e x (2x −3)−a 2x 2+ax ,∴f′(x)=e x (2x −1)−ax +a ,若要使f(x)在(−∞,1)内有两个极值点,只需f′(x)=0在(−∞,1)内有两个解,可转换为函数g(x)=e x (2x −1)与ℎ(x)=a(x −1)的图象在(−∞,1)内有两个交点,由g′(x)=e x (2x +1)知,当x ∈(−∞,−12)时,g′(x)<0,函数g(x)在(−∞,−12)上为减函数;当x ∈(−12,1)时,g′(x)>0,函数g(x)在(−12,1)上为增函数,当直线ℎ(x)=a(x −1)与曲线g(x)=e x (2x −1)相切时,设切点坐标为(x 0,y 0),由导数的几何意义可以得到{e x 0(2x 0+1)=ay 0=e x 0(2x 0−1)y 0=a(x 0−1),解得x 0=0或x 0=32(不合题意,舍去),可知a =e 0(2×0+1)=1,由图象可知,g(x)与ℎ(x)的图象在(−∞,1)内有两个交点,则a 的取值范围是(0,1).故答案为:(0,1).本题考查了利用函数的导数判断函数极值点的应用问题,也考查了转化思想与分析问题、解决问题的能力,是中档题.17.答案:解:(Ⅰ)4S n =(a n +1)2(n ∈N ∗),n =1时,4a 1=4S 1=(a 1+1)2,解得a 1=1,当n ≥2时,有a n =S n −S n−1=(a n +1)24−(a n−1+1)24,整理可得(a n +a n−1)(a n −a n−1−2)=0,因为数列{a n }各项均为正数,a n −a n−1=2(n ≥2),所以数列{a n }是首项为1,公差为2的等差数列,所以{a n }的通项公式为a n =2n −1;(Ⅱ)由b n =1a n ⋅a n+1=1(2n−1)(2n+1)=12(12n−1−12n+1),前n 项和T n =12(1−13+13−15+⋯+12n−1−12n+1)=12(1−12n+1)=n 2n+1.解析:(Ⅰ)由数列的递推式:n=1时,a1=S1,当n≥2时,a n=S n−S n−1,结合等差数列的定义和通项公式,可得所求通项公式;(Ⅱ)求得b n=1(2n−1)(2n+1)=12(12n−1−12n+1),运用数列的求和方法:裂项相消求和,化简整理,即可得到所求和.本题考查数列的通项公式的求法,注意运用数列的递推式,考查等差数列的定义和通项公式,考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.18.答案:解:(1)根据频率分布直方图,计算x=1×0.025×2+3×0.100×2+5×0.150×2+7×0.125×2+9×0.075×2+11×0.025×2=5.8;估计该校学生每周平均使用手机上网时间为5.8小时;(2)由频率分布直方图得1−2×(0.100+0.025)=0.75,估计该校学生每周使用手机上网时间超过4个小时的概率为0.75;(3)根据题意填写2×2列联表如下,近视不近视合计长时间使用手机651075不长时间使用手机101525合计7525100由表中数据,计算K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)=100×(65×15−10×10)275×25×75×25≈21.78>3.841,∴有95%的把握认为“该校学生的每周使用手机上网时间与近视程度有关”.解析:(1)根据频率分布直方图,计算平均数即可;(2)由频率分布直方图求得对应的频率值;(3)根据题意填写2×2列联表,计算观测值,对照临界值得出结论.本题考查了频率分布直方图与独立性检验的应用问题,是基础题.19.答案:(1)证明:由已知,得DC⊥SA,DC⊥DA,又SA∩DA=A,SA,DA⊂平面SAD,∴DC⊥平面SAD,∵AM⊂平面SAD,∴AM⊥DC.又∵SA =AD ,M 是SD 的中点,∴AM ⊥SD ,又AM ⊥DC ,SD ∩DC =D ,DC ⊂平面SDC ,∴AM ⊥平面SDC ,又SC ⊂平面SDC ,∴SC ⊥AM .由已知SC ⊥AN ,则SC ⊥平面AMN .∵MN ⊂平面AMN ,∴SC ⊥MN ;(2)解:由题意可知,在Rt △SAC 中,SA =2,AC =2√2,SC =2√3,由SA ⋅AC =SC ⋅AN ,可得AN =√22√3=√2√3, 则CN =2−AN 2=4√33,∴CN SC =4√332√3=23, 故三棱锥M −ANC 的体积V =12V D−ANC =12V N−ACD =12×23V S−ACD =(13)2×12×2×2×2=49.解析:(1)由已知利用线面垂直的判定可得DC ⊥平面SAD ,得到AM ⊥DC.再由已知得到AM ⊥SD ,可得AM ⊥平面SDC ,从而得到SC ⊥AM ,结合SC ⊥AN ,利用线面垂直的判定可得SC ⊥平面AMN.则SC ⊥MN ; (2)由已知求解三角形得到AN ,进一步求得CN ,得到CN SC =23,然后利用等积法求三棱锥M −ANC 的体积.本题考查空间中直线与直线、直线与平面位置关系的判定及其应用,考查空间想象能力与思维能力,训练了利用等积法求多面体的体积,是中档题. 20.答案:解:设A(x 1,y 1),B(x 2,y 2),将A ,B 点坐标代入方程得:mx 12+ny 12=1,mx 22+ny 22=1,两式相减得:m(x 1+x 2)(x 1−x 2)+n(y 1+y 2)(y 1−y 2)=0,设C(x 0,y 0),{x 1+x 2=2x 0y 1+y 2=2y 0, mx 0+ny 0⋅y 1−y0x 1−x 0=0, ∴mx 0+ny 0k OC =0,m =−ny 0x 0⋅k OC =−n ×√22×(−1)=√22n ,即n =√2m ,∴椭圆mx 2+√2my 2=1联立{mx 2+√2my 2=1y =−x +1,得(√2+1)mx 2−6√2mx +9√2m −1=0, x 1+x 2=√2√2+1,x 1x 2=√2m−1√2+1,2√2=|AB|=√2⋅(6√2√2+1)−49√2m−1√2+1,解得m =13,n =√23.解析:设A(x 1,y 1),B(x 2,y 2),由点差法得m(x 1+x 2)(x 1−x 2)+n(y 1+y 2)(y 1−y 2)=0,设C(x 0,y 0),得n =√2m ,椭圆mx 2+√2my 2=1,联立{mx 2+√2my 2=1y =−x +3,得(√2+1)mx 2−6√2mx +9√2m −1=0,由椭圆弦长公式能求出m ,n 的值.本题考查椭圆方程的求法,是中档题,解题时要认真审题,注意点差法和椭圆弦长公式的合理运用. 21.答案:解:(1)因为f(x)=x −lnx −a ,所以f′(x)=1−1x =x−1x ,则当x ∈(0,1)时,f′(x)<0;当x ∈(1,+∞)时,f′(x)>0.故f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,所以f(x)min =f(1)=1−a .①当a <1时,f(x)无零点;②当a =1时,f(x)有一个零点; ③当a >1时,因为f(e a )=e a −2a >0,f(1e )=1e>0,f(1)=1−a <0,所以f(x)有两个零点. (2)因为g(x)=e x−a −xlnx +(1−a)x ,所以g′(x)=e x−a −lnx −a =e x−a −x +x −lnx −a .由(1)可知当a ∈(1,e −1]时,f(x)有两个零点x 1,x 2(不妨设x 1<x 2),同时x 1,x 2也是F(x)=e x−a −x 的两个零点,且在定义域内f(x)与F(x)的符号完全相同, 所以g(x)在(0,x 1),(x 2,+∞)上单调递增,在(x 1,x 2)上单调递减,所以g(x)的极小值为ℎ(a)=g(x 2)=e x 2−a −x 2lnx 2+(1−a)x 2.因为x 2满足e x 2−a −x 2=0,所以a =x 2−lnx 2,则ℎ(a)=g(x 2)=x 2−x 2lnx 2+(1−x 2+lnx 2)x 2=2x 2−x 22. 因为a =x 2−lnx 2∈(1,e −1],所以x 2∈(1,e],所以ℎ(a)=g(x 2)∈[2e −e 2,1).解析:本题考查函数的导数的应用,函数的极值以及函数的最值的求法,考查转化思想以及计算能力,是难题,(1)求出f′(x)=1−1x =x−1x ,判断函数的单调性,求解函数的最小值,然后判断零点的个数.(2)通过g(x)=e x−a −xlnx +(1−a)x ,求出g′(x)=e x−a −lnx −a =e x−a −x +x −lnx −a.通过函数的零点与函数的单调性转化求解即可.22.答案:解:(1)圆锥曲线C 的参数方程为{x =2cosθy =√3sinθ(θ为参数), ∴普通方程为C :x 24+y 23=1,A(0,−√3),F 1(−1,0),F 2(1,0),k AF 2=√3,直线l 的方程为y =√3(x +1),∴直线l 极坐标方程为:ρsinθ=√3ρcosθ+√3,化为2ρsin(θ−π3)=√3.(2)直线的参数方程是{x =−1+12t y =√32t(t 为参数), 代入椭圆方程得5t 2−4t −12=0,∴t 1t 2=−125.∴|F 1M|⋅|F 1N|=|t 1t 2|=125.解析:(1)利用cos 2θ+sin 2θ=1可得曲线C 的普通方程,即可得出焦点坐标,得到直线l 的点斜式方程,化为极坐标方程即可;(2)直线的参数方程是{x =−1+12t y =√32t (t 为参数),代入椭圆方程得5t 2−4t −12=0,利用参数的意义即可得出.本题考查了直线的直角坐标方程化为极坐标、椭圆的参数方程化为普通方程、参数的应用,考查了推理能力与计算能力,属于中档题.23.答案:(1)解:因为不等式f(x)≤2的解集为{x|1≤x ≤5},则x =1和x =5是方程f(x)=|ax −3|=2的解,即{|a −3|=2|5a −3|=2,所以实数a 的值为1.不等式f(x)<2f(x +1)−1可化为|x −3|<2|x −2|−1,则{x ≥3x −3<2(x −2)−1或{2≤x <3−(x −3)<2(x −2)−1或x <2−(x −3)<−2(x −2)−1, 解得x ≥3或83<x <3或x <0,所以原不等式的解集为{x|x <0或x >83}.(2)证明:因为m ≥3,n ≥3,所以f(m)+f(n)=|m −3|+|n −3|=m −3+n −3=3, 即m +n =9.所以1m +4n =19(m +n)(1m +4n )=19(1+4+n m +4m n )≥19(5+2√n m ⋅4m n )=1,当且仅当n m =4m n ,即m =3,n =6时取等号.解析:(1)利用不等式f(x)≤2的解集为{x|1≤x ≤5},说明x =1和x =5是方程f(x)=|ax −3|=2的解,求出a ,然后转化不等式f(x)<2f(x +1)−1为|x −3|<2|x −2|−1,通过分类讨论转化求解即可.(2)化简f(m)+f(n)=3,得到m +n =9.利用基本不等式证明即可.本题考查解绝对值不等式和利用基本不等式证明不等式.是中档题.。
2020年黑龙江省哈尔滨三中高考数学一模试卷(理科)(附答案详解)

2020年黑龙江省哈尔滨三中高考数学一模试卷(理科)一、单选题(本大题共12小题,共60.0分)1.已知全集U=R,集合A={x|x2−3x−4>0},B={x|xx−5<0},那么集合(∁U A)∩B=()A. {x|−1≤x≤4}B. {x|0<x≤4}C. {x|0<x<5}D. {x|−1≤x<5}2.i为虚数单位,满足i⋅z=2+i的复数z的虚部是()A. 1B. iC. −2D. −2i3.(√3x2−x4)3的展开式中的常数项为()A. −3√3B. 3√3C. −9D. 94.我国南北朝时期的数学家祖暅提出了著名的祖暅原理:“幂势既同,则积不容异”.意思是如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等.现有同高的圆锥和棱锥满足祖咂原理的条件,若棱锥的体积为3π,圆锥的侧面展开图是半圆,则圆锥的母线长为()A. √33B. 1C. √3D. 2√35.某商场每天的食品销售额x(万元)与该商场的总销售额y(万元)具有相关关系,且回归方程为ŷ=9.7x+2.4.已知该商场平均每天的食品销售额为8万元,估计该商场平均每天的食品销售额与平均每天的总销售额的比值为()A. 110B. 19C. 18D. 176.已知S n为等比数列{a n}的前n项和,且S3是S4与S5的等差中项,则数列{a n}的公比为()A. −2B. −12C. 12D. −2或17.某地区有10000名高三学生参加了网上模拟考试,其中数学分数服从正态分布N(120,9),成绩在(117,126]之外的人数估计有()(附:若X服从N(μ,σ2),则P(μ−σ<X≤μ+σ)=0.682,P(μ−2σ<X≤μ+ 2σ)=0.9545)A. 1814人B. 3173人C. 5228人D. 5907人8.以F1(−√2,0),F2(√2,0)为焦点的椭圆与直线x−y+2√2=0有公共点,则满足条件A.x 26+y 24=1B.x 23+y 2=1C.x 25+y 23=1D.x 24+y 22=19. 已知某同学每次射箭射中的概率为p ,且每次射箭是否射中相互独立,该同学射箭3次射中多于1次的概率为0.784,则p =( )A. 0.5B. 0.6C. 0.7D. 0.810. 已知函数y =log 2x 和函数y =log 2(x −2)的图象分别为曲线C 1,C 2,直线y =k 与C 1,C 2分别交于M ,N 两点,P 为曲线C 1上的点.如果△PMN 为正三角形,则实数k 的值为( )A. log 2(2√3−1)B. −log 2(2√3−1)C. (2√3−1)12D. −(2√3−1)1211. 将一枚骰子抛掷3次,则最大点数与最小点数之差为3的概率是( )A. 13B. 14C. 15D. 1612. 已知函数f(x)={|−|x +1|+1|,x ≤0ln(ex)x+1,x >0,若方程[f(x)]2−mf(x)+n =0(n ≠0)有7个不同的实数解,则2m +3n 的取值范围( )A. (2,6)B. (6,9)C. (2,12)D. (4,13)二、单空题(本大题共4小题,共20.0分) 13. 已知函数f(x)=4cos(x −5π6)cosx −m 在[0,π2]上有两个不同的零点,则实数m 的取值范围是______.14. 已知点P 为圆(x −6)2+(y −8)2=1上任一点,F 1,F 2分别为椭圆x 24+y 23=1的两个焦点,求PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ 的取值范围______.15. 若直线y =kx +b 是曲线y =lnx 的切线,也是曲线y =e x−2的切线,则k =______. 16. 已知双曲线x 2a 2−y 2b 2=1(a >0,b >0)的焦距为2c ,A 1,A 2是实轴顶点,以A 1A 2为直径的圆与直线bx +cy −bc =0在第一象限有两个不同公共点,则双曲线离心率e 的取值范围是______.三、解答题(本大题共7小题,共82.0分)17. 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且bcosA +√32a =c .(1)若sinBsinC =cos 2A2,求C 的大小;(2)若AC 边上的中线BM 的长为1+√3,求△ABC 面积的最大值.18.如图,在四棱锥P−ABCD中,PA⊥平面ABCD,AD=CD=1,∠ADC=120°,PA=AB=BC=√3,点M是AC与BD的交点.(1)求二面角A−PC−B的余弦值;(2)若点N在线段PB上且MN//平面PDC,求直线MN与平面PAC所成角的正弦值.19.哈三中总务处的老师要购买学校教学用的粉笔,并且有非常明确的判断一盒粉笔是“优质产品”和“非优质产品”的方法.某品牌的粉笔整箱出售,每箱共有20盒,根据以往的经验,其中会有某些盒的粉笔为非优质产品,其余的都为优质产品.并且每箱含有0,1,2盒非优质产品粉笔的概率为0.7,0.2和0.1.为了购买该品牌的粉笔,校总务主任设计了一种购买的方案:欲买一箱粉笔,随机查看该箱的4盒粉笔,如果没有非优质产品,则购买,否则不购买.设“买下所查看的一箱粉笔”为事件A,“箱中有i件非优质产品”为事件B i(i=0,1,2).(1)求P(A|B0),P(A|B1),P(A|B2);(2)随机查看该品牌粉笔某一箱中的四盒,设X为非优质产品的盒数,求X的分布列及期望;(3)若购买100箱该品牌粉笔,如果按照主任所设计方案购买的粉笔中,箱中每盒粉期望大10,则所设计的方案有效.讨论该方案是否有效.20. 已知函数f(x)=x 2+mx +2lnx .(1)讨论f(x)在定义域内的极值点的个数;(2)若对∀x >0,f(x)−2e x −3x 2≤0恒成立,求实数m 的取值范围; (3)证明:若x ∈(0,+∞),不等式e x +x 2−(e +1)x +1x −1≥0成立.21. 过x 轴正半轴上一点M(m,0)做直线与抛物线E :y 2=x 交于A(x 1,y 1),B(x 2,y 2),(y 1>0>y 2)两点,且满足0<OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ <2,过定点N(4,0)与点A 做直线AC 与抛物线交于另一点C ,过点N(4,0)与点B 做直线BD 与抛物线交于另一点D.设三角形AMN 的面积为S 1,三角形DMN 的面积为S 2. (1)求正实数m 的取值范围;(2)连接C ,D 两点,设直线CD 的斜率为k 0;(i)当m =43时,直线AB 在y 轴的纵截距范围为[−83,−43],则求k 0的取值范围; (ii)当实数m 在(1)取到的范围内取值时,求S 2S 1的取值范围.22. 在平面直角坐标系中,曲线C 的参数方程为{x =2√3cosαy =√6sinα(α为参数),以原点为极点,x 轴的正半轴为极轴,建立极坐标系,直线l 的参数方程为{x =1+√22ty =√3+√22t,(t 为参数).(1)写出曲线C 的极坐标方程以及直线l 的普通方程;f(2)若点A(1,√3),直线l 与曲线C 交于P ,Q 两点,弦P ,Q 的中点为M ,求|AP|⋅|AQ||AM|的值.23. 设函数f(x)=|x +1|+|3−x|.(1)求f(x)≥5的解集;(2)若∀x ∈R ,使f(x)≥m 恒成立的m 的最大值为n.正数a ,b 满足12a+b +1a+3b =n ,求3a +4b 的最小值.答案和解析1.【答案】B【解析】解:因为集合A={x|x2−3x−4>0}={x|x<−1或x>4},B={x|0<x<5},则∁U A={x|−1≤x≤4},那么集合(∁U A)∩B={x|0<x≤4},故选:B.首先解不等式求出集合A,B,由补集的运算求出∁U A,再由交集的运算求出(∁U A)∩B.本题考查了解不等式和集合交、补集的混合运算,属于基础题.2.【答案】C【解析】解:由i⋅z=2+i,得z=2+ii =(2+i)(−i)−i2=1−2i,∴复数z的虚部是−2.故选:C.直接利用复数代数形式的乘除运算化简得答案.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.3.【答案】C【解析】解:∵(√3x2−x4)3的展开式中的通项公式为T r+1=C3r⋅(−1)r⋅(√3)3−r⋅x6r−6,令6r−6=0,求得r=1,可得常数项为−C31⋅3=−9,故选:C.先求出二项式展开式的通项公式,再令x的幂指数等于0,求得r的值,即可求得展开式中的常数项的值.本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.4.【答案】D【解析】解:现有同高的圆锥和棱锥满足祖暅原理的条件,棱锥的体积为3π,∴圆锥的体积为3π,∵圆锥的侧面展开图是半圆,设圆锥的侧面展开图这个半圆的半径是R,即圆锥的母线长是R,半圆的弧长是πR,圆锥的底面周长等于侧面展开图的扇形弧长,设圆锥的底面半径是r,则得到2πr=πR,∴R=2r,∴圆锥的高ℎ=√(2r)2−r2=√3r,∴圆锥的体积V=13×πr2×√3r=3π.解得r=√3,则圆锥的母线长为R=2r=2√3.故选:D.推导出圆锥的体积为3π,设圆锥的侧面展开图这个半圆的半径是R,即圆锥的母线长是R,半圆的弧长是πR,圆锥的底面周长等于侧面展开图的扇形弧长,设圆锥的底面半径是r,则R=2r,圆锥的高ℎ=√(2r)2−r2=√3r,由此能求出圆锥的母线长.本题考查圆锥的母线长的求法、考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.5.【答案】A【解析】解:∵商场每天的食品销售额x(万元)与该商场的总销售额y(万元)的线性回归方程为ŷ=9.7x+2.4,∴当商场平均每天的食品销售额为8万元时,该商场平均每天的总销售额为y=9.7×8+ 2.4=80,∴该商场平均每天的食品销售额与平均每天的总销售额的比值为:880=110,故选:A.根据线性回归方程得到该商场平均每天的总销售额,从而求出该商场平均每天的食品销售额与平均每天的总销售额的比值.本题主要考查了函数的实际应用,以及线性回归方程的应用,是基础题.6.【答案】A【解析】解:S3是S4与S5的等差中项,即为2S3=S4+S5,若公比q=1,则S n=na1,即有6a1=4a1+5a1,即a1=0,显然不成立,故q≠1,则2⋅a1(1−q 3)1−q =a1(1−q4)1−q+a1(1−q5)1−q,化为2q3=q4+q5,即q2+q−2=0,解得q=−2或1(舍去),故选:A.由等差数列的中项性质和等比数列的求和公式,解方程可得所求公比,注意公比为1的情况.本题考查等比数列的求和公式和等差数列的中项性质,考查方程思想和化简运算能力,属于基础题.7.【答案】A【解析】解:由数学分数服从正态分布N(120,9),得μ=120,σ=3.则P(117<x≤126)=P(117<X≤123)+P(123<X≤126)=P(μ−σ<X≤μ+σ)+12[P(μ−2σ<X≤μ+2σ)−P(μ−σ<X≤μ+σ)]=0.682+12(0.9545−0.682)=0.81825.则成绩在(117,126]之内的人数估计有8183,∴成绩在(117,126]之外的人数估计有1817,与1814最接近.故选:A.由已知可得μ=120,σ=3,则P(117<x≤126)=P(μ−σ<X≤μ+σ)+12[P(μ−2σ<X≤μ+2σ)−P(μ−σ<X≤μ+σ)],求出概率,乘以10000可得成绩在(117,126]之内人数的近似值,再由10000减去该近似值得答案.本题考查正态分布曲线的特点及曲线所表示的意义,考查正态分布中两个量μ和σ的应用,考查曲线的对称性,属于基础题.8.【答案】C【解析】解:以F1(−√2,0),F2(√2,0)为焦点的椭圆,设椭圆方程为x2a2+y2a2−2=1(a2>2),由{x 2a 2+y 2a 2−2=1x −y +2√2=0得(2a 2−2)x 2+4√2a 2x +10a 2−a 4=0, 由题意,a 有解,∴△=(4√2a 2)2−4(2a 2−2)(10a 2−a 4)≥0, ∴a 4−7a 2+10≥0,∴a 2≥5或a 2≤2(舍),∴a min 2=5,此时椭圆方程是:x 25+y 23=1.故选:C .先设椭圆方程,然后与直线方程联立方程组,再根据该方程组有解即可求出a 的最小值,则问题解决.本题主要考查由代数方法解决直线与椭圆交点问题,是中档题.9.【答案】C【解析】解:某同学每次射箭射中的概率为p ,且每次射箭是否射中相互独立, 该同学射箭3次射中多于1次的概率为0.784,则1−[C 31p(1−p)2+C 30p 0(1−p)3]=0.784,解得p =0.7. 故选:C .利用n 次独立重复试验中事件A 恰好发生一次的概率计算公式能求出结果.本题考查概率的求法,考查n 次独立重复试验中事件A 恰好发生一次的概率计算公式等基础知识,考查运算求解能力,是基础题.10.【答案】B【解析】解:由已知可设M(2k .k),N(2k +2,k),则P 点横坐标为2k +1, 又因为点P 在函数y =log 2x 的图象C 1上,所以P(2k +1,log(2k +1)),因为△PMN 为正三角形,则∠PMN =60°,故直线PM 的∴log2(2k+1)−k2k+1−2k=√3,即log2(2k+1)=k+√3,∴2k+√3=2k+1,即2k=2√3−1,∴k=−log2(2√3−1),故选:B.由已知条件设出M,N,P的坐标,利用直线PM的倾角是60°,即斜率为√3,利用斜率的坐标公式列出关于K的方程,解指对数方程即可本题主要考查对数函数的图象和性质应用,体现了数形结合和转化的数学思想,属于中档题.11.【答案】D【解析】解:将一枚骰子抛掷3次,基本事件总数n=6×6×6=216,最大点数与最小点数之差为3包含三种情况:①取最小点为1,最大点为4,另外1个点数可能为1,2,3,4,包含的基本事件个数为C32C41=12,②取点最小点为2,最大点为5,另外1个点数可能为2,3,4,5,包含的基本事件个数为C32C41=12,③取点最小点为3,最大点为6,另外1个点数可能为3,4,5,6,包含的基本事件个数为C32C41=12,则最大点数与最小点数之差为3的概率是:P=12+12+12216=16.故选:D.将一枚骰子抛掷3次,基本事件总数n=6×6×6=216,最大点数与最小点数之差为3包含三种情况:①取最小点为1,最大点为4,另外1个点数可能为1,2,3,4,包含的基本事件个数为C32C41=12,②取点最小点为2,最大点为5,另外1个点数可能为2,3,4,5,包含的基本事件个数为C32C41=12,③取点最小点为3,最大点为6,另外1个点数可能为3,4,5,6,包含的基本事件个数为C32C41=12,由此能求出最大点数与最小点数之差为3的概率.本题考查概率的求法,考查古典概型、排列组合等基础知识,考查运算求解能力,是基础题.12.【答案】C【解析】解:当x >0时,f′(x)=1−ln(ex)x 2,令f′(x)=0,解得x =1,故f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,且f(1)=2,x →+∞时,f(x)→1, 作出函数f(x)的图象如下图所示,令t =f(x),则t 2−mt +n =0有两个不同的实数根t 1,t 2,要使方程[f(x)]2−mf(x)+n =0(n ≠0)有7个不同的实数解,则t 1∈(0,1),t 2∈[1,2), ∴{n(1−m +n)<0(1−m +n)(4−2m +n)≤0,即{n(m −n −1)>0(m −n −1)(2m −n −4)≤0, 作出上述不等式组表示的可行域如下图所示,由可行域可知,当(m,n)取点(1,0)时,2m +3n 最小,且最小值为2; 当(m,n)取点(3,2)时,2m +3n 最大,且最大值为12. 故2m +3n 的取值范围为(2,12). 故选:C .利用导数研究函数f(x)的性质,可作出f(x)的草图,观察图象,结合题设条件可得方程t 2−mt +n =0有两个不同的实数根t 1,t 2,且t 1∈(0,1),t 2∈[1,2),利用二次函数根的分布,可以得到m ,n 满足的约束条件,由此作出可行域,再根据2m +3n 的几何意义,求得取值范围.本题考查分段函数的综合运用,涉及了利用导数研究函数的性质,“套套”函数,二次函数根的分布,简单的线性规划等知识点,考查换元思想,数形结合思想,函数与方程思想等数学思想,考查逻辑推理能力,运算求解能力,直观想象等数学能力,属于较难题目.13.【答案】[0,2−√3)【解析】解:依题意,函数g(x)=4cos(x−5π6)cosx,x∈[0,π2]上的图象与直线y=m有两个不同的交点,g(x)=4(cosxcos5π6+sinxsin5π6)cosx=4(−√32cosx+12sinx)cosx=2sinxcosx−2√3cos2x=sin2x−√3cos2x−√3=2sin(2x−π3)−√3,又x∈[0,π2],∴2x−π3∈[−π3,2π3],∴2sin(2x−π3)−√3∈[−2√3,2−√3],函数g(x)的图象如下,由图可知,m∈[0,2−√3).故答案为:[0,2−√3).依题意,函数g(x)=4cos(x−5π6)cosx,x∈[0,π2]上的图象与直线y=m有两个不同的交点,化简g(x)=2sin(2x−π3)−√3,作出函数g(x)在x∈[0,π2]上的图象,观察图象即可得到m的取值范围.本题主要考查函数零点与方程根的关系,考查三角恒等变换以及三角函数的图象及性质,考查数形结合思想及化简求解能力,属于中档题.14.【答案】[80,120]【解析】解:如图,椭圆x 24+y 23=1的焦点F 1(−1,0),F 2(1,0),设P(6+cosθ,8+sinθ),则PF 1⃗⃗⃗⃗⃗⃗⃗ =(−7−cosθ,−8−sinθ),PF 2⃗⃗⃗⃗⃗⃗⃗ =(−5−cosθ,−8−sinθ),则PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ =100+4(4sinθ+3cosθ)=100+20sin(θ+φ)(tanφ=34).∵−20≤20sin(θ+φ)≤20, ∴PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ 的取值范围是[80,120]. 故答案为:[80,120].由椭圆方程求出焦点坐标,设P(6+cosθ,8+sinθ),得到PF 1⃗⃗⃗⃗⃗⃗⃗ 与PF 2⃗⃗⃗⃗⃗⃗⃗ 的坐标,写出数量积,再由三角函数求最值可得PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ 的取值范围.本题考查圆与椭圆综合,考查平面向量的数量积运算,训练了利用三角函数求最值,是中档题.15.【答案】1或1e【解析】解:设y =kx +b 与y =e x−2和y =lnx 的切点分别为(x 1,e x 1−2)、(x 2,lnx 2); 由导数的几何意义可得k =e x 1−2=1x 2,曲线y =e x−2在(x 1,e x 1−2)处的切线方程为y −e x 1−2=e x 1−2(x −x 1), 即y =e x 1−2⋅x +(1−x 1)e x 1−2,曲线y =lnx 在点(x 2,lnx 2)处的切线方程为y −lnx 2=1x 2(x −x 2),即y =1x 2x +lnx 2−1,则{e x 1−2=1x2(1−x 1)e x 1−2=lnx 2−1, ∴(1x 2−1)(lnx 2−1)=0,解得x 2=1,或x 2=e .当x 2=1时,切线方程为y =x −1,即k =1, 当x 2=e 时,切线方程为y =xe ,即k =1e , ∴k =1或1e . 故答案为:1或1e .分别设出直线与两曲线的切点坐标,求出导数值,得到两切线方程,由两切线重合得答斜率和截距相等,从而求得切线方程得答案.本题考查利用导数研究过曲线上某点处的切线方程,考查计算能力,是中档题.16.【答案】(√2,√5+12)【解析】解:由题意如图,要使以A 1A 2为直径的圆与直线bx +cy −bc =0在第一象限有两个不同公共点, 可得直线在x ,y 轴的交点分别为:(c,0),(0,b), 则O 到直线的距离小于半径,且b >a ,即bc√b 2+c 2<a ,b >a ,整理可得:{b 2>a 2c 4−3a 2c 2+a 4<0,即{2a 2<c 2e 4−3e 2+1<0,解得√2<e <√5+12, 故答案为:(√2,√5+12).由题意可得O 到直线的距离小于半径,且b >a ,可得a ,c 的关系,进而求出离心率的范围.本题考查双曲线的性质及点到直线的距离公式,属于中档题.17.【答案】解:(1)∵bcosA +√32a =c .∴由正弦定理可得sinBcosA +√32sinA =sinC =sin(A +B)=sinAcosB +sinBcosA ,∴√32sinA =sinAcosB ,∴由sinA ≠0,可得cosB =√32,由B ∈(0,π),可得B =π3,∵由题意sinBsinC =cos 2A2=1+cosA 2,∴sinBsinC =1−cosCcosB , ∴cos(C −B)=1, ∵C ,B ∈(0,π), ∴C =B , ∴C =B =π3,(2)∵由(1)可得B =π3,∴由向量的中点表示可得BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ =2BM ⃗⃗⃗⃗⃗⃗ ,∴两边平方可得:BA ⃗⃗⃗⃗⃗ 2+BC ⃗⃗⃗⃗⃗ 2+2BA ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =4BM ⃗⃗⃗⃗⃗⃗ 2,可得:c 2+a 2+2⋅c ⋅a ⋅cosB =4(1+√3)2,可得:c 2+a 2+ac =16+8√3, ∴16+8√3≥2ac +ac =3ac ,解得ac ≤16+8√33,当且仅当a =c 时取等号,∴△ABC 的面积S =12acsinB =√34ac ≤4√3+63,当且仅当a =c 时取等号,即△ABC 面积的最大值是4√3+63.【解析】(1)由正弦定理,两角和的正弦函数公式可得√32sinA =sinAcosB ,结合sinA ≠0,可得cosB =√32,结合范围B ∈(0,π),可得B =π3,进而利用二倍角公式,两角差的余弦函数公式化简已知等式可得cos(C −B)=1,结合范围C ,B ∈(0,π),可得C =B =π3,即可得解.(2)由已知运用向量的中点表示可得BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ =2BM ⃗⃗⃗⃗⃗⃗ ,利用向量的模的平方即为向量的平方以及基本不等式即可得到ac 的最大值,进而根据三角形的面积公式即可求解. 本题主要考查了正弦定理,两角和的正弦函数公式,二倍角公式,两角差的余弦函数公式,基本不等式,三角形的面积公式以及平面向量的运算,考查了转化思想,属于中档题.18.【答案】解:(1)在△ACD 中,AC =√AD 2+CD 2−2AD ⋅CD ⋅cos120°=√3,cos∠DAC =AD 2+AC 2−CD 22AD⋅AC=√32,则∠DAC =π6. 在△ABC 中,cos∠BAC =AB 2+AC 2−BC 22AB⋅AC =12,则∠DAC =π6, 在△ABC 中,cos∠BAC =AB 2+AC 2−BC 22AB⋅AC=12,则∠BAC =π3, ∴∠BAD =π2,∴AB ⊥AD ,∵PA ⊥平面ABCD ,∴分别以直线AB ,AD ,AP 为x ,y ,z 轴建立空间直角坐标系, B(√3,0,0),C(√32,32,0),A(0,0,0),P(0,0,√3),N(√34,0,3√34),M(√34,34,0), AP ⃗⃗⃗⃗⃗ =(0,0,√3),AC ⃗⃗⃗⃗⃗ =(√32,32,0),BC ⃗⃗⃗⃗⃗ =(−√32,32,0),BP ⃗⃗⃗⃗⃗ =(−√3,0,√3), 设平面ACP 的法向量m⃗⃗⃗ =(x,y,z), 则{m ⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =√32x +32y =0m ⃗⃗⃗ ⋅AP ⃗⃗⃗⃗⃗ =√3z =0,取x =√3,则m ⃗⃗⃗ =(√3,−1,0), 设平面BCP 的法向量n⃗ =(a,b,c), 则{n ⃗ ⋅BC ⃗⃗⃗⃗⃗ =−√32a +32b =0n ⃗ ⋅BP ⃗⃗⃗⃗⃗ =−√3a +√3c =0,取a =√3,得n ⃗ =(√3,1,√3),则cos <m ⃗⃗⃗ ,n ⃗ >=m ⃗⃗⃗ ⋅n ⃗⃗ |m ⃗⃗⃗ |⋅|n ⃗⃗ |=√4×√7=√77, ∴二面角A −PC −B 的余弦值为√77. (2)设平面PCD 的法向量a ⃗ =(m,n,t), PC ⃗⃗⃗⃗⃗ =(√32,32,−√3),PD ⃗⃗⃗⃗⃗ =(0,1,−√3), 则{a ⃗ ⋅PC ⃗⃗⃗⃗⃗ =√32m +32n −√3t =0a ⃗ ⋅PD ⃗⃗⃗⃗⃗ =n −√3t =0,取n =√3,得a ⃗ =(−1,√3,1),设N(x,y,z),且BN⃗⃗⃗⃗⃗⃗ =λBP ⃗⃗⃗⃗⃗ ,(0≤λ≤1),满足(x −√3,y,z)=λ(−√3,0,√3), 则N(√3−√3λ,0,√3λ),MN⃗⃗⃗⃗⃗⃗⃗ =(3√34−√3λ,−34,√3λ),∵点N 在线段PB 上且MN//平面PDC , ∴MN ⃗⃗⃗⃗⃗⃗⃗ ⋅a ⃗ =√3λ−3√34−3√34+√3λ=0,解得λ=34.MN⃗⃗⃗⃗⃗⃗⃗ =(0,−34,3√34), ∵平面ACP 的法向量m ⃗⃗⃗ =(√3,−1,0),cos <m ⃗⃗⃗ ,MN ⃗⃗⃗⃗⃗⃗⃗ >=m ⃗⃗⃗ ⋅MN⃗⃗⃗⃗⃗⃗⃗|m ⃗⃗⃗ |⋅|MN⃗⃗⃗⃗⃗⃗⃗ |=342×32=14.∴直线MN与平面PAC所成角的正弦值为14.【解析】(1)分别以AB,AD,AP为x轴,y轴,z轴建立如图的空间直角坐标系,求出平面APC的法向量、平面PCD的法向量,利用向量法能求出二面角A−PC−D的正切值.(2)先根据条件求出点N的具体位置,再利用向量法能求出直线MN与平面PAC所成角的正弦值.本题考查线面角的正弦值、二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.19.【答案】解:(1)由已知P(A|B0)=1,P(A|B1)=C194C204=45,P(A|B2)=C184C204=1219.(2)X的可能取值为0,1,2,P(X=0)=0.7+0.2×C194C204+0.1×C184C204=877950,P(X=1)=0.2×C193C204+0.1×C21C138C204=70950,P(X=2)=0.1×C22C182C204=3950,∴随机变量X的分布列为:E(X)=1×70950+2×3950=38475.(3)由(1)知P(A)=P(X=0)=877950,按照设计方案购买的一箱粉笔中,箱中每盒粉笔都是优质产品的概率为:P(B0|A)=P(AB0)P(A)=P(A|B0)P(B0)P(A)=666877,∵100×665877−100×0.7<10,∴该方案无效.【解析】(1)利用古典概型概率计算公式能求出P(A|B0),P(A|B1),P(A|B2).(2)X的可能取值为0,1,2,分别求出相应的概率,由此能求出随机变量X的分布列和数学期望.(3)由P(A)=P(X=0)=877950,得到按照设计方案购买的一箱粉笔中,箱中每盒粉笔都是优质产品的概率为P(B0|A)=P(AB0)P(A)=P(A|B0)P(B0)P(A)=666877,由100×665877−100×0.7<10,得到该方案无效.本题考查概率、离散型随机变量的分布列、数学期望的求法,考查方案是否有效的判断与求法,考查古典概型、条件概率等基础知识,考查运算求解能力,是中档题.20.【答案】解:(1)f′(x)=2x+m+2x =2x2+mx+2x(x>0),对于方程2x2+mx+2=0,Δ=m2−16,①当−4≤m≤4时,Δ=m2−16≤0,f′(x)≥0,此时f(x)没有极值点;②当m<−4时,方程2x2+mx+2=0的两根为x1,x2,不妨设x1<x2,则x1+x2=−m2>0,x1x2=1,0<x1<x2,当0<x<x1或x>x2时,f′(x)>0,当x1<x<x2时,f′(x)<0,此时x1,x2是函数f(x)的两个极值点;③当m>4时,方程2x2+mx+2=0的两根为x3,x4,且x3+x4=−m2<0,x3x4=1,故x3<0,x4<0,当x∈(0,+∞)时,f′(x)>0,故f(x)没有极值点;综上,当m<−4时,函数f(x)有两个极值点;当m≥−4时,函数f(x)没有极值点;(2)f(x)−2e x−3x2=x2+mx+2lnx−2e x−3x2≤0,即mx+2lnx−2e x−2x2≤0,则m≤2x2+2e x−2lnxx,设g(x)=x2+e x−lnxx,g′(x)=x2−1+(x−1)e x+lnxx2,当x∈(0,1)时,g′(x)<0,g(x)单调递减,当x∈(1,+∞)时,g′(x)>0,g(x)单调递增,则g(x)≥g(1)=e+1,故m≤2(e+1);(3)证明:由(2)知当m=2(e+1)时,(e+1)x+lnx−e x−x2≤0恒成立,即e x+x2−(e+1)x≥lnx,欲证e x+x2−(e+1)x≥1−1x ,只需证lnx≥1−1x,设ℎ(x)=lnx−1+1x ,ℎ′(x)=x−1x2,∴当x ∈(0,1)时,ℎ′(x)<0,ℎ(x)单调递减, 当x ∈(1,+∞),ℎ′(x)>0,ℎ(x)单调递增, ∴ℎ(x)≥ℎ(1)=0,故lnx ≥1−1x ,∴对x ∈(0,+∞),不等式e x +x 2−(e +1)x +1x −1≥0成立.【解析】本题考查利用导数研究函数的极值,以及不等式的恒成立问题,考查分类讨论思想以及推理论证能力,属于较难题目.(1)函数的定义域为(0,+∞),求导后研究方程2x 2+mx +2=0,分类讨论得出函数的单调性情况,进而得出极值点情况; (2)问题等价于m ≤2x 2+2e x −2lnxx,设g(x)=x 2+e x −lnxx,利用导数求函数g(x)的最小值即可;(3)由(2)知,(e +1)x +lnx −e x −x 2≤0恒成立,则问题转化为证明lnx ≥1−1x ,设ℎ(x)=lnx −1+1x ,利用导数证明ℎ(x)≥0恒成立即可.21.【答案】解:(1)设直线AB 方程为x =ty +m ,联立直线AB 与抛物线方程得{x =ty +my 2=x ,解得y 2−ty −m =0,则△=t 2+4m >0且{x 1x 2=m 2y 1y 2=−m,又∵0<OA ⃗⃗⃗⃗⃗ ⋅OB⃗⃗⃗⃗⃗⃗ <2, ∴OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =x 1x 2+y 1y 2=m 2−m ∈(0,2),解得1<m <2, ∴正实数m 的取值范围为(1,2);(2)设A(y 12,y 1),B(y 22,y 2),C(y 32,y 3),D(y 42,y 4),设过点N(4,0)的直线为x =t 1y +4,过点M(43,0)的直线为x =t 2y +43,由{x =t 1y +4y 2=x ,联立解得y 2−t 1y −4=0, 由{x =t 2y +43y 2=x ,联立解得y 2−t 2y −43=0, ∴{y 1y 3=−4y 2y 4=−4y 1y 2=−43, ∴k ABkCD=y 1−y 2y 12−y 22y 3−y 4y 32−y 42=y 3+y 4y1+y 2=−4(1y 1+1y 2)y 1+y 2=−4y1y 2=3,(i)∵直线AB 在y 轴上的纵截距取值范围为[−83,−43], ∴k AB ∈[1,2],∴k CD =13k AB ∈[13,23],即k 0∈[13,23];(ii)S △AMN =12⋅MN ⋅y 1,S △DMN =12⋅MN ⋅y 4, 由(1)和(i)可知,{y 1y 2=−my 2y 4=−4,∴S 2S 1=y 4y 1=−4−m =4m ∈[2,4].【解析】(1)设直线AB 方程为x =ty +m ,与抛物线方程联立,由韦达定理可得{x 1x 2=m 2y 1y 2=−m,再结合已知条件0<OA ⃗⃗⃗⃗⃗ ⋅OB⃗⃗⃗⃗⃗⃗ <2,即可求得正实数m 的取值范围; (2)设A(y 12,y 1),B(y 22,y 2),C(y 32,y 3),D(y 42,y 4),设过点N(4,0)的直线为x =t 1y +4,过点M(43,0)的直线为x =t 2y +43,与抛物线方程联立后,可得{y 1y 3=−4y 2y 4=−4y 1y 2=−43,进而求得k AB =3k CD ,(i)由题意可知,k AB ∈[1,2],进而得到k 0∈[13,23];(ii)易知S 2S 1=y 4y 1=4m ,结合(1)中m 的范围即得解.本题主要考查直线与抛物线的位置关系,考查逻辑推理能力及运算求解能力,对计算能力要求较高,属于中档题.22.【答案】解:(1)曲线C 的参数方程为{x =2√3cosαy =√6sinα(α为参数),转换为直角坐标方程为x 212+y 26=1.直线l 的参数方程为{x =1+√22ty =√3+√22t ,(t 为参数).转换为直角坐标方程为x −y −1+√3=0.(2)把直线的参数方程{x =1+√22t y =√3+√22t ,(t 为参数),代入x 212+y 26=1,得到32t 2+(2√6+√2)t −5=0, 所以t 1+t 2=−4√6+2√23,t 1t 2=−103, 所以t 1+t 22=−2√6+√23,即|AM|=|t 2+t 22|=2√6+√23,|AP|⋅|AQ|=|t 1t 2|=103,所以|AP|⋅|AQ||AM|=1032√6+√23=10√6−5√211.【解析】(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换.(2)利用一元二次方程根和系数关系式的应用和二次函数性质的应用求出结果.本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,极径的应用,一元二次方程根和系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.23.【答案】解:(1)|x +1|+|3−x|≥5等价为{x ≥3x +1+x −3≥5或{−1<x <3x +1+3−x ≥5或{x ≤−1−x −1+3−x ≥5, 解得x ≥72或x ∈⌀或x ≤−32,则原不等式的解集为(−∞,−32]∪[72,+∞);(2)若∀x ∈R ,使f(x)≥m 恒成立,即为m ≤f(x)min ,由|x +1|+|3−x|≥|x +1+3−x|=4,当−1≤x ≤3时,取得等号,则f(x)的最小值为4,可得m ≤4,则n =4,即12a+b +1a+3b =n =4,由a >0,b >0,可得3a +4b =14[(2a +b)+(a +3b)](12a+b +1a+3b )=14(2+a+3b 2a+b +2a+b a+3b )≥14(2+2√a+3b 2a+b ⋅2a+ba+3b )=1, 当且仅当2a +b =a +3b ,即a =2b =15时取得等号,则3a +4b 的最小值为1.【解析】(1)由零点分区间法,结合绝对值的定义,去绝对值,解不等式,求并集,可得所求解集;(2)由题意可得m ≤f(x)min ,运用绝对值的性质可得其最小值,进而得到m 的最大值,再由乘1法和基本不等式,可得所求最小值,注意运用3a +4b =(2a +b)+(a +3b)的变形.本题考查绝对值不等式的解法,注意运用分类讨论思想,考查不等式恒成立问题解法,注意运用转化思想和绝对值不等式的性质,考查基本不等式的运用:求最值,化简整理的运算能力,属于中档题.。
2017年黑龙江省哈尔滨三中高考一模数学试卷(文科)【解析版】
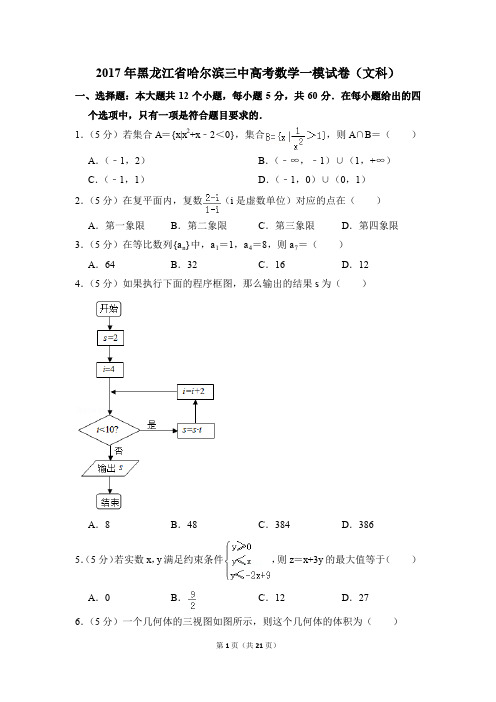
2017年黑龙江省哈尔滨三中高考数学一模试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若集合A={x|x2+x﹣2<0},集合,则A∩B=()A.(﹣1,2)B.(﹣∞,﹣1)∪(1,+∞)C.(﹣1,1)D.(﹣1,0)∪(0,1)2.(5分)在复平面内,复数(i是虚数单位)对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)在等比数列{a n}中,a1=1,a4=8,则a7=()A.64B.32C.16D.124.(5分)如果执行下面的程序框图,那么输出的结果s为()A.8B.48C.384D.3865.(5分)若实数x,y满足约束条件,则z=x+3y的最大值等于()A.0B.C.12D.276.(5分)一个几何体的三视图如图所示,则这个几何体的体积为()A.B.C.D.7.(5分)已知函数f(x)=sin wx+cos wx(w>0),y=f(x)的图象与直线y =2的两个相邻交点的距离等于π,则f(x)的单调递增区间是()A.[kπ﹣,kπ+],k∈Z B.[kπ+,kπ+],k∈ZC.[kπ﹣,kπ+],k∈Z D.[kπ+,kπ+],k∈Z8.(5分)已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的()A.既不充分也不必要的条件B.充分而不必要的条件C.必要而不充分的条件D.充要条件9.(5分)已知非零向量满足,则与的夹角为()A.B.C.D.10.(5分)过双曲线的右焦点且斜率为k的直线,与双曲线的右支只有一个公共点,则实数k的范围为()A.(﹣∞,﹣2]∪[2,+∞)B.[0,2]C.D.[﹣2,2]11.(5分)若△P AD所在平面与矩形ABCD所在平面互相垂直,P A=PD=AB=2,∠APD=60°,若点P,A,B,C,D都在同一个球面上,则此球的表面积为()A.πB.πC.πD.π12.(5分)已知椭圆,点A(c,b),右焦点F(c,0),椭圆上存在一点M,使得,且,则该椭圆的离心率为()A.B.C.D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)设等差数列{a n}的前n项和为S n,若a1+a13=4,则S13.14.(5分)某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是.15.(5分)进位制是人们为了计数和运算方便而约定的计数系统,“满几进一”就是几进制,不同进制之间可以相互转化,例如把十进制的89转化为二进制,根据二进制数“满二进一”的原则,可以用2连续去除89得商,然后取余数,具体计算方法如下:这种算法叫做“除二取把以上各步所得余数从下到上排列,得到89=1011001(2)余法”,上述方法也可以推广为把十进制数化为k进制数的方法,称为“除k 取余法”,那么用“除k取余法”把89化为七进制数为.16.(5分)当a时,关于x的不等式(e x﹣a)x﹣e x+2a<0的解集中有且只有两个整数值,则实数a的取值范围是.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(12分)在△ABC中,a,b,c分别是角A,B,C的对边,其外接圆半径为1,(c﹣2a)cos B+b cos C=0.(1)求角B的大小;(2)求△ABC周长的取值范围.18.(12分)某社区对社区内50名70岁以上老人的身体健康状况和对平时锻炼身体的积极性进行了调查,统计数据如表所示:(1)如果在被调查的老人中随机抽查一名,那么抽到积极锻炼身体的老人的概率是多少?抽到不积极锻炼身体且健康状况一般的老人的概率是多少?(2)试运用独立性检验思想方法判断能否有99%的把握说老人的身体健康状况与锻炼身体的积极性有关.(参考如表)参考公式:.19.(12分)已知四边形ABCD为直角梯形,AD∥BC,AB⊥BC,BC=2AB=4,AD=3,F为BC中点,EF∥AB,EF与AD交于点E,沿EF将四边形EFCD 折起,使得平面ABFE⊥平面EFCD,连接AD,BC,AC.(1)求证:BE∥平面ACD;(2)求三棱锥的B﹣ACD体积.20.(12分)已知抛物线E:x2=2py(p>0),其焦点为F,过F且斜率为1的直线被抛物线截得的弦长为8.(1)求抛物线E的方程;(2)设A为E上一动点(异于原点),E在点A处的切线交x轴于点P,原点O 关于直线PF的对称点为点B,直线AB与y轴交于点C,求△OBC面积的最大值.21.(12分)已知函数f(x)=ax,g(x)=lnx,(a∈R)(1)当a=1时,求函数y=在点(1,0)处的切线方程;(2)若在[1,+∞)上不等式xf(x﹣1)≥g(x)恒成立,求实数a的取值范围.[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系中,以原点为极点,x轴非负半轴为极轴建立极坐标系,直线l的参数方程为(t为参数),曲线C的极坐标方程为ρ=6cosθ(1)若l的参数方程中的t=时,得到M点,求M的极坐标和曲线C的直角坐标方程;(2)若点P(1,1),l和曲线C交于A,B两点,求.[选修4-5:不等式选讲]23.已知函数f(x)=|x+2|+|x﹣1|.(1)求不等式f(x)≥5的解集;(2)若关于x的不等式f(x)≥m2﹣2m的解集为R,求实数m的取值范围.2017年黑龙江省哈尔滨三中高考数学一模试卷(文科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若集合A={x|x2+x﹣2<0},集合,则A∩B=()A.(﹣1,2)B.(﹣∞,﹣1)∪(1,+∞)C.(﹣1,1)D.(﹣1,0)∪(0,1)【解答】解:A={x|x2+x﹣2<0}={x|(x+2)(x﹣1)<0}={x|﹣2<x<1},={x|﹣1<x<1且x≠0},则A∩B=(﹣1,0)∪(0,1),故选:D.2.(5分)在复平面内,复数(i是虚数单位)对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:在复平面内,复数==对应的点位于第一象限.故选:A.3.(5分)在等比数列{a n}中,a1=1,a4=8,则a7=()A.64B.32C.16D.12【解答】解:∵在等比数列{a n}中,a1=1,a4=8,∴,即8=q3,解得q=2,a7==1×26=64.故选:A.4.(5分)如果执行下面的程序框图,那么输出的结果s为()A.8B.48C.384D.386【解答】解:根据题意可知该循环体运行4次第一次:s=2,i=4<10,第二次:s=8,i=6<10,第三次:s=48,i=8<10,第四次:s=384,s=10≥10,结束循环,输出结果S=384,故选:C.5.(5分)若实数x,y满足约束条件,则z=x+3y的最大值等于()A.0B.C.12D.27【解答】解:由约束条件,作出可行域如图,联立,解得:A(3,3),化目标函数z=x+3y为y=﹣+,由图可知,当直线y=﹣+过A时,直线在y轴上的截距最大,z最大.此时z=3+3×3=12.故选:C.6.(5分)一个几何体的三视图如图所示,则这个几何体的体积为()A.B.C.D.【解答】解:该几何体为正八面体,即两个全等的正四棱锥,棱长为1,棱锥的高为,所以,其体积为:2×(1×1)×=,故选:A.7.(5分)已知函数f(x)=sin wx+cos wx(w>0),y=f(x)的图象与直线y =2的两个相邻交点的距离等于π,则f(x)的单调递增区间是()A.[kπ﹣,kπ+],k∈Z B.[kπ+,kπ+],k∈ZC.[kπ﹣,kπ+],k∈Z D.[kπ+,kπ+],k∈Z【解答】解:f(x)=sin wx+cos wx=2sin(wx+),(w>0).∵f(x)的图象与直线y=2的两个相邻交点的距离等于π,恰好是f(x)的一个周期,∴=π,w=2.f(x)=2sin(2x+).故其单调增区间应满足2kπ﹣≤2x+≤2kπ+,k∈Z.kπ﹣≤x≤kπ+,故选:C.8.(5分)已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的()A.既不充分也不必要的条件B.充分而不必要的条件C.必要而不充分的条件D.充要条件【解答】解:∵f(x)是定义在R上的偶函数,∴若f(x)为[0,1]上的增函数,则f(x)为[﹣1,0]上是减函数,又∵f(x)是定义在R上的以2为周期的函数,且[3,4]与[﹣1,0]相差两个周期,∴两区间上的单调性一致,所以可以得出f(x)为[3,4]上的减函数,故充分性成立.若f(x)为[3,4]上的减函数,同样由函数周期性可得出f(x)为[﹣1,0]上是减函数,再由函数是偶函数可得出f(x)为[0,1]上的增函数,故必要性成立.综上,“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的充要条件.故选:D.9.(5分)已知非零向量满足,则与的夹角为()A.B.C.D.【解答】解:非零向量满足,∴=,∴•=0,∴⊥;画出图形如图所示;∴||=,∴(+)•(﹣)=﹣=12﹣=﹣2,∴cos<+,﹣>===﹣,∵+与﹣夹角的取值范围为[0,π],∴与的夹角为.故选:C.10.(5分)过双曲线的右焦点且斜率为k的直线,与双曲线的右支只有一个公共点,则实数k的范围为()A.(﹣∞,﹣2]∪[2,+∞)B.[0,2]C.D.[﹣2,2]【解答】解:双曲线的渐近线方程y=±2x,当过焦点的两条直线与两条渐近线平行时,这两条直线与双曲线右支分别只有一个交点(因为双曲线正在与渐近线无限接近中),那么在斜率是[﹣2,2]两条直线之间的所有直线中,都与双曲线右支只有一个交点.此直线的斜率的取值范围[﹣2,2].故选:D.11.(5分)若△P AD所在平面与矩形ABCD所在平面互相垂直,P A=PD=AB =2,∠APD=60°,若点P,A,B,C,D都在同一个球面上,则此球的表面积为()A.πB.πC.πD.π【解答】解:设球心为O,如图,∵△P AD所在平面与矩形ABCD所在平面互相垂直,P A=PD=AB=2,∠APD =60°,∴AD=2,BD==2,设AC∩BD=E,则BE=,∵点P,A,B,C,D都在同一个球面上,∴OP=OB=R,设OE=x,在Rt△BOE中,OB2=BE2+OE2=2+x2,过O作线段OH⊥平面P AD于H点,H是垂足,∵O点到面P AD的距离与点E到平面P AD的距离相等,∴OH=1,∴在Rt△POH中,PO2=OH2+PH2=1+(﹣x)2=x2﹣2+4,∴2+x2=x2﹣2+4,解得x=,∴R=,∴此球的表面积S=4πR2=4π×=.故选:B.12.(5分)已知椭圆,点A(c,b),右焦点F(c,0),椭圆上存在一点M,使得,且,则该椭圆的离心率为()A.B.C.D.【解答】解:设M(x,y),∵∴,⇒⇒即OA⊥MF⇒cx+by=c2,…①.,因为,共线,cy﹣bx=bc…②由①②得x=,y=,…③把③代入椭圆得a4c2+4c6=a6⇒2c3=b3+bc2,c3﹣b3=bc2﹣c3,⇒(c﹣b)(b2+bc+2c2)=0⇒b=c⇒a=,椭圆的离心率e=.故选:A.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)设等差数列{a n}的前n项和为S n,若a1+a13=4,则S1326.【解答】解:∵等差数列{a n}的前n项和为S n,a1+a13=4,∴S13==.故答案为:26.14.(5分)某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是216.【解答】解:频率分布直方图中,从左到右的5个小矩形的面积之比为1:3:7:6:3,∴成绩在[16,18]的学生的频率为:=0.45,∴成绩在[16,18]的学生人数是:480×0.45=216. 故答案为:216.15.(5分)进位制是人们为了计数和运算方便而约定的计数系统,“满几进一”就是几进制,不同进制之间可以相互转化,例如把十进制的89转化为二进制,根据二进制数“满二进一”的原则,可以用2连续去除89得商,然后取余数,具体计算方法如下:把以上各步所得余数从下到上排列,得到89=1011001(2)这种算法叫做“除二取余法”,上述方法也可以推广为把十进制数化为k 进制数的方法,称为“除k 取余法”,那么用“除k 取余法”把89化为七进制数为 155(7) . 【解答】解:根据题意,89=12×7+5, 12=1×7+5, 1=0×7+1,则89=155(7),即89化为七进制数为155(7), 故答案为:155(7). 16.(5分)当a时,关于x 的不等式(e x ﹣a )x ﹣e x +2a <0的解集中有且只有两个整数值,则实数a 的取值范围是 [,) .【解答】解:当a时,关于x 的不等式(e x ﹣a )x ﹣e x +2a <0可化为e x (x ﹣1)﹣a (x ﹣2)<0, 即(x ﹣1)e x <a (x ﹣2); 设f (x )=(x ﹣1)e x ,g (x )=a (x ﹣2),其中a <;∴f′(x)=e x+(x﹣1)e x=xe x,令f′(x)=0,解得x=0;∴x>0时,f′(x)>0,f(x)单调递增;x<0时,f′(x)<0,f(x)单调递减;∴x=0时f(x)取得最小值为f(0)=﹣1;g(x)=a(x﹣2)是过定点(2,0)的直线;画出f(x)、g(x)的图象如图所示;要使不等式的解集中有且只有两个整数值,∴,∴,解≤a<,∴实数a的取值范围是[,).故答案为:[,).三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(12分)在△ABC中,a,b,c分别是角A,B,C的对边,其外接圆半径为1,(c﹣2a)cos B+b cos C=0.(1)求角B的大小;(2)求△ABC周长的取值范围.【解答】解:(1)根据题意,(2a﹣c)cos B=b cos C,由正弦定理得:(2sin A﹣sin C)cos B=sin B cos C,即2sin A•cos B﹣sin C•cos B=sin B cos C变形可得:2sin A•cos B=sin C•cos B+sin B cos C∴2sin A•cos B=sin(B+C)∵在△ABC中,sin(B+C)=sin A∴2sin A•cos B=sin A,即cos B=,则B=;(2)根据题意,由(1)可得B=,sin B=,又由正弦定理b=2R sin B=,a=2R sin A=2sin A,c=2R sin C=2sin C;则a+c=2(sin A+sin C)=2[sin(﹣C)+sin C]=2[cos C+sin C]=2sin (C+),又由0<C<,则<C+<,则有<sin(C+)≤1,故<a+c≤2,则有2<a+b+c≤3,即△ABC周长的取值范围为(2,3].18.(12分)某社区对社区内50名70岁以上老人的身体健康状况和对平时锻炼身体的积极性进行了调查,统计数据如表所示:(1)如果在被调查的老人中随机抽查一名,那么抽到积极锻炼身体的老人的概率是多少?抽到不积极锻炼身体且健康状况一般的老人的概率是多少?(2)试运用独立性检验思想方法判断能否有99%的把握说老人的身体健康状况与锻炼身体的积极性有关.(参考如表)参考公式:.【解答】解:(1)如果在被调查的老人中随机抽查一名, 那么抽到积极锻炼身体的老人的概率是P 1==,抽到不积极锻炼身体且健康状况一般的老人的概率是P 2=;(2)根据数表,计算观测值=≈11.538>6.635,对照数表知,有99%的把握认为老人的身体健康状况与积极锻炼身体有关. 19.(12分)已知四边形ABCD 为直角梯形,AD ∥BC ,AB ⊥BC ,BC =2AB =4,AD =3,F 为BC 中点,EF ∥AB ,EF 与AD 交于点E ,沿EF 将四边形EFCD 折起,使得平面ABFE ⊥平面EFCD ,连接AD ,BC ,AC . (1)求证:BE ∥平面ACD ; (2)求三棱锥的B ﹣ACD 体积.【解答】证明:(1)连结AF 交BE 于O , 则O 为AF 中点,设G 为AC 中点,连结OG ,DG ,则OG ∥CF ,且OG =CF . 由已知DE ∥CF ,且DE =CF .∴DE ∥OG ,且DE =OG ,∴四边形DEOG 为平行四边形. ∴EO ∥DG ,即BE ∥DG .∵BE ⊄平面ACD ,DG ⊂平面ACD , ∴BE ∥平面ACD .解:(2)∵CF ∥DE ,∴CF ∥平面AED ,∴点C 到平面ACD 的距离和点F 到平面ACD 的距离相等,均为2. ∴三棱锥的B ﹣ACD 体积V B ﹣ACD =V E ﹣ACD =V C ﹣ADE ==.20.(12分)已知抛物线E :x 2=2py (p >0),其焦点为F ,过F 且斜率为1的直线被抛物线截得的弦长为8. (1)求抛物线E 的方程;(2)设A 为E 上一动点(异于原点),E 在点A 处的切线交x 轴于点P ,原点O 关于直线PF 的对称点为点B ,直线AB 与y 轴交于点C ,求△OBC 面积的最大值.【解答】解:(1)由题可知F (0,),则该直线方程为:y =x +, 代入x 2=2py (p >0)得:x 2﹣2px ﹣p 2=0, 设M (x 1,y 1),N (x 2,y 2),则有x 1+x 2=2p , ∵|MN |=8,∴y 1+y 2+p =8,即3p +p =8,解得p =2 ∴抛物线的方程为:x 2=4y ; (2)设A (t ,),则E 在点A 处的切线方程为y =x ﹣,P (,0),B(,),直线AB 的方程是y =x +1,∴C (0,1)S △OBC =||≤,当且仅当t =±2时,取得等号,所以△OBC 面积的最大值为.21.(12分)已知函数f(x)=ax,g(x)=lnx,(a∈R)(1)当a=1时,求函数y=在点(1,0)处的切线方程;(2)若在[1,+∞)上不等式xf(x﹣1)≥g(x)恒成立,求实数a的取值范围.【解答】解:(1)当a=1时,函数y==,∴y′=,∴x=1时,y′=1,∴函数y=在点(1,0)处的切线方程为y=x﹣1;(2)设函数G(x)=a(x2﹣x)﹣lnx,且G(1)=0.G′(x)=①当a≤0时,有G(2)=2a﹣ln2<0,不成立,②当a<0时,(i)a≥1时,G′(x)=,当x≥1时,G′(x)≥所以G(x)在(0,+∞)上是单调增函数,所以G(x)≥G(1)=0(ii)0<a<1时,设h(x)=2ax2﹣ax﹣1,h(1)=a﹣1<0,所以存在x0,使得x∈(1,0)时,h(x)<0,∴G′(x)<0,G(x)<G(1)=0不成立综上所述a≥1.[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系中,以原点为极点,x轴非负半轴为极轴建立极坐标系,直线l的参数方程为(t为参数),曲线C的极坐标方程为ρ=6cosθ(1)若l的参数方程中的t=时,得到M点,求M的极坐标和曲线C的直角坐标方程;(2)若点P(1,1),l和曲线C交于A,B两点,求.【解答】解:(1)∵直线l的参数方程为(t为参数),l的参数方程中的t=时,得到M点,∴点M的直角坐标为M(0,2),∴,,∴点M的极坐标为M(2,),∵曲线C的极坐标方程为ρ=6cosθ,即ρ2=6ρcosθ,∴曲线C的直角坐标方程为x2﹣6x+y2=0.(2)联立直线l的参数方程和曲线C的直角坐标方程得:,则,∴=====.[选修4-5:不等式选讲]23.已知函数f(x)=|x+2|+|x﹣1|.(1)求不等式f(x)≥5的解集;(2)若关于x的不等式f(x)≥m2﹣2m的解集为R,求实数m的取值范围.【解答】解:(1)由|x+2|+|x﹣1|≥5.得:可得:x≤﹣3或,可得x∈∅或,可得x≥2解得:x≥2或x≤﹣3,故不等式的解集是{x|x≥2或x≤﹣3};(2)|x+2|+|x﹣1|≥m2﹣2m,若∀x∈R,使得不等式的解集为R,|x+2|+|x﹣1|≥3,当﹣2≤x≤1时取等号,可得3≥m2﹣2m,解得:﹣1≤m≤3.实数m的取值范围:[﹣1,3].第21页(共21页)。
2021年黑龙江省哈尔滨三中高考数学三模试卷(学生版+解析版)(理科)

2021年黑龙江省哈尔滨三中高考数学三模试卷(理科)一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合2{|20}A x x x =-,{|01000}B x lgx =<,{|}2aC x x =<,若(){|03}AB C x x =<,则(a = )A .lB .3C .6D .82.(5分)已知函数()f x 为奇函数,当0x >时,2()log (1)f x x ax =++,且(3)f a -=,则f (7)(= ) A .12B .12-C .2log 3D .23.(5分)为了让学生了解社会,拓宽视野,丰富知识,提高社会实践能力和综合素质,某中学团委组织学生参加了抽测一批棉花的纤维长度(单位:)cm 的社会实践活动.利用所学习的数学知识,同学们作出了样本的频率分布直方图.现在,由于原始数据不全,只能通过直方图来估计这一批棉花的纤维长度的平均值(同一组数据用这组数据所在区间的中点的值代替).则估计的平均值为( )A .21.75B .22.25C .23.75D .20.754.(5分)《九章算术》是我国一部经典的数学著作,《九章算术⋅商功》有这样的载述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也”.“堑堵”就是底面为直角三角形的直三棱柱,“鳖臑”是四个面均为直角三角形的三棱锥,将底面为短形,一条侧棱垂直于底面的四棱锥称为“阳马”.已知由某“堑堵”“阳马”“鳖臑”组成的几何体的三视图如图所示,则该几何体的体积为( )A .6B .5C .4D .35.(5分)有5条同样的生产线,生产的零件尺寸(单位:)mm 都服从正态分布2(20,)N σ,且2(1921)3P X <=,在每条生产线上各取一个零件,恰好有3个尺寸在区间(20,21]的概率为( ) A .64243B .80243C .1681D .402436.(5分)函数9()11x f x e x =+--的大致图象为( )A .B .C .D .7.(5分)已知直线2y x m =+与圆221x y +=相交于不同的两点A 、B ,O 为坐标原点,且0OA OB ⋅,则实数m 的取值范围是( ) A .(-∞,1010[,)+∞ B .(5-1010[,5) C .(-∞,55[,)+∞ D .[5-5]8.(5分)已知m 为常数,在某个相同的闭区间上,若()f x 为单调递增函数,()f x m +为单调递减函数,则称此区间为函数()f x 的“m LD -”区间.若函数()3sin(2)6f x x π=-,则此函数的“4LD π-”区间为( )A .[6k ππ-,]()12k k Z ππ+∈ B .[3k ππ+,7]()12k k Z ππ+∈C .[12k ππ+,]()3k k Z ππ+∈ D .7[12k ππ+,5]()6k k Z ππ+∈9.(5分)226(2)(1)x x +-的展开式中,5x 的系数为( ) A .52-B .88-C .62-D .110-10.(5分)已知双曲线2222:1(0,0)x y C a b a b-=>>,点M 为此渐近线上的一点,O 为坐标原点.双曲线C 的左、右顶点为A 、B ,焦距为2||OM ,则AM B∠为( ) A .2πB .6π C .3π D .4π 11.(5分)已知复数z 的模为1,复数23w z z =+,则在复平面内,复数w 所对应的点与点(4,0)的距离的最大值是( )A .6B .254C.D.12.(5分)复利是指一笔资金产生利息外,在下一个计息周期内,以前各计息周期内产生的利息也计算利总的计息方法.单利是指一笔资金只有本金计取利息,而以前各计息周期内产生的利息在下一个计息周期内不计算利息的计息方法.小闯同学一月初在某网贷平台贷款10000元,约定月利率为1.5%,按复利计算,从一月开始每月月底等额本息还款,共还款12次,直到十二月月底还清贷款,把还款总额记为x 元.如果前十一个月因故不还贷款,到十二月月底一次还清,则每月按照贷款金额的1.525%,并且按照单利计算利息,这样,把还款总额记为y 元,则y x -的值为( )(参考数据:121.015 1.2)≈ A .170-B .1200C .1030D .900二、填空题:本大愿共4小题,每小题5分,共20分.13.(5分)已知向量a ,b 的夹角为120︒,||2a =,||1b =,若(3)(2)a b a b λ+⊥+,则λ= .14.(5分)已知变量x ,y 满足3303020x y x y x y m -+⎧⎪+-⎨⎪-+⎩,若3z x y =+的最小值为5,则实数m = .15.(5分)已知点A 为椭圆2222:1(0)x y C a b a b+=>>的左顶点,(,0)F c 为椭圆的右焦点,B ,E 在椭圆上,四边形OABE 为平行四边形(O 为坐标原点),点F 到直线AE,则椭圆C 的离心率为 .16.(5分)已知数列{}n a 满足:152a =,2*112()2n n n a a a n N +=-+∈,若取整函数[]x 表示不小于x 的最小整数(例如:[1.2]2=,[3]3)=,设1n n na b a +=,数列{}n b 的前n 项和为n T ,则2021[]T = .三、解答题:共70分.解答应写出必要的文字说明,证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. 17.(12分)已知锐角ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,且满足(2)cos cos 0b c A a C --=.(1)求角A 的大小;(2)求cos cos B C +的取值范围.18.(12分)在刚刚过去的寒假,由于新冠疫情的影响,哈尔滨市的A 、B 两所同类学校的高三学年分别采用甲、乙两种方案进行线上教学,为观测其教学效果,分别在两所学校的高三学年各随机抽取60名学生,对每名学生进行综合测试评分,记综合评分为80及以上的学生为优秀学生.经统计得到两所学校抽取的学生中共有72名优秀学生.(1)用样本估计总体,以频率作为概率,若在A 、B 两个学校的高三学年随机抽取3名学生,求所抽取的学生中的优秀学生数的分布列和数学期望; (2)已知A 学校抽出的优秀学生占该校抽取总人数的23,填写列联表,并判断能否在犯错误的概率不超过0.1的前提下认为学生综合测试评分优秀与教学方案有关.附:k 2.072 2.70 3.841 5.024 6.6357.87910.82822()()()()()n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.19.(12分)如图,在三棱柱111ABC A B C-中,11BB AB AB BC===,D为AC的中点,1AB B D⊥,190B BC∠=︒.(1)求证:平面11ABB A⊥平面ABC;(2)求二面角1D BB A--的余弦值.20.(12分)已知抛物线2:2(0)C y px p=>的焦点为F,过点F且垂直于x轴的直线与C交于A,B两点,AOB∆(点O为坐标原点)的面积为2.(1)求抛物线C的方程;(2)设不经过原点O的直线l与抛物线交于P、Q两点,设直线OP、OQ的倾斜角分别为α和β,证明:当4παβ+=时,直线l恒过定点.21.(12分)已知函数f(x)=3(x﹣1)e x﹣ek有两个不同的零点(其中e为自然对数的底数).(1)当x<﹣1时,求证:(x﹣1)e x﹣1>﹣;(2)求实数k的取值范围;(3)若函数f(x)的两个零点为x1、x2,求证:<e.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4;坐标系与参数方程]22.(10分)在平面直角坐标系中,P为曲线122cos:(1sin2xCyααα=+⎧⎪⎨=⎪⎩为参数)上的动点,将P点纵坐标变为原来的2倍,横坐标变为原来的一半得到点Q,记点的轨迹为2C,以坐标原点O为极点,x轴非负半轴为极轴建立极坐标系.(1)求曲线C 的极坐标方程;(2)A ,B 是曲线2C 上不同于O 的两点,且(A 1ρ,)θ、2(,)6B πρθ+;求|||OA OB 的取值范围. [选修4-5:不等式选讲]23.已知函数()32f x x =-,()21g x x =-.(1)若()|()||()|h x f x g x =+,且()h x a 恒成立,求实数a 的最大值;(2)若()x ϕ,求()x ϕ的最大值.2021年黑龙江省哈尔滨三中高考数学三模试卷(理科)参考答案与试题解析一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合2{|20}A x x x =-,{|01000}B x lgx =<,{|}2aC x x =<,若(){|03}AB C x x =<,则(a = )A .lB .3C .6D .8【解答】解:220x x -,02x ∴,[0A ∴=,2], 01000lgx <<,1000110x ∴<<,(1B ∴=,100010),[0A B ∴=,100010),()[0AB C =,3),∴32a=,6a ∴=. 故选:C .2.(5分)已知函数()f x 为奇函数,当0x >时,2()log (1)f x x ax =++,且(3)f a -=,则f (7)(= ) A .12B .12-C .2log 3D .2【解答】解:因为函数()f x 为奇函数,当0x >时,2()log (1)f x x ax =++,且(3)f f -=-(3)a =,所以f (3)a =-, 即23a a +=-, 所以12a =-,则f (7)2log 873 3.50.5a =+=-=-. 故选:B .3.(5分)为了让学生了解社会,拓宽视野,丰富知识,提高社会实践能力和综合素质,某中学团委组织学生参加了抽测一批棉花的纤维长度(单位:)cm 的社会实践活动.利用所学习的数学知识,同学们作出了样本的频率分布直方图.现在,由于原始数据不全,只能通过直方图来估计这一批棉花的纤维长度的平均值(同一组数据用这组数据所在区间的中点的值代替).则估计的平均值为()A.21.75B.22.25C.23.75D.20.75【解答】解:由频率分布直方图可得,平均值为(0.0112.50.0717.50.0822.50.0227.50.0232.5)521.75⨯+⨯+⨯+⨯+⨯⨯=.故选:A.4.(5分)《九章算术》是我国一部经典的数学著作,《九章算术⋅商功》有这样的载述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也”.“堑堵”就是底面为直角三角形的直三棱柱,“鳖臑”是四个面均为直角三角形的三棱锥,将底面为短形,一条侧棱垂直于底面的四棱锥称为“阳马”.已知由某“堑堵”“阳马”“鳖臑”组成的几何体的三视图如图所示,则该几何体的体积为()A.6B.5C.4D.3【解答】解:根据几何体的三视图转换为直观图为:该几何体为棱锥和棱柱组成的组合体;如图所示:所以:111113223112313263223V =⨯⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=++=.故选:A .5.(5分)有5条同样的生产线,生产的零件尺寸(单位:)mm 都服从正态分布2(20,)N σ,且2(1921)3P X <=,在每条生产线上各取一个零件,恰好有3个尺寸在区间(20,21]的概率为( ) A .64243B .80243C .1681D .40243【解答】解:2~(20,)X N σ,∴正态分布曲线的对称轴为20x μ==,又2(1921)3P X <=, 11(2021)(1921)23P X P X ∴<=<=, 故在每条生产线上各取一个零件,恰好有3个尺寸在区间(20,21]的概率为: 3235114140(1)()1033927243P C =⨯-⨯=⨯⨯=. 故选:D .6.(5分)函数9()11x f x e x =+--的大致图象为( )A .B .C .D .【解答】解:根据题意,设()1x g x e x =--,其导数()1x g x e '=-, 在区间(,0)-∞上,()0g x '<,则()g x 为减函数, 在区间(0,)+∞上,()0g x '>,则()g x 为增函数, 则()(0)0min g x g ==, 故9()11xf x e x =+--的定义域为{|0}x x ≠,且()1f x >恒成立,其图像在1y =上方,排除BCD ,故选:A .7.(5分)已知直线2y x m =+与圆221x y +=相交于不同的两点A 、B ,O 为坐标原点,且0OA OB ⋅,则实数m 的取值范围是( ) A .(-∞,1010[,)+∞ B .(5-1010[,5) C .(-∞,55[,)+∞ D .[5-5]【解答】解:因为直线2y x m =+与圆221x y +=相交于不同的两点A 、B , 所以圆心到直线的距离114d =<+,解得55m -<<,又0OA OB ⋅,所以2d,即25,解得10m 或10m -②, 由①②得(5m ∈-1010][,5). 故选:B .8.(5分)已知m 为常数,在某个相同的闭区间上,若()f x 为单调递增函数,()f x m +为单调递减函数,则称此区间为函数()f x 的“m LD -”区间.若函数()3sin(2)6f x x π=-,则此函数的“4LD π-”区间为( )A .[6k ππ-,]()12k k Z ππ+∈ B .[3k ππ+,7]()12k k Z ππ+∈C .[12k ππ+,]()3k k Z ππ+∈ D .7[12k ππ+,5]()6k k Z ππ+∈【解答】解:由题意可知,函数()f x 在“4LD π-”区间单调递增,函数()4f x π+在“4LD π-”区间单调递减,函数()3sin(2)6f x x π=-,则令222,262k x k k Z πππππ-+-+∈,解得,63k xk k Z ππππ-++∈,故()f x 的单调递增区间为[,],63k k k Z ππππ-++∈,又()3sin(2)3sin(2)4263f x x x ππππ+=+-=+,令3222,232k x k k Z πππππ+++∈, 解得7,1212k xk k Z ππππ++∈, 故()4f x π+的单调递减区间为7[,],1212k k k Z ππππ++∈,两个单调区间的公共区间为[,],123k k k Z ππππ++∈,所以此函数的“4LD π-”区间为[,],123k k k Z ππππ++∈.故选:C .9.(5分)226(2)(1)x x +-的展开式中,5x 的系数为( ) A .52-B .88-C .62-D .110-【解答】解:因为226426426(2)(1)(44)(1)(44)(1)x x x x x x x x +-=++-=++-,则6(1)x -的展开式的通项公式为166()(1)r r rr r r T C x C x +=⋅-=-, 所以原二项式的展开式中含5x 项为41123335555666(1)4(1)4(1)110x C x x C x C x x ⋅-+⋅-+⋅-=-, 所以5x 的系数为110-, 故选:D .10.(5分)已知双曲线2222:1(0,0)x y C a b a b-=>>,点M 为此渐近线上的一点,O 为坐标原点.双曲线C 的左、右顶点为A 、B ,焦距为2||OM ,则AM B∠为( )A .2π B .6π C .3π D .4π【解答】解:由题意可得渐近线by x a=,即有b a =, 设(,)M m n ,(,0)m n >,可得bn m a=,① 又||OM c =,即222m n c +=,②由①②可得m a =,n b =,即(,)M a b , 又(,0)A a -,(,0)B a ,可得AB MB ⊥,直线AM 的斜率为tan 2b MAB a ∠== 可得6MAB π∠=, 所以263AMB πππ∠=-=.故选:C .11.(5分)已知复数z 的模为1,复数23w z z =+,则在复平面内,复数w 所对应的点与点(4,0)的距离的最大值是( )A .6B .254C .D .【解答】解:设z x yi =+,(,)x y R ∈,因为||1z =,则221x y +=,22223()3()(3)(23)w z z x yi x yi x y x xy y i =+=+++=-+++,故复数w 对应的点为22(3x y x -+,23)xy y +, 设复数w 所对应的点与点(4,0)的距离为d , 则22222(34)(23)d x y x xy y =-+-++2222(2134)(23)(1)x x x x =-+-++- 22(1)[(1)(25)(1)(23)]x x x x x =--+-++(1)(1634)x x =--- 2161834x x =--+,对称轴为916x =-,因为[1x ∈-,1],所以当916x =-时,225625(25)1616max d =-⨯-=, 故254max d =, 所以数w 所对应的点与点(4,0)的距离的最大值是254. 故选:B .12.(5分)复利是指一笔资金产生利息外,在下一个计息周期内,以前各计息周期内产生的利息也计算利总的计息方法.单利是指一笔资金只有本金计取利息,而以前各计息周期内产生的利息在下一个计息周期内不计算利息的计息方法.小闯同学一月初在某网贷平台贷款10000元,约定月利率为1.5%,按复利计算,从一月开始每月月底等额本息还款,共还款12次,直到十二月月底还清贷款,把还款总额记为x 元.如果前十一个月因故不还贷款,到十二月月底一次还清,则每月按照贷款金额的1.525%,并且按照单利计算利息,这样,把还款总额记为y 元,则y x -的值为( )(参考数据:121.015 1.2)≈ A .170-B .1200C .1030D .900【解答】解:由题意可得:121210000(1 1.5%)10000 1.01512000x =⨯+=⨯≈, 1000010000 1.525%1211830y =+⨯⨯=, 1183012000170y x ∴-=-=-,故选:A .二、填空题:本大愿共4小题,每小题5分,共20分.13.(5分)已知向量a ,b 的夹角为120︒,||2a =,||1b =,若(3)(2)a b a b λ+⊥+,则λ=1- .【解答】解:向量a ,b 的夹角为120︒,||2a =,||1b =,若(3)(2)a b a b λ+⊥+, 则22(3)(2)2(6)324(6)21cos12030a b a b a a b b λλλλλ+⋅+=++⋅+=⨯++⨯⨯⨯︒+=, 1λ=-,故答案为:1-.14.(5分)已知变量x ,y 满足3303020x y x y x y m -+⎧⎪+-⎨⎪-+⎩,若3z x y =+的最小值为5,则实数m = 0 .【解答】解:由约束条件作出可行域如图,联立3020x y x y m +-=⎧⎨-+=⎩,解得6(3m A -,3)3m +,由3z x y =+,化为33x z y =-+,由图可知,当直线33x zy =-+过A 时,直线在y 轴上的截距最小,z 有最小值为639533m m -++=,解得0m =. 故答案为:0.15.(5分)已知点A 为椭圆2222:1(0)x y C a b a b+=>>的左顶点,(,0)F c 为椭圆的右焦点,B ,E 在椭圆上,四边形OABE 为平行四边形(O 为坐标原点),点F 到直线AE 2,则椭圆C 的离心率为102- . 【解答】解:由题意可得(,0)A a -,设0(E x ,00)0y y >,由四边形OABE 为平行四边形可得1(B x ,0)y ,且OA EB =,所以(a -,100)(x x =-,0), 所以10x x a =-,即0(B x a -,0)y ,由B ,E 在椭圆上,所以220022220022()11x a y a b x y a b ⎧-+=⎪⎪⎨⎪+=⎪⎩,两式相减可得20220ax a a -=, 解得02ax =,代入可得03y =, 即(2aE 3), 所以3322AEbb k a a ==+ 所以直线AE 的方程为:3)by x a =+,30ay -=,右焦点(,0)F c 到直线AE的距离d =, 整理可得:23420e e +-=,解得:e ==,由椭圆的离心率可得:e =. 16.(5分)已知数列{}n a 满足:152a =,2*112()2n n n a a a n N +=-+∈,若取整函数[]x 表示不小于x 的最小整数(例如:[1.2]2=,[3]3)=,设1n n na b a +=,数列{}n b 的前n 项和为n T ,则2021[]T = 2023 .【解答】解:数列{}n a 满足:152a =,21122n n n a a a +=-+, 整理得111122n n na a a +=---,所以111122n n n a a a +=---. 所以1220211202120211111112222a a a a a a ++⋯+=-=----, 由于2211122(2)022n n n n n a a a a a +-=+-=->,所以数列{}n a 单调递增, 由于152a =,2218a =,3 2.82a ≈,4 3.16a ≈,故当4n 时,3n a >, 所以20213a >, 12202111112a a a <++⋯+<, 整理得122021111[]2a a a ++⋯+=. 111n n n na b a a +==+, 2021[]202122023T ∴=+=,故答案为:2023.三、解答题:共70分.解答应写出必要的文字说明,证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.17.(12分)已知锐角ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,且满足(2)cos cos 0b c A a C --=.(1)求角A 的大小;(2)求cos cos B C +的取值范围. 【解答】解:(1)由正弦定理知,sin sin sin a b cA B C==, (2)cos cos 0b c A a C --=,(2sin sin )cos sin cos 0B C A A C ∴--=,2sin cos sin cos sin cos 2sin cos sin()2sin cos sin 0B A C A A C B A A C B A B ∴--=-+=-=,sin 0B ≠,1cos 2A ∴=, (0,)2A π∈,3A π∴=.(2)由(1)知,23B C π+=, 锐角ABC ∆,∴022032B C B πππ⎧<<⎪⎪⎨⎪<=-<⎪⎩,解得62B ππ<<,211cos cos cos cos()cos cos cos sin()3226B C B B B B B B B B ππ∴+=+-=-=+=+,62B ππ<<,∴2363B πππ<+<,sin()6B π∴+∈,1], 故cos cos B C+的取值范围为,1]. 18.(12分)在刚刚过去的寒假,由于新冠疫情的影响,哈尔滨市的A 、B 两所同类学校的高三学年分别采用甲、乙两种方案进行线上教学,为观测其教学效果,分别在两所学校的高三学年各随机抽取60名学生,对每名学生进行综合测试评分,记综合评分为80及以上的学生为优秀学生.经统计得到两所学校抽取的学生中共有72名优秀学生.(1)用样本估计总体,以频率作为概率,若在A 、B 两个学校的高三学年随机抽取3名学生,求所抽取的学生中的优秀学生数的分布列和数学期望;(2)已知A 学校抽出的优秀学生占该校抽取总人数的23,填写列联表,并判断能否在犯错误的概率不超过0.1的前提下认为学生综合测试评分优秀与教学方案有关.附:2(()()()()n ad K a b c d a c b d =++++,其中n a b c d =+++.【解答】解:(1)由已知,学生为优秀的概率为720.6120=, 记优质学生数为X ,由题意可孩子,X 的所有可能取值为0,1,2,3,所以033(0)(0.4)0.064P X C ===, 123(1)(0.4)0.60.288P X C ==⨯=,223(2)0.4(0.6)0.432P X C ==⋅=,333(3)(0.6)0.216P X C ===,所以X 的分布列为:故X 的数学期望()30.6 1.8E X =⨯=; (2)22⨯列联表如下:所以222()120(40282032) 2.22 2.706()()()()60607248n ad bc K a b c d a c b d -⨯⨯-⨯==≈<++++⨯⨯⨯, 所以不能在犯错误的概率不超过0.1的前提下认为学生综合测试评分优秀与教学方案有关. 19.(12分)如图,在三棱柱111ABC A B C -中,11BB AB AB BC ===,D 为AC 的中点,1AB B D ⊥,190B BC ∠=︒.(1)求证:平面11ABB A ⊥平面ABC ; (2)求二面角1D BB A --的余弦值.【解答】(1)证明:取AB 中点O ,连接OD 、1OB ,所以//OD BC , 因为11BB AB =,所以1OB AB ⊥, 又因为1AB B D ⊥,111B DOB B =,所以AB ⊥平面1OB D ,又因为OD ⊂平面1OB D ,所以AB OD ⊥, 因为190B BC ∠=︒,//OD BC ,所以1OD B B ⊥, 又因为1B BAB B =,所以OD ⊥平面11ABB A ,又因为OD ⊂平面ABC ,所以平面ABC ⊥平面11ABB A , 于是平面11ABB A ⊥平面ABC .(2)解:由(1)知OD 、OA 、1OB 两两垂直, 建立如图所示的空间直角坐标系,不妨设2AB =,1(0BB =,13),(1BD =,1,0), 设平面1BB D 的法向量为(m x =,y ,)z ,130BB m y z BD m x y ⎧⋅=+=⎪⎨⋅=+=⎪⎩,令3y =-(3m =,3-1), 平面1BB A 的法向量为(1n =,0,0), 所以二面角1D BB A --的余弦值为||321||||71m n m n ⋅==⋅⋅.20.(12分)已知抛物线2:2(0)C y px p =>的焦点为F ,过点F 且垂直于x 轴的直线与C 交于A ,B 两点,AOB ∆(点O 为坐标原点)的面积为2. (1)求抛物线C 的方程;(2)设不经过原点O 的直线l 与抛物线交于P 、Q 两点,设直线OP 、OQ 的倾斜角分别为α和β,证明:当4παβ+=时,直线l 恒过定点.【解答】(1)解:根据题意可得焦点(2p F ,0),因此可得(,),(,)22p pA pB p -, 所以12222AOB pS p ∆=⋅⋅=,解之可得2p =,故可得抛物线的方程为:24y x =.(2)证明:根据题意,设1(P x ,1)y ,2(Q x ,2)y ,易知直线l 的斜率存在,假设直线l 的方程为y kx m =+,联立抛物线方程得,224404y kx mky y m y x=+⎧⇒-+=⎨=⎩, 由韦达定理可得,121244,my y y y k k+==,则222121212122142[()2]444y y m x x y y y y k k +=+=+-=-,2221212244y y m x x k =⋅=, ∴121212164OP OQ y y kk k x x y y m ⋅=⋅==, 12121212122()4OP OQ y y kx x m x x k k x x x x m+++=+==, 又因为tan OP k α=,tan OQ k β=, 所以4tan tan m αβ+=,4tan tan kmαβ⋅=,所以当4παβ+=时,4tan tan tan()141tan tan 1m k m αβαβαβ++===-⋅-,解得44m k =+,所以直线l 的方程即为:444(4)y kx k y k x =++⇔-=+, 即得直线l 恒过定点(4,4)-.21.(12分)已知函数f (x )=3(x ﹣1)e x ﹣ek 有两个不同的零点(其中e 为自然对数的底数).(1)当x <﹣1时,求证:(x ﹣1)e x ﹣1>﹣;(2)求实数k 的取值范围;(3)若函数f (x )的两个零点为x 1、x 2,求证:<e .【解答】证明:(1)当x <﹣1时,要证(x ﹣1)e x ﹣1>﹣,只需证明(x ﹣1)e +1>0,令x ﹣1=t ,则t <﹣2,设g (t )=te +1,则g ′(t )=e(1+t ),当t <﹣2时,g ′(t )<0,在(﹣∞,﹣2)上,g (t )为单调递减函数, 此时g (t )>g (﹣2)=1﹣>0,所以原不等式成立. 解:(2)∵f ′(x )=3xe x ,当x <0时,f ′(x )<0,当x <0时,当f ′(x )>0,可得函数f (x )在(﹣∞,0)上为单调递减函数,在(0,+∞)上为单调递增函数, 所以f (x )min =f (0)=﹣3﹣ek ,(i )当﹣ek ≥3时,f (x )min ≥0,不合题意,(ii )当﹣ek ≤0时,f (1)=﹣ek ,若x <1,则f (x )<﹣ek , 当x ≥1时,f (x )≥ek ,又因为当x <﹣1时,由(1)可得f (x )>﹣﹣ek ,由﹣﹣ek>0得x<2ln(﹣ek)+1,取x0满足x0<﹣1且x0<2ln(﹣ek)+1,则f(x0)>0,所以f(x)在(﹣∞,1)上有唯一的零点,综上所述,﹣<k<0.证明:(3)函数f(x)的两个零点为x1、x2,所以3(x1﹣1)e﹣ek=0,同理3(x2﹣1)e﹣ek=0,由(1)得(x1﹣1)e >﹣,(x2﹣1)e >﹣,所以,,所以<﹣(+),因为x1<1,所以<0,所以>﹣,同理>﹣,所以<1<e.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4;坐标系与参数方程]22.(10分)在平面直角坐标系中,P为曲线122cos:(1sin2xCyααα=+⎧⎪⎨=⎪⎩为参数)上的动点,将P点纵坐标变为原来的2倍,横坐标变为原来的一半得到点Q,记点的轨迹为2C,以坐标原点O为极点,x轴非负半轴为极轴建立极坐标系.(1)求曲线C的极坐标方程;(2)A ,B 是曲线2C 上不同于O 的两点,且(A 1ρ,)θ、2(,)6B πρθ+;求|||OA OB 的取值范围. 【解答】解:(1)P 为曲线122cos :(1sin 2x C y ααα=+⎧⎪⎨=⎪⎩为参数)上的动点, 设(,)P x y '',(,)Q x y ,则212x x y y '=⎧⎪⎨'=⎪⎩, 消去x '和y '得到:22(1)1x y -+=.即222x y x +=,根据222cos sin x y x y ρθρθρ=⎧⎪=⎨⎪+=⎩,转换为极坐标方程为2cos ρθ=.(2)A ,B 是曲线2C 上不同于O 的两点,且(A 1ρ,)θ、2(,)6B πρθ+; 由于(,)23ππθ∈-,故2(,)636πππθ-∈-,所以|||cos 2sin()[26A B OA OB πρθθθ=-=-∈-,1). [选修4-5:不等式选讲]23.已知函数()32f x x =-,()21g x x =-.(1)若()|()||()|h x f x g x =+,且()h x a 恒成立,求实数a 的最大值;(2)若()x ϕ,求()x ϕ的最大值.【解答】解:(1)()32f x x =-,()21g x x =-,()|()||()||32||21||(21)(32)|2h x f x g x x x x x ∴=+=-+--+-=, 当且仅当1322x 时等号成立. ()2min h x ∴=,又()h x a 恒成立,∴实数a 的最大值为2;(2)()x ϕ由柯西不等式可得,()11x ϕ22(11)(22+=.=1x =时等号成立.()x ϕ∴的最大值为2.。
黑龙江省哈尔滨三中2015-2016学年高二上学期期中考试数学(理)试题Word版含答案

哈三中2015—2016 学年度上学期高二第一学段考试数学(理) 试卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、抛物线的焦点坐标为()A.B.C.D.2、双曲线的实轴长是()A.B.C.D.3、圆与圆的位置关系是()A.内切B.相交C.外切D.相离4、若双曲线()的一个焦点与抛物线的焦点重合,则此双曲线的离心率为()A.B.C.D.5、设经过点的等轴双曲线的焦点为、,此双曲线上一点满足,则的面积为()A.B.C.D.6、直线被圆截得的弦长为()A.B.C.D.7、已知,是椭圆的两焦点,过点的直线交椭圆于,两点.在中,若有两边之和是,则第三边的长度为()A.B.C.D.8、若点是抛物线上一动点,则点到直线和轴的距离之和的最小值是()A.B.C.D.9、已知集合,集合,且,则的取值范围是()A.B.C.D.10、已知直线和双曲线的右支交于不同两点,则的取值范围是()A.B.C.D.11、若点和点分别为椭圆的中心和左焦点,点为椭圆上的任意一点,则的最大值为()A.B.C.D.12、椭圆()上存在一点满足,为椭圆的左焦点,为椭圆的右顶点,则椭圆的离心率的范围是()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分.将答案填在答题卡相应的位置上)13、若经过点的双曲线的渐近线方程为,则双曲线的标准方程为.14、圆上的点到直线的最小距离是.15、已知圆,圆,动圆和圆外切,和圆内切,则动圆圆心的轨迹方程为.16、设直线与抛物线相交于、两点,抛物线的焦点为,若,则的值为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17、(本小题满分10分)已知圆过点,,且圆心在直线上.(I)求圆的方程;(II)若点在圆上,求的最大值.18、(本小题满分12分)已知椭圆()的离心率为,过椭圆一焦点且与椭圆长轴垂直的弦长为.(I)求椭圆的方程;(II)若斜率为的直线与椭圆交于,两点,且,求该直线的方程.19、(本小题满分12分)已知中心在原点的双曲线的右焦点,且到双曲线的一条渐近线的距离为.(I)求双曲线的方程;(II)若直线与双曲线恒有两个不同的交点,,且(为原点),求的取值范围.20、(本小题满分12分)已知的三个顶点都在抛物线上,为抛物线的焦点.(I)若,求点的坐标;(II)若点,且,求证:直线过定点.21、(本小题满分12分)已知焦点为,的椭圆与直线交于,两点,为的中点,直线的斜率为.焦点在轴上的椭圆过定点,且与椭圆有相同的离心率.过椭圆上一点作直线()交椭圆于,两点.(I)求椭圆和椭圆的标准方程;(II)求面积的最大值.22、(本小题满分12分)若过点作直线交抛物线于,两点,且满足,过,两点分别作抛物线的切线,,,的交点为.参考公式:过抛物线上任一点作抛物线的切线,则切线方程为.(I)求证:点在一条定直线上;(II)若,求直线在轴上截距的取值范围.2015-2016高二考试数学(理科)答案一、选择题1-5 CBBBD 6-10 CADDA 11-12 CC二、填空题13.14.15.16.三、解答题17.(1)设圆心坐标为,则解得:,故圆的方程为:(2)令z=x+y,即,当这条直线与圆相切时,它在y轴上的截距最大或最小,可求得最大值为:18. (1)设焦点为(c,0),因为过椭圆一焦点且与椭圆长轴垂直的弦长为1,所以,,解得:故椭圆方程为:(2),19. (1)双曲线的一条渐近线方程为:,则,解得:故双曲线的标准方程为:(2)20.(1)抛物线为焦点为(0,1),准线为y=-1,因为|PF|=3,所以,点P到准线的距离为3,因此点P的纵坐标为2,纵坐标为,所以,P点坐标为(2)21. (1)依题意,可设椭圆方程为,将直线代入椭圆方程,得:,=0则,,所以,M(,)直线OM的斜率为2,可得:又解得b=1,,所以,椭圆方程是;(2)422.(1)(2)。
2019年黑龙江省哈尔滨三中高考数学一模试卷(文科)(内考)(解析版)

2019年黑龙江省哈尔滨三中高考数学一模试卷(文科)(内考)一、选择题:本大题共12小题,每小题5分,共60分.在题目给出的四个选项中,只有一个选项是符合题目要求.1.(5分)已知全集U=R,集合A={﹣2,﹣1,0,1,2},B={x|x2≥4},则如图中阴影部分所表示的集合为()A.{﹣2,﹣1,0,1}B.{0}C.{﹣1,0}D.{﹣1,0,1}2.(5分)若复数z=,则|z|=()A.8B.2C.2D.3.(5分)某三棱锥的三视图如图所示,则该三棱锥的体积为()A.B.C.2D.4.(5分)已知a=,b=,c=,则()A.b<a<c B.a<b<c C.b<c<a D.c<a<b5.(5分)已知数列{a n}的前n项和S n=2+λa n,且a1=1,则S5=()A.27B.C.D.316.(5分)已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是()A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β不平行,则在α内不存在与β平行的直线D.若m,n不平行,则m与n不可能垂直于同一平面7.(5分)函数f(x)=a x﹣1(a>0,a≠1)的图象恒过点A,则下列函数中图象不经过点A的是()A.y=B.y=|x﹣2|C.y=2x﹣1D.y=log2(2x)8.(5分)已知函数y=sin(ωx+φ)的最小正周期为,直线是其图象的一条对称轴,则下面各式中符合条件的解析式为()A.B.C.D.9.(5分)阅读如图所示的程序框图,若运行相应的程序输出的结果为0,则判断框中的条件不可能是()A.n≤2014B.n≤2015C.n≤2016D.n≤201810.(5分)已知双曲线C:﹣=1(a>0,b>0)的右焦点F2到渐近线的距离为4,且在双曲线C上到F2的距离为2的点有且仅有1个,则这个点到双曲线C的左焦点F1的距离为()A.2B.4C.6D.811.(5分)已知x2+y2=4,在这两个实数x,y之间插入三个实数,使这五个数构成等差数列,那么这个等差数列后三项和的最大值为()A.B.C.D.12.(5分)函数,方程[f(x)]2﹣(m+1)f(x)+1﹣m=0有4个不相等实根,则m的取值范围是()A.B.C.D.二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)已知向量=(2,﹣4),=(﹣3,﹣4),则向量与夹角的余弦值为.14.(5分)设x,y满足约束条件,则z=x﹣y的最大值是.15.(5分)学校艺术节对同一类的A,B,C,D四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“A作品获得一等奖”;乙说:“C作品获得一等奖”丙说:“B,D两项作品未获得一等奖”丁说:“是A或D作品获得一等奖”若这四位同学中只有两位说的话是对的,则获得一等奖的作品是.16.(5分)正四面体ABCD的棱长为4,E为棱BC的中点,过E作其外接球的截面,则截面面积的最小值为.三、解答题:本大题共5小题,满分60分.解答须写出文字说明、证明过程和演算步骤. 17.(12分)在△ABC,,BC=2.(1)若AC=3,求AB的长;(2)若点D在边AB上,AD=DC,DE⊥AC,E为垂足,,求角A的值.18.(12分)某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如表:(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为:S=,试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?附:k2=19.(12分)如图,多面体ABCDEF中,底面ABCD是菱形,∠BCD=60°,四边形BDEF 是正方形且DE⊥平面ABCD.(Ⅰ)求证:CF∥平面ADE;(Ⅱ)若AE=,求多面体ABCDEF的体积V.20.(12分)已知椭圆C:+=1(a>b>0)的离心率为,以M(1,0)为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+﹣1=0相切.(1)求椭圆C的标准方程;(2)已知点N(3,2),和平面内一点P(m,n)(m≠3),过点M任作直线l与椭圆C 相交于A,B两点,设直线AN,NP,BN的斜率分别为k1,k2,k3,k1+k3=3k2,试求m,n满足的关系式.21.(12分)已知函数f(x)=lnx﹣kx+1.(1)求函数f(x)的单调区间;(2)若f(x)≤0恒成立,试确定实数k的取值范围;(3)证明:请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题记分.答题时用2B 铅笔在答题卡上把所选的题号涂黑.[选修4-4:坐标系与参数方程]22.(10分)已知曲线C1:x+y=和C2:(φ为参数),以原点O为极点,x轴的正半轴为极轴,建立极坐标系,且两种坐标系中取相同的长度单位.(1)把曲线C1、C2的方程化为极坐标方程(2)设C1与x轴、y轴交于M,N两点,且线段MN的中点为P.若射线OP与C1、C2交于P、Q两点,求P,Q两点间的距离.[选修4-5:不等式选讲]23.设a,b,c>0,且ab+bc+ca=1,求证:(1)a+b+c≥;(2)++≥(++)2019年黑龙江省哈尔滨三中高考数学一模试卷(文科)(内考)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在题目给出的四个选项中,只有一个选项是符合题目要求.1.【解答】解:由Venn图可知阴影部分对应的集合为A∩(∁U B),∵B={x|x2≥4}={x|x≥2或x≤﹣2},A={﹣2,﹣1,0,1,2},∴∁U B={x|﹣2<x<2},即A∩(∁U B)={﹣1,0,1}故选:D.2.【解答】解:复数z=,则|z|===.故选:D.3.【解答】解:由主视图和侧视图可知棱锥的高h=2,结合侧视图和俯视图可知三棱锥的底面ABC为直角三角形,BC=1,AB=2,AB⊥BC,∴三棱锥的体积V==,故选:A.4.【解答】解:由a==b==根据指数函数的单调性,∴a>b.a==,c=,∴a<c,可得:b<a<c.故选:A.5.【解答】解:S n=2+λa n,且a1=1,∴1=a1=S1=2+λ,解得λ=﹣1.∴n≥2时,S n=2﹣a n=2﹣(S n﹣S n﹣1),化为:S n﹣2=(S n﹣1﹣2),S1﹣2=﹣1,∴S n﹣2=﹣,即S n=2﹣,则S5=2﹣=,故选:C.6.【解答】解:对于A,若α,β垂直于同一平面,则α与β不一定平行,例如墙角的三个平面;故A错误;对于B,若m,n平行于同一平面,则m与n平行.相交或者异面;故B错误;对于C,若α,β不平行,则在α内存在无数条与β平行的直线;故C错误;对于D,若m,n不平行,则m与n不可能垂直于同一平面;假设两条直线同时垂直同一个平面,则这两条在平行;故D正确;故选:D.7.【解答】解:函数f(x)=y=a x﹣1(a>0,a≠1)的图象恒过点A,即x﹣1=0,可得x=1,那么:y=1.∴恒过点A(1,1).把x=1,y=1带入各选项,经考查各选项,只有A没有经过A点.故选:A.8.【解答】解:函数y=sin(ωx+φ)的最小正周期为,故:,解得:ω=4,直线是其图象的一条对称轴,故:,(k∈Z)解得:φ=k(k∈Z),当k=1时,φ=,故选:A.9.【解答】解:模拟执行程序,可得前6步的执行结果如下:s=0,n=1;满足条件,执行循环体,s=,n=2;满足条件,执行循环体,s=0,n=3;满足条件,执行循环体,s=0,n=4;满足条件,执行循环体,s=,n=5;满足条件,执行循环体,s=0,n=6…观察可知,s的值以3为周期循环出现,当n的值除以3余1时,可得对应的s的值为,由于:2014=671×3+1所以:判断条件为n≤2014?时,s=符合题意.故选:A.10.【解答】解:设渐近线为,∵右焦点F2到渐近线的距离为4,∴,即b=4.∵双曲线C上到F2的距离为2的点有且仅有1个,这个点是右顶点,∴c﹣a=2.∴(c﹣a)2=4=b,⇒(c﹣a)4=b2=(c﹣a)(c+a),∴c+a=(c﹣a)3=8.则这个点到双曲线C的左焦点F1的距离为c+a=8,故选:D.11.【解答】解:根据题意,设插入的三个数为a、b、c,即构成等差数列的五个数分别为x,a,b,c,y,则有x+y=a+c=2b,则b=,c===,则这个等差数列后三项和为b+c+y=3b=,又由x2+y2=4,设x=2cosα,y=2sinα,则b+c+y=(x+3y)=(cosα+3sinα)=sin(α+φ)≤,即这个等差数列后三项和的最大值为;故选:D.12.【解答】解:函数是连续函数,x=0时,y=0.x>0时,函数的导数为f′(x)=,当0<x<1时,f′(x)>0,f(x)递增;当x>1时,f′(x)<0,f(x)递减,可得f(x)在x=1处取得极大值,f(x)∈(0,]x<0时,f′(x)=﹣<0,函数是减函数,作出y=f(x)的图象,设t=f(x),关于x的方程[f(x)]2﹣(m+1)f(x)+1﹣m=0即为t2﹣(m+1)t+1﹣m=0,有1个大于实根,一个根在(0,);由题意可得:解得m∈.故选:C.二、填空题:本大题共4小题,每小题5分,共20分.13.【解答】解:根据题意,设向量与夹角为θ,向量,,则||=2,||=5,且•=2×(﹣3)+(﹣4)×(﹣4)=10,cosθ===,故答案为:.14.【解答】解:作出不等式组对应的平面区域如图:由z=x﹣y得y=x﹣z,平移直线y=x﹣z,由图象直线当直线y=x﹣z经过B(2,0)时,直线y=x﹣z的截距最小,此时z最大为z=2﹣0=2,即z=x﹣y的最大值是2,故答案为:2.15.【解答】解:根据题意,A,B,C,D作品进行评奖,只评一项一等奖,假设参赛的作品A为一等奖,则甲、丙,丁的说法都正确,乙错误,不符合题意;假设参赛的作品B为一等奖,则甲、乙、丙、丁的说法都错误,不符合题意;假设参赛的作品C为一等奖,则乙,丙的说法正确,甲、丁的说法错误,符合题意;假设参赛的作品D为一等奖,则甲、乙,丙的说法都错误,丁的说法正确,不符合题意;故获得参赛的作品C为一等奖;故答案为:C.16.【解答】解:将四面体ABCD放置于正方体中,如图所示可得正方体的外接球就是四面体ABCD的外接球,∵正四面体ABCD的棱长为4,∴正方体的棱长为,可得外接球半径R满足,解得R=E为棱BC的中点,过E作其外接球的截面,当截面到球心O的距离最大时,截面圆的面积达最小值,此时球心O到截面的距离等于正方体棱长的一半,可得截面圆的半径为r==2,得到截面圆的面积最小值为S=πr2=4π.故答案为:4π三、解答题:本大题共5小题,满分60分.解答须写出文字说明、证明过程和演算步骤. 17.【解答】解:(1)设AB=x,则由余弦定理有:AC2=AB2+BC2﹣2AB•BC cos B,即32=22+x2﹣2x•2cos60°,解得:,所以;(2)因为,所以.在△BCD中,由正弦定理可得:,因为∠BDC=2∠A,所以.所以,所以.18.【解答】解:(1)设“在本年内随机抽取一天,该天经济损失S大于200元且不超过600元”为事件A…(1分)由200<S≤600,得150<ω≤250,频数为39,…(3分)∴P(A)=….(4分)(2)根据以上数据得到如表:….(8分)K2的观测值K2=≈4.575>3.841….(10分)所以有95%的把握认为空气重度污染与供暖有关.….(12分)19.【解答】(Ⅰ)证明:∵底面ABCD是菱形,∴AD∥BC,∵四边形BDEF是正方形,∴DE∥BF,∵BF∩BC=B,∴平面ADE∥平面BCF,∵CF⊂平面BCF,∴CF∥平面ADE.(Ⅱ)解:连结AC,交BD于O,∵四边形BDEF是正方形且DE⊥平面ABCD.∴DE⊥平面ABCD,又AC⊂平面ABCD,∴AC⊥DE,∵底面ABCD是菱形,∴AC⊥BD,又BD∩DE=D,∴AC⊥平面BDEF,∵AE=,∠BCD=60°,∴AD=DE=BD=1,∴AO=CO=,∴多面体ABCDEF的体积:V=2V A﹣BDEF=2×=2×=.20.【解答】解:(1)由椭圆C:+=1(a>b>0),焦点在x轴上,则M(1,0)到直线x﹣y+﹣1=0的距离d==1,∴b=d=1,离心率e===,解得:a=,∴椭圆C的标准方程;(2)①当直线斜率不存在时,由,解得x=1,,不妨设,,∵k1+k3=2,∴,∴m,n的关系式为3n=2m.②当直线的斜率存在时,设点A(x1,y1),B(x2,y2),直线l:y=k(x﹣1),联立椭圆整理得:(3k2+1)x2﹣6k2x+3k2﹣3=0,由韦达定理可知:x1+x2=,x1•x2=,∴,=,=.∴,∴m,n的关系式为3n=2m.21.【解答】解:(1)函数f(x)的定义域为,当k≤0时,在(0,+∞)上是增函数,当k>0时,若时,有,若时,有,则f(x)在上是增函数,在上是减函数.(2)由(1)知k≤0时,f(x)在(0,+∞)上是增函数,而f(1)=1﹣k>0,f(x)≤0不成立,故k>0,又由(1)知f(x)的最大值为,要使f(x)≤0恒成立,则即可,即﹣lnk≤0,得k≥1.(3)由(2)知,当k=1时,有f(x)≤0在(0,+∞)恒成立,且f(x)在(1,+∞)上是减函数,f(1)=0,即lnx<x﹣1,在x∈[2,+∞)上恒成立,令x=n2,则lnn2<n2﹣1,即2lnn<(n﹣1)(n+1),从而得证.请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题记分.答题时用2B 铅笔在答题卡上把所选的题号涂黑.[选修4-4:坐标系与参数方程]22.【解答】解:(1)线C1:x+y=和C2:(φ为参数),以原点O为极点,x轴的正半轴为极轴,建立极坐标系,因为x=ρcosθ,y=ρsinθ,所以C1:,即,所以;C2的普通方程为,所以其极坐标方程为,即.(2)由题意M(,0),N(0,1),所以P(),所以射线OP的极坐标方程为:,把代入C1得到ρ1=1,P(1,);把代入C2得到ρ2=2,Q(2,),所以|PQ|=|ρ2﹣ρ1|=1,即P,Q两点间的距离为1.[选修4-5:不等式选讲]23.【解答】证明:(1)运用分析法证明.要证a+b+c≥,即证(a+b+c)2≥3,由a,b,c均为正实数,且ab+bc+ca=1,即有a2+b2+c2+2(ab+bc+ca)≥3,即为a2+b2+c2≥1,①由a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac,相加可得a2+b2+c2≥zb+bc+ca=1,则①成立.综上可得,原不等式成立.(2)∵++=,而由(1)a+b+c≥,∴≥(++),故只需≥++,即a+b+c≤1,即:a+b+c≤ab+bc+ac,而a=•≤,b≤,c≤,∴a+b+c≤ab+bc+ac=1成立,(当且仅当a=b=c=时).。
(黑龙江)高三数学-2017年黑龙江省哈尔滨三中高考数学一模试卷(文科) Word版含解析
2017年黑龙江省哈尔滨三中高考数学一模试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={x|x2+x﹣2<0},集合,则A∩B=()A.(﹣1,2)B.(﹣∞,﹣1)∪(1,+∞) C.(﹣1,1)D.(﹣1,0)∪(0,1)2.在复平面内,复数(i是虚数单位)对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限3.在等比数列{a n}中,a1=1,a4=8,则a7=()A.64 B.32 C.16 D.124.如果执行下面的程序框图,那么输出的结果s为()A.8 B.48 C.384 D.3845.若实数x,y满足约束条件,则z=x+3y的最大值等于()A.0 B.C.12 D.276.一个几何体的三视图如图所示,则这个几何体的体积为()A. B.C.D.7.已知函数f(x)=sinwx+coswx(w>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是()A.[kπ﹣,kπ+],k∈Z B.[kπ+,kπ+],k∈ZC.[kπ﹣,kπ+],k∈Z D.[kπ+,kπ+],k∈Z8.已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的()A.既不充分也不必要的条件B.充分而不必要的条件C.必要而不充分的条件D.充要条件9.已知非零向量满足,则与的夹角为()A.B.C.D.10.过双曲线的右焦点且斜率为k的直线,与双曲线的右支只有一个公共点,则实数k的范围为()A.(﹣∞,﹣2]∪[2,+∞)B.[0,2]C.D.[﹣2,2] 11.若△PAD所在平面与矩形ABCD所在平面互相垂直,PA=PD=AB=2,∠APD=60°,若点P,A,B,C,D都在同一个球面上,则此球的表面积为()A.πB.πC.πD.π12.已知椭圆,点A(c,b),右焦点F(c,0),椭圆上存在一点M,使得,且,则该椭圆的离心率为()A. B.C.D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.设等差数列{a n}的前n项和为S n,若a1+a13=4,则S13.14.某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是.15.进位制是人们为了计数和运算方便而约定的计数系统,“满几进一”就是几进制,不同进制之间可以相互转化,例如把十进制的89转化为二进制,根据二进制数“满二进一”的原则,可以用2连续去除89得商,然后取余数,具体计算方法如下:这种算法叫做“除二取余把以上各步所得余数从下到上排列,得到89=1011001(2)法”,上述方法也可以推广为把十进制数化为k进制数的方法,称为“除k取余法”,那么用“除k取余法”把89化为七进制数为.16.当a时,关于x的不等式(e x﹣a)x﹣e x+2a<0的解集中有且只有两个整数值,则实数a的取值范围是.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在△ABC中,a,b,c分别是角A,B,C的对边,其外接圆半径为1,(c ﹣2a)cosB+bcosC=0.(1)求角B的大小;(2)求△ABC周长的取值范围.18.某社区对社区内50名70岁以上老人的身体健康状况和对平时锻炼身体的积极性进行了调查,统计数据如表所示:积极锻炼身体不积极锻炼身体合计健康状况良好18725健康状况一般61925合计242650(1)如果在被调查的老人中随机抽查一名,那么抽到积极锻炼身体的老人的概率是多少?抽到不积极锻炼身体且健康状况一般的老人的概率是多少?(2)试运用独立性检验思想方法判断能否有99%的把握说老人的身体健康状况与锻炼身体的积极性有关.(参考如表).19.已知四边形ABCD为直角梯形,AD∥BC,AB⊥BC,BC=2AB=4,AD=3,F为BC中点,EF∥AB,EF与AD交于点E,沿EF将四边形EFCD折起,使得平面ABFE⊥平面EFCD,连接AD,BC,AC.(1)求证:BE∥平面ACD;(2)求三棱锥的B﹣ACD体积.20.已知抛物线E:x2=2py(p>0),其焦点为F,过F且斜率为1的直线被抛物线截得的弦长为8.(1)求抛物线E的方程;(2)设A为E上一动点(异于原点),E在点A处的切线交x轴于点P,原点O 关于直线PF的对称点为点B,直线AB与y轴交于点C,求△OBC面积的最大值.21.已知函数f(x)=ax,g(x)=lnx,(a∈R)(1)当a=1时,求函数y=在点(1,0)处的切线方程;(2)若在[1,+∞)上不等式xf(x﹣1)≥g(x)恒成立,求实数a的取值范围.[选修4-4:坐标系与参数方程]22.在直角坐标系中,以原点为极点,x轴非负半轴为极轴建立极坐标系,直线l的参数方程为(t为参数),曲线C的极坐标方程为ρ=6cosθ(1)若l的参数方程中的t=时,得到M点,求M的极坐标和曲线C的直角坐标方程;(2)若点P(1,1),l和曲线C交于A,B两点,求.[选修4-5:不等式选讲]23.已知函数f(x)=|x+2|+|x﹣1|.(1)求不等式f(x)≥5的解集;(2)若关于x的不等式f(x)≥m2﹣2m的解集为R,求实数m的取值范围.2017年黑龙江省哈尔滨三中高考数学一模试卷(文科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={x|x2+x﹣2<0},集合,则A∩B=()A.(﹣1,2)B.(﹣∞,﹣1)∪(1,+∞) C.(﹣1,1)D.(﹣1,0)∪(0,1)【考点】交集及其运算.【分析】分别求出关于A、B的不等式,求出A、B的交集即可.【解答】解:A={x|x2+x﹣2<0}={x|(x+2)(x﹣1)<0}={x|﹣2<x<1},={x|﹣1<x<1且x≠0},则A∩B=(﹣1,0)∪(0,1),故选:D.2.在复平面内,复数(i是虚数单位)对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限【考点】复数的代数表示法及其几何意义.【分析】利用复数的运算法则、几何意义即可得出.【解答】解:在复平面内,复数==对应的点位于第一象限.故选:A.3.在等比数列{a n}中,a1=1,a4=8,则a7=()A.64 B.32 C.16 D.12【考点】等比数列的通项公式.【分析】利用等比数列的通项公式求出公比,由此能求出a7的值.【解答】解:∵在等比数列{a n}中,a1=1,a4=8,∴,即8=q3,解得q=2,a7==1×26=64.故选:A.4.如果执行下面的程序框图,那么输出的结果s为()A.8 B.48 C.384 D.384【考点】程序框图.【分析】先根据已知循环条件和循环体判定循环的次数,然后根据运行的后s的值找出规律,从而得出结论.【解答】解:根据题意可知该循环体运行4次第一次:s=2,i=4<10,第二次:s=8,i=6<10,第三次:s=48,i=8<10,第四次:s=384,s=10≥10,结束循环,输出结果S=384,故选:C.5.若实数x,y满足约束条件,则z=x+3y的最大值等于()A.0 B.C.12 D.27【考点】简单线性规划.【分析】由约束条件作出可行域,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.【解答】解:由约束条件,作出可行域如图,联立,解得:A(3,3),化目标函数z=x+3y为y=﹣+,由图可知,当直线y=﹣+过A时,直线在y轴上的截距最大,z最大.此时z=3+3×3=12.故选:C.6.一个几何体的三视图如图所示,则这个几何体的体积为()A. B.C.D.【考点】棱柱、棱锥、棱台的体积;由三视图求面积、体积.【分析】该几何体为正八面体,即两个全等的正四棱锥,棱长为1,棱锥的高为,即可求出体积【解答】解:该几何体为正八面体,即两个全等的正四棱锥,棱长为1,棱锥的高为,所以,其体积为:2×(1×1)×=,故选:A7.已知函数f(x)=sinwx+coswx(w>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是()A.[kπ﹣,kπ+],k∈Z B.[kπ+,kπ+],k∈ZC.[kπ﹣,kπ+],k∈Z D.[kπ+,kπ+],k∈Z【考点】两角和与差的正弦函数;正弦函数的单调性.【分析】先把函数化成y=Asin(ωx+φ)的形式,再根据三角函数单调区间的求法可得答案.【解答】解:f(x)=sinwx+coswx=2sin(wx+),(w>0).∵f(x)的图象与直线y=2的两个相邻交点的距离等于π,恰好是f(x)的一个周期,∴=π,w=2.f(x)=2sin(2x+).故其单调增区间应满足2kπ﹣≤2x+≤2kπ+,k∈Z.kπ﹣≤x≤kπ+,故选C.8.已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的()A.既不充分也不必要的条件B.充分而不必要的条件C.必要而不充分的条件D.充要条件【考点】必要条件、充分条件与充要条件的判断;奇偶性与单调性的综合.【分析】由题意,可由函数的性质得出f(x)为[﹣1,0]上是减函数,再由函数的周期性即可得出f(x)为[3,4]上的减函数,由此证明充分性,再由f(x)为[3,4]上的减函数结合周期性即可得出f(x)为[﹣1,0]上是减函数,再由函数是偶函数即可得出f(x)为[0,1]上的增函数,由此证明必要性,即可得出正确选项【解答】解:∵f(x)是定义在R上的偶函数,∴若f(x)为[0,1]上的增函数,则f(x)为[﹣1,0]上是减函数,又∵f(x)是定义在R上的以2为周期的函数,且[3,4]与[﹣1,0]相差两个周期,∴两区间上的单调性一致,所以可以得出f(x)为[3,4]上的减函数,故充分性成立.若f(x)为[3,4]上的减函数,同样由函数周期性可得出f(x)为[﹣1,0]上是减函数,再由函数是偶函数可得出f(x)为[0,1]上的增函数,故必要性成立.综上,“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的充要条件.故选D.9.已知非零向量满足,则与的夹角为()A.B.C.D.【考点】数量积表示两个向量的夹角.【分析】根据题意,得出•=0,⊥;求出||=,利用平面向量数量积的夹角公式求出夹角的大小.【解答】解:非零向量满足,∴=,∴•=0,∴⊥;画出图形如图所示;∴||=,∴(+)•(﹣)=﹣=12﹣=﹣2,∴cos<+,﹣>===﹣,∴与的夹角为.故选:C.10.过双曲线的右焦点且斜率为k的直线,与双曲线的右支只有一个公共点,则实数k的范围为()A.(﹣∞,﹣2]∪[2,+∞)B.[0,2]C.D.[﹣2,2]【考点】双曲线的简单性质.【分析】渐近线方程y=±2x,当过焦点的两条直线与两条渐近线平行时,这两条直线与双曲线右支分别只有一个交点,由此能求出此直线的斜率的取值范围.【解答】解:双曲线的渐近线方程y=±2x,当过焦点的两条直线与两条渐近线平行时,这两条直线与双曲线右支分别只有一个交点(因为双曲线正在与渐近线无限接近中),那么在斜率是[﹣2,2]两条直线之间的所有直线中,都与双曲线右支只有一个交点.此直线的斜率的取值范围[﹣2,2].故选:D.11.若△PAD所在平面与矩形ABCD所在平面互相垂直,PA=PD=AB=2,∠APD=60°,若点P,A,B,C,D都在同一个球面上,则此球的表面积为()A.πB.πC.πD.π【考点】球的体积和表面积.【分析】设球心为O,求出AD=2,BD=2,设AC∩BD=E,则BE=,OP=OB=R,设OE=x,则OB2=BE2+OE2=2+x2,过O作线段OH⊥平面PAD于H点,H是垂足,PO2=OH2+PH2=1+(﹣x)2,由此能求出球半径R,由此能求出此球的表面积.【解答】解:设球心为O,如图,∵△PAD所在平面与矩形ABCD所在平面互相垂直,PA=PD=AB=2,∠APD=60°,∴AD=2,BD==2,设AC∩BD=E,则BE=,∵点P,A,B,C,D都在同一个球面上,∴OP=OB=R,设OE=x,在Rt△BOE中,OB2=BE2+OE2=2+x2,过O作线段OH⊥平面PAD于H点,H是垂足,∵O点到面PAD的距离与点E到平面PAD的距离相等,∴OH=1,∴在Rt△POH中,PO2=OH2+PH2=1+(﹣x)2=x2﹣2+4,∴2+x2=x2﹣2+4,解得x=,∴R=,∴此球的表面积S=4πR2=4π×=.故选:B.12.已知椭圆,点A(c,b),右焦点F(c,0),椭圆上存在一点M,使得,且,则该椭圆的离心率为()A. B.C.D.【考点】椭圆的简单性质.【分析】设M(x,y),由⇒cx+by=c2,…①,由,cy﹣bx=bc…②由①②得x=,y=,…③把③代入椭圆得a4c2+4c6=a6⇒2c3=b3+bc2,c3﹣b3=bc2﹣c3,⇒(c﹣b)(b2+bc+2c2)=0⇒b=c.【解答】解:设M(x,y),∵∴,⇒⇒即OA⊥MF⇒cx+by=c2,…①.,因为,共线,cy﹣bx=bc…②由①②得x=,y=,…③把③代入椭圆得a4c2+4c6=a6⇒2c3=b3+bc2,c3﹣b3=bc2﹣c3,⇒(c﹣b)(b2+bc+2c2)=0⇒b=c⇒a=,椭圆的离心率e=.故选:A二、填空题(每题5分,满分20分,将答案填在答题纸上)13.设等差数列{a n}的前n项和为S n,若a1+a13=4,则S1326.【考点】等差数列的前n项和.【分析】利用等差数列通项公式直接求解.【解答】解:∵等差数列{a n}的前n项和为S n,a1+a13=4,∴S13==.故答案为:26.14.某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是216.【考点】频率分布直方图.【分析】先求出成绩在[16,18]的学生的频率,由此能求出成绩在[16,18]的学生人数.【解答】解:频率分布直方图中,从左到右的5个小矩形的面积之比为1:3:7:6:3,∴成绩在[16,18]的学生的频率为:=0.45,∴成绩在[16,18]的学生人数是:480×0.45=216.故答案为:216.15.进位制是人们为了计数和运算方便而约定的计数系统,“满几进一”就是几进制,不同进制之间可以相互转化,例如把十进制的89转化为二进制,根据二进制数“满二进一”的原则,可以用2连续去除89得商,然后取余数,具体计算方法如下:把以上各步所得余数从下到上排列,得到89=1011001(2)这种算法叫做“除二取余法”,上述方法也可以推广为把十进制数化为k 进制数的方法,称为“除k 取余法”,那么用“除k 取余法”把89化为七进制数为 155(7) . 【考点】进位制.【分析】根据题意,依据题意中“除k 取余法”的算法,分析可得89=12×7+5,12=1×7+5,1=0×7+1,则有89=155(7),即可得答案. 【解答】解:根据题意,89=12×7+5, 12=1×7+5, 1=0×7+1,则89=155(7),即89化为七进制数为155(7), 故答案为:155(7). 16.当a时,关于x 的不等式(e x ﹣a )x ﹣e x +2a <0的解集中有且只有两个整数值,则实数a 的取值范围是 (,) .【考点】指、对数不等式的解法.【分析】关于x 的不等式(e x ﹣a )x ﹣e x +2a <0可化为(x ﹣1)e x <a (x ﹣2); 设f (x )=(x ﹣1)e x ,g (x )=a (x ﹣2),其中a <;利用导数判断单调性、求出f (x )的最值,画出f (x )、g (x )的图象, 结合图象得出不等式的解集中有且只有两个整数时a 的取值范围. 【解答】解:当a时,关于x 的不等式(e x ﹣a )x ﹣e x +2a <0可化为e x (x ﹣1)﹣a (x ﹣2)<0, 即(x ﹣1)e x <a (x ﹣2); 设f (x )=(x ﹣1)e x ,g(x)=a(x﹣2),其中a<;∴f′(x)=e x+(x﹣1)e x=xe x,令f′(x)=0,解得x=0;∴x>0时,f′(x)>0,f(x)单调递增;x<0时,f′(x)<0,f(x)单调递减;∴x=0时f(x)取得最小值为f(0)=﹣1;g(x)=a(x﹣2)是过定点(2,0)的直线;画出f(x)、g(x)的图象如图所示;要使不等式的解集中有且只有两个整数值,∵a<,当x=0时y=﹣1,满足条件,0是整数解;当x=﹣1时,f(﹣1)=﹣2e﹣1;当x=﹣2时,f(x)=﹣3e﹣2,此时=>a,不等式有两个整数解为﹣1和0,∴实数a的取值范围是(,).故答案为:(,).三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在△ABC中,a,b,c分别是角A,B,C的对边,其外接圆半径为1,(c ﹣2a)cosB+bcosC=0.(1)求角B的大小;(2)求△ABC周长的取值范围.【考点】正弦定理;余弦定理;三角形中的几何计算.【分析】(1)根据题意,由正弦定理可以将(c﹣2a)cosB+bcosC=0整理变形可得2sinA•cosB=sinC•cosB+sinBcosC,又由三角函数的和差公式可得2sinA•cosB=sin(B+C),进而可得2sinA•cosB=sinA,即cosB=,由B的范围可得B的值.(2)根据题意,由正弦定理可得b的值,同时可得a+c=2(sinA+sinC),由三角函数的和差公式变形可得a+c=2sin(C+),结合C的范围,计算可得a+c 的范围,由b的值,即可得答案.【解答】解:(1)根据题意,(2a﹣c)cosB=bcosC,由正弦定理得:(2sinA﹣sinC)cosB=sinBcosC,即2sinA•cosB﹣sinC•cosB=sinBcosC变形可得:2sinA•cosB=sinC•cosB+sinBcosC∴2sinA•cosB=sin(B+C)∵在△ABC中,sin(B+C)=sinA∴2sinA•cosB=sinA,即cosB=,则B=;(2)根据题意,由(1)可得B=,sinB=,又由正弦定理b=2RsinB=,a=2RsinA=2sinA,c=2RsinC=2sinC;则a+c=2(sinA+sinC)=2[sin(﹣C)+sinC]=2[cosC+sinC]=2sin (C+),又由0<C<,则<C+<,则有<sin(C+)≤1,故<a+c≤2,则有2<a+b+c≤3,即△ABC周长的取值范围为(2,3].18.某社区对社区内50名70岁以上老人的身体健康状况和对平时锻炼身体的积极性进行了调查,统计数据如表所示:积极锻炼身体不积极锻炼身体合计健康状况良好18725健康状况一般61925合计242650(1)如果在被调查的老人中随机抽查一名,那么抽到积极锻炼身体的老人的概率是多少?抽到不积极锻炼身体且健康状况一般的老人的概率是多少?(2)试运用独立性检验思想方法判断能否有99%的把握说老人的身体健康状况与锻炼身体的积极性有关.(参考如表).【考点】独立性检验.【分析】(1)根据数表,计算对应的概率值即可;(2)根据数表,计算观测值,对照临界值表即可得出结论.【解答】解:(1)如果在被调查的老人中随机抽查一名,那么抽到积极锻炼身体的老人的概率是P1==,抽到不积极锻炼身体且健康状况一般的老人的概率是P2=;(2)根据数表,计算观测值=≈11.538>10.828,对照数表知,有99%的把握认为老人的身体健康状况与积极锻炼身体有关.19.已知四边形ABCD为直角梯形,AD∥BC,AB⊥BC,BC=2AB=4,AD=3,F为BC中点,EF∥AB,EF与AD交于点E,沿EF将四边形EFCD折起,使得平面ABFE⊥平面EFCD,连接AD,BC,AC.(1)求证:BE∥平面ACD;(2)求三棱锥的B﹣ACD体积.【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定.【分析】(1)连结AF 交BE 于O ,则O 为AF 中点,设G 为AC 中点,连结OG ,DG ,推导出四边形DEOG 为平行四边形,则BE ∥DG ,由此能证明BE ∥平面ACD .(2)点C 到平面ACD 的距离和点F 到平面ACD 的距离相等,均为2,从而三棱锥的B ﹣ACD 体积V B ﹣ACD =V E ﹣ACD =V C ﹣ADE ,由此能求出结果. 【解答】证明:(1)连结AF 交BE 于O , 则O 为AF 中点,设G 为AC 中点, 连结OG ,DG ,则OG ∥CF ,且OG=CF . 由已知DE ∥CF ,且DE=CF .∴DE ∥OG ,且DE=OG ,∴四边形DEOG 为平行四边形. ∴EO ∥DG ,即BE ∥DG .∵BE ⊄平面ACD ,DG ⊂平面ACD , ∴BE ∥平面ACD .解:(2)∵CF ∥DE ,∴CF ∥平面ACD ,∴点C 到平面ACD 的距离和点F 到平面ACD 的距离相等,均为2. ∴三棱锥的B ﹣ACD 体积V B ﹣ACD =V E ﹣ACD =V C ﹣ADE ==.20.已知抛物线E:x2=2py(p>0),其焦点为F,过F且斜率为1的直线被抛物线截得的弦长为8.(1)求抛物线E的方程;(2)设A为E上一动点(异于原点),E在点A处的切线交x轴于点P,原点O 关于直线PF的对称点为点B,直线AB与y轴交于点C,求△OBC面积的最大值.【考点】直线与抛物线的位置关系;抛物线的标准方程.(1)过点F且斜率为1的直线代入抛物线,利用|MN|=8,可得y1+y2+p=8,【分析】即可求抛物线C的方程;=||≤,(2)求出直线AB的方程是y=x+1,C(0,1),可得S△OBC即可求△OBC面积的最大值.【解答】解:(1)由题可知F(0,),则该直线方程为:y=x+,代入x2=2py(p>0)得:x2﹣2px﹣p2=0,设M(x1,y1),N(x2,y2),则有x1+x2=2p,∵|MN|=8,∴y1+y2+p=8,即3p+p=8,解得p=2∴抛物线的方程为:x2=4y;(2)设A(t,),则E在点A处的切线方程为y=x﹣,P(,0),B (,),直线AB的方程是y=x+1,∴C(0,1)S△OBC=||≤,当且仅当t=±2时,取得等号,所以△OBC面积的最大值为.21.已知函数f(x)=ax,g(x)=lnx,(a∈R)(1)当a=1时,求函数y=在点(1,0)处的切线方程;(2)若在[1,+∞)上不等式xf(x﹣1)≥g(x)恒成立,求实数a的取值范围.【考点】导数在最大值、最小值问题中的应用;利用导数研究曲线上某点切线方程.【分析】(1)当a=1时,求导数,求出切线的斜率,即可求函数y=在点(1,0)处的切线方程;(2)设函数G(x)=a(x2﹣x)﹣lnx,且G(1)=0,分类讨论,即可,求实数a的取值范围.【解答】解:(1)当a=1时,函数y==,∴y′=,∴x=1时,y′=1,∴函数y=在点(1,0)处的切线方程为y=x﹣1;(2)设函数G(x)=a(x2﹣x)﹣lnx,且G(1)=0.G′(x)=①当a≤0时,有G(2)=2a﹣ln2<0,不成立,②当a<0时,(i)a≥1时,G′(x)=,当x≥1时,G′(x)≥0所以G(x)在(0,+∞)上是单调增函数,所以G(x)≥G(1)=0(ii)0<a<1时,设h(x)=2ax2﹣ax﹣1,h(1)=a﹣1<0,所以存在x0,使得x∈(1,0)时,h(x)<0,∴G′(x)<0,G(x)<G(1)=0不成立综上所述a≥1.[选修4-4:坐标系与参数方程]22.在直角坐标系中,以原点为极点,x轴非负半轴为极轴建立极坐标系,直线l的参数方程为(t为参数),曲线C的极坐标方程为ρ=6cosθ(1)若l的参数方程中的t=时,得到M点,求M的极坐标和曲线C的直角坐标方程;(2)若点P(1,1),l和曲线C交于A,B两点,求.【考点】简单曲线的极坐标方程;参数方程化成普通方程.【分析】(1)t=代入直线l的参数方程求出M(0,2),从而求出点M的极坐标,由曲线C的极坐标方程能求出曲线C的直角坐标方程.(2)联立直线l的参数方程和曲线C的直角坐标方程得,由此利用韦达定理能求出的值.【解答】解:(1)∵直线l的参数方程为(t为参数),l的参数方程中的t=时,得到M点,∴点M的直角坐标为M(0,2),∴,,∴点M的极坐标为M(2,),∵曲线C的极坐标方程为ρ=6cosθ,即ρ2=6ρcosθ,∴曲线C的直角坐标方程为x2﹣6x+y2=0.(2)联立直线l的参数方程和曲线C的直角坐标方程得:,则,∴=====.[选修4-5:不等式选讲]23.已知函数f(x)=|x+2|+|x﹣1|.(1)求不等式f(x)≥5的解集;(2)若关于x的不等式f(x)≥m2﹣2m的解集为R,求实数m的取值范围.【考点】函数恒成立问题.【分析】(1)通过讨论x的范围,得到关于x的不等式组,解出即可;(2)求出f(x)的最小值,问题转化为3≥m2﹣2m,解出m即可.【解答】解:(1)由|x+2|+|x﹣1|≥5.得:可得:x≤﹣3或,可得x∈∅或,可得x≥2解得:x≥2或x≤﹣3,故不等式的解集是{x|x≥2或x≤﹣3};(2)|x+2|+|x﹣1|≥m2﹣2m,若∀x∈R,使得不等式的解集为R,|x+2|+|x﹣1|≥3,当﹣2≤x≤1时取等号,可得3≥m2﹣2m,解得:﹣1≤m≤3.实数m的取值范围:[﹣1,3].。
黑龙江省哈尔滨九中高考数学三模试卷 理(含解析)
黑龙江省哈尔滨九中2015届高考数学三模试卷(理科)一、选择题(本大题共12小题,每小题5分,每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)设复数,则在复平面内对应的点坐标为()A.(1,1)B.(﹣1,1)C.(﹣1,﹣1)D.(1,﹣1)2.(5分)已知两个集合A={x|y=ln(﹣x2+x+2)},则A∩B=()A.B.C.(﹣1,e)D.(2,e)3.(5分)=()A.4 B.2 C.﹣2 D.﹣44.(5分)如图所示,程序框图的功能是()A.求{}前10项和B.求{}前10项和C.求{}前11项和D.求{}前11项和5.(5分)一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为()A. m3B. m3C. m3D. m36.(5分)从1,2,3,4,5,6,7,8,9中不放回地依次取2个数,事件A=“第一次取到的是奇数”,B=“第二次取到的是奇数”,则P(B|A)=()A.B.C.D.7.(5分)直线l1:y=x、l2:y=x+2与⊙C:x2+y2﹣2mx﹣2ny=0 的四个交点把⊙C分成的四条弧长相等,则m=()A.0或1 B.0或﹣1 C.﹣1 D.18.(5分)如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC 所成的角是()A.90°B.60°C.45°D.30°9.(5分)点(1,1)在不等式组,表示的平面区域内,则m2+n2的取值范围是()A.[3,4] B.[2,4] C.[1,+∞)D.[1,3]10.(5分)给出下列四个结论:①若n组数据(x1,y1),…(x n,y n)的散点都在y=﹣2x+1上,则相关系数r=﹣1;②由直线,曲线及x轴围成的图形的面积是2ln2;③已知随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤﹣2)=0.21;④设回归直线方程为=2﹣2.5x,当变量x增加一个单位时,平均增加2个单位.其中正确结论的个数为()A.1 B.2 C.3 D.411.(5分)已知A,B,P是双曲线上的不同三点,且AB连线经过坐标原点,若直线PA,PB的斜率乘积,则该双曲线的离心率e=()A.B.C.D.12.(5分)已知函数,对∀a∈R,∃b∈(0,+∞),使得f (a)=g(b),则b﹣a的最小值为()A.B.C.D.二、填空题(本大题共4小题,每小题5分)13.(5分)若向量,是两个互相垂直的单位向量,则向量在向量方向上的投影为.14.(5分)已知f(x)=e x﹣x,求过原点与f(x)相切的直线方程.15.(5分)已知a>b>0,则a2+的最小值是.16.(5分)若数列{a n}与{b n}满足b n+1a n+b n a n+1=(﹣1)n+1,b n=,n∈N+,且a1=2,设数列{a n}的前n项和为S n,则S63=.三、解答题(解答应写出文字说明,证明过程或演算步骤)17.(12分)在△ABC中,角A,B,C的对边分别是a,b,c,且A,B,C成等差数列.(1)若=﹣,b=,求a+c的值;(2)求2sinA﹣sinC的取值范围.18.(12分)“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由;(下面的临界值表供参考)P(K2≥k0)0.10 0.05 0.010 0.005k0 2.706 3.841 6.635 7.879(2)现计划在这次场外调查中按年龄段选取9名选手,并抽取3名幸运选手,求3名幸运选手中在20~30岁之间的人数的分布列和数学期望.(参考公式:其中n=a+b+c+d)19.(12分)如图,斜三棱柱ABC﹣A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2,低面ABC是边长为2的正三角形,其重心为G点(重心为三条中线的交点).E是线段BC1上一点且.(1)求证:GE∥侧面AA1B1B;(2)求平面B1GE与底面ABC所成锐二面角的大小.20.(12分)已知抛物线y2=4x,过点M(0,2)的直线l与抛物线交于A、B两点,且直线l 与x交于点C.(1)求证:|MA|,|MC|、|MB|成等比数列;(2)设,,试问α+β是否为定值,若是,求出此定值;若不是,请说明理由.21.(12分)已知函数f(x)=x2﹣(a﹣2)x﹣alnx,(Ⅰ)求函数f(x)的单调区间;(Ⅱ)设函数g(x)=﹣x3﹣ax2+a﹣,若存在α,β∈(0,a],使得|f(α)﹣g(β)|<a成立,求a的取值范围;(Ⅲ)若方程f(x)=c有两个不相等的实数根x1,x2,求证:f′()>0.四、选修4-1:几何证明选讲.22.(10分)如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点 E,AD交BC于点F.(Ⅰ)求证:BC∥DE;(Ⅱ)若D,E,C,F四点共圆,且=,求∠BAC.五、选修4-4:坐标系与参数方程选讲23.在直角坐标系xoy中,曲线C1的参数方程为(t为参数),以原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为(1)求曲线C1的普通方程与曲线C2的直角坐标方程;(2)设点M(2,﹣1),曲线C1与曲线C2交于A,B,求|MA|•|MB|的值.六、选修4-5:不等式选讲24.已知函数f(x)=|x﹣a|.(1)若f(x)≤m的解集为{x|﹣1≤x≤5},求实数a,m的值.(2)当a=2且t≥0时,解关于x的不等式f(x)+t≥f(x+2t)黑龙江省哈尔滨九中2015届高考数学三模试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)设复数,则在复平面内对应的点坐标为()A.(1,1)B.(﹣1,1)C.(﹣1,﹣1)D.(1,﹣1)考点:复数代数形式的乘除运算;复数的代数表示法及其几何意义.专题:数系的扩充和复数.分析:利用复数的运算法则、共轭复数的定义、几何意义即可得出.解答:解:复数==﹣1+i,则在复平面内=i•(﹣1﹣i)=﹣i+1对应的点坐标为(1,﹣1),故选:D.点评:本题考查了复数的运算法则、共轭复数的定义、几何意义,考查了推理能力与计算能力,属于基础题.2.(5分)已知两个集合A={x|y=ln(﹣x2+x+2)},则A∩B=()A.B.C.(﹣1,e)D.(2,e)考点:交集及其运算.专题:集合.分析:求出A中x的范围确定出A,求出B中不等式的解集确定出B,找出A与B的交集即可.解答:解:由A中y=ln(﹣x2+x+2),得到﹣x2+x+2>0,即(x﹣2)(x+1)<0,解得:﹣1<x<2,即A=(﹣1,2),由B中不等式变形得:﹣2≤0,即≤0,整理得:(2x+1)(x﹣e)≥0,且x﹣e≠0,解得:x≤﹣或x>e,即B=(﹣∞,﹣]∪(e,+∞),则A∩B=(﹣1,﹣].故选:B.点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.3.(5分)=()A.4 B.2 C.﹣2 D.﹣4考点:诱导公式的作用;两角和与差的正弦函数.专题:三角函数的求值.分析:由已知可得原式等于,利用二倍角正弦公式及两角差的正弦公式化简可得结果.解答:解:========﹣4故选D点评:本题考查诱导公式和两角和与差的正弦函数的应用,属基础题.4.(5分)如图所示,程序框图的功能是()A.求{}前10项和B.求{}前10项和C.求{}前11项和D.求{}前11项和考点:程序框图.专题:算法和程序框图.分析:由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.解答:解:当k=1时,满足进行循环的条件,S=,n=4,k=2,当k=2时,满足进行循环的条件,S=,n=6,k=3,当k=3时,满足进行循环的条件,S=,n=8,k=4,当k=4时,满足进行循环的条件,S=,n=10,k=5,当k=5时,满足进行循环的条件,S=,n=12,k=6,当k=6时,满足进行循环的条件,S=,n=14,k=7,当k=7时,满足进行循环的条件,S=,n=16,k=8,当k=8时,满足进行循环的条件,S=,n=18,k=9,当k=9时,满足进行循环的条件,S=,n=20,k=10,当k=10时,满足进行循环的条件,S=,n=22,k=11,当k=11时,不满足进行循环的条件,故程序框图的功能是计算的S=值,即求{}前10项和,故选:B点评:本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.5.(5分)一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为()A. m3B. m3C. m3D. m3考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:由已知中的三视图,可知该几何体是一个以正视图为底面的七棱柱,分别计算底面面积和高,代入柱体体积公式,可得答案.解答:解:由已知中的三视图,可知该几何体是一个以正俯视图为底面的七棱柱,其底面面积S=m2,高h=1m,故几何体的体积V=Sh=m3,故选:D.点评:本题考查的知识点是简单空间图象的三视图,其中根据已知中的视图分析出几何体的形状及棱长是解答的关键.6.(5分)从1,2,3,4,5,6,7,8,9中不放回地依次取2个数,事件A=“第一次取到的是奇数”,B=“第二次取到的是奇数”,则P(B|A)=()A.B.C.D.考点:条件概率与独立事件.专题:计算题;概率与统计.分析:先计算P(AB)、P(A),再利用P(B|A)=,即可求得结论.解答:解:由题意,P(AB)==,P(A)==∴P(B|A)==.故选:D.点评:本题考查条件概率,考查学生的计算能力,属于基础题.7.(5分)直线l1:y=x、l2:y=x+2与⊙C:x2+y2﹣2mx﹣2ny=0 的四个交点把⊙C分成的四条弧长相等,则m=()A.0或1 B.0或﹣1 C.﹣1 D.1考点:直线与圆相交的性质.专题:数形结合法;直线与圆.分析:画出图形,直线l1∥l2,l1、l2把⊙C分成的四条弧长相等,结合选项讨论m的取值是否满足条件,从而得出结论.解答:解:∵直线l1∥l2,且l1、l2把⊙C分成的四条弧长相等,画出图形,如图所示;又⊙C可化为(x﹣m)2+(y﹣n)2=m2+n2,当m=0,n=1时,圆心为(0,1),半径r=1,此时l1、l2与⊙C的四个交点(0,0),(1,1),(0,2),(﹣1,1)把⊙C分成的四条弧长相等;当m=﹣1,n=0时,圆心为(﹣1,0),半径r=1,此时l1、l2与⊙C的四个交点(0,0),(﹣1,1),(﹣2,0),(﹣1,﹣1)也把⊙C分成的四条弧长相等;故选:B.点评:本题考查了直线与圆相交的性质问题,应画出图形,结合图形解答该题,是易错题.8.(5分)如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是()A.90°B.60°C.45°D.30°考点:直线与平面垂直的判定;异面直线及其所成的角.专题:计算题;空间位置关系与距离.分析:将其还原成正方体ABCD﹣PQRS,连接SC,AS,可得∠ASC(或其补角)即为所求角.解答:解:将其还原成正方体ABCD﹣PQRS,连接SC,AS,则PB∥SC,∴∠ACS(或其补角)是PB与AC所成的角∵△ACS为正三角形,∴∠ACS=60°∴PB与AC所成的角是60°故选B.点评:本题考查线线角的计算,考查学生分析解决问题的能力,属于中档题.9.(5分)点(1,1)在不等式组,表示的平面区域内,则m2+n2的取值范围是()A.[3,4] B.[2,4] C.[1,+∞)D.[1,3]考点:简单线性规划.专题:不等式的解法及应用.分析:求出约束条件,画出可行域,然后利用目标函数的几何意义求解即可.解答:解:点(1,1)在不等式组,表示的平面区域内,可得,不等式组表示的可行域如图:m2+n2的几何意义是可行域内的点到原点距离的平方,显然(1,0)到原点的距离最小,最小值为1,没有最大值,则m2+n2的取值范围是:{1,+∞).故选:点评:本题考查线性规划的应用,数形结合的应用,基本知识的考查.10.(5分)给出下列四个结论:①若n组数据(x1,y1),…(x n,y n)的散点都在y=﹣2x+1上,则相关系数r=﹣1;②由直线,曲线及x轴围成的图形的面积是2ln2;③已知随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤﹣2)=0.21;④设回归直线方程为=2﹣2.5x,当变量x增加一个单位时,平均增加2个单位.其中正确结论的个数为()A.1 B.2 C.3 D.4考点:命题的真假判断与应用.专题:简易逻辑.分析:①中,数据相关系数的意义,判定①正确.②利用定积分计算直线x=,x=2,曲线y=及x轴所围成的图形的面积.③已知随机变量ξ服从正态分布N(1,σ2),图象关于x=1对称,根据P(ξ≤4)=0.79,可得结论;④设回归直线方程为y=2﹣2.5x,当变量x增加一个单位时,y平均减少2.5个单位.解答:解:对于①,由题意,所有数据(x i,y i)(i=1,2,…,n)都在直线y=﹣x+1上,∴这组数据完全负相关,它的相关系数为﹣1,①正确.②由直线x=,x=2,曲线y=及x 轴所围成的图形的面积是=lnx =2ln2,正确;③已知随机变量ξ服从正态分布N (1,σ2),图象关于x=1对称,根据P (ξ≤4)=0.79,可得P (ξ≤﹣2)=0.21,正确;④设回归直线方程为y=2﹣2.5x ,当变量x 增加一个单位时,y 平均减少2.5个单位,故不正确. 故选:C点评: 本题以命题真假的判断为载体,着重考查了相关系数、定积分、正态分布、回归直线方程等知识点,属于中档题.11.(5分)已知A ,B ,P 是双曲线上的不同三点,且AB 连线经过坐标原点,若直线PA ,PB 的斜率乘积,则该双曲线的离心率e=()A .B .C .D .考点: 双曲线的简单性质.专题: 计算题;圆锥曲线的定义、性质与方程.分析: 设出点的坐标,求出斜率,将点的坐标代入方程,两式相减,再结合,即可求得结论.解答: 解:由题意,设A (x 1,y 1),P (x 2,y 2),则B (﹣x 1,﹣y 1) ∴k PA •k PB =,A ,B 代入两式相减可得=,∵,∴=,∴e 2=1+=,∴e=.故选:B .点评: 本题考查双曲线的标准方程,以及双曲线的简单性质的应用,得到=是解题的关键.12.(5分)已知函数,对∀a∈R,∃b∈(0,+∞),使得f (a)=g(b),则b﹣a的最小值为()A.B.C.D.考点:函数的值域.专题:函数的性质及应用;导数的概念及应用.分析:f(x)=e2x,g(x)=lnx+,得到f﹣1(x)=lnx,g﹣1(x)=,够造函数h(x)=h(x)=g﹣1(x)﹣f﹣1(x),则b﹣a的最小值,即为h(x)的最小值,利用导数法求出函数的最小值,可得答案.解答:解:∵f(x)=e2x,g(x)=lnx+,∴f﹣1(x)=lnx,g﹣1(x)=,令h(x)=g﹣1(x)﹣f﹣1(x)=﹣lnx,则b﹣a的最小值,即为h(x)的最小值,∵h′(x)=)=﹣,令h′(x)=0,解得x=,∵当x∈(0,)时,h′(x)<0,当x∈(,+∞)时,h′(x)>0,故当x=时,h(x)取最小值1﹣=1+,故选:A.点评:本题考查的知识点是反函数,利用导数法求函数的最值,其中将求b﹣a的最小值,转化为h(x)的最小值,是解答的关键,属于中档题.二、填空题(本大题共4小题,每小题5分)13.(5分)若向量,是两个互相垂直的单位向量,则向量在向量方向上的投影为﹣.考点:平面向量数量积的运算.专题:平面向量及应用.分析:先求得||的值,数形结合可得向量和向量的夹角为150°,根据在向量方向上的投影为||•cos150°,计算求得结果.解答:解:∵向量,是两个互相垂直的单位向量,∴=0,∴||===2.如图所示:设=,=,=,显然,向量和向量的夹角为150°,故在向量方向上的投影为2•cos150°=﹣.故答案为:﹣.点评:本题考查向量的投影,转化为向量的数量积和模长来运算是解决问题的关键,属于中档题.14.(5分)已知f(x)=e x﹣x,求过原点与f(x)相切的直线方程y=(e﹣1)x.考点:利用导数研究曲线上某点切线方程.专题:导数的综合应用.分析:根据函数f(x)的解析式设出切点的坐标,根据设出的切点坐标和原点求出切线的斜率,同时由f(x)求出其导函数,把切点的横坐标代入导函数中即可表示出切线的斜率,两次求出的斜率相等列出关于a的方程,求出方程的解即可得到a的值,进而得到切点坐标,根据切点坐标和切线过原点写出切线方程即可.解答:解:设切点坐标为(a,e a﹣a),又切线过(0,0),得到切线的斜率k=,又f′(x)=e x﹣1,把x=a代入得:斜率k=f′(a)=e a﹣1,则e a﹣1=,由于e a>0,则得到a=1,即切点坐标为(1,e﹣1),所以切线方程为:y﹣e+1=(e﹣1)(x﹣1).即y=(e﹣1)x.故答案为:y=(e﹣1)x点评:此题考查学生会利用导数求曲线上过某点切线方程,注意要区别在某点处的切线,解题的关键是确定切点,本题是一道中档题.15.(5分)已知a>b>0,则a2+的最小值是16.考点:基本不等式.专题:计算题.分析:先利用基本不等式求得b(a﹣b)范围,进而代入原式,进一步利用基本不等式求得问题答案.解答:解:∵b(a﹣b)≤()2=,∴a2+≥a2+≥16.当且仅当,即时取等号.故答案为:16点评:此题是中档题.本题主要考查了基本不等式在最值问题中的应用.解题的时候注意等号成立的条件.16.(5分)若数列{a n}与{b n}满足b n+1a n+b n a n+1=(﹣1)n+1,b n=,n∈N+,且a1=2,设数列{a n}的前n项和为S n,则S63=560.考点:数列的求和;数列递推式.专题:等差数列与等比数列.分析:由已知条件推导出b n=,a n=,由此能求出S63.解答:解:∵,∴b n=,∵,∴当n为奇数时,a n+2a n+1=0,当n为偶数时,2a n+a n+1=2,∵a1=2,∴a n=,∴S63=﹣=560故答案为:560.点评:本题考查数列求和等基础知识,考查计算能力、推理论证能力、综合发现问题解决问题的能力以及分类讨论思想.三、解答题(解答应写出文字说明,证明过程或演算步骤)17.(12分)在△ABC中,角A,B,C的对边分别是a,b,c,且A,B,C成等差数列.(1)若=﹣,b=,求a+c的值;(2)求2sinA﹣sinC的取值范围.考点:余弦定理的应用;数列的应用;向量在几何中的应用.专题:计算题.分析:(1)通过A,B,C成等差数列,求得B的值,通过已知的向量积求得ac的值,代入余弦定理即可求出a+c.(2)通过两角和公式对2sinA﹣sinC,再根据C的范围和余弦函数的单调性求出2sinA﹣sinC 的取值范围.解答:解:(1)∵A,B,C成等差数列,∴B=.∵•=﹣,∴a ccos(π﹣B)=﹣,∴ac=,即ac=3.∵b=,b2=a2+c2﹣2accosB,∴a2+c2﹣ac=3,即(a+c)2﹣3ac=3.∴(a+c)2=12,所以a+c=2.(2)2sinA﹣sinC=2sin(﹣C)﹣sinC=2(cosC+sinC)﹣sinC=cosC.∵0<C<,∴cosC∈(﹣,).∴2sinA﹣sinC的取值范围是(﹣,).点评:本题主要考查了余弦定理的应用.解决本题的关键就是充分利用了余弦定理的性质.18.(12分)“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由;(下面的临界值表供参考)P(K2≥k0)0.10 0.05 0.010 0.005k0 2.706 3.841 6.635 7.879(2)现计划在这次场外调查中按年龄段选取9名选手,并抽取3名幸运选手,求3名幸运选手中在20~30岁之间的人数的分布列和数学期望.(参考公式:其中n=a+b+c+d)考点:离散型随机变量的期望与方差;离散型随机变量及其分布列.专题:概率与统计.分析:(1)利用已知条件直接写出2×2列联表;求出K2,即可判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;(2)设3名选手中在20~30岁之间的人数为ξ,可能取值为0,1,2,3,20~30岁之间的人数是3人,求出概率得到分布列,然后求解期望即可.解答:解:(1)年龄/正误正确错误合计20~30 10 30 4030~40 10 70 80合计20 100 120有90%的把握认为猜对歌曲名称与否和年龄有关.﹣﹣﹣﹣﹣﹣(4分)(2)设3名选手中在20~30岁之间的人数为ξ,可能取值为0,1,2,3﹣﹣﹣﹣(5分)20~30岁之间的人数是3人﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分),,,﹣﹣﹣﹣﹣﹣﹣(10分)ξ0 1 2 3P﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(11分)E(ξ)==1﹣﹣﹣﹣﹣﹣(12分)点评:本题考查对立检验以及离散型随机变量的分布列以及期望的求法,考查计算能力.19.(12分)如图,斜三棱柱ABC﹣A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2,低面ABC是边长为2的正三角形,其重心为G点(重心为三条中线的交点).E是线段BC1上一点且.(1)求证:GE∥侧面AA1B1B;(2)求平面B1GE与底面ABC所成锐二面角的大小.考点:与二面角有关的立体几何综合题;直线与平面平行的判定.专题:计算题;证明题.分析:(1)欲证GE∥侧面AA1B1B,根据直线与平面平行的判定定理可知只需证GE与侧面AA1B1B 内一直线平行,延长B1E交BC于F,而GE∥AB1,GE⊄侧面AA1B1B,AB1⊂侧面AA1B1B,满足定理的条件;(2)过B1作B1H⊥AB,垂足为H,在底面ABC内,过H作HT⊥AF,垂足为T,连B1T,根据二面角平面角的定义可知∠B1TH为所求二面角的平面角,在Rt△B1HT中求出此角的正切值即可.解答:解:(1)延长B1E交BC于F,∵△B1EC1∽△FEB,BE=EC1∴BF=B1C1=BC,从而F为BC的中点.(2分)∵G为△ABC的重心,∴A、G、F三点共线,且=,∴GE∥AB1,又GE⊄侧面AA1B1B,AB1⊂侧面AA1B1B,∴GE∥侧面AA1B1B (4分)(2)在侧面AA1B1B内,过B1作B1H⊥AB,垂足为H,∵侧面AA1B1B⊥底面ABC,∴B1H⊥底面ABC.又侧棱AA1与底面ABC成60°的角,AA1=2,∴∠B1BH=60°,BH=1,B1H=(6分)在底面ABC内,过H作HT⊥AF,垂足为T,连B1T.由三垂线定理有B1T⊥AF,又平面B1GE与底面ABC的交线为AF,∴∠B1TH为所求二面角的平面角(8分)∴AH=AB+BH=3,∠HAT=30°,∴HT=AHsin30°=,在Rt△B1HT中,tan∠B1TH=(10分)从而平面B1GE与底面ABC所成锐二面角的大小为arctan(12分)点评:本题主要考查了直线与平面平行的判定,以及二面角的度量等基础知识,考查空间想象能力,运算能力和推理论证能力,属于中档题.20.(12分)已知抛物线y2=4x,过点M(0,2)的直线l与抛物线交于A、B两点,且直线l 与x交于点C.(1)求证:|MA|,|MC|、|MB|成等比数列;(2)设,,试问α+β是否为定值,若是,求出此定值;若不是,请说明理由.考点:直线与圆锥曲线的综合问题;等比关系的确定.专题:计算题;证明题.分析:(1)设直线l的方程为:y=kx+2,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得|MA|,|MC|、|MB|成等比数列,从而解决问题.(2)由,得,,,从而利用x1,x2,及k来表示α,β,最后结合(1)中根系数的关系即得故α+β为定值.解答:解:(1)设直线l的方程为:y=kx+2(k≠0),联立方程可得得:k2x2+(4k﹣4)x+4=0①设A(x1,y1),B(x2,y2),,则,②,而,∴|MC|2=|MA|•|MB|≠0,即|MA|,|MC|、|MB|成等比数列(7分)(2)由,得,,即得:,,则由(1)中②代入得α+β=﹣1,故α+β为定值且定值为﹣1(13分)点评:本小题主要考查等比关系的确定、向量坐标的应用、直线与圆锥曲线的综合问题等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.21.(12分)已知函数f(x)=x2﹣(a﹣2)x﹣alnx,(Ⅰ)求函数f(x)的单调区间;(Ⅱ)设函数g(x)=﹣x3﹣ax2+a﹣,若存在α,β∈(0,a],使得|f(α)﹣g(β)|<a成立,求a的取值范围;(Ⅲ)若方程f(x)=c有两个不相等的实数根x1,x2,求证:f′()>0.考点:利用导数研究函数的单调性;利用导数求闭区间上函数的最值.专题:导数的综合应用.分析:(Ⅰ)求出原函数的导函数,当a≤0时,f′(x)>0,当a>0时由导函数的零点对定义域分段,判断出导函数在不同区间段内的符号,则函数的单调区间可求;(Ⅱ)由题意可知a>0,由(Ⅰ)中的单调性求出f(x)在(0,a]上的最小值,利用导数求得g(x)在(0,a]上的函数值小于,求得f(x)的最小值与的差,然后分和讨论求解使得|f(α)﹣g(β)|<a成立的a的取值范围;(Ⅲ)把x1,x2代入方程f(x)=c,作差后得到,结合(Ⅰ)中函数的单调性把问题转化为证明,设t=换元后构造函数,利用导数加以证明.解答:解:(Ⅰ)由f(x)=x2﹣(a﹣2)x﹣alnx,得.当a≤0时,f′(x)>0,函数f(x)在(0,+∞)上单调递增.∴函数f(x)的增区间为(0,+∞).当a>0时,由f′(x)>0得x>,由f′(x)<0得0<x<.∴函数f(x)的增区间为(,+∞),减区间为(0,);(Ⅱ)当x∈(0,a]时,,由g(x)=﹣x3﹣ax2+a﹣,得.当a>0时,g′(x)<0在(0,+∞)恒成立,g(x)在(0,+∞)上为减函数,当x∈(0,a]时,g(x)<g(0)=..①当时,则|f(α)﹣g(β)|min=0<a显然成立,即a≥2.②当时,则,即.综上可知:a>;(Ⅲ)∵x1,x2是方程f(x)=c的两个不相等的实数根,不妨设0<x1<x2,则.两式相减得.即.又∵,当x>时f′(x)>0,当0<x<时f′(x)<0.故只要证明即可,即证.即证明.设t=,令,则.则在(0,+∞)上是增函数,又∵g(1)=0,∴t∈(0,1)时总有g(t)<0成立.即f′()>0.点评:本题考查利用导数研究函数的单调性,考查了利用导数求函数的最值,考查了数学转化思想方法和分类讨论的数学思想方法,是2015届高考试卷中的压轴题.四、选修4-1:几何证明选讲.22.(10分)如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点 E,AD交BC于点F.(Ⅰ)求证:BC∥DE;(Ⅱ)若D,E,C,F四点共圆,且=,求∠BAC.考点:与圆有关的比例线段.专题:推理和证明.分析:(Ⅰ)通过证明∠EDC=∠DCB,然后推出BC∥DE.(Ⅱ)解:证明∠CFA=∠CED,然后说明∠CFA=∠ACF.设∠DAC=∠DAB=x,在等腰△ACF中,π=∠CFA+∠ACF+∠CAF=7x,求解即可.解答:解:(Ⅰ)证明:因为∠EDC=∠DAC,∠DAC=∠DAB,∠DAB=∠DCB,所以∠EDC=∠DCB,所以BC∥DE.…(4分)(Ⅱ)解:因为D,E,C,F四点共圆,所以∠CFA=∠CED由(Ⅰ)知∠ACF=∠CED,所以∠CFA=∠ACF.设∠DAC=∠DAB=x,因为=,所以∠CBA=∠BAC=2x,所以∠CFA=∠FBA+∠FAB=3x,在等腰△ACF中,π=∠CFA+∠ACF+∠CAF=7x,则x=,所以∠BAC=2x=.…(10分)点评:本题考查内错角相等证明直线的平行,四点共圆条件的应用,考查推理与证明的基本方法.五、选修4-4:坐标系与参数方程选讲23.在直角坐标系xoy中,曲线C1的参数方程为(t为参数),以原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为(1)求曲线C1的普通方程与曲线C2的直角坐标方程;(2)设点M(2,﹣1),曲线C1与曲线C2交于A,B,求|MA|•|MB|的值.考点:简单曲线的极坐标方程;直线的参数方程.专题:坐标系和参数方程.分析:(1)曲线C1的参数方程为(t为参数),两式相加消去参数t即可化为普通方程;由曲线C2的极坐标方程为,平方化为ρ2+3ρ2sin2θ=4,利用即可化为直角坐标方程.(2)将代人C2直角坐标方程得,利用MA|•|MB|=t1•t2即可得出.解答:解:(1)曲线C1的参数方程为(t为参数),消去参数t化为x+y=1;由曲线C2的极坐标方程为,平方化为ρ2+3ρ2sin2θ=4,∴x2+4y2=4,化为直角坐标方程:=1.(2)将代人C2直角坐标方程得,∴,∴MA|•|MB|=.点评:本题考查了参数方程化为直角坐标方程、极坐标方程与直角坐标方程的互化、直线参数方程的应用,考查了推理能力与计算能力,属于中档题.六、选修4-5:不等式选讲24.已知函数f(x)=|x﹣a|.(1)若f(x)≤m的解集为{x|﹣1≤x≤5},求实数a,m的值.(2)当a=2且t≥0时,解关于x的不等式f(x)+t≥f(x+2t)考点:绝对值不等式的解法.专题:压轴题;不等式的解法及应用.分析:(Ⅰ)由题意可得a﹣m≤x≤a+m,比较题意可得,解之可得答案;(Ⅱ)当a=2时,f(x)=|x﹣2|,不等式可化为|x﹣2+2t|﹣|x﹣2|≤t,①分类讨论:当t=0时,不等式①恒成立,即x∈R;当t>0时,不等式等价于,或,或,解之综合可得答案.解答:解:(Ⅰ)由|x﹣a|≤m得a﹣m≤x≤a+m,结合题意可得,解得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)(Ⅱ)当a=2时,f(x)=|x﹣2|,所以f(x)+t≥f(x+2t)可化为|x﹣2+2t|﹣|x﹣2|≤t,①当t=0时,不等式①恒成立,即x∈R;当t>0时,不等式等价于,或,或,解得x<2﹣2t,或2﹣2t,或x∈ϕ,即x≤2﹣;综上,当t=0时,原不等式的解集为R,当t>0时,原不等式的解集为{x|x≤2﹣}﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)点评:本题考查绝对值不等式的解法,涉及分类讨论的思想,属中档题.。
黑龙江省哈尔滨市第三中学高三学年第一次模拟考试理科数学试题答案
2020年哈三中高三学年第一次模拟考试 数学试卷(理工类)答案及评分标准一、选择题:二、填空题: 13. [0,23) 14. [80,120] 15.1e或1 16. 152,2三、解答题:17. (1) 由 c a A b =+23cos , 余弦定理bc a c b A 2cos 222−+= 有c a bc a c b b =+−+⋅232222, 即ac c a b 3222−+= 有232cos 222=−+=ac b c a B由π<<B 0, 则6π=B ……………………………………………………..……3分又因为2cossin sin 2AC B = 有2cos 1sin 21A C +=, 即2)65cos(1sin 21C C −+=π, 有C C C sin 21cos 231sin +−=, 即1cos 23sin 21=+C C , 则1)3sin(=+πC , 由π<<C 0, 即23ππ=+C , 则6π=C ……………………………….………6分(2)延长线段AM 至D, 满足BM=MD, 联结AD在ABD ∆中, ()65,,,3122ππ=−=∠==+==B BAD c AB a AD AM BD , 满足余弦定理())23(2314222−−+=+ac c a ……………………………..9分 因为ac c a 222≥+,所以()ac ac c a )32()23(2314222+≥−−+=+, 则()ac )32(3142+≥+, 即8≤ac , 当且仅当c a =时取”=” 那么2218212121sin 21=⨯⨯≤==∆ac B ac S ABC, 当且仅当4==c a 时取”=” 则ABC ∆面积的最大值为2…………………………………….………………..12分18. (1)在ACD ∆中3111120cos 222=++=⋅⋅−+=︒CD AD CD AD AC ,232cos 222=⋅−+=∠AC AD CD AC AD DAC , 则6π=∠DAC在ABC ∆中212cos 222=⋅−+=∠AC AB BC AC AB BAC , 则3π=∠BAC ,那么2π=∠BAD , 即⊥AB AD因为⊥PA 平面ABCD …………………………………………………………………1分 所以, 分别以直线AB AD AP 为z y x ,,轴如图建立空间直角坐标系有()0,0,0A , ()0,0,3B , ⎪⎪⎭⎫ ⎝⎛0,23,23C , ()0,1,0D , ()3,0,0P , ⎪⎪⎭⎫ ⎝⎛0,43,43M ,设平面ACP 的法向量为()z y x m ,,=, 由于⎪⎪⎭⎫⎝⎛=0,23,23AC 且()3,0,0=AP满足⎪⎩⎪⎨⎧==+0302323z y x , 令3=x , 有⎪⎩⎪⎨⎧=−==013z y x , 则()0,1,3−=m ………...…….3分 设平面BCP 的法向量为()z y x n ,,=, 由于⎪⎪⎭⎫⎝⎛−=0,23,23BC 且()3,0,3−=BP 满足⎪⎩⎪⎨⎧=+−=+−03302323z x y x , 令3=x , 有⎪⎩⎪⎨⎧===313z y x , 则()3,1,3=n ……….……5分则7774013,cos =⨯+−>=<n m , 那么二面角B PC A −−的余弦值为77….…6分(2)设平面PCD 的法向量为()z y x a ,,=, 由于⎪⎪⎭⎫⎝⎛−=3,23,23PC 且()3,1,0−=PD满足⎪⎩⎪⎨⎧=−=−+03032323z y z y x , 令3=y , 有⎪⎩⎪⎨⎧==−=131z y x , 则()1,3,1−=a ……..…..8分 设()z y x N ,,且BP BN λ=,()10≤≤λ, 满足()()3,0,3,,3−=−λz y x有⎪⎩⎪⎨⎧==−=−λλ3033z y x , 则()λλ3,0,33−N , 则⎪⎭⎫⎝⎛−−=λλ3,43,3343MN则0=⋅a MN , 即033433433=+−−λλ, 有43=λ则⎪⎭⎫ ⎝⎛−=343,43,0MN ………………………………………………………………….10分 因为平面ACP 的法向量为()0,1,3−=m , 有4123243,cos =⨯>=<MN m那么直线MN 与平面PAC 所成角的正弦值为41………………………………………12分19. 解: (1) 由已知1)(0=B A P , 54)(4204191==C C B A P , 1912)(4204182==C C B A P …… 2分(2) X 可能的取值为2,1,0,· ……………………………… 3分所以9508771.02.07.0)0(420418420419=⨯+⨯+==C C C C X P ,950701.02.0)1(42031812420319=⨯+⨯==C C C C C X P , 95031.0)2(42021822=⨯==C C C X P . ………………………………… 6分 所以随机变量X 的分布列为4753895032950701=⨯+⨯=EX . ………………………………… 7分 (3) 由(1)知, =)(A P 950877)0(==X P , ………………………………… 8分按照设计方案购买的一箱粉笔中, 箱中每盒粉笔都是优质产品的概率为()A B P 0877665)()()()()(000===A PB P B A P A P AB P , ……………………………11分 因为107.0100877665100<⨯−⨯, 所以该方案无效. ……………………… 12分20.解(1)x mx x x m x x f 2222)(2++=++=‘()+∞∈,0x …………1分对于方程0222=++mx x 162−=∆m当44-≤≤m 时,0162≤−=∆m ,0)(≥x f ‘此时)(x f 没有极值点. …………………2分 当4−<m 时,方程0222=++mx x 两根为21,x x ,不妨设21x x <,0221>−=+mx x ,121=⋅x x ,210x x << 当0)(021>><<x f x x x x ‘,时或,当0)(21<<x f x x ‘时.此时21,x x 是函数)(x f 的两个极值点. ………………3分 当4>m 时,方程0222=++mx x 两根为43,x x ,0243<−=+mx x ,143=⋅x x ,所以004,3<<x x , ()+∞∈,0x 0)(>x f ‘,故)(x f 没有极值点.综上,当4−<m 时,函数)(x f 有两个极值点;当4−≥m 时,函数)(x f 没有极值点 …………. ………4分 (2)032ln 232-)(222≤−−++=−x e x mx x x e x f xx022ln 22≤−−+x e x mx x,x xe x x ln 222m 2−+≤x x e x x g x ln 222)(2−+=,22ln 11-)(x x e x x x g x +−+=)(‘……6分 ()1,0∈x ,0(<)‘x g ,)x g (单调递减;()+∞∈1,x ,0(>)‘x g )x g (单调递增; 11(+=≥e g x g )(),)1(2+≤e m ……8分(3)由(2)知当)1(2+=e m ,0ln )12≤−−++x e x x e x (恒成立,即 x x e x e x ln 1-2≥++)( 欲证xx e x e x 1-11-2≥++)( 只需证x x 1-1ln ≥,设x x x h 11ln )(+−=,21)(x x x h −=‘……10分 ()1,0∈x ,0('<)x h ,)x g (单调递减;()+∞∈1,x ,0(>)‘x h )x g (单调递增;01(=≥)()h x h ,所以xx 1-1ln ≥。
【附15套精选模拟试卷】黑龙江省哈尔滨三中2020届高三第一次模拟考试数学(理)试卷含解析
黑龙江省哈尔滨三中2020届高三第一次模拟考试数学(理)试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数3sin 4cos y x x =+,x ∈R 的值域是( ) A .[]7,7-B .[]5,5-C .[]4,4-D .[]3,3-2.已知等比数列{}n a 的前n 项和3nn S a =+(a 为常数),则数列2{}n a 的前n 项和为( )A .1(91)2n- B .1(91)4n- C .1(9)8na +D .3(91)8na +-3.已知函数()31log 5xf x x ⎛⎫=- ⎪⎝⎭,若实数x 0是方程f(x)=0的解,且0<x 1<x 0,则f(x 1)的值( )A .恒为负B .等于零C .恒为正D .不大于零4.1x >是21x >的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.将函数()2sin f x x =图象上各点的横坐标缩短到原来的12,纵坐标不变,然后向左平移6π个单位长度,得到()y g x =图象,若关于x 的方程()g x a =在,44ππ⎡⎤-⎢⎥⎣⎦上有两个不相等的实根,则实数a 的取值范围是( ) A .[]22-,B .[2,2)-C .[1,2)D .[1,2)-6.过双曲线2222:1(0,0)x y E a b a b-=>>的右焦点且垂直于x 轴的直线与双曲线E 交于,A B 两点,与双曲线E 的渐近线交于,C D两点,若AB ,则双曲线E 的渐近线方程为( ) A.y =B.y =C .2y x =± D.y =±7.设()f x 为定义在R 上的函数,当0x ≥时,()22()x f x x b b =++为常数,则(1)f -= A .-3B .-1C .1D .38.在三棱锥P ABC -中,平面PAB ⊥平面ABC ,V ABC是边长为PA PB ==,则该三棱锥外接球的表面积为( )A .654πB .16πC .6516πD .494π9.设11321log 2,log 3a b ==, c =0.3,则( )A .a<b<cB .a<c<bC .b<c<aD .b<a<c10.若将函数cos 2y x =的图象向左平移12π个单位长度,则平移后图象的对称轴为( ) A .()26k x k Z ππ=-∈ B .()26k x k Z x ππ=+∈ C .()212k x k Z ππ=-∈ D .()212k x k Z ππ=+∈11.设x ∈R ,定义符号函数1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩,则函数()f x =sgn x x 的图象大致是( )A .B .C .D .12.如图所示,等边ABC ∆的边长为2,AM BC P ,且6AM =.若N 为线段CM 的中点,则AN BM ⋅=u u u r u u u u r( )A .18B .22C .23D .24二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页(共21页) 2015年黑龙江省哈尔滨三中高考数学一模试卷(理科) 一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.(5分)集合P={x|>0},Q={x|y=},则P∩Q=( ) A.(1,2] B.[1,2] C.(﹣∞,﹣3)∪(1,+∞) D.[1,2) 2.(5分)等差数列{an}的前n项和为Sn,且S3=6,a1=4,则公差d等于( ) A.1 B. C.﹣2 D.3
3.(5分)在△ABC中,,AC=1,∠B=30°,△ABC的面积为,则∠C=( ) A.30° B.45° C.60° D.75° 4.(5分)下列函数在(0,+∞)上为减函数的是( ) A.y=﹣|x﹣1| B.y=ex C.y=ln(x+1) D.y=﹣x(x+2) 5.(5分)方程log2x+x=2的解所在的区间为( ) A.(0.5,1) B.(1,1.5) C.(1.5,2) D.(2,2.5) 6.(5分)将函数f(x)=sin(2x+φ)的图象向左平移个单位,所得到的函数图象关于y轴对称,则φ的一个可能取值为( ) A. B. C.0 D. 7.(5分)给出下列关于互不相同的直线m、l、n和平面α、β的四个命题: ①若m⊂α,l∩α=A,点A∉m,则l与m不共面; ②若m、l是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α; ③若l∥α,m∥β,α∥β,则l∥m; ④若l⊂α,m⊂α,l∩m=A,l∥β,m∥β,则α∥β, 其中为真命题的是( ) A.①③④ B.②③④ C.①②④ D.①②③
8.(5分)变量x、y满足条件,则(x﹣2)2+y2的最小值为( ) 第2页(共21页)
A. B. C.5 D. 9.(5分)如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,P为线段OC的中点,则•=( )
A.﹣1 B.﹣ C.﹣ D.﹣ 10.(5分)如图,四棱锥P﹣ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为( )
A.90° B.75° C.60° D.45° 11.(5分)已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若=3,则|QF|=( ) A. B. C.3 D.2 12.(5分)设函数f(x)在R上存在导数f′(x),∀x∈R,有f(﹣x)+f(x)=x2,在(0,+∞)上f′(x)<x,若f(4﹣m)﹣f(m)≥8﹣4m.则实数m的取值范围为( ) A.[﹣2,2] B.[2,+∞)
C.[0,+∞) D.(﹣∞,﹣2]∪[2,+∞) 二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题卡相应的位置上.) 13.(5分)正项等比数列{an}中,a2=4,a4=16,则数列{an}的前9项和等 第3页(共21页)
于 . 14.(5分)某几何体的三视图如图所示,则它的表面积为 .
15.(5分)已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=,椭圆的离心率为e1,双曲线的离心率e2,则= .
16.(5分)定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.如y=x2是[﹣1,1]上的平均值函数,0就是它的均值点.现有函数f(x)=x3+mx是区间[﹣1,1]上的平均值函数,则实数m的取值范围是 . 三、解答题(本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 17.(12分)设△ABC是锐角三角形,三个内角A,B,C所对的边分别记为a,b,c,并且(sinA﹣sinB)(sinA+sinB)=sin(﹣B)sin(+B). (Ⅰ)求角A的值; (Ⅱ)若•=12,a=2,求b,c(其中b<c). 18.(12分)已知数列{an}满足(an+1﹣1)(an﹣1)=3(an﹣an+1),a1=2,令. (Ⅰ)证明:数列{bn}是等差数列; 第4页(共21页)
(Ⅱ)求数列{an}的通项公式. 19.(12分)△ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点. (Ⅰ)求证:IH∥BC; (Ⅱ)求二面角A﹣GI﹣C的余弦值; (Ⅲ)求AG的长.
20.(12分)如图,抛物线C1:y2=2px与椭圆C2:+=1在第一象限的交点为B,O为坐标原点,A为椭圆的右顶点,△OAB的面积为. (Ⅰ)求抛物线C1的方程; (Ⅱ)过A点作直线l交C1于C、D 两点,射线OC、OD分别交C2于E、F两点,记△OEF和△OCD的面积分别为S1和S2,问是否存在直线l,使得S1:S2=3:77?若存在,求出直线l的方程;若不存在,请说明理由.
21.(12分)设函数f(x)=a(x+1)2ln(x+1)+bx(x>﹣1),曲线y=f(x)过点(e﹣1,e2﹣e+1),且在点(0,0)处的切线方程为y=0. (Ⅰ)求a,b的值; 第5页(共21页)
(Ⅱ)证明:当x≥0时,f(x)≥x2; (Ⅲ)若当x≥0时,f(x)≥mx2恒成立,求实数m的取值范围. 请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.【选修4-1:几何证明选讲】 22.(10分)如图,四边形ABCD是⊙O的内接四边形,延长BA和CD相交于点P,=,
=. (Ⅰ)求的值; (Ⅱ)若BD为⊙O的直径,且PA=1,求BC的长.
【选修4-4:坐标系与参数方程】 23.已知在平面直角坐标系xOy中,直线l的参数方程是(t是参数),以原点O为极点,x轴正半轴为极轴建立极坐标,曲线C的极坐标方程ρ=2cos(θ+).
(Ⅰ)判断直线l与曲线C的位置关系; (Ⅱ)设M为曲线C上任意一点,求x+y的取值范围. 【选修4-5:不等式选讲】 24.已知函数f(x)=|2x+1|﹣|x|﹣2 (Ⅰ)解不等式f(x)≥0 (Ⅱ)若存在实数x,使得f(x)≤|x|+a,求实数a的取值范围. 第6页(共21页)
2015年黑龙江省哈尔滨三中高考数学一模试卷(理科) 参考答案与试题解析 一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.(5分)集合P={x|>0},Q={x|y=},则P∩Q=( ) A.(1,2] B.[1,2] C.(﹣∞,﹣3)∪(1,+∞) D.[1,2) 【解答】解:集合P={x|>0}={x|x>1或x<﹣3},
Q={x|y=}={x|﹣2≤x≤2}, P∩Q={x|1<x≤2}=(1,2]. 故选:A. 2.(5分)等差数列{an}的前n项和为Sn,且S3=6,a1=4,则公差d等于( ) A.1 B. C.﹣2 D.3
【解答】解:∵S3=6=(a1+a3),且 a3=a1+2d,a1=4,∴d=﹣2, 故选:C. 3.(5分)在△ABC中,,AC=1,∠B=30°,△ABC的面积为,则∠C=( ) A.30° B.45° C.60° D.75° 【解答】解:∵△ABC中,B=30°,AC=1,AB=,由正弦定理可得: =,
∴sinC=, ∴C=60°或120°, C=60°时,A=90°;C=120°时A=30°, 当A=90°时,∴△ABC的面积为•AB•AC•sinA=,
当A=30°时,∴△ABC的面积为•AB•AC•sinA=,不满足题意, 则C=60°. 第7页(共21页)
故选:C. 4.(5分)下列函数在(0,+∞)上为减函数的是( ) A.y=﹣|x﹣1| B.y=ex C.y=ln(x+1) D.y=﹣x(x+2)
【解答】解:①y=﹣|x﹣1|= ∴(0,+∞)不是减函数, 故A不正确. ②y=ex,在(﹣∞,+∞)上为增函数,
故B不正确. ③y=ln(x+1)在(﹣1,+∞)上为增函数, 故C不正确. ④y=﹣x(x+2)在(﹣1,+∞)上为减函数, 所以在(0,+∞)上为减函数 故D正确. 故选:D. 5.(5分)方程log2x+x=2的解所在的区间为( ) A.(0.5,1) B.(1,1.5) C.(1.5,2) D.(2,2.5) 【解答】解:设f(x)=log2x+x﹣2,在(0,+∞)上单调递增. ∵f(1) =0+1﹣2=﹣1<0, f(1.5)=log21.5﹣0.5=log21.5﹣log2>0 ∴根据函数的零点存在性定理得出:f(x)的零点在(1,1.5)区间 内 ∴方程log2x+x=2的解所在的区间为(1,1.5) 故选:B. 6.(5分)将函数f(x)=sin(2x+φ)的图象向左平移个单位,所得到的函数图象关于y轴对称,则φ的一个可能取值为( ) A. B. C.0 D.
【解答】解:将函数f(x)=sin(2x+φ)的图象向左平移个单位,
