浅谈在弯矩作用下螺栓联接结构的计算方法
钢结构基础第五章 钢结构的紧固件连接

( N1y N1y )
V T
2
N m in
b
第五章 钢结构的紧固件连接
5.2 普通螺栓连接的构造和计算
5.2.3 螺栓群的计算
4. 螺栓群在轴心力作用下 的抗拉计算
n N Nt
b
5. 螺栓群在轴心力作用下 的抗拉计算 假定:中和轴在最下排 螺栓处
N
M 1
M y1 m y
第五章 钢结构的紧固件连接
5.2 普通螺栓连接的构造和计算
5.2.1 螺栓的排列和构造要求
排列要求
受力要求:钢板端部剪断,端距不应小于2d0;受拉时, 栓距和线距不应过小;受压时,沿作用力方向的栓距不 宜过大。 构造要求:栓距和线距不宜过大 施工要求:有一定的施工空间
第五章 钢结构的紧固件连接
图5-3 螺栓连接的 破坏情况
第五章 钢结构的紧固件连接
5.2 普通螺栓连接的构造和计算
5.2.2 普通螺栓连接受剪、受拉时的工作性能
1. 抗剪螺栓连接 受力状态:弹性时两端大而 中间小,进入塑性阶段后, 因内力重分布使各螺栓受力 趋于均匀。 为防止“解钮扣”破坏,当 连接长度l1较大时,应将螺栓 的承载力乘以折减系数。
第五章 钢结构的紧固件连接
5.3 高强度螺栓连接的性能和计算
5.3.1 高强度螺栓连接的性能
2. 高强度螺栓连接的摩擦面抗滑移系数 对于承压型连接,只要求清除油污及浮锈 对于摩擦型连接,对摩擦面抗滑移系数有要求 3. 高强度螺栓的排列 要求同普通螺栓,同样要考虑连接长度对承载力的不 利影响。
N t N1
M
M y1
m
yi
2
Nt
螺栓连接

螺栓连接——目录第一节:螺栓的分类 (1)第二节:普通螺栓连接的构造和计算 (2)一、螺栓的排列和构造 (2)二、普通螺栓连接的受力性能 (3)(一)、普通螺栓连接按照螺栓传力方式分为三种形式 (3)(二)、螺栓连接的破坏形式和解决方法 (3)三、单个螺栓的承载力设计值 (4)(一)、一个抗剪螺栓的承载力设计值 (4)(二)、一个抗拉螺栓的承载力设计值 (4)(三)、一个受剪受拉螺栓的设计值 (4)四、螺栓群计算 (5)(一)、螺栓群在板件轴心拉力作用下的抗剪计算 (5)(二)、螺栓群在扭矩作用下的抗剪计算 (7)(三)、螺栓群在扭矩、剪力和轴心拉力共同作用下的抗剪计算 (8)(四)、螺栓群在弯矩作用下的抗拉计算 (9)(五)、螺栓群在弯矩和剪力共同作用下的抗拉和抗剪计算 (11)(六)、螺栓群在弯矩和轴心拉力作用下的抗拉计算 (11)(七)、螺栓群在弯矩、轴心拉力和剪力共同作用下的抗拉和抗剪计算 (12)第三节:高强度螺栓连接的构造和计算 (13)一、高强度螺栓的排列和构造 (13)二、高强度螺栓的受力性能 (13)(一)、高强度螺栓连接从受力特征分为三种形式 (13)(二)、高强度螺栓的预拉力和连接表面的抗滑移系数 (13)三、高强度螺栓的承载力设计值 (15)(一)、高强度螺栓摩擦型连接的承载力设计值 (15)(二)、高强度螺栓承压型连接的承载力设计值 (16)四、高强度螺栓摩擦型螺栓群计算 (17)(一)、螺栓群在板件轴心拉力作用下的抗剪计算 (17)(二)、螺栓群在扭矩、剪力和轴心拉力共同作用下的抗剪计算 (18)(三)、螺栓群在弯矩作用下的抗拉计算 (19)(四)、螺栓群在弯矩和轴心拉力作用下的抗拉计算 (19)(五)、螺栓群在轴心拉力和剪力共同作用下的抗拉和抗剪计算 (20)(六)、螺栓群在弯矩、轴心拉力和剪力共同作用下的抗拉和抗剪计算 (20)第一节:螺栓的分类螺栓的分类:普通螺栓和高强度螺栓两种,两者的区别为:普通螺栓拧紧螺帽时产生的预拉力很小,由板面挤压产生的摩擦力可以忽略不计。
钢结构计算题(焊接、螺栓连接、稳定性)

Q235用。
由于翼缘处的剪应力很小,假定剪力全部由腹板的竖向焊缝均匀承受,而弯矩由整个T 形焊缝截面承受。
分别计算a 点与b 点的弯矩应力、腹板焊缝的剪应力及b 点的折算应力,按照各自应满足的强度条件,可以得到相应情况下焊缝能承受的力F i ,最后,取其最小的F 值即为所求。
1.确定对接焊缝计算截面的几何特性 (1)确定中和轴的位置()()()()8010102401020160)10115(1010240510201601≈⨯-+⨯-+⨯⨯-+⨯⨯-=ymm160802402=-=y mm(2)焊缝计算截面的几何特性()623231068.22)160115(230101014012151602301014023010121mm I x ⨯=-⨯⨯+⨯⨯++-⨯⨯+⨯⨯=腹板焊缝计算截面的面积:230010230=⨯=w A mm 22.确定焊缝所能承受的最大荷载设计值F 。
将力F 向焊缝截面形心简化得:F Fe M 160==(KN·mm) F V =(KN )查表得:215=w c f N/mm 2,185=w t f N/mm 2,125=wv f N/mm 2点a 的拉应力M a σ,且要求M a σ≤wt f 18552.01022688010160431===⨯⨯⨯==w t x M af F F I My σ N/mm 2 解得:278≈F KN点b 的压应力Mb σ,且要求Mb σ≤wc f 215129.110226816010160432===⨯⨯⨯==wc x Mbf F F I My σ N/mm 2 解得:5.190≈F KN由F V =产生的剪应力V τ,且要求V τ≤wV f125435.010231023===⨯⨯=wV V f F F τ N/mm 2 解得:7.290≈F KN点b 的折算应力,且要求起步大于1.1wt f ()()()w t V M bf F F 1.1435.03129.132222=⨯+=+τσ解得:168≈F KN缝的距离不相等,肢尖焊缝的受力小于肢背焊缝的受力,又题中给出了肢背、肢尖焊缝相同的长度和焊脚尺寸,所以,只要验算肢背焊缝的强度,若能满足,肢尖焊缝的强度就能肯定满足。
5 第一章-螺栓连接

N
(四)普通螺栓群在弯矩作用下
1 2 3 4 N1 N2 y1 N3 y y3 2 N4 中和轴
M
刨平顶紧 承托(板)
M
受压区
☻M作用下螺栓连接按弹性设计,其假定为: (1)连接板件绝对刚性,螺栓为弹性; (2)这种连接的受力有如下的特点:受拉截面只是螺栓的 几个点,而端板的受压区则是宽度很大的实体矩形截面当 计算形心位置作为中和轴时,端板的受压区高度很小,此 时把螺栓群的中和轴位于最下排螺栓的形心处,各螺栓所 受拉力与其至中和轴的距离呈正比。 离中和轴越远的螺栓所收拉力越大
2、承受静载的可拆卸结构连接; 3、临时固定构件的安装连接。
2.破坏形式
(1)螺栓杆被剪坏 栓杆较细而板件较厚时 (2)孔壁的挤压破坏 栓杆较粗而板件较薄时 (3)板件被拉断 截面削弱过多时 以上破坏形式予以计算解决。
N/2
N
N/2
N
N
N
N
(4)板件端部被剪坏(拉豁) 端矩过小时;端矩不应小于2dO
3)螺栓连接的构造要求
为了保证连接的可靠性,每个杆件的节点或拼接接头一 端不宜少于两个永久螺栓,但组合构件的缀条除外; 直接承受动荷载的普通螺栓连接应采用双螺帽,或其他 措施以防螺帽松动; C级螺栓宜用于沿杆轴方向的受拉连接,以下情况可用 于抗剪连接:
1、承受静载或间接动载的次要连接;
终拧—初拧基础上用长扳手或电动扳手再拧过一定的角度,一般为 120o~180o完成终拧。
特点:预拉力的建立简单、有效,但要防止欠拧、漏拧
和超拧; B、扭矩法 施工方法: 初拧—用力矩扳手拧至终拧力矩的30%~50%,使
板件贴紧密;
终拧—初拧基础上,按100%设计终拧力矩拧紧。 特点:简单、易实施,但得到的预拉力误差较大。
B73-弯矩、剪力共同作用下工字梁角焊缝连接计算
τf
x
x
(
fB
)2
f
2
f
f
w f
式中: he2lw 2 — 腹板焊缝有效截面积之和;
h — 腹板焊缝的长度。
方法二
假设腹板焊缝只承受剪力; 翼缘焊缝承担全部弯矩,并将弯矩 M 化为一对水平力
H=M/h1
V=F
翼缘焊缝按下式验算强度:
H fw
f
h le1 w1
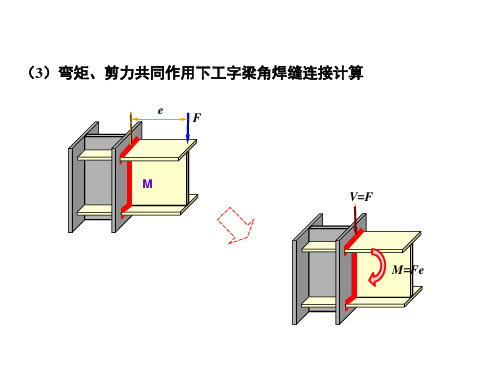
(3)弯矩、剪力共同作用下工字梁角焊缝连接计算
e
F
M V=F
M M=Fe
方法一
V=F
M=Fe M
h1 h h2 h1
A
B
x
x
σ fA
σ fB
τf
假设腹板焊缝承受全部剪力,弯矩则由全部焊缝承受
为分布合理,宜在每个翼缘的上下两侧均匀布置焊缝 弯曲应力沿梁高度呈三角形分布,最大应力发生在翼缘焊缝的最外 纤 维 A 处。
ff
腹板焊缝按下式验算强度:
H
M=Fe M
H
V 2he 2lw 2
fw ff式中源自 he1lw1 — 一个翼缘板焊缝有效截面积之和;
2he2lw2 — 两条腹板焊缝的有效截面积。
V=F
M=Fe M
h1 h h2 h1
A
B
x
x
σ fA
σ fB
τf
翼缘焊缝只承受垂直于焊缝长度方向的弯曲应力
对于控制点A:
M h1 f w
fA I w 2
ff
式中:
h1 — 上下翼缘焊缝的有效截面最外纤维之间的距离; Iw — 全部焊缝有效截面对中和轴的惯性矩; M — 全部焊缝所承受的弯矩。
钢结构钢结构的连接螺栓

例题2 试验算图所示C级普通螺栓连接。荷载设计值 F=100kN,螺栓M20,连接板件的钢材都为Q235—B。
解:1.单个螺栓的抗剪承载力: 单个螺栓的承剪承载力设计值为:
N
b v
nv
d 2 4
f
b v
1 3.14 20 2 4
140
43960
N 43.96 kN
01/07/2020
• 则螺栓1承受的最大剪力N1应满足: • 在N螺1 栓 群(为N一1Nx 狭 长N1布Tx )置2 时(,N1当Vy ymaNx>1Ty3)x2 max时N,mb in为计算方便,
上式可近似为
N1Tx 2
N
2 Vy
N
b m
in
01/07/2020
3.7 普通螺栓连接的构造和强度计算
4). 螺栓群在扭矩作用下的抗剪计算,常需先假定螺栓数目及布置,而后 进行验算。 设螺栓列数为m,每列螺栓有n个,螺栓据为p,等间距布置,端距为p/2, 每个螺栓的截面积为A,为此一确定螺栓数目的近似公式
• 支托承受剪力:螺栓群只承受弯矩M
支托和柱翼缘的角焊缝验算
α为考虑剪力V偏心对角焊缝的影响,取1.25~1.35
01/07/2020
例题4 其他条件同例题3,但牛腿下的支托仅在安装阶段
起作用,正常使用阶段不考虑支托承受剪力,即剪力由螺
栓群承担。验算螺栓群的强度。
解:1. 单个螺栓的承载力: 单个螺栓的承剪承载力设计值为:
3.7 普通螺栓连接的构造和强度计算
33).7..螺2普栓通群螺同栓时的承受抗剪拉力连和接拉力的计算
• 支托仅起安装作用:螺栓群承受弯矩M和剪力V
螺栓不发生拉剪破坏
钢结构的连接习题及答案

钢结构的连接习题及答案例 3.1 试验算图3-21所示钢板的对接焊缝的强度。
钢板宽度为200mm ,板厚为14mm ,轴心拉力设计值为N=490kN ,钢材为Q235 ,手工焊,焊条为E43型,焊缝质量标准为三级,施焊时不加引弧板。
(a ) (b )图3-21 例题3-1 (a )正缝;(b )斜缝解:焊缝计算长度 mm l w172142200=⨯-=焊缝正应力为223/185/5.2031417210490mm N f mm N w t =>=⨯⨯=σ不满足要求,改为斜对接焊缝。
取焊缝斜度为1.5:1,相应的倾角056=θ,焊缝长度mm l w 2.21314256sin 200'=⨯-=此时焊缝正应力为2203'/185/1.136142.21356sin 10490sin mm N f mm N tl N w f w =<=⨯⨯⨯==θσ剪应力为2203'/125/80.91142.21356cos 10490cos mm N f mm N tl N w v w =<=⨯⨯⨯==θτ 斜焊缝满足要求。
48.1560=tg ,这也说明当5.1≤θtg 时,焊缝强度能够保证,可不必计算。
例 3.2 计算图3-22所示T 形截面牛腿与柱翼缘连接的对接焊缝。
牛腿翼缘板宽130mm ,厚12mm ,腹板高200mm ,厚10mm 。
牛腿承受竖向荷载设计值V=100kN ,力作用点到焊缝截面距离e=200mm 。
钢材为Q345,焊条E50型,焊缝质量标准为三级,施焊时不加引弧板。
解:将力V 移到焊缝形心,可知焊缝受剪力V=100kN ,弯矩 m kN Ve M ⋅=⨯==202.0100翼缘焊缝计算长度为mm 106122130=⨯-腹板焊缝计算长度为mm 19010200=-(a ) (b )图3-22 例题3-2(a )T 形牛腿对接焊缝连接;(b )焊缝有效截面焊缝的有效截面如图3-22b 所示,焊缝有效截面形心轴x x -的位置cm y 65.60.1192.16.107.100.1196.02.16.101=⨯+⨯⨯⨯+⨯⨯=cm y 55.1365.62.1192=-+=焊缝有效截面惯性矩4223134905.62.16.1005.411919121cm I x =⨯⨯+⨯⨯+⨯=翼缘上边缘产生最大拉应力,其值为22461/265/59.981013491065.61020mm N f mm N I My w t x t =<=⨯⨯⨯⨯==σ 腹板下边缘压应力最大,其值为22462/310/89.2001013491055.131020mm N f mm N I My w c x a =<=⨯⨯⨯⨯==σ 为简化计算,认为剪力由腹板焊缝承受,并沿焊缝均匀分布223/180/63.521019010100mm N f mm N A V w v w =<=⨯⨯==τ腹板下边缘正应力和剪应力都存在,验算该点折算应力222222/5.2912651.11.1/6.22063.5239.2003mmN f mm N w t a =⨯=<=⨯+=+=τσσ焊缝强度满足要求。
盾构隧道管片连接螺栓设计计算方法探讨

盾构隧道管片连接螺栓设计计算方法探讨陈代秉;李德明;田贺卿【摘要】盾构隧道中管片连接螺栓是个重要的结构受力构件,施加于螺栓上的预紧力使管片缝间防水密封垫形成接触压应力而具有防水能力,同时,螺栓还承受着接缝面上水土压力或地震作用而产生的拉应力,现有设计规范对管片连接螺栓的设计配置无明确规定,造成设计和施工中的无章可循。
文章就管片连接横向螺栓、纵向螺栓、螺栓预加力和螺栓安装扭矩等设计计算理论和计算方法进行探讨。
%In shield tunnel, segment connecting bolts is an important structure component to bear forces which are applied in the segment joints by bolt pre-tightening force between waterproof gasket forming contact pressure stress with features of waterproof ability. At the same time, the bolt is also bearing force from joint surface water and soil pressure or the tensile stress from earthquake action. There is no clear stipulation in the existing design criterion on bolt design confi guration for segment connection, resulting in no design and construction rules to follow. The paper discusses the segment connecting bolts, horizontal and vertical bolts, bolt pre-load forces and the bolt installation torque design calculation theory and calculation methods etc.【期刊名称】《现代城市轨道交通》【年(卷),期】2016(000)004【总页数】4页(P64-67)【关键词】盾构管片;螺栓设计;计算方法;探讨【作者】陈代秉;李德明;田贺卿【作者单位】中铁成都轨道交通设计院有限公司,四川成都 611731;中铁成都轨道交通设计院有限公司,四川成都 611731;中铁成都轨道交通设计院有限公司,四川成都 611731【正文语种】中文【中图分类】U459.5在采用均质圆环理论计算盾构隧道结构时,常赋予管片接缝截面与管片主截面相同的强度和刚度,但这与实际情况严重不符,因为管片预制块体间的连接是通过连接螺栓实现的,这种连接形式使得接缝处具有一定力学铰接特性;另外,采用了错缝拼装形成的盾构隧道结构还具有一定的空间工作特性,即,采用均质圆环理论计算出的管片接缝面弯矩并不完全由接缝截面承担,一部分通过错缝传递到邻近管片主截面上,一部分由接缝处的螺栓承担。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浅谈在弯矩作用下螺栓联接结构的计算
方法
[摘要]在弯矩作用下的螺栓联接结构中,螺栓受力计算在国内不同的手册
中有不同的方法:〈水工设计手册3〉中采用的方法是以最下边一排螺栓为中性轴,所有螺栓都受拉,拉力大小与其到中性轴的距离成正比;〈钢结构设计规范
内部讲解〉中采用的方法是以构件中心为中性轴,中性轴以上螺栓受拉,中性轴
以下螺栓受压,中性轴上下对称位置上的一对螺栓组成一个力偶来对抗外来力矩。
第三种方法认为中性轴在构件中心以下某位置:中性轴以上所有螺栓对中性轴的
面积矩等于中性轴以下所联构件对中性轴的面积矩。
中性轴以上螺栓受拉,中性
轴以下螺栓不受力(预紧力除外),而是构件和构件之间产生挤压。
[关键词]弯矩作用下螺栓联接结构螺栓受力计算
用螺栓将两个结构联接起来,在联接处受弯矩(还有剪力)的工程实例很多,如水利工程的泄水阀,用螺栓将阀和预埋在混凝土中的钢管法兰相连;弧形闸门
支铰的固定铰座用预埋在混凝土中的锚栓与混凝土基础相连等。
在这种联接中,
剪力由摩擦力或专设的支托承担。
弯矩由螺栓承担,弯矩引起的螺栓受力怎样计算?联接处结构的应力怎样计算?国内有两种计算方法:下边列举的方法一是水
工设计手册3.结构计算(P3-96)中采用的方法;方法二是钢结构设计规范内部
讲解(P-82)中采用的方法。
方法三是本人在国外为一中东国家进行一座大型水
电工程金属结构设计咨询时及丹江口300吨级垂直升船机轨道梁连接方案审查时
使用的方法,现在把它写出来,供同行讨论、参考。
方法一
如图一所示,用螺栓将梁联接在柱子上,剪力由支托承受。
梁在联接处受弯
矩M,用m列每列i+1个螺栓联接(图中只画出了2列)。
以最下边一排螺栓处
为中性轴,中性轴以上螺栓受拉,受拉力大小与其到中性轴的距离成正比。
最上
边一排螺栓受力最大,设最上边一排每个螺栓受力为N1,其它螺栓受力从大到小依次为N2,N3,…,Ni 。
N 2= N 1。
Y 2/ Y 1 , N 3= N 1。
Y 3/ Y 1 , …, N i = N 1。
Y i / Y 1 根据力矩平衡原理,
N 1。
Y 1+ N 1。
Y 22/ Y 1+ N 1。
Y 32/ Y 1+…+ N 1。
Y i 2/ Y 1=M/m
N 1= M. Y 1/m.∑Y i 2 (∑Y i 2—一列螺栓到中性轴的平方和,m —螺栓列数) 螺栓最大受力计算出来了,现在从螺栓处切开一个断面,如图二所示,分析断面右侧物体的平衡。
从图二可以看出,
断面右侧物体所受弯矩
不平衡,在水平方向所
受拉压力也不平衡。
另
外,被联接的两个构件
之间的相互作用力怎样
计算,也没有给出结论。
方法二
如图三
所示,螺栓在
上下方向对称
布置,以构件
中心为中性轴。
认为在中性轴
以上,螺栓受
拉;在中性轴
以下,螺栓受
压。
中性轴上
下对称位置上
的一对螺栓组成一个力偶,来对抗外力矩M。
中性轴上下对称位置上的螺栓受力
大小相等,方向相反。
螺栓受力大小与其到中性轴的距离成正比,设最上、最下一排螺栓受力为N
1
,其它螺栓受力依次为(从大到小):
N
2= N
1
.Y
2
/ Y
3
, N
3
= N
1
.Y
1
/ Y
3
根据力矩平衡原理得:
2.N
1.Y
3
+2.N
1
.Y
2
2/ Y
3
+ 2.N
1
.Y
1
2/ Y
3
=M/2
2.N
1/ Y
3
(Y
3
2+ Y
2
2+ Y
1
2)= M/2
N
1= Y
3
.M/[4( Y
3
2+ Y
2
2+ Y
1
2)]
螺栓最大受力计算出来了,现在从螺栓处切开一个断面,如图四所示,分析断面右侧物体的平衡。
从图四可以看出,断面右侧物体所受弯矩平衡了,在水平方向所受拉压力也平衡了。
但是在中性轴下边,螺栓是不受压力的,只在被联接的两个构件之间产生挤压应力。
另外,被联接的两个构件之间的相互作用力怎样计算,也没有给出结论。
方法三
如图五所示,认为中性轴不在对称构件的中心位置,也不在最下边一排螺栓处,而是位于构件中心位置以下的某位置c<e<。
在中性轴位置,被联接的两个构件之间的拉压应力为零;在中性轴以上,螺栓受拉,被联接的两个构件之间不产生相互作用力;在中性轴以下,螺栓不受力(预紧力除外),被联接的两个构件之间产生相互作用的压应力(与实体构件相同)。
下边分两种不同的联接情况(钢构件与钢构件联接;钢构件联接在混凝土建筑物上)进行分析计算。
情况一:被联接的两个构件都是钢结构,如泄水阀联接在预埋钢管的法兰上,丹江口垂直升船机改造工程中钢轨道梁之间的联接(位于大坝上游1根及下游2根梁需将梁联接起来悬臂推拉过去)。
1. 确定中性轴位置
原理:中性轴以上各螺栓面积对中性轴的面积矩等于中性轴以下实体断面对中性轴的面积矩。
求中性轴的方法有两种,一种是一个螺栓一个螺栓的去求面积矩;第二种是,若螺栓间距相等,可将螺栓面积换算成长方形的实体断面来求面积矩,如图五所示。
本文就介绍这种方法。
先将各螺栓面积均摊开来变为两个各宽f的长方形,f= .(s——单个螺
栓面积,d——螺栓间距)。
接下来的问题就变为求上边两个各宽f的长方形和下
边宽a这样一个形状的形心位置(图五中画的是d=2c的情况)。
设中性轴(形心位置)到构件底边距离为e,则:
a.e.=2f(b-e).
.e2 = fb2-2fbe+fe2
(-f) e2+2fbe-fb2=0
e=。
2.求上边两个长方形断面和下边一个构件的实体断面对中性轴的惯性矩J
=(b-e)3+ (b-e)3+ e3+ e3
J
J
= f(b-e)3+ e3
= e
被联接构件之间最大压应力σ
压
= (b-e-c)
联接螺栓最大拉应力σ
螺栓
联接螺栓最大拉力 F=σ
.s (s—螺栓有效断面积)
螺栓
情况二:钢结构联接在混凝土上,如弧形闸门固定铰座用锚栓联接在混凝
土牛腿上。
如图五所示,这种方式的联接,中性轴以下是钢结构压在混凝土上,中性轴以上是螺栓受拉。
计算中性轴时,需根据钢与混凝土弹模比将螺栓受拉换算为混凝土受拉。
1. 确定中性轴位置
原理:中性轴以上各螺栓换算为混凝土后的面积(等于7倍螺栓面积)对中性轴的面积矩等于中性轴以下实体断面对中性轴的面积矩。
求中性轴的方法同情况一。
将各螺栓换算为混凝土后的面积均摊开来变为两个各宽7f的长方形,f= .(s——单个螺栓面积,d——螺栓间距)。
接下来的问题就变为求上边两个各宽7f的长方形和下边宽a这样一个形状的形心位置(图五中画的是d=2c的情况)。
设中性轴(形心位置)到构件底边距离为e,则:
a.e.=2×7f(b-e).
a.e2 = 14fb2-28fbe+14fe2
(a-14f) e2+28fbe-14fb2=0
e=。
2.求上边两个长方形断面和下边一个构件的实体断面对中性轴的惯性矩J
0= .7(b-e)3+ .7(b-e)3+ e3+ e3
J
J
= .e3+ f(b-e)3
= e
混凝土最大压应力σ
压
螺栓最大拉应力σ
= (b-e-c)
螺栓
.s (s—螺栓有效断面积)
联接螺栓最大拉力 F=σ
螺栓
从螺栓联接处切开一个断面,如图六所示,中性轴以上,螺栓受拉;中性轴以下是实体构件受压区。
