3单纯形法第1部分
单纯形法及应用举例

❖ 力求总运费最省
34
cij xij d13 d13 2950
i1 j1
❖ 目标函数为:
min z P1d 4 P2d 5 P3(d6 d 7 d 8 d 9)
P4d
10
P5
d
11
P6 (d
12
d
12)
P7d
13
17
第4节 应用举例
2x1 x2 xs
11
x1
x2 d1 d1 0
满足约束条件:
x1 2x2 d2 d2 10
8x1 10x2 d3 d3 56
x1, x2, xs , di, di 0, i 1,2,3
3
第3节 解目标规划的单纯形法
x12+x22+x32+d2− − d2+=100
x13+x23+x33+d3− − d3+=450
x14+x24+x34+d4− − d4+=250
❖ A3向B1提供的产品量不少于100
x31+d5−− d5+=100
15
第4节 应用举例
❖ 每个销地的供应量不小于其需要量的80%
x11+x21+x31+d6−−d6+=200×0.8 x12+x22+x32+d7− − d7+=100×0.8 x13+x23+x33+d8− − d8+=450×0.8 x14+x24+x34+d9− − d9+=250×0.8 ❖ 调运方案的总运费不超过最小运费调运方案的10%
1-3 单纯形法原理

由于任意系数列向量均可由基向量组线性表示,则非基向 量中的 Pj 用基向量组线性表示为:
Pj a ijPi
i 1
2017/5/5
m
Pj a ijPi 0,
i 1
m
( j m 1,...,n )
12
设有 0,则
( Pj aij Pi ) 0
i 1
只要取
(0) (0) x x min i aij 0 l 为
正,于是非零分量的个数
m
,并可证得
P P2 ... Pl 1 Pl 1 ... Pm , Pj 1
线性无关,所以 X (1) 是新的基可行解。
2017/5/5
a12 a22
a1n a2 n
am 2 amn
1 0 0 0 1 0 0 0 1
9
由于该矩阵含有一个单位子矩阵,因此,这个单位阵就是一组 基,就可以求出一个基可行解:
X 0,,0, b1,, bm
令:X X (1) (1 ) X ( 2 )
0 1
则AX A(X (1) (1 ) X ( 2 ) ) AX (1) AX ( 2 ) AX ( 2 ) b
X C C 为凸集
引理:线性规划问题的可行解X=(x1,x2,……xn)为基可行解的充要条件是 X的正分量所对应的系数列向量是线性独立的(所组成的矩阵是非奇 异的)。
11
由构造初始可行基的方法知前m 个基向量恰好是一个单位
阵,所以约束方程组的增广矩阵为
P1 P2 ... Pm Pm1 ... Pj ... Pn b
1 0 ... 0 0 ... 0 1 ... 0 ... ... ... 0 ... 1 a1,m 1 ... ... a1, j ... ... a2,m 1 ... a2, j am,m 1 ... am , j ... a1,n b1 ... a2,n b2 ... ... ... ... am,n bm
(整理)单纯形法解例1.

例1 用单纯形法解下列问题:解:将原问题化成标准形:x 4与添加的松弛变量x 5,x 6在约束方程组中其系数列正好构成一个3阶单位阵,它们可以作为初始基变量,初始基可行解为X =(0, 0, 0,10, 8, 4)T列出初始单纯形表,见表1。
22x 2的系数列的正分量对应去除常数列,最小比值所在行对应的基变量作为换出的基变量。
242)24,110(m in ===θ 因此确定2为主元素(表1中以防括号[]括起),意味着将以非基变量x 2去置换基变量x 6,采取的做法是对约束方程组的系数增广矩阵实施初等行变换,将x 2的系数列(1, -1, 2)T 变换成x 6的系数列(0, 0, 1)T ,变换之后重新计算检验数。
变换结果见表2。
1231234123123min 2..210,248,244,0,1,,4.j x x x s t x x x x x x x x x x x j -++-+=-+≤-+-≤≥=123123412351236max 2..210,248,244,0,1,,6.j x x x s t x x x x x x x x x x x x x j -+-+-+=-++=-+-+=≥=检验数σ3=3>0,当前基可行解仍然不是最优解。
继续“换基”,确定2为主元素,即以非基变量x 3置换基变量x 5。
变换结果见表3。
表3此时,3个非基变量的检验数都小于0,σ1= -9/4,σ5= -3/2,σ5= -7/4,表明已求得最优解:T)0,0,8,5,12,0(=*X 。
去除添加的松弛变量,原问题的最优解为:T )8,5,12,0(=*X ,最小值为-19例2 用大M 法求解下列问题:12312312313min 3..211,243,21,0,1,,3.j x x x s t x x x x x x x x x j +--+≤+-≥-=≥=解 引进松弛变量x 4、、剩余变量x 5和人工变量x 6、x 7,解下列问题:1234567123412356137min 300()..211243210,1,2,,7j x x x x x M x x s t x x x x x x x x x x x x x j +-++++-++=+--+=-+=≥=用单纯形法计算如下:由于σ1<2< 0,说明表中基可行解不是最优解,所以确定x 1为换入非基变量;以x 1的系数列的正分量对应去除常数列,最小比值所在行对应的基变量作为换出的基变量。
单纯形法

C X B b
0 x 360 0 x 200 0 x 300
7 12 0 0 0
xx x x x
1
2
3
4
5
9 4 100
90
4 5 010
40
3 [10] 0 0 1
30
7 12 0 0 0
9
其中检验数 c C
1
1
B
1
p 1
7
(0 0
0) 4
7;
3
360 90
4
[ ] 中表示进基列与出基行的交叉元,下一张表将实 行以它为主元的初等行变换(称高斯消去)。方法是: 先将主元消成1,再用此1将其所在列的其余元消成0。
每个基B都对应于一个基本解
非负的基本解就是基本可行解
几种解之间的关系:
基本可行解
非可行解 可行解
基本解
问题:基本可行解是可行域中的哪些点?
3.基本定理
(1)线性规划的可行域是一个凸多面体。 (2)线性规划的最优解(若存在的话)必能在可行
域的角点获得。
(3)线性规划可行域的角点与基本可行解一一对应。
7 12 0 0 0
0
x 3
240
0
x 4
50
12 x 30 2
7.8 0
[2.5] 0
0.3 1
3.4 0
1 0 - 0.4 1 0 - 0.5 0 0 0.1
0 0 -1.2
回顾单纯形法步骤
B
X
0
B
01b 0
c
C B 1P
0
0
min
(B 01b )
(B
1 0
P
)
B1
第一章 线性规划及单纯形法

线性规划问题的标准形式: 线性规划问题的标准形式:
max f = ∑ c j x
j =1 j n
n ∑ aij x j = bi , i = 1,2,L , m j =1 x j ≥ 0, j = 1,2,L , n
日产量( 日产量(吨) 9 5 7 21
11
)(模型 例2(运输问题)(模型) (运输问题)(模型)
minf = 2 x11 + 9 x12 + 10 x13 + 7 x14 + x21 + 3 x22 + 4 x23 + 2 x24 + 8 x31 + 4 x32 + 2 x33 + 5 x34 x11 + x12 + x13 + x14 = 9 x +x +x +x =5 23 24 21 22 x31 + x32 + x33 + x34 = 7 x11 + x21 + x31 = 3 s.t. x12 + x22 + x32 = 8 x13 + x23 + x33 = 4 x14 + x24 + x34 = 6 xij ≥ 0(i = 1,2,3; j = 1,2,3,4)
18
3、(线性规划)数学模型的三要素 、(线性规划) 、(线性规划 变量/决策变量 决策变量; ①变量 决策变量; 目标函数( ②目标函数(max/min); ); 约束条件。 ③约束条件。
19
决策变量: ①变量/决策变量:指决策者为实现规划目标采 变量 决策变量 取的方案、措施,是问题中要确定的未知量; 取的方案、措施,是问题中要确定的未知量;
单纯形法——精选推荐

单纯形法第⼆章单纯形法2.1 单纯形法原理(⼤M法)例3 min z=4x1+3x2+8x3x1+x3≥2x2+2x3≥5x j≥0(j=1,2,3)⼀、构造初始可⾏基(m×m单位阵)每个约束都有⼀个系数为+1的独有变量(基变量)1.引⼊附加变量,化为标准型(⾸先变为b≥0)x1+x3-x4=2x2+2x3-x5=5x j≥0(j=1,2,...,5)(x4、x5为附加变量)min z=4x1+3x2+8x3+0x4+0x5假设化为标准型后,仍⽆初始可⾏基2. 若约束中附加变量系数为-1或原约束为等式,必须引⼊⼈⼯变量x1+x3-x4+x6=2 ① (基变量为x6)x2+2x3-x5+x7=5 ② (基变量为x7)x j≥0(j=1,2,...,7)(x6、x7为⼈⼯变量)⼈⼯变量>0时,约束被篡改3. ⽬标函数中附加变量系数为0,⽽⼈⼯变量系数为Mmin z=4x1+3x2+8x3+0x4+0x5+M x6+M x7③M——罚因⼦(很⼤正数)⼤M法——罚函数法⼆、求出⼀个基本可⾏解1. ⽤⾮基变量表⽰基变量和⽬标函数由①:x6=2-x1-x3+x4④由②:x7=5-x2-2x3+x5⑤将④、⑤代⼊③:z=(4-M)x1+(3-M)x2+(8-3M)x3+M x4+M x5+7M ⑥检验数σj= ⑥式中各⾮基变量x j的系数,z=z0+∑σ∈Jj jj x(J为⾮基变量下标的集合)基变量的检验数=02、求出⼀个基本可⾏解及相应z值令各⾮基变量为0,x1=x2=x3=x4=x5=0由④、⑤、⑥得x6=2,x7=5,z=7M三、最优性检验(求min)1.最优性检验的依据——检验数σj2.最优解判别定理:若在极⼩化问题中,对于某个基本可⾏解,所有检验数σj≥0,且⼈⼯变量为0,则这个基本可⾏解是最优解。
例3中,σ1<0,σ2<0,σ3<0,需继续迭代3.⽆穷多组最优解判别定理:若在极⼩化问题中,对于某个基本可⾏解,所有检验数σj≥0,⼜有某个⾮基变量检验数为0,且⼈⼯变量为0,则线性规划问题有⽆穷多组最优解。
求解线性规划的单纯形法(1)

◦ 确定移动的方向 ◦ 确定在何处停下 ◦ 确定新的基本可行解
求解线性规划的单纯形法
例:用单纯形法求解以下线性规划问题
求解线性规划的单纯形法 首先将模型转化成标准形式
求解线性规划的单纯形法
Q1:确定初始的基本可行解
• 选择原点:
– 令决策变量 x1= x2 = 0得:X0 = ( 0,0,3,4)T
xx33 = 1 -x2 ≥=0 → x2 ≤ 1/1
x4 = 2 -x2 ≥ 0 → x2 ≤ 2/1
离基(最小比值规则) :
x2 ≤ min {1/1,2/1 } = 1 x2 = min {1/1,2/1 } = 1
x3为离基变量
X1 = ( 0, 1, 0, 1)T
求解线性规划的单纯形法
3
x1 + 2x2
+ x4 =4
初等数学 变换
新的BF解 x1 =0,x4 =0 x3 =?1 ,x2 =2
新方程
Z x1/2
+ 3x4 /2 =6
x1/2 + x3 - x4 / 2 1
x1/2 + 2x2 + x4 /2 =2
非最优解!
• 寻找新的基本可行解:
– 初等数学变换
非基变量 x1的系数 X*=(0, 2, 1, 0) 是正数!
x1 2
x1 2
-
x1 4
初等行变换
x3
0
确定x3为离基变量
Z*=7,X*=(2,1,0,0)
非基变量系 数>0,最优!
Z x1/2
+ 3x4 /2 =6
x1/2 + x3 - x4 / 2 1
第一章 线性规划及单纯形法1图解2006
简写为:
n
ma或 x(minz) cjxj
j1
jn1aijxj (,)bi (i 1,,m)
xj 0 (j 1,,n)
向量表达形式:
ma或 xm ( izn)CX
n
j 1
Pj
x
j
(, )b
X 0
C(c1,c2,,cn)
x 1
X
x2 xn
a 1 j
Pj
a2j
目标函数 mzi n 28(x1 0 1x 0 2 1x3 1x4)145(x1 02 0 x22 x3)260(x1 0 3x 0 2)373x10 4 0
约束条件
x11 x12 x13 x14 15
xx1132
x13 x14
x14 x22
x21 x23
x22 x31
x23 x32
第一章 线性规划及单纯形法
第一节 线性规划问题及其数学模型
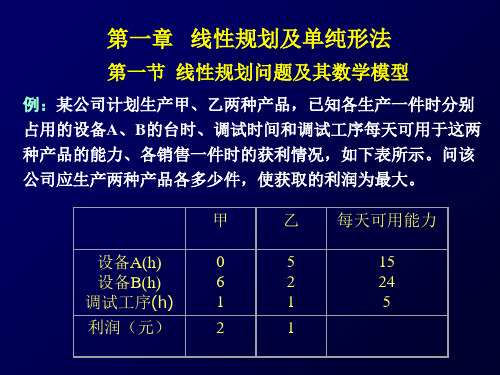
例:某公司计划生产甲、乙两种产品,已知各生产一件时分别 占用的设备A、B的台时、调试时间和调试工序每天可用于这两 种产品的能力、各销售一件时的获利情况,如下表所示。问该 公司应生产两种产品各多少件,使获取的利润为最大。
甲
乙 每天可用能力
设备A(h)
可行域中使目标函数值达到最优的可行解称为最优解。
图解法的步骤:
(1)在平面上建立直角坐标系 (2)图示约束条件,找出可行域 (3)图示目标函数,寻求最优解
线性规划的图解
max z = x1+3x2 s.t. x1+ x2≤6
-x1+2x2≤8 x1 ≥0, x2≥0
x2 6
4
最优解 可行域
-8
0
目标函数等ห้องสมุดไป่ตู้线
