2012学年第一学期七年级数学校本作业
后安中学2012-2013学年度第一学期“元旦杯”七年级数学竞赛试题

后安中学2012—2013学年度第一学期“元旦杯” 七年级数学竞赛试题 (时间:110分钟 总分:120分) 命题者:莫玉明 分 数_____________ 一、选择题(每小题4分,共40分) 1. 下列语句正确的是( ) A. 1是最小的自然数; B. 平方等于它本身的数只有1 C. 绝对值最小的数是0; D. 任何有理数都有倒数 2.下列各项是一元一次方程的是( ) A. 2x ―1=0 B. x 1=4 C. 4x x 22-=0 D. 5x -y =8 3. 化简4856--的结果为( ) A. 67- B. -76 C. 67 D. 76 4. 下列变形属于移項的是( ) A. 由2x =2,得x =1 B. 由2x =-1,得x =-2 C. 由3x -27=0,得3x =27 D. 由-x -1=0,得x +1=0 5. 数轴上,在表示-1.5与29之间,整数点有( ) A. 7个 B. 6个 C. 5个 D. 4个 6. 若a =3x ―5,b =x -7,a +b =20,则x 的值为( ) A. 22 B. 12 C. 32 D. 87. 某品牌电脑原价为m 元,先降价n 元,又降低20%后的售价为( )A. 0.8(m +n )元B. 0.8(m -n )元C. 0.2(m +n )元D. 0.2(m -n )元8. 已知a . b 都是非零数,则abab b b a a ||||||++的值为( ) A. -1或3, B. 1 C. -1 D. ±1或±3 学校 班级 姓名 座号9. 观察图中正方形四个顶点所标的数字规律,可知数2011应标在( )A. 第502个正方形的左下角B. 第502个正方形的右下角C. 第503个正方形的左上角D. 第503个正方形的右下角10. 如图,从边长为(a +4)cm 的正方纸片中剪去一个边长为()1a +cm 的正方形(0)a >,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( ).A. 22(25)cm a a +B. 2(315)cm a +C. 2(69)cm a +D. 2(615)cm a +二、填空题(每小题4分,共32分) 11.32-的倒数的相反数是 。
七年级数学第一学期《字母表示数》习题(含答案)

七年级数学《字母表示数》一、耐心填一填:1、32x y 5-的系数是 2、当x= __________时,的值为自然数;312-x3、a 是13的倒数,b 是最小的质数,则21a b-= 。
4、三角形的面积为S ,底为a ,则高h= __________5、去括号:-2a 2 - [3a 3- (a - 2)] = __________6、若-7x m+2y 与-3x 3y n 是同类项,则m n +=7、化简:3(4x -2)-3(-1+8x )= 8、y 与10的积的平方,用代数式表示为________ 9、当x=3时,代数式________132的值是--x x10、当x=________时,|x|=16;当y=________时,y 2=16; 二、精心选一选: 1、 a 的2倍与b 的31的差的平方,用代数式表示应为( )A 22312ba -B ba 3122-C2312⎪⎭⎫ ⎝⎛-b a D2312⎪⎭⎫⎝⎛-b a2、下列说法中错误的是( )A x 与y 平方的差是x 2-y 2B x 加上y 除以x 的商是x+xyC x 减去y 的2倍所得的差是x-2yD x 与y 和的平方的2倍是2(x+y)23、已知2x 6y 2和321,9m- 5m n -173mn xy -是同类项则的值是 ( )A -1B -2C -3D -4 4、已知a=3b, c=) (cb a cb a ,2a的值为则-+++A 、712D 611C 115B 511、、、5、已知:a<0, b>0,且|a|>|b|, 则|b+1|-|a-b|等于( )A 、2b-a+1 B.1+a C.a-1 D.-1-a6、上等米每千克售价为x 元,次等米每千克售价为y 元,取上等米a 千克和次等米b 千克,混合后的大米每千克售价为( )Aa b x y++Bax by ab+ Cax by a b++ Dx y 2+7、 小华的存款是x 元小林的存款比小华的一半还多2元,则小林的存款是( )A )2(21+xB )2(21-xC 221+xD 221-x8、m-[n-2m-(m-n)]等于( )A -2mB 2mC 4m-2nD 2m-2n 9、若k 为有理数,则|k|-k 一定是( )A 0B 负数C 正数D 非负数 10、已知长方形的周长是45㎝,一边长是a ㎝,则这个长方形的面积是( )A 、平方厘米、平方厘米245aB 2)45(a a - C 、平方厘米、平方厘米-a)-245a( D a)245( 三、化简题1、2222(835)(223)a ab b a ab b ----+2、)231(34x xy xy -+-3、)(2)2(333c b a c b a b a ---+ 4、 ()⎪⎭⎫⎝⎛++-+--13431354b a b a5、2223[723()1]a a a a a ----+ 6、2222(876)[8()]x y xy xy xy x y y x -+---+四、化简求值1、523531411()[2()()][()()]2323x y x y x y x y x y +++-+-+-+,其中3x y +=2、2225[(53)6()]a a a a a a -+---,其中12a =-3、已知:2(2)10x y +++=,求222225{2[3(42)]}xy xy xy xy x y ----的值。
2012学年第一学期高一数学校本作业第12周3-

2012学年第一学期高一数学校本作业第12周【3】
向量减法运算及其几何意义
命题人:王璐 审题人:郭春
一、选择题
1.在△ABC 中,向量BC →可表示为( )
①AB →-AC →;②AC →-AB →;③BA →+AC →;④BA →-CA →.
A .①②③
B .①③④
C .②③④
D .①②④
2.当|a |=|b |≠0且a 、b 不共线时,a +b 与a -b 的关系是( )
A .平行
B .垂直
C .相交但不垂直
D .相等
3.下列各式结果是AB →的是( )
A.AM →-MN →+MB →
B.AC →-BF →+CF →
C.AB →-DC →+CB →
D.AB →-FC →+BC →
4.若|OA →|=8,|OB →|=5,则|AB →|的取值范围是( )
A .[3,8]
B .(3,8)
C .[3,13]
D .(3,13)
二、填空题
5.若向量a 与b 共线,|a|=|b|=1,|a -b|=________.
6.如图K -17-1所示的四边形ABCD 中,设AB →=a ,AD →=b ,BC →=c ,则用a ,b ,c 表示出DC →为________.
图K -17-1 三、解答题
7.已知非零向量a ,b 满足|a |=7+1,|b |=7-1,且|a -b |=4,求|a +b |的值.
8.如图K -17-2,已知O 为平行四边形ABCD 内一点,OA →=a ,OB →=b ,OC →=c ,求OD →.
图K -17-2
[选做题]
证明:对于任意两个向量a,b,都有||a|-|b||≤|a-b|≤|a|+|b|.。
2012学年第一学期七年级练习卷

文档供参考,可复制、编制,期待您的好评与关注! 1 / 7 2012学年第一学期七年级练习卷(一) 科学练习卷 (出卷:陈步先) 温馨提示:本次考试时间为90分钟,满分100分。 一、选择题(本题共25小题,每小题2分,共50分) 1、科学已经与我们的生活密不可分,下列不属于科学研究的是 ( ) A.小明到椒江的大陈岛旅游,为“甲午岩”的雄伟而叹服 B.麦哲伦航海探险,发现地球是圆的 C.苹果落在牛顿身上,结果他发现了万有引力 D.天空布满了乌云,小明觉得特别闷热,由此他认为天快要下雨了 2、下列哪种生物只能通过摄取食物以获得养料才能维持生活? ( ) A.青莱 B.睡莲 C.蜻蜓 D.红松 3、下列实验操作正确的是( )
4、植物细胞有而动物细胞没有的结构是( )。 A.细胞壁 B.细胞膜 C.细胞质 D. 细胞核 5、某同学用同一把卷尺三次测得教室门的宽度为80.19厘米,80.20厘米,80.21厘米,则下列说法错误的是( ) A.80.21厘米这个记录结果是正确的 B.此卷尺的最小刻度是1毫米 C.测量结果最后应记作80.2厘米 D.80.20中最末一位数字“0”是有意义 6、我国北方的冬天,气温很低,有时能达到-39℃,河流会结上厚厚的一层冰,冰下有流动的河水,那么冰的下表面与水交界处的温度是( ) A.4℃ B.0℃ C.-39℃ D.略高于-39℃ 7、以下不属于长度单位的是( ) A、微米 B、纳米 C、 光年 D、 毫米3 8、在使用温度计测液体温度时,下列做法不正确的是……………………………… ( ) A.使用前必须观察它的量程,认清它的最小刻度值 B.温度计的玻璃泡应全部浸入被测液体中,不要碰到容器底或容器壁 C.温度计玻璃泡浸入被测液体中,应立即读数 D.读数时玻璃泡要留在被测液体中,视线要与温度计的液面相平 9、小虎在寻找蜗牛时,记录了不同环境下发现蜗牛的数量(如右图所示)。据此,你可
2012年国培数学第一次作业
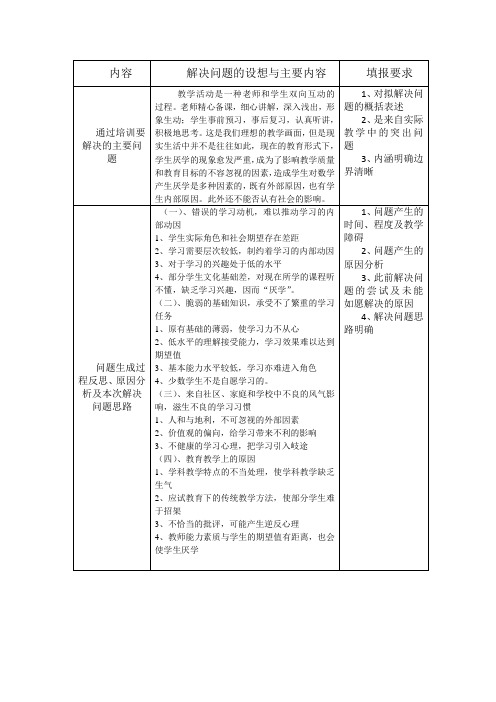
内容解决问题的设想与主要内容填报要求通过培训要解决的主要问题教学活动是一种老师和学生双向互动的过程。
老师精心备课,细心讲解,深入浅出,形象生动;学生事前预习,事后复习,认真听讲,积极地思考。
这是我们理想的教学画面,但是现实生活中并不是往往如此,现在的教育形式下,学生厌学的现象愈发严重,成为了影响教学质量和教育目标的不容忽视的因素,造成学生对数学产生厌学是多种因素的,既有外部原因,也有学生内部原因。
此外还不能否认有社会的影响。
1、对拟解决问题的概括表述2、是来自实际教学中的突出问题3、内涵明确边界清晰问题生成过程反思、原因分析及本次解决问题思路(一)、错误的学习动机,难以推动学习的内部动因1、学生实际角色和社会期望存在差距2、学习需要层次较低,制约着学习的内部动因3、对于学习的兴趣处于低的水平4、部分学生文化基础差,对现在所学的课程听不懂,缺乏学习兴趣,因而“厌学”。
(二)、脆弱的基础知识,承受不了繁重的学习任务1、原有基础的薄弱,使学习力不从心2、低水平的理解接受能力,学习效果难以达到期望值3、基本能力水平较低,学习亦难进入角色4、少数学生不是自愿学习的。
(三)、来自社区、家庭和学校中不良的风气影响,滋生不良的学习习惯1、人和与地利,不可忽视的外部因素2、价值观的偏向,给学习带来不利的影响3、不健康的学习心理,把学习引入岐途(四)、教育教学上的原因1、学科教学特点的不当处理,使学科教学缺乏生气2、应试教育下的传统教学方法,使部分学生难于招架3、不恰当的批评,可能产生逆反心理4、教师能力素质与学生的期望值有距离,也会使学生厌学1、问题产生的时间、程度及教学障碍2、问题产生的原因分析3、此前解决问题的尝试及未能如愿解决的原因4、解决问题思路明确此次问题解决的预期目标(一)改进和加强思想教育工作,帮助学生端正学习态度。
1、针对性要强。
中学生“厌学”的根本原因是这些学生没有树立正确的世界观和人生观,对自己的人生座标不明确,没有树立远大的理想。
2012-2013学年度第一学期教学质量自查七年级数学

2012-2013学年度第一学期教学质量自查七年级数学(满分100分)一、选择题(每小题3分,共15分)1. 用科学记数法表示56 700 000,正确的是 ( )A. 567×105B. 56.7×106C. 5.67×107D. 5.67×1082. 下列算式中,运算结果为负数的是 () A. -(-3) B. 3- C. -32 D. (-3)23. 方程931=-x 的解是 () A. x=3 B. x=-3 C.x=27 D. x=-274. 一本新书按标价的九折出售,仍可获利20%,若该书的进货价为21元,则标价为 () A. 26元 B. 27元 C. 28元 D. 29元5. 下列图形可以作为一个长方体的展开图的是 ( )A. B. C. D.二、填空题(每小题3分,共15分)6. -3的绝对值是 .7. “比x 的2倍小7的数”用式子表示是 .8. 关于x 的方程mx +4=3x +5的解是x =1,则m= .9. 若单项式3x 2y n 与-2x m y 3是同类项,则m+n= .10. 25°31′的角的补角等于 .三、解答题(每小题6分,共30分)11. 计算:2(4x -0.5)-6(1-x 31) .12. 计算:40+(-2)3×5-(-0.28)÷(-2)2 .13. 解方程:3.5x -2=4.5x +0.25 .14. 先化简,再求值:)412()85(22xy x x xy +---,其中x =-21,y =2 .15. 如图1,A 、B 、C 、D 在同一直线上,AB=8,AD=14,C 是BD 的中点,求AC 的长 .图1四、解答题(每小题8分,共40分)16. 解方程:2133210-=--x x x .17. 已知a 为一个有理数,解答下列问题:(1)如果a 的相反数是a ,求a 的值;(2) 10a 一定大于a 吗?说明你的理由.18. 某车间每天能制作甲种零件500只,或者制作乙种零件250只,甲、乙两种零件各一只配成一套产品,现在要在30天内制作最多的成套产品,则甲、乙两种零件各应制作多少天?19. 如图2,O 是直线AC 上一点,OA 是一条射线,OD 平分∠AOB ,OE 在∠BOC 内,∠BOE=31∠EOC ,∠EOC=90°. (1)求∠DOE 的度数;(2)哪些角与∠AOD 互为余角?请说明理由;(3)互为补角的角有几对?20. 一张长方形桌子可坐6人,按图3方式将桌子拼在一起.图3 (1) 2张桌子拼在一起可坐 人,4张桌子拼在一起可坐 人,n 张桌子拼在一起可坐 人.(2) 一家餐厅有40张这样的长方形桌子,按照上图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?。
七年级数学课时学案作业本答案上册
七年级数学课时学案作业本答案上册
七年级上册数学课案作业本答案内容包括:
1. 有理数的基本运算;
2. 比较大小、判断正负号;
3. 绝对值;
4. 比例与比例系数;
5. 分式及运算;
6. 平行四边形、垂直四边形、三角形的面积;
7. 解一元二次不等式;
8. 平行线、垂直线、垂直平分线;
9. 正方形、长方形的面积和周长;
10. 正多边形的边数与角度;
11. 长方体、圆柱体的体积;
12. 求和、积分和分式的乘除法;
13. 找出最小公倍数与最小公约数;
14. 找出最大公约数;
15. 找出方程组的解;
16. 找出等差数列、等比数列和递推数列的前n项和;
17. 找出三角形的内角和;
18. 学习算法和解决问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9.1 字母表示数一、填空题1、已知长方形的长为,a宽为10,用表a示长方形的周长。
2、如果圆的周长为C,那么它的半径是。
3、一个正方形的周长是C,那么这个正方形的边长是。
4、每件上衣售价元a,用字母a表示降价10%后的售价是。
5、设甲数为x,乙数为y,用x、y表示甲数与乙数和的平方是。
6、设甲数为x,乙数为y,用x、y表示甲数与乙数平方的和是。
7、三个连续奇数中,中间的一个为n,用式子表示这三个连续奇数的和为。
二、选择题1、一批运动服装按原价八五折出售,每套a元,则它的原价为()A、0.85 a元 B 2017a元C、0.15 a元D、203a元2、若x表示一个两位数,y也表示一个两位数,小明想用x、y来组成一个四位数且把x 放在y的右边,你认为下列表达式中哪一个是正确的()A、y xB、x+yC、100x+yD、100y+x拓展:1、观察:13=12,13+23=(1+2)2,13+23+33=(1+2+3)2,则13+23+33+43+…+103= ,请你将这个规律用含n的等式表示。
2、观察下列各式,你发现了什么规律?3×5=15,15=42-15×7=35,35=62-17×9=63,63=82-1……11×13=143,143=122-1将你猜想得到的规律用只含一个字母的式子表示。
9.2代数式一、下列式子中,属于代数式的是。
①23x-②5-③1a b+④s vt=⑤1xx+⑥25x=二、用代数式表示:⒈x的2倍与35的差是。
⒉x的35%与0.4的和是。
⒊x除以的y商是。
⒋x与a的14的和的平方是。
⒌x的平方的倒数减去12的差是。
⒍一件上衣原价a元,打八折后的售价是元。
⒎学校7月份用电度a,8月份比7月份节约10%,8月份用电度。
8 、铅笔的单价是元a,钢笔的单价是b元,小明买了x支铅笔,y支钢笔,总共应付元。
三、简答题:1、若一个三位数个位数字为a,十位数字为b,百位数字为c,表示这个三位数。
2、有三个连续偶数,中间的一个数是2n,用n的代数式表示其它的两个数。
3、某种商品进价为a元,商店将价格提高40%做为零售价销售,在销售旺季过后,商店又以8折的价格开展促销活动,求这时一件商品的售价。
4、某商店进了一款服装,其进价为每件125元,标价为元x,为了促销,决定以8折优惠出售,计算每件服装可以赚多少元。
5、学校操场上有400米的圆形跑道,甲、乙两人从同一地点同时反向出发,甲的速度是每秒钟x米,乙的速度是每秒钟米y,它们经过多少时间第一次相遇。
拓展:1、“循环赛”是指参赛选手间都要互相比赛一次的比赛方式,如果一次乒乓球比赛有名x 选手报名参加,比赛方式采用“循环赛”,那么这次乒乓球比赛共有场。
2、某商品原售价a元,现受季节影响,降价b元后又降价20%,那么该商品现在的售价是元(用a,b的代数式表示)3、如图,半径为R的圆中挖出一个边长为的a正方形,求余下部分的周长与面积。
9.3 代数式的值1.已知x=y-1,y=3,则代数式8y-3x 的值是 .2.当a=8,b=9时,代数式b-1a 的值是 .3.若m-1=0,代数式m- 1m的值是 . 4.填表:5.已知长方形的长是宽的2倍,如果用a 表示长,那么长方形的周长为 ;当a=5cm 时,这个长方形的周长为 .6.下列说法正确的个数有( )①一般情况下,一个代数式的值与代数式中字母的取值有关. ②代数式中字母可以取任何值. ③代数式a 2的值一定为正.④n 为整数,则2n+2表示偶数.A.1个B.2个C.3个D.4个 7.当a=2时,代数式a 2+ 2b=8,则b=( )A.2B.- 2C.3D.- 3 8.使代数式2x- 1x- 3的值是0的x 是( )A.3B.12C.13 D.29.若x 、y 互为相反数,a 、b 互为倒数.则13 (x+y)+3ab 的值是( )A.3B.- 8C.- 3D.以上都不对 10.若|x- 1|+|y+3|=0,求1- xy- xy 2的值. 拓展:1. 填表:从填好的表中,你能发现什么规律?请写出 2. 已知代数式x 2+3x+5的值为7,求代数式3x 2+9x- 2的值. 3. 已知y=ax 3+bx+1,当x=2时,y=- 5,求x=- 2时,y 的值.4. 小明在计算15- 12 x 的值时,不小心将“-”看成“+”,结果得24,求15- 12x 的正确结果为多少?9.4 整式一、填空题1.42234263y y x y x x --+-的次数是 ; 2.当y = 时,代数式3y -2与43+y 的值相等; 3.-23ab 的系数是 ,次数是 次.4.把代数式2a 2b 2c 和a 3b 2的相同点填在横线上:(1)都是 式;(2)都是 次.5.多项式x 3y 2-2xy 2-43xy-9是___次___项式,其中最高次项的系数是 ,二次项是 ,常数项是 . 6.若2313mx y z -与2343x y z 是同类项,则m = . 7.在x 2,21(x +y),π1,-3中,单项式是 ,多项式是 ,整式是 .8.单项式7532c ab 的系数是____________,次数是____________.9.多项式x 2y +xy -xy 2-53中的三次项是____________. 二、选择题1.下列说法正确的是( ) A .x(x +a)是单项式 B .π12+x 不是整式 C .0是单项式 D .单项式-31x 2y 的系数是31 2.下列说法正确的是( )A .x 的指数是0B .x 的系数是0C .-10是一次单项式D .-10是单项式 拓展:1、当a=____________时,整式x 2+a -1是单项式.2、若多项式2-6-22++nn xx 是三次三项式,求代数式12-2+n n 的值。
9.5 合并同类项1、所含的 相同,且 也相同的单项式叫做同类项。
2、找出多项式41594532222++---ab a ab a 中的同类项 。
3、写出b a 2的一个同类项,你写的是 。
4、下列各组单项式为同类项的是( )①2232yx y x -与 ②ab abc 321-与 ③32235b a b a 与- ④03与- ⑤b a 与 ⑥a a 33与 ⑦3344xy ab --与(A )①③④⑥ (B )①②④⑦ (C )②③⑥ (D )①④ 5、合并同类项:(1)222a ab a +- (2)b a ab a ab ---+32(3)22223221ab b a a b b a +-- (4)22222123y xy x y x -+++ 6、化简求值:(1)x x x x x x 822345222-+---,其中21-=x ;(2)x x xy yx xy y x 9757632222-+++--,其中31,1-=-=y x 。
7、把(y x -)当作一个因式,合并同类项:5(y x -)2+(y x -)-(y x -)3+5(y x -)+2(y x -)3-3(y x -)28、已知多项式7425233223-+---+-x x x x x x a 、 当212=x 时,求这个多项式的值 b 、 当x 为何值时,这个多项式的值为-431拓展:已知:单项式312y x n +-与354-m y x 是同类项,求代数式:mn mn mn m n 45734.222--+的值。
9.6 整式的加减1、去括号法则:括号前面是“+”号,去掉“+”号和括号,括号里的各项 ;括号前面是“-”号,去掉“-”号和括号,括号里的各项 。
2、去括号:(1)()23422xx x ---+= ;(2)()323223yxy y x x ---= ; (3)()443335b a ab b a -+--= 。
3、化简:(1)(-x+2x 2+5)+(-3+4x 2-6x) (2)(3a 2-ab+7)-(-4a 2+6ab+7) (3)⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+b a ab ab b a 222243413(4)⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛++-32323231m n m m n m4、先化简,再求代数式()()xy yxy x 745352222+++-的值,其中1-=x ,2-=y 。
5、整式15++b a 与一个整式的和是223+-b a ,求这个整式。
6、已知:()222++-=x x A ,221-=x B ,计算:B A 2+。
7、先化简,再求代数式153.021353322-+⎥⎦⎤⎢⎣⎡+⎪⎭⎫⎝⎛+--+x x x x x x 的值,其中31-=x 。
拓展:已知3--,212-==c b a c 。
求代数式1-)-(2-)-(2b a b a 的值。
9.8幂的乘方1、32)21(⎥⎦⎤⎢⎣⎡-= a 15=( )5 ()32m x =2、()()4352aa -⋅-=_______。
3、(y m )3·y n= 。
4、=⋅-+⋅-+-3421213()(m m m x x x x) 。
5、已知921684=⋅⋅m m ,则m= 。
6、计算:①2324)(a a a +⋅ ②223)(2x x x +⋅ ③2582)(a a a -⋅7、计算: (1)[]3232)5()5(-- (2)m m m x x x 3233)(2)()(-⋅(3))()()()(624523x x x x x -⋅--⋅⋅-8、计算:(1)23)]()[(a b b a -- (2)532)3()3()3(x y x y y x --- 9、化简:632525125⨯⨯(结果用幂的形式表示)§ 9.9 积的乘方1. __________)3(432=-b a . =-22)3(xy ____________. 42)2(a -=____________.2. 342)(2b a =____________. __________])3(31[232=-⋅x x .3. 432])(31[b a y x --=____________.[把)(y x -看作一个因式]4. 200320023)31(⋅-=____________. 3423)()()3(y x y x -⋅-⋅-=____________.5. 当9638b a x -=,则=x ____________.6. 若12,3==nmx x ,(n m ,都是正整数),那么=+nm x3____________. 7. 计算:(1)32)3(b a - (2)425)2(y x - (3)432)21(b a - (4)pn m b a )3(8. 计算:(1)384463)()(b a b a -+- (2)232232)()()(x x x x ---⋅--(3)nnb a b a )()(322+ (4)22132)2()(+-⋅+n n nnb b a b a9. 用简便方法计算:(1)665.24⨯ (2)200720075.1)32(⨯-(3)128)41(8-⨯ (4)3272322)4()2(]2)21([÷+⨯-§ 9.10 整式的成法一、单项式与单项式相乘1. __________232=⋅⋅b a a . __________)3()2(32=-⋅-x x . 2. __________)32()21(22=-⋅b a ab . __________2)3(12=⋅--y x y x n n . 3. =⨯⋅⨯⋅⨯)102()107()106(235____________.222)21()2()2(y xy x ⋅-⋅=____________.4. 计算:(1)232221)3()2(y xy x ⋅--(2))34()23(322c ab bc a -⋅-(3)1000200016)5.2(⨯(4)23)21()21()21(-⋅-⋅-(5)2)2()()2(a a a --⋅- (5)322)2()3(4ab b a ab +-⋅(7)222322)()32(3b a b a b a ---⋅ (8))31()2()23()32(7223232ab b a ab b a ⋅---⋅-二、单项式与多项式相乘5. __________)25(32=+--x x x .__________2)23(22=⋅+xy y x .6. )5132()5(2+-⋅-x x x =____________. )1(2+-a a a mm=____________.7. 计算:(1))(c b a m -+- (2))478)(21(3+--x x x(3)2)52(41x x ⋅+- (4))123()4(2+--⋅-xy x xy(5) )33(61)3(3123-++x x (6)222222)2()(4xy y x y x -+-8. 化简求值(1))32102()1(22322----+-x x x x x x x ,其中,21-=x (2))](2)2([)31(22y xy x y x xy xy ---⋅-,其中,5.1-=x ,2=y三、多项式与多项式相乘 9. __________)31)(326(222=-+-y x y xy x . 10.))((d c b a ++=____________. __________)19)(9(=+-a a . 11. 计算:(1))4)(3(+-x x (2)))((22y xy x y x +-+(3))53)(12(2--x x (4))21)(2)(5(2--+x x x12. 若c bx ax x x ++=-+2)25)(32(,则___________,_____,===c b a .13. 计算:(1)))(2())(23(b a b a b a b a +-+-+ (2))2)(1()3)(2(---++y x y x14. 化简求值:(1))152()96)(2(22------x x x x x x ,其中5.0=x(2)1)1())(1(2322+-+--+x x x x x x ,其中213=x .15. 已知))(1(22y a a ax a -+++的展开式中不含2a 、3a 项,试求x 、y 的值.16. 解方程:4)73()1)(12()3)(13(22++=+--+-x x x x x x x17. 已知:b a c C a c b B c b a A --=--=--=2,2,2, 求证:0)()()(=-+-+-C b a B a c A c b9.11平方差公式基础题 一、填空:=---))()(1(y x y x ________ ))()(2(x y y x ++-=__________=-+)23)(32)(3(b a b a _______ 161___)___)()(4(22-=-+b a ab ab22))(________)(5(xy y x -=--二、选择:(1)下列计算中,正确的是( )(A )2)2)(2(2-=-+m m m (B )252)52)(52(2-=-+a a a (C )116)14)(1422-=-+y x xy xy (D )12)12)(12(2-=-+m m m (2)下列各式中能用平方差公式计算的是( )(A ))352)(523(3223a cbc b a --(B )))((b a b a --+ (C ))32)(23(-+a a (D ))4332)(4332(3232b a b a ---三、计算:①(-3+x )(3+x ) ② )34)(34(22n m n m -+③)4)(2)(2(2a a a ++- ④ 122×118⑤-49.9×50.1 ⑥41194320⨯四、化简:(1))2)(2()2)(2(y x y x y x y x ++-++--- (2)))()((22q p q p q p +-+ (3)))(())(())((a c a c c b c b b a b a +-++-+-+ 拓展:已知==-=-yxy x y x ,则,21222。
