相交线与平行线难题集锦
相交线与平行线难题汇编含答案解析

【答案】B
【解析】
【分析】
利用E、F分别是线段BC、BA的中点得到EF是△BAC的中位线,得出∠CAB的大小,再利用CD∥AB得到∠DCA的大小,最后在等腰△DCA中推导得到∠D.
【详解】
∵点E、F分别是线段CB、AB的中点,∴EF是△BAC的中位线
∴EF∥AC
∵∠1=40°,∴∠CAB=40°
A.5B.6C.7D.8
【答案】C
【解析】
解:∵FM平分∠EFD,∴∠EFM=∠DFM= ∠CFE.∵EG平分∠AEF,∴∠AEG=∠GEF= ∠AEF.∵EM平分∠BEF,∴∠BEM=∠FEM= ∠BEF,∴∠GEF+∠FEM= (∠AEF+∠BEF)=90°,即∠GEM=90°,∠FEM+∠EFM= (∠BEF+∠CFE).∵AB∥CD,∴∠EGF=∠AEG,∠CFE=∠AEF,∴∠FEM+∠EFM= (∠BEF+∠CFE)= (BEF+∠AEF)=90°,∴在△EMF中,∠EMF=90°,∴∠GEM=∠EMF,∴EG∥FM,∴与∠DFM相等的角有:∠EFM、∠GEF、∠EGF、∠AEG以及∠GEF、∠EGF、∠AEG三个角的对顶角.故选C.
∵OB⊥CD,
∴∠1+∠3=90°,
∵∠1=∠2,
∴∠2+∠3=90°,
∴∠2与∠3互余,
故选:C.
【点睛】
本题考查了垂线和余角,关键是掌握垂线的定义当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
15.如图所示,下列条件中,能判定直线a∥b的是()
【详解】
当b∥d时a∥c;
相交线与平行线难题集锦(精)

相交线与平行线难题集锦1. 如图,BE∥AO,∠1=∠2,OE⊥OA于点O,EH⊥CO于点H,那么∠5=∠6,为什么?2.如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E = 140º,求∠BFD 的度数.3.如图,DE⊥AB,EF∥AC,∠A=35°,求∠DEF的度数。
4、如图1-26所示.AE ∥BD ,∠1=3∠2,∠2=25°,求∠C .5.如图,直线AB 、CD 被直线EF 所截,∠AEF +∠CFE =180°,∠1=∠2,则图中的∠H 与∠G 相等吗?说明你的理由.6.夹在两条平行线间的正方形ABCD 如图所示,顶点分别在两条平行线上,证明∠1=∠27. 已知DB ∥FG ∥EC ,A 是FG 上一点,∠ABD =60°,∠ACE =36°,AP 平分∠BAC ,求:⑴∠BAC 的大小;⑵∠PAG 的大小.A 1BC DE F G H 2 21A B C D a b8、如图在△ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,CE是∠ACB的平分线。
求证:∠EDF=∠BDF9.如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在C、D之间有一点P,如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化.若点P在C、D 两点的外侧运动时(P在直线l3上,但P点与点C、D不重合,试探索∠PAC,∠APB,∠PBD 之间的关系又是如何?10、如图,已知l1∥l2,MN分别和直线l1、l2交于点A、B,ME分别和直线l1、l2交于点C、D,点P在MN上(P点与A、B、M三点不重合.(1如果点P在A、B两点之间运动时,∠α、∠β、∠γ之间有何数量关系请说明理由;(2如果点P在A、B两点外侧运动时,∠α、∠β、∠γ有何数量关系(只须写出结论.。
七年级下册数学难题

七年级下册数学难题一、相交线与平行线类1. 如图,已知直线AB∥CD,∠1 = 30°,∠2 = 90°,则∠3等于多少度?解析:因为AB∥CD,所以∠1 = ∠4(两直线平行,同位角相等),已知∠1 = 30°,所以∠4 = 30°。
又因为∠2 = 90°,在三角形中,∠3+∠4+∠2 = 180°(三角形内角和为180°)。
把∠4 = 30°,∠2 = 90°代入可得:∠3+30°+90° = 180°。
解得∠3 = 180° 30° 90° = 60°。
2. 已知:如图,EF⊥AB,CD⊥AB,∠1 = ∠2,试说明∠AGD=∠ACB。
解析:因为EF⊥AB,CD⊥AB,所以EF∥CD(在同一平面内,垂直于同一条直线的两条直线互相平行)。
所以∠2 = ∠3(两直线平行,同位角相等)。
又因为∠1 = ∠2,所以∠1 = ∠3(等量代换)。
所以DG∥BC(内错角相等,两直线平行)。
所以∠AGD = ∠ACB(两直线平行,同位角相等)。
二、实数类1. 已知a=√(5)+2,b=√(5)-2,求a^2+b^2+7的值。
解析:先求a + b的值:a + b=√(5)+2+√(5)-2 = 2√(5)。
再求ab的值:ab=(√(5)+2)(√(5)-2)=(√(5))^2-2^2=5 4 = 1。
然后a^2+b^2=(a + b)^2-2ab=(2√(5))^2-2×1=20 2=18。
所以a^2+b^2+7=18 + 7=25。
2. 若√(1 3a)+|8b 3| = 0,求ab的值。
解析:因为√(1 3a)≥slant0,|8b 3|≥slant0,要使√(1 3a)+|8b 3| = 0成立。
则√(1 3a)=0,解得a=(1)/(3);|8b 3| = 0,解得b=(3)/(8)。
相交线与平行线难题集锦

相交线与平行线难题集锦1.要将角钢(1)弯成120°的钢架(2),则需要在角钢(1)上截去的缺口是多少度?2.将矩形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF的度数是多少?3.将三角尺的直角顶点放在直尺的一边上,已知∠1=30°,∠2=50°,则∠3的度数等于多少?4.直线AC∥BD,连结AB,直线AC,BD及线段AB把平面分成①、②、③、④四个部分。
当动点P落在第①部分时,证明∠APB=∠PAC+∠PBD;当动点P落在第②部分时,∠APB=∠PAC+∠PBD不成立;当动点P在第③部分时,探究∠PAC,∠APB,∠PBD之间的关系,并给出结论并证明之一。
6.在将直尺与三角尺叠放在一起的图中,与∠2互余的角是哪一个?8.光线a照射到平面镜CD上,然后在平面镜之间来回反射,已知∠1=55°,∠3=75°,求∠2的度数。
9.在图1-26中,已知AE∥BD,∠2=25°且∠1=3∠2,求∠C的度数。
10.直线AB、CD被直线EF所截,已知∠AEF+∠XXX°且∠1=∠2,问图中的∠H与∠G是否相等。
12.如图所示是XXX自制对顶角的“小仪器”示意图:将直角三角板ABC的AC边延长且使AC固定;另一个三角板CDE的直角顶点与前一个三角板直角顶点重合;延长DC,已知∠1=30°,求∠ACF的度数。
FD将一块直尺和一块三角板放在一起,如图所示。
如果∠1的度数为45°,那么∠2的度数是多少?XXX所示,将三角板的直角顶点放在平行线a、b中的直线b上。
如果∠1的度数为40°,那么∠2的度数是多少?如图所示,l∥m,等腰直角三角形ABC的直角顶点C在直线m上。
如果∠β的度数为20°,那么∠α的度数是多少?选项如下:A、25°B、30°C、20°D、35°XXX所示,AB∥EF∥CD,且∠ABC的度数为46°,∠CEF的度数为154°。
初中数学相交线与平行线难题汇编附答案

初中数学相交线与平行线难题汇编附答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初中数学相交线与平行线难题汇编附答案一、选择题1.如图,将一张含有30角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠的大小为()∠=,则1244α-A.14B.16C.90α-D.44【答案】A【解析】分析:依据平行线的性质,即可得到∠2=∠3=44°,再根据三角形外角性质,可得∠3=∠1+30°,进而得出结论.详解:如图,∵矩形的对边平行,∴∠2=∠3=44°,根据三角形外角性质,可得:∠3=∠1+30°,∴∠1=44°﹣30°=14°.故选A.点睛:本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:两直线平行,同位角相等.2.如图所示,有下列五种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6旁内角;④∠5和∠2是同位角;⑤<1和∠3是同旁内角;其中正确的是()A.①②③④B.①②③④C.①②③④⑤D.①②④⑤【答案】D【解析】如图,①∠1和∠4是直线AC和直线BC被直线AB截得的同位角,所以①正确;②∠3和∠5是直线BC和直线AB被直线AC截得的内错角,所以②正确;③∠2和∠6是直线AB和直线AC被直线CB截得的内错角,所以③错误;④∠5和∠2是直线AC和直线BC被直线AB截得的同位角,所以④正确;⑤∠1和∠3是直线BC和直线AB被直线AC截得的同旁内角,所以⑤正确.故答案选D.点睛:(1)准确识别同位角、内错角、同旁内角的关键,是弄清两角是由哪两条直线被哪条直线截得,这其中的关键是辨别出截线,在截线的两旁的是内错角,在截线的同旁的为同位角或同旁内角;(2)辨别截线方法:先找出两角的边所在直线,公共直线即是截线.3.下列说法中,正确的是()A.过一点有且只有一条直线与已知直线垂直B.过直线外一点有且只有一条直线与已知直线平行C.垂于同一条直线的两条直线平行D.如果两个角的两边分别平行,那么这两个角一定相等【答案】B【解析】【分析】根据平行线的性质和判定,平行线公理及推论逐个判断即可.【详解】A、在同一平面内,过一点有且只有一条直线与已知直线垂直,故本选项不符合题意;B、过直线外一点有且只有一条直线与已知直线平行,故本选项符合题意;C、在同一平面内,垂直于同一条直线的两直线平行,故本选项不符合题意;D、如果两个角的两边分别平行,那么这两个角相等或互补,故本选项不符合题意;故选:B.【点睛】此题考查平行线的性质和判定,平行线公理及推论,能熟记知识点的内容是解题的关键.∥的条件有()个.4.如图,下列能判定AB CD(1)180B BCD ∠+∠=︒; (2)12∠=∠;(3)34∠=∠; (4)5B ∠=∠.A .1B .2C .3D .4 【答案】C【解析】【分析】根据平行线的判定定理依次判断即可.【详解】∵180B BCD ∠+∠=︒,∴AB ∥CD ,故(1)正确;∵12∠=∠,∴AD ∥BC ,故(2)不符合题意;∵34∠=∠,∴AB ∥CD ,故(3)正确;∵5B ∠=∠,∴AB ∥CD ,故(4)正确;故选:C.【点睛】此题考查平行线的判定定理,熟记定理及两个角之间的位置关系是解题的关键.5.如图,直线a ∥b ,直线c 分别交a ,b 于点A ,C ,∠BAC 的平分线交直线b 于点D ,若∠1=50°,则∠2的度数是( )A .50°B .70°C .80°D .110°【答案】C【解析】【分析】 根据平行线的性质可得∠BAD=∠1,再根据AD 是∠BAC 的平分线,进而可得∠BAC 的度数,再根据补角定义可得答案.【详解】因为a ∥b ,所以∠1=∠BAD=50°,因为AD是∠BAC的平分线,所以∠BAC=2∠BAD=100°,所以∠2=180°-∠BAC=180°-100°=80°.故本题正确答案为C.【点睛】本题考查的知识点是平行线的性质,解题关键是掌握两直线平行,内错角相等.6.将一个矩形纸片按如图所示折叠,若∠1=40°,则∠2的度数是()A.40°B.50°C.60°D.70°【答案】D【解析】【分析】根据折叠的知识和直线平行判定即可解答.【详解】解:如图可知折叠后的图案∠ABC=∠EBC,又因为矩形对边平行,根据直线平行内错角相等可得∠2=∠DBC,又因为∠2+∠ABC=180°,所以∠EBC+∠2=180°,即∠DBC+∠2=2∠2=180°-∠1=140°.可求出∠2=70°.【点睛】掌握折叠图形的过程中有些角度是对称相等的是解答本题的关键.7.如图,直线AB∥CD,直线EF分别交AB、CD于E、F两点,EG平分∠AEF,如果∠1=32°,那么∠2的度数是()A .64°B .68°C .58°D .60°【答案】A【解析】【分析】 首先根据平行线性质得出∠1=∠AEG ,再进一步利用角平分线性质可得∠AEF 的度数,最后再利用平行线性质进一步求解即可.【详解】∵AB ∥CD ,∴∠1=∠AEG .∵EG 平分∠AEF ,∴∠AEF=2∠AEG ,∴∠AEF=2∠1=64°,∵AB ∥CD ,∴∠2=64°.故选:A .【点睛】本题主要考查了角平分线性质以及平行线的性质,熟练掌握相关概念是解题关键.8.如图,将一张矩形纸片折叠,若170∠=︒,则2∠的度数是( )A .65︒B .55︒C .70︒D .40︒【答案】B【解析】【分析】根据平行线的性质求出∠3=170∠=︒,得到∠2+∠4=110°,由折叠得到∠2=∠4即可得到∠2的度数.【详解】∵a ∥b ,∴∠3=170∠=︒,∴∠2+∠4=110°,由折叠得∠2=∠4,∴∠2=55 ,故选:B.【点睛】此题考查平行线的性质,折叠的性质.9.如图,11∥l2,∠1=100°,∠2=135°,则∠3的度数为()A.50°B.55°C.65°D.70°【答案】B【解析】【分析】如图,延长l2,交∠1的边于一点,由平行线的性质,求得∠4的度数,再根据三角形外角性质,即可求得∠3的度数.【详解】如图,延长l2,交∠1的边于一点,∵11∥l2,∴∠4=180°﹣∠1=180°﹣100°=80°,由三角形外角性质,可得∠2=∠3+∠4,∴∠3=∠2﹣∠4=135°﹣80°=55°,故选B.【点睛】本题考查了平行线的性质及三角形外角的性质,熟练运用平行线的性质是解决问题的关键.10.如图AD∥BC,∠B=30,DB平分∠ADE,则∠DEC的度数为()A.30B.60C.90D.120【答案】B【解析】∵AD∥BC,∴∠ADB=∠DBC,∵DB平分∠ADE,∴∠ADB=∠ADE,∵∠B=30°,∴∠ADB=∠BDE=30°,则∠DEC=∠B+∠BDE=60°.故选B.【点睛】此题主要考查了平行线的性质,正确得出∠ADB的度数是解题关键.11.如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是()A.110°B.120°C.140°D.150°【答案】B【解析】【详解】解:∵AD∥BC,∴∠DEF=∠EFB=20°,图b中∠GFC=180°-2∠EFG=140°,在图c中∠CFE=∠GFC-∠EFG=120°,故选B.12.如图,ABCD为一长方形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应,若∠1=2∠2,则∠AEF的度数为( )A.75°B.72°C.70°D.65°【答案】B【解析】【分析】如图,由折叠的性质可知∠3=∠4,已知AB∥CD,根据两直线平行,内错角相等可得∠3=∠1,再由∠1=2∠2,∠3+∠4+∠2=180°,可得5∠2=180°,即可求得∠2=36°,所以∠AEF=∠3=∠1=72°【详解】如图,由折叠的性质可知∠3=∠4,∵AB∥CD,∴∠3=∠1,∵∠1=2∠2,∠3+∠4+∠2=180°,∴5∠2=180°,即∠2=36°,∴∠AEF=∠3=∠1=72°故选B.【点睛】本题考查的是图形翻折变换的性质及平行线的性质,熟知折叠的性质及平行线的性质是解决问题的关键.13.如图所示,b∥c,a⊥b,∠1=130°,则∠2=().A.30°B.40°C.50°D.60°【答案】B【解析】【分析】证明∠3=90°,利用三角形的外角的性质求出∠4即可解决问题.【详解】如图,反向延长射线a交c于点M,∵b∥c,a⊥b,∴a⊥c,∴∠3=90°,∵∠1=90°+∠4,∴130°=90°+∠4,∴∠4=40°,∴∠2=∠4=40°,故选B.【点睛】本题考查平行线的性质,垂线的性质,三角形的外角的性质等知识,解题的关键是熟练掌握基本知识14.如图所示,某同学的家在P处,他想尽快赶到附近公路边搭公交车,他选择P→C路线,用几何知识解释其道理正确的是()A.两点确定一条直线B.垂直线段最短C.两点之间线段最短D.三角形两边之和大于第三边【答案】B【解析】【分析】根据垂线段的定义判断即可.【详解】解:直线外一点与直线上各点连接的所有线段中,垂线段最短,选:B.【点睛】直线外任意一点到这条直线的垂线段的长度,叫做点到这条直线的距离.直线外一点与直线上各点连接的所有线段中,垂线段最短.简称“垂线段最短”.15.下列四个命题:①对顶角相等;②内错角相等;③平行于同一条直线的两条直线互相平行;④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等.其中真命题的个数是( )A.1个B.2个C.3个D.4个【答案】B【解析】解:①符合对顶角的性质,故本小题正确;②两直线平行,内错角相等,故本小题错误;③符合平行线的判定定理,故本小题正确;④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补,故本小题错误.故选B.16.如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在边AC、BC上,BD平分∠ABC,DE∥AB.图中的等腰三角形共有()A.3个B.4个C.5个D.6个【答案】C【解析】【分析】已知条件,根据三角形内角和等于180,角的平分线的性质求得各个角的度数,然后利用等腰三角形的判定进行判断即可.【详解】解:∵AB=AC,∠A=36°,∴∠ABC=∠C=72°,∵BD平分∠ABC,∴∠ABD=∠DBC=36°,∴∠BDC=180°﹣36°﹣72°=72°,∵DE∥AB,∴∠EDB=∠ABD=36°,∴∠EDC=72°﹣36°=36°,∴∠DEC=180°﹣72°﹣36°=72°,∴∠A=∠ABD,∠DBE=∠BDE,∠DEC=∠C,∠BDC=∠C,∠ABC=∠C,∴△ABC、△ABD、△DEB、△BDC、△DEC都是等腰三角形,共5个,故选C.【点睛】本题考查了等腰三角形判定和性质、角平分线的性质、平行线的性质,由已知条件利用相关的性质求得各个角相等是解题的关键.17.如图,直线//a b ,将一块含45︒角的直角三角尺(90︒∠=C )按所示摆放.若180︒∠=,则2∠的大小是( )A .80︒B .75︒C .55︒D .35︒【答案】C【解析】【分析】 先根据//a b 得到31∠=∠,再通过对顶角的性质得到34,25∠=∠∠=∠,最后利用三角形的内角和即可求出答案.【详解】解:给图中各角标上序号,如图所示:∵//a b∴3180︒∠=∠=(两直线平行,同位角相等),又∵34,25∠=∠∠=∠(对顶角相等),∴251804180804555A ∠=∠=︒-∠-∠=︒-︒-︒=︒.故C 为答案.【点睛】本题主要考查了直线平行的性质(两直线平行,同位角相等)、对顶角的性质(对顶角相等),熟练掌握直线平行的性质是解题的关键.18.如图,直线//,175a b ︒∠=,则2∠的大小是( )A .75︒B .85︒C .95︒D .105︒【答案】D【解析】【分析】 把2∠的对顶角标记为3∠,根据对顶角的性质得到2∠与3∠得关系,再根据直线平行的性质得到1∠与3∠得关系,最后由等量替换得到2∠得度数.【详解】解:如图,把2∠的对顶角标记为3∠,∵2∠与3∠互为对顶角,∴23∠∠=,又∵//a b ,175︒∠=,∴13180∠+∠=︒(两直线平行,同旁内角互补),∴12180∠+∠=︒(等量替换),∴2180118075105∠=︒-∠=︒-︒=︒故D 为答案.【点睛】本题主要考查了对顶角的性质(对顶角相等)、直线平行的性质(两直线平行,同旁内角互补),学会运用等量替换原则是解题的关键.19.如图,小慧从A 处出发沿北偏东60°方向行走至B 处,又沿北偏西20°方向行走至C 处,此时需要将方向调整到与出发时一致,则方向的调整应为( )A.左转80°B.右转80°C.左转100°D.右转100°【答案】B【解析】【分析】如图,延长AB到D,过C作CE//AD,由题意可得∠A=60°,∠1=20°,根据平行线的性质可得∠A=∠2,∠3=∠1+∠2,进而可得答案.【详解】如图,延长AB到D,过C作CE//AD,∵此时需要将方向调整到与出发时一致,∴此时沿CE方向行走,∵从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,∴∠A=60°,∠1=20°,AM∥BN,CE∥AB,∴∠A=∠2=60°,∠1+∠2=∠3∴∠3=∠1+∠2=20°+60°=80°,∴应右转80°.故选B.【点睛】本题考查了方向角有关的知识及平行线的性质,解答时要注意以北方为参照方向,进行角度调整.20.如图,点P是直线a外一点,PB⊥a,点A,B,C,D都在直线a上,下列线段中最短的是( )A.PA B.PB C.PC D.PD 【答案】B【解析】如图,PB是点P到a的垂线段,∴线段中最短的是PB.故选B.。
相交线与平行线难题集锦
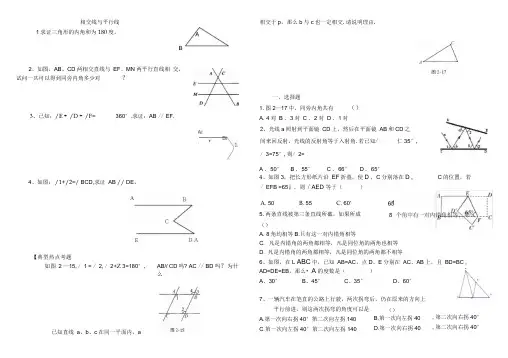
相交线与平行线1求证三角形的内角和为180度。
相交于p,那么b与c也一定相交.请说明理由.2、如图,AB、CD两相交直线与EF、MN两平行直线相交,试问一共可以得到同旁内角多少对?3、已知:/E + /D + /F= 360°.求证:AB // EF.4、如图,/1+/2=/ BCD,求证AB // DE。
【典型热点考题】如图 2 —15,/ 1 = / 2,/ 2+Z 3=180°,已知直线a、b、c在同一平面内,aAiBi'AB// CD吗? AC // BD吗?为什么一、选择题1.图2—17中,同旁内角共有()A. 4对B . 3对C . 2对D . 1对2、光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知/ 仁35°,/ 3=75°,则/ 2=A . 50°B . 55°C . 66°D . 65°4、如图3,把长方形纸片沿EF折叠,使D , C分别落在D ,/ EFB =65』,则/ AED 等于()A. 50B. 55C. 60'5.两条直线被第三条直线所截,如果所成()A. 8角均相等B.只有这一对内错角相等C的位置,若C. 凡是内错角的两角都相等,凡是同位角的两角也相等D. 凡是内错角的两角都相等,凡是同位角的两角都不相等6、如图,在L ABC中,已知AB=AC,点D、E分别在AC、AB上,且BD=BC ,AD=DE=EB,那么• A的度数是()A、30°B、45°C、35°D、60°7、一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则这两次拐弯的角度可以是A.第一次向右拐40°第二次向左拐140C.第一次向左拐40°第二次向左拐140()B.第一次向左拐40D.第一次向右拐40BDA,第二次向右拐40°,第二次向右拐40°&已知: A 、 + C 、 + 如图,AB//CD , + =360 -=180则图中 B 、 D 、三个角之间的数量关系为(=180 =909、如图, 把三角形纸片沿 DE 折叠, 当点A 落在四边形BCED 内部时,则/ A 与/ 1 +/ 2之间有一种数量关系始终保持不变•请试着找一找这个规律,你发现的规律是 (A) Z A =Z 1 + Z 2 (B)2 / A =Z 1+Z 2 (C)3 (D)3 二、填空题 Z A=2( Z 1 十Z 2)E1、用等腰直角三角板画Z AOB =45:,并将三角板沿OB 方向平移到如图17所示的虚线处后绕点 M 逆时针方向旋转 22,则三角板的斜边与射线 OA 的夹角[为1、已知:如图 2—33,Z ABC 玄ADC BF 、DE 是Z ABC Z ADC 的角平分线,Z 1 = Z 2 .求证:DC// AB.2、已知:如图, CD//EF , Z 1=65 , Z 2=35解:2、如图2— 31,直线a 、b 被直线 AB 所截,且 AB 丄BC,(1) Z 1和Z 2是 _______ 角; ⑵若Z 1与Z 2互补,则Z 1- Z 3= ________ . 三、解答题3、实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平 面镜所夹的锐角相等•(1)如图,一束光线m 射到平面镜a 上,被a 反射到平面镜b 上,又被b 反射•若被b 反 射出的光线n 与光线m 平行,且Z 仁50° ,则Z 2=⑵在(1)中,若Z 仁55 ° ,则Z 3=,Z3=;若 Z 1= 40° ,则 Z 3=⑶ 由⑴、(2),请你猜想:当两平面镜a 、b 的夹角Z 3=时,可以使任何射到平面镜a 上的光线m 经过平面镜a 、b 的两次反射后,入射光线 m 与反射光线n 平行. 你能说明理由吗?7、潜望镜中的两个镜子MN和PQ是互相平行的,如图所示,光线AB经镜面反射后,/仁/ 2,/ 3=/4,试说明,进入的光线AB与射出的光线CD平行吗?为什么?8、女口图:已知' ABC与ADEF是一副三角板的拼图,A,E,C,D在同一条线上(1)、求证EF//BC ; (2)、求与区2的度数D。
相交线与平行线难题汇编含答案
∴OD=CD=3.
∵ 到 的距离是2.4,
∴ 到 的距离是2.4,
∴ 的面积= .
故选A.
【点睛】
本题考查了等腰三角形的判定、角平分线的定义、平行线的性质、以及角平分线的性质,利用角平分线的性质得出 到 的距离是2.4是解题的关键.
6.如图 ∥ ,∠ = , 平分∠ ,则∠ 的度数为()
A. B. C. D.
【答案】B
【解析】
∵AD∥BC,
∴∠ADB=∠DBC,
∵DB平分∠ADE,
∴∠ADB=∠ADE,
∵∠B=30°,
∴∠ADB=∠BDE=30°,
则∠DEC=∠B+∠BDE=60°.
故选B.
【点睛】此题主要考查了平行线的性质,正确得出∠ADB的度数是解题关键.
B、两直线平行,内错角相等,正确;
C、等腰三角形的两个底角相等,正确;
D、若两实数的平方相等,则这两个实数相等或互为相反数,故D错误;
故选:D.
【点睛】
本题考查了判断命题的真假,以及平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义,解题的关键是熟练掌握所学的性质进行解题.
16.若∠A与∠B是对顶角且互补,则它们两边所在的直线( )
∵∠1=90°+∠4,
∴130°=90°+∠4,
∴∠4=40°,
∴∠2=∠4=40°,
故选B.
【点睛】
本题考查平行线的性质,本知识
2.如图,已知 ,若 , , ,下列结论:① ;② ;③ ;④ 与 互补;⑤ ,其中正确的有()
A.2个B.3个C.4个D.5个
∴∠ACD=38°,
∴∠2=∠BCD=60°﹣38°=22°,
七下第七章相交线与平行线难题训练(有答案)
七下第七章相交线与平行线难题训练一、选择题1.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,请你数一数,错误的个数为()A. 1个B. 2个C. 3个D. 4个2.下列说法正确的个数是()①同位角相等;②过一点有且只有一条直线与已知直线垂直;③过一点有且只有一条直线与已知直线平行;④三条直线两两相交,总有三个交点;⑤若a//b,b//c,则a//c.A. 1个B. 2个C. 3个D. 4个3.如图,已知AB//CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是()A. ∠E=∠FB. ∠E+∠F=180°C. 3∠E+∠F=360°D. 2∠E−∠F=90°4.已知:如图AB//EF,BC⊥CD,则∠α,∠β,∠γ之间的关系是()A. ∠β=∠α+∠γB. ∠α+∠β+∠γ=180°C. ∠α+∠β−∠γ=90°D. ∠β+∠γ−∠α=90°5.若∠α与∠β是内错角,且∠α=50°时,则∠β的度数为()A. 50°B. 130°C. 50°或130°D. 无法确定6.给出下列说法:(1)两条直线被第三条直线所截,同位角相等;(2过平面内一点有且只有一条直线与已知直线平行;(3)相等的两个角是对顶角;(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;(5)不相交的两条直线叫做平行线(6)垂直于同一条直线的两条直线平行。
其中正确的有()A. 0个B. 1个C. 2个D. 3个7.一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH 折叠,发现GD与GC重合,HF与HE重合.则下列判断正确的是()A. 纸带①的边线平行,纸带②的边线不平行B. 纸带①的边线不平行,纸带②的边线平行C. 纸带①、②的边线都平行D. 纸带①、②的边线都不平行8.已知:如图,点E、F分别在直线AB、CD上,点G、H在两直线之间,线段EF与GH相交于点O,且有∠AEF+∠CFE=180°,∠AEF−∠1=∠2,则在图中相等的角共有()A. 5对B. 6对C. 7对D. 8对二、填空题9.用一张长方形纸条折成如图所示图形,如果∠1=130°,那么∠2=______.10.如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,则∠FGD的度数是______度,再沿BF折叠成图c,则图c中的∠DHF的度数是______.11.如果∠A的两边分别与∠B的两边平行,且∠A比∠B的3倍少40°,则这两个角的度数分别为______ .12.如图,将一条两边沿互相平行的纸带折叠,若∠1=30°,则∠α=______°.13.如图,AD⊥BC,EF⊥BC,∠1=∠2,求证:∠BAC+∠AGD=180°证明的过程如下,请将括号内的理由填写完整。
相交线与平行线难题汇编及答案解析
在△ODB和△OEC中
∴△ODB≌△OEC
∴OD=OE
∴△ODE是顶角为120°的等腰三角形,
∴ 形状不变,故①正确;
过点O作OH⊥DE,则DH=EH
∵△ODE是顶角为120°的等腰三角形
∴∠ODE=∠OED= (180°-120°)=30°
∴OH=OE·sin∠OED= OE,EH= OE·cos∠OED= OE
∴∠3=∠EDB,故③正确,④错误;
∵AC⊥BC,CD⊥AB,
∴∠ACB=∠CDA=90°,
∴∠A+∠B=90°,∠1+∠A=90°,
∴∠1=∠B,故⑤正确;
即正确的个数是4个,
故选:C.
【点睛】
此题考查平行线的判定和性质,三角形内角和定理,垂直定义,能综合运用知识点进行推理是解题的关键.
3.如图,点 分别在 的边 上,点 在 的内部,若 ,则 的度数是()
9.如图,若AB∥CD,则∠α、∠β、∠γ之间关系是()
A.∠α+∠β+∠γ=180°B.∠α+∠β﹣∠γ=360°
C.∠α﹣∠β+∠γ=180°D.∠α+∠β﹣∠γ=180°
【答案】D
【解析】
试题解析:如图,作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∵EF∥AB,
∴∠α+∠AEF=180°,
∵EF∥CD,
相交线与平行线难题汇编及答案解析
一、选择题
1.如图,△ABC中,∠C=90°,则点B到直线AC的距离是( )
A.线段ABB.线段ACC.线段BCD.无法确定
【答案】C
【解析】
【分析】
直接利用点到直线的距离定义得出答案.
相交线与平行线难题汇编附解析
相交线与平行线难题汇编附解析一、选择题1.如图所示,某同学的家在P处,他想尽快赶到附近公路边搭公交车,他选择P→C路线,用几何知识解释其道理正确的是()A.两点确定一条直线B.垂直线段最短C.两点之间线段最短D.三角形两边之和大于第三边【答案】B【解析】【分析】根据垂线段的定义判断即可.【详解】解:Q直线外一点与直线上各点连接的所有线段中,垂线段最短,选:B.【点睛】直线外任意一点到这条直线的垂线段的长度,叫做点到这条直线的距离.直线外一点与直线上各点连接的所有线段中,垂线段最短.简称“垂线段最短”.2.如图,直线a∥b,直线c分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=50°,则∠2的度数是()A.50°B.70°C.80°D.110°【答案】C【解析】【分析】根据平行线的性质可得∠BAD=∠1,再根据AD是∠BAC的平分线,进而可得∠BAC的度数,再根据补角定义可得答案.【详解】因为a∥b,所以∠1=∠BAD=50°,因为AD 是∠BAC 的平分线,所以∠BAC=2∠BAD=100°,所以∠2=180°-∠BAC=180°-100°=80°.故本题正确答案为C.【点睛】本题考查的知识点是平行线的性质,解题关键是掌握两直线平行,内错角相等.3.如图,能判定EB ∥AC 的条件是( )A .∠C =∠ABEB .∠A =∠EBDC .∠C =∠ABCD .∠A =∠ABE 【答案】D【解析】【分析】在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线.【详解】A 、∠C =∠ABE 不能判断出EB ∥AC ,故A 选项不符合题意;B 、∠A =∠EBD 不能判断出EB ∥AC ,故B 选项不符合题意;C 、∠C =∠ABC 只能判断出AB =AC ,不能判断出EB ∥AC ,故C 选项不符合题意;D 、∠A =∠ABE ,根据内错角相等,两直线平行,可以得出EB ∥AC ,故D 选项符合题意. 故选:D .【点睛】此题考查平行线的性质,正确识别“三线八角”中的同位角、内错角、同旁内角是解题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.4.如图,已知//AB CD ,直线EF 分别交AB ,CD 于M ,N 两点,将一个含有30°角的直角三角尺按如图所示的方式放置(30PNG ∠=︒),若75EMB ∠=︒,则PNM ∠的度数是()A .30°B .45︒C .60︒D .75︒【答案】B【解析】根据75EMB ∠=︒,可以计算75END ∠=︒(两直线平行,同位角相等),又由75END PNM PNG ∠=∠+∠=︒,30PNG ∠=︒从而得到PNM ∠的度数.【详解】解:∵//AB CD ,∴75EMB EFD ∠=∠=︒(两直线平行,同位角相等),又∵30PNG ∠=︒,75END PNM PNG ∠=∠+∠=︒,∴753045PNM END PNG ∠=∠-∠=︒-︒=︒,故答案为B.【点睛】本题主要考查了两直线平行的性质. 牢记知识点: 两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;5.如图,ABCD 为一长方形纸带,AB ∥CD ,将ABCD 沿EF 折叠,A 、D 两点分别与A′、D′对应,若∠1=2∠2,则∠AEF 的度数为( )A .75°B .72°C .70°D .65°【答案】B【解析】【分析】 如图,由折叠的性质可知∠3=∠4,已知AB ∥CD ,根据两直线平行,内错角相等可得∠3=∠1,再由∠1=2∠2,∠3+∠4+∠2=180°,可得5∠2=180°,即可求得∠2=36°,所以∠AEF=∠3=∠1=72°【详解】如图,由折叠的性质可知∠3=∠4,∵AB ∥CD ,∴∠3=∠1,∵∠1=2∠2,∠3+∠4+∠2=180°,∴5∠2=180°,即∠2=36°,∴∠AEF=∠3=∠1=72°故选B .本题考查的是图形翻折变换的性质及平行线的性质,熟知折叠的性质及平行线的性质是解决问题的关键.6.如图,AB CD ∥,BF 平分ABE ∠,且BF DE P ,则ABE ∠与D ∠的关系是( )A .2ABE D ∠=∠B .180ABE D ∠+∠=︒C .90ABED ∠=∠=︒D .3ABE D ∠=∠【答案】A【解析】【分析】 延长DE 交AB 的延长线于G ,根据两直线平行,内错角相等可得D G ∠=∠,再根据两直线平行,同位角相等可得G ABF ∠=∠,然后根据角平分线的定义解答.【详解】证明:如图,延长DE 交AB 的延长线于G ,//AB CD Q ,D G ∴∠=∠,//BF DE Q ,G ABF ∴∠=∠,D ABF ∴∠=∠,BF Q 平分ABE ∠,22ABE ABF D ∴∠=∠=∠,即2ABE D ∠=∠.故选:A .【点睛】本题考查了平行线的性质,角平分线的定义,熟记性质并作辅助线是解题的关键.7.如图,12180∠+∠=︒,3100∠=︒,则4∠=( )A.60︒B.70︒C.80︒D.100︒【答案】C【解析】【分析】首先证明a∥b,再根据两直线平行同位角相等可得∠3=∠6,再根据对顶角相等可得∠4.【详解】解:∵∠1+∠5=180°,∠1+∠2=180°,∴∠2=∠5,a∥b,∴∠3=∠6=100°,∴∠4=180°-100°=80°.故选:C.【点睛】此题考查平行线的判定与性质,解题关键是掌握两直线平行同位角相等.8.如图,BE平分∠DBC,点A是BD上一点,过点A作AE∥BC交BE于点E,∠DAE=56°,则∠E的度数为()A.56°B.36°C.26°D.28°【答案】D【解析】分析:根据平行线的性质,可得∠DBC=56°,∠E=∠EBC,根据角平分线的定义,可得∠EBC=12∠DBC=28°,进而得到∠E=28°.详解:∵AE∥BC,∠DAE=56°,∴∠DBC=56°,∠E=∠EBC,∵BE平分∠DBC,∴∠EBC=12∠DBC=28°,∴∠E=28°,故选D.点睛:本题主要考查了角平分线的定义和平行线的性质,熟练掌握角平分线的定义和平行线的性质是解题的关键.9.如图,若AB∥CD,则∠α、∠β、∠γ之间关系是()A.∠α+∠β+∠γ=180°B.∠α+∠β﹣∠γ=360°C.∠α﹣∠β+∠γ=180°D.∠α+∠β﹣∠γ=180°【答案】D【解析】试题解析:如图,作EF∥AB,∵AB∥CD,∴EF∥CD,∵EF∥AB,∴∠α+∠AEF=180°,∵EF∥CD,∴∠γ=∠DEF,而∠AEF+∠DEF=∠β,∴∠α+∠β=180°+∠γ,即∠α+∠β-∠γ=180°.故选:D.10.把一副三角板放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是()A.45°B.60°C.75°D.82.5°【答案】C【解析】【分析】直接利用平行线的性质结合已知角得出答案.【详解】如图,作直线l平行于直角三角板的斜边,可得:∠3=∠2=45°,∠4=∠5=30°,故∠1的度数是:45°+30°=75°,故选C.【点睛】本题主要考查了平行线的性质,正确作出辅助线是解题关键.11.在下图中,∠1,∠2是对顶角的图形是()A.B.C.D.【答案】B【解析】略12.如图,△ABC中,∠C=90°,则点B到直线AC的距离是 ( )A.线段AB B.线段AC C.线段BC D.无法确定【答案】C【解析】【分析】直接利用点到直线的距离定义得出答案.【详解】解:如图,三角形ABC中,∠C=90°,则点B到直线AC的距离是:线段BC.故选:C .【点睛】本题考查点到之间的距离,正确把握相关定义是解题关键.13.下列四个说法:①两点之间,线段最短;②连接两点之间的线段叫做这两点间的距离;③经过直线外一点,有且只有一条直线与这条直线平行;④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.其中正确的个数有( )A .1个B .2个C .3个D .4个【答案】C【解析】【分析】根据线段公理,两点之间的距离的概念,平行公理,垂线段最短等知识一一判断即可.【详解】解:①两点之间,线段最短,正确.②连接两点之间的线段叫做这两点间的距离,错误,应该是连接两点之间的线段的距离叫做这两点间的距离.③经过直线外一点,有且只有一条直线与这条直线平行,正确.④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.正确.故选C .【点睛】本题考查线段公理,两点之间的距离的概念,平行公理,垂线段最短等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.14.如图,等边ABC V 边长为a ,点O 是ABC V 的内心,120FOG ∠=︒,绕点O 旋转FOG ∠,分别交线段AB 、BC 于D 、E 两点,连接DE ,给出下列四个结论:①ODE V 形状不变;②ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一;③四边形ODBE 的面积始终不变;④BDE V 周长的最小值为1.5a .上述结论中正确的个数是( )A .4B .3C .2D .1【答案】A【解析】【分析】 连接OB 、OC ,利用SAS 证出△ODB ≌△OEC ,从而得出△ODE 是顶角为120°的等腰三角形,即可判断①;过点O 作OH ⊥DE ,则DH=EH ,利用锐角三角函数可得OH=12OE 和OE ,然后三角形的面积公式可得S △ODE=4OE 2,从而得出OE 最小时,S △ODE 最小,根据垂线段最短即可求出S △ODE 的最小值,然后证出S 四边形ODBE =S △OBC=212即可判断②和③;求出BDE V 的周长=a +DE ,求出DE 的最小值即可判断④.【详解】解:连接OB 、OC∵ABC V 是等边三角形,点O 是ABC V 的内心,∴∠ABC=∠ACB=60°,BO=CO ,BO 、CO 平分∠ABC 和∠ACB ∴∠OBA=∠OBC=12∠ABC=30°,∠OCA=∠OCB=12∠ACB=30° ∴∠OBA=∠OCB ,∠BOC=180°-∠OBC -∠OCB=120° ∵120FOG ∠=︒∴∠=FOG ∠BOC∴∠FOG -∠BOE=∠BOC -∠BOE∴∠BOD=∠COE在△ODB 和△OEC 中BOD COE BO COOBD OCE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ODB ≌△OEC∴OD=OE∴△ODE 是顶角为120°的等腰三角形,∴ODE V 形状不变,故①正确;过点O 作OH ⊥DE ,则DH=EH∵△ODE 是顶角为120°的等腰三角形∴∠ODE=∠OED=12(180°-120°)=30° ∴OH=OE·sin ∠OED=12OE ,EH= OE·cos ∠∴∴S △ODE =12DE·2 ∴OE 最小时,S △ODE 最小,过点O 作OE′⊥BC 于E′,根据垂线段最短,OE′即为OE 的最小值∴BE ′=12BC=12a 在Rt △OBE ′中 OE′=BE′·tan ∠OBE ′=12a 33 ∴S △ODE 3223 ∵△ODB ≌△OEC∴S 四边形ODBE =S △ODB +S △OBE = S △OEC +S △OBE =S △OBC =12BC 23 23=1423 ∴S △ODE ≤14S 四边形ODBE 即ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一,故②正确; ∵S 四边形ODBE 23 ∴四边形ODBE 的面积始终不变,故③正确; ∵△ODB ≌△OEC∴DB=EC∴BDE V 的周长=DB +BE +DE= EC +BE +DE=BC +DE=a +DE ∴DE 最小时BDE V 的周长最小∵3OE∴OE 最小时,DE 最小而OE 的最小值为OE′=36a ∴DE 336a =12a ∴BDE V 的周长的最小值为a +12a =1.5a ,故④正确; 综上:4个结论都正确,故选A .【点睛】此题考查的是等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短的应用,掌握等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短是解决此题的关键.15.如图,下列判断:①若12A C ∠=∠∠=∠,,则B D ∠=∠;②若12B D ∠=∠∠=∠,,则A C ∠=∠:③若,A C B D ∠=∠∠=∠,则12∠=∠.其中,正确的个数是( ).A .0B .1C .2D .3【答案】D【解析】【分析】 ①根据12A C ∠=∠∠=∠,证明四边形DEBF 是平行四边形即可判断;②根据12B D ∠=∠∠=∠,证明DC ∥AB 即可判断;③根据,A C B D ∠=∠∠=∠证明DC ∥AB 即可判断.【详解】解:如图,标出∠3,①∵A C ∠=∠,∴DC ∥AB (内错角相等,两直线平行),∵2,3∠∠是对顶角,∴23∠∠=,∴13∠=∠(等量替换),∴DE ∥FB (同位角相等,两直线平行),∴四边形DEBF 是平行四边形(两组对边分别平行),∴B D ∠=∠,②∵2,3∠∠是对顶角,∴23∠∠=,∴13∠=∠(等量替换),∴DE ∥FB (同位角相等,两直线平行),∴∠B+∠DEB=180°,又∵B D ∠=∠,∴∠D+∠DEB=180°,∴DC ∥AB (同旁内角互补,两直线平行),∴A C ∠=∠(两直线平行,内错角相等);故②正确;③∵A C ∠=∠,∴DC ∥AB (内错角相等,两直线平行),∴B CFB ∠=∠(两直线平行,内错角相等),又∵B D ∠=∠,∴D CFB ∠=∠,∴DE ∥FB (同位角相等,两直线平行),∴13∠=∠(两直线平行,同位角相等),∵2,3∠∠是对顶角,∴23∠∠=,∴12∠=∠(等量替换),故③正确.故D 为答案.【点睛】本题主要考查了直线平行的判定(同位角相等、内错角相等、同旁内角互补,两直线平行)、直线平行的性质、等量替换的相关知识点,掌握直线平行的判定和性质是解题的关键.16.如图,直线,AB CD 相交于点,50,O AOC OE AB ︒∠=⊥,则DOE ∠的大小是( )A .40︒B .50︒C .70︒D .90︒【答案】A【解析】根据对顶角的性质,把BOD ∠的度数计算出来,再结合OE AB ⊥,即可得到答案.【详解】解:∵50AOC ∠=︒,∴50BOD ∠=︒(对顶角相等),又∵OE AB ⊥,∴90EOB ∠=︒,∴905040DOE BOE DOB ∠=∠-∠=︒-︒=︒,故A 为答案.【点睛】本题主要考查了对顶角的性质(对顶角相等),判断,BOD AOC ∠∠是对顶角是解题的关键.17.如图,在ABC V 中,AB AC =,30A ∠=︒,直线a b ∥,顶点C 在直线b 上,直线a 交AB 于点D ,交AC 与点E ,若1145∠=︒,则2∠的度数是( )A .30°B .35°C .40°D .45°【答案】C【解析】【分析】 先根据等腰三角形的性质和三角形内角和可得ACB ∠度数,由三角形外角的性质可得AED ∠的度数,再根据平行线的性质得同位角相等,即可求得2∠.【详解】∵AB AC =,且30A ∠=︒, ∴18030752ACB ∠︒-︒==︒, 在ADE ∆中,∵1145A AED ∠∠∠=+=︒,∴14514530115AED A ∠∠=︒-=︒-︒=︒,∵//a b ,∴2AED ACB ∠∠∠=+,即21157540∠=︒-︒=︒,故选:C .【点睛】本题考查综合等腰三角形的性质、三角形内角和定理、三角形外角的性质以及平行直线的性质等知识内容.等腰三角形的性质定理:等腰三角形两底角相等;三角形内角和定理:三角形三个内角的和等于180 ;三角形外角的性质:三角形的外角等于与它不相邻的两个内角之和;两直线平行,同位角相等.18.下列说法中错误的个数是( )(1)过一点有且只有一条直线与已知直线平行;(2)过一点有且只有一条直线与已知直线垂直;(3)不相交的两条直线叫做平行线;(4)有公共顶点且有一条公共边的两个互补的角互为邻补角.A.1个B.2个C.3个D.4个【答案】C【解析】(1)应强调过直线外一点,故错误;(2)正确;(3)不相交的两条直线叫做平行线,没有说明是否是在同一平面内,所以错误;(4)有公共顶点且有一条公共边的两个角不一定互为邻补角,角平分线的两个角也满足,但可以不是,故错误.错误的有3个,故选C.19.下列图形中线段PQ的长度表示点P到直线a的距离的是()A.B.C.D.【答案】C【解析】【分析】根据点到直线的距离的定义,可得答案.【详解】由题意得PQ⊥a,P到a的距离是PQ垂线段的长,故选C.【点睛】本题考查了点到直线的距离,点到直线的距离是解题关键.20.如图,直线AB,CD相交于点O,∠2-∠1=15°,∠3=130°.则∠2的度数是()A.37.5°B.75°C.50°D.65°【答案】D【解析】【分析】先根据条件和邻补角的性质求出∠1的度数,然后即可求出∠2的度数.【详解】)∵∠3=130°,∠1+∠3=180°,∴∠1=180°-∠3=50°,∵∠2-∠1=15°,∴∠2=15°+∠1=65°;故答案为D.【点睛】本题考查角的运算,邻补角的性质,比较简单.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
