最新勾股定理知识点与常见题型总结
第18章.勾股定理知识点与常见题型总结

第18章 勾股定理复习一.知识归纳 1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方 2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 常见方法如下: 方法一:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证.cbaHG F EDCB A方法二:bacbac cabcab四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证a bcc baE D CBA3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形 4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则cb =,a ②知道直角三角形一边,可得另外两边之间的数量关系 ③可运用勾股定理解决一些实际问题 5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形 6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等 ③用含字母的代数式表示n 组勾股数: 221,2,1n n n -+(2,n ≥n 为正整数); 2221,22,221n n n n n ++++(n 为正整数) 2222,2,m n mn m n -+(,m n >m ,n 为正整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.8..勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论. 9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决. 常见图形:ABC30°D CB A ADB CCB DA题型一:直接考查勾股定理 例1.在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长 ⑵已知17AB =,15AC =,求BC 的长 分析:直接应用勾股定理222a b c +=解:⑴10AB =⑵8BC ==题型二:应用勾股定理建立方程 例2.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD = ⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为 ⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积.有时可根据勾股定理列方程求解 解:⑴4AC , 2.4AC BCCD AB⋅== DBAC⑵设两直角边的长分别为3k ,4k ∴222(3)(4)15k k +=,3k ∴=,54S =⑶设两直角边分别为a ,b ,则17a b +=,22289a b +=,可得60ab =1302S ab ∴==2cm例3.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长21DCBA分析:此题将勾股定理与全等三角形的知识结合起来 解:作DE AB ⊥于E , 12∠=∠,90C ∠=︒ ∴ 1.5DE CD == 在BDE ∆中90,2BED BE ∠=︒=Rt ACD Rt AED ∆≅∆ AC AE ∴=在Rt ABC ∆中,90C ∠=︒222AB AC BC ∴=+,222()4AE EB AC +=+3AC ∴=例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积答案:6题型三:实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 mABCD E分析:根据题意建立数学模型,如图8AB =m ,2CD =m ,8BC =m ,过点D 作DE AB ⊥,垂足为E ,则6AE =m ,8DE =m在Rt ADE ∆中,由勾股定理得10AD答案:10m题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形例6.已知三角形的三边长为a ,b ,c ,判定ABC ∆是否为Rt ∆ ① 1.5a =,2b =, 2.5c = ②54a =,1b =,23c = 解:①22221.52 6.25a b +=+= ,222.5 6.25c ==∴ABC ∆是直角三角形且90C ∠=︒②22139b c +=,22516a =,222bc a +≠ABC ∴∆不是直角三角形 例7.三边长为a ,b ,c 满足10a b +=,18ab =,8c =的三角形是什么形状?解:此三角形是直角三角形理由:222()264a b a b ab +=+-= ,且264c = 222a b c ∴+= 所以此三角形是直角三角形题型五:勾股定理与勾股定理的逆定理综合应用例8.已知ABC ∆中,13AB =cm ,10BC =cm ,BC 边上的中线12AD =cm ,求证:AB AC =证明:D CBAAD 为中线,5BD DC ∴==cm在ABD ∆中,22169AD BD += ,2169AB =222AD BD AB ∴+=, 90ADB ∴∠=︒,222169AC AD DC ∴=+=,13AC =cm ,AB AC ∴=。
初中数学58种模型之31、勾股定理知识点与常见题型总结

勾股定理复习一.知识归纳1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:方法一:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则22c a b =+,22b c a =-,22a cb =-②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等③用含字母的代数式表示n 组勾股数:221,2,1n n n -+(2,n ≥n 为正整数);2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.8..勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论.9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决.常见图形:题型一:直接考查勾股定理例1.在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长⑵已知17AB =,15AC =,求BC 的长分析:直接应用勾股定理222a b c +=解:⑴2210AB AC BC =+=⑵228BC AB AC =-=题型二:应用勾股定理建立方程例2.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD =⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积.有时可根据勾股定理列方程求解解:⑴224AC AB BC =-=, 2.4AC BC CD AB⋅==⑵设两直角边的长分别为3k ,4k ∴222(3)(4)15k k +=,3k ∴=,54S =⑶设两直角边分别为a ,b ,则17a b +=,22289a b +=,可得60ab =1302S ab ∴==2cm 例3.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长分析:此题将勾股定理与全等三角形的知识结合起来解:作DE AB ⊥于E ,12∠=∠,90C ∠=︒∴ 1.5DE CD ==在BDE ∆中2290,2BED BE BD DE ∠=︒=-= Rt ACD Rt AED∆≅∆ AC AE∴=在Rt ABC ∆中,90C ∠=︒222AB AC BC ∴=+,222()4AE EB AC +=+3AC ∴=例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积答案:6题型三:实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了m分析:根据题意建立数学模型,如图8AB =m ,2CD =m ,8BC =m ,过点D 作DE AB ⊥,垂足为E ,则6AE =m ,8DE =m在Rt ADE ∆中,由勾股定理得10AD =答案:10m题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形例6.已知三角形的三边长为a ,b ,c ,判定ABC ∆是否为Rt ∆① 1.5a =,2b =, 2.5c =②54a =,1b =,23c =解:①22221.52 6.25a b +=+= ,222.5 6.25c ==∴ABC ∆是直角三角形且90C ∠=︒②22139b c += ,22516a =,222b c a +≠ABC ∴∆不是直角三角形例7.三边长为a ,b ,c 满足10a b +=,18ab =,8c =的三角形是什么形状?解:此三角形是直角三角形理由:222()264a b a b ab +=+-= ,且264c =222a b c ∴+=所以此三角形是直角三角形题型五:勾股定理与勾股定理的逆定理综合应用例8.已知ABC ∆中,13AB =cm ,10BC =cm ,BC 边上的中线12AD =cm ,求证:AB AC =证明:AD 为中线,5BD DC ∴==cm在ABD ∆中,22169AD BD += ,2169AB =222AD BD AB ∴+=,90ADB ∴∠=︒,222169AC AD DC ∴=+=,13AC =cm ,AB AC ∴=。
勾股定理(知识归纳+题型突破)(原卷版)-2023-2024学年八年级数学上册单元速记巧练

勾股定理(知识归纳+题型突破)1.了解勾股定理的历史,掌握勾股定理的证明方法;2.理解并掌握勾股定理及逆定理的内容;3.能应用勾股定理及逆定理解决有关的实际问题.一、勾股定理1.勾股定理:直角三角形两直角边a b 、的平方和等于斜边c 的平方.(即:222a b c +=)二、勾股定理的逆定理1.勾股定理的逆定理如果三角形的三边长a b c 、、,满足222a b c +=,那么这个三角形是直角三角形.要点:应用勾股定理的逆定理判定一个三角形是不是直角三角形的基本步骤:(1)首先确定最大边,不妨设最大边长为c ;(2)验证:22a b +与2c 是否具有相等关系:若222a b c +=,则△ABC 是以∠C 为90°的直角三角形;若222a b c +>时,△ABC 是锐角三角形;若222a b c +<时,△ABC 是钝角三角形.2.勾股数满足不定方程222x y z +=的三个正整数,称为勾股数(又称为高数或毕达哥拉斯数),显然,以x y z 、、为三边长的三角形一定是直角三角形.要点:常见的勾股数:①3、4、5;②5、12、13;③8、15、17;④7、24、25;⑤9、40、41.如果(a b c 、、)是勾股数,当t 为正整数时,以at bt ct 、、为三角形的三边长,此三角形必为直角三角形.观察上面的①、②、④、⑤四组勾股数,它们具有以下特征:1.较小的直角边为连续奇数;2.较长的直角边与对应斜边相差1.3.假设三个数分别为a b c 、、,且a b c <<,那么存在2a b c =+成立.(例如④中存在27=24+25、29=40+41等)三、勾股定理与勾股定理逆定理的区别与联系区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理;联系:勾股定理与其逆定理的题设和结论正好相反,两者互为逆定理,都与直角三角形有关.四、勾股定理的应用勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用是:(1)已知直角三角形的两边,求第三边;(2)利用勾股定理可以证明有关线段平方关系的问题;(3)解决与勾股定理有关的面积计算;(4)勾股定理在实际生活中的应用.题型一用勾股定理理解三角形【例1】若一个直角三角形的两条直角边长分别是6和8,则斜边长是()A .6B .7C .8D .101.在直角ABC 中,∠B=90°,3AB =,4AC =,则BC 的长为()A .5B .7C .5或7D .5或32.如图,在Rt ABC △中,90A ∠=︒,2BC =,则222AC AB BC ++的值为()A .8B .2C .4D .223.已知直角三角形的两边长分别为5和12,则斜边长是4.如图所示,已知ABC 中,6AB =,9AC =,AD BC ⊥于D ,M 为AD 上任一点,则22MC MB -等于.题型二勾股数【例2】下列各组数中,是勾股数的是()A .0.3,0.4,0.5B .3,7,4C .52,6,132D .9,40,411.下列各组数,是勾股数的一组是()A .8,15,17B .13,14,15C .3,5,7D .2,34,542.《九章算术》提供了许多勾股数如()3,4,5,()5,12,13等一组勾股数最大的数称为“弦数”.经研究,若m 是大于1的奇数,把它平方后拆成相邻的两个整数,那么m 与这两个数组成勾股数,若m 是大于1的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1,得到两个整数,那么m 与这两个数组成勾股数,根据上面的规律,由10生成的勾股数的“弦数”是()A .16B .24C .26D .32题型三勾股定理的逆定理【例3】a ,b ,c 是ABC 的A ∠,B ∠,C ∠的对边,下列条件中,能判断是直角三角形的有()①222+=a b c ②222a b c =-③A B ∠∠=︒+90④123AB C ∠∠∠=∶∶∶∶A .1个B .2个C .3个D .4个1.在ABC 中,A ∠,B ∠,C ∠的对边分别为a ,b ,c ,则下列命题中为假命题的是()A .如果C AB ∠=∠+∠,则ABC 是直角三角形B .如果()()2b c a c a =+-,则ABC 是直角三角形C .如果222a c b -=.则ABC 是直角三角形,且90C ∠=︒D .若523A B C =∠∶∠∶∠∶∶,则ABC 是直角三角形.2.下列由三条线段a 、b 、c 构成的三角形:①2a mn =,22b m n =-,()220c m n m n =+>>,②21a n =+,2221b n n =++,()2220c n n n =+>,③3a k =,4b k =,()50c k k =>,④::1:3:2a b c =,其中能构成直角三角形的有()A .1个B .2个C .3个D .4个题型四勾股定理的逆定理的实际应用【例4】.ABC 的三边分别是a 、b 、c ,且满足2268250a b a b +--+=,5c =,则ABC 的形状是.如图,某住宅小区在施工后留下了一块空地,已知4=AD 米,3CD =米,13AB =米,12BC =米,90ADC ∠=︒,小区为美化环境,欲在空地上铺草坪.若草坪每平方米30元,则用该草坪铺满这块空地需花费多少元?巩固训练:1.为了绿化环境,我市某中学有一块四边形的空地ABCD ,如图所示,学校计划在空地上种植草皮,经测量903m 4m 12m 13m A AB DA BC CD ∠=︒====,,,,.(1)求出空地ABCD 的面积.(2)若每种植1平方米草皮需要300元,问总共需投入多少元?题型五勾股定理与无理数的表示A .7B .8C .9D .101.如图,OA OB =,(1)写出数轴上点A 表示的数;(2)比较点A 表示的数与 1.5-的大小;(3)在数轴上作出5所对应的点.2.如图,在数轴上以1个单位长度画一个正方形,以原点为圆心,以正方形的对角线长为半径画弧,与正半轴的交点为B ,且点B 表示的是一个无理数,因此我们得出一个结论.(1)点B 表示的数为_________;得出的结论是:_________与数轴上的点是一一对应的.(2)若将图中数轴上标的A ,C ,D 各点与所给的三个实数5,3和π-对应起来,则点A 表示的实数为_________,点C 表示的实数为_________,点D 表示的实数为_________.题型六网格问题【例6】.如图,在44⨯的正方形方格图中,小正方形的顶点称为格点,ABC 的顶点都在格点上,则ABC 是三角形.1.如图,在3×3的网格中,每个小正方形的边长均为1,点A ,B ,C 都在格点上,若BD 是ABC 的高,则BD 的长为()A .101313B .191313C .181313D .713132.如图,小正方形边长为1,连接小正方形的三个顶点,可得ABC ,则AC 边上的高长度为()A .355B .3510C .55D .5103.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.(1)在图1中以格点A 为顶点画一个面积为5的正方形ABCD ;(2)①在图2中以格点E 为顶点画一个EFG ,使得2EF =,32EG =,25FG =;②求出EFG 的面积.题型七利用勾股定理证明平方关系【例7】.在ABC 中,A ∠、B ∠、C ∠的对应边分别是a 、b 、c ,若90A C ∠+∠=︒,则下列等式中成立的是()A .222+=a b cB .222b c a +=C .222a c b +=D .222c a b -=1.如图,ABC 中,90BAC ∠=︒,点A 向上平移后到A ',得到A BC ' .下面说法错误的是()A .ABC 的内角和仍为180︒B .BAC BAC '∠<∠C .222AB AC BC +=D .222A B A C BC ''+<2.如图,在ABC 中,AB AC >,AH BC ⊥于H ,M 为AH 上异于A 的一点,比较AB AC -与MB MC -的大小,则AB AC -()MB MC -.A .大于B .等于C .小于D .大小关系不确定题型八、九、十一以直角三角形三边的面积问题、勾股树、以弘图为背景的计算题【例8】.如图是一株美丽的勾股树,图中所有四边形都是正方形,所有的三角形都是直角三角形,若正方形A ,B 的面积分别为5,3,则正方形C 的面积是.【例9】.“勾股树”是以正方形-边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这-过程所画出来的图形,因为重复数次后的形状好似--棵树而得名.假设下图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第五代勾股树中正方形的个数为()A .31B .63C .65D .67【例10】.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD 、正方形EFGH 、正方形MNKT 的面积分别为123S S S 、、.若12318S S S ++=,则2S 的值是()1.如图,在四边形ABCD 中,90ABC ADC ∠=∠=︒,分别以AB BC CD DA ,,,为一边向外作正方形甲、乙、丙、丁,若用S 甲,S 乙,S 丙,S 丁来表示它们的面积,则S S +甲乙S S +丙丁(填>,<或=).2.毕达哥拉斯树也叫“勾股树”,是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树状图形,其中所有的四边形都是正方形,所有的三角形都是直角三角形.如图,若正方形A ,B ,C ,D 的边长分别是2,3,1,2,则正方形G 的边长是()A .8B .22C .32D .5A .125B .6C .5D .1543.如图,有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,就变成了如图所示的形状,若继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2023次后形成的图形中所有的正方形的面积和是()A .2024B .2023C .2022D .14.勾股定理是数学定理中证明方法最多的定理之一,也是用代数思想解决几何问题最重要的工具之一.下列图形中可以证明勾股定理的有()A .①③B .②③C .②④D .①④5.如图,在四边形ABDE 中,AB DE ∥,AB BD ⊥,点C 是边BD 上一点,BC DE a ==,CD AB b ==.AC CE c ==.下列结论;①ABC CDE △≌△;②90ACE ∠=︒;③四边形ABDE 的面积是()2212a b +;④()2221112222a b c ab +-=⨯;⑤该图可以验证勾股定理.其中正确的结论个数是()A .5B .4C .3D .26.意大利著名画家达·芬奇用一张纸片剪拼出不一样的空洞,而两个空洞的面积是相等的,如图所示,证明了勾股定理,若设图1中空白部分的面积为1S ,图2中空白部分的面积为2S ,则下列对1S ,2S 所列等式不正确的是()A .2212S a b ab =++B .22S c ab =+C .12S S =D .222+=a b c 7.勾股定理又称毕达哥拉斯定理、商高定理、新娘座椅定理、百牛定理等,是人类早期发现并证明的重要数学定理之一,大约有五百多种证明方法,我国古代数学家赵爽和刘徽也分别利用《赵爽弦图》和《青朱出入图》证明了勾股定理,以下四个图形,哪一个是赵爽弦图()A .B .C .D .题型十一勾股定理的实际应用题【例11】.如图,A ,C 之间隔有一湖,在与AC 方向成90︒角的CB 方向上的点B 处测得500m AB =,400m BC =,则AC 的长为()A .300mB .400mC .500mD .600m巩固训练:1.海洋热浪对全球生态带来了严重影响,全球变暖导致华南地区汛期更长、降水强度更大,使得登录广东的台风减少,但是北上的台风增多.如图,一棵大树在一次强台风中距地面5m 处折断,倒下后树顶端着地点A 距树底端B 的距离为12m ,这棵大树在折断前的高度为()A .10mB .15mC .18mD .20m2.如图,圆柱的底面周长为6,高为4,蚂蚁在圆柱表面爬行,从点A 爬到点B 的最短路程是()A .213B .5C .13D .103.将一根长为17cm 的筷子,置于内径为6cm 高为8cm 的圆柱形水杯中,设筷子露在杯子外面的长度为x cm ,则x 的取值范围是()A .68x ≤≤B .79x ≤≤C .810x ≤≤D .911x ≤≤4.一棵高10m 的大树倒在了高8m 的墙上,大树的顶端正好落在墙的最高处,如果随着大树的顶端沿着墙面向下滑动,请回答下列各题.(1)如果大树的顶端沿着墙面向下滑动了2m ,那么大树的另一端点是否也左滑动了2m ?说明理由.(2)如果大树的顶端沿着墙面向下滑动了m a ,那么大树的另一端点是否也左滑动了m a ?说明理由.5.如图,圆柱形玻璃杯高为16cm ,底面周长为40cm ,在杯内壁离杯底4cm 的点B 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm 且与蜂蜜相对的点A 处,则蚂蚁从外壁A 处到内壁B 处的最短距离为()cm .(杯壁厚度不计)A .20B .25C .30D .406.为了积极响应国家新农村建设的号召,遂宁市某镇政府采用了移动宣讲的形式进行广播宣传.如图,笔直的公路MN 的一侧点A 处有一村庄,村庄到公路MN 的距离为600m ,假使宣讲车P 周围1000m 以内能听到广播宣传,宣讲车P 在公路MN 上沿PN 方向行驶.(1)村庄能否听到广播宣传?请说明理由.(2)已知宣讲车的速度是200m /min ,如果村庄能听到广播宣传,那么总共能听多长时间?7.在海平面上有A ,B ,C 三个标记点,其中A 在C 的北偏西54︒方向上,与C 的距离是800海里,B 在C 的南偏西36︒方向上,与C 的距离是600海里.(1)求点A 与点B 之间的距离;(2)若在点C 处有一灯塔,灯塔的信号有效覆盖半径为500海里,每隔半小时会发射一次信号,此时在点B 处有一艘轮船准备沿直线向点A 处航行,轮船航行的速度为每小时20海里.轮船在驶向A 处的过程中,最多能收到多少次信号?(信号传播的时间忽略不计).题型十二勾股定理的折叠问题【例12】.如图所示,在ABC 中,∠B=90°,3AB =,5AC =,将ABC 折叠,使点C 与点A 重合,折痕为DE ,则ABE 的周长是()A .7B .7.5C .8D .73+1.如图,在Rt ABC △中,90C ∠=︒,5cm AB =,3cm BC =,D 为AC 上的一点,将BCD △沿BD 折叠,使点C 恰好落在AB 上的点E 处,求AD 的长.2.如图,将一张正方形纸片ABCD 对折,使CD 与AB 重合,得到折痕MN 后展开,E 为CN 上一点,将CDE 沿DE 所在的直线折叠,使得点C 落在折痕MN 上的点F 处,连接AF .若2AB =,则CE 的长度为()A .423-B .23-C .12D .31-题型十三勾股定理的解答证明题【例13】.如图,已知在ABC 中,CD AB ⊥于点D ,20AC =,15BC =,9DB =.(1)求AD 的长;(2)求证:ABC 是直角三角形.1.如图,AC 是四边形ABCD 的对角线,25456890.AB BC AD CD B ====∠=︒,,,,(1)试判断ADC △的形状,并说明理由;(2)求四边形ABCD 的面积.2.在ABC 中,90ACB ∠=︒,AC BC =,D ,E 是边AB 上两点,45DCE ∠=︒.(1)求证:222AD BE DE +=;(2)若2EB AD =,求DE AD的值.3.用四个全等的直角三角形拼成如图①所示的大正方形,中间也是一个正方形,它是美丽的弦图,其中四个直角三角形的直角边长分别为a 、()b a b <,斜边长为c .(1)结合图①,求证:222+=a b c .(2)如图②,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH .若该图形的周长为24,3OB =.求该图形的面积.4.如图,ABC 的周长为425+,其中4AB =,53BC =-.(1)AC =______;(2)判断ABC 是否为直角三角形,并说明理由.(3)过点A 作AE AB ⊥,22AE =,在AB 上取一点D ,使得DB DE =,求AD 的长度.5.阅读材料:一般地,设平面上任意两点()11,A x y 和()22,B x y ,可以用AB 表示,A B 两点之间的距离,那么该如何计算AB 呢?作AA x '⊥轴、作BB x '⊥轴,垂足分别是点A B ''、;作AA y ''⊥轴,垂足为点A ''、作BB y ''⊥轴,垂足为点B '',且与AA '交于点C ,则四边形BB A C ACB A ''''''、是矩形.∵2121,BC x x AC y y =-=-∴()()222222121||||||AB AC BC x x y y =+=-+-,∴()()222121AB x x y y =-+-.这就是平面直角坐标系中两点之间的距离公式.如:点()1,4A 和点()5,2B 之间的距离22(51)(24)2025AB =-+-==.(1)请运用公式计算点()4,2M 和点()2,1N -之间的距离;(2)在(1)的条件下,点O 为原点,求MNO 的周长.。
勾股定理知识点+类型+题型有答案版
勾股定理知识点知识点一:勾股定理如果直角三角形的两直角边长分别为:a,b,斜边长为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方.要点诠释:(1)勾股定理揭示的是直角三角形平方关系的定理。
(2)勾股定理只适用于直角三角形,而不适用于锐角三角形和钝角三角。
(3)勾股定理的一些变式:c2=a2+b2, a2=c2-b2, b2=c2-a2, c2=(a+b)2-2ab知识点二:用面积证明勾股定理方法一:将四个全等的直角三角形拼成如图(1)所示的正方形。
图(1)中,所以。
方法二:将四个全等的直角三角形拼成如图(2)所示的正方形。
图(2)中,所以。
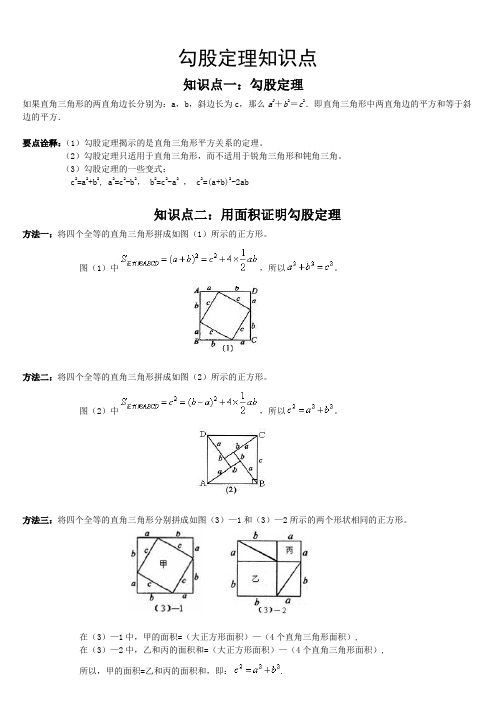
方法三:将四个全等的直角三角形分别拼成如图(3)—1和(3)—2所示的两个形状相同的正方形。
在(3)—1中,甲的面积=(大正方形面积)—(4个直角三角形面积),在(3)—2中,乙和丙的面积和=(大正方形面积)—(4个直角三角形面积),所以,甲的面积=乙和丙的面积和,即:.方法四:如图(4)所示,将两个直角三角形拼成直角梯形。
,所以。
知识点三:勾股定理的作用1.已知直角三角形的两条边长求第三边;2.已知直角三角形的一条边,求另两边的关系;3.用于证明平方关系的问题;4.利用勾股定理,作出长为的线段。
知识点四:勾股数满足不定方程x2+y2=z2的三个正整数,称为勾股数(又称为高数或毕达哥拉斯数),显然,以x,y,z为三边长的三角形一定是直角三角形。
熟悉下列勾股数,对解题有很大帮助:①3、4、5②5、12、13;③8、15、17;④7、24、25;⑤10、24、26;⑥9、40、41.②如果(a,b,c)是勾股数,当t>0时,以at,bt,ct为三角形的三边长,此三角形必为直角三角形。
勾股定理考查类型类型一:勾股定理的直接用法在Rt△ABC中,∠C=90°(1)已知a=6, c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a.思路点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。
初中八年级的上第一章勾股定理学习知识点与常见题型总结计划及练习.docx

八年级上第一章勾股定理知识点与常见题型总结及练习一.知识归纳1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为 a ,b,斜边为 c ,那么 a 2b2c22 .勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法DC b a A aDH a cb bcEc GF cb c E bca aaA cB a b B bC3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC 中, C 90 ,则c a2b2, b c2a2, ac2b2②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5 .勾股定理的逆定理如果三角形三边长 a ,b, c 满足 a2b2c2,那么这个三角形是直角三角形,其中 c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和a2b2与较长边的平方 c2 作比较,若它们相等时,以 a ,b, c 为三边的三角形是直角三角形;若a2b2c2,时,以 a ,b, c 为三边的三角形是钝角三角形;若 a 2b2c2,时,以 a ,b, c 为三边的三角形是锐角三角形;②定理中 a ,b, c 及 a2b2c2只是一种表现形式,不可认为是唯一的,如若三角形三边长 a ,b, c 满足a2c2b2,那么以 a ,b, c 为三边的三角形是直角三角形,但是 b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6 .勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即 a 2 b 2c2中, a ,b, c 为正整数时,称 a ,b, c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5 ; 6,8,10 ; 5,12,13 ; 7,24,25 等③用含字母的代数式表示n 组勾股数:n21,2n, n2 1 ( n2, n 为正整数);2n1,2n22n,2n 2 2 n 1 ( n 为正整数)m2n2 ,2 mn,m2n 2(m n, m,n为正整数)7.勾股定理的应用8..勾股定理逆定理的应用9 .勾股定理及其逆定理的应用CCC30°A DB B DAA B B二、常见考题分析题型一:直接考查勾股定理例1 .在ABC 中, C 90.⑴已知 AC 6 , BC 8 .求 AB 的长⑵已知 AB 17, AC15 ,求 BC 的长分析:直接应用勾股定理222a b c题型二:应用勾股定理建立方程例2 .⑴在ABC中,ACB90 , AB5cm ,BC 3 cm ,CD AB于D,CD=⑵已知直角三角形的两直角边长之比为3:4,斜边长为 15,则这个三角形的面积为⑶已知直角三角形的周长为30 cm,斜边长为 13 cm,则这个三角形的面积为分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积.列方程求解例3 .如图ABC中,C90,1 2,CD 1.5,BD 2.5,求AC的长CD1A2E B分析:此题将勾股定理与全等三角形的知识结合起来例 4.如图Rt ABC,C90 AC3,BC 4 ,分别以各边为直径作半圆,求阴影部分面积CAB题型三:实际问题中应用勾股定理例 5.如图有两棵树,一棵高8 cm,另一棵高 2 cm,两树相距 8 cm,一只小鸟从一棵树至少飞了mA8、如 ,一 直角三角形的 片,两直角AC=6㎝, BC=8㎝。
勾股定理知识点与常见题型总结

勾股定理知识点与常见题型总结大正方形面积为所以方法三:,,化简得证3、勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形4、勾股定理的应用①已知直角三角形的任意两边长,求第三边在中,,则,,②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5、勾股定理的逆定理如果三角形三边长,,满足,那么这个三角形是直角三角形,其中为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和与较长边的平方作比较,若它们相等时,以,,为三边的三角形是直角三角形;若,时,以,,为三边的三角形是钝角三角形;若,时,以,,为三边的三角形是锐角三角形;②定理中,,及只是一种表现形式,不可认为是唯一的,如若三角形三边长,,满足,那么以,,为三边的三角形是直角三角形,但是为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6、勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即中,,,为正整数时,称,,为一组勾股数②记住常见的勾股数可以提高解题速度,如;;;等③用含字母的代数式表示组勾股数:(为正整数);(为正整数)(,为正整数)7、勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题、在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解、8、、勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论、9、勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体、通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决、常见图形:题型一:直接考查勾股定理例1、在中,、⑴已知,、求的长⑵已知,,求的长分析:直接应用勾股定理解:⑴⑵题型二:应用勾股定理建立方程例2、⑴在中,,,,于,=⑵已知直角三角形的两直角边长之比为,斜边长为,则这个三角形的面积为⑶已知直角三角形的周长为,斜边长为,则这个三角形的面积为分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积、有时可根据勾股定理列方程求解解:⑴,⑵设两直角边的长分别为,,,⑶设两直角边分别为,,则,,可得例3、如图中,,,,,求的长分析:此题将勾股定理与全等三角形的知识结合起来解:作于,,在中在中,,例4、如图,,分别以各边为直径作半圆,求阴影部分面积答案:6题型三:实际问题中应用勾股定理例5、如图有两棵树,一棵高,另一棵高,两树相距,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了分析:根据题意建立数学模型,如图,,,过点作,垂足为,则,在中,由勾股定理得答案:题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形例6、已知三角形的三边长为,,,判定是否为①,,②,,解:①,是直角三角形且②,,不是直角三角形例7、三边长为,,满足,,的三角形是什么形状?解:此三角形是直角三角形理由:,且所以此三角形是直角三角形题型五:勾股定理与勾股定理的逆定理综合应用例8、已知中,,,边上的中线,求证:证明:为中线,在中,,,,,,。
勾股定理知识点与常见题型总结,强列推荐
第18章勾股定理复习一.知识归纳1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222ab c勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:方法一:4EFGHSS S 正方形正方形ABCD ,2214()2abba c ,化简可证.cbaHG F EDCBA方法二:bacbaccabcab四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422Sab cab c大正方形面积为222()2Sa b aab b所以222abc方法三:1()()2S a b ab 梯形,2112S 222ADE ABES Sabc 梯形,化简得证a bccbaE D CBA3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC 中,90C,则22cab ,22bca ,22acb②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222abc ,那么这个三角形是直角三角形,其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22ab 与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a bc ,时,以a ,b ,c 为三边的三角形是钝角三角形;若222abc ,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222abc 只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222acb ,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222abc 中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等③用含字母的代数式表示n 组勾股数:221,2,1nn n(2,n n 为正整数);2221,22,221n n n nn (n 为正整数)2222,2,mn mn mn (,m n m ,n 为正整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.8..勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论.9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决.常见图形:ABC30°DCBAADBCCBDA题型一:直接考查勾股定理例1.在ABC 中,90C.⑴已知6AC ,8BC.求AB 的长⑵已知17AB ,15AC ,求BC 的长分析:直接应用勾股定理222abc解:⑴2210ABAC BC ⑵228BCABAC题型二:应用勾股定理建立方程例2. ⑴在ABC 中,90ACB,5ABcm ,3BCcm ,CDAB 于D ,CD =⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积.有时可根据勾股定理列方程求解解:⑴224ACABBC, 2.4AC BC CDABDBAC⑵设两直角边的长分别为3k ,4k222(3)(4)15k k ,3k ,54S ⑶设两直角边分别为a ,b ,则17a b ,22289ab,可得60ab1302Sab2cm例3.如图ABC 中,90C,12, 1.5CD , 2.5BD,求AC 的长21EDCBA分析:此题将勾股定理与全等三角形的知识结合起来解:作DEAB 于E ,12,90C 1.5DE CD在BDE 中2290,2BED BE BDDERt ACD Rt AEDACAE在Rt ABC 中,90C222ABACBC ,222()4AEEB AC3AC 例4.如图Rt ABC ,90C3,4AC BC ,分别以各边为直径作半圆,求阴影部分面积BAC答案:6题型三:实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了mABCD E分析:根据题意建立数学模型,如图8ABm ,2CD m ,8BC m ,过点D 作DE AB ,垂足为E ,则6AEm ,8DEm在Rt ADE 中,由勾股定理得2210ADAEDE答案:10m题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形例6.已知三角形的三边长为a ,b ,c ,判定ABC 是否为Rt ① 1.5a,2b, 2.5c ②54a ,1b ,23c 解:①22221.526.25ab,222.56.25cABC 是直角三角形且90C ②22139bc,22516a,222b caABC 不是直角三角形例7.三边长为a ,b ,c 满足10a b,18ab,8c的三角形是什么形状?解:此三角形是直角三角形理由:222()264a b a b ab,且264c222abc所以此三角形是直角三角形题型五:勾股定理与勾股定理的逆定理综合应用例8.已知ABC 中,13ABcm ,10BC cm ,BC 边上的中线12AD cm ,求证:ABAC证明:DCBAAD 为中线,5BD DC cm 在ABD 中,22169ADBD,2169AB222ADBDAB ,90ADB,222169AC AD DC,13AC cm ,ABAC。
(word完整版)勾股定理知识点总结及练习,推荐文档
勾股定理知识总结一.基础知识点:1:勾股定理直角三角形两直角边a、b的平方和等于斜边c的平方。
(即:a2+b2=c2)要点诠释:勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:(1)已知直角三角形的两边求第三边(在ABC∆中,90C∠=︒,则c=,b=,a=)(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边(3)利用勾股定理可以证明线段平方关系的问题2:勾股定理的逆定理如果三角形的三边长:a、b、c,则有关系a2+b2=c2,那么这个三角形是直角三角形。
要点诠释:勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时应注意:(1)首先确定最大边,不妨设最长边长为:c;(2)验证c2与a2+b2是否具有相等关系,若c2=a2+b2,则△ABC是以∠C为直角的直角三角形(若c2>a2+b2,则△ABC是以∠C为钝角的钝角三角形;若c2<a2+b2,则△ABC为锐角三角形)。
(定理中a,b,c及222a b c+=只是一种表现形式,不可认为是唯一的,如若三角形三边长a,b,c满足222a c b+=,那么以a,b,c为三边的三角形是直角三角形,但是b为斜边)3:勾股定理与勾股定理逆定理的区别与联系区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理;联系:勾股定理与其逆定理的题设和结论正好相反,都与直角三角形有关。
规律方法指导1.勾股定理的证明实际采用的是图形面积与代数恒等式的关系相互转化证明的。
2.勾股定理反映的是直角三角形的三边的数量关系,可以用于解决求解直角三角形边边关系的题目。
3.勾股定理在应用时一定要注意弄清谁是斜边谁直角边,这是这个知识在应用过程中易犯的主要错误。
4. 勾股定理的逆定理:如果三角形的三条边长a,b,c有下列关系:a2+b2=c2,•那么这个三角形是直角三角形;该逆定理给出判定一个三角形是否是直角三角形的判定方法.5.•应用勾股定理的逆定理判定一个三角形是不是直角三角形的过程主要是进行代数运算,通过学习加深对“数形结合”的理解.5:勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:方法一:4EFGHS S S∆+=正方形正方形ABCD,2214()2ab b a c⨯+-=,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c=⨯+=+大正方形面积为222()2S a b a ab b=+=++所以222a b c+=cb aHGFEDCBAcb aHGFEDCBAbacbaccabcab6:勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25;8,15,17;9,40,41等勾股定理练习一.填空题:1. 在Rt △ABC 中,∠C=90°(1)若a=5,b=12,则c=________; (2)b=8,c=17,则S △ABC =________。
勾股定理知识点总结归纳与经典习题型归纳
精心整理
-来源网络
勾股定理
知识点
1.勾股定理:直角三角形两直角边的平方和等于斜边的平方.即222a b c +=
2.勾股定理逆定理:若三角形的三边长,,a b c 满足222a b c +=,则这个三角形是直角三角形.
3.常见的勾股数:3,4,5;5,12,13;7,24,25;8,15,17;9,12,15.
注意:勾股数的任意倍还是勾股数. 1_cm___2.在1直角三角形纸片,两直角边B 与点A 2.如图,已知,将它的锐角BC 边3为DE 4EF ,则△1体的底面周长为2__25___.
34个侧面4.如图,圆柱形玻璃杯,高为12cm ,底面周长为18cm ,在杯内离杯底3cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离的平方是多少?
解:如图,将杯子侧面展开,作A 关于EF 的对称点A′,连接A′C 即为最短距离.A′C 2=A ′D 2+CD 2=92+132=250(cm 2).
1.如图5,∠OAB =∠OBC =∠OCD =90°,AB =BC =CD =1,OA =2,则2OD =__7__.
2.一个三角形的三边长之比为5∶12∶13,它的周长为60,则它的面积是__120_.
精心整理
-来源网络。
勾股定理(题型归纳)(解析版)
勾股定理的性质应用【思维导图】◎考点题型1:用勾股定理解三角形例.(2022·全国·八年级课前预习)直角△ABC 的两直角边BC =12,AC =16,则△ABC 的斜边AB 的长是( ) A .20 B .10C .9.6D .8【答案】A 【解析】 略变式1.(2021·山东沂源·七年级期中)已知ABC 中,10AB AC ==,BD 是AC 边上的高线,2DC=,那么BD等于()A.2B.4C.6D.8【答案】C【解析】【分析】由题意根据已知可求得AD的长,再根据勾股定理即可求得BD的长.【详解】解:∵AB=AC=10,DC=2,∴AD= AC-DC=8,∴6BD.故选:C.【点睛】本题主要考查勾股定理的应用,熟练掌握直角三角形勾股定理是解题的关键.变式2.(2022·全国·八年级)已知,Rt△ABC中,∠A=90°,AB=4,BC=5,AC边的长为()A.3B C.3D【答案】A【解析】【分析】根据勾股定理求解即可.【详解】解:如图所示,∵∠A=90°,AB=4,BC=5,∴3AC =. 故选:A . 【点睛】此题考查了勾股定理的运用,解题的关键是熟练掌握勾股定理.勾股定理:在直角三角形中,两条直角边的平方和等于斜边的平方.变式3.(2021·山东章丘·八年级期中)直角三角形的边长分别为a ,b ,c ,且∠C =90°,若a 2=9,b 2=16,那么c 2的值是( ) A .5 B .7C .25D .49【答案】C 【解析】 【分析】根据勾股定理,即可求解. 【详解】解:∵直角三角形的边长分别为a ,b ,c ,且∠C =90°, ∴c 2=a 2+b 29+16=25, 故选C . 【点睛】本题主要考查勾股定理,掌握直角三角形中,直角边的平方和等于斜边长的平方,是解题的关键.◎考点题型2:求两点间的距离例.(2022·甘肃玉门·八年级期末)点P (-3,4)到坐标原点的距离是( ) A .3 B .4C .-4D .5【答案】D 【解析】 【分析】利用两点之间的距离公式即可得. 【详解】解:点(3,4)P -到坐标原点(0,0)5=, 故选:D . 【点睛】本题考查了两点之间的距离公式,熟练掌握两点之间的距离公式是解题关键.变式1.(2022·河北·宽城满族自治县教研室八年级期末)如图,数轴上点A 对应的数是0,点B 对应的数是1,BC AB ⊥,垂足为B ,且2BC =,以A 为圆心,AC 为半径画弧,交数轴于点D ,则点D 表示的数为( )A .2.2BCD 【答案】D 【解析】 【分析】首先根据勾股定理求出AC 的长,再根据同圆的半径相等可知AD =AC ,再根据条件:点A 对应的数是原点,可求出D 点坐标. 【详解】解:∵BC AB ⊥, ∴ABC ∠=90︒,∴AC =∵以A 为圆心,AC 为半径画弧,交数轴于点D ,∴AD AC ==,∴点D 故选D . 【点睛】此题考查实数与数轴,勾股定理,解题关键是利用勾股定理求出AC .变式2.(2021·湖南永兴·八年级期末)关于点P (﹣3,4),下列说法正确的个数有( )(1)点P到x轴的距离为4;(2)点P到y轴的距离为﹣3;(3)点P在第四象限;(4)点P到原点的距离为5;(5)点P关于x轴的对称点的坐标是(﹣3,﹣4).A.2个B.3个C.4个D.5个【答案】B【解析】【分析】根据已知点所在象限,画出图形,进而分析得出答案.【详解】解:如图所示:(1)点P到x轴的距离为4,故(1)正确;(2)点P到y轴的距离为3,故(2)错误;(3)点P在第二象限,故(3)错误;(4)点P到x轴的距离为4,点P到y轴的距离为3,根据勾股定理可得,点P到原点的距离为5,故(4)正确;(5)点P关于x轴的对称点的坐标是(﹣3,﹣4),故(5)正确.所以正确的个数有3个.故选:B.【点睛】本题主要考查了点的坐标,正确确定P点位置是解题关键.变式3.(2021·广东·高州市长坡中学八年级期中)在直角坐标系中,点A(3,2)到原点的距离是()B C D.2A【解析】【分析】根据勾股定理求解即可.【详解】解:如图,AB⊥x轴于点B,∵A(3,2),∴OB=3,AB=2,∴OA∴点A(3,2故选:C.【点睛】本题考查的是勾股定理,利用勾股定理求解是解答此题的关键.◎考点题型3:勾股数问题例.(2022·福建省福州第十六中学八年级期末)在下列四组数中,不是..勾股数的一组是()A.15,8,7B.4,5,6C.24,25,7D.5,12,13【答案】B【解析】【分析】利用勾股数的定义(勾股数就是可以构成一个直角三角形三边的一组正整数),最大数的平方=最小数的平方和,直接判断即可.【详解】解:A、222+=,故A不符合题意.8715B、222+≠,故B符合题意.456C、222+=,故C不符合题意.72425D、222+=,故D不符合题意.51213【点睛】本题主要是考查了勾股数的判别,熟练掌握勾股数的定义,是求解该题的关键.变式1.(2022·甘肃会宁·八年级期末)下列各组数,是勾股数的是()A.13,14,15B.0.3,0.4,0.5C.6,7,8D.5,12,13【答案】D【解析】【分析】根据能够成为直角三角形三条边长的三个正整数,称为勾股数,即可求解【详解】解:A、不是正整数,则不是勾股数,故本选项不符合题意;B、不是正整数,则不是勾股数,故本选项不符合题意;C、222678+≠,则不是勾股数,故本选项不符合题意;D、2225+12=13,是勾股数,故本选项符合题意;故选:D【点睛】本题主要考查了勾股数的定义,熟练掌握能够成为直角三角形三条边长的三个正整数,称为勾股数是解题的关键.变式2.(2021·江苏江都·八年级阶段练习)下列各组数中,是勾股数的是()A2B.0.3 0.4 0.5,,C.5,12,13D.9,12,13【答案】C【解析】【分析】根据勾股数的定义,对选项逐个判断即可,勾股数是指满足222+=a b c的正整数.【详解】解:A和B不是正整数,不符合题意;C、22251213+=,且为正整数,为勾股数,符合题意;D、22291222513+=≠,不是勾股数,不符合题意;故选:C【点睛】此题考查了勾股数的判断,解题的关键是掌握勾股数的定义.变式3.(2021·陕西莲湖·八年级期中)下列四组数中,是勾股数的是()A.5,12,13B.32,42,52C.1D.7,24,26【答案】A【解析】【分析】、、为勾股数.根据勾股数的概念求解即可,满足222a b c的正整数a b c+=【详解】解:A、∵222+=,∴5,12,13是勾股数,符合题意;51213B、∵22≠,∴32,42,52不是勾股数,不符合题意;52=2704,27882704+,23227842=8C1D、22≠,∴7,24,26不是勾股数,不符合题意;72462526=676,625676+=,2故选A【点睛】此题考查了勾股数的判断,解题的关键是熟练掌握勾股数的概念.◎考点题型4:以直角三角形的三边长为边的三角形的面积例.(2021·福建福安·八年级期中)图中字母A所代表的正方形的面积为().A.64B.8C.16D.6【答案】A【解析】【分析】根据勾股定理和正方形的性质即可得出结果.【详解】解:根据勾股定理以及正方形的面积公式知:以直角三角形的两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,所以A=289-225=64.故选:A.【点睛】本题考查了勾股定理,以及正方形的面积公式,勾股定理最大的贡献就是沟通“数”与“形”的关系,它的验证和利用都体现了数形结合的思想,即把图形的性质问题转化为数量关系的问题来解决.能否由实际的问题,联想到用勾股定理的知识来求解是本题的关键.变式1.(2021·四川东坡·八年级期中)如图,黑色部分长方形的面积为()A.24B.30C.40D.48【答案】B【解析】【分析】根据勾股定理求出直角三角形的斜边,再利用长方形面积公式进行求解即可.【详解】解:在直角三角形中,两直角边为6和8,=,10⨯=,∴长方形面积为:10330故选B.【点睛】本题考查了勾股定理的应用,长方形面积的计算,解题的关键是熟练掌握勾股定理.变式2.(2021·江西乐平·八年级期中)如图,分别以直角三角形的三条边向外部作了三个正方形A、B、C,已知正方形A的面积是67cm2,正方形C的面积是100cm2,那么,正方形B的面积是()A.33cm2B.36cm2C.43cm2D.50cm2【答案】A【解析】【分析】根据勾股定理得出三个正方形A 、B 、C 之间的面积关系,然后代入数据求解即可. 【详解】解:如图,设直角三角形三边分别为:a ,b ,c , 则由勾股定理得:222+=a b c ,∴三个正方形的面积之间关系为:A B C S S S +=,∵267cm A S =,2100cm C S =,∴21006733cm B C A S S S =-=-=,故选:A .【点睛】本题考查勾股定理的运用,理解并熟练运用勾股定理是解题关键.变式3.(2021·浙江·温州市南浦实验中学八年级期中)如图,在Rt △ABC 中,∠ACB =90°,分别以AB ,BC ,AC 为边向外作三个正方形,已知其中两个正方形面积分别为25,169,则正方形M 的面积为( )A .100B .144C .154D .194【答案】B 【解析】 【分析】根据勾股定理和正方形的面积公式即可得到结论. 【详解】解:在Rt △ABC 中,∠ACB =90°, ∴AC 2=AB 2﹣BC 2=169﹣25=144, ∴正方形M 的面积为144,【点睛】本题考查了勾股定理,正方形的面积,熟练掌握勾股定理是解题的关键.◎考点题型5:勾股定理与网格问题例.(2021·广东清新·八年级期中)如图,大正方形是由4个小正方形组成,小正方形的边长为2,连接小正方形的三个顶点,得到△ABC ,则△ABC 的面积为( )A .4B .6C .8D .10【答案】B 【解析】 【分析】 根据题意可得ABCS =S 正方形DEF A -ADC CEB ABF S S S --△△△,代入求解即可.【详解】 如图所示,∵大正方形是由4个小正方形组成,小正方形的边长为2, ∴由题意可得, ABCS=S 正方形DEF A -ADC CEB ABF S S S --△△△11122211144422242222164246AD DE AD CD CE BE AF BF =---=⨯-⨯⨯-⨯⨯-⨯⨯=---=【点睛】此题考查了割补法求三角形面积,解题的关键是根据题意正确得到ABCS =S 正方形DEF A -ADC CEB ABF S S S --△△△.变式1.(2021·广西·南宁市第八中学八年级阶段练习)如图,△ABC 的顶点A ,B ,C 在边长为1的正方形网格的格点上,则BC 边长的高为( )A B C D 【答案】B 【解析】 【分析】求出△ABC 的面积,根据勾股定理求出BC 长,利用面积公式求解即可. 【详解】解:∵11134232124222ABC S ∆=⨯-⨯⨯-⨯⨯-⨯⨯=4,∵BC∴BC=, 故选:B . 【点睛】此题考查勾股定理和三角形面积公式,解题关键是会用三角形面积公式求高,利用勾股定理求出边长.变式2.(2021·辽宁铁东·八年级期中)如图,在由边长均为1的小正方形组成的4×4网格中,将连接任意两个格点的线段称作“格点线”,则“格点线”的长度不可能为( )A.5B C D【答案】B【解析】【分析】根据题意和各个选项中的数据,可以得到哪个数据不可能是“格点线”的长度,从而可以解答本题.【详解】解:∵5可能是“格点线”的长度,故选项A不符合题意;“格点线”的长度,故选项B符合题意;“格点线”的长度,故选项C不符合题意;“格点线”的长度,故选项D不符合题意.故选:B【点睛】本题考查勾股定理,解答本题的关键是明确题意,利用勾股定理的知识解答.变式3.(2020·陕西·西安市黄河中学八年级阶段练习)如图,网格中的每个小正方形的边长为1,四边形的顶点A,B,C,D都在格点上,则下面5)A.AB B.BC C.CD D.AD【答案】D【解析】【分析】根据勾股定理求得每条线段的长度即可.【详解】解:AB BC=3,CD=ADAD,故选:D.【点睛】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.◎考点题型6:勾股定理与折叠问题例.(2021·山东·滕州市大坞镇大坞中学九年级阶段练习)已知,如图长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.3B.4C.6D.12【答案】C【解析】【分析】首先翻折方法得到ED=BE,再设出未知数,分别表示出线段AE,ED,BE的长度,然后在Rt△ABE 中利用勾股定理求出AE的长度,知道AE的长度后,就可以利用面积公式求得△ABE的面积了.【详解】解:∵长方形折叠,使点B与点D重合,∴ED=BE,设AE=x cm,则ED=BE=(9-x)cm,在Rt△ABE中,AB2+AE2=BE2,∴32+x2=(9-x)2,解得:x=4,= 6(cm2),∴△ABE的面积为:3×4×12故选C.本题考查了利用勾股定理解直角三角形的能力:直角三角形两直角边的平方和等于斜边的平方.变式1.(2021·浙江浙江·八年级期中)如果将长为6cm,宽为5cm的矩形纸片折叠一次,那么这条折痕的长不可能是()A.8cm B.C.5.5cm D.3cm【答案】A【解析】【分析】根据勾股定理计算出最长折痕即可作出判断.【详解】,故折痕长不可能为8cm.故选:A.【点睛】本题考查了折叠问题,勾股定理,根据勾股定理计算后即可做出选择,难度不大.变式2.(2019·河南卧龙·七年级期末)如图,在△ABC中,AB=10,AC=6,BC=8,将△ABC折叠,使点C落在AB边上的点E处,AD是折痕,则△BDE的周长为()A.6B.8C.12D.14【答案】C【解析】【分析】利用勾股定理求出AB=10,利用翻折不变性可得AE=AC=6,推出BE=4即可解决问题.【详解】在Rt△ABC中,∵AC=6,BC=8,∠C=90°,∴AB=10,由翻折的性质可知:AE=AC=6,CD=DE,∴△BDE 的周长=DE +BD +BE =CD +BD +E =BC +BE =8+4=12. 故选:C . 【点睛】本题考查翻折变换,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型. 变式3.(2021·江苏江都·八年级阶段练习)如图,有一张直角三角形纸片,90ACB ∠=︒,5cm AB =,3cm AC =,现将ABC ∆折叠,使边AC 与AB 重合,折痕为AE ,则CE 的长为( )A .1cmB .2cmC .3cm 2D .5cm 2【答案】C 【解析】 【分析】先根据勾股定理求出BC 的长度,再由折叠的性质可得CE=DE ,设CE x =,然后在Rt BDE 中利用勾股定理即可求出x 的值. 【详解】∵90ACB ∠=︒,5cm AB =,3cm AC =∴4BC ==由折叠可知CE=DE,AC=AD ,90ADE ACE ∠=∠=︒ 设CE x =,则4,2,BE x BD AB AD =-=-= 在Rt BDE 中 ∵222DE BD BE +=∴2222(4)x x +=-解得32x = 故选C本题主要考查勾股定理,掌握勾股定理的内容及方程的思想是解题的关键.◎考点题型7:利用勾股定理求两条线段的平方的和或差例.(2018·全国·八年级单元测试)在Rt △ABC 中,斜边BC=10,则BC 2+AB 2+AC 2等于( ) A .20 B .100C .200D .144【答案】C 【解析】 【分析】根据勾股定理得出,AB 2+AC 2= BC 2,即可求出答案 【详解】∵在Rt △ABC 中,斜边BC =10 ∴AB 2+AC 2= BC 2=100∴BC 2+AB 2+AC 2=100+100=200 故答案为C 【点睛】此题考查了勾股定理的基本运用,三边平方关系是解决此题的关键变式1.(2021·贵州六盘水·八年级阶段练习)在△ABC 中,∠C =90°,AB =3,则AB 2+BC 2+AC 2的值为( ) A .6 B .9C .12D .18【答案】D 【解析】 【分析】根据90C ∠=︒,利用勾股定理可得222AB BC AC =+,据此求解即可. 【详解】解:如图示,90C ∠=︒∴在Rt ABC 中,222AB BC AC =+∴222222222318AB BC AC AB AB AB =+==+=+⨯, 故选:D . 【点睛】本题主要考查了勾股定理的性质,掌握直角三角形中,三角形的三边长a ,b ,c 满足222+=a b c 是解题的关键.变式2.(2021·全国·八年级课时练习)在Rt ABC △中,90C ∠=︒,10AB =,则2222AB AC BC ++=( ).A .100 B .200C .300D .400【答案】C 【解析】 【分析】根据题意90C ∠=︒,那么AB 就为斜边,则根据勾股定理可得:222AC BC AB +=,那么原式则为23AB ,再将AB 的值代入即可求出答案.【详解】解:∵在Rt ABC △中,且90C ∠=︒, ∴AB 为Rt ABC △的斜边,∴根据勾股定理得:222AC BC AB +=, ∴2222223310300AB AC BC AB ++==⨯=, 故选:C . 【点睛】本题主要考查了勾股定理,正确对应斜边并能灵活运用勾股定理是解题的关键.变式3.(2021·江苏滨海·八年级期中)如图,在ABC ∆中,90C ∠=︒,4AC =,2BC =.以AB 为一条边向三角形外部作正方形,则正方形的面积是( )A .8B .12C .18D .20【答案】D 【解析】 【分析】根据勾股定理解得2AB 的值,再结合正方形的面积公式解题即可. 【详解】在ABC ∆中,90C ∠=︒,4AC =,2BC =,222224220AB AC BC ∴=+=+=∴以AB 为一条边向三角形外部作的正方形的面积为220AB =,故选:D . 【点睛】本题考查勾股定理的应用,是重要考点,难度较易,掌握相关知识是解题关键.◎考点题型8:利用勾股定理证明线段平方关系例.(2021·江苏兴化·八年级期中)对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD ,点E 为对角线BD 上任意一点,连接AE 、CE . 若AB =5,BC =3,则AE 2-CE 2等于( )A .7B .9C .16D .25【答案】C 【解析】 【分析】连接AC ,与BD 交于点O ,根据题意可得AC BD ⊥,在在Rt AOE 与Rt COE 中,利用勾股定理可得2222AE CE AO CO -=-,在在Rt AOB 与Rt COB 中,继续利用勾股定理可得2222AO CO AB BC -=-,求解即可得.【详解】解:如图所示:连接AC ,与BD 交于点O ,∵对角线互相垂直的四边形叫做“垂美”四边形, ∴AC BD ⊥,在Rt AOE 中,222AE AO OE =+, 在Rt COE 中,222CE CO OE =+, ∴2222AE CE AO CO -=-, 在Rt AOB 中,222AO AB OB =-, 在Rt COB 中,222CO BC OB =-, ∴2222225316AO CO AB BC -=-=-=, ∴2216AE CE -=, 故选:C . 【点睛】题目主要考查勾股定理的应用,理解题意,熟练运用勾股定理是解题关键.变式1.(2021·全国·八年级课时练习)如图,在ABC 中,AB AC >,AH BC ⊥于H ,M 为AH 上异于A 的一点,比较AB AC -与MB MC -的大小,则AB AC -( )MB MC -.A .大于B .等于C .小于D .大小关系不确定【答案】C 【解析】 【分析】由题意得,AB 2=AH 2+BH 2,AC 2=AH 2+HC 2,则AB 2−AC 2=BH 2−HC 2,同理有MB 2−MC 2=BH 2−HC 2,则AB 2−AC 2=MB 2−MC 2.再根据平方差公式即可求解. 【详解】解:∵AH ⊥BC ,有AB 2=AH 2+BH 2,AC 2=AH 2+HC 2,∴AB 2−AC 2=BH 2−HC 2,又∵MH ⊥BC ,同理有MB 2−MC 2=BH 2−HC 2, ∴AB 2−AC 2=MB 2−MC 2,即(AB +AC )(AB −AC )=(MB +MC )(MB −MC ), 又∵M 点在△ABC 内,∵AB +AC >MB +MC , 则AB −AC <MB −MC . 故选C . 【点睛】本题考查了勾股定理,解题的关键是熟知勾股定理及平方差公式的应用.变式2.(2019·江苏·常熟市第一中学八年级阶段练习)在ABC 中,A ∠、B 、C ∠的对应边分别是a 、b 、c ,若90A C ∠+∠=︒,则下列等式中成立的是( ) A .222+=a b c B .222b c a +=C .222a c b +=D .222c a b -=【答案】C 【解析】 【分析】由已知两角之和为90度,利用三角形内角和定理得到三角形为直角三角形,利用勾股定理即可得到结果. 【详解】解:∵在ABC 中,90A C ∠+∠=︒, ∴90B ∠=︒,∴ABC 为直角三角形, 则根据勾股定理得:222a c b +=. 故选:C . 【点睛】此题考查了勾股定理,熟练掌握勾股定理是解题的关键.变式3.(2020·江苏东台·八年级阶段练习)在ABC 中,∠BAC=90°,则下列结论成立的是( ) A .BC=AC+BC B .AC 2=AB 2+BC 2 C .AB 2=AC 2+BC 2 D .BC 2 =AB 2+AC 2【答案】D 【解析】【分析】根据勾股定理即可求解. 【详解】解:在 △ ABC 中,∠BAC =90°,根据勾股定理可得222BC AB AC =+, 故选:D . 【点睛】本题考查勾股定理,掌握勾股定理的内容是解题的关键.◎考点题型9:勾股定理的证明方法例.(2022·全国·八年级)勾股定理与黄金分割并称为几何学中的两大瑰宝勾股定理的发现可以称为是数学史上的里程碑,2000多年来,人们对它进行了大量的研究,至今已有几百种证法.利用图形中有关面积的等量关系可以证明勾股定理,利用如图①的直角三角形纸片拼成的②③④⑤四个图形中,可以证明勾股定理的图形有( )A .1个B .2个C .3个D .4个【答案】C 【解析】 【分析】利用面积与恒等式,②中矩形面积等于两个直角三角形面积之和,都为ab ,无法证明勾股定理; ③中梯形面积等于两个直角边分别为a ,b 的直角三角形与一个直角边为c 的等腰直角三角形面积之和;④中大正方形的面积等于4个小直角三角形面积与一个小正方形面积之和;⑤中大正方形的面积等于4个小直角三角形面积与一个小正方形面积之和,即可求解. 【详解】解:根据题意得:②中矩形面积等于两个直角三角形面积之和,都为ab ,无法证明勾股定理; ③中梯形面积等于两个直角边分别为a ,b 的直角三角形与一个直角边为c 的等腰直角三角形面积之和,即()221112222a b ab c +=⨯+ ,整理得:222+=a b c ,可以证得勾股定理;④中大正方形的面积等于4个小直角三角形面积与一个小正方形面积之和,即 ()22142c ab b a =⨯+- ,整理得:222+=a b c ,可以证得勾股定理;⑤中大正方形的面积等于4个小直角三角形面积与一个小正方形面积之和,即()22142a b ab c +=⨯+, 整理得:222+=a b c ,可以证得勾股定理; 所以可以证明勾股定理的图形有③④⑤,共3个. 故选:C 【点睛】本题主要考查了勾股定理的证明,熟练掌握梯形,正方形的面积的不同求法是解题的关键. 变式1.(2021·山东梁山·八年级期末)如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD ,正方形EFGH ,正方形MNPQ 的面积分别为S 1,S 2,S 3,若S 1+S 2+S 3=45,则S 2的值是( )A .12B .15C .20D .25【答案】B 【解析】 【分析】设每个小直角三角形的面积为m ,则S 1=4m +S 2,S 3=S 2﹣4m ,依据S 1+S 2+S 3=60,可得4m +S 2+S 2+S 2﹣4m =60,进而得出S 2的值. 【详解】解:设每个小直角三角形的面积为m ,则S 1=4m +S 2,S 3=S 2﹣4m , ∵S 1+S 2+S 3=45, ∴4m +S 2+S 2+S 2﹣4m =45, 即3S 2=45, 解得S 2=15.故选B . 【点睛】本题主要考查了勾股定理和正方形、全等三角形的性质的运用,证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用大图形的面积等于几个小图形的面积和化简整理得到勾股定理.变式2.(2021·河北·临漳县教育体育局教研室八年级期中)勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中不能证明勾股定理的是( )A .B .C .D .【答案】D 【解析】 【分析】利用两个以a 和b 为直角边三角形面积与一个直角边为c 的等腰直角三角形面积和等于上底为a,下第为b,高为(a+b)的梯形面积推导勾股定理可判断A ,利用以a 与b 为两直角边四个全等三角形面积与边长为c 的小正方形面积和等于以a+b 的和为边正方形面积推导勾股定理可判断B ,利用以a 与(a+b )为两直角边四个全等三角形面积与边长为b 的小正方形面积和等于以c 为边正方形面积推导勾股定理可判断C ,利用四个小图形面积和等于大正方形面积推导完全平方公式可判断D . 【详解】解: A 、两个以a 和b 为直角边三角形面积与一个直角边为c 的等腰直角三角形面积和等于上底为a,下第为b,高为(a+b)的梯形面积,故()2211112222ab ab c a b ++=+,整理得: 222a b c +=,即能证明勾股定理,故本选项不符合题意;B 、以a 与b 为两直角边四个全等三角形面积与边长为c 的小正方形面积和等于以a+b 的和为边正方形面积,故()22142ab c a b ⨯+=+,整理得: 222a b c +=,即能证明勾股定理,故本选项不符合题意;C 、以a 与(a+b )为两直角边四个全等三角形面积与边长为b 的小正方形面积和等于以c 为边正方形面积,()22142a ab bc ⨯++=,整理得: 222a b c +=,即能证明勾股定理,故本选项不符合题意;D 、四个小图形面积和等于大正方形面积,()2222ab a b a b ++=+ ,根据图形证明完全平方公式,不能证明勾股定理,故本选项符合题意; 故选:D . 【点睛】本题考查利用面积推导勾股定理与完全平方公式,掌握利用面积推导勾股定理与完全平方公公式是关键.变式3.(2019·山东·青岛大学市北附属中学八年级阶段练习)如图1是边长分别为,a b 的两个正方形,经如图2所示的割补可以得到边长为c 的正方形,且面积等于割补前的两正方形的面积之和.利用这个方法可以推得或验证勾股定理.现请你通过对图2的观察指出下面对割补过程的理解不正确的是( )A .割⑤补⑥B .割③补①C .割①补④D .割③补②【答案】B 【解析】 【分析】根据图2所示可以判断如何剪拼能够拼成正方形. 【详解】 解:由题意可得:要拼成一个正方形,应当割⑤补⑥,割①补④,割③补②, 故选B . 【点睛】本题主要考查了图形的设计,正确理解小正方形的面积的和等于拼成的正方形的面积是解题的关键.◎考点题型10:以弦图为背景的计算题例.(2021·北京·北方工业大学附属学校八年级期中)如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x ,y 表示直角三角形的两直角边(x >y ),则下列四个说法:①x 2+y 2=49,②x ﹣y =2,③2xy +4=49,④x +y =9. 其中说法正确的是( )A .②③B .①②③C .②④D .①②④【答案】B 【解析】 【分析】根据正方形的性质,直角三角形的性质,直角三角形面积的计算公式及勾股定理解答即可. 【详解】 如图所示,∵△ABC 是直角三角形,∴根据勾股定理:22249x y AB +==,故①正确;由图可知2x y CE -===,故②正确;由图可知,四个直角三角形的面积与小正方形的面积之和为大正方形的面积, 列出等式为144492xy ⨯⨯+=,即2449xy +=,故③正确; 由2449xy +=可得245xy =,又∵2249x y +=,两式相加得:2224945x xy y ++=+,整理得:()294x y +=,9x y +=≠,故④错误;故正确的是①②③. 故答案选B . 【点睛】本题主要考查了勾股定理的应用,正方形性质,完全平方公式的应用,算术平方根,准确分析判断是解题的关键.变式1.(2022·北京房山·八年级期末)如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它被第24届国际数学家大会选定为会徽,是国际数学界对我国古代数学伟大成就的肯定.“弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,若直角三角形的两条直角边分别为a 、b ,大正方形边长为3,小正方形边长为1,那么ab 的值为( )A .3B .4C .5D .6【答案】B 【解析】 【分析】根据大正方形的面积是9,小正方形的面积是1,可得直角三角形的面积,即可求得ab 的值. 【详解】解:∵大正方形边长为3,小正方形边长为1, ∴大正方形的面积是9,小正方形的面积是1, ∴一个直角三角形的面积是(9-1)÷4=2, 又∵一个直角三角形的面积是12ab =2, ∴ab =4. 故选:B . 【点睛】本题考查了与弦图有关的计算,还要注意图形的面积和a ,b 之间的关系.变式2.(2022·山西襄汾·八年级期末)如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中90ABC ∠=︒,13cm AC =,5cm AB =,则阴影部分的面积是( )2cmA .169B .25C .49D .64【答案】C 【解析】 【分析】先利用勾股定理求出12BC =,再利用大正方形的面积减去四个全等直角三角形的面积即可得. 【详解】解:90ABC ∠=︒,13cm AC =,5cm AB =,12(cm)BC ∴,则阴影部分的面积是211313451249(cm )2⨯-⨯⨯⨯=,故选:C . 【点睛】本题考查了勾股定理、全等三角形的性质,熟练掌握勾股定理是解题关键.变式3.(2021·吉林珲春·八年级期中)我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a 、b (b >a ),则(a +b )2的值为( ).A .24B .25C .49D .13【答案】C 【解析】 【分析】根据勾股定理,可得2225a b += ,再由四个全等的直角三角形的面积之和等于大正方形的面积减去小正方形的面积,可得224ab = ,然后利用完全平方公式,即可求解. 【详解】解:根据题意得:2225a b += ,四个全等的直角三角形的面积之和为25124-= ,∴14242ab ⨯= ,即224ab = ,∴()2222252449a b a b ab +=++=+= . 故选:C 【点睛】本题主要考查了勾股定理,完全平方公式的应用,勾股定理,完全平方公式是解题的关键.◎考点题型11:用勾股定理构造图形解决问题例.(2021·吉林朝阳·八年级期末)如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm ,内壁高12cm .若这支铅笔长为18cm ,则这只铅笔在笔筒外面部分长度不可能的是( )A .3cmB .5cmC .6cmD .8cm【答案】D 【解析】 【分析】当铅笔不垂直于底面放置时,利用勾股定理可求得铅笔露出笔筒部分的最小长度;考虑当铅笔垂直于笔筒底面放置时,铅笔在笔筒外面部分的长度是露出的最大长度;从而可确定答案. 【详解】15(cm)=,则铅笔在笔筒外部分的最小长度为:18−15=3(cm);当铅笔垂直于笔筒底面放置时,铅笔在笔筒外面部分的长度为18−12=6(cm ),即铅笔在笔筒外面最长不超过6cm ,从而铅笔露出笔筒部分的长度不短于3cm ,不超过6cm .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理
一.知识归纳 1.勾股定理
内容:直角三角形两直角边的平方和等于斜边的平方;
表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=
勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方 2.勾股定理的证明
勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是 ①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 常见方法如下:
方法一:4EFGH S S S ∆+=正方形正方形ABCD ,221
4()2
ab b a c ⨯+-=,化简可证.
c
b
a
H
G F E
D
C
B A
方法二:
b
a
c
b
a
c c
a
b
c
a
b
四个直角三角形的面积与小正方形面积的和等于大正方形的面积.
四个直角三角形的面积与小正方形面积的和为221
422S ab c ab c =⨯+=+
大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=
方法三:1()()2S a b a b =+⋅+梯形,211
2S 222
ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证
a b
c
c b
a
E D C
B
A
3.勾股定理的适用范围
勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形 4.勾股定理的应用 ①已知直角三角形的任意两边长,求第三边
在ABC ∆中,90C ∠=︒
,则c
,b
,a
②知道直角三角形一边,可得另外两边之间的数量关系 ③可运用勾股定理解决一些实际问题 5.勾股定理的逆定理
如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边 ①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形; ②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边 ③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形 6.勾股数 ①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数 ②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等 ③用含字母的代数式表示n 组勾股数: 221,2,1n n n -+(2,n ≥n 为正整数); 2221,22,221n n n n n ++++(n 为正整数) 2222,2,m n mn m n -+(,m n >m ,n 为正整数)
7.勾股定理的应用
勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.
8..勾股定理逆定理的应用
勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体
推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论. 9.勾股定理及其逆定理的应用
勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决. 常见图形:
A
B
C
30°D C
B A A
D
B C
C
B D
A
题型一:直接考查勾股定理 例1.在ABC ∆中,90C ∠=︒.
⑴已知6AC =,8BC =.求AB 的长 ⑵已知17AB =,15AC =,求BC 的长 分析:直接应用勾股定理222a b c +=
解:⑴10AB =
⑵8BC
题型二:应用勾股定理建立方程 例2.
⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD = ⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为 ⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为
分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积.有时可根据勾股定理列方程求解 解:
⑴4AC , 2.4AC BC
CD AB
⋅=
= D
B
A
C
⑵设两直角边的长分别为3k ,4k ∴222(3)(4)15k k +=,3k ∴=,54S =
⑶设两直角边分别为a ,b ,则17a b +=,22289a b +=,可得60ab =1
30
2
S ab ∴==2cm
例3.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长
2
1
D
C
B
A
分析:此题将勾股定理与全等三角形的知识结合起来 解:作DE AB ⊥于E , 12∠=∠,90C ∠=︒ ∴ 1.5DE CD == 在BDE ∆中
90,2BED BE ∠=︒ Rt ACD Rt AED ∆≅∆ AC AE ∴=
在Rt ABC ∆中,90C ∠=︒
222AB AC BC ∴=+,222()4AE EB AC +=+3AC ∴=
例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积
答案:6
题型三:实际问题中应用勾股定理
例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 m
A
B
C
D E
分析:根据题意建立数学模型,如图8AB =m ,2CD =m ,8BC =m ,过点D 作DE AB ⊥,垂足为E ,则6AE =m ,8DE =m
在Rt ADE ∆
中,由勾股定理得10AD
答案:10m
题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形
例6.已知三角形的三边长为a ,b ,c ,判定ABC ∆是否为Rt ∆
① 1.5a =,2b =, 2.5c = ②54a =,1b =,2
3c =
解:①22221.52 6.25a b +=+= ,222.5 6.25c ==
∴ABC ∆是直角三角形且90C ∠=︒
②22139b c +=
,22516
a =,222
b
c a +≠ABC ∴∆不是直角三角形 例7.三边长为a ,b ,c 满足10a b +=,18ab =,8c =的三角形是什么形状? 解:此三角形是直角三角形
理由:222()264a b a b ab +=+-= ,且264c = 222a b c ∴+= 所以此三角形是直角三角形
题型五:勾股定理与勾股定理的逆定理综合应用
例8.已知ABC ∆中,13AB =cm ,10BC =cm ,BC 边上的中线12AD =cm ,求证:AB AC =
证明:
D C
B
A
AD 为中线,5BD DC ∴==cm
在ABD ∆中,22169AD BD += ,2169AB =222AD BD AB ∴+=, 90ADB ∴∠=︒,222169AC AD DC ∴=+=,13AC =cm ,AB AC ∴=。
