公路路面不平度的数值模拟方法研究
基于功率谱密度的路面不平整度数值模拟

e - 2  ̄ f . m a a At
( , ) 。 ( f ) e - Z , : , d t l
【 3 1
l
l 2 =
一 2 7 t n m _ i l
2At X
=
( 4 )
式中: x 为x Ⅲ 的离散傅里 叶变换 ( m= 0 , 1 …N 一 1 o 以上分析推导 出离散 时间信号 与离 散功率谱 密度之 间的相关 关系, 按照式( 4 ) 即可计算得出离散功率谱 密度 G  ̄ ( f 3 。 3采样 与 混淆
・
5 6・
科 技 论 坛
基于功率谱 密度 的路 面不平整度数值模 拟
寸
任思润
雒 晓 东
( 西 安 市 政设 计研 究 院有 限公 司 . 陕 西 西安 7 1 0 0 6 8 )
摘 要: 路 面不平整是 引起车辆振动进而导致车辆对路 面产生 附加动载 的主要原 因。为了了解路 面不平整对车辆动力特性的影响 , 采 用基 于离散傅里叶逆 变换的方法 , 首先将路面功率谱 密度进行 离散 , 然后模 拟路 面的不平顺情况。模 拟 出的路 面不平整信 号的功率谱
r _ o。 : 、
由式( 6 ) 确定出合适的 △ f 和L 后, 即可得 出频率分辨率为 采样点总数 为 一 。根据傅里叶变换可得 :
△f
—
l i mX r f t ) =x ( t 1 。 此时, 存在傅里叶变换对:
’
( , ) = e ( ¨ e - 2  ̄ : , d t
Ⅳ ≥ 壶 ’ 正 号
,
( 6 )
引 起 激 励 的 位移 或加 速 度 响应 极 小 , 所 以 在 积分 计算 过 程 中 不 需 要 波叠加法 、 积分 单 位 白噪 声 法 、 滤波器整形 白噪声法和 A R MA模 型 考虑这些频率范围的影响 。 设路面有效空间频率范围的上下限分别 法等 , 这些所得到的路面不平整度与实际情况都有较大差别 。本文 为n 、 n 。 , 常用 的车速 为 v , 车辆 固有频率 为 , f 0 , 路 面不平度空 间频 采用 基于离散傅里 叶逆变换 的方 法 , 首先将路面功率谱密度进行离 率为 n , 则频率 f 与 n的关系为 f = v n 。所以: 散, 然后模拟路面的不平顺情况。 2功率谱 密度的离散化
关于路面不平度重构的研究
T NOLO GY TR N D[摘要]通过对GB7031-1986建议的公路路面功率谱密度的拟合表达式进行研究,可以得出采用谐波叠加法进行模拟得到的路面不平度所对应的功率谱密度可以很好地逼近目标谱的结论。
[关键词]谐波叠加;路面不平度;仿真在进行汽车动力响应分析和平顺性研究中,时域路面模型日益受到重视,因为路面输人模型能否准确的反映实际研究的路面对分析研究的准确性有着根本的影响。
所以,建立合理的路面输人模型是进行汽车平顺性和操稳性研究需首先解决的问题之一。
对于时域内的路面激励(也即路面不平度或高程)可以利用路面不平度数据和汽车行驶速度获得,获得方法有:1)试验测试方法;2)将给定的路面功率谱密度变换为路面不平度。
本文通过对GB7031-1986建议的公路路面功率谱密度的拟合表达式进行研究后,采用谐波叠加法进行模拟得到的路面不平度所对应的功率谱密度可以很好地逼近目标谱。
1路面不平度的功率谱密度的描述根据国际标准化组织文件,功率谱密度G q (n )可以用下式作为拟合表达式:G q (n )=G q (n 0)(n n 0)-W(1)式中,n 为空间频率,其带宽为[n 1,n 2],分别为有效频带的上限和下限,带宽的确定应保证汽车在一平均速度行驶时,不平度引起的振动要包括汽车振动的主要固有频率;n 0(0.1m -1)为参考空间频率;G q (n 0)为参考空间频率下的路面功率谱密度,称为路面不平度系数,数据取决于公路的路面等级;W 为频率指数,为双对数坐标上斜线的频率,它决定路面功率谱密度的频率结构,分级路面铺的频率指数W =2。
国际标准化组织提出了把路面的不平度分为8级。
表1列举出了部分等级路面的功率谱密度值及几何平均值。
表1路面不平度8级分类标准2谐波叠加算法模拟路面不平度2.1谐波叠加法模型的建立谐波叠加法是将随机激励表示成大量具有随机相位的正弦或余弦之和。
本文采用余弦谐波叠加法生成路面不平度仿真数据,其主要思想就是将路面不平度表示成大量具有随机相位的余弦级数之和。
路面不平度的模拟与汽车非线性随机振动的研究报告

清华大学学报自然科学版JOURNALOF TSINGHUAUNIVERSITY SCIENCEANDTECHNOLOGY1999年第39卷第8期Vol.39 No.81999路面不平度的模拟与汽车非线性随机振动的研究*金睿臣,宋健文摘预测汽车的随机振动响应对汽车的开发设计是非常重要的。
实际汽车存在许多非线性环节,需采用非线性振动模型进行研究,在这种情况下,通常采用的频域分析方法一般不再适用。
应用机械系统分析软件ADAMS建立了11自由度汽车非线性振动模型,并用由伪白噪声法生成的符合实际路面统计特性的伪随机序列来模拟路面不平度。
在此基础上,利用数值算法在时域中对汽车的非线性随机振动响应进行了计算机仿真计算研究。
结果表明,这种方法对研究汽车的非线性随机振动是有效的。
关键词汽车动力学;ADAMS软件;非线性随机振动;路面不平度分类号U 461;O 322Simulation of the road irregularity and study of nonlinear randomvibration of the automobileJIN Ruichen,SONG JianDepartment of Automotive Engineering,State Key Laboratory of Automotive Safety and Energy Conservation,Tsinghua University,Beijing 100084,China Abstract To use the simulation technique is very important to predict the random vibration of the automobile.Because there are many nonlinear factors in a real automobile,a nonlinear vibration model should be necessarily used.In this case,the frequency domain methods can not be applicable.Under the help of the mechanical system simulation program ADAMS,an 11 DOF nonlinear vibration model of the automobile was built.By means of pseudo white noise,pseudo random sequences,which can simulate the random irregularities of a road,were generated.Based on these,using numerical method,the random vibration of the automobile was studied.The results of simulation have demonstrated the validity of the method.Key words vehicle dynamics;program ADAMS;nonlinear random vibration; road irregularities汽车以一定的速度行驶时,路面的随机不平度通过轮胎、悬架等弹性、阻尼元件传递到车身上,并通过座椅将振动传递到人体。
路面不平度数学模型的研究进展

杨益 明 刘奕贯 ( 南京交通职业技术学院, 南京 2 18) 118
【 摘要】 分别阐 述了 路面不平度的功率谱分析模型、 时间序列分析模型、 分形分析模型及小波分析模
型, 对每一种路面模型进行 了系统评价 , 并指 出了路面不平度研究发展方向。
的分析 方法 , 时域 分 析 方 法 有 利 于 导 出 良好 的 用
控制律 。
1 1 三角级 数法 .
从 理论上 讲 , 意 一 条路 面轨 迹 均 可 由一 系 任 列 离散 的正 弦波叠 加 而成 。假 如 已知 路 面频 域模 型 , 么每个 正 弦 波 的振 幅 可 由相 应 频 率 的频 率 那
进行傅 立 叶 逆 变 换 , 而 得 到 路 面 不平 度值 。其 进 路 面模 型 为 :
N
—
—
q = I t
,
( =0 1 m , …N 一1 )
() 4
式 中 ,为前 、 轮激 励输 人 点位 置 ;为 左 、 i 后 . 右 轮 激励输 入点位 置 ; 随机 路 面 激励 ;t 与路 q O为 面等 级 有 关 的 常 数 ; V为 车 速 ; 为 零 均 值 的
【 主题词】 振动系统
路面不平度
汽车
线性 或耦合 动力学 分 析 , 时 , 此 时域 分析 是 最基 本
0 引言
路 面不平 度 是 车 辆振 动 系 统 的 主要 振 源 , 它 使车辆 在行驶 中产 生 行驶 阻力 和振 动 。汽 车 的平
顺性是 车体 对 路 面 激 励 的综 合 反 映 , 平 路 面 的 不
1 2 线性 滤 波 白噪声 法 .
般性 路面 的激励 为 随机过程 , 把路 面纵 剖 面
整车路面不平度激励的仿真方法研究

整车路面不平度激励的仿真方法研究徐东镇;张祖芳;夏公川【摘要】Analysis of road surface roughness on the three axle vehicle random excitation input, using white noise method and the transfer function method is used to derive the vehicle six rounds of road roughness input state equations are obtained. In Matlab/Simulink to build a two-dimensional pavement roughness mathematical model, and standard pavement roughness the comparison and validation, indicating the accuracy of the model to build. Through the vehicle state equation to build six rounds of pavement roughness mathematical model. The simulation results show that the with the axle of the power density of the two wheels of the spectrum differences, on the same side of the front and rear wheels of power density spectrum difference of smaller, more in line with the actual situation of multi vehicle bridge heavy truck and in order to further validate the simulation results, the correlation coefficient of the road roughness of the six round of the vehicle is analyzed, and the results are consistent with the above conclusions.%分析了路面不平度对三轴式整车的随机激励输入,利用白噪声法和传递函数法推导得出整车六轮路面不平度输入的状态方程。
路面不平度的数值模拟与测量

路面不平度的数值模拟与测量路面不平度的数值模拟与测量引言:路面不平度是指道路表面的高低起伏或凹凸不平的程度,是衡量道路平整度和舒适性的重要指标。
路面不平度对于车辆行驶安全和驾驶员的舒适感受都有较大影响。
因此,精确的路面不平度模拟与测量方法对于道路设计、养护以及交通安全具有重要意义。
一、数值模拟数值模拟是一种利用计算机科学与技术手段对真实现象进行仿真与模拟的方法。
在路面不平度的数值模拟中,研究者一般将路面分割为小网格,并基于路面几何、弹性力学等理论,通过计算机程序模拟车辆行驶中与路面不平度的相互作用过程。
1.1 路面几何模型在路面不平度模拟中,首先要建立路面几何模型。
常用的模型有横向几何模型和纵向几何模型。
横向几何模型是指路面在横向方向上的曲率变化规律,包括平面曲率和横向坡度等信息。
纵向几何模型是指路面在纵向方向上的高低起伏规律,通常用高程和纵向坡度描述。
1.2 路面材料模型路面不平度的模拟需要考虑路面材料的物理特性,包括弹性模量、泊松比、厚度等。
通过分析路面材料的应力、应变关系,可以计算得到车辆在不同材料上行驶时的反应。
1.3 车辆模型在路面不平度模拟中,车辆模型是一个重要的因素。
车辆模型通常包括车身、轮胎、悬挂系统等。
不同车型对路面不平度的响应不同,因此需要根据实际情况选择合适的车辆模型进行模拟。
二、测量方法测量路面不平度的方法有多种,包括直接测量方法和间接测量方法。
直接测量方法是指直接对路面进行测量,如高程测量、采样测量等。
2.1 高程测量高程测量是指通过使用高程仪、激光测距仪等设备直接获取路面高程信息的方法。
高程测量可以快速获取路面的高低起伏,但缺点是测量范围有限,准确度较低。
2.2 采样测量采样测量是指通过在路面上采集样本,然后利用实验室设备对路面样本进行分析与测试的方法。
常用的采样方法有岩心采样和拓样等。
采样测量可以获得路面材料的物理力学性质,从而更好地了解路面不平度的形成原因。
2.3 间接测量方法间接测量方法是指通过车辆或传感器等设备间接测量路面不平度信息的方法。
基于IFFT法的路面不平度时域模拟方法

基于IFFT法的路面不平度时域模拟方法作者:鲍家定伍建伟王瀚超莫秋云来源:《现代电子技术》2016年第20期摘要:路面不平度时域模拟方法存在模拟精度低下等问题。
考虑到IFFT法能够精确而又简单地重构道路的时域模型,是一种普适性的方法,其具有计算量小、计算简单高效等的特点,可为后续车辆动力学仿真分析提供实时的时域模型。
基于IFFT法(逆快速傅里叶变换法)进行路面不平度的时域模拟,总结了IFFT法时域模拟的五个步骤,并利用Matlab语言开发了基于该方法的时域模拟函数。
通过与标准的功率谱密度曲线比较,其吻合程度高,表明该方法是正确可靠的,同时也说明了模拟参数选取的合理性。
关键词:路面不平度; IFFT;时域模拟; Matlab;功率谱密度中图分类号: TN911.71⁃34; U461.4 文献标识码: A 文章编号: 1004⁃373X(2016)20⁃0008⁃04Abstract: Currently, there are some problems in the time⁃domain simulation of road roughness, such as low simulation precision. Therefore, IFFT (inverse fast Fourier transform)is used to do time⁃domain simulation of road roughness because it can reconstruct time⁃domain model of road accurately and simply. It has the characteristics of small computational amount,simple calculation, etc. The time⁃domain simulation of road roughness was performed on the basis of IFFT method. Five steps of the time⁃domain simulation of IFFT method were summarized. The time⁃domain simulation function based on the method was developed with Matlab language. In comparison with the standard power spectral density curve, its match degree is high, which shows that the method is right and reliable, and also illustrates the rationality of the simulation parameter.Keywords: road roughness; IFFT; time⁃domain simulation; Matlab; power spectral density随着人们对汽车平顺性的要求不断提高,研究人员逐渐认识到汽车振动系统非线性动力学分析的重要性,纷纷通过建立非线性动力学模型来提高平顺性仿真的精度和优化的质量。
关于路面不平度测量研究

关于路面不平度测量研究摘要:随着传感器技术、计算机技术和信号处理技术的飞速发展,人们对路面不平度的采集、测量和各种试验方法也在不断的更新和改进。
近年来,这一领域已经涌现出了多种测量和试验分析的新方法。
本文分析了传统路面不平度的测试方法,为行内探讨提供参考或借鉴。
关键词:路面不平度;测量;仪器引言:路面不平度是指道路表面相对于理想参考平面的偏离。
近年来,随着对公路服务质量要求的不断提高及路面管理系统的不断发展,随着传感器技术、计算机技术和信号处理技术的飞速发展,人们对路面不平度的采集、测量和试验的方法也在不断的更新和改进,这一领域陆续出现了多种测量和试验分析的新方法。
一、国内路面不平度测量历史与现状国内于20 世纪60 年代开始路面不平度的测量与研究。
1965 年,长春汽车研究所用标杆法测量了江苏、安徽等省的若干公路的路面不平度,并进行了谱估计。
70 年代以来,一汽和吉林大学合作,在路面测量和统计分析方面作了较深入的工作,并完成了海南试验场可靠性跑道的设计与构筑。
目前,较为完善的中国道路路谱数据相对匮乏,但其在汽车研发阶段的作用日益受到各大汽车公司的关注。
早在1988 年,为了使富康轿车能够适应中国的道路条件和使用条件,中法双方专家就共同组织了在中国不同地区的行驶试验,包括多种地形、多种路况,记录了大量试验数据通过对试验过程记录数据的分析,中法专家对将要引进的产品提出了30 项改进意见,以适应中国的道路条件和使用条件。
1996 年,美国通用公司派专家测量了中国的部分路谱,根据路谱统计结果对上海通用公司生产的轿车的悬挂系统做了改进。
近些年,一些企业、大学进行了越来越多的道路谱数据测量工作。
从2008 年8 月起,国家“863”计划资助的项目开始在全国大范围内进行道路谱数据采集,旨在结合实际道路特点,测量道路谱信息、地理信息以及视频信息,建立道路谱数据库,实现室内道路模拟等。
数据采集及应用流程如图1 所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
器整形白噪声法[5] 以及利用 ARMA 模型的方法[2] 等 ,这些方法所得路面不平度对应的功率谱密度 与给定的功率谱密度相比都存在一定误差. 文献 [6 ]研究了利用基于频域功率谱采样的数值模拟 方法对铁路轨道的随机不平度进行的研究 ,在此 文献的基础上 , 本文通过对 GB703121986[7] 建议 的公路路面功率谱密度的拟和表达式进行研究 , 在分析了所关心的汽车固有振动频率和行驶速度 的影响后 ,获得分布在一定频率范围内的离散功 率谱密度数据 ,利用计算 、分析获得路面不平度的 离散傅立叶变换 ,进而利用离散傅立叶逆变换得 到路面不平度值. 通过对整个过程以及算例进行 分析 ,可以得出 :这种方法思路明确 、便于操作 ,并 且利用这种方法得到的路面不平度对应的功率谱 密度可以达到与给定的功率谱密度一致.
系数 ,数据取决于公路的路面等级 ,单位 :m2Πm- 1 ;
W 为频率指数 ,为双对数坐标上斜线的频率 ,它
决定路面功率谱密度的频率结构 ,取 W = 2.
由于汽车隔振系统的作用 ,使汽车对某些频
率路面激励的位移或加速度响应极小 ,所以在进
行路面不平度计算时 ,可以不考虑这些频率成分
的影响. 设需要的路面空间频率成分 (或称有效空
间频率) 的上 、下限分别为 nu 、nl ,则有[3]
Gx ( n) =
Gx ( n0 )
n n0
-W
0
nl ≤ n ≤ nu (2) 其它
有效频率上 、下限 nu 和 nl 的选取要保证使汽车
以常用速度行驶时由路面不平度激起的振动频率
范围包括汽车系统振动的主要固有频率. 假设汽 车的行驶速度为 v (单位 : mΠs) ,路面不平度的空 间频率为 n ,那么汽车轮胎受到的激振频率为 : f = vn. 若汽车振动的主要固有频率范围为 ( f l , f u ) ,可以得出路面不平度功率谱密度的有效空间 频率上 、下限 nu 、nl 分别为
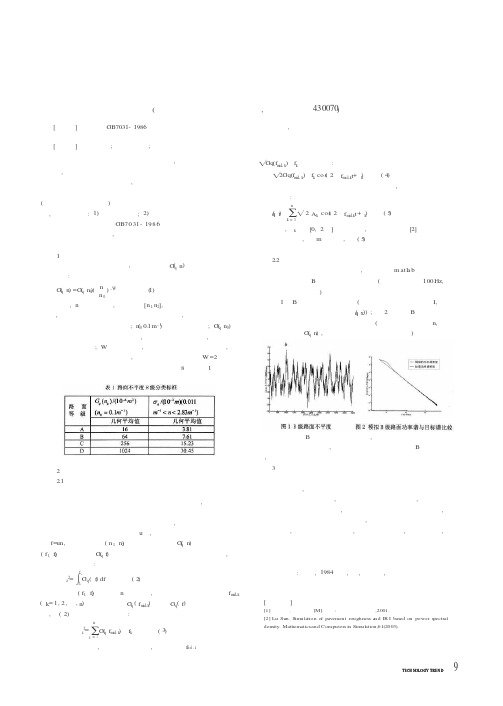
图 1 为 C 级公路的路面不平度曲线 (该图的 横坐标是沿道路走向的长度 I ,纵坐标是路面相 对基准平面的高度或路面不平度 x) .
2 算 例
某轿车振动系统的固有频率分布在 017 ~ 15 Hz ,常用车速为 36 ~180 kmΠh (10~50 mΠs) . 若 取地面作用于轮胎的激励时间频率下限为 f l = 0. 5 Hz 、上限为 f u = 30 Hz ,那么在此激励的频率范 围内研究该轿车的振动可以满足要求. 由 (3) 式可 知 ,研究轿车振动时需要的空间频率的上 、下限分 别为
(4) 、(5) 可得
Δl
≤1 2 nu
= 01166 7 m L
≥1
nl
= 100 m
在本算例中 ,取Δl = 011 m、L = 40916 m ,可以满足
以上要求. 因此有 ,采样点数 N =ΔLl = 4 096 、空间
频率间隔Δn =
1 L
= 01002 44 m- 1 .
根据 GBΠT703121986 ,按照功率谱密度 ,公路
…, N - 1) ,其离散傅立叶变换有 N 个数据 ,但在
计算其功率谱密度时只需其离散傅立叶变换的前
N 2
+1
个数据 .
现在利用 (7)
、(8)
式得到了其离散
傅立叶变换的前
N 2
+
1
个数据 ,所以若要通过离
散傅立叶逆变换得出离散信号 xm ( m = 0 ,1 , …,
N - 1) ,就必须补齐其离散傅立叶变换的后部分
Key words : power spectral density ; road roughness ; Fourier transform ; sampling
汽车振动系统中包括许多非线性元件 ,为获 得准确的结果 ,需采用非线性振动模型[1] . 对于非 线性系统 ,需要在时域中进行研究. 近年来 ,主动 、 半主动控制悬架的研究已经得到了人们充分重 视 ,控制系统的反馈信号是时域信号 ,所以在进行 控制策略研究时 ,也需在时域中进行. 因为研究时 所需路面激励是时域信号 ,时域内的路面激励需 利用路面不平度数据 (空间域路面激励) 和汽车行 驶速度获得. 路面不平度可利用以下 2 种方法得 到 :1) 试验测试方法 ;2) 将给定的路面不平度功率 谱密度变换为路面不平度的方法 ,近年来这种方 法受到了广泛重视[1~5] .
nu
=
fu v
=
30 10
= 3 m- 1
nl
=
fl v
=
015 50
=
0101 m- 1
可见 ,只需在 0. 01~3 m- 1 的空间频率范围内模拟
路面不平度 ,便可覆盖该轿车振动系统的固有频
率 ,从而保证利用所得路面不平度作为激励研究
汽车的振动情况时 ,所得结论符合真实情况. 为避
免频率混叠和使有效空间频率下限 nl 准确 ,由
| Xk | =
N
2Δl
Gx
(
nk )
(
k
=
0
,1
,2
,
…,
N 2
)
(7)
上式中 , nk = kΔn.
由 (7) 式得到的只是离散傅立叶变换的模值 ,
而
Xk
是复数
,若相角为
φ k
,则有
Xk
=|
Xk |
ejφk ( k
=
0
,1
,2
,
…,
N 2
)
(8)
φ k
可以在[ 0
,2π]内随机选取.
对具有 N 个数据的离散采样 xm ( m = 0 , 1 ,
(北京航空航天大学 汽车工程系 , 北京 100083)
摘 要 : 研究了一种公路路面不平度的数值模拟新方法 ,该方法直接对给 定的公路路面不平度功率谱密度进行研究 ,经过一系列处理获得路面的不平度值. 充 分考虑了所关心的汽车固有振动频率和行驶速度影响后 ,利用该方法对 C 级公路路 面进行数值模拟 ,模拟结果表明 :利用该方法所得路面不平度的功率谱密度与给定的 功率谱密度是准确一致的.
845
逆变换便得到路面不平度
∑ xm
=
1 N
N- 1 k=0
j2πkm
Xk e N ( m
= 0 ,1 ,2 , …, N - 1)
(9)
由于上述获得路面不平度的过程是计算其功率谱
密度的逆过程 ,所以理论上可保证所得路面不平
度的功率谱密度与给定的功率谱密度准确一致.
据 ,最后对这些数据利用 (9) 式进行离散傅立叶逆 变换便得到路面不平度数据.
离散的功率谱密度
Gx
(
nk )
(k
=0
,1
,2
,
…,
N) 2
,由
(7) 式得到路面不平度的离散傅立叶变换前
N 2
+1
个模值 ,然后利用 (8) 式得出其复数形式 ,接着根
nu
=
fu v
(3)
nl
=
fl v
在计算功率谱密度时为避免频率混叠 ,距离采样
间隔Δl 应满足[8]
Δl
≤1 2 nu
(4)
若采样点数为 N ,总采样距离为 L = NΔl ,则采样
的空间频率分辨率为Δn
=
1 L
. 为保证在计算离散
的功率谱密度时其有效空间频率下限 nl 准确 ,应
有 nl ≥Δn ,即
收稿日期 : 2003203226 基金项目 :“凡舟”科研基金资助项目 (20021313) 作者简介 : 刘献栋 (1966 - ) ,男 ,河北赵县人 ,教授 ,l9236 @163. com.
© 1995-2006 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
2第00239
年 卷
9月 第9期
北京航空航天大学学报 Journal of Beijing Univer sit y o f A er onautics and Astronautics
September 2003 Vol. 29 No19
公路路面不平度的数值模拟方法研究
刘献栋 邓志党 高 峰
关 键 词 : 功率谱密度 ; 路面不平度 ; 傅立叶变换 ; 采样 中图分类号 : U 467 ; TP 273 文献标识码 : A 文 章 编 号 : 100125965 (2003) 0920843204
Re search o n the metho d of simulating ro ad ro ughne ss numerically
=
0
,1
,2
,
…,
N 2
)
进行补齐
,于是得到
Xk
(k
= 0 ,1 ,2 ,
…,
N 2
,
N 2
+ 1 , …, N
-
1) . 对
Xk
进行离散傅立叶
© 1995-2006 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
第 9 期 刘献栋等 :公路路面不平度的数值模拟方法研究
Liu Xiandong Deng Zhidang Gao Feng
(Dept . of Automobile Engineering , Beijing University of Aeronautics and Astronautics , Beijing 100083 , China)
