初中常用三角函数值对照表
(完整版)三角函数特殊角值表

角度 函数 0 30 45 60 90 120 135 150 180 270 360 角a 的弧度0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 3π/2 2π sin 0 1/2 √2/2 √3/2 1 √3/2 √2/2 1/2 0 -1 0 cos 1 √3/2 √2/2 1/2 0 -1/2 -√2/2 -√3/2 -1 0 1 tan√3/31√3-√3-1-√3/31、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出: sin30°=cos60°=21,sin45°=cos45°=22, tan30°=cot60°=33, tan 45°=cot45°=1正弦函数 sinθ=y/r 余弦函数 cosθ=x/r 正切函数 tanθ=y/x 余切函数 cotθ=x/y 正割函数 secθ=r/x 余割函数 cscθ=r/y2、列表法:说明:正弦值随角度变化,即0˚ 30˚ 45˚ 60˚ 90˚变化;值从02122 23 1变化,其余类似记忆.3、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:① 有界性:(锐角三角函数值都是正值)即当0°<α<90°时,则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A <B <90°时,则sin A <sin B ;tan A <tan B ; cos A >cos B ;cot A >cot B ;特别地:若0°<α<45°,则sin A <cos A ;tan A <cot A 若45°<A <90°,则sin A >cos A ;tan A >cot A . 4、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为2m 形式,正切、余切值可表示为3m 形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.30˚ 123145˚ 1212 60˚ 3函数名正弦余弦正切余切正割余割符号sin cos tan cot sec csc正弦函数sin(A)=a/c余弦函数cos(A)=b/c正切函数tan(A)=a/b余切函数cot(A)=b/a其中a为对边,b为邻边,c为斜边三角函数对照表三角函数SIN COS TAN 三角函数SIN COS TAN 0°0 1 0 90° 1 0 无1°0.0174 0.9998 0.0174 89°0.9998 0.0174 57.2899 2°0.0348 0.9993 0.0349 88°0.9993 0.0348 28.6362 3°0.0523 0.9986 0.0524 87°0.9986 0.0523 19.0811 4°0.0697 0.9975 0.0699 86°0.9975 0.0697 14.3006 5°0.0871 0.9961 0.0874 85°0.9961 0.0871 11.4300 6°0.1045 0.9945 0.1051 84°0.9945 0.1045 9.5143 7°0.1218 0.9925 0.1227 83°0.9925 0.1218 8.1443 8°0.1391 0.9902 0.1405 82°0.9902 0.1391 7.1153 9°0.1564 0.9876 0.1583 81°0.9876 0.1564 6.3137 10°0.1736 0.9848 0.1763 80°0.9848 0.1736 5.6712 11°0.1908 0.9816 0.1943 79°0.9816 0.1908 5.1445 12°0.2079 0.9781 0.2125 78°0.9781 0.2079 4.7046 13°0.2249 0.9743 0.2308 77°0.9743 0.2249 4.3314 14°0.2419 0.9702 0.2493 76°0.9702 0.2419 4.0107 15°0.2588 0.9659 0.2679 75°0.9659 0.2588 3.7320二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin 22sin cos cos 2cos 2sin 22cos 2112sin 2αααααααα==-=-=-2tan tan 21tan 2ααα=--sin 33sin 4sin 3cos34cos33cos .3tan tan 3tan 313tan 2αααααααααα=-=--=--三角函数的和差化积公式 三角函数的积化和差公式sin sin 2sincos 22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅[][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+--化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)22sin cos sin()a x b x a b x φ±=+±其中φ角所在的象限由a 、b 的符号确定,φ角的值由tan ba φ=确定六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
三角函数公式表(全)

三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系:平方关系:tanα·cotα=1sinα·cscα=1 sinα/cosα=tanαsin2α+cos2α=11+tan2α=sec2α(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=———----———1-tanα·tanβtanα-tanβtan(α-β)=—————-------—1+tanα·tanβ2tan(α/2) sinα=——————1+tan2(α/2)1-tan2(α/2) cosα=——————1+tan2(α/2)2tan(α/2) tanα=——————1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式Sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2] sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2] cos α+cos β=2cos[(α+β)/2]·cos[(α-β)/2] cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2]1sinα·cosβ=-[sin(α+β)+sin(α-β)]21cosα·sinβ=-[sin(α+β)-sin(α-β)]21cosα·cosβ=-[cos(α+β)+cos(α-β)]21sinα·sinβ=— -[cos(α+β)-cos(α-β)]2化asinα±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)THANKS致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。
初中三角函数详细数值表.doc

本篇是关于初中三角函数的速记与理解,皆来自于课本与网络,所以免费。
欢迎曾经与我一样不理解的初学者观阅 ~~~~~本品仅用于学习交流,谢绝转载。
首先,我们先理解基础概念,如下:SinA=CosA=TanA=CotA=还有一点很重要,0 < sinA < 10 < sinA <1根据三角函数的定义,我们还可以得出SinA*2+CosA*2=1TanA·CotA=1TanA=SinA/CosACotA=CosA/SinATanA=1/CotAsin A= cos(90- A )tan A =cotA (90 - A )此为必背图表角度0度30度45度60度90度三角函数sin01/2 2 3 12 2cos1 3 2 1/202 2tan0 3 1 3 ――3cot―― 3 1 3 03相对应的示意图见下页~~~~~~~~~~~~~~~~~<A=30度<A=45度<A=60度如何用计算器计算函数值(1)求已知锐角的三角函数值求 sin63 °52′41″的值.(精确到 0.0001)先用如下方法将角度单位状态设定为“度”:SHIFT MODE(SETUP)3显示D依次键入sin 63°52′41″=得到结果;求 cot70 °45′的值.(精确到 0.0001)在角度单位状态为“度”的情况下(屏幕显示),按下列顺序依次按键:1÷ cot 70°45′=得到结果(2)由锐角三角函数值求锐角已知 tanx =0.7410,求锐角 x.(精确到 1′)在角度单位状态为“度”的情况下(屏幕显示),按下列顺序依次按键:SHIFT tan(tan1)0·741=0得到结果再次键入SHIFT o’’’完成接下来如标题示,整理好的三角函数表sin15= (√ 6- √2)/4 ,sin75=( √6+√2)/2 ,sin105= √2/2*( √3/2+1/2)sin120= √3/2sin135= √2/2sin150=1/2sin165= (√ 6- √ 2)/4sin180=0sin270=-1sin360=0(上为特殊值)sin1=sin2=sin3=sin4=sin6= sin7= sin8= sin9= sin10= sin11= sin12= sin13= sin14= sin15= sin16= sin17= sin18= sin19= sin20=sin21= sin22= sin23= sin24= sin25= sin26= sin27= sin28= sin29= sin30=sin32= sin33= sin34= sin35= sin36= sin37= sin38= sin39= sin40= sin41= sin42= sin43= sin44= sin45= sin46= sin47= sin48= sin49= sin50= sin51= sin52= sin53= sin54= sin55= sin56= sin57=sin59= sin60= sin61= sin62= sin63= sin64= sin65= sin66= sin67= sin68= sin69= sin70= sin71= sin72= sin73= sin74= sin75= sin76= sin77= sin78= sin79= sin80= sin81= sin82= sin83= sin84=sin86= sin87= sin88= sin89= sin90=1 cos1= cos2= cos3= cos4= cos5= cos6= cos7= cos8= cos9= cos10= cos11= cos12= cos13= cos14= cos15= cos16= cos17= cos18= cos19= cos20= cos21=cos23= cos24= cos25= cos26= cos27= cos28= cos29= cos30= cos31= cos32= cos33= cos34= cos35= cos36= cos37= cos38= cos39= cos40= cos41= cos42= cos43= cos44= cos45= cos46= cos47= cos48=cos50= cos51= cos52= cos53= cos54= cos55= cos56= cos57= cos58= cos59= cos60= cos61= cos62= cos63= cos64= cos65= cos66= cos67= cos68= cos69= cos70= cos71= cos72= cos73= cos74= cos75=cos77= cos78= cos79= cos80= cos81= cos82= cos83= cos84= cos85= cos86= cos87= cos88= cos89= cos90=0 tan1= tan2= tan3= tan4= tan5= tan6= tan7= tan8= tan9= tan10= tan11= tan12=tan14= tan15= tan16= tan17= tan18= tan19= tan20= tan21= tan22= tan23= tan24= tan25= tan26= an27= tan28= tan29= tan30= tan31= tan32= tan33= tan34= tan35= tan36= tan37= tan38= tan39=tan41= tan42= tan43= tan44= tan45= tan46= tan47= tan48= tan49= tan50= tan51= tan52= tan53= tan54= tan55= tan56= tan57= tan58= tan59= tan60= tan61= tan62= tan63= tan64= tan65= tan66=tan68=tan69=tan70=tan71=tan72=tan73=tan74=tan75=tan76=tan77=tan78=tan79=tan80=tan81=tan82=tan83=tan84=tan85=tan86=tan87=tan88=tan89=tan90= 无取值如果求精确度的话,还可以看下面sin1=sin3= sin4= sin5= sin6= sin7= sin8= sin9= sin10= sin11= sin12= sin13= sin14= sin15= sin16= sin17= sin18= sin19=0. sin20=0. sin21= sin22= sin23= sin24= sin25= sin26= sin27= sin28= sin29=sin31= sin32= sin33= sin34= sin35= sin36=0. sin37= sin38= sin39=0. sin40=0. sin41=0. sin42= sin43= sin44= sin45= sin46= sin47= sin48= sin49= sin50= sin51= sin52= sin53= sin54= sin55= sin56=0.sin58= sin59= sin60=0. sin61= sin62=0. sin63= sin64= sin65=0. sin66= sin67=0. sin68= sin69=0. sin70= sin71= sin72= sin73=0. sin74= sin75=0. sin76=0. sin77=0. sin78= sin79= sin80= sin81= sin82=0. sin83=sin85= sin86= sin87=0. sin88=0. sin89=0. sin90=1cos1=0. cos2=0. cos3=0. cos4= cos5= cos6= cos7= cos8=0. cos9= cos10= cos11= cos12= cos13=0. cos14=0. cos15=0. cos16= cos17=0. cos18= cos19= cos20=cos22= cos23=0. cos24= cos25=0. cos26= cos27= cos28= cos29= cos30=0. cos31= cos32= cos33= cos34=0. cos35= cos36= cos37= cos38= cos39= cos40= cos41= cos42= cos43= cos44= cos45= cos46= cos47=cos49=0. cos50=0. cos51=0. cos52= cos53= cos54=0. cos55=0. cos56= cos57=0. cos58= cos59= cos60= cos61= cos62= cos63=0. cos64= cos65= cos66=0. cos67= cos68=0. cos69= cos70=0. cos71= cos72= cos73= cos74=cos76= cos77= cos78= cos79= cos80= cos81= cos82= cos83= cos84= cos85= cos86= cos87= cos88= cos89= cos90=0tan1= tan2= tan3= tan4= tan5= tan6= tan7= tan8= tan9= tan10= tan11=tan13=0. tan14= tan15=0. tan16=0. tan17= tan18= tan19= tan20= tan21=0. tan22=0. tan23=0. tan24=0. tan25=0. tan26=0. tan27=0. tan28= tan29= tan30=0. tan31=0. tan32=0. tan33=0. tan34=0. tan35=0. tan36=0. tan37= tan38=tan40=0. tan41=0. tan42=0. tan43= tan44=0. tan45=0. tan46= tan47= tan48= tan49= tan50= tan51= tan52= tan53=1. tan54= tan55= tan56=1. tan57=1. tan58=1. tan59=1. tan60=1. tan61=1. tan62=1. tan63= tan64= tan65=tan67=tan68=2.tan69=2.tan70=2.tan71=tan72=tan73=3.tan74=tan75=3.tan76=tan77=tan78=tan79=tan80=tan81=tan82=tan83=tan84=tan85=tan86=tan87=tan88=tan89=tan90=( 无限 )终于完了,本人冒着长针眼的危险整理出了这个东东以下鸣谢百度文库上的资料:初中数学锐角三角形讲解初中三角函数值表计算器三角函数求值还有百度知道:三角函数表以及数学课本和提分教练里的资料后话:虽然说细数只借鉴了这么多,但是找资料的时候也费了很多时间,网页的历史记录竟然已经达到5 , 6页了。
初中三角函数数值表格

初中三角函数数值表格
在初中数学中,学习三角函数是十分重要的一部分。
三角函数主要指正弦、余弦和正切这三个函数,在数学和实际生活中有着广泛的应用。
通过建立一个数值表格,我们可以更好地理解三角函数的性质和变化规律。
正弦函数值表
下表展示了正弦函数在0°到360°范围内的数值:
角度0°30°45°60°90°180°270°360°
正弦值00.50.7070.86610-10余弦函数值表
下表展示了余弦函数在0°到360°范围内的数值:
角度0°30°45°60°90°180°270°360°
余弦值10.8660.7070.50-101正切函数值表
下表展示了正切函数在0°到360°范围内的数值:
角度0°30°45°60°90°180°270°360°正切值00.5771 1.732无穷大0无穷小0结论
通过以上数值表格可以看出,正弦函数在0°和180°时达到最大值1,余弦函数在0°和360°时达到最大值1,正切函数在45°时达到最大值1。
这些表格展示了三角函数在不同角度下的数值,有助于我们更好地理解三角函数的性质和特点。
在学习数学的过程中,通过一些如此简单的数值表格,我们可以更好地理解抽象的数学概念,希望这些数值表格能帮助您更深入地理解三角函数的奥秘。
三角函数及取值表

(1)特殊角三角函数值sin0=0sin30=0.5sin45=0.7071 二分之根号2sin60=0.8660 二分之根号3sin90=1cos0=1cos30=0.866025404 二分之根号3cos45=0.707106781 二分之根号2cos60=0.5cos90=0tan0=0tan30=0.577350269 三分之根号3tan45=1tan60=1.732050808 根号3tan90=无cot0=无cot30=1.732050808 根号3cot45=1cot60=0.577350269 三分之根号3cot90=0(2)0°~90°的任意角的三角函数值,查三角函数表。
(见下)(3)锐角三角函数值的变化情况(i)锐角三角函数值都是正值(ii)当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)余切值随着角度的增大(或减小)而减小(或增大)(iii)当角度在0°≤α≤90°间变化时,0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时,tanα>0, cotα>0.“锐角三角函数”属于三角学,是《数学课程标准》中“空间与图形”领域的重要内容。
从《数学课程标准》看,中学数学把三角学内容分成两个部分,第一部分放在义务教育第三学段,第二部分放在高中阶段。
在义务教育第三学段,主要研究锐角三角函数和解直角三角形的内容,本套教科书安排了一章的内容,就是本章“锐角三角函数”。
在高中阶段的三角内容是三角学的主体部分,包括解斜三角形、三角函数、反三角函数和简单的三角方程。
无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
初中三角函数详细数值表

初中三角函数详细数值表本篇是关于初中三角函数的速记与理解,皆来自于课本与网络,所以免费。
欢迎曾经与我一样不理解的初学者观阅~~~~~本品仅用于学习交流,谢绝转载。
首先,我们先理解基础概念,如下:SinA=斜边的对边A ∠ CosA=斜边的邻边A ∠ TanA=的邻边的对边A A ∠∠ CotA=的对边的邻边A A ∠∠还有一点很重要,0<sinA<1 0<sinA<1根据三角函数的定义,我们还可以得出SinA*2+CosA*2=1 TanA · CotA=1TanA=SinA/CosACotA=CosA/SinATanA=1/CotAsinA=cos(90?-A)tanA=cotA(90?-A)此为必背图表相对应的示意图见下页~~~~~~~~~~~~~~~~~<A=30度<A=45度<A=60度如何用计算器计算函数值(1)求已知锐角的三角函数值求sin63°52′41″的值.(精确到0.0001)先用如下方法将角度单位状态设定为“度”:SHIFT MODE(SETUP)3显示D依次键入sin 63 °52 ′41 ″=得到结果;求cot70°45′的值.(精确到0.0001)在角度单位状态为“度”的情况下(屏幕显示),按下列顺序依次按键:1÷cot 70 °45 ′=得到结果(2)由锐角三角函数值求锐角已知tanx=0.7410,求锐角x.(精确到1′)在角度单位状态为“度”的情况下(屏幕显示),按下列顺序依次按键:SHIFT tan (1tan )0 ·741=0得到结果再次键入SHIFT o’’’完成接下来如标题示,整理好的三角函数表sin15=(√6-√2)/4,sin75=(√6+√2)/2,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/2sin150=1/2sin165=(√6-√2)/4sin180=0sin270=-1sin360=0(上为特殊值)sin1=0.01745sin2=0.034899sin3=0.052335sin4=0.069756sin5=0.087155sin7=0.121869 sin8=0.139173 sin9=0.156434 sin10=0.17364 sin11=0.19080 sin12=0.20791 sin13=0.22495 sin14=0.24192 sin15=0.25881 sin16=0.27563 sin17=0.29237 sin18=0.30901 sin19=0.32556 sin20=0.34202 sin21=0.35836 sin22=0.37460 sin23=0.39073 sin24=0.40673 sin25=0.42261 sin26=0.43837 sin27=0.45399 sin28=0.46947 sin29=0.48480 sin30=0.49999 sin31=0.51503 sin32=0.52991 sin33=0.54463 sin34=0.55919sin36=0.58778 sin37=0.60181 sin38=0.61566 sin39=0.62932 sin40=0.64278 sin41=0.65605 sin42=0.66913 sin43=0.68199 sin44=0.69465 sin45=0.70710 sin46=0.71933 sin47=0.73135 sin48=0.74314 sin49=0.75470 sin50=0.76604 sin51=0.77714 sin52=0.78801 sin53=0.79863 sin54=0.80901 sin55=0.81915 sin56=0.82903 sin57=0.83867 sin58=0.84804 sin59=0.85716 sin60=0.86602 sin61=0.87461 sin62=0.88294 sin63=0.89100sin65=0.90630 sin66=0.91354 sin67=0.92050 sin68=0.92718 sin69=0.93358 sin70=0.93969 sin71=0.94551 sin72=0.95105 sin73=0.95630 sin74=0.96126 sin75=0.96592 sin76=0.97029 sin77=0.97437 sin78=0.97814 sin79=0.98162 sin80=0.98480 sin81=0.98768 sin82=0.99026 sin83=0.99254 sin84=0.99452 sin85=0.99619 sin86=0.99756 sin87=0.99862 sin88=0.99939 sin89=0.99984 sin90=1cos1=0.99984 cos2=0.99939cos4=0.99756 cos5=0.99619 cos6=0.99452 cos7=0.99254 cos8=0.99026 cos9=0.98768 cos10=0.9848 cos11=0.9816 cos12=0.97814 cos13=0.9743 cos14=0.9702 cos15=0.9659 cos16=0.9612 cos17=0.9563 cos18=0.9510 cos19=0.9455 cos20=0.9396 cos21=0.9335 cos22=0.9271 cos23=0.9205 cos24=0.9135 cos25=0.9063 cos26=0.8987 cos27=0.8910 cos28=0.8829 cos29=0.8746 cos30=0.8660 cos31=0.8571cos33=0.8386 cos34=0.8290 cos35=0.8191 cos36=0.8090 cos37=0.7986 cos38=0.7880 cos39=0.7771 cos40=0.7660 cos41=0.7547 cos42=0.7431 cos43=0.7313 cos44=0.7193 cos45=0.7071 cos46=0.6946 cos47=0.6819 cos48=0.6691 cos49=0.6560 cos50=0.6427 cos51=0.6293 cos52=0.6156 cos53=0.6018 cos54=0.5877 cos55=0.5735 cos56=0.5592 cos57=0.5446 cos58=0.5299 cos59=0.5150 cos60=0.5000cos62=0.4694 cos63=0.4539 cos64=0.4383 cos65=0.4226 cos66=0.4067 cos67=0.3907 cos68=0.3746 cos69=0.3583 cos70=0.3420 cos71=0.3255 cos72=0.3090 cos73=0.2923 cos74=0.2756 cos75=0.2588 cos76=0.2419 cos77=0.2249 cos78=0.2079 cos79=0.1908 cos80=0.1736 cos81=0.1564 cos82=0.1391 cos83=0.1218 cos84=0.1045 cos85=0.0871 cos86=0.06973 cos87=0.052 cos88=0.0348 cos89=0.0174cos90=0tan1=0.017455 tan2=0.034920 tan3=0.052407 tan4=0.069926 tan5=0.087488 tan6=0.105104 tan7=0.122784 tan8=0.140540 tan9=0.158384 tan10=0.17632 tan11=0.19438 tan12=0.21255 tan13=0.23086 tan14=0.24932 tan15=0.26794 tan16=0.28674 tan17=0.30573 tan18=0.32491 tan19=0.34432 tan20=0.36397 tan21=0.38386 tan22=0.40402 tan23=0.42447 tan24=0.44522 tan25=0.46630 tan26=0.48773 an27=0.50952 tan28=0.53170tan29=0.55430 tan30=0.57735 tan31=0.60086 tan32=0.62486 tan33=0.64940 tan34=0.67450 tan35=0.70020 tan36=0.72654 tan37=0.75355 tan38=0.78128 tan39=0.80978 tan40=0.83909 tan41=0.86928 tan42=0.90040 tan43=0.93251 tan44=0.96568 tan45=0.99999 tan46=1.03553 tan47=1.07236 tan48=1.11061 tan49=1.15036 tan50=1.19175 tan51=1.23489 tan52=1.27994 tan53=1.32704 tan54=1.3763 tan55=1.42814 tan56=1.48256 tan57=1.53986tan59=1.66427 tan60=1.73205 tan61=1.80404 tan62=1.88072 tan63=1.96261 tan64=2.05030 tan65=2.14450 tan66=2.24603 tan67=2.35585 tan68=2.47508 tan69=2.60508 tan70=2.74747 tan71=2.90421 tan72=3.07768 tan73=3.27085 tan74=3.48741 tan75=3.73205 tan76=4.01078 tan77=4.33147 tan78=4.70463 tan79=5.14455 tan80=5.67128 tan81=6.31375 tan82=7.11536 tan83=8.14434 tan84=9.51436 tan85=11.4300 tan86=14.3006tan88=28.6362tan89=57.2899tan90=无取值如果求精确度的话,还可以看下面sinsin90=1cos90=0tan90=(无限)终于完了,本人冒着长针眼的危险整理出了这个东东以下鸣谢百度文库上的资料:初中数学?锐角三角形讲解初中三角函数值表计算器三角函数求值还有百度知道:三角函数表以及数学课本和提分教练里的资料后话:虽然说细数只借鉴了这么多,但是找资料的时候也费了很多时间,网页的历史记录竟然已经达到5,6页了。
初中数学:三角函数

初中数学:三角函数三角函数是数学中经典的概念之一,是数学分析、数学物理、工程等领域的基础工具。
本篇文章将从初中三角函数的定义、性质、常见角度及其应用等方面进行介绍。
一、三角函数的定义1. 正弦函数正弦函数Sine,简写为sin,是一个经典的周期函数,它的周期是2π。
在数学上,正弦函数可以用一个圆上的角的对边长度与斜边长度之比来定义。
设一个半径为r的圆上有一个角α,则该角的正弦值为:sinα = 对边/ 斜边2. 余弦函数余弦函数Cosine,简写为cos,同样是一个经典的周期函数,它的周期也是2π。
在数学上,余弦函数可以用一个圆上的角的邻边长度与斜边长度之比来定义。
设一个半径为r的圆上有一个角α,则该角的余弦值为:cosα = 邻边/ 斜边3. 正切函数正切函数Tangent,简写为tan,用一个直角三角形的对边长度与邻边长度之比来描述。
设一个直角三角形中的一个角为α,则该角的正切值为:tanα = 对边/ 邻边4. 余切函数余切函数Cotangent,简写为cot,是正切函数的倒数,它用邻边长度与对边长度之比来描述。
设一个直角三角形中的一个角为α,则该角的余切值为:cotα = 邻边/ 对边二、三角函数的性质1. 正弦函数和余弦函数的特点正弦函数与余弦函数具有如下特点:(1)周期性:正弦函数和余弦函数都是周期函数,周期均为2π。
(2)奇偶性:正弦函数是奇函数,余弦函数是偶函数。
(3)取值范围:正弦函数的取值范围是[-1,1],余弦函数的取值范围也是[-1,1]。
2. 正切函数和余切函数的特点正切函数与余切函数具有如下特点:(1)周期性:正切函数和余切函数都是周期函数,周期均为π。
(2)奇偶性:正切函数是奇函数,余切函数也是奇函数。
(3)取值范围:正切函数的取值范围是R(实数集),余切函数的取值范围也是R,但余切函数的定义域不包括π的整数倍。
三、常见角度的三角函数值1. 30°、45°、60°三角函数值(1)30°角正弦函数:sin30° = 1/2余弦函数:cos30° = √3/2正切函数:tan30° = 1/√3余切函数:cot30° = √3(2)45°角正弦函数:sin45° = √2/2余弦函数:cos45° = √2/2正切函数:tan45° = 1余切函数:cot45° = 1(3)60°角正弦函数:sin60° = √3/2余弦函数:cos60° = 1/2正切函数:tan60° = √3余切函数:cot60° = 1/√32. 常用角度的三角函数值(1)0°和180°角正弦函数:sin0° = 0,sin180° = 0余弦函数:cos0° = 1,cos180° = -1正切函数:tan0° = 0,tan180° = 0余切函数:cot0° = 无穷大,cot180° = 无穷大(2)90°和270°角正弦函数:sin90° = 1,sin270° = -1余弦函数:cos90° = 0,cos270° = 0正切函数:tan90° = 无穷大,tan270° = 无穷大余切函数:cot90° = 0,cot270° = 0四、三角函数的应用1. 三角函数在直角三角形中的应用在直角三角形中,三角函数可以用来计算三角形的各个边与角。
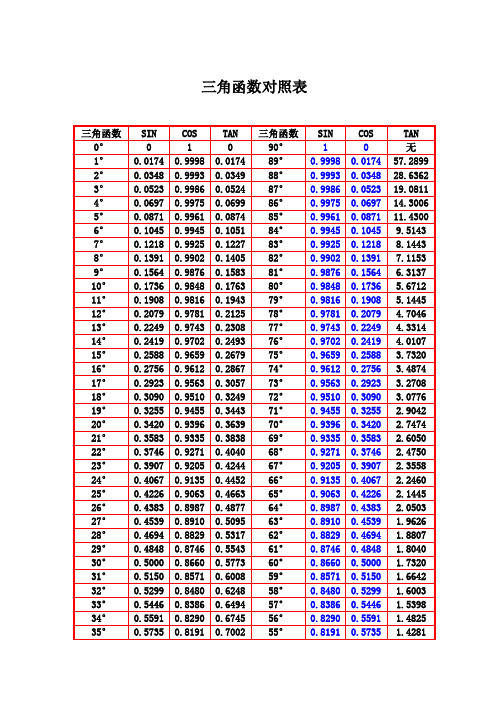
三角函数对照表
商的关系
sin tan sec
cos
csc
cos cot csc
sin
sec
平方关系
2
2
sin cos 1
2
2
1 tan sec
2
2
1 cot csc
诱导公式
sin() sin
cos( ) cos tan() tan
cot() cot
sin( ) cos 2
cos( ) sin 2
0.9998 0.9993 0.9986 0.9975 0.9961 0.9945 0.9925 0.9902 0.9876 0.9848 0.9816 0.9781 0.9743 0.9702 0.9659 0.9612 0.9563 0.9510 0.9455 0.9396 0.9335 0.9271 0.9205 0.9135 0.9063 0.8987 0.8910 0.8829 0.8746 0.8660 0.8571 0.8480 0.8386 0.8290 0.8191
36° 37° 38° 39° 40° 41° 42° 43° 44° 45°
0.5877 0.6018 0.6156 0.6293 0.6427 0.6560 0.6691 0.6819 0.6946 0.7071
0.8090 0.7986 0.7880 0.7771 0.7660 0.7547 0.7431 0.7313 0.7193 0.7071
TAN 0
0.0174 0.0349 0.0524 0.0699 0.0874 0.1051 0.1227 0.1405 0.1583 0.1763 0.1943 0.2125 0.2308 0.2493 0.2679 0.2867 0.3057 0.3249 0.3443 0.3639 0.3838 0.4040 0.4244 0.4452 0.4663 0.4877 0.5095 0.5317 0.5543 0.5773 0.6008 0.6248 0.6494 0.6745 0.7002
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中常用三角函数值对照表
初中常用的三角函数有正弦函数、余弦函数和正切函数等等,接下来分享具体的三角函数值表,供参考。
常用三角函数值对照表
sin0=sin0°=0
cos0=cos0°=1
tan0=tan0°=0sin15=0.650;
sin15°=0.259
cos15=-0.759;cos15°=0.966
tan15=-0.855;tan15°=0.268
sin30°=1/2
cos30°=0.866;
tan30°=0.577;
sin45°=0.707;
cos45°=0.707
tan45=1.620;tan45°=1
sin60=-0.305;sin60°=0.866
cos60=-0.952;cos60°=1/2
tan60=0.320;tan60°=1.732
sin75=-0.388;sin75°=0.966
cos75=0.922;cos75°=0.259
tan75=-0.421;tan75°=sin75°/cos75°=3.732
sin90=0.894;sin90°=cos0°=1
cos90=-0.448;cos90°=sin0°=0
tan90=-1.995;tan90°不存在
sin105=-0.971;sin105°=cos15°
cos105=-0.241;cos105°=-sin15°
tan105=4.028;tan105°=-cot15°
sin120=0.581;sin120°=cos30°
cos120=0.814;cos120°=-sin30°
tan120=0.713;tan120°=-tan60°
sin135=0.088;sin135°=sin45°
cos135=-0.996;cos135°=-cos45°
tan135=-0.0887;tan135°=-tan45°
sin150=-0.7149;sin150°=sin30°
cos150=-0.699;cos150°=-cos30°
tan150=-1.022;tan150°=-tan30°
sin165=0.998;sin165°=sin15°
cos165=-0.066;cos165°=-cos15°
tan165=-15.041;tan165°=-tan15°
sin180=-0.801;sin180°=sin0°=0
cos180=-0.598;cos180°=-cos0°=-1
tan180=1.339;tan180°=0
sin195=0.219;sin195°=-sin15°
cos195=0.976;cos195°=-cos15°
tan195=0.225;tan195°=tan15°
sin360=0.959;sin360°=sin0°=0
cos360=-0.284;cos360°=cos0°=1
tan360=-3.380;tan360°=tan0°=0
三角函数值的特点
(1)当角度在0°~90°间变化时,
正弦值随着角度的增大(或减小)而增大(或减小)。
余弦值随着角度的增大(或减小)而减小(或增大)。
正切值随着角度的增大(或减小)而增大(或减小)。
余切值随着角度的增大(或减小)而减小(或增大)。
(2)当角度在0°≤α≤90°间变化时,
0≤sinα≤1,1≥cosα≥0。
三角函数两角和公式
sin(A+B)=sinAcosB+cosAsinB
sin(A-B)=sinAcosB-cosAsinB
cos(A+B)=cosAcosB-sinAsinB
cos(A-B)=cosAcosB+sinAsinB
tan(A+B)=(tanA+tanB)/(1-tanAtanB)
tan(A-B)=(tanA-tanB)/(1+tanAtanB)
cot(A+B)=(cotAcotB-1)/(cotB+cotA)
cot(A-B)=(cotAcotB+1)/(cotB-cotA)
三角函数倍角公式
tan2A=2tanA/(1-tan²A)
Sin2A=2SinA•C osA
Cos2A=Cos^2A--Sin²A
=2Cos²A—1
=1—2sin^2A
三角函数三倍角公式
sin3A=3sinA-4(sinA)³;
cos3A=4(cosA)³-3cosA
tan3a=tana•tan(π/3+a)•tan(π/3-a)
三角函数半角公式
sin(A/2=√{(1--cosA)/2}
cos(A/2)=√{(1+cosA)/2}
tan(A/2)=√{(1--cosA)/(1+cosA)}
cot(A/2)=√{(1+cosA)/(1-cosA)}
tan(A/2)=(1--cosA)/sinA=sinA/(1+cosA) 三角函数和差化积
sin(a)+sin(b)=2sin[(a+b)/2]cos[(a-b)/2]
sin(a)-sin(b)=2cos[(a+b)/2]sin[(a-b)/2]
cos(a)+cos(b)=2cos[(a+b)/2]cos[(a-b)/2] cos(a)-cos(b)=-2sin[(a+b)/2]sin[(a-b)/2]
tanA+tanB=sin(A+B)/cosAcosB
三角函数积化和差
sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)] cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)] sin(a)cos(b)1/2*[sin(a+b)+sin(a-b)] cos(a)sin(b)1/2*[sin(a+b)-sin(a-b)]。
