初中数学竞赛:三角函数
三角函数竞赛试题与方法

三角函数竞赛试题与方法二、方法与例题 1.结合图象解题。
例1 求方程s inx =lg |x |的解的个数。
【解】在同一坐标系内画出函数y =s inx 与y =lg |x |的图象(见图),由图象可知两者有6个交点,故方程有6个解。
2.三角函数性质的应用。
例2 设x ∈(0, π), 试比较co s(s inx )与s in (co s x )的大小。
【解】 若⎪⎭⎫⎢⎣⎡∈ππ,2x ,则co s x ≤1且co s x >-1,所以co s ⎥⎦⎤ ⎝⎛-∈0,2πx ,所以s in (co s x ) ≤0,又0<s inx ≤1, 所以co s(s inx )>0,所以co s(s inx )>s in (co s x ). 若⎥⎦⎤⎝⎛-∈2,0πx ,则因为s inx +co s x =2cos 22sin 222=⎪⎪⎭⎫ ⎝⎛+x x (s inxco s 4π+s in 4πco s x )=2s in (x +4π)≤2<2π, 所以0<s inx <2π-co s x <2π, 所以co s(s inx )>co s(2π-co s x )=s in (co s x ).综上,当x ∈(0,π)时,总有co s(s inx )<s in (co s x ).例3 已知α,β为锐角,且x ·(α+β-2π)>0,求证:.2sin cos sin cos <⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛xxαββα【证明】 若α+β>2π,则x >0,由α>2π-β>0得co s α<co s(2π-β)=s in β,所以0<βαsin cos <1,又s in α>s in (2π-β)=co s β, 所以0<αβsin cos <1,所以.2sin cos sin cos sin cos sin cos 0=⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛αββααββαxx若α+β<2π,则x <0,由0<α<2π-β<2π得co s α>co s(2π-β)=s in β>0, 所以βαsin cos >1。
全国初中数学竞赛试题及答案

全国初中数学竞赛试题及答案
全国初中数学竞赛试题及答案
1. 角函数的计算和证明问题
在解三角函数问题之前,除了熟知初三教材中的有关知识外,还应该掌握:
(1)三角函数的单调性当a为锐角时,sina与tga的值随a的值增大而增大;cosa与ctga随a的值增大而减小;当a为钝角时,利用诱导公式转化为锐角三角函数讨论.
注意到sin45=cos45= ,由(1)可知,当时0sina;当45
(2)三角函数的有界性|sina|1,|cosa|1,tga、ctga可取任意实数值(这一点可直接利用三角函数定义导出).
例1(1986年全国初中数学竞赛备用题)在△ABC中,如果等式sinA+cosA= 成立,那么角A是( )
(A)锐角 (B)钝角 (C)直角
分析对A分类,结合sinA和cosA的单调性用枚举法讨论.
解当A=90时,sinA和cosA=1;
当45 ,cosA0,
sinA+cosA 当A=45时,sinA+cosA= 当00,cosA sinA+cosA ∵ 1, 都大于 .
淘汰(A)、(C),选(B).
例2(1982年上海初中数学竞赛题)ctg6730的值是( )
(A) -1 (B)2- (C) -1
(D) (E) 分析构造一个有一锐角恰为6730的Rt△,再用余切定义求之.
解如图36-1,作等腰Rt△ABC,设B=90,AB=BC=1.延长BA到D使AD=AC,连DC,则AD=AC= ,D=22.5,DCB=67.5.这时,
ctg6730=ctgDCB= 选(A).。
初中数学竞赛专题:三角函数

初中数学竞赛专题:三角函数§7.1锐角三角函数7.1.1★比较下列各组三角函数值的大小:(1)sin19︒与cos70︒;(2)cot65︒与cos40︒;(3)cos1︒,tan46︒,sin88︒和cot38︒.解析(1)利用互余角的三角函数关系式,将cos70︒化sin20︒,再与sin19︒比大小.因为()︒=︒-︒=︒,而cos70cos9020sin20︒<︒,sin19sin20所以sin19cos70︒<︒.(2)余切函数与余弦函数无法化为同名函数,但是可以利用某些特殊的三角函数值,间接比较它们的大小.cot60cos45︒=<︒=,再将cot65︒,cos40︒分别与cot60︒,cos45︒比大小.因为︒>︒>,︒<︒=,cos40cos45cot65cot60所以cot60cos45︒<︒,所以cot65cos40︒<︒.(3)tan451︒=,显然cos1︒,sin88︒均小于1,而tan46︒,cot38︒均大于1.再分别比较cos1︒与sin88︒,以及tan46︒与cot38︒的大小即可.因为()cos38cot9052tan52︒=︒-︒=︒,所以︒>︒>︒=.tan52tan46tan451因为()︒=︒-︒=︒,cos1cos9089sin89所以sin88sin891︒<︒<,所以cot38tan46cos1sin88︒>︒>︒>︒.评注比较三角函数值的大小,一般分为三种类型:(1)同名的两个锐角三角函数值,可直接利用三角函数值随角变化的规律,通过比较角的大小来确定三角函数值的大小.(2)互为余函数的两锐角三角函数值,可利用互余角的三角函数关系式化为同名三角函数,比较其大小.(3)不能化为同名的两个三角函数,可通过与某些“标准量”比大小,间接判断它们的大小关系,常选择的标准量有:0,1以及其他一些特殊角如30︒,45︒,60︒的三角函数值.7.1.2 ★化简求值:(1)tan1tan2tan3tan89︒⋅︒⋅︒⋅⋅︒; (2sin83︒;(3)2222tan sin tan sin αααα⋅-;(4cos 79sin 79︒-︒;(5)若tan 3α=求2sin sin 13sin cos αααα-+的值.解析(1)原式=tan1tan2tan3tan44tan45cot 44cot 43cot3cot 2cot1︒⋅︒⋅︒⋅⋅︒⋅︒⋅︒⋅︒⋅⋅︒⋅︒⋅︒()()()tan1cot1tan 2cot 2tan 44cot 44tan 45=︒⋅︒⋅︒⋅︒⋅⋅︒⋅︒⋅︒1111=⋅⋅⋅=.(2)原式1cos7cos71cos7=︒=⋅︒=︒. (3)原式()22442242222sin sin sin sin cos 1sin sin sin 1cos sin cos ααααααααααα⋅====--. (4)原式sin11cos11sin11cos11sin11cos110︒-︒=︒-︒-︒-︒=.(5)原式2222sin cos sin sin cos sin 13sin cos sin cos 3sin cos αααααααααααα--==+++ 2222tan tan 336tan 13tan 313319αααα--===-++++⨯. 评注 同角三角函数关系式以及互余两角三角函数关系式,在三角式变形、化简、求值及证明中是重要的依据.7.1.3★试证明在锐角三角形中,任何一个角的正弦大于其他两个角的余弦. 解析在锐角三角形里,显然有90A B ∠+∠=︒,所以有9090A B ︒>∠>︒-∠.由于在0︒~90︒范围内,当A ∠增加时,其正弦值是增加的,于是我们知道()sin sin 90cos A B B >︒-=.同理可以证明其他的五组. 7.1.4★下列四个数中哪个最大: A .tan48cot 48︒+︒ B .sin48cos48︒+︒ C .tan48cos48︒+︒D .cot 48sin48︒+︒解析显然0sin481<︒<,0cos481<︒<0<cos48°<1.因此有:sin 48sin 48tan 48cos48︒︒<=︒︒, cos48cos48cot 48sin 48︒︒<=︒︒所以A 最大.7.1.5★设x 为锐角,且满足sin 3cos x x =,求sin cos x x . 解析 我们将sin 3cos x x =代入22sin cos 1x x +=,得到210cos 1x =,并且x 是锐角,因此cos x =所以sin x =因此3sin cos 10x x =. 7.1.6★★在ABC △中,3C A ∠=∠,27BC =,48AB =.证明:2A ∠是锐角,并计算cos2A 的值. 解析若290A ∠︒≥,则45A ∠︒≥,3135C A ∠=∠︒≥,于是180A B C ∠+∠+∠>︒,矛盾.为计算cos2A ,必须构造出一个以2A ∠为其一锐角的直角三角形.如图,过C 作CD 交AB 于D ,使ACD A ∠=∠,则32BCD A A A ∠=∠-∠=∠.ABC DE又CDB A ACD ∠=∠+∠ =2A BCD ∠=∠ 所以27BD BC ==,21AD AB BD =-=, 21DC AD ==.作BE CD 丄于E ,则212CE DE ==,故217cos2cos 5418CE A BCE BC =∠===. 7.1.7★已知sin cos αα+,求sin cos αα的值.解析 由sin cos αα+两边平方得()22sin cos αα+=.又22sin cos 1αα+=,所以12sin cos 2αα+=,得1sin cos 2αα=. 评注 (1)当已知sin α与cos α之间和或差的值时,常常考虑运用22sin cos 1αα+=转化问题.(2)总结此题解答过程,该问题实际上是读者都熟悉的问题:已知a b +221a b +=,求ab 的值.这里用三角函数式sin α、cos α来替代a 、b ,变化了一下问题的形式.因此,在解题时,弄清问题的本质是非常重要的.7.1.8★已知m 为实数,且sin α、cos α是关于x 的方程2310x mx -+=的两根.求44sin cos αα+的值. 解析由根与系数的关系知1sin cos 3αα=.则有()()2244227sin cos sin cos 2sin cos 9αααααα+=+-=.7.1.9★★设A 、B 是一个直角三角形的两个锐角,满足sin sin A B -=sin A 及sin B 的值. 解析由于90A B +=︒,故由互余关系得()sin sin 90cos B A A =︒-=.因此条件即为sin cos A A -=①将上式平方,得221sin cos 2sin cos 2A A A A +-=, 由正、余弦的平方关系,即有12sin cos 2A A =,所以()2223sin cos sin cos 2sin cos 12sin cos 2A A A A A A A A +=++=+=,因sin A 、cos A 均为正数,故sin cos 0A A +>.因此由上式得sin cos A A +=②由①、②得sin A,cos A =故sin B =. 评注本题也可如下解答:由①得sin cos 2A A =+两边平方,得221sin cos 2A A A =++, ③因22sin 1cos A A =-,代入上式并整理,得212cos 02A A -=, ④解得cos A =.因cos 0A >,故只有cos A =sin A =. 7.1.10★若存在实数x 和y ,使得222225sin cos , 43cos sin ,4x y a x y a ⎧+=⎪⎪⎨⎪+=⎪⎩ 求实数a 的所有可能值. 解析把两式相加,得2358a a +=,解得1a =,或83a =-(舍去).当1a =时,π4x =,π6y =满足方程.故1a =. 7.1.11★★已知关于x 的一元二次方程()()22211120m x m x +--+=的两个根是一个直角三角形的两个锐角的正弦,求实数m 的值.解析设方程的两个实根1x 、2x 分别是直角三角形ABC 的锐角A 、B 的正弦.则()22222212sin sin sin cos 190x x A B A A A B +=+=+=+=︒,又122112m x x m -+=+,12122x x m =+, 所以()2222111212211242122m x x x x x x m m -⎛⎫+=+-=-= ⎪++⎝⎭. 化简得224230m m -+=,解得1m =或23.检验,当1m =时,()()22114820m m =--+<△;当23m =时,()()22114820m m =--+△≥.所以23m =.评注本题是三角函数与一元二次方程的综合,基本解法是利用韦达定理和22sin cos 1αα+=列方程求解.要注意最后检验方程有无实数根.7.1.12★★已知方程2450x x k -+=的两根是直角三角形的两个锐角的正弦,求k .解析根据韦达定理,有12125 , 4.4x x k x x ⎧+=-⎪⎪⎨⎪=⎪⎩并且由于其两根是直角三角形的两个锐角的正弦,所以又有22121x x +=. 于是有()2222121212512244k x x x x x x ⎛⎫=+=+-=--⨯ ⎪⎝⎭.解得98k =.7.1.13★★★若直角三角形中的两个锐角A 、B 的正弦是方程20x px q ++=的两个根; (1)那么,实数p 、q 应满足哪些条件?(2)如果p 、q 满足这些条件,方程20x px q ++=的两个根是否等于直角三角形的两个锐角A 、B 的正弦?解析 (1)设A 、B 是某个直角三角形两个锐角,sin A 、sin B 是方程20x px q ++=的两个根,则有240p q =-△≥. ①由韦达定理,sin sin A B p +=-,sin sin A B q =.又sin 0A >,sin 0B >,于是0p <,0q >. 由于()sin sin 90cos B A A =︒-=.所以sin cos A A p +=-,sin cos A A q =, 所以()()22sin cos 1sin cos 12p A A A A q -=+=+=+,即221p q -=.由①得21240q p q -=-≥,则12q ≤. 故所求条件是0p <,102p <≤,221p q -=.②(2)设条件②成立,则24120p q q -=-≥,故方程有两个实根:α==β==.由②知p -=又p -,所以0p p <---,故0βα>≥. 又()2222221p q αβαβαβ+=+-=-=,故01αβ<<≤. 所以,α、β为直角三角形两个锐角的正弦. 评注一般地,有()sin 90cos αα︒-=,()cos 90sin αα︒-=.即在Rt ABC△中()90C ∠=︒,sin cos A B =,cos sin A B =.7.1.14★★已知方程()24210x m x m -++=的两个根恰好是一个直角三角形的两个锐角的余弦,试求m 的值. 解析设题中所述的两个锐角为A 及B ,由题设得()241160 , 1cos cos , 2cos cos .4m m m A B m A B ⎧=+-⎪⎪+⎪+=⎨⎪⎪=⎪⎩△≥ 因为cos sin B A =,故()2, 1cos sin , 2cos sin , 410m A A m A m m A ++==⎧=-⇒⎪⎪⎪⎨⎪⎪⎪⎩可△≥取任意实数①② ①式两边平方,并利用恒等式22sin cos 1A A +=,得()()221cos sin 12sin cos 4m A A A A ++=+=.再由②得()21124m m ++=,解得m =.由cos 0A >,sin 0A >及②知0m >.所以m =.7.1.15★★不查表,求15︒的四种三角函数值. 解析30︒、45︒、60︒这些特殊角的三角函数值,我们可以利用含有这些特殊角的直角三角形的几何性质及勾股定理直接推出.同样,15︒角的三角函数值,也可以利用直角三角形的性质将其推出.如图所示.在ABC △中,90C ∠=︒,30ABC ∠=︒,延长CB 到D ,使BD BA =,则1152D BAD ABC ∠=∠=∠=︒.A BCD130°15°设1AC =,则2AB =,BC 2BD =,所以2CD CB BD =+=+所以)1AD ====.所以sin15AC AD ︒===, cos15CD AD ︒===, tan152AC CD ︒===cot152CDAC︒==. 评注 将15︒角的三角函数求值问题,通过构造适当的三角形,将它转化为30︒角的三角函数问题,这种将新的未知问题通过一定途径转化为旧的已解决了的问题的方法,是我们研究解决新问题的重要方法.根据互余三角函数关系式,我们很容易得到75︒角的四种三角函数值. 7.1.16★★求22.5︒角的正切值(不查表,不借助计算器). 解析4522.52︒︒=,所以设法构造一个含22.5︒角的直角三角形,用定义求值. 如图,Rt ABC △中,90C ∠=︒,45B ∠=︒,延长CB 到D ,使BD BA =,则122.52D B ∠=∠=︒.设AC b=,有AB,)1DC DB BC b =+=+.AB CD故tan 22.51ACDC︒===.7.1.17★★求sin18︒的值. 解析构造一个顶角A 为36︒的等腰ABC △,AB AC =,如图,作内角平分线则36ABD DBC ∠=∠=︒,设1AC =,BC x =.AB CDH由于36DBA DAB ∠=∠=︒,72BDC BCD ∠=∠=︒,故CB BD DA x ===,而CAB △∽CBD △(36CAB CBD ∠=∠=︒),故AC BC BC DC =,故11xx x=-,有x =(舍去). 再作AH BC ⊥于H,则18CAH ∠=︒,CH =.所以sin18︒. 评注本题所构造的等腰三角形是圆内接正十边形的相邻顶点与圆心确定的三角形,利用它可以求出半径为R 的圆内接正十边形的边长.7.1.18★已知直角三角形ABC 中,90C ∠=︒,sin sin A B m +=,求证:21sin sin 2m A B -=.解析 因为90A B ∠+∠=︒,所以sin cos B A =.从而2222sin sin sin cos 1A B A A +=+=.又sin sin A B m +=,所以()22sin sin m A B =+22sin sin 2sin sin A B A B =++,即()22222sin sin sin cos 1A B m A A m =-+=-.7.1.19★★在ABC △中,a 、b 、c 分别是角A 、B 、C 的对边,且101511b c c a a b+++==,求sin :sin :sin A B C .解析 依题意,可将边转化为角.设sin sin sin a b ck A B C===,则 sin a k A =,sin b k B =,sin c k C =.于是题中条件化为sin sin sin sin sin sin 101511B C C A A B+++==. 令上述比值为t ,那么sin sin 10B C t +=, sin sin 15C A t +=,sin sin 11A B t +=.所以有sin 8A t =,sin 7C t =,sin 3B t =,从而得sin :sin :sin 8:3:7A B C =. 7.1.20★★★若θ为三角形的最小内角,试求关于x 的方程)543284cos 0x x x θ-+-=的所有实根.解析 原方程显然有根0x =,再求方程)43284cos 0x x x θ-+-+=①的实根.θ为三角形最小内角,则060θ︒<︒≤,所以1cos 12θ<≤.方程①可整理变形为22221122cos 022x x x θ⎛⎫⎛⎫-+-+-+= ⎪ ⎪⎝⎭⎝⎭,2212202x x ⎛⎫- ⎪⎝⎭≥,21cos 02x θ⎛⎫- ⎪⎝⎭≥.令()2f x =-由(240=--△知()f x 恒大于零,即不存在使方程①成立的实数x .故原方程仅有一个实根0x =.7.1.21★★已知函数2cos 4sin 6y x x αα=-+对于任意实数x 都有0y >,且α是三角形的一个内角,求cos α的取值范围. 解析由于方程没有实数根,()24sin 24cos 0αα-<.并根据22sin cos 1αα+=,可以得到22cos 3cos 20αα+->.因此cos 0.5α>或cos 2α<-. 由于1cos 0α>>,所以1cos 0.5α>>. 7.1.22★★已知α、β是钝角,求证: (1)关于x 的方程22cos 0x α-=①有两个不相等的实根;(2)若sin β是方程①的根,则cos β也是方程①的根. 解析(1)因α是钝角,故cos 0α<,于是()()41cos 8cos 41cos 0ααα=+-=->△,所以,方程①有两个不相等的实根.(2)设r 是方程①的另一根,则sin r β≠.由韦达定理,得sin r β+=② cos sin 02r αβ=<.③由于sin 0β>,故0r <.由②、③两式得()()222sin sin 2sin 1cos cos 1r r r βββαα+=+-=+-=.所以cos r β==,即cos β也是①的根.7.1.23★★已知()()2cos 4sin 6y x x αα=-+,对于任意实数x ,都有0y >,且是三角形的一个内角,求α的取值范围. 解析因对任意实数x ,二次函数()()2cos 4sin 6y x x αα=-+y 恒大于0,所以cos 0α>,并且()24sin 24cos 0αα=-<△,所以()2161cos 24cos 0αα--<,整理得()()2cos 1cos 20αα-+>.因cos 20α+>,故2cos 10α->,1cos 2α>. 所以060α︒<<︒.7.1.24★★若x 、y 为实数,221x y +=,α为锐角,求证:sin cos x y αα+的绝对值不大于1. 解析由221x y +=,22sin cos 1αα+=,得()()2222sin cos 1x y αα++=,即22222222sin cos cos sin 1x y x y αααα+++=,加一项减一项,得22222222sin 2sin cos cos cos 2cos sin sin 1x xy y x xy y αααααααα+++-+=.即()()2sin cos cos sin 1x y x y αααα2++-=, 因为()2cos sin 0x y αα-≥, 所以()2sin cos 1x y αα+≤, 故sin cos 1x y αα+≤.7.1.25★已知090αβ︒<<<︒,求证:(1)sin sin αβ<;(2)cos cos αβ>;(3)tan tan αβ<. 解析用定义将三角比表示成直角三角形对应边的比,然后利用边的不等关系证明.作1AOB α∠=,2A OB β∠=,使121AO A O ==,作11A H OB ⊥于1H ,22A H OB ⊥于2H . BCOA 1A 2H 1H 2由21A OB AOB ∠>∠得射线1OA 与线段22A H 相交,设交于C ,则12OA OA OC =>,所以1A 在OC 的延长线上,所以1H 在2OH 的延长线上,得12OH OH >.又11A H =22A H 所以1122A H A H <. 因为11111sin A H A H OA α==,111cos OH OH OA α==,111tan A H OH α=,22222sin A H A H OA β==,222cos OH OH OA β==,222tan A H OH β=,所以sin sin αβ<,cos cos αβ>,tan tan αβ<. 7.1.26★★ 已知090α︒<<︒,求证: 解析1 构造Rt ABC△,90C ∠=︒,1AB =,CAB α∠=,如图,则sin sin BC AB αα==,cos cos AC AB αα==.(1)由+BC AC AB +>,得co si s 1n αα+>;(2)作高CH ,中线CD ,则CH CD ≤,1122CD AB ==,211112244ABC S AB CH AB CD AB =⋅⋅==△≤(ABC △以中线CD ,高线CH 重合为面积最大).CABDHαcos αsin α而11sin cos 22ABC S BC AC αα=⋅=△,所以2sin cos 1αα≤. 有12sin cos 2αα+≤,即()2sin cos 2αα+≤. 又sin cos 0αα+>,所以sin cos αα+. 由(1),(2)知,1sin cos αα<+ 解析2 ()2sin cos 12sin cos 1αααα+=+>.又由()()222sin cos 12sin cos sin cos 0αααααα-+=-=-≥,得()22sin cos αα+≥, 故有()21sin cos 2αα<+≤,由sin cos 0αα+>,知1sin cos αα<+ 评注 解析1同时也证明了“斜边给定的直角三角形中,等腰直角三角形的面积最大”这一结论.7.1.27★★★证明:对于任何实数x 、y ,有()22sin sin sin sin sin sin 2x y x y ⎛⎫+ ⎪⎝⎭≥. 解析 因为对于任意x 、y ,都有1sin 1x -≤≤,1sin 1y -≤≤,所以22πsin sin π1sin sin 1222x y x y +-<-<≤≤≤.而函数sin x 在ππ22x -≤≤上的值是随着x 的增加而增加的,故()22sin sin sin sin sin sin 2x y x y ⎛⎫+⎪⎝⎭≥. 7.1.28★★★若0a b >>,090α︒︒≤≤,试证明sin sin a b a b αα+-不能介于a b a b -+及a ba b+-之间.解析假设sin sin a b a b a b a b a b a b αα-++<<+--,则有sin sin a b a ba b a bαα++<--. 由题意知0sin 1α≤≤,0a >,则sin a a α≤,即sin a b a b α--≤,又0b >,从而2211sin b ba b a bα++--≥,即sin sin a b a ba b a bαα++--≥,所以假设不成立,即命题成立. 7.1.29★★★设221x y +=,且1x ≠-,1y ≠-,求证:()2111y x y x x yx y-=-++++. 解析本题如果直接用代数方法,通过代数式的运算证明等式成立,比较复杂.根据已知条件221x y +=,联想到22sin cos 1αα+=,因此可设sin x α=,cos y α=,则将代数式转化为三角式,利用三角函数有关公式进行变形,这样会简便一些. 设sin x α=,cos y α=,则11y x x y -++cos sin 1sin 1cos αααα=-++()()22cos cos sin sin 1sin 1cos αααααα+--=++ ()()cos sin 1cos sin 1sin cos sin cos αααααααα-+=+++()()2cos sin 1cos sin 22sin 2cos 2sin cos αααααααα-++=+++()()222cos sin 1cos sin 1sin cos 2sin 2cos 2sin cos αααααααααα-++=+++++()()()22cos sin 1cos sin 1cos sin αααααα-++=++()()2cos 2sin 21cos sin 1y x x yαααα--==++++.评注在一些代数等式的证明中,如果已知条件221x y +=或()220x y a a +=>,则可设cos , sin ;x y αα=⎧⎨=⎩或 , ,x y αα⎧=⎪⎨⎪⎩从而将代数式转化为三角等式的证明问题,我们称这种转化为三角代换法.由于三角函数的公式较多,因此化为三角式后,运算化简常比较方便.§7.2解直角三角形7.2.1★★如图,在直角三角形ABC 中,90C ∠=︒,AD 是A ∠的平分线,且CD =,DB =求ABC △的三边长.ABC DE解析 由角平分线想到对称性,考虑过D 作DE AB ⊥,交AB 于E ,则由90C ∠=︒得CD DE ==.在直角三角形BDE 中,1sin 2DE B DB ===,则60B ∠=︒,所以tan AC BC B ===2sin ACAB AC B===, BC CD DB =+=故ABC △的三边长分别为7.2.2★★在Rt ABC △中(如图),D 、E 是斜边AB 的三等分点,已知sin CD x =,()cos 090CE x x =︒<<︒.试求AB 的长.AB C DEFP QG解析 作DF AC ⊥于F ,EG AC ⊥于G ;DP BC ⊥于P ,EQ BC ⊥于Q .令BP PQ QC a ===,AG GF FC b ===.则2DF a =,EG a =.在Rt CDF △和Rt CEG △中,由勾股定理,得()2222sin a b x +=,及()2222cos a b x +=, 两式相加得()2251a b +=,2215a b +=.所以3AB BD == 7.2.3★★如图,ABC △中,90C ∠=︒,10AB =,6AC =,AD 是BAC ∠的平分线,求点B 到直线AD 的距离BH .ABCD EH解析 已知Rt ABH △中,10AB =,要求BH ,可求出BAH ∠的正弦值,而BAH CAD ∠=∠,因而可先求出DC 的长.作DE AB ⊥于E ,有6AE AC ==,ED CD =. 设3DC k =,由三角形内角平分线性质有106BD DC =,则5BD k =. Rt BDE △中,222DE BE BD +=,即()()()22231065k k +-=,得1k =. 33CD k ==,AD =sin 10BHDAC ∠==,故BH = 7.2.4★已知ABC △是非等腰直角三角形,90BAC ∠=︒,在BC 所在直线上取两点D 、E 使DB BC CE ==,连结AD 、AE .已知45BAD ∠=︒.求tan CAE ∠的值.解析 如图,过B 、C 两点作BM AC ∥、CN AB ∥分别交AD 、AE 于M 、N .易知AB CDEMN2AC BM =,2AB CN =,tan BM BAD AB ∠=,tan CNCAE AC∠=, 从而,1tan tan 4BAD CAE ∠∠=. 因为tan 1BAD ∠=,则1tan 4CAE ∠=.7.2.5★★设有一张矩形纸片ABCD (如图),3AB =,4BC =.现将纸片折叠,使C 点与A 点重合,试求折痕EF 的长.ABCDEOF解析 设O 是矩形对角线AC 的中点.连结CF ,由折叠知CF AF =,故FO AC ⊥,即EF AC ⊥.由3AB =,4BC =,得5AC =,从而1522AO AC ==. 在Rt AOF △中,90AOF ∠=︒,故tan OF AO FAO =⋅∠.又由Rt ADC △得3tan tan 4DC FAO DAC AD ∠=∠==, 所以5315248OF =⋅=,1524EF OF ==. 7.2.6★★已知三角形两边之和是10,这两边的夹角为30︒,面积为254,求证:此三角形为等腰三角形.解析由题意可设10a b +=,30α=︒,则125sin 24S ab α==△,即1125224ab ⋅=, 得25ab =.于是,由10a b +=,25ab =,得a 、b 是方程210250x x -+=的两个根.而此方程有两个相等的根,所以5a b ==,即此三角形为等腰三角形. 评注也可以直接由()()2240a b a b ab -=+-=,得a b =.7.2.7★★在ABC △中,90C ∠=︒,其周长为2+且已知斜边上的中线长为1.如果BC AC >,求tan A 的值. 解析由于斜边长是斜边上中线长的2倍,故2AB c ==.于是,由题设及勾股定理,得224. a b a b ⎧++==⎪⎨⎪⎩①② 把①式两边平方,得2226a ab b ++=.再由②得 1ab =. ③由①、③知,a 、b 分别是二次方程210u +=的两根,解得u .因为BC AC >(即a b >),故12BC =,12AC =,所以tan 2BC A AC === 7.2.8★★已知a 、b 、c 分别是ABC △中A ∠、B ∠,C ∠的对边,且a 、b 是关于x 的一元二次方程()()2424x c c x ++=+的两个根. (1)判断ABC △的形状;(2)若3tan 4A =求a 、b 、c . 解析(1)根据题意,尝试从边来判断.因为4a b c +=+,()42ab c =+,所以()2222a b a b ab +=+-()()224242c c c =+-⨯+=, 从而知ABC △是直角三角形,90C ∠=︒. (2)由90C ∠=︒,3tan 4A ∠=,得34a b=.令3a =,()40b k k =>,则5c k =,于是754k k =+,得2k =,从而有6a =,8b =,10c =.7.2.9★★在Rt ABC △中,90C ∠=︒,12ABC S m =△,且两直角边长满足条件32a b m +=. (1)证明:24m ≥;(2)当m 取最小值时,求ABC △中最小内角的正切值. 解析(1)由题设得,32.ab m a b m =⎧⎨+=⎩消去b ,得32m a a m -⎛⎫=⎪⎝⎭,故实数a 满足二次方程2320x mx m -+=. ①所以()224240m m m m =-=-△≥. 因为0m >,所以24m ≥.(2)当24m =时,方程①只有一个实数根4a =,从而6b =.由b a >,知ABC △的最小内角为A ∠,其正切值2tanA 3a b ==.7.2.10★★如图所示.90A BEF EBC ECD ∠=∠=∠=∠=︒,30ABF ∠=︒,45BFE ∠=︒,60ECB ∠=︒且2AB CD =.求tan CDE ∠的值.ABCDEF解析 因为tan CECDE CD∠=,已知2AB CD =,因此,只需求出AB 与CE 的比值即可. 不妨设1CD =,则2AB =.在Rt ABF △中,90A ∠=︒,30ABF ∠=︒,所以cos30AB BF ==︒. 在Rt BEF △中,90BEF ∠=︒,45BFE ∠=︒,所以cos 45BE BF =︒==在Rt BEC △中,90EBC ∠=︒,60ECB ∠=︒, sin 60BE CE ==︒,所以tan 3CE CDE CD ∠==. 7.2.11★★如图所示.在锐角ABC △中,4sin 5B =,tan 2C =,且10ABC S =△.求BC .AB CD解析 作AD BC ⊥于D ,设AD x =,在Rt ABD △中,因为4sin 5B =,所以3cos 5B ==,所以sin 4tan cos 3B B B ==,所以43AD BD =,34BD x =. 在Rt ADC △中,因为tan 2AD C DC ==,所以22AD x CD ==,所以35424x BC BD CD x x =+=+=. ① 因为1102ABC S BC AD =⨯=△, 所以151024x x ⨯⋅=, 所以4x =.由①知5454BC =⨯=. 评注在一般三角形中,在适当位置作高线,将其转化为直角三角形求解,这是解斜三角形常采用的方法.7.2.12★★如图所示.在ACD △中,45A ∠=︒,5CB =,7CD =,3BD =.求CBD ∠及AC .A B E DC解析1 作CE AD ⊥于E ,设CE x =,BE y =,则有()2222225 , 37. x y x y ⎧+=⎪⎨++=⎪⎩①②②-①得22697524y +=-=,所以52y =.因为x ,所以512cos 52BE CBE CB ∠===,所以60CBE ∠=︒,18060120CBD ∠=︒-︒=︒,所以sin 45CE AC ===︒. 解析2 在CBD △中,5BC =,3BD =,7CD =,由余弦定理得2222cos CD BC BD BC BD CBD =+-⋅⋅∠,所以2222227531cos 22532CD BC BD CBD BC BD ----∠===--⋅⋅-⨯⨯,所以120CBD ∠=︒,从而60CBA ∠=︒.在ABC △中,由正弦定理得sin sin AC BCCBA A=∠,所以5sin sin BC CBAAC A⨯∠==A .7.2.13★★如图,已知ABC △中,1AB =,D 是AB 的中点,90DCA ∠=︒,45DCB ∠=︒.求BC 的长.ABCD E解析 作BE AC⊥B,交AC的延长线于E,设BC x=.则sin 45BE BC =⨯︒=cos45CE BC =⋅︒由DC BE ∥,D 是AB 的中点,知2AE EC ==而222AE BE AB +=,得221+=.即x =,所以BC =.评注通过构造直角三角形,使用三角函数、勾股定理等知识将边角联系起来是求线段长的常用方法.7.2.14★★如图,ABC △中,90ACB ∠=︒,CD AB ⊥于D ,DE AC ⊥于E ,DF BC ⊥于F .求证:33AE AC BF BC=. ABCDE F解析 ADE ACD B ∠=∠=∠,而tan AE ADE DE ∠=,tan ED ACD EC ∠=,tan DF B BF=,所以 tan AE ED DFB DE EC FB===, 又DF EC =,所以3tan AE ED EC B DE EC BF ⋅⋅=,所以3tan AEB BF=. 又tan ACB BC=,所以33AE AC BF BC =. 评注 本题直角三角形较多,直接用相似三角形往往找不好关系,利用等角的三角函数作边的转化,使关系明确.7.2.15★★如图,在ABC △中,90A ∠=︒,AB AC =,M 是AC 边的中点,AD 垂直于BM 且交BC 于D .AB CDF M求证:AMB CMD ∠=∠. 解析作DF AC ⊥于F ,不妨设3AB =,因AD BM ⊥,90BAM ∠=︒,所以DAF ABM ∠=∠.又112tan 2ACMA ABM AB AB ∠===.1tan 2DF DAF FA ∠==.又90BAC ∠=︒,AB AC =,45C ∠=︒,而90DFC ∠=︒,故FC FD =. 由于12FC FA =,而3FC FA +=,1FC =,2FA =,而32MC =,31122FM =-=,1FD =, 即1tan 212FD CMD FM ∠===,又tan 2ABAMB AM∠==,AMB ∠,CMD ∠是锐角. 因此AMB CMD ∠=∠. 评注利用解三角形的知识把结论中有关的线段用常数或适当的参数表示,通过计算证明几何命题,这种方法称为几何题的三角证法.7.2.16★★在等腰直角三角形ABC 中,1AB =,90A ∠=︒,点E 为腰AC 上任意一点,AE a =,点F 在底边BC 上,且FE BE ⊥,求证:()()2121CEF a a S a -=+△.解析如图,过点F 作FD AC ⊥,垂足为D .ABCDEF因为ABE BEA BEA DEF ∠+∠=∠+∠,所以ABE DEF ∠=∠,从而知ABE △∽DEF △, 得AB AEDE DF=. 又因为FD CD =,则令FD x =,那么1DE a x =--. 于是11aa x x=--,得()11a a x a -=+. 故()()()()21111122121CEFa a a a S EC FD a a a --=⋅=⋅-⋅=++△. 7.2.17★★★如图,在直角三角形ABC 中,90A ∠=︒,AB a =,ACb =,E 是AC 上一动点,F 在BC 上,E 从点A 开始向C 运动且保持EF BE ⊥,试写出EFC S △与点E 运动时到点A 距离x 的关系式.ABCDEF解析 如图,过点C 作CD EF ⊥,交直线EF 于D ,则ABE △∽DEC △,得AB BE AEED EC CD==. 由AE x =,得EC b x =-,则a xDE CD =,得a b x DE -=b x x CD -=. 又BEF△∽CDF△,则BE EFCD DF=,即BE EF EFBE CD EF FD ED==++,得(2a b x EF a bx -==+.故()221122CEFax b x S EF CD a bx-=⋅=⋅+△. 7.2.18★★如图(a ),正方形ABCD 的边长E 、F 分别是AB 、BC 的中点,AF 分别交DE 、DB 于点M 、N ,求DMN △的面积.ABCDEFM N(a)CF B EN MDA(b)解析 记正方形ABCD 的边长为2a .由题设易知BFN △∽DAN △,则有21AD AN DN BF NF BN ===, 得2AN NF =,所以23AN AF=.在直角ABF △中,2AB a =,BF a =,则AF ==,于是cos AB BAF AF ∠= 由题设可知ADE△≌BAF△,所以AED AFB ∠=∠,18018090AME BAF AED BAF AFB ∠=︒-∠-∠=︒-∠-∠=︒.于是cos AM AE BAF =⋅∠=,23MN AN AM AF AM =-=-=, 从而415MND AFD S MN S AF ==△△. 又()()212222AFD S a a a =⋅⋅=△,所以2481515MND AFD S S a ==△△. 因a =故8MND S =△.7.2.19★★已知a 、b 、c 是ABC △三边的长,其中b a c >=,且方程20ax c +=两根的差的ABC △中最大角的度数. 解析由已知条件b a c >=可知,这是一个等腰三角形,且底边b 最长,则最大角为B ∠,求出ABC △中的底角A (或C )即可.我们可以先求角A (或C )的三角函数值,再确定角的大小,如图所示.由图知A BCD abc2cos 2b AD bA AB c c===,则关键是求出b 与c 的比值.通过一元二次方程中的条件,可得到关于c 、b 的方程,则问题得到解决.因为a c =,所以方程为20cx c +=. 设1x 、2x 为方程的两个根,则有12x x +=121x x =.因为12x x -=()2122x x -=,即()2121242x x x x +-=,所以242c ⎛⎫-= ⎪ ⎪⎝⎭,c,b c ,所以cos 2b A c =, 所以30A ∠=︒,所以1803030120B ∠=︒-︒-︒=︒. 评注这是一道方程与几何知识的综合题.三角形的边是一元二次方程的系数,利用方程条件导出边的关系,由边的关系再进一步求角的大小. 7.2.20★★在ABC △中,90C ∠=︒,则cot 2A b c a +=;反过来,如果在ABC △中,cot 2A b ca+=,则ABC △是直角三角形. 解析(1)作角平分线AD (图略),则在Rt ACD △中,cot2A ACDC=. 由角平分线的比例性质,有DC ACBD AB=. 所以DC AC BD DC AB AC =++,即DC ba b c=+.所以abDC b c=+. 所以cot2A b ca+=. (2)我们证明:B ∠或C ∠是直角.设90C ∠≠︒,下证90B ∠=︒.如图,作ABC △的角平分线AD ,在直线AD 上取一点E ,使90ACE ∠=︒.由题设有AB CD EFcot 2AC A b c EC a +==,所以abEC b c=+ 又由(1)中的计算,abDC b c=+,所以CD CE =,作CF DE ⊥于F ,则 22DCE FCE DAC BAC ∠=∠=∠=∠.所以180********ABC ACB BAC ACB DCE ACE ∠=︒-∠-∠=︒-∠-∠=︒-∠=︒.7.2.21★★如图,AB 是圆的直径,弦CD AB ∥,AC 与BD 相交于E ,已知AED θ∠=,试求:CDE ABE S S △△.DC ABEθ解析由AB CD ∥,得CDE △∽ABE △.所以22::CDE ABE S S DE BE =△△.连结AD ,则90ADB ∠=︒.故由Rt ADE △,有cos DEAEθ=,又AE BE =,所以2:cos CDE ABE S S θ=△△. 7.2.22★★★如图,延长锐角ABC △的高AD 、BE 、CF 分别交外接圆于L 、M 、N .设垂心为外接圆半径为R .求证:A(1)a b c a b cHA HB HC HL HM HN++=++; (2)sin sin sin 8sinAsin sin AL A BM B CN C R B C ++=. 解析(1)由于CBF △∽AHF △,所以a CFHA AF=. 在Rt AFC △中,tan CF A AF =,所以tan aA HA=. 同理tan b B HB =,tan cC HC=,于是左边tan tan tan A B C =++. 由于H 、D 、C 、E 共圆,所以BHD C ∠=∠.在直角三角形BHD 中,tan BD BHD HD =∠,所以tan BDC HD=.同理tan CDB HD=. 相加得tan tan aC B HD=+. 由于H 是ABC △的垂心,易证HD DL =,所以12HD HL =,()1tan tan 2a C B HL =+. 同理()1tan tan 2b A C HM =+,()1tan tan 2c B A HN =+. 相加后得右边tan tan tan A B C =++.(2)由于H 是垂心,所以HD DL =,可得HBC △≌LBC △. 由于1sin 2ABLC S AL a R AL A =⋅=⨯⨯四边形, 所以sin ABC BCL ABC HBC R AL A S S S S ⋅⨯=+=+△△△△.同理可证sin ABC HCA R BM B S S ⨯⨯=+△,sin ABC HAB R CN C S S ⨯⨯=+△△.相加后得()1sin sin sin 44sin 2ABC R AL A BM B CN C S ab C ++==⋅△22sin 2sin sin R A R B C =⋅⋅⋅,所以sin sin sin 8sin sin sin AL A BM B CN C R A B C ++=.7.2.23★★如图所示,已知电线杆AB 直立于地面上,它的影子恰好照在土坡的坡面CD 和地面BC 上.如果CD 与地面成45︒,60A ∠=︒,4m CD =,(m BC =,求电线杆AB 的长(精确到0.1m ).解析 如图,延长AD 交地面于点E ,过点D 作DF CE ⊥于点F . 因为45DCF ∠=︒,60A ∠=︒,4CD =,所以sin 4542CF DF CD ==︒=⨯=tan 60EF DF =︒==因为tan 30AB BE =︒=,所以(()8.5m AB ==≈. 7.2.24★如图,某岛S 周围42海里内存在着大量的暗礁.现在一轮船自西向东以每小时15海里的速度航行,在、A 处测得S 在北偏东60︒,2小时后在B 处测得S 在正东北方向,试问轮船是否需要改变航行方向行驶,才能避免触礁危险,说明理由.SA B C解析 若设船不改变航向,与小岛S 的最近距离为SC .则有tan60tan45152SC SC ︒-︒=⨯,解得1542SC =<. 因此需要改变航向,以免触礁.7.2.25★★★如图,某污水处理站计划砌一段截面为等腰梯形的排污渠,如果渠深为h ,截面积为S ,试求当倾角θ为多少时造价最小?解析 要使造价最小,只需考虑AD DC CB ++最小,故首先设法用h 、S 、θ表示AD DC CB ++.()()()1122cot cot 22S AB CD h CD h h CD h h θθ=+=+=+. 有cot S CD h h θ=-,则2AD DC CB AD CD ++=+2cot sin h S h θθ⎛⎫=+- ⎪⎝⎭()2cos sin h S h θθ-=+. 因S 、h 为常数,则要求AD DC CB ++的最小值,只需求2cos sin m θθ-=的最小值. 设2cos sin m θθ-=,两边平方整理得 ()()2221cos 4cos 40m m θθ+---=,cos θ==.由上式知()2230m m -≥,解得m 故当m 时,2cos sin θθ-有最小值.当m =时,221cos 12m θ==+,从而得60θ=︒,此时排污渠造价最小.。
三角函数在初中数学中的应用

三角函数在初中数学中的应用在初中数学学习中,三角函数是比较重要的内容。
在初中阶段,学生主要学习正弦函数、余弦函数和正切函数。
这三个函数在生活中的应用非常广泛,几乎涉及到生活的各个方面。
三角函数在初中数学中的应用,主要分为以下几个方面。
一、图形的模拟三角函数可以用来模拟一些具有规律性的图形,例如:正弦函数可以模拟海浪般的波形,余弦函数可以模拟钟摆的运动,正切函数可以模拟图形的变化趋势。
在初中阶段,学生可以通过计算出每个函数在不同角度下的值,来绘制出完整的图形。
通过这种方式,可以让学生更好地理解三角函数的定义、性质和应用。
二、三角函数在几何中的应用三角函数在初中数学中的应用,最重要的一个方面是在几何学中的应用。
初中阶段学生主要学习平面几何、立体几何和三角形几何。
而正弦函数、余弦函数和正切函数都可以用来计算三角形的各种参数。
例如:学生可以利用正弦定理来计算三角形的角度或者利用余弦定理来计算三角形的边长。
而计算三角形的高度、面积等参数,可以使用三角函数中的正切函数进行计算。
三、三角函数在物理中的应用三角函数在初中数学中的应用,还可以用在物理学中。
在物理学中,三角函数尤其是正弦函数和余弦函数,常常被用来描述周期性的现象。
例如:学生可以利用正弦函数和余弦函数来模拟电磁波的传播、声波的振动以及光的折射等现象。
而在物理学中,正切函数通常用于计算速度、加速度和力等物理量的变化趋势。
四、三角函数在工程领域中的应用三角函数在初中数学中的应用还可以用在工程领域中。
例如在建筑、制造、电子工程、汽车制造等领域,都需要用到三角函数。
例如:在建筑领域中,工人需要计算出房屋的倾斜角度和高度,以此来安装楼梯、门框和捆绑钢管等工作。
而在制造领域中,设计师需要计算出各个部件之间的角度和长度,以此来制作出精确的机械。
五、三角函数在数学竞赛中的应用三角函数在初中数学中的应用,最后一个方面是在数学竞赛中的应用。
学生只有深入理解了三角函数的定义、性质和应用,才能在数学竞赛中取得好成绩。
初三数学三角函数(含答案)

初中数学三角函数1、勾股定理:直角三角形两直角边 a 、b 的平方和等于斜边c 的平方。
a 2b 2c 24、任意锐角的正切值等于它的余角的余切值; 任意锐角的余切值等于它的余角的正切值。
tan A cot B cot A tan Bcot-1 ~3~6、 正弦、余弦的增减性:当0°w < 90°时,sin 随 的增大而增大,cos 随 的增大而减小7、 正切、余切的增减性:当0° < <90°时,tan 随 的增大而增大,cot 随 的增大而减小。
1、解直角三角形的定义:已知边和角(两个,其中必有一边)一所有未知的 边和角。
依据:①边的关系: a 2b 2c 2;②角的关系:A+B=90 °;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)2、应用举例:(1)仰角:视线在水平线上方的角; 俯角:视线在水平线下方的角(2)坡面的铅直高度 h 和水平宽度I 的比叫做坡度(坡比)。
用字母i 表示,即i y 。
坡度一 般写成1: m 的形式,如i 1:5等。
把坡面与水平面的夹角记作 (叫做坡角),那么h + i tan 。
l3、 从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图 3, OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
4、 指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30° (东北方向), 南 偏东45° (东南方向),南偏西60° (西南方向), 北偏西60° (西北方向)。
铅垂线*视线 ‘ 仰角水平线俯角1*视线初三数学三角函数综合试题一、填空题: 1、在 Rt △ ABC 中/C = 90°, a = 2, b = 3,则 cosA =_, sinB =_ , tanB = ___ 2、直角三角形 3、已知tan ABC 的面积为24cm 2,直角边AB 为6cm , / A 是锐角,则sinA = =—, 是锐角,贝U sin 12 + ) + cos 2(40 ° 4、 cos 2(50° — _______ ? 5、 如图1,机器人从A 点,沿着西南方向,行了个4,:2单位,至U 达 60°的方向上,贝U 原来 )—tan(30)tan(60 ° + 到原点O 在它的南偏东 保留根号).A 的坐标为B 点后观察 _ (结果 NMNC 0(2)10cm 周长为36cm 则一底角的正切值为_、3的山坡走了 50米,则他离地面 米高。
专题探究课二--中学生数学竞赛中三角函数问题的热点题型

专题探究课二--中学生数学竞赛中三角函数问题的热点题型三角函数是中学数学中的重要内容之一,也是中学生数学竞赛中经常涉及的题型之一。
本文将探讨中学生数学竞赛中三角函数问题的热点题型,以帮助学生更好地应对这类题目。
1. 正弦函数与余弦函数问题1.1 角度转换在数学竞赛中,经常出现要求将弧度转换为角度或者将角度转换为弧度的问题。
考生需要熟悉如何使用正弦函数和余弦函数的定义来进行转换,并灵活运用。
1.2 函数图像理解正弦函数和余弦函数的函数图像是解题的关键。
考生需要熟悉函数图像的特点,如振幅、周期、相位等,并能利用这些特点解决各种类型的问题。
1.3 同角三角函数的关系正弦函数、余弦函数与其他三角函数之间存在一定的关系,如正切函数、余切函数等。
考生需要了解这些关系,并能够利用它们简化计算、求解方程等。
2. 三角恒等式与方程2.1 基本恒等式三角函数的基本恒等式是解题中常用的工具,如正弦函数的和差公式、倍角公式、半角公式等。
考生需要熟悉这些恒等式的推导和应用,并能够利用它们求解各类三角函数方程。
2.2 复杂方程与恒等式的转化在数学竞赛中,有时会出现较为复杂的三角函数方程或者恒等式,考生需要能够灵活运用恒等式的性质将其转化为较为简单的形式,从而更好地解决问题。
2.3 解三角形三角函数的性质可以用来解决三角形相关的问题,如求解三角形的边长、角度等。
考生需要了解三角形的基本概念和性质,并能够运用三角函数解决各类三角形问题。
3. 应用题型数学竞赛中的应用题目常常涉及到三角函数的应用,如航空、导航、建筑等领域。
考生需要能够理解问题背景,灵活运用三角函数的概念和性质解决实际问题,并能够给出合理的解释和推理过程。
总结中学生数学竞赛中三角函数问题是较为常见的题型,要解决这类问题,考生需要熟悉正弦函数和余弦函数的性质,掌握三角函数的基本恒等式和转化方法,并能够灵活应用于各类题目中。
通过不断练习和探索,考生将能够在数学竞赛中取得更好的成绩。
初中数学-三角函数详解

初中数学-三角函数详解我选择介绍初中数学中的三角函数的概念、公式及应用。
一、三角函数的概念三角函数是指在直角三角形中,以某个角为自变量,另外两个角的函数关系。
常见的三角函数有正弦函数、余弦函数和正切函数。
正弦函数sinA表示直角三角形中A角的对边与斜边的比值。
余弦函数cosA表示直角三角形中A角的邻边与斜边的比值。
正切函数tanA表示直角三角形中A角的对边与邻边的比值。
二、三角函数的公式三角函数的公式有很多,其中比较重要的有:1)三角函数的基本关系式sin^2A + cos^2A = 12)正切函数与正弦、余弦函数的关系式tanA = sinA / cosA3)三角函数的和差公式sin(A ± B) = sinAcosB ± cosAsinBcos(A ± B) = cosAcosB ∓ sinAsinBtan(A ± B) = (tanA ± tanB)/(1 ∓ tanAtanB)三、三角函数的应用三角函数广泛应用于几何问题和物理问题中。
下面是两个应用例题:例题1:已知一座房屋的高度为10米,从房屋前面的道路上斜向房屋上方仰视,仰角为30度,求房屋前面道路上的水平距离。
解:设房屋前面道路上的水平距离为x米,则可以列出以下等式:tan30° = 10 / x通过换元和化简,可以求得x的值:x = 10 / tan30° ≈ 17.32因此,房屋前面道路上的水平距离为17.32米。
例题2:已知一辆车从A点出发,向北行驶200公里到达B点,然后向东行驶150公里到达C点,求从C点观察A 点与B点的夹角α。
解:通过勾股定理可以求出直线AB和直线AC的长度:AB = √(200^2 + 150^2) ≈ 250AC = 200根据余弦定理可以求出∓BAC的角度:cosα = (AB^2 + AC^2 - BC^2) / (2 × AB × AC)= (250^2 + 200^2 - 150^2) / (2 × 250 × 200)≈ 0.628通过反余弦函数可以计算出夹角α的度数:α = arccos(0.628) ≈ 51.5°因此,从C点观察A点与B点的夹角α约为51.5度。
三角函数及解直角三角形竞赛试题
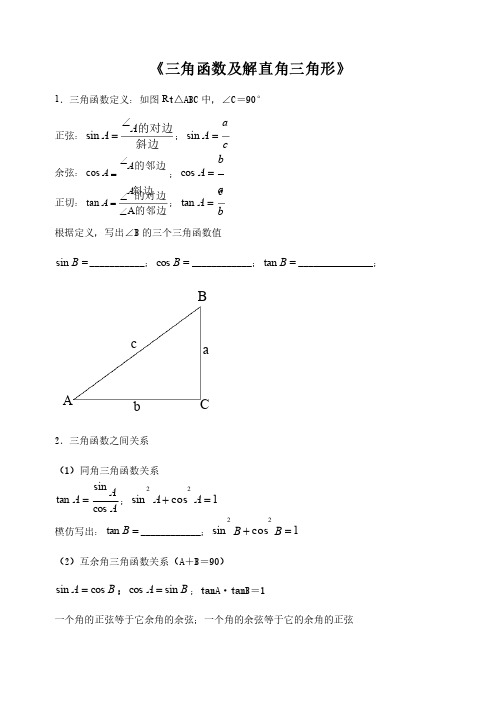
《三角函数及解直角三角形》1.三角函数定义:如图R t △ABC 中,∠中,∠C C =9090°°正弦:斜边的对边A A Ð=sin ;c aA =sin余弦:斜边的邻边A A Ð=cos ;c b A =cos正切:的邻边的对边A tan ÐÐ=A A ;ba A =tan根据定义,写出∠根据定义,写出∠B B 的三个三角函数值的三个三角函数值=B sin ______________________;;=B cos ________________________;;=B tan ______________________________;;cabBCA2.三角函数之间关系.三角函数之间关系 (1)同角三角函数关系)同角三角函数关系AAA cos sintan =;1cos sin 22=+A A模仿写出:=B tan ________________________;;1cos sin 22=+B B (2)互余角三角函数关系()互余角三角函数关系(A A +B =9090))B A cos sin =;B A sin cos =;tanA tanA··tanB tanB==1一个角的正弦等于它余角的余弦;一个角的余弦等于它的余角的正弦3.特殊角的三角函数值3030°、°、°、454545°、°、°、606060°°三角函数三角函数 3030°° 4545°° 6060°° a sina cos a tan4.会设计并根据三角函数关系计算15°、°、757575°角的三角函数°角的三角函数°角的三角函数DC BA5.根据表格中数据总结正弦、余弦、正切的增减性.根据表格中数据总结正弦、余弦、正切的增减性 当0°≤a ≤9090°时,°时,°时,sin a 随a 的增大而的增大而_____________________;;cos a 随a 的增大而的增大而_____________________;;tan a 随a 的增大而的增大而_______ _______6.已知一个三角函数值,求其他三角函数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学竞赛:三角函数
直角三角形中有两条直角边和一条斜边,从这三条边中适当取两条边可以得到不同的比,这些比值的大小显然只与直角三角形中锐角的大小有关,这佯便定义了直角三角形中锐角的三角函数(如图3-14),常用的有:
利用比例的变形并且结合勾股定理,可以从三角函数定义中推出同角三角函数间的关系式:
(1)倒数关系
tgα·ctgα=1;
(2)商的关系
(3)平方关系
sin2α+cos2α=1.
这些同角三角函数关系式对任意锐角都成立,它们在求值、化简以及三角式的变形中有着重要的应用.
如图3-15所示,在直角三角形ABC中,∠A与∠B互为余角,根据三角函数定义不难得到互为余角的三角函数之间的关系:
sinB=sin(90°-A)=cosA,
cosB=cos(90°-A)=sinA,
tgB=tg(90°-A)=ctgA,
ctgB=ctg(90°-A)=tgA.
上述四个公式可以概括为:一个锐角的余角的三角函数值,等于该锐角相应的余函数的函数值
由图3-16可以看到,在直角三角形ABC中,如果斜边长度不变,当锐角A增大时,sinA 与tgA的值也随之增大,而cosA与ctgA的值随之减小.特别地,当A=0时,sin0=0,tg0=0,cos0=1,ctg0值不存在;当A=90°时,sin90°=1,tg90°值不存在,cos90°=0,ctg90°=0.
由于一个角的正弦或余弦值等于直角边与斜边的比,而直角三角形的斜边总是大于直角边,所以,当α为锐角时,总有
0<sinα<1,0<cosα<1.
我们利用以上锐角三角函数的定义及性质,可以解决一些求值、化简以及等式证明等问题.
例1 不查表,求15°的四种三角函数值.
分析 30°,45°,60°这些特殊角的三角函数值,我们可以利用含有这些特殊角的直角三角形的几何性质及勾股定理直接推出.同样,15°角的三角函数值,也可以利用直角三角形的性质将其推出.
解如图3-17所示.在△ABC中,∠C=90°,∠ABC=30°,延长CB到D,使BD=BA,则
所以
所以
说明将15°角的三角函数求值问题,通过构造适当的三角形,将它转化为30°角的三角函数问题,这种将新的未知问题通过一定途径转化为旧的已解决了的问题的方法,是我们研究解决新问题的重要方法.根据互余三角函数关系式,我们很容易得到75°角的四种三角函数值.
例2 比较下列各组三角函数值的大小:
(1)sin19°与cos70°;
(2)ctg65°与cos40°;
(3)cos1°,tg46°,sin88°和ctg38°.
分析 (1)利用互余角的三角函数关系式,将cos70°化为sin20°,再与sin19°比大小.
(2)余切函数与余弦函数无法化为同名函数,但是可以利用某些特殊
再将
ctg65°,cos40°分别与ctg60°,cos45°比大小.
(3)tg45°=1,显然cos1°,sin88°均小于1,而tg46°,ctg38°均大于1.再分别比较cos1°与sin88°,以及tg46°与ctg38°的大小即可.
解 (1)因为cos70°=cos(90°-20°)=sin20°,而
sin19°<sin20°,
所以sin19°<cos70°.
(2)因为
所以 ctg60°<cos45°,
所以 ctg65°<cos40°.
(3)因为ctg38°=ctg(90°-52°)=tg52°,所以
tg52°>tg46°>tg45°=1.
因为
cos1°=cos(90°-89°)=sin89°,
所以sin88°<sin89°<1,
所以ctg38°>tg46°>cos1°>sin88°.
说明比较三角函数值的大小,一般分为三种类型:
(1)同名的两个锐角三角函数值,可直接利用三角函数值随角变化的规律,通过比较角的大小来确定三角函数值的大小.
(2)互为余函数的两锐角三角函数值,可利用互余角的三角函数关系式化为同名三角函数,比较其大小.
(3)不能化为同名的两个三角函数,可通过与某些“标准量”比大小,间接判断它们的大小关系,常选择的标准量有:0,1以及其他一些特殊角如30°,45°,60°的三角函数值.
例3 化简求值:
(1)tg1°·tg2°·tg3°·…·tg89°;
分析 (1)因为tg89°=tg(90°-1°)=ctg1°,而tg1°·ctg1°=1,所以,可将连乘积中的第一个因式与倒数第一个因式相乘,结果为1.同样方法,将第二个因式与倒数第二个因式相乘,其积也是1.依次类推.
(3)利用同角三角函数关系将正切函数化为正弦函数与余弦函数,再进一步化简求值.
(4)将被开方式化为完全平方的形式,即
1-2sin11°·cos11°=sin211°-2sin11°·cos11°+cos211°
=(sin11°-cos11°)2.
因为sin1l°<cos11°,所以根式化简后得cos11°-sin11°.
(5)根据tgα=3,求出sinα与cosα的值.也可以将所求分式的分子、分母同除以cos2α,将其化为用tgα表示的分式.
解 (1)原式=tg1°·tg2°·tg3°·…·tg44°·tg45°
·ctg44°·ctg43°·…·ctg3°·ctg2°·ctg1°
=(tg1°·ctg1°)·(tg2°·ctg2°)·…·(
tg44°·ctg44°)·tg45°
=1·1·…·1=1.
说明同角三角函数关系式以及互余两角三角函数关系式,在三角式变形、化简、求值及证明中是重要的依据.
例4 设α是锐角,若
求以tgα,ctgα为两根的一元二次方程.
分析根据韦达定理,以tgα,ctgα为两根的一元二次方程是
x2-(tgα+ctgα)x+tgα·ctgα=0,
因此,解决问题的关键是求出tgα+ctgα的值.
解由已知条件
可得
所以
(1)当sinα=cosα时,tgα=ctgα=1,所求方程为
x2-2x+1=0,
所求方程为
即4x2-9x+4=0.
说明这是一道一元二次方程与三角函数相结合的综合题,应注意运用分析法、综合法,寻求解题途径.
例5 设x2+y2=1,且x≠-1,y≠-2,求证:
分析本题如果直接用代数方法,通过代数式的运算证明等式成立,比较复杂.根据已知条件x2+y2=1,联想到sin2α+cos2α=1,因此可设x=sinα,y=cosα,则将代数式转化为三角式,利用三角函数有关公式进行变形,这样会简便一些.
证设x=sinα,y=cosα,则
说明在一些代数等式的证明中,如果已知条件
x2+y2=1或x2+y2=a(a>0),
则可设
从而将代数式转化为三角等式的证明问题,我们称这种转化为三角代换法.由于三角函数的公式较多,因此化为三角式后,运算化简常比较方便.
【练习】
3.求值:sin6α+cos6α+3sin2α·cos2α+4.
4.求证:
(1)sin(90°-A)ctg(90°-A)=sinA;
(2)sinAcos(90°-A)+cosAsin(90°-A)=1;
5.化简下列各式,并求出它们的值:
(1)(sinA+cosA)2+(sinA-cosA)2;
6.证明:
sin2A·tgA+cos2A·ctgA+2sinA·cosA=tgA+ctgA.。
