九年级三角函数竞赛题(含答案)
初三数学三角函数(含答案)
则电线杆的高度为 ( A．9 米 B．28 米
)
C． 7 3米
D. 14 2 3 米
19、如图 6,两建筑物的水平距离为 am,从 A 点测得 D 点的俯角为 a,测得 C 点的
俯角为β,则较低建筑物 CD 的高为 ( )
A.a m
B.(a·tanα)m
C. a m tan
D.a(tanα－tanβ)m
24、已知 Rt△ABC 的斜边 AB 的长为 10cm , sinA、sinB 是方程 m(x2－2x)+5(x2+x)+12=0 的两根。 （1）求 m 的值 （2）求 Rt△ABC 的内切圆的面积
25、如图,△ABC 是等腰三角形,∠ACB=90°,过 BC 的中点 D 作 DE⊥AB,垂足为 E,连结 CE,求 sin∠ACE 的值.
1、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的 边和角。
依据：①边的关系： a2 b2 c2 ；②角的关系：A+B=90°；③边角关系：三角函
数的定义。(注意：尽量避免使用中间数据和除法)
2、应用举例： (1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。
铅垂线
视线
A.(cosα,1)
B.(1,sinα) C.(sinα,cosα)
D.(cosα,sinα)
14、如图 4，在△ABC 中，∠C=90°，AC=8cm，AB 的垂直平分线 MN 交 AC 于 D，
连结 BD，若 cos∠BDC= 3 ，则 BC 的长是（
5
A、4cm
B、6cm C、8cm
） D、10cm
tan A cotB cot A tanB tan A 1 (倒数)
初中数学三角函数难题(含答案)
1．已知等边△ABC内接于⊙O，点D是⊙O上任意一点，则sin∠ADB的值为（）A．1 B．C． D．2．在Rt△ABC中，∠C=90°，BD是△ABC的角平分线，将△BCD沿着直线BD折叠，点C落在点C1处，如果AB=5，AC=4，那么sin∠ADC1的值是．3．观察下列等式①sin30°=cos60°=②sin45°=cos45°=③sin60°=cos30°=…根据上述规律，计算sin2a+sin2（90°﹣a）= ．4．有四个命题：①若45°＜a＜90°，则sina＞cosa；②已知两边及其中一边的对角能作出唯一一个三角形；③已知x1，x2是关于x的方程2x2+px+p+1=0的两根，则x1+x2+x1x2的值是负数；④某细菌每半小时分裂一次（每个分裂为两个），则经过2小时它由1个分裂为16个．其中正确命题的序号是（注：把所有正确命题的序号都填上）．5．如图，一束光线从点A（3，3）出发，经过y轴上点C反射后经过点B（1，0），则光线从点A到点B经过的路径长为．6．在Rt△ABC中，∠C=90°，BC：AC=3：4，则cosA= ．7．如果α是锐角，且sin2α十cos235°=1，那么α=度．8．因为cos30°=，cos210°=﹣，所以cos210°=cos（180°+30°）=﹣cos30°=﹣；因为cos45°=，cos225°=﹣，所以cos225°=cos（180°+45°）=﹣cos45°=﹣；猜想：一般地，当a为锐角时，有cos（180°+a）=﹣cosa，由此可知cos240°的值等于．9．在△ABC中，已知sinA=，cosB=，则∠C= ．10．在△ABC中，（tanC﹣1）2+|﹣2cosB|=0，则∠A= ．11．若α、β均为锐角，则以下有4个命题：①若sinα＜sinβ，则α＜β；②若α+β=90°，则sinα=cosβ；③存在一个角α，使sinα=1.02；④tanα=．其中正确命题的序号是．（多填或错填得0分，少填的酌情给分）12．附加题：如图，在Rt△ABC中，BC、AC、AB三边的长分别为a、b、c，则sinA=，cosA=，tanA=．我们不难发现：sin260°+cos260°=1，…试探求sinA、cosA、tanA之间存在的一般关系，并说明理由．13．对于钝角α，定义它的三角函数值如下：sinα=sin（180°﹣α），cosα=﹣cos（180°﹣α）（1）求sin120°，cos120°，sin150°的值；（2）若一个三角形的三个内角的比是1：1：4，A，B是这个三角形的两个顶点，sinA，cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根，求m的值及∠A和∠B 的大小．14．如图，在梯形ABCD中，AD∥BC，AD=3，DC=5，AB=4，∠B=45°．动点M 从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动．设运动的时间为t 秒．（1）求BC的长；（2）当MN∥AB时，求t的值；（3）试探究：t为何值时，△MNC为等腰三角形．15．如图，从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度．如果这时气球的高度CD为90米．且点A、D、B在同一直线上，求建筑物A、B间的距离．16．钓鱼岛自古以来就是我国的神圣领土，为维护国家主权和海洋权利，我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理．如图，某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B，B船在A船的正东方向，且两船保持20海里的距离，某一时刻两海监船同时测得在A的东北方向，B的北偏东15°方向有一我国渔政执法船C，求此时船C与船B的距离是多少．（结果保留根号1．已知等边△ABC内接于⊙O，点D是⊙O上任意一点，则sin∠ADB的值为（）A．1 B．C． D．【解答】解：∵△ABC是等边三角形，∴∠ACB=60°．∵∠ADB与∠ACB是同弧所对的圆周角，∴∠ADB=60°．∴sin∠ADB=sin60°=．故选C．2．（2013•崇明县一模）在Rt△ABC中，∠C=90°，BD是△ABC的角平分线，将△BCD沿着直线BD折叠，点C落在点C1处，如果AB=5，AC=4，那么sin∠ADC1的值是．【解答】解：∵∠C=90°，BD是△ABC的角平分线，∵将△BCD沿着直线BD折叠，∴C1点恰好在斜边AB上，∴∠DC1A=90°，∴∠ADC1=∠ABC，∵AB=5，AC=4，∴sin∠ADC1=．故答案为：．3．（2012•衡阳）观察下列等式①sin30°=cos60°=②sin45°=cos45°=③sin60°=cos30°=…根据上述规律，计算sin2a+sin2（90°﹣a）= 1 ．【解答】解：由题意得，sin230°+sin2（90°﹣30°）=1；sin245°+sin2（90°﹣45°）=1；sin260°+sin2（90°﹣60°）=1；故可得sin2a+sin2（90°﹣a）=1．故答案为：1．4．（2010•防城港）有四个命题：①若45°＜a＜90°，则sina＞cosa；②已知两边及其中一边的对角能作出唯一一个三角形；③已知x1，x2是关于x的方程2x2+px+p+1=0的两根，则x1+x2+x1x2的值是负数；④某细菌每半小时分裂一次（每个分裂为两个），则经过2小时它由1个分裂为16个．其中正确命题的序号是①④（注：把所有正确命题的序号都填上）．【解答】解：①因为sin45°=cos45°=，再结合锐角三角函数的变化规律，故此选项正确；②不一定能够判定两个三角形全等，故此选项错误；③根据根与系数的关系，得x1+x2=﹣，x1x2=．∴x1+x2+x1x2=，是正数．故此选项错误；④根据题意，得2小时它由1个分裂24个，即16个，故此选项正确．故正确的有①④．5．（2011•莆田）如图，一束光线从点A（3，3）出发，经过y轴上点C反射后经过点B（1，0），则光线从点A到点B经过的路径长为 5 ．【解答】解：如图所示，延长AC交x轴于B′．则点B、B′关于y轴对称，CB=CB′．作AD⊥x轴于D点．则AD=3，DB′=3+1=4．∴AB′=AC+CB′=AC+CB=5．即光线从点A到点B经过的路径长为5．6．（2007•眉山）在Rt△ABC中，∠C=90°，BC：AC=3：4，则cosA= ．【解答】解：∵Rt△ABC中，∠C=90°，BC：AC=3：4，∴设BC=3x，则AC=4x，∴AB=5x，∴cosA===．7．（2002•西城区）如果α是锐角，且sin2α十cos235°=1，那么α=35 度．【解答】解：∵sin2α十cos235°=1，∴α=35°．8．（2010•湛江）因为cos30°=，cos210°=﹣，所以cos210°=cos（180°+30°）=﹣cos30°=﹣；因为cos45°=，cos225°=﹣，所以cos225°=cos（180°+45°）=﹣cos45°=﹣；猜想：一般地，当a为锐角时，有cos（180°+a）=﹣cosa，由此可知cos240°的值等于﹣．【解答】解：∵当a为锐角时，有cos（180°+a）=﹣cosa，∴cos240°=cos（180°+60°）=﹣cos60°=﹣．9．（2013•邵阳模拟）在△ABC中，已知sinA=，cosB=，则∠C= 105°．【解答】解：∵sinA=，cosB=，∴∠A=30°，∠B=45°，∴∠C=180°﹣30°﹣45°=105°．故答案为：105°．10．（2012•海南模拟）在△ABC中，（tanC﹣1）2+|﹣2cosB|=0，则∠A= 105°．【解答】解：∵（tanC﹣1）2+|﹣2cosB|=0，∴tanC﹣1=0，﹣2cosB=0，即tanC=1，cosB=，又∵B、C在同一个三角形中，∴B=30°，C=45°，∴A=180°﹣30°﹣45°=105°．故答案是105°．11．（2011•九江模拟）若α、β均为锐角，则以下有4个命题：①若sinα＜sinβ，则α＜β；②若α+β=90°，则sinα=cosβ；③存在一个角α，使sinα=1.02；④tanα=．其中正确命题的序号是①②④．（多填或错填得0分，少填的酌情给分）【解答】解：∵sinα＜sinβ，则α＜β；故此选项正确；②若α+β=90°，则sinα=cos（90°﹣α）=cosβ，∴故此选项正确；③存在一个角α，sinα=，∴sinα≤1，∴sinα=1.02，故此选项错误；④tanα=．根据对应边之间关系得出，故此选项正确．故答案为：①②④．12．（2008•庆阳）附加题：如图，在Rt△ABC中，BC、AC、AB三边的长分别为a、b、c，则sinA=，cosA=，tanA=．我们不难发现：sin260°+cos260°=1，…试探求sinA、cosA、tanA之间存在的一般关系，并说明理由．【解答】解：存在的一般关系有：（1）sin2A+cos2A=1；（2）tanA=．证明：（1）∵sinA=，cosA=，a2+b2=c2，∴sin2A+cos2A==1．（2）∵sinA=，cosA=，∴tanA==，=．13．（2013•大庆）对于钝角α，定义它的三角函数值如下：sinα=sin（180°﹣α），cosα=﹣cos（180°﹣α）（1）求sin120°，cos120°，sin150°的值；（2）若一个三角形的三个内角的比是1：1：4，A，B是这个三角形的两个顶点，sinA，cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根，求m的值及∠A和∠B 的大小．【解答】解：（1）由题意得，sin120°=sin（180°﹣120°）=sin60°=，cos120°=﹣cos（180°﹣120°）=﹣cos60°=﹣，sin150°=sin（180°﹣150°）=sin30°=；（2）∵三角形的三个内角的比是1：1：4，∴三个内角分别为30°，30°，120°，①当∠A=30°，∠B=120°时，方程的两根为，﹣，将代入方程得：4×（）2﹣m×﹣1=0，解得：m=0，经检验﹣是方程4x2﹣1=0的根，∴m=0符合题意；②当∠A=120°，∠B=30°时，两根为，，不符合题意；③当∠A=30°，∠B=30°时，两根为，，将代入方程得：4×（）2﹣m×﹣1=0，解得：m=0，经检验不是方程4x2﹣1=0的根．综上所述：m=0，∠A=30°，∠B=120°．14．（2010•密云县）如图，在梯形ABCD中，AD∥BC，AD=3，DC=5，AB=4，∠B=45°．动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动．设运动的时间为t秒．（1）求BC的长；（2）当MN∥AB时，求t的值；（3）试探究：t为何值时，△MNC为等腰三角形．【解答】解：（1）如图①，过A、D分别作AK⊥BC于K，DH⊥BC于H，则四边形ADHK是矩形．∴KH=AD=3．在Rt△ABK中，AK=AB•sin45°=4•=4，BK=AB•cos45°=4=4．在Rt△CDH中，由勾股定理得，HC==3．∴BC=BK+KH+HC=4+3+3=10．（2）如图②，过D作DG∥AB交BC于G点，则四边形ADGB是平行四边形．∵MN∥AB，∴MN∥DG．∴BG=AD=3．∴GC=10﹣3=7．由题意知，当M、N运动到t秒时，CN=t，CM=10﹣2t．∵DG∥MN，∴∠NMC=∠DGC．又∵∠C=∠C，∴△MNC∽△GDC．∴，即．解得，．（3）分三种情况讨论：①当NC=MC时，如图③，即t=10﹣2t，∴．②当MN=NC时，如图④，过N作NE⊥MC于E．解法一：由等腰三角形三线合一性质得：EC=MC=（10﹣2t）=5﹣t．在Rt△CEN中，cosC==，又在Rt△DHC中，cosC=，∴．解得t=．解法二：∵∠C=∠C，∠DHC=∠NEC=90°，∴△NEC∽△DHC．∴，即．∴t=．③当MN=MC时，如图⑤，过M作MF⊥CN于F点．FC=NC=t．解法一：（方法同②中解法一），解得．解法二：∵∠C=∠C，∠MFC=∠DHC=90°，∴△MFC∽△DHC．∴，即，∴．综上所述，当t=、t=或t=时，△MNC为等腰三角形．15．（2015•甘南州）如图，从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度．如果这时气球的高度CD为90米．且点A、D、B在同一直线上，求建筑物A、B间的距离．【解答】解：由已知，得∠ECA=30°，∠FCB=60°，CD=90，EF∥AB，CD⊥AB于点D．∴∠A=∠ECA=30°，∠B=∠FCB=60°．在Rt△ACD中，∠CDA=90°，tanA=，∴AD==90×=90．在Rt△BCD中，∠CDB=90°，tanB=，∴DB==30．∴AB=AD+BD=90+30=120．答：建筑物A、B间的距离为120米．16．（2013•遂宁）钓鱼岛自古以来就是我国的神圣领土，为维护国家主权和海洋权利，我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理．如图，某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B，B船在A船的正东方向，且两船保持20海里的距离，某一时刻两海监船同时测得在A的东北方向，（结B的北偏东15°方向有一我国渔政执法船C，求此时船C与船B的距离是多少．果保留根号）【解答】解：过点B作BD⊥AC于D．由题意可知，∠BAC=45°，∠ABC=90°+15°=105°，∴∠ACB=180°﹣∠BAC﹣∠ABC=30°，在Rt△ABD中，BD=AB•sin∠BAD=20×=10（海里），在Rt△BCD中，BC===20（海里）．答：此时船C与船B的距离是20海里．。
三角函数练习题(含答案)
三角函数练习题及答案（一）选择题1、在直角三角形中，各边都扩大2倍，则锐角A 的正弦值与余弦值都（ ）A 、缩小2倍B 、扩大2倍C 、不变D 、不能确定12、在Rt △ABC 中，∠C=900，BC=4，sinA=45，则AC=（ ） A 、3 B 、4 C 、5 D 、6 3、若∠A 是锐角，且sinA=13，则（ ）A 、00<∠A<300B 、300<∠A<450C 、450<∠A<600D 、600<∠A<9004、若cosA=13，则A A AA tan 2sin 4tan sin 3+-=（ ） A 、47B 、 13C 、 12D 、0 5、在△ABC 中，∠A ：∠B ：∠C=1：1：2，则a ：b ：c=（ ）A 、1：1：2B 、1：1：√2C 、1：1：√3D 、1：1：√226、在Rt △ABC 中，∠C=900，则下列式子成立的是（ ）A 、sinA=sinB B 、sinA=cosBC 、tanA=tanBD 、cosA=tanB7．已知Rt △ABC 中，∠C=90°，AC=2，BC=3，那么下列各式中，正确的是（ ）A ．sinB= 23B ．cosB= 23C ．tanB= 23D ．tanB=32 8．点（-sin60°，cos60°）关于y 轴对称的点的坐标是（ ） A ．（32，12） B ．（-32，12） C ．（-32，-12） D ．（-12，-32）9．每周一学校都要举行庄严的升国旗仪式，让我们感受到了国旗的神圣．某同学站在离旗杆12米远的地方，当国旗升起到旗杆顶时，他测得视线的仰角为30°，若这位同学的目高1.6米，则旗杆的高度约为（ ）A ．6.9米B ．8.5米C ．10.3米D ．12.0米10．王英同学从A 地沿北偏西60º方向走100m 到B 地，再从B 地向正南方向走200m 到C 地，此时王英同学离A 地 （ ）（A ）350m （B ）100 m （C ）150m （D ）3100m11、如图1，在高楼前D点测得楼顶的仰角为300，向高楼前进60米到C点，又测得仰角为450，则该高楼的高度大约为（）A.82米B.163米C.52米D.70米12、一艘轮船由海平面上A地出发向南偏西40º的方向行驶40海里到达B地，再由B地向北偏西10º的方向行驶40海里到达C地，则A、C两地相距（）．（A）30海里（B）40海里（C）50海里（D）60海里（二）填空题1．在Rt△ABC中，∠C=90°，AB=5，AC=3，则sinB=_____．2．在△ABC中，若BC=2，AB=7，AC=3，则cosA=________．3．在△ABC中，AB=2，AC=2，∠B=30°，则∠BAC的度数是______．4．如图，如果△APB绕点B按逆时针方向旋转30°后得到△A＇P＇B，且BP=2，那么PP＇的长为________． (不取近似值. 以下数据供解题使用：sin15°=，cos15°=624+)5．如图，在甲、乙两地之间修一条笔直的公路，从甲地测得公路的走向是北偏东48°．甲、乙两地间同时开工，若干天后，公路准确接通，则乙地所修公路的走向是南偏西___________度．6．如图，机器人从A点，沿着西南方向，行了个42单位，到达B 点后观察到原点O在它的南偏东60°的方向上，则原来A的坐标为___________结果保留根号）．7．求值：sin260°+cos260°=___________．8．在直角三角形ABC中，∠A=090，BC=13，AB=12，那么tan B=___________．9．根据图中所给的数据，求得避雷针CD的长约为_______m（结果精确的到0.01m）．（可用计算器求，也可用下列参考数据求：sin43°≈0.6802，sin40°≈0.6428，cos43°≈0.7341，cos40°≈0.7660，tan43°≈0.9325，tan40°≈0.8391）10．如图，自动扶梯AB 段的长度为20米，倾斜角A 为α，高度BC 为___________米（结果用含α的三角比表示）．11．如图2所示，太阳光线与地面成60°角，一棵倾斜的大树与地面成30°角，这时测得大树在地面上的影子约为10米，则大树的高约为________米．（保留两个有效数字，2≈1.41，3≈1.73）三、简答题：1，计算：sin cos cot tan tan 3060456030︒+︒-︒-︒⋅︒分析：可利用特殊角的三角函数值代入直接计算；2计算：22459044211(cos sin )()()︒-︒+-︒+--π分析：利用特殊角的三角函数值和零指数及负整数次幂的知识求解。
三角函数10道大题(带答案)
三角函数10道大题(带答案)三角函数1.已知函数$f(x)=4\cos x\sin(x+\frac{\pi}{6})+\sin(2x-\frac{\pi}{4})+2\cos2x-1,x\in R$。
Ⅰ）求$f(x)$的最小正周期；Ⅱ）求$f(x)$在区间$[-\frac{\pi}{4},\frac{\pi}{4}]$上的最大值和最小值。
2.已知函数$f(x)=\tan(2x+\frac{\pi}{4}),x\in R$。
Ⅰ）求$f(x)$的定义域与最小正周期；II）设$\alpha\in(\frac{\pi}{4},\frac{\pi}{2})$，若$f(\alpha+\frac{\pi}{4})=2\cos2\alpha$，求$\alpha$的大小。
3.已知函数$f(x)=\frac{(sinx-cosx)\sin2x}{\sin x}$。
1）求$f(x)$的定义域及最小正周期；2）求$f(x)$的单调递减区间。
4.设函数$f(x)=\frac{2\pi\cos(2x+\frac{\pi}{4})+\sin2x}{24}$。
Ⅰ）求函数$f(x)$的最小正周期；II）设函数$g(x)$对任意$x\in R$，有$g(x+\pi)=g(x)$，且当$x\in[0,\frac{\pi}{2}]$时，$2\pi g(x)=1-f(x)$，求函数$g(x)$在$[-\pi,0]$上的解析式。
5.函数$f(x)=A\sin(\omega x-\frac{\pi}{6})+1(A>0,\omega>\frac{\pi}{6})$的最大值为3，其图像相邻两条对称轴之间的距离为$\frac{\pi}{2}$。
1）求函数$f(x)$的解析式；2）设$\alpha\in(0,\frac{\pi}{2})$，则$f(\alpha)=2$，求$\alpha$的值。
6.设$f(x)=4\cos(\omega x-\frac{\pi}{6})\sin\omegax+\cos2\omega x$，其中$\omega>0$。
三角函数及解直角三角形竞赛试题
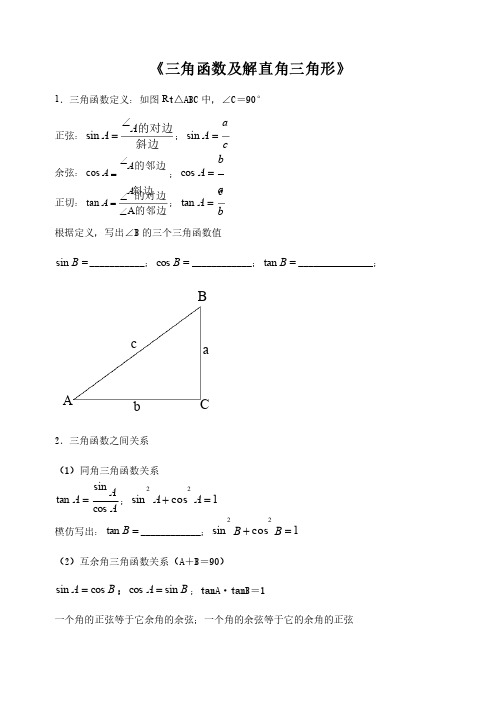
《三角函数及解直角三角形》1．三角函数定义：如图R t △ABC 中，∠中，∠C C ＝9090°°正弦：斜边的对边A A Ð=sin ；c aA =sin余弦：斜边的邻边A A Ð=cos ；c b A =cos正切：的邻边的对边A tan ÐÐ=A A ；ba A =tan根据定义，写出∠根据定义，写出∠B B 的三个三角函数值的三个三角函数值=B sin ______________________；；=B cos ________________________；；=B tan ______________________________；；cabBCA2．三角函数之间关系．三角函数之间关系 （1）同角三角函数关系）同角三角函数关系AAA cos sintan =；1cos sin 22=+A A模仿写出：=B tan ________________________；；1cos sin 22=+B B （2）互余角三角函数关系（）互余角三角函数关系（A A ＋B ＝9090））B A cos sin =；B A sin cos =；tanA tanA··tanB tanB＝＝1一个角的正弦等于它余角的余弦；一个角的余弦等于它的余角的正弦3．特殊角的三角函数值3030°、°、°、454545°、°、°、606060°°三角函数三角函数 3030°° 4545°° 6060°° a sina cos a tan4．会设计并根据三角函数关系计算15°、°、757575°角的三角函数°角的三角函数°角的三角函数DC BA5．根据表格中数据总结正弦、余弦、正切的增减性．根据表格中数据总结正弦、余弦、正切的增减性 当0°≤a ≤9090°时，°时，°时，sin a 随a 的增大而的增大而_____________________；；cos a 随a 的增大而的增大而_____________________；；tan a 随a 的增大而的增大而_______ _______6．已知一个三角函数值，求其他三角函数值。
三角函数试题及答案初中
三角函数试题及答案初中一、选择题（每题3分，共30分）1. 若sinα=1/2，则α的度数是（）A. 30°B. 60°C. 90°D. 120°2. cos30°的值是（）A. 1/2B. √3/2C. √2/2D. 13. 已知tan45°=1，则sin45°的值是（）A. 1/√2B. √2/2C. √2D. 14. 如果sinβ=3/5，且β为锐角，则cosβ的值是（）A. 4/5B. -4/5C. 3/5D. -3/55. 根据三角函数的定义，下列哪个选项是错误的（）A. sin0°=0B. cos90°=0C. tan60°=√3D. sin180°=-16. 已知sinA=1/2，那么cos2A的值是（）A. 1/4B. 1/2C. 3/4D. 07. 在直角三角形中，如果一个锐角的正弦值是1/3，那么它的余弦值是（）A. 2√2/3B. √2/3C. √6/3D. 3√2/38. 根据三角函数的周期性，sin(360°+α)等于（）A. sinαB. -sinαC. co sαD. -cosα9. 一个角的正切值是-√3，那么这个角的度数是（）A. 60°B. 120°C. 240°D. 300°10. 根据三角函数的和角公式，sin(α+β)=sinαcosβ+cosαsinβ，那么cos(α+β)的值是（）A. cosαcosβ-sinαsinβB. cosαcosβ+sinαsinβC. sinαcosβ-cosαsinβD. -cosαcosβ-sinαsinβ二、填空题（每题4分，共20分）1. sin60°的值是______。
2. 一个角的余弦值是-1/2，那么这个角的正弦值是______。
3. 已知tanA=2，则sinA的值是______。
九年级三角函数竞赛题(含答案)
锐角三角函数古希腊数学家和古代中国数学家为了测量的需要，他们发现并经常利用下列几何结论：在两个大小不同的直角三角形中，只要有一个锐角相等，那么这两个三角形的对应边的比值一定相等．正是古人对天文观察和测量的需要才引起人们对三角函数的研究，1748年经过瑞士的著名数学家欧拉的应用，才逐渐形成现在的sin 、cos 、tg 、ctg 的通用形式．三角函数揭示了直角三角形中边与锐角之间的关系，是数形结合的桥梁之一，有以下丰富的性质：1．单调性；2．互余三角函数间的关系；3．同角三角函数间的关系．平方关系：sin 2α+cos 2α=1；商数关系：tg α=ααcos sin ，ctg α=ααsin cos ； 倒数关系：tg αctg α=1．【例题求解】【例1】 已知在△ABC 中，∠A 、∠B 是锐角，且sinA ＝135，tanB=2，AB=29cm ， 则S △ABC = ．思路点拨 过C 作CD ⊥AB 于D ，这样由三角函数定义得到线段的比，sinA=135=AC CD ，tanB=2=BDCD ，设CD=5m ，AC ＝13m ，CD ＝2n ，BD ＝n ，解题的关键是求出m 、n 的值． 注：设△ABC 中，a 、b 、c 为∠A 、∠B 、∠C 的对边，R 为△ABC 外接圆的半径，不难证明：与锐角三角函数相关的几个重要结论：(1) S △ABC =C ab B ac A bc sin 21sin 21sin 21==； （2）R Cc B b A a 2sin sin sin ===． 【例2】 如图，在△ABC 中．∠ACB ＝90°，∠ABC ＝15°，BC=1，则AC=( )A ．32+B ．32-C ．0.3D ．23-思路点拨 由15°构造特殊角，用特殊角的三角函数促使边角转化．注：（1）求(已知)非特角三角函数值的关是构造出含特殊角直角三角形．（2）求(已知)锐角角函数值常根据定转化为求对应线段比，有时需通过等的比来转换．【例3】 如图，已知△ABC 是等腰直角三角形，∠ACB ＝90°，过BC 的中点D 作DE ⊥AB 于E ，连结CE ，求sin ∠ACE 的值．思路点拨 作垂线把∠ACE 变成直角三角形的一个锐角，将问题转化成求线段的比．【例4】 如图，在△ABC 中，AD 是BC 边上的高，tanB=cos ∠DAC ，(1)求证：AC ＝BD ；(2)若sinC=1312，BC=12，求AD 的长． 思路点拨 (1)把三角函数转化为线段的比，利用比例线段证明； (2) sinC=AC AD =1312，引入参数可设AD=12k ，AC ＝13k ．【例5】 已知：在Rt △ABC 中，∠C=90°，sinA 、sinB 是方程02=++q px x 的两个根．(1)求实数p 、q 应满足的条件；(2)若p 、q 满足(1)的条件，方程02=++q px x 的两个根是否等于Rt △ABC 中两锐角A 、B 的正弦?思路点拨 由韦达定理、三角函数关系建立p 、q 等式，注意判别式、三角函数值的有界性，建立严密约束条件的不等式，才能准确求出实数p 、q 应满足的条件．学历训练A 组1．已知α为锐角，下列结论①sin α+cos α=l ；②如果α>45°，那么sin α>cos α；③如果cos α>21 ，那么α<60°； ④αsin 11)-(sin 2-=α．正确的有 ． 2．如图，在菱形ABCD 中，AE ⊥BC 于E ，BC=1，cosB 135，则这个菱形的面积为 ． 3．如图，∠C=90°，∠DBC=30°，AB ＝BD ，利用此图可求得tan75°= ．4．化简:(1)263tan 27tan 22-+ = ．(2)sin 2l °+sin 22°+…+sin 288°+sin 289°= ．5．身高相等的三名同学甲、乙、丙参加风筝比赛．三人放出风筝线长、线与地面夹角如下表(假设风筝线是拉直的)，则三人所放的风筝中( )A ．甲的最高B ．丙的最高C ．乙的最低D ．丙的最低6．已知 sin αcos α=81，且0°<α<45°则co α-sin α的值为( ) A ．23 B ．23- C ．43 D ．43- 7．在△ABC 中，∠C ＝90°，∠ABC ＝30°，D 是AC 的中点，则ctg ∠DBC 的值是( ) A ．3 B ．32 C ． 23 D ．43 8．在等腰Rt △ABC 中．∠C ＝90°，AC ＝6，D 是AC 上一点，若tan ∠DBA=51，则AD 的长为( )A ．2B ．2C ． 1D ．229．已知关于x 的方程0)1(242=++-m x m x 的两根恰是某直角三角形两锐角的正弦，求m 的值．10．D 是△ABC 的边AC 上的一点，CD=2AD ，AE ⊥BC 于E ，若BD ＝8，sin ∠CBD=43，求AE 的长．B 组 11．若0°<α<45°，且sin αcon α=1673，则sin α= ． 12．已知关于x 的方程0)cos 1(2sin 423=-+⋅-ααx x 有两个不相等的实数根，α为锐角，那么α的取值范围是 ．13．已知是△ABC 的三边，a 、b 、c 满足等式))((4)2(2a c a c b -+=，且有035=-c a ，则sinA+sinB+sinC 的值为 ．14．设α为锐角，且满足sin α=3cos α，则sin αcos α等于( )A ．61B ．51 C ．92 D ．103 15．如图，若两条宽度为1的带子相交成30°的角，则重叠部分(图中阴影部分)的面积是( )A ．2B ．23 C ．1 D ．2116．如图，在△ABC 中，∠A ＝30°，tanB=23，AC=32，则AB 的长是( ) A ．33+ B ．322+ C ．5 D ．29 17．己在△ABC 中，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，且c=35，若关于x 的方程0)35(2)35(2=-+++b ax x b 有两个相等的实根，又方程0sin 5)sin 10(22=+-A x A x 的两实根的平方和为6，求△ABC 的面积．18．如图，已知AB=CD=1，∠ABC ＝90°，∠CBD °=30°，求AC 的长．19．设 a 、b 、c 是直角三角形的三边，c 为斜边，n 为正整数，试判断n n b a 与n c 的关系，并证明你的结论．20．如图，已知边长为2的正三角形ABC 沿直线l 滚动．(1)当△ABC 滚动一周到△A l B 1C 1的位置，此时A 点所运动的路程为 ，约为 (精确到0.1，π=3.14)(2)设△ABC 滚动240°，C 点的位置为C ˊ，△ABC 滚动480°时，A 点的位置在A ˊ，请你利用三角函数中正切的两角和公式tan(α+β)=(tan α+tan β)÷(1-tan α·tan β)，求出∠CAC ˊ+∠CAA ˊ的度数．参考答案。
三角函数10道大题（带答案）
三角函数大题转练三角函数大题转练1.已知函数()4cos sin()16f x x x p =+-.（Ⅰ）求（Ⅰ）求 ()f x 的最小正周期；的最小正周期；（Ⅱ）求()f x 在区间[,]64p p-上的最大值和最小值.2、已知函数.,1cos 2)32sin()32sin()(2R x x x x x f Î-+-++=p p（Ⅰ）求函数)(x f 的最小正周期；的最小正周期；（Ⅱ）求函数)(x f 在区间]4,4[pp -上的最大值和最小值. 3、已知函数()tan(2),4f x x =+p（Ⅰ）求()f x 的定义域与最小正周期；的定义域与最小正周期；（II II）设）设0,4æöÎç÷èøpa ，若()2cos 2,2f =a a 求a 的大小的大小4、已知函数x x x x x f sin2sin )cos (sin )(-=.（1）求)(x f 的定义域及最小正周期；的定义域及最小正周期； （2）求)(x f 的单调递减区间. 5、 设函数22()cos(2)sin 24f x x x p=++. （I ）求函数()f x 的最小正周期；的最小正周期；（II ）设函数()g x 对任意x R Î，有()()2g x g x p +=，且当[0,]2x pÎ时，1()()2g x f x =-，求函数()g x 在[,0]p -上的解析式. 6、函数()sin()16f x A x pw =-+（0,0A w >>）的最大值为3， 其图像相邻两条对称轴之间的距离为2p ，（1）求函数()f x 的解析式；的解析式；（2）设(0,)2pa Î，则()22f a =，求a 的值. 7、设426f (x )cos(x )sin x cos x p =w -w +w ，其中.0>w（Ⅰ）求函数y f (x )= 的值域的值域（Ⅱ）若y f (x )=在区间322,p p éù-êúëû上为增函数，求上为增函数，求 w 的最大值. 8、函数2()6cos3cos 3(0)2xf x x w w w =+->在一个周期内的图象如图所示，A 为图象的最高点，B 、C 为图象与x 轴的交点，且ABC D 为正三角形. （Ⅰ）求w 的值及函数()f x 的值域；的值域；（Ⅱ）若083()5f x =，且0102(,)33x Î-，求0(1)f x +的值. 9、已知,,a b c 分别为ABC D 三个内角,,A B C 的对边，cos 3sin 0a C a C b c +--=（1）求A ； （2）若2a =，ABC D 的面积为3；求,b c . 10、在D ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ．已知cos A ＝23，sin B ＝5cos C ．(Ⅰ)求tan C 的值；的值； (Ⅱ)若a ＝2，求D ABC的面积．的面积．答案答案1、【思路点拨】先利用和角公式展开，再利用降幂公式、化一公式转化为正弦型函数，最后求周期及闭区间上的最值. 【精讲精析】（Ⅰ）因为()4cos sin()16f x x x p=+-314cos (sin cos )122x x x =+-23sin 22cos 1x x =+-3sin 2cos 22sin(2)6x x x p =+=+，所以()f x 的最小正周期为p .（Ⅱ）因为64x p p-££，所以22663x p pp-£+£.于是，当262x pp+=，即6x p=时，()f x 取得最大值2；当266x p p +=-，即6x p=-时，()f x 取得最小值－1. 2、【解析】 （1）2()=sin (2+)+sin(2)+2cos 133f x x x x p p --2sin 2cos cos 22sin(2)34x x x p p =+=+ 函数()f x 的最小正周期为22T p p ==（2）322sin(2)11()24444424x x x f x p p p p p p -££Þ-£+£Þ-£+£Û-££当2()428x x p p p +==时，()2maxf x =，当2()444x x p p p +=-=-时，mi min n ()1f x =- 【点评】该试题关键在于将已知的函数表达式化为=sin (+)y A x w j 的数学模型，再根据此三角模型的图像与性质进行解题即可数的有关公式进行变换、化简求值.【精讲精析】（I ）【解析】由2,42+¹+Îx k k Z p p p ， 得,82¹+Îk x k Z p p .所以()f x 的定义域为{|,}82ι+Îkx R x k Z p p ，()f x 的最小正周期为.2p（II ）【解析】由(())2cos 2,2f =a a 得tan()2cos 2,4+=pa a22sin()42(cos sin ),cos()4+=-+p a a a p a 整理得sin cos2(cos sin )(cos sin ).cos sin +=+--a a a a a a a a因为(0,)4Îp a ，所以sin cos 0.+¹a a 因此211(cos sin ),sin 2.22-==a a a 即 由(0,)4Îp a ，得2(0,)2Îp a .所以2,.612==p pa a 即4、解（1）：s i n 0()x x k k Z p¹Û¹Î得：函数()f x 的定义域为{,}x x k k Z p ¹Î(sin cos )sin 2()(sin cos )2cos sin x x x f x x x xx-==-´sin 2(1cos 2)2sin(2)14x x x p=-+=--得：)(x f 的最小正周期为22T p p ==；（2）函数sin y x =的单调递增区间为[2,2]()22k k k Z p p p p -+Î 则322224288k x k k x k p p p p pp p p p -£-£+Û-££+得：)(x f 的单调递增区间为3[,),(,]()88k k k k k Z p pp p p p -+Î5、本题考查两角和与差的三角函数公式、二倍角公式、三角函数的周期等性质、分段函数解析式等基础知识，考查分类讨论思想和运算求解能力. 【解析】2211()co 242f x x xp=++11sin 222x =-， （I ）函数()f x 的最小正周期22T p p ==（II ）当[0,]2x p Î时，11()()sin 222g x f x x =-=当[,0]2x p Î-时，()[0,]22x p p +Î 11()()sin 2()sin 22222g x g x x x pp=+=+=- 当[,)2x p p Î--时，()[0,)2x p p +Î 11()()sin 2()sin 222g x g x x x p p =+=+=得函数()g x 在[,0]p -上的解析式为1sin 2(0)22()1sin 2()22x x g x x x p p p ì--££ïï=íï-£<ïî. 6、【解析】（1）∵函数()f x 的最大值是3，∴13A +=，即2A =. ∵函数图像的相邻两条对称轴之间的距离为2p ，∴最小正周期T p=，∴2w =. 故函数()f x 的解析式为()2sin(2)16f x x p=-+. （2）∵()2f a 2sin()126p a =-+=，即1sin()62p a -=， ∵02p a <<，∴663p p pa -<-<，∴66p p a -=，故3p a =. 7、解：（1）()314cos sin sin cos 222f x x x x x w w w w æö=++ç÷ç÷èø22223sin cos 2sin cos sin x x x x x w w w w w =++-3sin 21x w =+因1sin 21x w -££，所以函数()y f x =的值域为13,13éù-+ëû（2）因sin y x =在每个闭区间()2,222k k k Z p p p péù-+Îêúëû上为增函数， 故()3sin 21f x x w =+()0w >在每个闭区间(),44k k k Z p p p p w w w w éù-+Îêúëû上为增函数. 依题意知3,22p p éù-Íêúëû,44k k p p pp w w w w éù-+êúëû对某个k Z Î成立，此时必有0k =，于是32424p p w p pwì-³-ïïíï£ïî，解得16w £，故w 的最大值为16. 8. 本题主要考查三角函数的图像与性质、同角三角函数的关系、两角和差公式，倍角公式等基础知识，考查基本运算能力，以及数形结合思想，化归与转化思想. [解析]（Ⅰ）由已知可得：2()6cos3cos 3(0)2xf x x w w w =+->=3cosωx+)3sin(32sin 3pw w +=x x又由于正三角形ABC 的高为23，则BC=4 所以，函数482824)(p w wp ===´=，得，即的周期T x f所以，函数]32,32[)(-的值域为x f .……………………6分 （Ⅱ）因为，由538)(0=x f （Ⅰ）有，538)34(sin 32)(00=+=p p x x f 54)34(s i n 0=+p p x 即 由x 0)2,2()34x (323100pp p p -Î+-Î），得，（所以，53)54(1)34(cos 20=-=+p p x 即故=+)1(0x f =++)344(sin 320p p p x ]4)34(sin[320p p p ++x )22532254(324sin)34cos(4cos )34([sin 3200´+´=+++=pp p p p p x x567=………………………………………………………12分 9..解：（1）由正弦定理得：cos 3sin 0sin cos 3sin sin sin sin a C a C b c A C A C B C+--=Û-=+sin cos 3sin sin sin()sin 13sin cos 1sin(30)2303060A C A C a C CA A A A A °°°°Û+=++Û-=Û-=Û-=Û=（2）1sin 342S bc A bc ==Û=， 2222cos 4a b c bc A b c =+-Û+= 10. 本题主要考查三角恒等变换，正弦定理，余弦定理及三角形面积求法等知识点. (Ⅰ)∵cos A ＝23＞0，∴sin A ＝251cos 3A -=，又5cos C ＝sin B ＝sin(A ＋C )＝sin A cos C ＋sin C cos A ＝53cos C ＋23sin C ．整理得：tan C ＝5．(Ⅱ)由图辅助三角形知：sin C ＝56．又由正弦定理知：sin sin a c A C=， 故3c =． (1) 对角A运用余弦定理：cos A ＝222223b c abc +-=． (2) 解(1) (2)得：3b = or b ＝33(舍去)． ∴D ABC 的面积为：S＝52．。
三角函数习题及答案
任意角的三角函数一、选择题：1．使得函数有意义的角在（）（Ａ）第一，四象限（Ｂ）第一，三象限（Ｃ）第一、二象限（Ｄ）第二、四象限２．角α、β的终边关于У轴对称，（κ∈Ζ）。
则（Ａ）α＋β＝２κπ（Ｂ）α－β＝２κπ（Ｃ）α＋β＝２κπ－π（Ｄ）α－β＝２κπ－π３．设θ为第三象限的角，则必有（）（Ａ）（Ｂ）（Ｃ）（Ｄ）４．若，则θ只可能是（）（Ａ）第一象限角（Ｂ）第二象限角（C）第三象限角（Ｄ）第四象限角５．若且，则θ的终边在（）(A)第一象限（B）第二象限（C）第三象限（D）第四象限二、填空题：6．已知α是第二象限角且则2α是第▁▁▁▁象限角，是第▁▁▁象限角。
7．已知锐角α终边上一点A的坐标为（2sina3,-2cos3）,则α角弧度数为▁▁▁▁。
8．设则Y的取值范围是▁▁▁▁▁▁▁。
9．已知cosx-sinx<-1，则x是第▁▁▁象限角。
三、解答题：10．已知角α的终边在直线上，求sinα及cot的值。
11．已知Cos(α+β)+1=0, 求证：sin(2α+β)+sinβ=0。
12．已知，求ƒ（1）+ƒ（2）+ƒ（3）+……+ƒ（2000）的值。
同角三角函数的基本关系式及诱导公式一、选择题：1．化简结果是（）（A）0 （B）（C）22．若，且，则的值为（）或3. 已知，且，则的值为（）4. 已知，并且是第一象限角，则的值是（）5. 化简的结果是（）6. 若且，则角所在的象限是（）（A）一、二象限（B）二、三象限（C）一、三象限（D）一、四象限填空题：7．化简▁▁▁▁▁▁。
8．已知，则的值为▁▁▁▁▁▁。
9．=▁▁▁▁▁。
10．若关于的方程的两根是直角三角形两锐角的正弦值，则▁▁▁▁。
解答题：11．已知：，求的值。
12．已知，求证：13．已知，且，求的值。
14．若化简：两角和与差的三角函数1．“”是“”的（）（A）充分必要条件（B）必要不充分条件（C）充要条件（D）既不充分也不必要条件2．已知且为锐角，则为（）或非以上答案3．设则下列各式正确的是（）4．已知，且则的值是（）二、填空题：5．已知则的值为6．已知且则7．已知则8．在中，是方程的两根，则三、解答题：9．求值。
数学三角函数专题测试题（附答案）
数学三⾓函数专题测试题（附答案）三⾓函数测试题第I 卷（共50分）⼀. 选择题（每⼩题5分，共50分）1、已知sin α=54, 并且α是第⼆象限⾓, 那么tan α的值为 ( ) A －34 B －43 C 43 D 342、若θθθ则⾓且,02sin ,0cos <>的终边所在象限是 ( )A ．第⼀象限B ．第⼆象限C ．第三象限D ．第四象限3、下列函数中，周期为1的奇函数是（）A ．x y π2sin 21-=B ．)32(sin ππ+=x yC ．tan2y x π= D ．x x y ππcos sin =4、函数y = sin(2x+25π)的图象的⼀条对称轴⽅程是 ( )A x = －2πB x = －4πC x = 8πD x =45π5、函数)2(3cos 2cos )(ππ-≤≤-+-=x x x x f 有（）A ．最⼤值3，最⼩值2B ．最⼤值5，最⼩值3C ．最⼤值5，最⼩值2D ．最⼤值3，最⼩值815 6、函数y=asinx －bcosx 的⼀条对称轴⽅程为4π=x ，则直线ax －by+c=0的倾斜⾓是（）A ．45°B ．135°C ．60°D ．120°7、若函数)sin()(?ω+=x x f 的图象（部分）如图所⽰，则?ω和的取值是 ( )A ．3,1πω==B ．3,1πω-==C ．6,21π?ω==D ．6,21π?ω-==8、若f ( x ) = tan (x +4π) ，则 A f (－１) > f ( 0 ) > f (1 ) Ｂ f (1 ) > f (0 )> f ( – 1 ) C f (0 ) > f (1 ) > f ( – 1 ) D f (0 ) > f ( – 1 ) > f ( 1 ) 9、若sin x 是减函数，且cos x 是增函数，则2x是第（）象限⾓ A ⼆ B ⼀或⼆ C ⼆或三 D ⼆或四10、函数y = 12cos 2sin -+x x 的定义域是A [ 0 ,4π] B [ 42,2πππ+k k ] C [4,πππ+k k ] D [432,42ππππ++k k ]第II 卷（共100分）⼆.填空题（每⼩题5分，共25分） 11.已知=-=-ααααcos sin ,45cos sin 则 12.已知等于则)2cos(),,0(,31cos θππθθ+∈=13、函数)4sin(cos )4cos(sin ππ+++=x x x x y 的最⼩正周期T= 。
(完整版)三角函数练习题(含答案)
三角函数练习题及答案（一）选择题1、在直角三角形中，各边都扩大2倍，则锐角A 的正弦值与余弦值都（ ）A 、缩小2倍B 、扩大2倍C 、不变D 、不能确定12、在Rt △ABC 中，∠C=900，BC=4，sinA=45，则AC=（ ） A 、3 B 、4 C 、5 D 、6 3、若∠A 是锐角，且sinA=13，则（ ）A 、00<∠A<300B 、300<∠A<450C 、450<∠A<600D 、600<∠A<9004、若cosA=13，则A A AA tan 2sin 4tan sin 3+-=（ ） A 、47B 、 13C 、 12D 、0 5、在△ABC 中，∠A ：∠B ：∠C=1：1：2，则a ：b ：c=（ ）A 、1：1：2B 、1：1：√2C 、1：1：√3D 、1：1：√226、在Rt △ABC 中，∠C=900，则下列式子成立的是（ ）A 、sinA=sinB B 、sinA=cosBC 、tanA=tanBD 、cosA=tanB7．已知Rt △ABC 中，∠C=90°，AC=2，BC=3，那么下列各式中，正确的是（ ）A ．sinB= 23B ．cosB= 23C ．tanB= 23D ．tanB=32 8．点（-sin60°，cos60°）关于y 轴对称的点的坐标是（ ） A ．（32，12） B ．（-32，12） C ．（-32，-12） D ．（-12，-32）9．每周一学校都要举行庄严的升国旗仪式，让我们感受到了国旗的神圣．某同学站在离旗杆12米远的地方，当国旗升起到旗杆顶时，他测得视线的仰角为30°，若这位同学的目高1.6米，则旗杆的高度约为（ ）A ．6.9米B ．8.5米C ．10.3米D ．12.0米10．王英同学从A 地沿北偏西60º方向走100m 到B 地，再从B 地向正南方向走200m 到C 地，此时王英同学离A 地 （ ）（A ）350m （B ）100 m （C ）150m （D ）3100m11、如图1，在高楼前D点测得楼顶的仰角为300，向高楼前进60米到C点，又测得仰角为450，则该高楼的高度大约为（）A.82米B.163米C.52米D.70米12、一艘轮船由海平面上A地出发向南偏西40º的方向行驶40海里到达B地，再由B地向北偏西10º的方向行驶40海里到达C地，则A、C两地相距（）．（A）30海里（B）40海里（C）50海里（D）60海里（二）填空题1．在Rt△ABC中，∠C=90°，AB=5，AC=3，则sinB=_____．2．在△ABC中，若BC=2，AB=7，AC=3，则cosA=________．3．在△ABC中，AB=2，AC=2，∠B=30°，则∠BAC的度数是______．4．如图，如果△APB绕点B按逆时针方向旋转30°后得到△A＇P＇B，且BP=2，那么PP＇的长为________． (不取近似值. 以下数据供解题使用：sin15°=，cos15°=62+)5．如图，在甲、乙两地之间修一条笔直的公路，从甲地测得公路的走向是北偏东48°．甲、乙两地间同时开工，若干天后，公路准确接通，则乙地所修公路的走向是南偏西___________度．6．如图，机器人从A点，沿着西南方向，行了个42单位，到达B 点后观察到原点O在它的南偏东60°的方向上，则原来A的坐标为___________结果保留根号）．7．求值：sin260°+cos260°=___________．8．在直角三角形ABC中，∠A=090，BC=13，AB=12，那么tan B=___________．9．根据图中所给的数据，求得避雷针CD的长约为_______m（结果精确的到0.01m）．（可用计算器求，也可用下列参考数据求：sin43°≈0.6802，sin40°≈0.6428，cos43°≈0.7341，cos40°≈0.7660，tan43°≈0.9325，tan40°≈0.8391）10．如图，自动扶梯AB 段的长度为20米，倾斜角A 为α，高度BC 为___________米（结果用含α的三角比表示）．11．如图2所示，太阳光线与地面成60°角，一棵倾斜的大树与地面成30°角，这时测得大树在地面上的影子约为10米，则大树的高约为________米．（保留两个有效数字，2≈1.41，3≈1.73）三、简答题：1，计算：sin cos cot tan tan 3060456030︒+︒-︒-︒⋅︒分析：可利用特殊角的三角函数值代入直接计算；2计算：22459044211(cos sin )()()︒-︒+-︒+--π分析：利用特殊角的三角函数值和零指数及负整数次幂的知识求解。
全国各地初中(九年级)数学竞赛《函数》真题大全 (附答案)
全国各地初中（9年级）数学竞赛专题大全竞赛专题6 函数一、单选题1．（2021·全国·九年级竞赛）2420x x y -+，则x y -的值为（ ）． A ．2B ．6C ．2或2-D ．6或6-2．（2021·全国·九年级竞赛）如图，两个反比例函数1k y x=和2ky x =在第一象限内的图象分别是1l 和2l ，设点P 在1l 上，PC x ⊥轴于点C ，交2l 于点,A PD y ⊥轴于点D ，交2l 于点B ，则四边形PAOB 的面积为（ ）．A ．12k k +B ．12k k -C ．12k kD ．21k k -3．（2021·全国·九年级竞赛）如右图，点P 是x 轴正半轴上一个动点，过点P 作x 轴的垂线交双曲线1y x=于点Q ，连接OQ ，当点P 向右运动时，Rt QOP 的面积（ ）．A ．逐渐增大B ．逐渐减小C ．保持不变D ．无法确定4．（2021·全国·九年级竞赛）设a ，b ，c 是ABC 三边的长，二次函数2()22b b y a x cx a =----在1x =取最小值83b -，则ABC 是（ ）A ．等腰三角形B ．锐角三角形C ．钝角三角形D ．直角三角形5．（2021·全国·九年级竞赛）若函数22(1)32y k x x k k =++++-的图象与x 轴交点的纵坐标为4-，则k 的值是（ ） A ．1-B ．2-C ．1-或2D ．1-或2-6．（2021·全国·九年级竞赛）设[]x 表示不超过实数x 的最大整数，{}[]x x x =-，则200983201083401783200920092009⨯⨯⨯⎡⎤⎡⎤⎡⎤+++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦（ ）． A ．249075 B ．250958 C ．174696 D ．2510007．（2021·全国·九年级竞赛）在实数范围内，设1988(2)(1)(2)(1)511111a a a a a x a a ⎡⎤--+--⎢⎥+=⎢⎥-⎢⎥+-⎣⎦，则x 的个位数字是（ ）． A ．1B ．2C ．4D ．68．（2021·全国·九年级竞赛）设抛物线24y x kx =++与x 轴有两个不同交点()()12,0,,0x x ，则下列结论中一定成立的是（ ）．A ．221217x x += B ．22128x x +=C ．221217x x +< D ．22128x x +>9．（2021·全国·九年级竞赛）设Rt ABC △的三个顶点A ，B ，C 均在抛物线2y x 上，并且斜边AB 平行于x 轴，若斜边上的高为h ，则（ ） A ．1h <B ．1h =C ．12h <<D ．2h >10．（2021·全国·九年级竞赛）设,n k 为正整数，12132(3)(1)4,(5)4,(7)4A n n A n A A n A +-+=++=++431(9)4,,(21)4,k k A n A A n k A -++=+++，已知1002005A =，则n 的值为（ ）．A ．1806B ．2005C ．3612D ．4100二、填空题11．（2021·全国·九年级竞赛）边长为整数的等腰三角形一腰上的中线将其周长分为1:2的两部分，那么所有这些等腰三角形中，面积最小的三角形的面积是_________． 12．（2021·全国·九年级竞赛）若0abc ≠，则||||||||a b c abca b c abc +++的最大值是________，最小值是__________． 13．（2021·全国·九年级竞赛）若0x >，则24411x x x y ++-+=的最大值是________．14．（2021·全国·九年级竞赛）设x 为正实数，则函数21y x x x=-+的最小值是______．15．（2021·全国·九年级竞赛）已知,a b 为抛物线()()2y x c x c d =----与x 轴交点的横坐标，a b <，则||||a c c b -+-的值为______．16．（2021·全国·九年级竞赛）设正ABC 的边长为2，M 是AB 边上的中点，P 是BC 边上任意一点，PA PM 十的最大值和最小值分别记为s 和t ，则22s t -=_______． 17．（2021·全国·九年级竞赛）若2008个数122008,,,a a a 满足：12a =，2n a -1112008n n n a a a --⎛⎫+ ⎪⎝⎭102008+=，其中，2n =，3，…，2008．那么2008a 可能达到的最大值是_________．18．（2021·全国·九年级竞赛）设333199519961997,0x y z xyz ==>，且2223333199519961997199519961997x y z ++111x y z++=_______． 19．（2021·全国·九年级竞赛）如果代数式535ax bx cx ++-当2x =-时的值为7，那么当2x =时，该式的值是_________．20．（2021·全国·九年级竞赛）函数23||7y x x =-+的图象与函数22336y x x x x =-+-+的图象的交点个数是_______．21．（2021·全国·九年级竞赛）不论m 取任何实数，抛物线2221y x mx m m =+++-的顶点都在一条直线上，则这条直线的解析式是______．22．（2021·全国·九年级竞赛）如果一次函数y mx n =+与反比例函数3n x y x -=的图象相交于点1,22⎛⎫⎪⎝⎭，那么该直线与双曲线的另一个交点为________．23．（2021·全国·九年级竞赛）函数|1||2||3|y x x x =+++++，当x =_______时，y 有最小值，最小值等于_______．24．（2021·全国·九年级竞赛）当x 变化时，分式22365112x x x x ++++的最小值是_______．25．（2021·全国·九年级竞赛）代数式21133110x x +的最小值是_______．26．（2021·全国·九年级竞赛）已知a ，b 是正数，并且二次函数22y x ax b =++和22y x bx a =++的图象都与x 轴相交，则22a b +的最小值是________． 三、解答题27．（2021·全国·九年级竞赛）在直径为5的圆内放入10个点，证明其中必有两点的距离小于2． 28．（2021·全国·九年级竞赛）试求1231997x x x x -+-+-++-的最小值．29．（2021·全国·九年级竞赛）当12x ≤≤2121x x x x +---30．（2021·全国·九年级竞赛）一幢33层的大楼里有一部电梯停在第一层，它一次最多容纳32人，而且只能在第2层至第33层中某一层停一次．对每个人来讲，他往下走一层楼感到1分不满意，往上走一层感到3分不满意．现有32个人在第一层，并且他们分别住在第2层至第33层的每一层，问：电梯停在哪一层，可以使得这32个人不满意的总分达到最小值？最小值是多少？（有些人可以不坐电梯直接从楼梯上楼） 31．（2021·全国·九年级竞赛）求函数22233x y x x +=++的最大值和最小值．32．（2021·全国·九年级竞赛）已知,,a b c 都是正整数，且抛物线2y ax bx c =++与x 轴有2个不同的交点A 和B ，若,A B 到原点的距离都小于1，求a b c ++的最小值．33．（2021·全国·九年级竞赛）求2221026249T x y z xy yz z =++---+的最小值．34．（2021·全国·九年级竞赛）在40与100之间任取一个实数x ，如果[]7x =，那么1610x ⎡=⎣的概率是多少?这是[]a 表示不超过a 的最大整数（要求答案写成最简分数的形式）．35．（2021·全国·九年级竞赛）如图，D E F 、、分别是ABC 的三边BC CA AB 、、上任意一点，证明：,,AEF BFD CDE △△△中至少有一个三角形的面积不大于ABC 的面积的四分之一．36．（2021·全国·九年级竞赛）某林场安排了7天的植树工作，从第二天起每天都比前一天增加5个植树的人，但从第二天起每人每天都比前一天少植5棵树，且同一天植树的人，植相同数量的树．若7天共植树9947棵，则植树最多的那天共植了多少棵？植树最少的那天，有多少人在植树？37．（2021·全国·九年级竞赛）一幢33层的大楼有一部电梯停在第一层，它一次最多能容纳32人，而且只能在第2层至第33层中某一层停一次．对于每个人来说他往下走一层楼梯感到1分不满意，往上走一层楼梯感到3分不满意．现在有32个人在第一层，并且他们分别在第2至第33层的每一层，问：电梯停在哪一层，可以使32人不满意的总分达到最小？最小值是多少？（有些人可以不坐电梯而直接从楼梯上楼）． 38．（2021·全国·九年级竞赛）已知正整数m ，n 17434m m n -+=，求n 的最大值． 39．（2021·全国·九年级竞赛）对于1,2,3,,i n =，有|| 1 i x <且有12||||||n x x x +++=122009||n x x x ++++．求正整数n 的最小值．40．（2021·全国·九年级竞赛）整数012010,,,x x x 满足条件：00x =，10|||1|x x =+，21|||1|x x =+，…，201020091x x =+，求122010x x x +++的最小值．41．（2021·全国·九年级竞赛）平面内给定一个方向l 和一个凸图形F ，其面积为()S F ，内接于F 且有一边平行于l 的所有三角形中面积最大的记为，其面积记()S ．求最大正实数c ，使对平面内任意给定的凸图形F ，都有()()S c S F ≥⋅．42．（2021·全国·九年级竞赛）已知x ，y ，z 是正数且1x y z ++=，比较149A x y z=++与36B =的大小，并问A 能否等于B ?43．（2021·全国·九年级竞赛）（1）证明：若x 取任意整数时，二次函数2y ax bx c =++总取整数值，那么2,,a a b c -都是整数；（2）写出上述命题的逆命题，并判断真假，且证明你的结论．44．（2021·全国·九年级竞赛）已知一次函数12y x =，二次函数221y x =+，是否存在二次函数23y ax bx c =++，其图象经过点(5,2)-，且对任意实数，这三个函数对应的函数值123,,y y y ，都有132y y y ≤≤成立？若存在，求出函数3y 的解析式；若不存在，请说明理由．45．（2021·全国·九年级竞赛）点(4,0),(0,3)A B 与点C 构成边长是3,4,5的直角三角形．如果点C 在反比例函数ky x=的图象上，求k 可能取到的一切值． 46．（2021·全国·九年级竞赛）已知一次函数y ax b =+的图象经过点(3,32),(3),(,2)A B C c c --，求222a b c ab bc ca ++---的值．47．（2021·全国·九年级竞赛）如图，在直角梯形OABC 中，//OA BC ，A ，B 两点的坐标分别是(13,0)A ，(11,12)B ，动点P ，Q 分别从O ，B 两点同时出发，点P 以每秒3个单位长的速度沿OA 方向运动，点Q 以每秒1个单位长的速度沿线段BC 运动，线段OB 与PQ 的交点为D ，过D 作//DE OA 交AB 于E ，射线QE 交x 轴于点F ，设P ，Q 运动的时间为t 秒．（1）当t 为何值时，以P A B Q 、、、为顶点的四边形是平行四边形，请写出推理过程．（2）设以P A E Q 、、、为顶点的图形面积为y ，求y 关于运动时间t 的函数关系式，并求出y 的最大值． （3）当t 为何值时，PQF △为等腰三角形？请写出推理过程．48．（2021·全国·九年级竞赛）已知抛物线21:34c y x x =--+和抛物线22:34c y x x =--相交于A ，B 两点，点P 在抛物线1c 上，且位于点A 与点B 之间；点Q 在抛物线2c 上，也位于点A 与点B 之间． （1）求线段AB 的长；（2）当//PQ y 轴时，求PQ 长度的最大值．49．（2021·全国·九年级竞赛）已知x ，y ，z 为实数，且满足2023x y z x y z +-=⎧⎨-+=⎩，求222x y z ++的最小值．50．（2021·全国·九年级竞赛）函数22(21)y x k x k =+-+的图象与x 轴的两个交点是否都在直线1x =的右侧，若是，请说明理由；若不一定，请求出两个交点在直线1x =的右侧时，k 的取值范围．竞赛专题6 函数答案解析一、单选题1．（2021·全国·九年级竞赛）2420x x y -+，则x y -的值为（ ）． A ．2 B ．6C ．2或2-D ．6或6-【答案】D 【解析】 【分析】 【详解】解：2420x x y -+，2420x x y -+=，240x -，20x y +=，即2,2x y x =±=-，于是()236x y x x x -=--==或6-． 故选：D ．2．（2021·全国·九年级竞赛）如图，两个反比例函数1k y x=和2ky x =在第一象限内的图象分别是1l 和2l ，设点P 在1l 上，PC x ⊥轴于点C ，交2l 于点,A PD y ⊥轴于点D ，交2l 于点B ，则四边形PAOB 的面积为（ ）．A ．12k k +B ．12k k -C ．12k kD ．21k k -【答案】B 【解析】 【分析】 【详解】OACOBDPOOD PAOB S S SS=--长方形四边形．设(,),(,),(,)P a b A c d B e f ，则122,,ab k cd k ef k ===，所以12212111111222222PAOB S PC PD AC OC BD OD ab cd ef k k k k k =⨯-⨯⨯-⨯⨯=--=--=-四边形．故选：B ．3．（2021·全国·九年级竞赛）如右图，点P 是x 轴正半轴上一个动点，过点P 作x 轴的垂线交双曲线1y x=于点Q ，连接OQ ，当点P 向右运动时，Rt QOP 的面积（ ）．A ．逐渐增大B ．逐渐减小C ．保持不变D ．无法确定【答案】C 【解析】 【分析】 【详解】设(,)Q a b ，则,OP a PQ b ==，且1b a=，所以111222OPQS OP PQ ab =⨯⨯=⨯=． 故选：C ．4．（2021·全国·九年级竞赛）设a ，b ，c 是ABC 三边的长，二次函数2()22b by a x cx a =----在1x =取最小值83b -，则ABC 是（ ）A ．等腰三角形B ．锐角三角形C ．钝角三角形D ．直角三角形【答案】D 【解析】 【分析】 【详解】解 依题意可得2220,,42,231,2,52()52338()223ba b a a b c b c a a b c ABC b a c b c b b b a c a b⎧⎪->⎧⎪>⎧⎪⎪=⎪⎪-⎪⎪=⇒+=⇒⇒+=⇒⎨⎨⎨⎪⎪⎪-=⎪⎪⎪=⎩⎩⎪----=-⎪⎩是直角三角形．故应选D ．注：从前面的例题可以看出，解有关二次函数的最值问题，不仅要熟悉有关二次函数的性质，还要灵活运用相关的不等式知识、几何知识等，才能使问题得到顺利解决．5．（2021·全国·九年级竞赛）若函数22(1)32y k x x k k =++++-的图象与x 轴交点的纵坐标为4-，则k 的值是（ ） A ．1- B ．2-C ．1-或2D ．1-或2-【答案】B【分析】 【详解】解 因0x =时，4y =-代入函数关系得2432k k -=+-，即(1)(2)0k k ++=，所以1k =-或2k =-．故应选D ．注：本题中的函数可以是一次函数，也可以是二次函数．不能一开始就默认它是二次函数，约定10k +≠，从而错误地选择了B ．6．（2021·全国·九年级竞赛）设[]x 表示不超过实数x 的最大整数，{}[]x x x =-，则200983201083401783200920092009⨯⨯⨯⎡⎤⎡⎤⎡⎤+++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦（ ）． A ．249075 B ．250958 C ．174696 D ．251000【答案】A 【解析】 【分析】 【详解】原式(20090)83(20091)83(20092008)83200920092009+⨯+⨯+⨯⎡⎤⎡⎤⎡⎤=+++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦083183200883838383200920092009⨯⨯⨯⎡⎤⎡⎤⎡⎤=++++++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦083183200883083183200883832009200920092009200920092009⨯⨯⨯⨯⨯⨯⎧⎫⎧⎫⎧⎫=⨯++++----⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭83083183200883200983(122008)2009200920092009⨯⨯⨯⎧⎫⎧⎫⎧⎫=⨯++++----⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭083183200883200983831004200920092009⨯⨯⨯⎧⎫⎧⎫⎧⎫=⨯+⨯----⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭．显然，2009与83互质，083,183,,200883⨯⨯⨯除以2009有2009个不同的余数．所以，08318320088301200810042009200920092009⨯⨯⨯+++⎧⎧⎫⎧⎫+++==⎨⎨⎬⎨⎬⎩⎩⎭⎩⎭． 故原式200983831004100416674782328249075=⨯+⨯-=+=．7．（2021·全国·九年级竞赛）在实数范围内，设1988(2)(1)(2)(1)511111a a a a a x a a ⎡⎤--+--⎢⎥+=⎢⎥-⎢⎥+-⎣⎦，则x 的个位数字是（ ）． A ．1 B ．2C ．4D ．6【答案】D【分析】 【详解】解：要使x 有意义，必须且只需(2)(1)0,(2)(1)0,(2)(1)0,1,110,21101a a a a a a a a a a a⎧--≥⎪⎧--=--≥⎪⎪⎪⇒≠⇒=-⎨⎨-≠⎪⎪≠⎩⎪+≠⎪-⎩． 所以1988198********05(1)1()(2)(2)1611(1)12x ⨯⨯-+=+=-=-=--+， 故x 的个位数字为6， 故选：D ．8．（2021·全国·九年级竞赛）设抛物线24y x kx =++与x 轴有两个不同交点()()12,0,,0x x ，则下列结论中一定成立的是（ ）．A ．221217x x += B ．22128x x += C ．221217x x +< D ．22128x x +> 【答案】D 【解析】 【分析】 【详解】由2244016k k =-⨯>⇒>．又因1212,4x x k x x +=-=，所以()2222121212281688x x x x x x k +=+-=->-=． 故选：D ．9．（2021·全国·九年级竞赛）设Rt ABC △的三个顶点A ，B ，C 均在抛物线2y x 上，并且斜边AB 平行于x 轴，若斜边上的高为h ，则（ ） A ．1h < B ．1h = C ．12h << D ．2h >【答案】B 【解析】 【分析】 【详解】解 设A 的坐标为()2,a a ，点C 的坐标为()2,(|||| )c c c a <，则B 点的坐标为()2,a a -．由勾股定理可得()22222()AC a c a c =-+-，()22222()BC c a a c =++-，则22222(2)4AC BC AB a a +===， 于是()()222222224a c a c a ++-=，即()22222a c a c -=-．由于22a c >，所以221a c -=，即斜边上的高h =（A 的纵坐标）-（C 的纵坐标）221a c =-=． 注：（1）如图仅画出了0c a <<的情形，在其他情形下，计算是完全相同的．（2）设()()1122,,,A x y B x y ，利用勾股定理可得计算A 与B 的距离的公式为()()2222121AB x x y y =-+-．10．（2021·全国·九年级竞赛）设,n k 为正整数，12132(3)(1)4,(5)4,(7)4A n n A n A A n A +-+=++=++431(9)4,,(21)4,k k A n A A n k A -++=+++，已知1002005A =，则n 的值为（ ）．A ．1806B ．2005C ．3612D ．4100【答案】A 【解析】 【分析】 【详解】2221[(1)2][(1)2]4(1)24(1)1A n n n n n +++-+=+-++=+， 2222[(3)2][(3)2]4(3)24(3)3A n n n n n +++-+=+-+=+=+， 2223[(5)2][(5)2]4(5)24(5)5A n n n n n +++-++-+++，同理451007,9,,21001199200520051991806A n A n A n n n =+=+=+⨯-=+=⇒=-=．故选：A ． 二、填空题11．（2021·全国·九年级竞赛）边长为整数的等腰三角形一腰上的中线将其周长分为1:2的两部分，那么所有这些等腰三角形中，面积最小的三角形的面积是_________． 37【解析】 【分析】设等腰三角形的腰为x ，底为y ，周长被分为的两部分的长分别为n 和2n ，则222x x n x y n ⎧+=⎪⎪⎨⎪+=⎪⎩或222x x n x y n ⎧+=⎪⎪⎨⎪+=⎪⎩，解得25(,),33n n x y ⎛⎫= ⎪⎝⎭或4,33n n ⎛⎫ ⎪⎝⎭．因为25233n n ⨯<（此时不能够成三角形，舍去），所以4(,),33n n x y ⎛⎫= ⎪⎝⎭，其中n 是3的倍数．则三角形面积2221472336n n n S ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭．当0n ≥时，S 随着n 的增大而增大．所以3n =时．S 37 12．（2021·全国·九年级竞赛）若0abc ≠，则||||||||a b c abca b c abc +++的最大值是________，最小值是__________． 【答案】 4 -4 【解析】 【分析】 【详解】 因为1||a a =±，1||b b =±，1||c c =±，1||abc abc =±，所以44||||||a b ca b c -≤++≤． 当a ，b ，c 全为正时等于4，当a ，b ，c 全为负时等于4-，故其最大值是4，最小值是4-． 13．（2021·全国·九年级竞赛）若0x >，则24411x x x y ++-+=的最大值是________．32 【解析】 【分析】 【详解】因0x >，244222441111111x x x x y xx x x ++++==++++-+22222211121232x x x x x x+⋅+⋅等号成立当且仅当221(0)x x x =>，即1x =，所以0x >时，1y 32y 3232=+ 故答案为：0x >时，1y 32y 3232=+ 14．（2021·全国·九年级竞赛）设x 为正实数，则函数21y x x x=-+的最小值是______．【答案】1【分析】 【详解】 211(1)10211(0)y x x x x x x=-++-≥+⋅=>，等号当且仅当1x =且1x x =，即1x =时成立，故y 的最小值为1， 故答案为：1．15．（2021·全国·九年级竞赛）已知,a b 为抛物线()()2y x c x c d =----与x 轴交点的横坐标，a b <，则||||a c c b -+-的值为______． 【答案】b a - 【解析】 【分析】 【详解】依题意，该抛物线开口向上，又当x a =或b 时，0y =．当x c =时，20y =-<，所以a c b <<，故||||a c c b c a b c b a -+-=-+-=-．故答案为：b a -．16．（2021·全国·九年级竞赛）设正ABC 的边长为2，M 是AB 边上的中点，P 是BC 边上任意一点，PA PM 十的最大值和最小值分别记为s 和t ，则22s t -=_______． 【答案】43 【解析】 【分析】 【详解】因为PA CA ≤，PM CM ≤，故当P 处于BC 边顶点C 这一极端位置时，PM PA 十取最大值，最大值为32s CM CA =+=．如图4-1，作正'A BC ，设'M 为'A B 的中点，则由'PBM PBM ≌得'PM PM ，于是''PA PM PA PM AM +=+≥．连'CM ，则'ACM ∠='ACB BCM ∠+∠=603090︒+︒=︒，所以'AM =22'AC CM +=222(3)7+'7PA AM PM +≥=A 、P 、'M 共线时等号成立，即PA AM +的最小值为7t =22s t -=22(32)(7)3-=4317．（2021·全国·九年级竞赛）若2008个数122008,,,a a a 满足：12a =，2n a -1112008n n n a a a --⎛⎫+ ⎪⎝⎭102008+=，其中，2n =，3，…，2008．那么2008a 可能达到的最大值是_________．【答案】200620082 【解析】 【分析】 【详解】依题意11102008n n nn a a a a --⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭，12008n n a a -= ①或11n n a a -=② 于是连续两次第②类变换互相抵消，保持原数不变，并且当连续三次变换依次是“第①类变换，第②类变换，第①类变换”时，其效果相当为进行一次第②类变换，故从12a =出发变到2008a ，一共要经过2007次变换，相当于进行若干次第①类变换和至多2次第②类变换，并且第②类变换只有第一次、最后一次进行才可能使2008a 最大．其中以前2006次进行第①类变换，最后一次进行第②类变换时，2008a 达到最大值200620082．18．（2021·全国·九年级竞赛）设333199519961997,0x y z xyz ==>，且2223333199519961997199519961997x y z ++111x y z++=_______． 【答案】1 【解析】 【分析】 【详解】解：因0xyz >，故3331995199619970x y z k ===>，则3331995,1996,1997k k k x y z ===， 3333333k k k k k kx y z x y z++， 两端三次方得3111111()x y z x y z++=++．又0,0,0x y z >>>，所以1111x y z++=．故答案为：1．19．（2021·全国·九年级竞赛）如果代数式535ax bx cx ++-当2x =-时的值为7，那么当2x =时，该式的值是_________． 【答案】17- 【解析】 【分析】 【详解】解：因为当2x =-时，535328257ax bx cx a b c ++-=----=， 所以328212a b c +=-＋，于是当2x =时，5353282512517ax bx cx a b c ++-=++-=--=-． 故答案为：17-．20．（2021·全国·九年级竞赛）函数23||7y x x =-+的图象与函数22336y x x x x =-+-+的图象的交点个数是_______． 【答案】4 【解析】 【分析】 【详解】第一个函数化为2237(0),37(0),x x x y x x x ⎧++<=⎨-+≥⎩第二个函数化为26(03),266(03).x y x x x x ≤≤⎧=⎨-+⎩或 分别作它们的图象知，它们共有4个交点．或者分别解方程组(22237,37,(0),00)2666y x x y x x x x y x x y ⎧=++=-+<≤≤⎨=-+=⎩及2237,(3)266y x x x y x x ⎧=-+>⎨=-+⎩，可得4个交点为(1111(985,6285,(35),6,(35),6,(313),82222A B C D ⎛⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎝⎭⎝⎭⎝⎭．故答案为：4．21．（2021·全国·九年级竞赛）不论m 取任何实数，抛物线2221y x mx m m =+++-的顶点都在一条直线上，则这条直线的解析式是______． 【答案】1y x =-- 【解析】 【分析】 【详解】二次函数化为2()1y x m m =++-，得顶点坐标为,1,x m y m =-⎧⎨=-⎩消去m 得1y x =--．故答案为：1y x =--．22．（2021·全国·九年级竞赛）如果一次函数y mx n =+与反比例函数3n x y x -=的图象相交于点1,22⎛⎫⎪⎝⎭，那么该直线与双曲线的另一个交点为________． 【答案】51,2⎛⎫-- ⎪⎝⎭【解析】 【分析】 【详解】将1,22x y ==代入,31y mx n ny x =+⎧⎪⎨=-⎪⎩得12,2261,m n n ⎧=+⎪⎨⎪=-⎩于是1,23.n m ⎧=⎪⎨⎪=⎩ 解方程13,2312y x y x ⎧=+⎪⎪⎨⎪=-⎪⎩得1,22x y ⎧=⎪⎨⎪=⎩或1,5.2x y =-⎧⎪⎨=-⎪⎩故另一交点为51,2⎛⎫-- ⎪⎝⎭．故答案为：51,2⎛⎫-- ⎪⎝⎭．23．（2021·全国·九年级竞赛）函数|1||2||3|y x x x =+++++，当x =_______时，y 有最小值，最小值等于_______．【答案】 2- 2 【解析】 【分析】 【详解】解 当3x ≤-时，(1)(2)(3)3(2)y x x x x =-+-+-+=-+； 当32x -<≤-时，(1)(2)(3)y x x x x =-+-+++=-；当21x -<≤-时，(1)(2)(3)4y x x x x =-+++++=+； 当1x >-时，(1)(2)(3)3(2)y x x x x =+++++=+．故|1||2||3|y x x x =+++++在(,2]-∞-上递减，在[2,)-+∞上递增，当2x =-时，y 取最小值2．故应填2,2-（如图）．注：①一般说来，对于含绝对值的一次函数，应分区间将绝对值符号去掉变成折线函数，再根据函数的增减性（一次项系数为正时递增，为负时递减）就不难得出所求函数的最大（或最小）值．如果作出其图象，那么其结果是一目了然的．②本题的一种简单解法是利用差的绝对值的几何意义来求解：因为||x a -表示数轴上坐标为x 的点P 到坐标为a 的点A 的距离，故|1||2||3|y x x x =+++++表示数轴上坐标为x 的点P 到坐标分别为1,2,3---的点,,A B C 的距离之和．显然当P 与B 重合时，即2x =-时，这个距离之和为最小，其最小值为线段AC 的长度|(1)(3)|2---=．又如，若要求|9||8||3||1||5||6|y x x x x x x =-+-+-++++++的最小值，则它等价于求数轴上坐标为x 的点P ，分别到坐标为9,8,3,1,5,6---的各点,,,,,A B C D E F 的距离之和的最小值． 显然当P 在线段CD 上，即当13x -≤≤时，这个距离之和取最小值，并且最小值|9(6)||8(5)||3(1)|32AF BE CD =++=--+--+--=．24．（2021·全国·九年级竞赛）当x 变化时，分式22365112x x x x ++++的最小值是_______．【答案】4 【解析】 【分析】 【详解】解 令22365112x x y x x ++=++，去分母整理得 2(6)(212)2100y x y x y -+-+-=．若6y =，则①化为20=，矛盾．故6y ≠． 因为作为x 的方程①有实根x ，故()22(212)4(6)(210)410244(4)(6)0y y y y y y y =----=--+=---≥，即(4)(6)0y y --≤，解得46y ≤≤． 而6y ≠，所以46y ≤<．4y =代入①可得1x =-，故当1x =-时，y 取最小值4．故应填4．注：例5~7中求最值的方法叫做判别式法．这是求函数最值的重要方法之一．但应该注意的是，化简整理为一个关于x 的二次方程后（其余数是变量y 的函数），对其二次项系数是否为零应进行讨论，只有在二次项系数不等于零的情形才能应用判别式法（若使二次项系数等于0的y 的值存在，则这个值也是函数y 可取到的值，在求最值时，应将这个值考虑在内进行讨论）．25．（2021·全国·九年级竞赛）代数式21133110x x +的最小值是_______． 【答案】3223【解析】 【分析】 【详解】解 设21133110y x x =+，则()222(110)1133y x x +=+，即22222032233113y xy x +=⨯+⨯．关于x 的方程222322322031130x yx y ⨯-+⨯-=有实根，所以 ()()222222(220)432233113411332230y y y =--⨯⨯⨯⨯-=⨯-⨯≥（因为22220432234113+⨯⨯=⨯），所以3223y ≥． 当且仅当223x =y 取最小值3223 故应填322326．（2021·全国·九年级竞赛）已知a ，b 是正数，并且二次函数22y x ax b =++和22y x bx a =++的图象都与x 轴相交，则22a b +的最小值是________． 【答案】20 【解析】 【分析】 【详解】解 因两条抛物线都与x 轴相交，故其判别式218a b =-及22(2)4b a =-都不小于零，即22222280,8,8440a b a b a b a b b a b a⎧⎧-≥≥⎪⇒⇒+≥+⎨⎨-≥≥⎪⎩⎩． 因,a b 都是正数，所以423(8)64644a b a a a ≥≥⇒≥⇒≥，及242b a b ≥≥⇒≥，所以22224220a b +≥+=，即22a b +的最小值为20．故应填20．注：本题中求最值的方法叫做放缩法，即根据题目条件，将各变量的值适当放缩为一个常数，从而求出其最值． 三、解答题27．（2021·全国·九年级竞赛）在直径为5的圆内放入10个点，证明其中必有两点的距离小于2． 【答案】见解析 【解析】 【分析】 【详解】分析 把圆等分为9个扇形显然不行（虽然必有一扇形内至少有2点，但不保证它们的距离小于2），因此，我们先作一个与已知圆同心的小圆（其直径必须小于2，但不能太小），然后将余下的圆环部分8等分． 证明 设O 是已知圆心，如图，以O 为圆心作半径为0.9的圆，再将余下的圆环8等分，于是将已知圆面分成了9个部分，由抽屉原理知其中必有一部分内至少有已知10点中的101129-⎡⎤+=⎢⎥⎣⎦点,M N ，若,M N 在小圆内，则220.9 1.82MN OC ≤=⨯=<． 若,M N 同在一个扇面形内，则由余弦定理，有222cos45MN AC OC OA OC OA ≤+-⋅︒0.81 6.2520.9 2.50.7 3.912+-⨯⨯⨯<．从例2可以看出，分割图形制造“抽屉”时，可能不是将图形等分为几部分，而是要求分割的每一部分图形都具有所需要的性质（例2中每一部分图形内任意两点的距离都小于2），读者应用这种方法解题时，应该注意到这一点．28．（2021·全国·九年级竞赛）试求1231997x x x x -+-+-++-的最小值．【答案】997002． 【解析】 【分析】 【详解】解：要求1219961997x x x x -+-+⋯+-+-的最小值，只要在数轴上找出x 所对应的点，使这点到1，2，3，…，1997所对应的点的距离之和最小即可． 如图1-1所示，当999x =时，原式的值最小，最小值为999199929999989999999991000999100199919969991997-+-+⋯+--+-+-+⋯+-+-＋99899721012997998=++⋯++++++⋯++(9981)99822+⨯=⨯997002=．29．（2021·全国·九年级竞赛）当12x ≤≤2121x x x x +--- 【答案】21x -． 【解析】 【分析】 【详解】解：令2121(12)A x x x x x +---≤≤，则 222212(21)21A x x x x x x =+-----22224422(2)x x x x x =--+=--()()22222241x x x x x =--=--=-，又0,12A x >≤≤，所以1A x =-30．（2021·全国·九年级竞赛）一幢33层的大楼里有一部电梯停在第一层，它一次最多容纳32人，而且只能在第2层至第33层中某一层停一次．对每个人来讲，他往下走一层楼感到1分不满意，往上走一层感到3分不满意．现有32个人在第一层，并且他们分别住在第2层至第33层的每一层，问：电梯停在哪一层，可以使得这32个人不满意的总分达到最小值？最小值是多少？（有些人可以不坐电梯直接从楼梯上楼） 【答案】当电梯停在第27层时，不满意总分最小，最小值为316分 【解析】 【分析】 【详解】解易知这32人恰好是从第2层到第33层各住1人．对于每个乘电梯上下楼的人，他所住的层数一定不小于直接上楼的人所住的层数（事实上，设住s 层的人乘电梯，而住第t 层的人直接上楼，s t <，则这2人不满意分数之和为3t ；若两人交换上楼方式，则2人不满意分数之和为33s t <，即不满意总分减小． 设电梯停在第x 层，在第一层有y 人没有乘电梯而直接上楼，那么不满意总分为3[12(33)]3(12)[12(2)]S x y x y =+++-++++++++--，其中3[12(33)]x +++-是住在第1x +层至第33层的人（共33x -人）的不满意总分之和，3(12)y +++是直接从楼梯上楼的人（共y 人）的不满意总分之和，12(2)x y +++--是从第2y +层至第1x -层的人（共2x y --人）的不满意总分之和，于是331(33)(34)(1)(2)(1)222S x x y y x y x y =--+++----222102231684x xy x y y =--+++ 222(102)231684x y x y y =-++++()221021215180308648y x y y +⎛⎫=-+-+ ⎪⎝⎭22102152(6)31631648y x y +⎛⎫=-+-+≥ ⎪⎝⎭，且当27,6x y ==时，316S =．答：当电梯停在第27层时，不满意总分最小，最小值为316分．注：求含2个或2个以上变量的代数式的最大（小）值时，配方法是其中有效方法之一；另一种方法则是利用已有不等式将含有变量的代数式化为一个不大于（或不小于）一个常数c 的不等式，并能确定等号可以成立，则常数c 便是所求的最大值（或最小值）；第三种方法就是化为一元二次方程用判别式法（参看§5例4~7），等等．31．（2021·全国·九年级竞赛）求函数22233x y x x +=++的最大值和最小值．【答案】当2x =-时，y 取最小值2-；当0x =时，y 取最大值23，理由见解析． 【解析】 【分析】 【详解】将原式整理为关于x 的方程：2(32)(32)0yx y x y +-+-=．若0y =，则1x =-，即0y =是函数的一个值；若0y ≠，则因关于x 的方程有实根，所以2(32)4(32)(32)(324)0y y y y y y =---=---≥，即(32)(2)0y y -+≤，解得223y -≤≤．由此可看出0y =即不是最大值也不是最小值． 当2y =-时，由222233x x x +-=++，解得2x =-；当23y =时，由2222333x x x +=++，解得0x =．所以当2x =-时，y 取最小值2-；当0x =时，y 取最大值23．32．（2021·全国·九年级竞赛）已知,,a b c 都是正整数，且抛物线2y ax bx c =++与x 轴有2个不同的交点A 和B ，若,A B 到原点的距离都小于1，求a b c ++的最小值． 【答案】11，见解析． 【解析】 【分析】【详解】设()()()1212,0,,0A x B x x x <，则1212120,0,00b x x ax x c x x a ⎧+=-<⎪⎪⇒<<⎨⎪⋅=>⎪⎩． 又2402b ac b ac =->⇒>① 又因为121,1OA x OB x =<=<， 故121210,101cx x x x c a a-<<-<<⇒=<⇒<．② 因0a >，抛物线开口向上，故1x =-时，0y a b c =-+>，得b a c <+．而,b a c +均为正整数，故1a c b +≥+，于是由①得21()1a c ac a c +>⇒>，由②1a c >，即1a c >，于是22(1)(11)4a c >≥+=，所以5a ≥．又22514b ac >⨯，所以5b ≥．取5,5,1a b c ===时，2551y x x =++满足题目条件，故a b c ++的最小值为55111++=． 33．（2021·全国·九年级竞赛）求2221026249T x y z xy yz z =++---+的最小值． 【答案】5 【解析】 【分析】 【详解】解 ()()()22222692445T x xy y y yz z z z =-++-++-++222(3)()(2)55x y y z z =-+-+-+≥．当6,2x y z ===时，T 取最小值5．注：例2~3中求最值的方法是常用的配方法．34．（2021·全国·九年级竞赛）在40与100之间任取一个实数x ，如果[]7x =，那么1610x ⎡=⎣的概率是多少?这是[]a 表示不超过a 的最大整数（要求答案写成最简分数的形式）． 【答案】780【解析】 【分析】 【详解】因[]7x =，故2278,78x x <≤≤≤．而要使[16]10x =，即22101611,2.5 2. 75,2.5 2.75x x x ≤≤≤，故所求概率22222.75 2.25 1.31257871580p -===-． 35．（2021·全国·九年级竞赛）如图，D E F 、、分别是ABC 的三边BC CA AB 、、上任意一点，证明：,,AEF BFD CDE △△△中至少有一个三角形的面积不大于ABC 的面积的四分之一．【答案】见解析 【解析】 【分析】 【详解】证明 记123,,,ABC AEF BFD CDE S S S S S S S S ====，于是11sin 21sin 2AE AF A S AE AFS AB ACAB AC A ⋅⋅⋅⋅==⋅⋅⋅⋅．同理32,S S BF BD CD CE S BA BC S CA CB⋅⋅==⋅⋅， 所以1233222()()()S S S AF FB BD DC CE EA S AB BC CA ⋅⋅⋅⋅⋅=⋅⋅ 222222122264AF FB BD DC CE EA AB BC CA +++⎛⎫⎛⎫⎛⎫⋅⋅ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭≤=⋅⋅． 31234S S S S ． 由平均值原理得123,,S S S 中必有一个不大于S4．即证． 36．（2021·全国·九年级竞赛）某林场安排了7天的植树工作，从第二天起每天都比前一天增加5个植树的人，但从第二天起每人每天都比前一天少植5棵树，且同一天植树的人，植相同数量的树．若7天共植树9947棵，则植树最多的那天共植了多少棵？植树最少的那天，有多少人在植树？ 【答案】植树最少的那天有54人或24人植树． 【解析】 【分析】 【详解】设第4天有m 人植树，每人植树n 棵，则第4天共植树mn 棵；第3天有5m -人植树，每人植5n +棵，则第3天共植树(5)(5)m n -+棵．同理，第2天共植树(10)(10)m n -+棵；第1天共植树(15)(15)m n -+棵；第5天共植树(5)(5)m n +-棵；第6天共植树(10)(10)m n +-棵；第7天共植树(15)(15)m n +-棵．由七天共植树9947棵得(15)(15)(10)(10)m n m n -++-++(5)(5)(5)(5)m n mn m n -++++-(10)(10)m n ++-(15)(15)9947m n ++-=．化简得77009947mn -=，1521mn =．因221521313=⨯．又每天都有人植树，所以15m >，15n >，故39m n ==．因为第4天植树棵数为39391521⨯=，其他各天植树棵数为(39)(39)a a -+=21521a -（5a =，10或15），所以第4天植树最多，这一天共植树1521棵． 当15a =时，2239a -的植树棵数最少．又当15a =时，植树人数为391554+=或391524-=，所以植树最少的那天有54人或24人植树． 37．（2021·全国·九年级竞赛）一幢33层的大楼有一部电梯停在第一层，它一次最多能容纳32人，而且只能在第2层至第33层中某一层停一次．对于每个人来说他往下走一层楼梯感到1分不满意，往上走一层楼梯感到3分不满意．现在有32个人在第一层，并且他们分别在第2至第33层的每一层，问：电梯停在哪一层，可以使32人不满意的总分达到最小？最小值是多少？（有些人可以不坐电梯而直接从楼梯上楼）． 【答案】当电梯停在第27层时，这32人不满意的总分达到最小，最小值为316分． 【解析】 【分析】 【详解】易知，这32人恰好是第2至第33层各住一人，对于每个乘电梯上、下梯的人，他所住的层数一定大于直接走楼梯上楼的人所住的层数．事实上，设住s 层的人乘电梯，而住第t 层的人直接走楼梯上楼，且s t <，交换两人上楼方式，其余人不变，则不满意总分不增．现分别证明如下：设电梯停在第x 层，①当x s t ≤<时，若住在第s 层的坐电梯，住第t 层的人直接走楼梯上楼，则这两者不满意总分为3(1)3()t s x -+-=3333t s x +--；交换两人上楼方式，则两者不满意总分为3(1)3()s t x -+-=3333t s x +--，两者相等；②当s x t <<时，若住s 层的人乘电梯，而住第t 层的人直接走楼梯上楼，则这两人不满意总分为3(1)()t x s -+-=33t x s +--；交换两人上楼方式，则这两者不满意总分为3(1)3()s t x -+-=3333t x s -+-，前者比后者多4()0x s ->；③当s t x <≤时，若住s 层的人乘电梯，住t 层的人直接走楼梯上楼，则这两者不满意总分为3(1)()t x s -+-=33t x s +--；交换两人上楼方式，则这两者的不满意总分为3(1)()s x t -+-=33s x t +--，前者比后者多4()0t s ->．今设电梯停在第x 层，设有y 人直接走楼梯上楼，则11y x +≤-，那么不满意总分为3(12)s y =+++3[12(33)]x ++++-[12(11)]x y ++++---3(1)3(33)(34)22y y x x +--=++(2)(1)2x y x y ----222102231684x xy x y y =--+++222(102)231684x y x y y =-++++=210224y x +⎡⎤-⎢⎥⎣⎦()211518030688y y +-+210224y x +⎛⎫=-+ ⎪⎝⎭215(6)3163168y +-+≥． 当27x =，6y =时，316s =，所以，当电梯停在第27层时，这32人不满意的总分达到最小，最小值为316分．38．（2021·全国·九年级竞赛）已知正整数m ，n 17434m m n -+=，求n 的最大值． 【答案】104 【解析】 【分析】 【详解】设70a m =-，104104a a n -+=，两边平方得22222104a a n +-=．令222104a b -=（b 为正整数），则2()()104a b a b -+=．由于-a b 与a b +同奇偶，即同为偶数，所以当2a b -=时，a b +取最大值52104⨯．这时，222()104n a b =+=为最大，所以n 的最大值为104． 39．（2021·全国·九年级竞赛）对于1,2,3,,i n =，有|| 1 i x <且有12||||||n x x x +++=122009||n x x x ++++．求正整数n 的最小值．【答案】正整数n 的最小值为2010． 【解析】 【分析】 【详解】 作整体估计如下：2009=1212||||||||n n x x x x x x +++-+++12||||||n x x x n ≤+++<，所以2010n ≥．当2010n =时，取121005x x x ===20092010=，10061007x x ===201020092010x =-，则||1i x <(1,2,,2010) i =且122010|||||x x x +++2009=+122010||x x x +++，满足题目条件，故所求n 的最小值为2010．40．（2021·全国·九年级竞赛）整数012010,,,x x x 满足条件：00x =，10|||1|x x =+，21|||1|x x =+，…，201020091x x =+，求122010x x x +++的最小值．【答案】122010x x x +++的最小值为7．【解析】 【分析】 【详解】由已知条件可得：2210021x x x =++，2221121x x x =++，…，2220102009200921x x x =++，各式相加整理后得22010x =()2001200922010x x x x +++++．又00x =，故有122010x x x +++=2201020101220102x x +-()220101120112x =+-． 因122010x x x +++为整数，故()220101x +为奇数，又2243201045<<且2432011-=16214>=2452011-，所以122010x x x +++2145201172≥-=．。
三角函数大题专项(含答案)
三角函数博项锻炼之阳早格格创做1．正在△ABC中，角A、B、C对于应边a、b、c，中交圆半径为1，已知2（sin2A﹣sin2C）＝（a﹣b）sinB．（1）说明a2+b2﹣c2＝ab；（2）供角C战边c．2．正在△ABC中，内角A，B，C所对于的边分别为a，b，c．已知bsinA＝acos（B﹣）．（Ⅰ）供角B的大小；（Ⅱ）设a＝2，c＝3，供b战sin（2A﹣B）的值．3．已知α，β为钝角，tanα＝，cos（α+β）＝﹣．（1）供cos2α的值；（2）供tan（α﹣β）的值．4．正在仄里四边形ABCD中，∠ADC＝90°，∠A＝45°，AB＝2，BD＝5．（1）供cos∠ADB；（2）若DC＝2，供BC．5．已知函数f（x）＝sin2x+sinxcosx．（Ⅰ）供f（x）的最小正周期；（Ⅱ）若f（x）正在区间[﹣，m]上的最大值为，供m 的最小值．6．正在△ABC中，内角A，B，C所对于的边分别为a，b，c．已知asinA＝4bsinB，ac＝（a2﹣b2﹣c2）（Ⅰ）供cosA的值；（Ⅱ）供sin（2B﹣A）的值7．设函数f（x）＝sin（ωx﹣）+sin（ωx﹣），其中0＜ω＜3，已知f（）＝0．（Ⅰ）供ω；（Ⅱ）将函数y＝f（x）的图象上各面的横坐标伸少为本去的2倍（纵坐标没有变），再将得到的图象背左仄移个单位，得到函数y＝g（x）的图象，供g（x）正在[﹣，]上的最小值．8．正在△ABC中，内角A，B，C所对于的边分别为a，b，c．已知a＞b，a＝5，c＝6，sinB＝．（Ⅰ）供b战sinA的值；（Ⅱ）供sin（2A+）的值．9．△ABC的内角A，B，C的对于边分别为a，b，c，已知△ABC的里积为．（1）供sinBsinC；（2）若6cosBcosC＝1，a＝3，供△ABC的周少．10．△ABC的内角A，B，C的对于边分别为a，b，c，已知sin（A+C）＝8sin2．（1）供cosB；（2）若a+c＝6，△ABC的里积为2，供b．11．已知函数f（x）＝cos（2x﹣）﹣2sinxcosx．（I）供f（x）的最小正周期；（II）供证：当x∈[﹣，]时，f（x）≥﹣．12．已知背量＝（cosx，sinx），＝（3，﹣），x∈[0，π]．（1）若，供x的值；（2）记f（x）＝，供f（x）的最大值战最小值以及对于应的x的值．13．正在△ABC中，∠A＝60°，c＝a．（1）供sinC的值；（2）若a＝7，供△ABC的里积．14．已知函数f（x）＝2sinωxcosωx+cos2ωx（ω＞0）的最小正周期为π．（1）供ω的值；（2）供f（x）的单调递加区间．15．正在△ABC中，内角A，B，C所对于的边分别为a，b，c，已知b+c＝2acosB．（1）说明：A＝2B；（2）若cosB＝，供cosC的值．16．设f（x）＝2sin（π﹣x）sinx﹣（sinx﹣cosx）2．（Ⅰ）供f（x）的单调递加区间；（Ⅱ）把y＝f（x）的图象上所有面的横坐标伸少到本去的2倍（纵坐标没有变），再把得到的图象背左仄移个单位，得到函数y＝g（x）的图象，供g（）的值．17．正在△ABC中，内角A，B，C所对于的边分别为a，b，c，已知asin2B＝bsinA．（1）供B；（2）已知cosA＝，供sinC的值．18．正在△ABC中，内角A，B，C所对于的边分别为a，b，c，已知b+c＝2acosB．（Ⅰ）说明：A＝2B；（Ⅱ）若△ABC的里积S＝，供角A的大小．19．正在△ABC中，角A，B，C所对于的边分别是a，b，c，且+＝．（Ⅰ）说明：sinAsinB＝sinC；（Ⅱ）若b2+c2﹣a2＝bc，供tanB．20．正在△ABC中，AC＝6，cosB＝，C＝．（1）供AB的少；（2）供cos（A﹣）的值．21．已知函数f（x）＝4tanxsin（﹣x）cos（x﹣）﹣．（1）供f（x）的定义域与最小正周期；（2）计划f（x）正在区间[﹣，]上的单调性．22．△ABC的内角A，B，C的对于边分别为a，b，c，已知2cosC（acosB+bcosA）＝c．（Ⅰ）供C；（Ⅱ）若c＝，△ABC的里积为，供△ABC的周少．参照问案1．正在△ABC中，角A、B、C对于应边a、b、c，中交圆半径为1，已知2（sin2A﹣sin2C）＝（a﹣b）sinB．（1）说明a2+b2﹣c2＝ab；（2）供角C战边c．【解问】说明：（1）∵正在△ABC中，角A、B、C对于应边a、b、c，中交圆半径为1，∴由正弦定理得：＝2R＝2，∴sinA＝，sinB＝，sinC＝，∵2（sin2A﹣sin2C）＝（a﹣b）sinB，∴2（）＝（a﹣b）•，化简，得：a2+b2﹣c2＝ab，故a2+b2﹣c2＝ab．解：（2）∵a2+b2﹣c2＝ab，∴cosC＝＝＝，解得C＝，∴c＝2sinC＝2•＝．2．正在△ABC中，内角A，B，C所对于的边分别为a，b，c．已知bsinA＝acos（B﹣）．（Ⅰ）供角B的大小；（Ⅱ）设a＝2，c＝3，供b战sin（2A﹣B）的值．【解问】解：（Ⅰ）正在△ABC中，由正弦定理得，得bsinA＝asinB，又bsinA＝acos（B﹣）．∴asinB＝acos（B﹣），即sinB＝cos（B﹣）＝cosBcos+sinBsin＝cosB+，∴tanB＝，又B∈（0，π），∴B＝．（Ⅱ）正在△ABC中，a＝2，c＝3，B＝，由余弦定理得b＝＝，由bsinA＝acos（B ﹣），得sinA＝，∵a＜c，∴cosA＝，∴sin2A＝2sinAcosA＝，cos2A＝2cos2A﹣1＝，∴sin（2A﹣B）＝sin2AcosB﹣cos2AsinB＝＝．3．已知α，β为钝角，tanα＝，cos（α+β）＝﹣．（1）供cos2α的值；（2）供tan（α﹣β）的值．【解问】解：（1）由，解得，∴cos2α＝；（2）由（1）得，sin2，则tan2α＝．∵α，β∈（0，），∴α+β∈（0，π），∴sin（α+β）＝＝．则tan（α+β）＝．∴tan（α﹣β）＝tan[2α﹣（α+β）]＝＝．4．正在仄里四边形ABCD中，∠ADC＝90°，∠A＝45°，AB＝2，BD＝5．（1）供cos∠ADB；（2）若DC＝2，供BC．【解问】解：（1）∵∠ADC＝90°，∠A＝45°，AB＝2，BD＝5．∴由正弦定理得：＝，即＝，∴sin∠ADB＝＝，∵AB＜BD，∴∠ADB＜∠A，∴cos∠ADB＝＝．（2）∵∠ADC＝90°，∴cos∠BDC＝sin∠ADB＝，∵DC＝2，∴BC＝＝＝5．5．已知函数f（x）＝sin2x+sinxcosx．（Ⅰ）供f（x）的最小正周期；（Ⅱ）若f（x）正在区间[﹣，m]上的最大值为，供m 的最小值．【解问】解：（I）函数f（x）＝sin2x+sinxcosx＝+sin2x＝sin（2x﹣）+，f（x）的最小正周期为T＝＝π；（Ⅱ）若f（x）正在区间[﹣，m]上的最大值为，可得2x﹣∈[﹣，2m﹣]，即有2m﹣≥，解得m≥，则m的最小值为．6．正在△ABC中，内角A，B，C所对于的边分别为a，b，c．已知asinA＝4bsinB，ac＝（a2﹣b2﹣c2）（Ⅰ）供cosA的值；（Ⅱ）供sin（2B﹣A）的值【解问】（Ⅰ）解：由，得asinB＝bsinA，又asinA＝4bsinB，得4bsinB＝asinA，二式做比得：，∴a＝2b．由，得，由余弦定理，得；（Ⅱ）解：由（Ⅰ），可得，代进asinA＝4bsinB，得．由（Ⅰ）知，A为钝角，则B为钝角，∴．于是，，故．7．设函数f（x）＝sin（ωx﹣）+sin（ωx﹣），其中0＜ω＜3，已知f（）＝0．（Ⅰ）供ω；（Ⅱ）将函数y＝f（x）的图象上各面的横坐标伸少为本去的2倍（纵坐标没有变），再将得到的图象背左仄移个单位，得到函数y＝g（x）的图象，供g（x）正在[﹣，]上的最小值．【解问】解：（Ⅰ）函数f（x）＝sin（ωx﹣）+sin（ωx ﹣）＝sinωxcos﹣cosωxsin﹣sin（﹣ωx）＝sinωx﹣cosωx＝sin（ωx﹣），又f（）＝sin（ω﹣）＝0，∴ω﹣＝kπ，k∈Z，解得ω＝6k+2，又0＜ω＜3，∴ω＝2；（Ⅱ）由（Ⅰ）知，f（x）＝sin（2x﹣），将函数y＝f（x）的图象上各面的横坐标伸少为本去的2倍（纵坐标没有变），得到函数y＝sin（x﹣）的图象；再将得到的图象背左仄移个单位，得到y＝sin（x+﹣）的图象，∴函数y＝g（x）＝sin（x﹣）；当x∈[﹣，]时，x﹣∈[﹣，]，∴sin（x﹣）∈[﹣，1]，∴当x＝﹣时，g（x）博得最小值是﹣×＝﹣．8．正在△ABC中，内角A，B，C所对于的边分别为a，b，c．已知a＞b，a＝5，c＝6，sinB＝．（Ⅰ）供b战sinA的值；（Ⅱ）供sin（2A+）的值．【解问】解：（Ⅰ）正在△ABC中，∵a＞b，故由sinB＝，可得cosB＝．由已知及余弦定理，有＝13，∴b＝．由正弦定理，得sinA＝．∴b＝，sinA＝；（Ⅱ）由（Ⅰ）及a＜c，得cosA＝，∴sin2A＝2sinAcosA ＝，cos2A＝1﹣2sin2A＝﹣．故sin（2A+）＝＝．9．△ABC的内角A，B，C的对于边分别为a，b，c，已知△ABC的里积为．（1）供sinBsinC；（2）若6cosBcosC＝1，a＝3，供△ABC的周少．【解问】解：（1）由三角形的里积公式可得S△ABC＝acsinB＝，∴3csinBsinA＝2a，由正弦定理可得3sinCsinBsinA＝2sinA，∵sinA≠0，∴sinBsinC＝；（2）∵6cosBcosC＝1，∴cosBcosC＝，∴cosBcosC﹣sinBsinC＝﹣＝﹣，∴cos（B+C）＝﹣，∴cosA＝，∵0＜A＜π，∴A＝，∵＝＝＝2R＝＝2，∴sinBsinC＝•＝＝＝，∴bc＝8，∵a2＝b2+c2﹣2bccosA，∴b2+c2﹣bc＝9，∴（b+c）2＝9+3cb＝9+24＝33，∴b+c＝∴周少a+b+c＝3+．10．△ABC的内角A，B，C的对于边分别为a，b，c，已知sin（A+C）＝8sin2．（1）供cosB；（2）若a+c＝6，△ABC的里积为2，供b．【解问】解：（1）sin（A+C）＝8sin2，∴sinB＝4（1﹣cosB），∵sin2B+cos2B＝1，∴16（1﹣cosB）2+cos2B＝1，∴16（1﹣cosB）2+cos2B﹣1＝0，∴16（cosB﹣1）2+（cosB﹣1）（cosB+1）＝0，∴（17cosB﹣15）（cosB﹣1）＝0，∴cosB＝；（2）由（1）可知sinB＝，∵S△ABC＝ac•sinB＝2，∴ac＝，∴b2＝a2+c2﹣2accosB＝a2+c2﹣2××＝a2+c2﹣15＝（a+c）2﹣2ac﹣15＝36﹣17﹣15＝4，∴b＝2．11．已知函数f（x）＝cos（2x﹣）﹣2sinxcosx．（I）供f（x）的最小正周期；（II）供证：当x∈[﹣，]时，f（x）≥﹣．【解问】解：（Ⅰ）f（x）＝cos（2x﹣）﹣2sinxcosx，＝（co2x+sin2x）﹣sin2x，＝cos2x+sin2x，＝sin（2x+），∴T＝＝π，∴f（x）的最小正周期为π，（Ⅱ）∵x∈[﹣，]，∴2x+∈[﹣，]，∴﹣≤sin（2x+）≤1，∴f（x）≥﹣12．已知背量＝（cosx，sinx），＝（3，﹣），x∈[0，π]．（1）若，供x的值；（2）记f（x）＝，供f（x）的最大值战最小值以及对于应的x的值．【解问】解：（1）∵＝（cosx，sinx），＝（3，﹣），∥，∴﹣cosx＝3sinx，当cosx＝0时，sinx＝1，分歧题意，当cosx≠0时，tanx＝﹣，∵x∈[0，π]，∴x＝，（2）f（x）＝＝3cosx﹣sinx＝2（cosx﹣sinx）＝2cos（x+），∵x∈[0，π]，∴x+∈[，]，∴﹣1≤cos（x+）≤，当x＝0时，f（x）有最大值，最大值3，当x＝时，f（x）有最小值，最小值﹣2．13．正在△ABC中，∠A＝60°，c＝a．（1）供sinC的值；（2）若a＝7，供△ABC的里积．【解问】解：（1）∠A＝60°，c＝a，由正弦定理可得sinC＝sinA＝×＝，（2）a＝7，则c＝3，∴C＜A，∵sin2C+cos2C＝1，又由（1）可得cosC＝，∴sinB＝sin（A+C）＝sinAcosC+cosAsinC＝×+×＝，∴S△ABC＝acsinB＝×7×3×＝6．14．已知函数f（x）＝2sinωxcosωx+cos2ωx（ω＞0）的最小正周期为π．（1）供ω的值；（2）供f（x）的单调递加区间．【解问】解：f（x）＝2sinωxcosωx+cos2ωx，＝sin2ωx+cos2ωx，＝，由于函数的最小正周期为π，则：T＝，解得：ω＝1．（2）由（1）得：函数f（x）＝，令（k∈Z），解得：（k∈Z），所以函数的单调递加区间为：[]（k∈Z）．15．正在△ABC中，内角A，B，C所对于的边分别为a，b，c，已知b+c＝2acosB．（1）说明：A＝2B；（2）若cosB＝，供cosC的值．【解问】（1）说明：∵b+c＝2acosB，∴sinB+sinC＝2sinAcosB，∵sinC＝sin（A+B）＝sinAcosB+cosAsinB，∴sinB＝sinAcosB﹣cosAsinB＝sin（A﹣B），由A，B∈（0，π），∴0＜A﹣B＜π，∴B＝A﹣B，或者B＝π﹣（A﹣B），化为A＝2B，或者A＝π（舍去）．∴A＝2B．（II）解：cosB＝，∴sinB＝＝．cosA＝cos2B＝2cos2B﹣1＝，sinA＝＝．∴cosC＝﹣cos（A+B）＝﹣cosAcosB+sinAsinB＝+×＝．16．设f（x）＝2sin（π﹣x）sinx﹣（sinx﹣cosx）2．（Ⅰ）供f（x）的单调递加区间；（Ⅱ）把y＝f（x）的图象上所有面的横坐标伸少到本去的2倍（纵坐标没有变），再把得到的图象背左仄移个单位，得到函数y＝g（x）的图象，供g（）的值．【解问】解：（Ⅰ）∵f（x）＝2sin（π﹣x）sinx﹣（sinx ﹣cosx）2 ＝2sin2x﹣1+sin2x＝2•﹣1+sin2x＝sin2x﹣cos2x+﹣1＝2sin（2x﹣）+﹣1，令2kπ﹣≤2x﹣≤2kπ+，供得kπ﹣≤x≤kπ+，可得函数的删区间为[kπ﹣，kπ+]，k∈Z．（Ⅱ）把y＝f（x）的图象上所有面的横坐标伸少到本去的2倍（纵坐标没有变），可得y＝2sin（x﹣）+﹣1的图象；再把得到的图象背左仄移个单位，得到函数y＝g（x）＝2sinx+﹣1的图象，∴g（）＝2sin+﹣1＝．17．正在△ABC中，内角A，B，C所对于的边分别为a，b，c，已知asin2B＝bsinA．（1）供B；（2）已知cosA＝，供sinC的值．【解问】解：（1）∵asin2B＝bsinA，∴2sinAsinBcosB＝sinBsinA，∴cosB＝，∴B＝．（2）∵cosA＝，∴sinA＝，∴sinC＝sin（A+B）＝sinAcosB+cosAsinB＝＝．18．正在△ABC中，内角A，B，C所对于的边分别为a，b，c，已知b+c＝2acosB．（Ⅰ）说明：A＝2B；（Ⅱ）若△ABC的里积S＝，供角A的大小．【解问】（Ⅰ）说明：∵b+c＝2acosB，∴sinB+sinC＝2sinAcosB，∴sinB+sin（A+B）＝2sinAcosB∴sinB+sinAcosB+cosAsinB＝2sinAcosB∴sinB＝sinAcosB﹣cosAsinB＝sin（A﹣B）∵A，B是三角形中的角，∴B＝A﹣B，∴A＝2B；（Ⅱ）解：∵△ABC的里积S＝，∴bcsinA＝，∴2bcsinA＝a2，∴2sinBsinC＝sinA＝sin2B，∴sinC＝cosB，∴B+C＝90°，或者C＝B+90°，∴A＝90°或者A＝45°．19．正在△ABC中，角A，B，C所对于的边分别是a，b，c，且+＝．（Ⅰ）说明：sinAsinB＝sinC；（Ⅱ）若b2+c2﹣a2＝bc，供tanB．【解问】（Ⅰ）说明：正在△ABC中，∵+＝，∴由正弦定理得：，∴＝，∵sin（A+B）＝sinC．∴整治可得：sinAsinB＝sinC，（Ⅱ）解：b2+c2﹣a2＝bc，由余弦定理可得cosA＝．sinA＝，＝+＝＝1，＝，tanB＝4．20．正在△ABC中，AC＝6，cosB＝，C＝．（1）供AB的少；（2）供cos（A﹣）的值．【解问】解：（1）∵△ABC中，cosB＝，B∈（0，π），∴sinB＝，∵，∴AB＝＝5；（2）cosA═﹣cos（π﹣A）＝﹣cos（C+B）＝sinBsinC﹣cosBcosC＝﹣．∵A为三角形的内角，∴sinA＝，∴cos（A﹣）＝cosA+sinA＝．21．已知函数f（x）＝4tanxsin（﹣x）cos（x﹣）﹣．（1）供f（x）的定义域与最小正周期；（2）计划f（x）正在区间[﹣，]上的单调性．【解问】解：（1）∵f（x）＝4tanxsin（﹣x）cos（x﹣）﹣．∴x≠kπ+，即函数的定义域为{x|x≠kπ+，k∈Z}，则f（x）＝4tanxcosx•（cosx+sinx）﹣＝4sinx（cosx+sinx）﹣＝2sinxcosx+2sin2x﹣＝sin2x+（1﹣cos2x）﹣＝sin2x﹣cos2x＝2sin（2x﹣），则函数的周期T＝；（2）由2kπ﹣＜2x﹣＜2kπ+，k∈Z，得kπ﹣＜x＜kπ+，k∈Z，即函数的删区间为（kπ﹣，kπ+），k∈Z，当k＝0时，删区间为（﹣，），k∈Z，∵x∈[﹣，]，∴此时x∈（﹣，]，由2kπ+＜2x﹣＜2kπ+，k∈Z，得kπ+＜x＜kπ+，k∈Z，即函数的减区间为（kπ+，kπ+），k∈Z，当k＝﹣1时，减区间为（﹣，﹣），k∈Z，∵x∈[﹣，]，∴此时x∈[﹣，﹣），即正在区间[﹣，]上，函数的减区间为∈[﹣，﹣），删区间为（﹣，]．22．△ABC的内角A，B，C的对于边分别为a，b，c，已知2cosC（acosB+bcosA）＝c．（Ⅰ）供C；（Ⅱ）若c＝，△ABC的里积为，供△ABC的周少．【解问】解：（Ⅰ）∵正在△ABC中，0＜C＜π，∴sinC≠0已知等式利用正弦定理化简得：2cosC （sinAcosB+sinBcosA）＝sinC，整治得：2cosCsin（A+B）＝sinC，即2cosCsin（π﹣（A+B））＝sinC2cosCsinC＝sinC∴cosC＝，∴C＝；（Ⅱ）由余弦定理得7＝a2+b2﹣2ab•，∴（a+b）2﹣3ab＝7，∵S＝absinC＝ab＝，∴ab＝6，∴（a+b）2﹣18＝7，∴a+b＝5，∴△ABC的周少为5+．。
三角函数50题精选题附答案
1. 已知方程（a 为大于1的常数）的两根为，，且、，则的值是_________________.解析：属于易错题，由于限定了角的范围，所以最终答案只有一个，1>a ∴a 4tan tan -=+βα0<，o a >+=⋅13tan tan βα∴βαtan ,tan 是方程01342=+++a ax x 的两个负根 又⎪⎭⎫ ⎝⎛-∈2,2,ππβα ⎪⎭⎫⎝⎛-∈∴0,2,πβα 即⎪⎭⎫ ⎝⎛-∈+0,22πβα由tan ()βα+=βαβαtan tan 1tan tan ⋅-+=()1314+--a a =34可得.22tan -=+βα2.函数f(x)=的值域为______________。
解析：易错题，错因：令x x t cos sin +=后忽视1-≠t ,从而121)(-≠-=t t g ，得到错解：⎥⎦⎤⎢⎣⎡---2122,2122 正解：⎥⎦⎤ ⎝⎛--⋃⎪⎪⎭⎫⎢⎣⎡---2122,11,2122 3.在△ABC 中，2sinA+cosB=2，sinB+2cosA=，则∠C 的大小应为( )A ．B ．C ．或D ．或解析：遇到这类型题，首先排除两个答案，因为给定条件就是让我们去排除4.已知tana tanb 是方程x 2+3x+4=0的两根，若a ，b ∈(-)，则a+b=（ ）A ．B ．或-C ．-或D ．-解析：tana .tanb=4；tana +tanb=-3，所以tana tanb 均为负，即a ，b 都属于四象限 5.在中，，则的大小为（ ）A. B. C.D.解析：由3s i n 463c o s 41A B A B +=+=⎧⎨⎩c o s s i n 平方相加得115sin()sin 2266A B C C ππ+=∴=∴=或若C =56π， 则A B +=π6113cos 4sin 0cos 3A B A -=>∴<又1312<5366A C C πππ∴>∴≠∴= ∴选A ，实际上首先排除两个答案的6.函数为增函数的区间是……………… ( ) A.B.C.D.解析：注意x 前面系数为负7.已知且，这下列各式中成立的是（ ） A.B.C.D.解析：解法1sin β＞-cos α=sin （3π/2-α），因为β、（3π/2-α）都在二象限，sinx 二象限为减函数，所以β＜（3π/2-α）解法2：首先排除AC（为什么），由特殊值法排除B8.△ABC中，已知cosA=，sinB=，则cosC的值为（）A、 B、 C、或 D、9.设cos1000=k，则tan800是（）A、 B、 C、 D、10.函数的单调减区间是（）A、（）B、C、 D、11.在△ABC中，则∠C的大小为（）A、30°B、150°C、30°或150°D、60°或150°12.若,且,则_______________.13、设ω>0，函数f(x)=2sinωx在上为增函数，那么ω的取值范围是_____14已知奇函数单调减函数，又α，β为锐角三角形内角，则（）A、f(cosα)＞ f(cosβ)B、f(sinα)＞ f(sinβ)C、f(sinα)＜f(cosβ)D、f(sinα)＞ f(cosβ)15.函数的值域是．16.若，α是第二象限角，则=__________17.已知定义在区间[-p，]上的函数y=f(x)的图象关于直线x= -对称，当xÎ[-，]时，函数f(x)=Asin(wx+j)(A>0, w>0,-<j<)，其图象如图所示。
初中三角函数试题及答案
初中三角函数试题及答案一、选择题（每题3分，共30分）1. 若sinA=1/2，则cosA的值为：A. 1/2B. √3/2C. -√3/2D. -1/22. 已知一个角的正弦值为0.6，那么这个角的余弦值的范围是：A. (0,1)B. (-1,0)C. (0,1)D. (-1,1)3. 函数y=sin(x)的周期是：A. 2πB. πC. 2D. 14. 函数y=cos(x)的图像关于：A. y轴对称B. x轴对称C. 原点对称D. 以上都不对5. 已知tanA=2，那么sinA/cosA的值为：A. 2B. 1/2C. -2D. -1/26. 函数y=sin(x)+cos(x)的最大值是：A. 1B. √2C. 2D. √37. 如果一个角的余弦值为-1，则这个角的度数是：A. 0°B. 90°C. 180°D. 270°8. 函数y=sin(x)在区间[0,π]上是：A. 增函数B. 减函数C. 先增后减D. 先减后增9. 函数y=cos(x)的图像在x=π/2处的切线斜率是：A. 0B. 1C. -1D. 不存在10. 已知sin(A+B)=sinAcosB+cosAsinB，那么cos(A+B)的表达式是：A. cosAcosB-sinAsinBB. cosAcosB+sinAsinBC. -cosAcosB-sinAsinBD. -cosAcosB+sinAsinB二、填空题（每题3分，共30分）1. 若sinA=3/5，且A为锐角，则cosA=______。
2. 函数y=cos(x-π/3)的图像关于点______对称。
3. 函数y=tan(x)的周期是______。
4. 如果一个角的正弦值为1/2，则这个角的余弦值可以是______。
5. 函数y=sin(x)在x=π/2处的值是______。
6. 函数y=cos(x)在x=0处的值是______。
九年级数学竞赛专题12 三角函数_答案
专题12三角函数例1 AC 2－BC 2＝(1993＋1992)(1993－1992)＝1993＋1992＝AB 2，∴AC 2＝AB 2＋BC 2，得∠B＝90°，故原式＝(19921993)2.例2 AD ＝227m ，BC ＝146m .解法一:延长AD ，BC 交于点E ，如图1.在Rt △ABE 中，AB ＝200m ，∠A ＝60°，∴BE ＝AB ·tanA ＝200 3 (m )，AE ＝AB cos 60°＝2000.5＝400(m ).在Rt △CDE 中，CD ＝100m .∠E ＝90°－∠A ＝30°，∴CE ＝2CD ＝200(m .∵cot ∠E ＝DE CD ，DE ＝CD ·cot 30°＝100 3 (m )，∴AD＝AE －DE ＝400－1003≈227(m )，BC ＝BE －CE ＝2003－200≈146(m ).解法二:如图2，过点D 作矩形ABEF .设AD ＝x .在Rt △AFD 中，∠DAF ＝90°－60°＝30°，∴DF ＝12AD ＝12x ，AF ＝32x ，在Rt △CED 中，∠CDE ＝30°，∴CE ＝12CD ＝50(m )，DE ＝32CD ＝503(m )，∵DE ＋DF ＝AB .∴503＋12x ＝200，解得x ＝400－100 3.∴AD ＝400－1003≈227(m ).∵BC ＋CE ＝AF ，∴BC ＝AF －CE ＝32(400－1003)－50＝2003－200≈146(m ).例3 ⑴103 ⑵35 提示：tan ∠AEN ＝tan ∠EAB ＝EB AB .例4 ⑴设DE ＝x (海里)，则客轮从A 点出发到相遇之处E 点的距离为2x 海里.若2x <200，则x <100，即DE <12AB ，而从D 点出发，货轮到相遇点E 处的最短距离是100海里，所以x ≥100，即2x ≥200，故相遇处E 点应在CB 上，选B . ⑵设货轮从出发点D 到两船相遇处E 共航行了x 海里，如图，过D 作DF ⊥CB 于F ，连DE ，则DE ＝x ，AB ＋BE ＝2x ，DF ＝100，EF ＝300－2x ，由x 2＝1002＋(300－2x )2，得x ＝200－10063(海里).例5 ⑴p ，q 应满足以下条件：⎩⎪⎨⎪⎧△＝p 2－4q ≥0sinA ＋sinB ＝－p sinA ·sinB ＝q 0＜sinA ＜10＜sinB ＜1sin 2A ＋cos 2A ＝1.由此推得⎩⎨⎧p <00<q ≤12p 2－2q ＝1 ,⑵先设方程x 2＋px ＋q ＝0的两个根为α，β，若α，β满足⎩⎪⎨⎪⎧p 2－4q ≥0 ①0＜α＜1，0＜β＜1②α2＋β2＝1 ③，则α，β必定是直角三角形的两个锐角的正弦;若α，β不满足条件①②③式中任何一个，则结论是否定的.例6 设α为直角三角形一锐角，则sinα＝a c ，cosα＝b c .∵0<sinα<1，0<cosα<1∴当n ≥3时，sin n α<sin 2α，cos n α<cos 2α，于是sin n α＋cos n α<sin 2α＋cos 2α＝1，即(a c )n ＋(b c )n <1，故a n＋b n<c n ..9 2. 5 1 提示：用换元法. 3.43－213 4.116 5.A 6.B 7.A 8.B9.⑴在Rt △DCE 中，∠CED ＝60°，DE ＝76.∵sin ∠CED ＝DC DE ，∴DC ＝DE ·sin ∠CED ＝383(厘米).故垂直支架CD 的长度为383厘米.⑵设水箱半径OD ＝x 厘米，则OC ＝(383＋x )厘米，AO ＝(150＋x )厘米.∵Rt △OAC 中，∠BAC ＝30°，∴AO ＝2OC ，即150＋x ＝2(383＋x ），解得x ＝150－763≈18.52≈18.5(厘米).故水箱半径OD 的长度为18.5厘米. 10.(1sinα－1)＋(1cosα－1)＋(1sinαcosα－2)＝1－sinαsinα＋1－cosαcosα＋1－2sinαcosαsinαcosα，∵0<sinα<1，0<cosα<1，于是有1－ sinα>0,1－ cosα>0,∴1－sinαsinα＋1－cosαcosα＋(sinα－cosα)2sinαcosα>0，即1sinα＋1cosα＋1sinαcosα>4.11.过C 作CE ∥AB 交BD 于E ，设AC ＝x ，则CB CE ＝BC ·tan ∠CBE由△DCE ∽△DAB ，得CD CE AD AB =，即11x =+，化简得（x ＋2）（x 3－2）＝0，解得x AC . 12. P ＝－2q ＝1，x 1,2＝1.提示：tan A －tan B ＝()CD CD CD BD AD AD BD AD BD-=-⋅. B 级1. 1163m k k <<-2. 43. 145cm 24. 13 提示：延长MN 交BC 的延长线于T ，设MB 的中点为O ，连接TO ，则△BAM ∽△TOB .5. B6. D7.D8. （1）如图，延长线段BE ，与AC 相交于点F ，∴DE ＝AF ，∠BFC ＝∠A ＝37°.在Rt △BCF 中，tan ∠BFC ＝BF CF ，∴CF ＝ 4.8 6.4tan 370.75BC ==︒（米），∴DE ＝AF ＝AC －CF ＝8－6.4＝1.6（米）.故水平平台DE 的长度为1.6米. （2）延长线段DE ，交BC 于点G .∵DG ∥AC ，∴∠BGM ＝∠C ＝90°，∴四边形MNCG 是矩形，∴CG ＝MN ＝3（米）.∵BC ＝4.8（米），∴BG ＝BC －CG ＝1.8（米）.∵DG ∥AC ，∴1.834.88BE BG BF CB ===，∴53EF BE =，而AD ＝EF ，故53AD BE =.9. 18 提示：222a b c +=，3sin 5A =. 10. 提示：（1）S =S △EFG ＋S △FGH ＝1sin 2EG FH θ⋅. （2）过E ，F ，G ，H 分别作正方形ABCD 的垂线，得矩形PQRT .设ABCD 的边长为a ，PQ ＝b ，QR ＝c ，则b，c 由S △AEH ＝S △THE ，S △BEF ＝S △PEF ，S △GFC ＝S △QFG ，S △DGH ＝S △RGH ，得S ABCD ＋S PQRT ＝2S EFGH ，∴a 2＋bc ＝2S，即22a S .∴222222(4)4k l S a k l S +-=-，由（1）知22sin S kl S θ=>，∴2224k l kl S +≥>.故22222244k l S a k l S -=+-. 11. （1）S 梯形ABCD ＝56. （2）E ，F 分别是BC ，DC 的中点，设运动时间为x 秒，则S △EFC ＝22224(5)1055x x x -+=--+，当x ＝5时，S △EFC 面积最大，最大值为10. 12. （1）折冬天太阳最低时，甲楼最高处A 点的影子落在乙楼的C 处，那么图中CD 的长度就是甲楼的影子在乙楼上的高度.设CE ⊥AB 于点E ，则∠AEC ＝90°，∠ACE ＝30°，EC ＝20米，∴AE ＝EC tan ∠ACE ＝20tan30°≈11.6（米），CD ＝EB ＝AB －AE ＝4.4（米）.（2）设点A 的影子落在地面上某点C ，则∠ACB ＝30°，AB ＝16米，∴BC ＝AB cot30°≈27.7（米），故要使甲楼的影子不影响乙楼，那么乙楼距离甲楼至少要27.7米. 第8题图。
2024年数学九年级三角函数专项练习题1(含答案)
2024年数学九年级三角函数专项练习题1（含答案）试题部分一、选择题：1. 已知角A是锐角，sinA = 3/5，则cosA的值为（）A. 4/5B. 3/4C. 4/3D. 2/32. 在直角三角形ABC中，∠C=90°，若sinA = cosB，则∠A的度数是（）A. 30°B. 45°C. 60°D. 90°3. 下列函数中，最小正周期为π的是（）A. y = sin2xB. y = cos3xC. y = tanxD. y = cot2x4. 若0°＜α＜90°，则下列各式中正确的是（）A. sinα＜cosαB. tanα＜cotαC. sinα＜tanαD. cosα＜tanα5. 已知0°＜θ＜90°，且sinθ = √3/2，则cosθ的值为（）A. 1/2B. √3/2C. 1/√2D. 1/√36. 在直角坐标系中，点P（2，√3）位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限7. 已知sinα = 1/2，则cosα的值可能是（）A. √3/2B. √3/2C. 1/2D. 1/28. 若0°＜θ＜90°，且tanθ = 1，则sinθ的值为（）A. 1B. 1/√2C. √2/2D. √3/29. 在直角三角形中，若一个锐角的正弦值等于另一个锐角的余弦值，则这两个角的度数之和为（）A. 45°B. 90°C. 135°D. 180°10. 已知sinα = cos(90° α)，则α的取值范围是（）A. 0°＜α＜45°B. 45°＜α＜90°C. 90°＜α＜135°D. 135°＜α＜180°二、判断题：1. 在直角三角形中，锐角的正弦值随着角度的增大而增大。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
锐角三角函数
古希腊数学家和古代中国数学家为了测量的需要，他们发现并经常利用下列几何结论：在两个大小不同的直角三角形中，只要有一个锐角相等，那么这两个三角形的对应边的比值一定相等．正是古人对天文观察和测量的需要才引起人们对三角函数的研究，1748年经过瑞士的著名数学家欧拉的应用，才逐渐形成现在的sin 、cos 、tg 、ctg 的通用形式．
三角函数揭示了直角三角形中边与锐角之间的关系，是数形结合的桥梁之一，有以下丰富的性质：
1．单调性；
2．互余三角函数间的关系；
3．同角三角函数间的关系．
平方关系：sin 2α+cos 2α=1；
商数关系：tg α=ααcos sin ，ctg α=ααsin cos ； 倒数关系：tg αctg α=1．
【例题求解】
【例1】 已知在△ABC 中，∠A 、∠B 是锐角，且sinA ＝
135，tanB=2，AB=29cm ， 则S △ABC = ．
思路点拨 过C 作CD ⊥AB 于D ，这样由三角函数定义得到线段的比，sinA=
135=AC CD ，tanB=2=BD
CD ，设CD=5m ，AC ＝13m ，CD ＝2n ，BD ＝n ，解题的关键是求出m 、n 的值． 注：设△ABC 中，a 、b 、c 为∠A 、∠B 、∠C 的对边，R 为△ABC 外接圆的半径，不难证明：与锐角三角函数相关的几个重要结论：
(1) S △ABC =C ab B ac A bc sin 21sin 21sin 21==
； （2）R C
c B b A a 2sin sin sin ===． 【例2】 如图，在△ABC 中．∠ACB ＝90°，∠ABC ＝15°，BC=1，则AC=( )
A ．32+
B ．32-
C ．0.3
D ．23-
思路点拨 由15°构造特殊角，用特殊角的三角函数促使边角转化．
注：（1）求(已知)非特角三角函数值的关是构造出含特殊角直角三角形．
（2）求(已知)锐角角函数值常根据定转化为求对应线段比，有时需通过等的比来转换．
【例3】 如图，已知△ABC 是等腰直角三角形，∠ACB ＝90°，过BC 的中点D 作DE ⊥AB 于E ，连结CE ，求sin ∠ACE 的值．
思路点拨 作垂线把∠ACE 变成直角三角形的一个锐角，将问题转化成求线段的比．
【例4】 如图，在△ABC 中，AD 是BC 边上的高，tanB=cos ∠DAC ，
(1)求证：AC ＝BD ；
(2)若sinC=1312，BC=12，求AD 的长． 思路点拨 (1)把三角函数转化为线段的比，利用比例线段证明； (2) sinC=
AC AD =1312，引入参数可设AD=12k ，AC ＝13k ．
【例5】 已知：在Rt △ABC 中，∠C=90°，sinA 、sinB 是方程02=++q px x 的两个根．
(1)求实数p 、q 应满足的条件；
(2)若p 、q 满足(1)的条件，方程02=++q px x 的两个根是否等于Rt △ABC 中两锐角A 、B 的正弦?
思路点拨 由韦达定理、三角函数关系建立p 、q 等式，注意判别式、三角函数值的有界性，建立严密约束条件的不等式，才能准确求出实数p 、q 应满足的条件．
学历训练
A 组
1．已知α为锐角，下列结论①sin α+cos α=l ；②如果α>45°，那么sin α>cos α；③如果cos α>21 ，那么α<60°； ④αsin 11)-(sin 2-=α．正确的有 ． 2．如图，在菱形ABCD 中，AE ⊥BC 于E ，BC=1，cosB 13
5，则这个菱形的面积为 ． 3．如图，∠C=90°，∠DBC=30°，AB ＝BD ，利用此图可求得tan75°= ．
4．化简:
(1)263tan 27tan 22-+ = ．
(2)sin 2l °+sin 22°+…+sin 288°+sin 289°= ．
5．身高相等的三名同学甲、乙、丙参加风筝比赛．三人放出风筝线长、线与地面夹角如下表(假设风筝线是拉直的)，则三人所放的风筝中( )
A ．甲的最高
B ．丙的最高
C ．乙的最低
D ．丙的最低
6．已知 sin αcos α=8
1，且0°<α<45°则co α-sin α的值为( ) A ．
23 B ．2
3- C ．43 D ．43- 7．在△ABC 中，∠C ＝90°，∠ABC ＝30°，D 是AC 的中点，则ctg ∠DBC 的值是( ) A ．3 B ．32 C ． 23 D ．4
3 8．在等腰Rt △ABC 中．∠C ＝90°，AC ＝6，D 是AC 上一点，若tan ∠DBA=5
1，则AD 的长为( )
A ．2
B ．2
C ． 1
D ．22
9．已知关于x 的方程0)1(242=++-m x m x 的两根恰是某直角三角形两锐角的正弦，求m 的值．
10．D 是△ABC 的边AC 上的一点，CD=2AD ，AE ⊥BC 于E ，若BD ＝8，sin ∠CBD=
4
3，求AE 的长．
B 组 11．若0°<α<45°，且sin αcon α=16
73，则sin α= ． 12．已知关于x 的方程0)cos 1(2sin 423=-+⋅-ααx x 有两个不相等的实数根，α为锐角，那么α的取值范围是 ．
13．已知是△ABC 的三边，a 、b 、c 满足等式))((4)2(2a c a c b -+=，且有035=-c a ，则sinA+sinB+sinC 的值为 ．
14．设α为锐角，且满足sin α=3cos α，则sin αcos α等于( )
A ．61
B ．5
1 C ．9
2 D ．10
3 15．如图，若两条宽度为1的带子相交成30°的角，则重叠部分(图中阴影部分)的面积是
( )
A ．2
B ．
23 C ．1 D ．21
16．如图，在△ABC 中，∠A ＝30°，tanB=2
3，AC=32，则AB 的长是( ) A ．33+ B ．322+ C ．5 D ．
29 17．己在△ABC 中，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，且c=35，若关于x 的方程0)35(2)35(2=-+++b ax x b 有两个相等的实根，又方程0sin 5)sin 10(22=+-A x A x 的两实根的平方和为6，求△ABC 的面积．
18．如图，已知AB=CD=1，∠ABC ＝90°，∠CBD °=30°，求AC 的长．
19．设 a 、b 、c 是直角三角形的三边，c 为斜边，n 为正整数，试判断n n b a 与n c 的关系，并证明你的结论．
20．如图，已知边长为2的正三角形ABC 沿直线l 滚动．
(1)当△ABC 滚动一周到△A l B 1C 1的位置，此时A 点所运动的路程为 ，约为 (精确到0.1，π=3.14)
(2)设△ABC 滚动240°，C 点的位置为C ˊ，△ABC 滚动480°时，A 点的位置在A ˊ，请你利用三角函数中正切的两角和公式tan(α+β)=(tan α+tan β)÷(1-tan α·tan β)，求出∠CAC ˊ+∠CAA ˊ的度数．
参考答案。