数据结构 迷宫求解
数据结构课程设计迷宫问题求解

数据结构课程设计迷宫问题求解正文:一、引言在数据结构课程设计中,迷宫问题求解是一个经典且常见的问题。
迷宫问题求解是指通过编程实现在迷宫中找到一条从起点到终点的路径。
本文将详细介绍如何用数据结构来解决迷宫问题。
二、问题分析1.迷宫定义:迷宫是由多个格子组成的矩形区域,其中包括起点和终点。
迷宫中的格子可以是墙壁(无法通过)或者通道(可以通过)。
2.求解目标:在给定的迷宫中,找到从起点到终点的一条路径。
3.输入:迷宫的大小、起点坐标、终点坐标以及墙壁的位置。
4.输出:从起点到终点的路径,或者提示无解。
三、算法设计1.基础概念a) 迷宫的表示:可以使用二维数组来表示迷宫,数组的元素可以是墙壁、通道或者路径上的点。
b) 坐标系统:可以使用(x, y)来表示迷宫中各个点的坐标。
c) 方向定义:可以用上、下、左、右等四个方向来表示移动的方向。
2.深度优先搜索算法(DFS)a) 算法思想:从起点开始,沿着一个方向一直走到无法继续为止,然后回退到上一个点,再选择其他方向继续探索。
b) 算法步骤:i) 标记当前点为已访问。
ii) 判断当前点是否为终点,如果是则返回路径;否则继续。
iii) 遍历四个方向:1.如果该方向的下一个点是通道且未访问,则继续向该方向前进。
2.如果该方向的下一个点是墙壁或已访问,则尝试下一个方向。
iv) 如果四个方向都无法前进,则回退到上一个点,继续向其他方向探索。
3.广度优先搜索算法(BFS)a) 算法思想:从起点开始,逐层向外探索,直到找到终点或者所有点都被访问。
b) 算法步骤:i) 标记起点为已访问,加入队列。
ii) 循环以下步骤直到队列为空:1.取出队首元素。
2.判断当前点是否为终点,如果是则返回路径;否则继续。
3.遍历四个方向:a.如果该方向的下一个点是通道且未访问,则标记为已访问,加入队列。
iii) 如果队列为空仍未找到终点,则提示无解。
四、算法实现1.选择合适的编程语言和开发环境。
数据结构迷宫求解

数据结构迷宫求解迷宫问题是一种常见的求解问题,通过在迷宫中找到从起点到终点的路径。
在计算机科学中,使用数据结构来解决迷宫问题非常方便。
本文将介绍迷宫问题的基本原理、常见的求解方法以及使用不同数据结构的优缺点。
首先,我们需要明确迷宫的基本定义。
迷宫可以看作是一个二维的网格,其中包含一些墙壁和通路。
起点是迷宫的入口,终点则是迷宫的出口。
我们的目标是找到从起点到终点的一条路径。
迷宫问题可以使用多种算法求解,包括深度优先(DFS)、广度优先(BFS)、最短路径算法等。
以下将详细介绍这些算法以及它们在迷宫问题中的应用。
同时,我们还会讨论不同数据结构在求解迷宫问题中的优缺点。
首先,深度优先(DFS)是一种常用的求解迷宫问题的算法。
该算法从起点开始,一直到终点,期间遇到墙壁或已经访问过的点则回溯到上一个节点。
DFS可以使用递归实现,也可以使用栈来保存需要回溯的节点。
DFS的优点是简单易懂,易于实现。
然而,它可能会陷入死循环或者找到一条较长的路径而不是最短路径。
另一种常见的算法是广度优先(BFS),它从起点开始,逐层扩展,直到找到终点为止。
BFS可以使用队列来保存每一层的节点。
与DFS相比,BFS能够找到最短路径,但它需要维护一个较大的队列,从而增加了空间复杂度。
除了DFS和BFS,还有一些其他算法可以应用于迷宫问题。
例如,迪杰斯特拉算法和A*算法可以找到最短路径。
这些算法使用了图的概念,将迷宫中的通道表示为图的边,将各个节点之间的距离表示为图的权重。
然后,通过计算最短路径的权重,找到从起点到终点的最短路径。
迪杰斯特拉算法和A*算法的优点是能够找到最短路径,但它们的实现较为复杂。
在使用这些算法求解迷宫问题时,我们需要选择适合的数据结构来存储迷宫和过程中的状态。
以下是几种常见的数据结构以及它们的优缺点:1.数组:数组是一种常见的数据结构,它可以用来表示迷宫。
可以使用二维数组来表示迷宫的网格,并使用特定的值表示墙壁和通路。
数据结构 迷宫求解

数据结构迷宫求解数据结构迷宫求解一、引言数据结构是计算机科学中最基础、最重要的内容之一。
它能帮助我们存储和组织数据,并提供了各种算法来对这些数据进行处理和操作。
迷宫求解是其中一种经典的应用场景,通过使用适当的数据结构和算法,能够在迷宫中寻找到一条从起点到终点的路径。
本文将介绍一种常用的迷宫求解算法,并给出相应的数据结构实现。
二、问题描述1:迷宫定义:迷宫是一个由墙壁和路障组成的二维矩阵,其中墙壁表示不可通行的区域,路障表示可通行但需要绕过的区域。
迷宫通常具有一个起点和一个终点,我们需要找到一条从起点到终点的路径。
2:算法目标:实现一个算法,能够在给定的迷宫中找到一条从起点到终点的路径,并输出该路径。
三、数据结构设计1:迷宫的存储结构:为了方便表示迷宫,我们可以使用一个二维数组来表示迷宫的格子,其中每个格子表示一个迷宫的单元。
我们可以使用0表示可通行的空格,使用1表示墙壁,使用2表示路障。
同时,我们需要记录每个格子的状态,以标记是否已经被访问过。
2:路径的存储结构:为了记录找到的路径,我们可以使用一个栈来存储路径上的各个节点。
在访问迷宫时,我们将访问过的格子入栈,并在找到终点后,按照栈的顺序依次弹出格子,即可得到路径。
四、算法设计1:深度优先搜索算法:深度优先搜索是一种常用的图遍历算法,适用于解决迷宫问题。
其基本思想是从起点出发,沿着某一条路径一直向前,直到终点或者无法前进为止。
当无法前进时,回退到上一个节点,并尝试其他路径,直到找到终点或者所有路径都尝试完毕。
2:算法步骤:- 将起点入栈,并标记其为已访问;- 当栈不为空时,弹出栈顶元素,并尝试向上、下、左、右四个方向前进,如果某一方向可以前进且未被访问过,则将该方向上的格子入栈,并标记为已访问;- 当找到终点时,输出路径;- 当所有路径都尝试完毕时,结束算法。
五、算法实现1:迷宫的表示:我们可以使用一个二维数组来存储迷宫,如下所示: ```pythonmaze = [[0, 1, 0, 0, 0],[0, 1, 0, 1, 0],[0, 0, 0, 0, 0],[0, 1, 1, 1, 0],[0, 0, 0, 1, 0]]```2:深度优先搜索的实现:我们可以使用递归来实现深度优先搜索算法,如下所示:```pythondef dfs(maze, start, end, path):if start == end:return Truei, j = startmaze[i][j] = 2path:append(start)if i > 0 and maze[i - 1][j] == 0 anddfs(maze, (i - 1, j), end, path):return Trueif i < len(maze) - 1 and maze[i + 1][j] == 0 and dfs(maze, (i + 1, j), end, path):return Trueif j > 0 and maze[i][j - 1] == 0 anddfs(maze, (i, j - 1), end, path):return Trueif j < len(maze[0]) - 1 and maze[i][j + 1] == 0 and dfs(maze, (i, j + 1), end, path):return Truepath:pop()return Falsedef solve_maze(maze, start, end):path = []dfs(maze, start, end, path)return path```六、待解决的问题1:如何处理迷宫中存在的死胡同(即无法找到终点的路径)?2:如何处理迷宫中存在的多条路径(即多个路径都能到达终点)?附件:- 迷宫示例图片- 算法实现示例代码- 数据结构设计图法律名词及注释:1:数据结构:在计算机科学中,数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。
数据结构课程设计 迷宫求解

考虑使用一个二维数组表示迷宫.所有的通路用0表示,墙用1表示,出口用9表示,入口用6表示,已经过点用3表示.输出走出迷宫的过程.从这个问题的求解过程中可以简单总结出两个算法,一是探路过程,二是输出路线.1.探路过程探路过程算法可归纳为:[1]从入口位置开始,检查东西南北四个方向上的通路,如果发现出口则成功退出,否则将所有通路坐标压入栈;[2]从栈中取出一个坐标,将其标记为当前位置(标记数字3),再次判断通路情况;[3]如此进行,直到发现出口则成功退出,若栈空而且未发现出口,则失败退出.这里使用到的回溯过程可描述为: 每到达一点时,会将所有可能的通路坐标(标记数字0的节点)压入栈.所以当到达一点,而不存在可能的通路时,自然没有相应的坐标压入栈,而此时便从栈中取出上一个点所压入的可能的一个通路坐标,并继续作通路判断,这便是一个回溯的过程.2.输出某一较短路线将所有在探路过程中经过的点(标记数字3的节点)按实际探路路线存入队列,对头为入口,队尾为出口.这些点可能存在绕路的情况,所以可用下面的算法输出某一较短路线.[1]将队尾(出口)节点设置为当前判断节点;[2]从当前判断节点(x,y)的前驱节点开始,向前遍历队列,如果发现相邻节点(其坐标可以为(x+1,y),(x-1,y),(x,y+1),(x,y-1)之一),则删除该相临节点至当前判断节点的前驱节点之间的所有节点;[3]将该相临节点设置为当前判断节点,继续判断相临节点;[4]当当前判断节点为对头节点时退出.该算法所得到的路线不一定是最短路线,想得到最短路线,可考虑使用树结构将所有由出口至入口的路线保留为一子树,树高最短的子树即为最短路线.但此算法可保证所得路线不会存在绕路情况.3.表示节点坐标的类public class MazeCell {private int x, y;//表示x轴y轴坐标public MazeCell() {}public MazeCell(int i, int j) {x = i;y = j;}public boolean equals(Object o) {if (!(o instanceof MazeCell))return false;MazeCell cell = (MazeCell) o;return cell.x == x && cell.y == y;}public String toString() {return x + "," + y;}public int getX() {return x;}public void setX(int x) {this.x = x;}public int getY() {return y;}public void setY(int y) {this.y = y;}}4.所使用的栈数据结构import java.util.LinkedList;public class Stack<T> {private LinkedList<T> storage = new LinkedList<T>(); /** 入栈*/public void push(T v) {storage.addFirst(v);}/** 出栈,但不删除*/public T peek() {return storage.getFirst();}/** 出栈*/public T pop() {return storage.removeFirst();}/** 栈是否为空*/public boolean empty() {return storage.isEmpty();}/** 打印栈元素*/public String toString() {return storage.toString();}}5.求解迷宫问题import java.io.BufferedReader;import java.io.IOException;import java.io.InputStreamReader;import java.io.PrintStream;import java.util.Iterator;import java.util.LinkedList;import java.util.List;import java.util.ListIterator;public class Maze {private int rows = 0, cols = 0;// 迷宫的行数与列数private char[][] store, path;// 迷宫矩阵private MazeCell currentCell, exitCell = new MazeCell(),entryCell = new MazeCell();// 当前节点,出口节点,入口节点private static final char EXIT = '9', ENTRY = '6', VISITED = '3';// 出口标记,入口标记,已经过节点标记private static final char PASS = '0', W ALL = '1';// 通路标记,墙标记private Stack<MazeCell> mazeStack = new Stack<MazeCell>();// 探路过程所使用栈private List<MazeCell> currentList = new LinkedList<MazeCell>();// 路经的路线队列public Maze() {// 构造迷宫int row = 0, col = 0;Stack<String> mazeRows = new Stack<String>();InputStreamReader isr = new InputStreamReader(System.in);BufferedReader buffer = new BufferedReader(isr);System.out.println("Enter a rectangular maze using the following" + " characters: \n6-entry\n9-exit\n1-wall\n0-passage\n"+ "Enter one line at a time; end with Ctrl-d;");try {String str = buffer.readLine();while (str != null) {row++;cols = str.length();str = "1" + str + "1";mazeRows.push(str);if (str.indexOf(EXIT) != -1) {exitCell.setX(row);exitCell.setY(str.indexOf(EXIT));}if (str.indexOf(ENTRY) != -1) {entryCell.setX(row);entryCell.setY(str.indexOf(ENTRY));}str = buffer.readLine();}} catch (IOException e) {e.printStackTrace();}rows = row;store = new char[rows + 2][];store[0] = new char[cols + 2];for (; !mazeRows.empty(); row--)store[row] = (mazeRows.pop()).toCharArray();store[rows + 1] = new char[cols + 2];for (col = 0; col <= cols + 1; col++) {store[0][col] = WALL;store[rows + 1][col] = WALL;}path = new char[rows + 2][];copyArray(store, path);}/** 二维数组复制*/private void copyArray(char[][] src, char[][] tar) {for (int i = 0; i < src.length; i++) {tar[i] = new char[cols + 2];for (int j = 0; j < src[i].length; j++)tar[i][j] = src[i][j];}}/** 二维数组输出*/private void display(PrintStream out, char[][] carray) {for (int row = 0; row <= rows + 1; row++)out.println(carray[row]);out.println();}/** 将未访问并可通路的节点压入栈*/private void pushUnvisited(int row, int col) {if (store[row][col] == PASS || store[row][col] == EXIT) mazeStack.push(new MazeCell(row, col));}/** 探路过程*/public void exitMaze(PrintStream out) {currentCell = entryCell;currentList.add(currentCell);out.println();while (!currentCell.equals(exitCell)) {int row = currentCell.getX();int col = currentCell.getY();display(System.out, store);if (!currentCell.equals(entryCell))store[row][col] = VISITED;pushUnvisited(row - 1, col);pushUnvisited(row + 1, col);pushUnvisited(row, col - 1);pushUnvisited(row, col + 1);if (mazeStack.empty()) {display(out, store);out.println("Failure");return;} else {currentCell = mazeStack.pop();currentList.add(currentCell);}}display(out, store);out.println("Success");}/** 得到某一输出路线*/private void getPath() {if (currentList.size() <= 0)return;MazeCell cell = currentList.get(currentList.size() - 1);while (cell != currentList.get(0)) {List<MazeCell> subList = currentList.subList(0, currentList.indexOf(cell));ListIterator<MazeCell> itr = subList.listIterator();while (itr.hasNext()) {MazeCell target = itr.next();if (adjoin(cell, target)) {removeElements(currentList.indexOf(target) + 1, currentList .indexOf(cell));cell = target;break;}}}}/** 删除队列中由from至to的连续元素*/private void removeElements(int from, int to) {int turn = to - from;while (turn > 0) {currentList.remove(from);turn--;}}/** 判断两个节点是否相邻*/private boolean adjoin(MazeCell current, MazeCell target) {if ((current.getX() == target.getX() + 1 || current.getX() == target.getX() - 1)&& (current.getY() == target.getY()))return true;if ((current.getY() == target.getY() + 1 || current.getY() == target.getY() - 1)&& (current.getX() == target.getX()))return true;return false;}/** 输出路线*/public void printPath(PrintStream out) {getPath();out.println("Path:");if (currentList.size() >= 2) {currentList.remove(currentList.size() - 1);currentList.remove(0);}Iterator<MazeCell> itr = currentList.iterator();while (itr.hasNext()) {MazeCell cell = itr.next();path[cell.getX()][cell.getY()] = VISITED;}display(System.out, path);}public static void main(String[] args) {Maze maze = new Maze();maze.exitMaze(System.out);maze.printPath(System.out);}}6.结果输出Enter a rectangular maze using the following characters: 6-entry9-exit1-wall0-passageEnter one line at a time; end with Ctrl-d;90000110110000000600//构造的迷宫如下111111119000011110111100000110060011111111//开始探路11111111900001111011110000011006001 11111111111111 1900001 1110111 1000001 1006301 11111111111111 1900001 1110111 1000001 1006331 1111111 1111111 1900001 1110111 1000031 1006331 11111111111111 1900001 1110111 1000331 1006331 1111111 1111111 1900001 1110111 1003331 1006331 11111111111111 1900001 1110111 1033331 1006331 1111111111111119000011110111133333110063311111111111111119000011110111133333113063311111111111111119000011110111133333113363311111111//下一步为回溯过程111111119000011110111133333113363311111111111111119000011113111133333113363311111111111111119030011113111133333113363311111111111111119033011113111133333113363311111111111111119033311113111133333113363311111111//下一步为回溯过程111111119333311113111133333113363311111111SuccessPath:111111119330011113111100300110060011111111。
数据结构 迷宫求解

实验二:迷宫1.需求分析[迷宫求解] 求迷宫中从入口到出口的所有路径;计算机接迷宫问题时,通常使用的是“穷举求解”的方法,即从入口出发,顺某一方向向前探索,若能走通,则继续往前走;否则,沿原路返回,换一个方向再继续探索,直至所有可能的通路都探索到为止。
因此,在求解迷宫通路问题的算法中可应用“栈”设计一个先进后出的结构来保存从入口到当前位置的路径。
在计算机中构造一个方块图表示迷宫,图中每个方块或为通道(即空白方块),或为墙(即阴影方块)。
所求路径必须为简单路径,即在求得的路径上不能重复出现同一通道块。
假设“当前位置”指的是“在搜索过程中某一时刻所在图中某个方块位置”,则求迷宫中一条路径的基本思想是:若当前位置“可通”,则纳入“当前路径”,并继续朝下一个“位置”探索,即切换“下一位置”为“当前位置”,如此重复直至到达出口;若当前位置“不可通,则应顺着“来向”退回到“迁移通道块”,然后朝着除了“来向”之外的其他方向继续探索;若该通道块的四周4个方块均“不可通”,则应该“从当前路径”删除该通道块。
所谓“下一位置”指的是“当前位置”四周4个方向(东西南北)上相邻的方块。
假设以栈S记录“当前路径”,则栈顶中存放的是“当前路径上最后一个通道块”。
由此,“纳入路径”的操作即为“当前位置入栈”;“从当前路径上删除前衣通道块”的操作即为“出栈”。
2.概要设计void EnQueue(int i,int j,int k); //入队一个节点void DeQueue(int *i,int *j,int *k); //获取当前节点的序号和对应的迷宫坐标,然后出列bool GetNextPos(int *i ,int *j,int count); //得到下一个邻接点的位置void ShortestPath_BFS(int i,int j); //广度优先遍历寻找最短路径void ShortestPath(); //输出最短路径void Print(); //输出迷宫形状int Map[10][10] = {{1,1,1,1,1,1,1,1,1,1},{1,0,0,1,0,0,0,1,0,1},{1,0,0,1,0,0,0,1,0,1},{1,0,0,0,0,1,1,0,0,1},{1,0,1,1,1,0,0,0,0,1},{1,0,0,0,1,0,0,0,0,1},{1,0,1,0,0,0,1,0,0,1},{1,0,1,1,1,0,1,1,0,1},{1,1,0,0,0,0,0,0,0,0},{1,1,1,1,1,1,1,1,1,1}};struct Node{int parent_id; //保存父节点的位置int node_id; //当前节点的序号,以便传递给子节点int x,y; //当前结点对应的坐标}Q[10*10]; //每个节点包含迷宫坐标、队列中的序号、父节点的序号,多个节点形成队列int front = 0,rear = 0; //队列头指针和尾指针void EnQueue(int i,int j,int k){Q[rear].x = i;Q[rear].y = j; //保存当前节点对应的坐标位置Q[rear].parent_id = k; //保存父节点的序号Q[rear].node_id = rear; //保存当前节点序号rear++;}void DeQueue(int *i,int *j,int *k){*i = Q[front].x;*j = Q[front].y;*k = Q[front].node_id;front++; //出列一个节点}bool GetNextPos(int *i ,int *j,int count){switch(count){case 1:(*j)++; return 1; //右(东)case 2:(*i)++; return 1; //下(南)case 3:(*j)--; return 1; //左(西)case 4:(*i)--; return 1; //上(北)default: return 0;}}void ShortestPath_BFS(int i ,int j){int count,m,n,k;EnQueue(i,j,-1); Map[1][1] = 1; //起点入队,标记起点已走过while(true){count = 1;DeQueue(&i,&j,&k);n = i,m = j; //保存当前位置while(GetNextPos(&i,&j,count)){count++;if(!Map[i][j]){EnQueue(i,j,k); Map[i][j] = 1;if(i == 8 && j == 9) return; //到达终点,(8,9)是默认终点,可以任意修改}i = n; j = m; //保证遍历当前坐标的所有相邻位置}}}3.详细设计主函数部分:#include"maze.h"#include<iostream>using namespace std;void main(){cout<<"程序说明:"<<'\n'<<"1.输出路径为最短路径;"<<'\n'<<"2.默认的出口在最右下角,如有需要可以调整。
数据结构之迷宫求解实验报告武汉大学
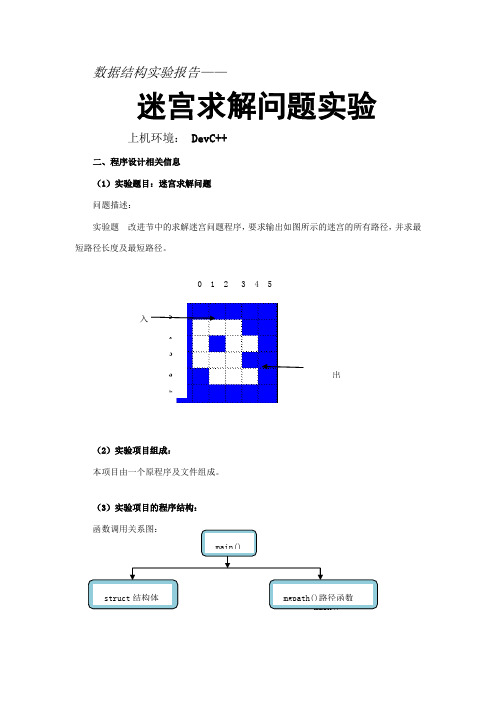
数据结构实验报告——迷宫求解问题实验上机环境: DevC++二、程序设计相关信息(1)实验题目:迷宫求解问题问题描述:实验题 改进节中的求解迷宫问题程序,要求输出如图所示的迷宫的所有路径,并求最短路径长度及最短路径。
(2)实验项目组成:本项目由一个原程序及文件组成。
(3)实验项目的程序结构: 函数调用关系图:0 1 2 3 4 5 01234 出入main() main()struct 结构体 mgpath()路径函数(4)实验项目包含的函数的功能描述: mg[M+1][N+1] =1;Stack[top].j=1;Stack[top].di=-1;mg[1][1]=-1;printf("迷宫所有路径如下:\n");while(top>-1){i=Stack[top].i;j=Stack[top].j;di=Stack[top].di; if(i==M-2&&j==N-2){printf("%4d:",count++);for(k=0;k<=top;k++){printf("(%d,%d)",Stack[k].i,Stack[k].j); if((k+1)%5==0) mg=0回mg=1进循环for下一下一个方块前一个方块值下一个方块值输出方位坐标入口结束printf("\n ");}printf("\n");if(top+1<min){for(k=0;k<=top;k++)Path[k]=Stack[k];min=top+1;}mg[Stack[top].i][Stack[top].j]=0;top--;i=Stack[top].i;j=Stack[top].j;di=Stack[top].di; }find=0;while(di<4&&find==0){di++;switch(di){case 0:i=Stack[top].i-1;j=Stack[top].j;break; case 1:i=Stack[top].i;j=Stack[top].j+1;break; case 2:i=Stack[top].i+1;j=Stack[top].j;break; case 3:i=Stack[top].i;j=Stack[top].j-1;break; }if(mg[i][j]==0)find=1;}if(find==1){Stack[top].di=di;top++;Stack[top].i=i;Stack[top].j=j;Stack[top].di=-1;mg[i][j]=-1;}else{mg[Stack[top].i][Stack[top].j]=0; top--;}}printf("\n");printf("最短路径如下:\n");printf("路径最短长度:%d\n",min);printf("最短路径路径:\n");for(k=0;k<min;k++){printf("(%d,%d)",Path[k].i,Path[k].j); }printf("\n\n");}int main(){mgpath();system("PAUSE"); return 0;}。
栈的迷宫求解(数据结构试验)
实验二:迷宫问题班级:姓名:学号:一、需求分析(1 )以二维数据Maze[m+2][n+2] 表示迷宫,其中:Maze[0][j] 和Maze[m+1][j](0<=j<=n+1)及Maze[i][0]和Maze[i][n+1](0<=i<=m+1)为添加一圈障碍。
数组中以元素值为0 表示通路,1 表示障碍,限定迷宫的大小m,n<=100。
(2)用户输入迷宫的规模m,n;并按照此规模输入迷宫的具体数据。
(3)迷宫的入口位置和出口位置可由用户随时设定。
(4)若设定的迷宫存在通路,则以长方阵形式将迷宫及其通路输出到标准输出文件(即终端)上,其中,字符“#”表示障碍,字符“*”表示路径上的位置,字符“@”表示“死胡同”,即曾途径然而不能到达出口的位置,余者用空格符印出。
若设定的迷宫不存在通路,则报告相应信息。
(5)本程序只求出一条成功的通路。
然而,只需要对迷宫求解的函数作小量修改,便可求得全部路径。
(6)测试数据见原题,当入口位置为(1,1),出口位置为(9,8)时,输出数据应为:* * # @ @ @ #* # @ @ @ #* * @ @ # # #* # # # # @* * * # * * * @# * * * # * ## # # # * ## # # * ## # * *(7)程序执行的命令为:1)创建迷宫;2)求解迷宫;3)输出迷宫的解。
二、概要设计1. 设定栈的抽象数据类型定义:ADT Stack{数据对象:D={a i|a i∈CharSet,i=1,2,…,n,n>=0}数据关系:R1={<a i-1,a i>|a i-1,a i∈D,i=2,…,n}基本操作:InitStack(&S)操作结果:构造一个空栈S。
DestroyStack(&S)初始条件:栈S 已存在。
操作结果:销毁栈S。
ClearStack(&S)初始条件:栈S 已存在。
数据结构课程设计_迷宫求解
迷宫求解一.问题描述对迷宫问题的求解过程实际就是从入口开始,一步一步地走到出口的过程。
基本要求:输入一个任意大小的迷宫数据,用递归和非递归两种方法求出一条走出迷宫的路径,并将路径输出。
二.设计思路在本程序中用两种方法求解迷宫问题-非递归算法和递归算法。
对于非递归算法采用回溯的思想,即从入口出发,按某一方向向前探索,若能走通,并且未走过,则说明某处可以到达,即能到达新点,否则试探下一方向;若所有的方向均没有通路,或无路可走又返回到入口点。
在求解过程中,为了保证在到达某一点后不能向前继续行走(无路)时,能正确返回前一点以便继续从下一个方向向前试探,则需要用一个栈保存所能到达的没一点的下标与该点前进的方向,然后通过对各个点的进出栈操作来求得迷宫通路。
对于递归算法,在当前位置按照一定的策略寻找下个位置,在下个位置又按照相同的策略寻找下下个位置…;直到当前位置就是出口点,每一步的走法都是这样的。
随着一步一步的移动,求解的规模不断减小;如果起始位置是出口,说明路径找到,算法结束,如果起始位置的四个方向都走不通,说明迷宫没有路径,算法也结束。
另外,为了保证迷宫的每个点都有四个方向可以试探,简化求解过程,将迷宫四周的值全部设为1,因此将m行n列的迷宫扩建为m+2行,n+2列,同时用数组来保存迷宫阵列。
三.数据结构设计在迷宫阵列中每个点都有四个方向可以试探,假设当前点的坐标(x,y),与其相邻的四个点的坐标都可根据该点的相邻方位而得到,为了简化问题,方便求出新点的坐标,将从正东开始沿顺时针进行的这四个方向的坐标增量放在一个结构数组move[4]中,每个元素有两个域组成,其中x为横坐标增量,y为纵坐标增量,定义如下:typedef struct{int x,y;}item;为到达了某点而无路可走时需返回前一点,再从前一点开始向下一个方向继续试探。
因此,还要将从前一点到本点的方向压入栈中。
栈中的元素由行、列、方向组成,定义如下:typedef struct{int x,y,d;}DataType;由于在非递归算法求解迷宫的过程中用到栈,所以需定义栈的类型,本程序中用的是顺序栈,类型定义如下;typedef struct{DataType data[MAXSIZE];int top;}SeqStack, *PSeqStack;四.功能函数设计(1)函数PSeqStack Init_SeqStack()此函数实现对栈的初始化工作。
数据结构-迷宫求解
3.2.4 迷宫求解对如上图所示的迷宫进行求解,上图为4*4的矩形,“0”表示可以行走的通道,“1”表示的为墙;则有输入如下:4 40 0 1 00 1 0 10 0 0 00 1 0 0源程序如下:#include<stdio.h>#include <malloc.h>typedef struct node{int x;int y;int dir;struct node *pre;struct node *next;}NODE;//nodemain(){int map[100][100],m,n,i,j,x1,y1,flag=0; NODE *head,*end,*p;p=(NODE*)malloc(sizeof(NODE)); head=end=p;scanf("%d %d",&m,&n);for(i=0;i<=m+1;i++)for(j=0;j<=n+1;j++){if(i==0||j==0||i==m+1||j==n+1)map[i][j]=1;else scanf("%d",&map[i][j]);}//forx1=1;y1=1;do{if(map[x1][y1]==0){map[x1][y1]=1;p=(NODE*)malloc(sizeof(NODE));p->x=x1;p->y=y1;p->dir=0;p->dir++;p->pre=end;end->next=p;end=p;if(end->x==m&&end->y==n){ flag=1;end->next=NULL;head=head->next;while(head->next!=NULL){printf("<%d,%d> ",head->x,head->y);head=head->next;}//whileprintf("<%d,%d>\n",head->x,head->y);break;}//ifx1++;}//ifelse {//当前位置不能通过if(head!=end){if(end->dir==5){end=end->pre;x1=end->x;y1=end->y;continue;}x1=end->x;y1=end->y;if(end->dir==1){x1++;end->dir++;}else if(end->dir==2){y1++;end->dir++;}else if(end->dir==3){x1--;end->dir++;}else if(end->dir==4){y1--;end->dir++;}}//if}//else}while(head!=end);if(flag==0)printf("there is no solution!\n"); return 0;}//main效果如下:生成的数组为其路径。
数据结构迷宫求解
#include<stdio.h>#include<stdlib.h>#include<time.h>#include<malloc.h>typedef int Status;#define OK 1#define ERROR 0#define STACK_INIT_SIZE 100#define STACKINCREMENT 10typedef struct{int x;int y;}PosType;//迷宫中的位置类型typedef struct{int ord;PosType seat;int di;}SelemType;//栈元素类型typedef struct{SelemType *base;SelemType *top;int stacksize;}SqStack;//栈类型Status InitStack (SqStack &S){S.base = (SelemType *)malloc(STACK_INIT_SIZE * sizeof(SelemType));if(!S.base)exit(-2);S.top = S.base;S.stacksize = STACK_INIT_SIZE;return OK;}Status Push(SqStack &S,SelemType e){if(S.top - S.base >= S.stacksize){S.base = (SelemType *)realloc(S.base,(S.stacksize + STACKINCREMENT)*sizeof(SelemType));if(!S.base)exit(-2);S.top = S.base + S.stacksize;S.stacksize += STACKINCREMENT;}*S.top++ = e;return OK;}Status Pop(SqStack &S,SelemType &e){if(S.top == S.base)return 0;e = *--S.top;return OK;}Status StackEmpty(SqStack S){if(S.top == S.base)return OK;elsereturn ERROR;}void InitMaze(int maze[17][17]){srand((int)time(NULL));for(int i = 0;i<16;i++)maze[0][i] = 0;for(i = 1; i<15; i++){maze[i][0] = 1;for(int j = 1;j<15;j++){maze[i][j] = rand()%2;}maze[i][15] = 1;}for(i = 0;i<10;i++)maze[15][i] = 1;}void OutputmazeFirst(int maze[17][17]){printf("\n\n");printf("所建迷宫为(#为外墙):\n\n");for(int i = 0;i<16;i++)printf("# ");printf("\n");for(i=1;i<15;i++){printf("# ");for(int j = 1;j<15;j++)printf("%d ",maze[i][j]);printf("# ");printf("\n");}for(i = 0;i<16;i++)printf("# ");printf("\n");}void OutputmazeEnd(int maze[17][17],SqStack S) {printf("\n迷宫通路路径为:\n\n");SelemType *p = S.base;while(p!=S.top){maze[p->seat.x][p->seat.y] = 2;p++;}for(int i = 0;i<16;i++)printf("# ");printf("\n");for(i=1;i<15;i++){printf("# ");for(int j = 1;j<15;j++){if(maze[i][j] == 2)printf("* ");elseprintf(" ");}printf("# ");printf("\n");}for(i = 0;i<16;i++)printf("# ");printf("\n");}Status Pass( int maze[17][17],PosType CurPos) {if (maze[CurPos.x][CurPos.y]==0)return OK;elsereturn ERROR;}void MarkFoot( int maze[17][17],PosType CurPos) {maze[CurPos.x][CurPos.y]=1;}PosType NextPos(PosType CurPos, int Dir){PosType ReturnPos;switch (Dir){case 1:ReturnPos.x=CurPos.x;ReturnPos.y=CurPos.y+1;break;case 2:ReturnPos.x=CurPos.x+1;ReturnPos.y=CurPos.y;break;case 3:ReturnPos.x=CurPos.x;ReturnPos.y=CurPos.y-1;break;case 4:ReturnPos.x=CurPos.x-1;ReturnPos.y=CurPos.y;break;}return ReturnPos;}Status MazePath(int maze[17][17],SqStack &S, PosType start, PosType end) {// 若迷宫maze中从入口 start到出口 end的通道,则求得一条存放在栈中// (从栈底到栈顶),并返回TRUE;否则返回FALSEPosType curpos;int curstep;SelemType e;InitStack(S);curpos = start; // 设定"当前位置"为"入口位置"curstep = 1; // 探索第一步do{if (Pass(maze,curpos)){ // 当前位置可通过,即是未曾走到过的通道块MarkFoot(maze,curpos); // 留下足迹e.di =1;e.ord = curstep;e.seat= curpos;Push(S,e); // 加入路径if (curpos.x == end.x && curpos.y==end.y)return OK; // 到达终点(出口)curpos = NextPos(curpos, 1); // 下一位置是当前位置的东邻curstep++; // 探索下一步}else{ // 当前位置不能通过if (!StackEmpty(S)){Pop(S,e);while (e.di==4 && !StackEmpty(S)){MarkFoot(maze,e.seat);Pop(S,e); // 留下不能通过的标记,并退回一步} // whileif (e.di<4){e.di++;Push(S, e); // 换下一个方向探索curpos = NextPos(e.seat, e.di); // 当前位置设为新方向的相邻块}}}} while (!StackEmpty(S) );return 0;}int main(){SqStack S;int maze[17][17];printf("创建一个正方形迷宫,大小为15 X 15(不算墙):\n");InitMaze(maze);OutputmazeFirst(maze);PosType start,end;printf("\n请输入入口坐标(行,列):");scanf("%d",&start.x);scanf("%d",&start.y);printf("\n请输入出口坐标(行,列):");scanf("%d",&end.x);scanf("%d",&end.y);if(MazePath(maze,S,start,end)){OutputmazeEnd(maze,S);printf("\n通路如上图所示!\n");}elseprintf("\n无通路!\n");return 0;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据结构迷宫求解
数据结构迷宫求解
⒈引言
⑴背景
迷宫是一种抽象的概念,常用于解决路径导航、游戏等问题。
在这个文档中,我们将介绍如何使用数据结构来解决迷宫问题。
⑵目的
本文档的目的是提供一个详细的说明,如何使用数据结构来表示和解决迷宫问题。
读者将能够了解迷宫问题的相关概念、常见解决方法以及使用数据结构来实现这些方法的步骤。
⒉迷宫问题概述
⑴定义迷宫
迷宫是一个由方块构成的正方形网格,其中某些方块可能是墙壁,而其他方块是可以通过的路径。
⑵目标
在迷宫中,我们需要找到从入口到出口的一条路径,该路径应遵循特定的规则,如不穿墙壁、尽量最短等。
⑶问题解决方法
解决迷宫问题的常用方法包括深度优先搜索(DFS)、广度优先搜索(BFS)等。
⒊数据结构的选择
⑴迷宫表示
迷宫可以使用二维数组来表示,其中墙壁用特定的值表示,可通过的路径用另一个值表示。
⑵路径记录
使用栈或队列数据结构来记录路径,以便对路径进行操作。
⒋深度优先搜索(DFS)
⑴算法介绍
深度优先搜索是一种常用的解决迷宫问题的方法。
它通过递归地进入迷宫的不同路径,直到找到解决方案。
⑵算法步骤
⒋⑴初始化栈并将起点入栈。
⒋⑵从栈中弹出一个节点,将其标记为已访问。
⒋⑶检查该节点的邻居,如果邻居是未访问过的路径,则将其入栈。
⒋⑷重复步骤2和3,直到找到目标或栈为空。
⒌广度优先搜索(BFS)
⑴算法介绍
广度优先搜索是另一种常用的解决迷宫问题的方法。
它通过逐层遍历迷宫中的路径,直到找到解决方案。
⑵算法步骤
⒌⑴初始化队列并将起点入队。
⒌⑵从队列中弹出一个节点,将其标记为已访问。
⒌⑶检查该节点的邻居,如果邻居是未访问过的路径,则将其入队。
⒌⑷重复步骤2和3,直到找到目标或队列为空。
⒍其他解决方法
⑴ A算法
A算法是一种启发式搜索方法,通过估计到目标的距离来优化搜索过程。
在处理大型迷宫时,A算法通常比DFS和BFS更高效。
⑵迭代深化搜索
迭代深化搜索是一种结合了DFS和BFS的方法,通过限
制DFS的搜索深度和逐步增加深度的方式,降低了内存的使用量。
⒎结论
在本文档中,我们介绍了使用数据结构解决迷宫问题的方法,包括深度优先搜索、广度优先搜索、A算法和迭代深化搜索。
读者
可以根据自己的需求选择适合的方法来解决具体问题。
附件:无
法律名词及注释:
无。
