维纳滤波复原的基本原理
运动图像模糊

一、运动模糊的定义数字图像处理研究有很大部分是在图像恢复方面进行的,包括对算法的研究和针对特定问题的图像处理程序的编写。
数字图像处理中很多值得注意的成就就是在这个方面取得的。
在图像成像的过程中,图像系统中存在着许多退化源。
一些退化因素只影响一幅图像中某些个别点的灰度;而另外一些退化因素则可以使一幅图像中的一个空间区域变得模糊起来。
前者称为点退化,后者称为空间退化。
此外还有数字化、显示器、时间、彩色,以及化学作用引起的退化。
总之,使图像发生退化的原因很多,但这些退化现象都可用卷积来描述,图像的复原过程就可以看成是一个反卷积的问题。
反卷积属于数学物理问题中的一类“反问题”,反问题的一个共同的重要属性是其病态,即其方程的解不是连续地依赖于观测数据,换句话说,观测数据的微小变动就可能导致解的很大变动。
因此,由于采集图像受噪声的影响,最后对于图像的复原结果可能偏离真实图像非常远。
由于以上的这些特性,图像复原的过程无论是理论分析或是数值计算都有特定的困难。
但由于图像复原技术在许多领域的广泛应用,因而己经成为迅速兴起的研究热点。
在拍摄期间, 如果相机与景物之间存在足够大的相对运动, 就会造成照片的模糊, 称之为运动模糊。
运动模糊是成像过程中普遍存在的问题, 在飞机或宇宙飞行器上拍下来的照片,用照相机拍摄高速运动物体的照片, 在突发事件的场合(通常用于侦破), 以及战场上飞行中的导弹均可能存在这种现象。
运动模糊图像的复原是图像复原中的重要课题之一, 可广泛用于天文、军事、道路交通、医学图像、工业控制及侦破领域, 具有重要的现实意义。
运动模糊初期研究的主要原因是为了对卫星所拍摄的图像进行复原, 因为卫星相对地球是运动的, 所以拍出的图像是模糊的(当然, 卫星所拍摄图像的模糊原因不仅仅是相对运动而造成的, 还有其他原因如大气湍流所造成的模糊等等)。
1965 年徘徊者8 号发回37137 张照片, 这些照片由于飞行器的高速运动都带有运动模糊。
维纳滤波(Wiener Filtering)ppt课件

求得H后,这时的均方误差为最小:记最佳的H为
H Hopt (n)
.
E
e 2 (n ) min
E
(
s(
n
)
hopt (m ) x(n
m0
m
)
)
2
E[s2(n) 2s(n) h(m)x(n m) m0
hopt (m ) x(n m )hopt (r ) x(n r )]
h(n) x(n)s(n)w(n)
y(n) sˆ(n)
.
解:已知信号的自相关和噪声的自相关为:
Rss(m)0.6m Rww(m)(m)
1
Rss(j) hopt(m)[Rss(jm)Rww(jm)] m0
j 0 12h(0)0.6h(1) j 1 0.60.6h(0)2h(1) 解得: h (0 ) 0 .4 5 1h ( 1 ) 0 .1 6 5
.
设有一个线性系统,它的单位脉冲响应是 h ( n ) , 当输入一个观测到的随机信号 x ( n ) ,简称观测值,
且该信号包含噪声 和w (有n )用信号 ,s ( n简) 称信
号,也即
x(n)s(n)w (n) (1)
则输出为
y(n)x(n)h(n)h(m )x(nm ) (2) m
.
求得最小均方误差:
1
E [e 2 (n )]m in R s s(0 )h (m )R s s(m ) 1 h (0 ) 0 .6 h (1 ) 0 .4 5 m 0
.
2 维纳滤波器的应用
要设计维纳滤波器必须知道观测信号和估计信号 之间的相关函数,即先验知识。如果我们不知道 它们之间的相关函数,就必须先对它们的统计特 性做估计,然后才能设计出维纳滤波器,这样设 计出的滤波器被称为“后验维纳滤波器”。
解模糊化方法

解模糊化方法解模糊化是图像处理中的一种技术,用于提高图像的清晰度和细节。
图像模糊是由于图像在捕捉或传输过程中被模糊或失真所引起的。
解模糊化是一个复杂的过程,不同的方法会应用于不同的场合,例如时间相关的问题或者在图像处理中的降噪问题。
下面我们将介绍一些常用的解模糊化方法。
1. 维纳滤波维纳滤波是一种在频域中操作的解模糊方法。
该方法通过滤波处理实现图像的恢复。
维纳滤波通过最小化噪声和失真之和的误差来实现图像恢复,同时考虑到信噪比和模糊度等参数。
该方法有时可能会导致图像中出现了一些伪影或其他问题。
2. 盲去卷积盲去卷积是一种基于信号处理的解模糊方法。
该方法的主要好处是,它不需要知道捕获或传输过程中发生的任何失真。
该方法通过计算图像的自相关矩阵来推断捕捉或传输过程中的失真,然后将图像恢复到原来的样子。
3. 基于最大后验概率(MAP)的方法基于最大后验概率的方法是一种通过概率模型来实现解模糊的技术。
该方法通过先验模型和图像模型进行建模,即在估计损失函数的同时,对图像和失真进行了建模。
基于最大后验概率的解模糊化方法可以通过损失函数进行最小化,从而实现图像的恢复。
该方法具有较高的准确度和鲁棒性。
非盲去卷积是一种可以基于已知的卷积核进行解模糊的方法。
在非盲去卷积中,通过计算捕捉或传输过程中被卷积的图像和卷积核之间的卷积,计算出白噪声和失真的实际值,然后通过滤波来恢复原始图像。
总之,解模糊化是一个具有挑战性的问题。
针对不同的场合和问题,应用各种方法进行解决。
深入了解每种技术的优缺点并适当地选择才能获得最佳的效果。
RLS、LMS及维纳滤波

图3.2 LMS算法下的误差信号以及滤波处理后的输出信号
图3.3维纳滤波的输入受干扰信号以及滤波输出信号
上图中红色是滤波后的输出信号,通过对比可以发现RLS算法下的输出信号比LMS算法下的输出信号要稳定的多。可以看到在RLS算法下的误差信号在迭代次数200次左右的时候变化较快较大,这是因为滤波器的阶数是200。可以看到在LMS算法下的输出信号在迭代次数200次以前是还没有达到收敛的,这是因为自适应滤波器的阶数是200阶,在200次之后,信号才是真正的滤波器的输出信号。由维纳滤波器的输出信号可以看到,在前200次,波形都是不稳定的,这是因为滤波器的阶数是200,在这之前还没有求得最佳的滤波器的系数,之后输出波形基本稳定,并且有效的抑制了噪声。但是基于维纳滤波器的求解过程中要求知道信号的统计特性,因此适用范围有限,并且计算自相关矩阵以及求其逆时需要占用极大的内存。
四
[1]张贤达.现代信号处理[M].北京:清华大学出版社,2004.
[2]丁玉美.数字信号处理[M].西安:西安电子科技大学出版社,2003.
[3]王正林,刘明.精通MATLAB 7[M].北京:电子工业出版社,2006(7).
五
课程设计
RLS、LMS及维纳滤波算法在噪声背景下的信号提取
院系:
专业:
学生姓名:
学号:
指导教授:
二○一三年十二月
一
噪声无处不在,在通信领域,噪声干扰是屡见不鲜的事情。前人做了很多从噪声中提取信号的相关工作。在本次实验中,主要是运用经典的最小均方误差方法,使用的是LMS准则,以及最小二乘方法,使用的是RLS准则,对这两种方法的降噪效果进行对比和分析。
3
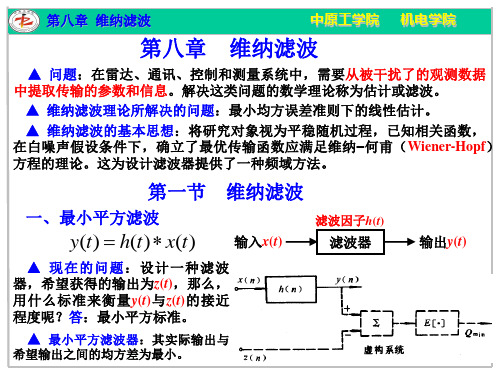
第八章 维纳滤波
rxx(λ-k)
rzx(λ)
第八章 维纳滤波 维纳-何甫积分方 程式(离散形式):
中原工学院
N xx
机电学院
h(k )r
k 0
N
( k ) rzx ( ) 或 h(k )rxx (k ) rzx ( )
k 0
自相关函数为偶函数
▲ 维纳滤波器 如果已知x(n)与所要求的输出信号z(n),则当x(n)的自相关函 数和z(n)与x(n)的互相关函数为已知时,求解维纳-何甫方程,即可求得满足均 方误差最小的滤波因子h(n)。这就是按照最小平方准则设计的线性滤波系统, 它是一个最佳系统,通常称为维纳滤波器。 这是一个对 称 矩阵 。 卷积形式:
第八章 维纳滤波
中原工学院
机电学院
第二节
反滤波
一、回声鸣震现象及反滤波
问题的提出:在某些情况下(例如,在大礼堂内演讲,由于墙壁多次反射, 而造成回声交混,形成一片轰鸣声,使人们听不清讲话内容)所录取的信号, 可认为是原始信号经过几个物理系统(信号传输的路径或通道)作用的结果, 或者看成是源信号经过几个物理滤波器以串联形式滤波的结果。这时,采用 反滤波方法可以使真正源信号从干扰中恢复出来。
n n n n
期望输出s(n)与输入x(n)的互相关函数为
n n
rsx (k ) s(n k ) x(n) s(n k )[s(n) n(n)] rss (k )
如果以 Rss(ejω) 和 Rnn(ejω) 分别表示 rss(k) 和 rnn(k) 的频谱,即分别为 s(n) 和 n(n) 的功率谱,则在对维纳滤波的时间范围不加限制的情况下,由式H(ejω)=Rzs(ejω)/ Rxx(ejω),可以得到维纳滤波器的频率响应应为:
图像复原——逆滤波复原与维纳滤波复原方法及比较

图像复原——逆滤波复原与维纳滤波复原⽅法及⽐较图像复原——逆滤波复原与维纳滤波复原⽅法及⽐较鲁东⼤学信息与电⽓⼯程学院学年第-----1----学期逆滤波复原与维纳滤波复原⽅法及⽐较《》课程论⽂课程号:摘要任课教师成绩图像复原,即利⽤退化过程的先验知识,去恢复已被退化图像的本来⾯⽬。
对遥论⽂题⽬:逆滤波复原与维纳滤波复原⽅法及⽐较感图像资料进⾏⼤⽓影响的校正、⼏何校正以及对由于设备原因造成的扫描线漏失、根据课程介绍的相关内容,从图像复原、分割、修复等⽅⾯,对⽬错位等的改正,将降质图像重建成接近于或完全⽆退化的原始理想图像的过程。
图像在形成,记录,处理和传输的过程中,因为成像系统,记录设备,传输介质和处理⽅前采⽤的前沿的⽅法理论及技术进⾏总结分析,题⽬⾃拟。
法的不完备导致图像质量的下降,也就是常说的图像退化。
图像复原是对发⽣退化的论⽂要求:(对论⽂题⽬、内容、⾏⽂、字数等作出判分规定。
) 图像进⾏补偿,某种意义上对图像进⾏改进,改善输⼊图像的质量。
我的这篇论⽂主要求论⽂结构合理,逻辑性强,重复率不能超过40%,内容具有⼀要介绍逆滤波图像复原,维纳滤波图像复原等⽅法,以及对他们之间进⾏⽐较。
学号_________________姓名__________________ 本专关键词:图像复原、逆滤波复原、维纳滤波复原定的前沿性。
对于全⽂抄袭、逻辑混乱等情况均判0分。
题⽬字体⿊体,⼩⼆。
正⽂,宋体,⼩四,段落间距1.2倍⾏距。
⼀(图像复原的意义字数不少于3000字。
论⽂结尾应附⾄少5篇相关参考⽂献。
复原是图像处理的⼀个重要内容,它的主要⽬的是改善给定的图像质量并尽可能教师评语: 恢复原图像。
图像在形成、传输和记录过程中,受各种因素的影响,图像的质量都会有所下降,典型表现有图像模糊、失真、有噪声等。
这⼀质量下降的过程称为图像的退化。
图像复原的⽬的就是尽可能恢复退化图像本来⾯⽬。
⼆(维纳滤波的介绍密封线学⽣须将⽂字写在此线以下图像复原是图像处理中的⼀个重要问题。
维纳滤波的应用研究
维纳滤波的应用研究一、本文概述《维纳滤波的应用研究》一文旨在深入探讨维纳滤波理论在多个领域中的实际应用及其效果评估。
维纳滤波,作为一种经典的信号处理方法,自其诞生以来便在通信、图像处理、控制理论等多个领域发挥了重要作用。
本文将从理论到实践,系统介绍维纳滤波的基本原理、发展历程以及在各个领域中的具体应用案例。
本文将首先回顾维纳滤波的基本理论,包括其数学原理、算法实现以及性能评估方法。
在此基础上,文章将重点关注维纳滤波在不同领域中的应用实践,例如,在通信系统中如何提高信号传输质量、在图像处理中如何实现噪声抑制和图像增强、在控制理论中如何优化系统性能等。
文章还将对维纳滤波的应用效果进行定量分析和评估,以展示其在实际应用中的优势和局限性。
本文还将对维纳滤波的未来发展趋势进行展望,探讨其在新技术、新领域中的应用前景,以期为推动维纳滤波技术的进一步发展和应用提供有益的参考和启示。
二、维纳滤波器的理论基础维纳滤波器,以诺贝尔物理学奖得主诺伯特·维纳的名字命名,是一种用于估计信号的最优线性滤波器。
其理论基础主要源于最小均方误差准则和线性系统理论。
维纳滤波器可以在存在噪声的情况下,从观测数据中提取出有用的信号,其性能优于其他简单的滤波器,如移动平均滤波器或低通滤波器。
维纳滤波器的设计关键在于求解维纳-霍普夫方程,这是一个以信号的自相关函数和噪声的自相关函数为输入的线性方程。
解这个方程可以得到滤波器的最优权系数,这些权系数被用于构建滤波器,使得输出信号与原始信号的均方误差最小。
维纳滤波器的另一个重要特性是其频域表示。
通过将维纳滤波器的权系数转换为频域表示,我们可以更直观地理解滤波器的性能。
在频域中,维纳滤波器可以看作是一个频率依赖的增益函数,该函数根据信号的频率和噪声的功率谱来确定每个频率分量的增益。
维纳滤波器的理论基础是线性系统理论和最小均方误差准则。
通过求解维纳-霍普夫方程,我们可以得到最优的滤波器权系数,从而实现信号的最优估计。
Lucy-Richardson与维纳滤波算法比较分析
Lucy-Richardson与维纳滤波算法比较分析颜伟;朱煜峰【摘要】图像复原在数字图像处理中有着非常重要的研究意义,目的在于去除图像中的噪声而不会丢失图像的细节信息,而图像模糊以及噪声同样是造成图像不清晰原因之一.实验通过对图像加入高斯噪声和运动模糊的先后次序不同,对Lucy-Richardson复原和维纳滤波复原算法进行比较,同时对加入噪声和模糊函数相同参数与顺序2种算法进行500次仿真实验.实验结果表明:当图像加入模糊函数再加入高斯噪声时,维纳滤波算法优于L-R算法,且在L-R算法迭代次数不断增加过程中,图像清晰度越来越差.当先对图像加入高斯噪声再加入模糊函数时,L-R算法复原效果比维纳滤波算法好;同时迭代次数的增加,L-R算法图像复原效果更好,PSNR更高.【期刊名称】《江西科学》【年(卷),期】2017(035)005【总页数】5页(P785-789)【关键词】高斯噪声;Lucy-Richardson;维纳滤波;图像去噪【作者】颜伟;朱煜峰【作者单位】东华理工大学测绘工程学院,330013,南昌;东华理工大学测绘工程学院,330013,南昌【正文语种】中文【中图分类】TP391.41Abstract:Image restoration has a very important research significance in digital image processing,The purpose is to remove the noise in the image without losing the details of the image.While the image blur and noise is also cause one of the reasons why the image is not clear.In this experiment, Lucy-Richardson restoration and Wiener filter restoration algorithm are compared by adding the Gaussian noise and motion blur to the image in different order,at the same time,we add 500 simulation experiments on the same parameters and order of adding noise and fuzzyfunction.Experimental results show:When the image is added to the fuzzy function and the Gaussian noise is added,the Wiener filter algorithm is superior to the L-R algorithm,and the image clarity is getting worse When the image is added to the gaussian noise before adding the fuzzy function,the L-R algorithm is better than the Wiener filter algorithm.And Increased number of iterations,L-R Algorithm image recovery better,PSNR higher.Key words:gaussian noise;Lucy-Richardson;wiener filtering;image denoising图像在获取过程中往往会因为外在因素如:噪声、模糊、失真等因素导致图像不清晰,图像复原就是对退化图像的清晰模型化过程。
0606逆滤波和维纳滤波
逆滤波没有说明怎样处 理噪声,维纳滤波综合 考虑退化函数和噪声统 计特征.
Sn (u, v) | N (u, v) |2 噪声的功率谱 S f (u, v) | F (u, v) |2 未退化图像的功率谱
8
6.7 最小均方误差滤波 –维纳滤波 (Minimum Mean Square Error Filtering-Wiener Filtering)
Fˆ (u, v) F (u, v) N (u, v) H (u, v)
再作傅立叶逆变换得
fˆ (x, y) f (x, y) N (u, v)H 1 (u, v) e j2 (uxvy)dudv
2. 当噪声作用范围很 大时,逆滤波不能 从噪声中提取图像。
5
维纳滤波器
Fˆ
(u,
v)
H
1 (u,
v)
|
H
(u,
v)
| |2
H (u, v) |2 Sn (u, v)
/
S
f
(u,
v)
G(u,
v)
括号中的项组成的滤波器就是最小均方误差滤波器。
H (u, v) H *(u, v) | H (u, v) |2
退化函数 H (u, v)的复共轭 H *(u, v)H (u, v)
采用维纳滤波要求:
未退化图像和噪声的功率必须是已知的。 一般用下式近似,也可以得到比较好的效果(K为特
殊常数):
Fˆ
(u,
v)
H
1 (u,
v)
|
| H
H (u, v) (u, v) |2
|2 K
最佳维纳滤波的原理
最佳维纳滤波的原理
最佳维纳滤波(Optimal Wiener Filtering)是一种常用的信号处理技术,其原理基于最小均方误差准则(Minimum Mean Square Error,MMSE)。
该滤波器可以用于去噪、图像恢复、语音增强等领域。
最佳维纳滤波的原理可以概括为以下几个步骤:
1. 建立系统模型:首先,我们要建立一个观察模型,用于描述输入信号和系统的关系。
通常,我们假设输入信号经过系统传递后受到了加性高斯噪声的影响,这个模型可以表示为:Y = HX + N,其中Y是观察到的信号,X是输入信号,H是系统的频率响应,N是高斯噪声。
2. 计算滤波器的频率响应:为了最小化估计信号与原信号之间的均方误差,我们需要求解滤波器的频率响应。
通过求解Wiener-Hopf方程,可以得到最佳滤波器的频率响应,这个频率响应最小化了估计信号和原信号之间的误差。
3. 对输入信号进行滤波:根据得到的最佳滤波器的频率响应,我们可以将输入信号通过滤波器进行滤波,得到估计信号。
这一步可以通过频域滤波、时域滤波等方式实现。
4. 提取估计信号:最后,我们可以从滤波后的信号中提取出估计信号,用于后续的应用。
最佳维纳滤波的原理在处理信号时考虑了输入信号的特性以及噪声的影响,通过最小化均方误差的准则,使得估计信号与原信号尽可能接近。
这种滤波方法可以有效去除噪声,恢复信号的质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
维纳滤波复原的基本原理
维纳滤波(Wiener Filter)是一种经典的自适应滤波方法,可
用于信号复原和图像恢复等任务。
其基本原理是最小化输出信号与原始信号之间的均方误差,从而实现信号的最佳估计。
维纳滤波的基本假设是,原始信号和噪声是在频率域上相互独立的。
根据这一假设,维纳滤波通过对输入信号进行频域上的加权来实现信号的复原。
其具体步骤如下:
1. 将输入信号和噪声信号进行傅里叶变换,得到它们在频率域上的表示。
2. 根据信号自相关函数和噪声自相关函数的频谱表示,计算维纳滤波器的频率响应函数。
3. 将输入信号和噪声信号的频率表示与维纳滤波器的频率响应函数相乘,得到输出信号的频率表示。
4. 对输出信号进行傅里叶逆变换,得到复原后的信号。
维纳滤波的关键是确定维纳滤波器的频率响应函数。
通常情况下,维纳滤波器的频率响应函数需要对输入信号和噪声信号的功率谱进行估计。
常用的估计方法包括最小均方误差(MSE)准则、最大似然估计(MLE)准则和谱因子化方法等。
需要注意的是,维纳滤波在实际应用中并不总是能够获得满意的效果。
其有效性依赖于对输入信号和噪声信号的统计性质的
准确估计,以及对维纳滤波器的频率响应函数的合理选择。
在噪声强度较高、信号与噪声相关性较强或噪声功率谱存在峰值等情况下,维纳滤波可能失效或效果较差,此时可能需要使用其他更适合的滤波方法。
