20172018学年高一物理力学专题提升专题19双星和多星问题
2018高中物理第六章万有引力与航天9双星和多星系统难点破解学案新人教版必修2
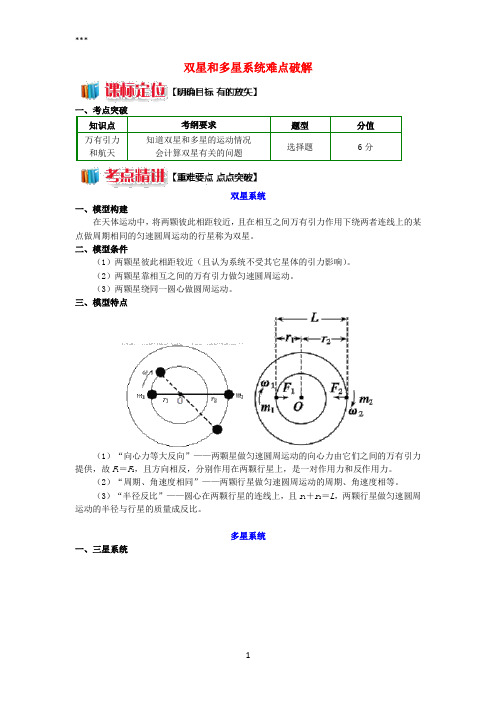
双星和多星系统难点破解双星系统一、模型构建在天体运动中,将两颗彼此相距较近,且在相互之间万有引力作用下绕两者连线上的某点做周期相同的匀速圆周运动的行星称为双星。
二、模型条件(1)两颗星彼此相距较近(且认为系统不受其它星体的引力影响)。
(2)两颗星靠相互之间的万有引力做匀速圆周运动。
(3)两颗星绕同一圆心做圆周运动。
三、模型特点(1)“向心力等大反向”——两颗星做匀速圆周运动的向心力由它们之间的万有引力提供,故F1=F2,且方向相反,分别作用在两颗行星上,是一对作用力和反作用力。
(2)“周期、角速度相同”——两颗行星做匀速圆周运动的周期、角速度相等。
(3)“半径反比”——圆心在两颗行星的连线上,且r1+r2=L,两颗行星做匀速圆周运动的半径与行星的质量成反比。
多星系统一、三星系统图一图二图一中,三颗质量相等的行星分别处于等边三角形的三个定点上,围绕正三角形的几何中心O点各自做匀速圆周运动。
三颗星的周期、半径均相同。
图二中,三颗质量相等的行星位于一条直线上,其中一颗星位于直线的中点O(可视为静止不动),另外两颗行星绕O点做匀速圆周运动。
运行的两颗星的周期相同。
二、四星系统图三图四图三中,三颗质量相等的行星分别处于等边三角形的三个定点上,围绕正三角形的几何中心O点各自做匀速圆周运动,第四颗星位于O点(可视为静止不动)。
运行的三颗星的周期相同。
图四中,四颗质量相等的行星位于正方向的四角,绕正方形的几何中心O点做匀速圆周运动。
四颗星的运行周期相同。
三、解决多星系统的关键多星系统与双星系统相似,首先选取其中一颗星为研究对象,分析各行星之间的万有引力关系并确定向心力的大小。
接着找到行星做圆周运动的圆心,确定半径。
然后结合圆周运动和牛顿运动定律进行计算。
例题 1 (重庆高考)冥王星与其附近的另一星体卡戎可视为双星系统,质量比约为7∶1,同时绕它们连线上某点O做匀速圆周运动。
由此可知,冥王星绕O点运动的()1A. 轨道半径约为卡戎的71B. 角速度大小约为卡戎的7C. 线速度大小约为卡戎的7倍D. 向心力大小约为卡戎的7倍思路分析:本题是双星问题,设冥王星的质量、轨道半径、线速度分别为m1、r1、v1,卡戎的质量、轨道半径、线速度分别为m2、r2、v2,由双星问题的规律可得,两星间的万有引力分别给两星提供做匀速圆周运动的向心力,且两星的角速度相等,故B、D均错;由G221L m m =m 1ω2r 1=m 2ω2r 2(L 为两星间的距离),因此1221211221,71m m r r v v m m r r ====ωω=71,故A 对,C 错。
高中物理双星四星问题和卫星变轨考点归纳复习

高中物理双星问题和卫星变轨考点归纳考点1:双星问题一、 要明确双星中两颗子星做匀速圆周运动的向心力来源双星中两颗子星相互绕着旋转可看作匀速圆周运动,其向心力由两恒星间的万有引力提供。
由于力的作用是相互的,所以两子星做圆周运动的向心力大小是相等的,利用万有引力定律可以求得其大小。
二、 要明确双星中两颗子星匀速圆周运动的运动参量的关系两子星绕着连线上的一点做圆周运动,所以它们的运动周期是相等的,角速度也是相等的,所以线速度与两子星的轨道半径成正比。
三、 要明确两子星圆周运动的动力学关系。
设双星的两子星的质量分别为M 1和M 2,相距L ,M 1和M 2的线速度分别为v 1和v 2,角速度分别为ω1和ω2,由万有引力定律和牛顿第二定律得:M 1:22121111121M M v G M M r L r ω== M 2: 22122222222M M v G M M r L r ω== 在这里要特别注意的是在求两子星间的万有引力时两子星间的距离不能代成了两子星做圆周运动的轨道半径。
四、“双星”问题的分析思路质量m 1,m 2;球心间距离L ;轨道半径 r 1 ,r 2 ;周期T 1,T 2 ;2 2角速度ω1,ω2线速度V1 V2角速度相同:(参考同轴转动问题)ω1 =ω2(由于在双星运动问题中,忽略其他星体引力的情况下向心力由双星彼此间万有引力提供,可理解为一对作用力与反作用力)m1ω2r1=m2ω2r2m1r1=m2r2r1:r2=m2:m1线速度之比与质量比相反:(由半径之比推导)V1=ωr1V2=ωr2V1:V2=r1:r2=m2:m1两颗质量可以相比的恒星相互绕着旋转的现象,叫双星。
双星问题是万有引力定律在天文学上的应用的一个重要内容,现就这类问题的处理作简要分析。
考点2:卫星变轨一、人造卫星基本原理绕地球做匀速圆周运动的人造卫星所需向心力由万有引力提供。
轨道半径r确定后,与之对应的卫星线速度r GMv =、周期GM r T 32π=、向心加速度2rGM a =也都是确定的。
(word完整版)高三物理一轮复习专题练习:双星及多星问题

双星及多星问题一、双星问题1.模型构建:在天体运动中,将两颗彼此相距较近,且在相互之间万有引力作用下绕两者连线上的某点做角速度、周期相同的匀速圆周运动的恒星称为双星。
2.模型条件: (1)两颗星彼此相距较近。
(2)两颗星靠相互之间的万有引力提供向心力做匀速圆周运动。
(3)两颗星绕同一圆心做圆周运动。
3.模型特点: (1)“向心力等大反向”——两颗星做匀速圆周运动的向心力由它们之间的万有引力提供。
(2)“周期、角速度相同”——两颗恒星做匀速圆周运动的周期、角速度相等。
(3)三个反比关系:m1r1=m2r2;m1v1=m2v2;m1a1=m2a2推导:根据两球的向心力大小相等可得,m1ω2r1=m2ω2r2,即m1r1=m2r2;等式m1r1=m2r2两边同乘以角速度ω,得m1r1ω=m2r2ω,即m1v1=m2v2;由m1ω2r1=m2ω2r2直接可得,m1a1=m2a2。
(4)巧妙求质量和:Gm1m2L2=m1ω2r1①Gm1m2L2=m2ω2r2②由①+②得:G m1+m2L2=ω2L ∴m1+m2=ω2L3G4. 解答双星问题应注意“两等”“两不等”(1)“两等”: ①它们的角速度相等。
②双星做匀速圆周运动向心力由它们之间的万有引力提供,即它们受到的向心力大小总是相等。
(2)“两不等”:①双星做匀速圆周运动的圆心是它们连线上的一点,所以双星做匀速圆周运动的半径与双星间的距离是不相等的,它们的轨道半径之和才等于它们间的距离。
②由m1ω2r1=m2ω2r2知由于m1与m2一般不相等,故r1与r2一般也不相等。
二、多星模型(1)定义:所研究星体的万有引力的合力提供做圆周运动的向心力,除中央星体外,各星体的角速度或周期相同.(2)三星模型:①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示).(3)四星模型:①其中一种是四颗质量相等的恒星位于正方形的四个顶点上,沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙).②另一种是三颗恒星始终位于正三角形的三个顶点上,另一颗位于中心O,外围三颗星绕O做匀速圆周运动(如图丁所示).三、卫星的追及相遇问题1、某星体的两颗卫星从相距最近到再次相距最近遵从的规律:内轨道卫星所转过的圆心角与外轨道卫星所转过的圆心角之差为2π的整数倍。
(新课标)高考物理大一轮复习思想方法4“双星”、“多星”问题的处理方法

(2)如右图所示,三颗质量相等的行星位于一正三角形的顶点处,都 绕三角形的中心做圆周运动.每颗行星运行所需向心力都由其余两颗行 星对其万有引力的合力来提供.
Gm2 ×2×cos 30° =ma向,其中L=2rcos 30° . L2 三颗行星转动的方向相同,周期、角速度、线速度的大小相等.
[典例]
Gm m′g,解得g= 2 ,故C正确;由万有引力定律和向心力公式得 R Gm2 2Gm2 4π2 2a =m 2 ,T=2πa 2 2+ a T 2 2a 2a ,故D正确. 4+ 2Gm
2.宇宙三星或多星 (1)如右图所示,三颗质量相等的行星,一颗行星位于中心位 置不动,另外两颗行星围绕它做圆周运动.这三颗行星始终位于 同一直线上,中心行星受力平衡.运转的行星由其余两颗行星的 Gm2 Gm2 引力提供向心力: 2 + =ma向 r 2r2
两行星转动的方向相同,周期、角速度、线速度的大小相等.
2π m T 2RC,可得T=π
a3 Gm.
答案 (4)π
m2 (1)2 3G 2 a a3 Gm
m2 (2) 7G 2 a
7 (3) a 4
[突破训练] 1.2015年4月,科学家通过欧航局天文望远镜在一个河外星 系中,发现了一对相互环绕旋转的超大质量双黑洞系统,如图所 示.这也是天文学家首次在正常星系中发现超大质量双黑洞.这 对验证宇宙学与星系演化模型、广义相对论在极端条件下的适应 性等都具有十分重要的意义.我国今年底也将发射全球功能最强 的暗物质探测卫星.若图中双黑洞的质量分别为M1和M2,它们 以两者连线上的某一点为圆心做匀速圆周运动.根据所学知识, 下列选项正确的是( )
mAmB (2)同上,B星体所受A、C星体引力大小分别为FAB=G r2 2m 2 =G 2 , a m Cm B m2 FCB=G 2 =G 2 ,方向如图所示. r a m2 由FBx=FABcos 60° +FCB=2G 2 ,FBy=FABsin 60° = a
高考专题10 双星及多星问题-高考物理一轮复习专题详解 Word版含解析

高考重点难点热点快速突破1.双星模型(1)定义:绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示.(2)特点:①各自所需的向心力由彼此间的万有引力相互提供,即Gm 1m 2L 2=m 1ω 21r 1,Gm 1m 2L2=m 2ω 22r 2 ②两颗星的周期及角速度都相同,即T 1=T 2,ω1=ω2③两颗星的半径与它们之间的距离关系为:r 1+r 2=L (3)两颗星到圆心的距离r 1、r 2与星体质量成反比,即m 1m 2=r 2r 1. 2.多星模型(1)定义:所研究星体的万有引力的合力提供做圆周运动的向心力,除中央星体外,各星体的角速度或周期相同.(2)三星模型:①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R 的圆形轨道上运行(如图3甲所示).②三颗质量均为m 的星体位于等边三角形的三个顶点上(如图乙所示).(3)四星模型:①其中一种是四颗质量相等的恒星位于正方形的四个顶点上,沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙所示).②另一种是三颗恒星始终位于正三角形的三个顶点上,另一颗位于中心O ,外围三颗星绕O 做匀速圆周运动(如图丁所示).典例分析【例1】 (多选)(2017年昆明模拟)宇宙中两颗相距很近的恒星常常组成一个系统,它们以相互间的万有引力彼此提供向心力,从而使它们绕着某一共同的圆心做匀速圆周运动,若已知它们的运转周期为T ,两星到某一共同圆心的距离分别为R 1和R 2,那么,系统中两颗恒星的质量关系是( )A .这两颗恒星的质量必定相等B .这两颗恒星的质量之和为4π2R 1+R 23GT 2C .这两颗恒星的质量之比为m 1∶m 2=R 2∶R 1D .其中必有一颗恒星的质量为4π2R 1+R 23GT 2【答案】 BC【例2】:2016年2月11日,美国科学家宣布探测到引力波的存在,引力波的发现将为人类探索宇宙提供新视角,这是一个划时代的发现.在如图所示的双星系统中,A、B两个恒星靠着相互之间的引力正在做匀速圆周运动,已知恒星A的质量为太阳质量的29倍,恒星B的质量为太阳质量的36倍,两星之间的距离L=2×105 m,太阳质量M=2×1030 kg,引力常量G=6.67×10-11N·m2/kg2,π2=10.若两星在环绕过程中会辐射出引力波,该引力波的频率与两星做圆周运动的频率具有相同的数量级,则根据题目所给信息估算该引力波频率的数量级是( )A.102 Hz B.104 Hz C.106 Hz D.108 Hz【答案】 A【例3】:.经过用天文望远镜长期观测,人们在宇宙中已经发现了许多双星系统,通过对它们的研究,使我们对宇宙中物质的存在形式和分布情况有了较深刻的认识,双星系统由两个星体组成,其中每个星体的线度都远小于两星体之间的距离,一般双星系统距离其他星体很远,可以当成孤立系统来处理.现根据对某一双星系统的测量确定,该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动.(1)计算出该双星系统的运动周期T;(2)若该实验中观测到的运动周期为T 观测,且T 观测∶T =1∶N (N >1).为了理解T 观测与T 的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质.作为一种简化模型,我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质.若不考虑其他暗物质的影响,根据这一模型和上述观测结果确定该星系间这种暗物质的密度.【答案】 (1)πL2L GM (2)3N -1M2πL3 【解析】 (1)双星均绕它们连线的中点做圆周运动,万有引力提供向心力,则G M 2L 2=M ⎝⎛⎭⎪⎫2πT 2·L 2,解得T =πL2L GM.【例4】:由三颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式,三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O 在三角形所在的平面内做相同角速度的圆周运动(图为A 、B 、C 三颗星体质量不相同时的一般情况).若A 星体质量为2m 、B 、C 两星体的质量均为m ,三角形的边长为a ,求:(1)A 星体所受合力大小F A ; (2)B 星体所受合力大小F B ; (3)C 星体的轨道半径R C ; (4)三星体做圆周运动的周期T .【答案 】 (1)23G m 2a 2 (2)7G m 2a 2 (3)74a (4)πa 3Gm【解析】(1)由万有引力定律,A 星体所受B 、C 星体引力大小为F BA =G m A m B r 2=G 2m 2a2=F CA方向如图所示则合力大小为F A =F BA ·cos 30°+F CA ·cos 30°=23G m 2a2(3)由于m A =2m ,m B =m C =m通过分析可知,圆心O 在BC 的中垂线AD 的中点 则R C =⎝ ⎛⎭⎪⎫34a 2+⎝ ⎛⎭⎪⎫12a 2=74a (4)三星体运动周期相同,对C 星体,由F C =F B =7G m 2a 2=m (2πT)2R C ,可得T =πa 3Gm. 专题练习1:宇宙间存在一些离其他恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m 的星位于等边三角形的三个顶点,三角形边长为R ,忽略其他星体对它们的引力作用,三星在同一平面内绕三角形中心O 做匀速圆周运动,万有引力常量为G ,则( )A .每颗星做圆周运动的线速度为 Gm RB .每颗星做圆周运动的角速度为 3GmR 3C .每颗星做圆周运动的周期为2πR 33GmD .每颗星做圆周运动的加速度与三星的质量无关 【答案】 ABC【解析】由图可知,每颗星做匀速圆周运动的半径r =R2cos 30°=33R .由牛顿第二定律得Gm 2R 2·2cos 30°=m v 2r =mω2r =m 4π2T2r =ma ,可解得v =GmR,ω= 3GmR 3,T =2πR 33Gm ,a =3GmR2,故A 、B 、C 均正确,D 错误. 2.宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.设四星系统中每个星体的质量均为m ,半径均为R ,四颗星稳定分布在边长为a 的正方形的四个顶点上.已知引力常量为G.关于宇宙四星系统,下列说法错误的是( )A . 四颗星围绕正方形对角线的交点做匀速圆周运动B . 四颗星的轨道半径均为C . 四颗星表面的重力加速度均为D . 四颗星的周期均为2πa【答案】B3.宇宙中存在一些离其他恒星较远,由质量相等的三个星体组成的三星系统,通常可忽略其他星体对它们的引力作用.已观测到稳定的三星系统存在的一种形式是三个星体位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行,如图所示.设每个星体的质量均为m,相邻的两个星体之间的距离为L,引力常量为G,则( )A.该圆形轨道的半径为3 2 LB.每个星体的运行周期均为3πL3 2GmC.每个星体做圆周运动的线速度均为Gm LD.每个星体做圆周运动的加速度均与星体的质量无关【答案】:C4.双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动,研究发现,双星系统演化过程中,两星的总质量、距离和周期均可能发生变化,若某双星系统中两星做圆周运动的周期为T ,经过一段时间演化后,两星总质量变为原来的k 倍,两星之间的距离变为原来的n 倍,则此时圆周运动的周期为( )A.n 3k 2B.n 3k T C.n 2kT D.n kT 【答案】:B【解析】:设m 1的轨道半径为r 1,m 2的轨道半径为r 2,由于它们之间的距离恒定,因此双星在空间的绕向一定相同,同时角速度和周期也都相同,两星之间的万有引力提供两星做圆周运动的向心力,即Gm 1m 2r 1+r 22=m 1r 1⎝⎛⎭⎪⎫2πT 2,Gm 1m 2r 1+r 22=m 2r 2⎝ ⎛⎭⎪⎫2πT 2,可得T =2πr 1+r 23G m 1+m 2,故当两恒星总质量变为原来的k倍,两星间距变为原来的n 倍时,圆周运动的周期变为n 3kT ,B 正确. 5.经长期观测,人们在宇宙中已经发现了“双星系统”,“双星系统”由两颗相距较近的恒星组成,每个恒星的直径远小于两个星体之间的距离,而且双星系统一般远离其他天体.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O 点做周期相同的匀速圆周运动.现测得两颗星之间的距离为L ,质量之比为m 1∶m 2=3∶2.则可知( )A .m 1、m 2做圆周运动的角速度之比为2∶3B .m 1、m 2做圆周运动的线速度之比为3∶2C .m 1做圆周运动的半径为r 1=25LD .m 2做圆周运动的半径为r 2=25L【答案:】C6. (多选)宇宙中,两颗靠得比较近的恒星,只受到彼此之间的万有引力作用互相绕转,称之为双星系统.在浩瀚的银河系中,多数恒星都是双星系统.设某双星系统P、Q绕其连线上的O点做匀速圆周运动,如图所示.若PO>OQ,则( )A.星球P的质量一定大于Q的质量B.星球P的线速度一定大于Q的线速度C.双星间距离一定,双星的质量越大,其转动周期越大D.双星的质量一定,双星之间的距离越大,其转动周期越大【答案】BD7. (多选)宇宙中两个相距较近的星球可以看成双星,它们只在相互间的万有引力作用下,绕两球心连线上的某一固定点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动,则下列说法正确的是( ) A.双星相互间的万有引力不变B.双星做圆周运动的角速度均增大C.双星做圆周运动的速度均减小D.双星做圆周运动的半径均增大【答案】CD【解析】双星间的距离在不断缓慢增加,由万有引力定律,F=G,知万有引力减小,A错误;根据万有引力提供向心力得G=m1r1ω2=m2r2ω2,可知m1r1=m2r2,知轨道半径比等于质量之反比,双星间的距离变大,则双星的轨道半径都变大,B 错误,D 正确;根据G=m 1v 1ω=m 2v 2ω,可得线速度减小,C 正确8. (多选)双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动.若某双星系统中两星做圆周运动的周期为T ,两星总质量为M ,两星之间的距离为r ,两星质量分别为m 1、m 2,做圆周运动的轨道半径分别为r 1、r 2,则下列关系式中正确的是( )A . M =B . r 1=rC . T =2πD . =【答案】AC【解析】由于它们之间的距离恒定,因此双星在空间的绕向一定相同,同时角速度和周期也都相同.由向心力公式可得:对m 1:=m 1ω2r 1① 对m 2:=m 2ω2r 2②;由①②式可得:m 1r 1=m 2r 2 ,即=,D 错误.r 1+r 2=r ,得:r 1=r =r ,B 错误.将ω=,r 1=r 代入①式,可得:=m 1·r,得:T =2π,M =,A 、C 正确.9.宇宙中存在由质量相等的四颗星组成的四星系统,四星系统离其他恒星较远,通常可忽略其他星体对四星系统的引力作用.已观测到稳定的四星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为a 的正方形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动,其运动周期为T 1;另一种形式是有三颗星位于边长为a 的等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行,其运动周期为T 2,而第四颗星刚好位于三角形的中心不动.试求两种形式下,星体运动的周期之比T 1T 2.【答案】T 1T 2=6+634+2【解析】:对于第一种形式,一个星体在其它三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动,其轨道半径为:r1=22a.。
高一物理双星试题及答案

高一物理双星试题及答案一、选择题(每题4分,共40分)1. 双星系统是指两颗恒星围绕共同的质心做圆周运动的系统,下列关于双星系统的描述中,正确的是()。
A. 两颗恒星的角速度相等B. 两颗恒星的线速度相等C. 两颗恒星的向心加速度相等D. 两颗恒星的向心力相等答案:A2. 在双星系统中,两颗恒星之间的万有引力提供各自做圆周运动的向心力,下列关于万有引力的描述中,正确的是()。
A. 两颗恒星之间的万有引力大小相等B. 两颗恒星之间的万有引力大小不相等C. 两颗恒星之间的万有引力方向相同D. 两颗恒星之间的万有引力方向相反答案:A3. 双星系统中,两颗恒星的轨道半径之比为2:1,下列关于它们的描述中,正确的是()。
A. 它们的周期之比为1:2B. 它们的周期之比为2:1C. 它们的角速度之比为1:2D. 它们的角速度之比为2:1答案:D4. 双星系统中,两颗恒星的质量分别为M1和M2,轨道半径分别为r1和r2,下列关于它们的描述中,正确的是()。
A. M1/r1 = M2/r2B. M1/r1 ≠ M2/r2C. M1/r1 = 2M2/r2D. M1/r1 = 1/2M2/r2答案:A5. 双星系统中,两颗恒星的线速度分别为v1和v2,下列关于它们的描述中,正确的是()。
A. v1 = v2B. v1 ≠ v2C. v1 = 2v2D. v1 = 1/2v2答案:B6. 双星系统中,两颗恒星的向心加速度分别为a1和a2,下列关于它们的描述中,正确的是()。
A. a1 = a2B. a1 ≠ a2C. a1 = 2a2D. a1 = 1/2a2答案:B7. 双星系统中,两颗恒星的向心力分别为F1和F2,下列关于它们的描述中,正确的是()。
A. F1 = F2B. F1 ≠ F2C. F1 = 2F2D. F1 = 1/2F2答案:A8. 双星系统中,两颗恒星的周期分别为T1和T2,下列关于它们的描述中,正确的是()。
(广东专用)2018年高考物理一轮复习 第5章 万有引力定律 微专题25 双星与多星问题试题 粤教版
25 双星与多星问题[方法点拨] (1)核心问题是“谁”提供向心力的问题.(2)“双星问题”的隐含条件是两者的向心力相同、周期相同、角速度相同;双星中轨道半径与质量成反比;(3)多星问题中,每颗行星做圆周运动所需的向心力是由它们之间的万有引力的合力提供,即F 合=m v 2r,以此列向心力方程进行求解.1.(双星问题)“双星体系”由两颗相距较近的恒星组成,每个恒星的半径远小于两个星球之间的距离,而且双星系统一般远离其他天体.如图1所示,相距为L 的A 、B 两恒星绕共同的圆心O 做圆周运动,A 、B 的质量分别为m 1、m 2,周期均为T .若有间距也为L 的双星C 、D ,C 、D 的质量分别为A 、B 的两倍,则( )图1A .A 、B 运动的轨道半径之比为m 1m 2B .A 、B 运动的速率之比为m 1m 2C .C 运动的速率为A 的2倍D .C 、D 运动的周期均为22T 2.(多星问题)(多选)太空中存在一些离其他恒星很远的、由三颗星体组成的三星系统,可忽略其他星体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式:一种是直线三星系统——三颗星体始终在一条直线上;另一种是三角形三星系统——三颗星体位于等边三角形的三个顶点上.已知某直线三星系统A 每颗星体的质量均为m ,相邻两颗星中心间的距离都为R ;某三角形三星系统B 的每颗星体的质量恰好也均为m ,且三星系统A 外侧的两颗星体做匀速圆周运动的周期和三星系统B 每颗星体做匀速圆周运动的周期相等.引力常量为G ,则( )A .三星系统A 外侧两颗星体运动的线速度大小为v =GmRB .三星系统A 外侧两颗星体运动的角速度大小为ω=12R5GmRC .三星系统B 的运动周期为T =4πRR 5GmD.三星系统B任意两颗星体中心间的距离为L=3125R3.引力波的发现证实了爱因斯坦100年前所做的预测.1974年发现了脉冲双星间的距离在减小就已间接地证明了引力波的存在.如果将该双星系统简化为理想的圆周运动模型,如图2所示,两星在相互的万有引力作用下,绕O点做匀速圆周运动.由于双星间的距离减小,则 ( )A.两星的运动周期均逐渐减小图2 B.两星的运动角速度均逐渐减小C.两星的向心加速度均逐渐减小D.两星的运动速度均逐渐减小4.(多选)宇宙中有这样一种三星系统,系统由两个质量为m的小星体和一个质量为M的大星体组成,两个小星体围绕大星体在同一圆形轨道上运行,轨道半径为r.关于该三星系统的说法中正确的是( )A.在稳定运行的情况下,大星体提供两小星体做圆周运动的向心力B.在稳定运行的情况下,大星体应在小星体轨道中心,两小星体在大星体相对的两侧C.小星体运行的周期为T=4πr32 G M+mD.大星体运行的周期为T=4πr32 G M+m5.(多选)神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图3所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T,可见星A所受暗星B的引力可等效为位于O点质量为m′的星体(视为质点)对它的引力,设A和B的质量分别为m1、m2,则( )图3A .m ′与m 1、m 2的关系为m ′=m 32m 1+m 22B .m ′与m 1、m 2的关系为m ′=m 1m 22m 1+m 22C .暗星B 的质量m 2与可见星A 的速率v 、周期T 和质量m 1之间的关系为m 32m 1+m 22=v 3T2πG D .暗星B 的质量m 2与可见星A 的速率v 、周期T 和质量m 1之间的关系为m 31m 1+m 22=v 3T2πG6.(多选)宇宙间存在一个离其他星体遥远的系统,其中有一种系统如图4所示,四颗质量均为m 的星体位于正方形的顶点,正方形的边长为a ,忽略其他星体对它们的引力作用,每颗星都在同一平面内绕正方形对角线的交点O 做匀速圆周运动,引力常量为G ,则( ) A .每颗星做圆周运动的线速度大小为 +24Gma图4 B .每颗星做圆周运动的角速度大小为Gm 2a3 C .每颗星做圆周运动的周期为2π2a3GmD .每颗星做圆周运动的加速度与质量m 有关7.(多选)宇宙中两颗相距很近的恒星常常组成一个系统,它们以相互间的万有引力彼此提供向心力,从而使它们绕着某一共同的圆心做匀速圆周运动,若已知它们的运转周期为T ,两星到某一共同圆心的距离分别为R 1和R 2,那么,系统中两颗恒星的质量关系是( ) A .这两颗恒星的质量必定相等 B .这两颗恒星的质量之和为4π2R 1+R 23GT 2C .这两颗恒星的质量之比为m 1∶m 2=R 2∶R 1D .其中必有一颗恒星的质量为4π2R 1+R 23GT 2答案精析1.D [对于双星A 、B ,有Gm 1m 2L 2=m 1(2πT )2r 1=m 2(2πT )2r 2,r 1+r 2=L ,得r 1=m 2m 1+m 2L ,r 2=m 1m 1+m 2L ,T =2πLL G m 1+m 2,A 、B 运动的轨道半径之比为r 1r 2=m 2m 1,A 错误;由v =2πr T得,A 、B 运动的速率之比为v 1v 2=r 1r 2=m 2m 1,B 错误;C 、D 运动的周期T ′=2πL L G m 1+2m 2=22T ,D 正确;C 的轨道半径r 1′=2m 22m 1+2m 2L =r 1,C 运动的速率为v 1′=2πr 1′T ′=2v 1,C 错误.]2.BCD [三星系统A 中,三颗星体位于同一直线上,两颗星体围绕中央星体在同一半径为R 的圆轨道上运行.其中外侧的一颗星体由中央星体和另一颗外侧星体的合万有引力提供向心力,有:G m 2R 2+Gm 2R2=m v 2R,解得v = 5Gm 4R ,A 错误;三星系统A 中,周期T =2πR v=4πR R 5Gm ,则其角速度为ω=2πT =12R5GmR,B 正确;由于两种系统周期相等,即T=4πRR5Gm,C 正确;三星系统B 中,三颗星体位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行,如图所示,对某颗星体,由万有引力定律和牛顿第二定律得:2Gm 2L 2cos 30°=m L 2cos 30°·4π2T 2,L =3125R ,D 正确.] 3.A [设双星之间的距离为L ,质量较大的星球与O 点的距离为r ,质量为M ,另一星球质量为m ,由万有引力定律和匀速圆周运动知识得,G MmL2=Mr ω2,G Mm L2=m (L -r )ω2,联立解得ω=G M +mL 3,由于双星之间的距离L 减小,故两星运动的角速度增大,选项B 错误;由周期T =2πω,可知两星的运动周期减小,选项A 正确;由G MmL2=Ma 可知,由于双星之间的距离L 减小,两星运动的向心加速度增大,选项C 错误;由G Mm L 2=M v 2r 可知,v = GmrL 2,因双星质量不变,rL不变,又由于双星之间的距离L 减小,故两星运动的速度增大,选项D 错误.]4.BC [在稳定运行的情况下,对某一个环绕星体而言,受到其他两个星体的万有引力,两个万有引力的合力提供环绕星体做圆周运动的向心力,故A 错误;在稳定运行的情况下,大星体应在小星体轨道中心,两小星体在大星体相对的两侧,故B 正确;对某一个小星体有:GMmr 2+Gmm r 2=4π2rmT 2,解得小星体运行的周期为T =4πr32GM +m,故C 正确;大星体相对静止,故D 错误.]5.AC [由m 1r 1ω2=m 2r 2ω2可得:m 1m 2=r 2r 1,由Gm 1m 2r 1+r 22=Gm 1m ′r 21可得:m ′m 2=r 21r 1+r 22,因此m ′=m 2r 21r 1+r 22=m 32m 1+m 22,A 项正确,B 项错误;由Gm 1m ′r 21=m 1v 2r 1,可得m ′=r 1v 2G ,又由v =2πr 1T可知m 32m 1+m 22=v 2r 1G =v 3T2πG,C 项正确,D 项错误.] 6.AD [由星体均围绕正方形对角线的交点做匀速圆周运动可知,星体做匀速圆周运动的轨道半径r =22a ,每颗星体在其他三个星体万有引力的合力作用下围绕正方形对角线的交点做匀速圆周运动,由万有引力定律和向心力公式得:Gm 22a2+2G m 2a 2cos 45°=m v 222a,解得v =+24Gm a ,角速度为ω=vr=+22Gm a 3,周期为T =2πω=2π2a3+2Gm,加速度a =v 2r =2+Gm2a 2,故选项A 、D 正确,B 、C 错误.]7.BC [对m 1有:G m 1m 2R 1+R 22=m 1R 14π2T 2,解得m 2=4π2R 1R 1+R 22GT 2,同理可得m 1=4π2R 2R 1+R 22GT 2,故两者质量不相等,故选项A 错误;将两者质量相加得m 1+m 2=4π2R 1+R 23GT 2,故选项B 正确;m 1∶m 2=R 2∶R 1,故选项C 正确;两者质量之和为4π2R 1+R 23GT 2,则不可能其中一个的质量为4π2R 1+R 23GT 2,故选项D 错误.]。
专题2:双星与多星系统(课件)
恒星较远,通常可忽略其他星体对四星系统的引力作用。已观测到稳定的四
星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为a的正方
形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动;另一种形式
是有三颗星位于边长为a的等边三角形的三个顶点上,并沿外接于等边三角形
的圆形轨道运行,而第四颗星刚好位于三角形的中心不动。设每个星体的质
AB
C
速圆周运动的向心力;对C,A、B对
C的万有引力提供A做匀速圆周运动
的向心力;B在连线的中点处,所受
的合力为零。
三、三星系统
【计算1】设每颗星的质量均为m,轨道半径为R,求第一种形式 (直线等间距排列)下星体的线速度和周期;
【解析】对A受力分析如图:
Gm2 F1 R2
①
Gm2
v 5GmR 2R
为r1和r2,若运动周期为T,求两星的总质量。
对A:
G
m1m2 L2
m1
(
2
T
)
2
r1
G
m2 L2
( 2 T
)2 r1
①
A
r1 o L
r2
对B: B
G
m1m2 L2
m2
(
2 T
)
2
r2
G
m1 L2
( 2 T
)2 r2
①+②得:
G
m1 m2 L2
( 2
T
)2 (r1 r2 )
②
m1
m2
4 2 L3
量均为m,试求两种形式下星体运动的周期T1和T2。(已知引力常量为G)
【答案】
T1 2 a
(4
2a 2
高中物理双星问题和卫星变轨考点归纳
高中物理双星问题和卫星变轨考点归纳考点1:双星问题一、 要明确双星中两颗子星做匀速圆周运动的向心力来源双星中两颗子星相互绕着旋转可看作匀速圆周运动,其向心力由两恒星间的万有引力提供。
由于力的作用是相互的,所以两子星做圆周运动的向心力大小是相等的,利用万有引力定律可以求得其大小。
二、 要明确双星中两颗子星匀速圆周运动的运动参量的关系两子星绕着连线上的一点做圆周运动,所以它们的运动周期是相等的,角速度也是相等的,所以线速度与两子星的轨道半径成正比。
三、 要明确两子星圆周运动的动力学关系。
设双星的两子星的质量分别为M 1和M 2,相距L ,M 1和M 2的线速度分别为v 1和v 2,角速度分别为ω1和ω2,由万有引力定律和牛顿第二定律得: M 1: 22121111121M M v G M M r L r ω== M 2: 22122222222M M v G M M r L r ω== 在这里要特别注意的是在求两子星间的万有引力时两子星间的距离不能代成了两子星做圆周运动的轨道半径。
四、“双星”问题的分析思路质量m 1,m 2;球心间距离L ;轨道半径 r 1 ,r 2 ;周期T 1,T 2 ;角速度ω1,ω2 线速度V 1 V 2;角速度相同:(参考同轴转动问题)ω1 =ω2(由于在双星运动问题中,忽略其他星体引力的情况下向心力由双星彼此间万有引力提供,可理解为一对作用力与反作用力)m 1ω2r 1=m 2ω2r 2m 1r 1=m 2r 2 r 1:r 2=m2:m 12 2线速度之比与质量比相反:(由半径之比推导)V 1=ωr 1 V 2=ωr 2V 1:V 2=r 1:r 2=m 2:m 1两颗质量可以相比的恒星相互绕着旋转的现象,叫双星。
双星问题是万有引力定律在天文学上的应用的一个重要内容,现就这类问题的处理作简要分析。
考点2:卫星变轨一、人造卫星基本原理绕地球做匀速圆周运动的人造卫星所需向心力由万有引力提供。
高三物理一轮复习专题练习:双星及多星问题
1112一、双星问题双星及多星问题1.模型构建:在天体运动中,将两颗彼此相距较近,且在相互之间万有引力作用下绕两者连线上的某点做角速度、周期相同的匀速圆周运动的恒星称为双星。
2.模型条件: (1)两颗星彼此相距较近。
(2)两颗星靠相互之间的万有引力提供向心力做匀速圆周运动。
(3)两颗星绕同一圆心做圆周运动。
3.模型特点: (1)“向心力等大反向”——两颗星做匀速圆周运动的向心力由它们之间的万有引力提供。
(2)“周期、角速度相同”——两颗恒星做匀速圆周运动的周期、角速度相等。
(3)三个反比关系:m1r1=m2r2;m1v1=m2v2;m1a1=m2a2推导:根据两球的向心力大小相等可得,mω2r=mω2r,即mr=mr;等式mr=mr两边同乘以角速度ω,得mrω=mr1 12 2 1 1 2 2 1 1 2 2 1 1 2 2ω,即mv=mv;由mω2r=mω2r直接可得,ma=ma。
1 12 2 1 1 2Gmm 2 Gmm 1 1 2 2 G m+m ω2L3(4)巧妙求质量和:12=mω2r①12=mωr②2由①+②得:12=ωL2∴m+m=L2L2L2G4.解答双星问题应注意“两等”“两不等”(1)“两等”: ①它们的角速度相等。
②双星做匀速圆周运动向心力由它们之间的万有引力提供,即它们受到的向心力大小总是相等。
(2)“两不等”:①双星做匀速圆周运动的圆心是它们连线上的一点,所以双星做匀速圆周运动的半径与双星间的距离是不相等的,它们的轨道半径之和才等于它们间的距离。
②由mω2r=mω2r知由于m与m一般不相等,故r与r一般也不相等。
1 12 2 1 2 1 2二、多星模型(1)定义:所研究星体的万有引力的合力提供做圆周运动的向心力,除中央星体外,各星体的角速度或周期相同.(2)三星模型:①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示).(3)四星模型:①其中一种是四颗质量相等的恒星位于正方形的四个顶点上,沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙).②另一种是三颗恒星始终位于正三角形的三个顶点上,另一颗位于中心O,外围三颗星绕O做匀速圆周运动(如图丁所示).三、卫星的追及相遇问题1、某星体的两颗卫星从相距最近到再次相距最近遵从的规律:内轨道卫星所转过的圆心角与外轨道卫星所转过的圆心角之差为2π的整数倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
百度文库 - 让每个人平等地提升自我 1 专题19 双星和多星问题 【专题概述】 1.双星模型 (1)定义:绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示.
(2)特点: ①各自所需的向心力由彼此间的万有引力相互提供,即 Gm1m2L2=m1ω 21r1,Gm1m2
L2=m2ω 22r2
②两颗星的周期及角速度都相同,即 T1=T2,ω1=ω2
③两颗星的半径与它们之间的距离关系为:r1+r2=L
(3)两颗星到圆心的距离r1、r2与星体质量成反比,即m1m2=r2r1. 2.多星模型 (1)定义:所研究星体的万有引力的合力提供做圆周运动的向心力,除中央星体外,各星体的角速度或周期相同. (2)三星模型: ①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示). ②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示). 百度文库 - 让每个人平等地提升自我
2 (3)四星模型: ①其中一种是四颗质量相等的恒星位于正方形的四个顶点上,沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙所示). ②另一种是三颗恒星始终位于正三角形的三个顶点上,另一颗位于中心O,外围三颗星绕O做匀速圆周运动(如图丁所示). 【典例精讲】 1. 双星问题 典例1:2016年2月11日,美国科学家宣布探测到引力波的存在,引力波的发现将为人类探索宇宙提供新视角,这是一个划时代的发现.在如图所示的双星系统中,A、B两个恒星靠着相互之间的引力正在做匀速圆周运动,已知恒星A的质量为太阳质量的29倍,恒星B的质量为太阳质量的36倍,两星之间的距离L=2×105 m,太阳质量M=2×1030 kg,引力常量G=×10-11 N·m2/kg2,π2=10.若两星在环绕过程中会辐射出引力波,该引力波的频率与两星做圆周运动的频率具有相同的数量级,则根据题目所给信息估算该引力波频率的数量级是( )
A.102 Hz B.104 Hz C.106 Hz D.108 Hz 【答案】A 百度文库 - 让每个人平等地提升自我
3 由①得T= 4π2L3×3665GMB, 则f=1T= GMB4π2L3×3665= 错误! Hz≈×102 Hz.
典例2:经过用天文望远镜长期观测,人们在宇宙中已经发现了许多双星系统,通过对它们的研究,使我们对宇宙中物质的存在形式和分布情况有了较深刻的认识,双星系统由两个星体组成,其中每个星体的线度都远小于两星体之间的距离,一般双星系统距离其他星体很远,可以当成孤立系统来处理.现根据对某一双星系统的测量确定,该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动. (1)计算出该双星系统的运动周期T; (2)若该实验中观测到的运动周期为T观测,且T观测∶T=1∶N(N>1).为了理解T观测与T的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质.作为一种简化模型,我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质.若不考虑其他暗物质的影响,根据这一模型和上述观测结果确定该星系间这种暗物质的密度.
【答案】(1)πL2LGM (2)3N-1M2πL3
2. 三星问题: 典例3:由三颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式,三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内百度文库 - 让每个人平等地提升自我 4 做相同角速度的圆周运动(图为A、B、C三颗星体质量不相同时的一般情况).若A星体质量为2m、B、C两星体的质量均为m,三角形的边长为a,求:
(1)A星体所受合力大小FA; (2)B星体所受合力大小FB; (3)C星体的轨道半径RC; (4)三星体做圆周运动的周期T.
【答案】(1)23Gm2a2 (2)7Gm2a2 (3)74a (4)πa3Gm 百度文库 - 让每个人平等地提升自我
5 (3)由于mA=2m,mB=mC=m 通过分析可知,圆心O在BC的中垂线AD的中点
则RC= 34a2+12a2=74a (4)三星体运动周期相同,对C星体,由FC=FB=7Gm2a2=m(2πT)2RC,可得T=π a3Gm. 典例4: 宇宙间存在一些离其他恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为R,忽略其他星体对它们的引力作用,三星在同一平面内
绕三角形中心O做匀速圆周运动,万有引力常量为G,则( )
A.每颗星做圆周运动的线速度为 GmR B.每颗星做圆周运动的角速度为 3GmR3 C.每颗星做圆周运动的周期为2πR33Gm D.每颗星做圆周运动的加速度与三星的质量无关 【答案】ABC
3. 四星问题: 典例5:宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.设四星系统中每个星体的质量均为m,半径均为R,四颗星稳定分布在边长为a的正方形的四个顶点上.已知引力常量为G.关于宇宙四星系统,下列说法错误的是( ) A. 四颗星围绕正方形对角线的交点做匀速圆周运动
B. 四颗星的轨道半径均为 百度文库 - 让每个人平等地提升自我 6 C. 四颗星表面的重力加速度均为 D. 四颗星的周期均为2πa 【答案】B
【总结提升】 我们在解双星问题时应该有这样的思路: 1 要明确双星中两个子星做匀速圆周运动的向心力来源。 2要明确双星中两个子星做匀速圆周运动的运动参量直接的关系。 3 两个子星的运动的周期和角速度 3双星模型的重要结论 两颗星到轨道圆心的距离r与星体质量成反比
双星的运动周期为T=2π 双星的总质量 M=, 【专练提升】
1. 2015年9月14日,美国的LIGO探测设施接收到一个来自GW150914的引力波信号,此信号是由两个黑洞的合并过程产生的.如果将某个双黑洞系统简化为如图所示的圆周运动模型,两黑洞绕O点做匀速圆周运动.在相互强大的引力作用下,两黑洞间的距离逐渐减小,在此过程中,两黑洞做圆周运动的( ) 百度文库 - 让每个人平等地提升自我
7 A. 周期均逐渐增大 B. 线速度均逐渐减小 C. 角速度均逐渐增大 D. 向心加速度均逐渐减小 【答案】C
2. 现代观测表明,由于引力作用,恒星有“聚集”的特点,众多的恒星组成了不同层次的恒星系统,最简单的恒星系统是两颗互相绕转的双星,事实上,冥王星也是和另一星体构成双星,如图所示,这两颗行星m1、m2各以一定速率绕它们连线上某一中心O匀速转动,这样才不至于因万有引力作用而吸引在一起,现测出双星间的距离始终为L,且它们做匀速圆周运动的半径r1与r2之比为3∶2,则( )
A. 它们的角速度大小之比为2∶3 B. 它们的线速度大小之比为3∶2 C. 它们的质量之比为3∶2 D. 它们的周期之比为2∶3 【答案】B 【解析】双星的角速度和周期都相同,故A、D均错;由=m1ω2r1,=m2ω2r2,解得m1∶m2=r2∶r1=2∶3,C错误;由v=ωr知,v1∶v2=r1∶r2=3∶2,B正确. 3 宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其他星体对百度文库 - 让每个人平等地提升自我 8 它们的引力作用,已观测到稳定的三星系统存在形式之一是:如图所示,三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行,设每个星体的质量均为M,则( )
A. 环绕星运动的线速度为 B. 环绕星运动的角速度为 C. 环绕星运动的周期为T=4π D. 环绕星运动的周期为T=2π 【答案】C
4 (多选)宇宙中,两颗靠得比较近的恒星,只受到彼此之间的万有引力作用互相绕转,称之为双星系统.在浩瀚的银河系中,多数恒星都是双星系统.设某双星系统P、Q绕其连线上的O点做匀速圆周运动,如图所示.若PO>OQ,则( )
A. 星球P的质量一定大于Q的质量 B. 星球P的线速度一定大于Q的线速度 C. 双星间距离一定,双星的质量越大,其转动周期越大 D. 双星的质量一定,双星之间的距离越大,其转动周期越大 百度文库 - 让每个人平等地提升自我 9 【答案】BD
5. (多选)宇宙中两个相距较近的星球可以看成双星,它们只在相互间的万有引力作用下,绕两球心连线上的某一固定点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动,则下列说法正确的是( ) A. 双星相互间的万有引力不变 B. 双星做圆周运动的角速度均增大 C. 双星做圆周运动的速度均减小 D. 双星做圆周运动的半径均增大 【答案】CD 【解析】双星间的距离在不断缓慢增加,由万有引力定律,F=G,知万有引力减小,A错误;根据万有引力提供向心力得G=m1r1ω2=m2r2ω2,可知m1r1=m2r2,知轨道半径比等于质量之反比,双星间的距离变大,则双星的轨道半径都变大,B错误,D正确;根据G=m1v1ω=m2v2ω,可得线速度减小,C正确. 6 (多选)双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动.若某双星系统中两星做圆周运动的周期为T,两星总质量为M,两星之间的距离为r,两星质量分别为m1、m2,做圆周运动的轨道半径分别为r1、r2,则下列关系式中正确的是( ) A. M= B. r1=r
C. T=2π D. = 【答案】AC
