南京市2011届高三第一次模拟考试(卷)
2012高考语文备考:2011届江苏省各市历次模拟考试文科加试题汇编(一)

2012高考语文备考2011届江苏省各市历次模拟考试文科加试题汇编(一)新高考新题目2011-09-19 07202012高考语文备考2011届江苏省各市历次模拟考试文科加试题汇编(一)2011南京三模附加题练习一、阅读材料,完成19~21题。
(10分)杨补凡为余夫妇写载花小影,神情确肖。
是夜月色颇佳,兰影上粉墙,别有幽致,星澜醉后兴发曰“补凡能为君写真,我能为花图影。
”余笑曰“花影能如人影否’”星澜取素纸铺于墙即就兰影用墨浓淡图之日间取视虽不成画而花叶萧疏自有月下之趣。
芸宝之,各有题咏。
(选自沈复《浮生六记·醉图兰影》)19.用斜线“/”给材料中画线的文言文断句。
(限6处)(6分)20.与“兰”并称为“花中四君子”的是、、。
(2分)21.请各用一个字概括“载花小影”和“醉图之兰影”的艺术效果。
(2分)答、。
二、名著阅读题(15分)22.下列有关名著名篇的说明,不正确的两项是(5分)( ▲ )( ▲ )A.曹操求贤若渴,曾从敌对阵营里招降过许多人才,如董卓的属下才华出众的陈琳,虽在檄文里痛骂过曹操,但董卓失败后,曹操没有杀他,而是收为己用。
B.“白光”是小说《白光》中的情节线索,白光一直在诱惑着陈士成的思维和行动,他在疯人的恍惚感觉中追寻着穷途末路中的一丝“白光”样的希望,直至出城门,投水而死。
C.《边城》中赛龙舟,捉鸭子,月下对歌,推动了情节发展;河街的吊角楼,古老的白塔,拉缆的渡船,象征了人物的命运。
这些事、物都形象地体现了湘西的地域文化特色。
D.《女神》中,无论是古代神话、历史故事中的人物,还是人格化的自然景象,其形象的选择都十分贴切,如山岳海洋、日月星辰、风云雷电等,都与表达的内容感情相一致。
E.“脆弱啊,你的名字就叫女人!……”出自哈姆雷特之口,是其被鬼魂告知谋杀真相之前的一段内心独自,表达了哈姆雷特对母亲强烈的愤怒和怨恨。
23.简答题(10分)(1)《欧也妮·葛朗台》中的拿依是一个什么样的人?请结合作品简要分析。
2011南京市高三第三次模拟考试数学试卷
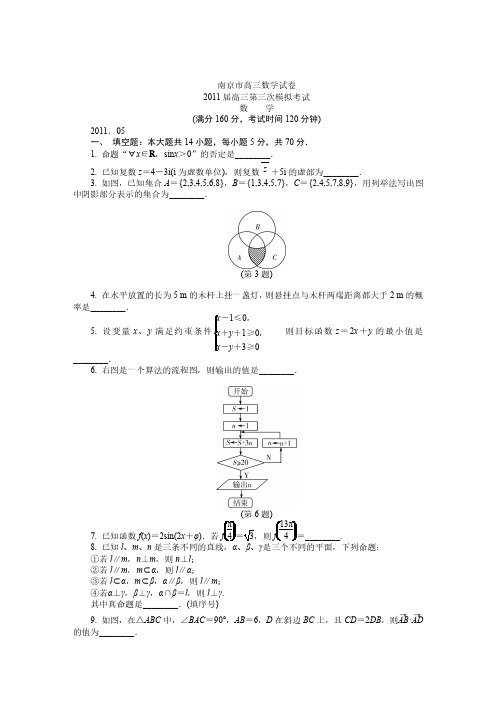
南京市高三数学试卷2011届高三第三次模拟考试数学(满分160分,考试时间120分钟)2011.05一、填空题:本大题共14小题,每小题5分,共70分.1.命题“∀x∈R,sin x>0”的否定是________.2.已知复数z=4-3i(i为虚数单位),则复数z+5i的虚部为________.3.如图,已知集合A={2,3,4,5,6,8},B={1,3,4,5,7},C={2,4,5,7,8,9},用列举法写出图中阴影部分表示的集合为________.(第3题)4.在水平放置的长为5m的木杆上挂一盏灯,则悬挂点与木杆两端距离都大于2m的概率是________.5.设变量x、y满足约束条件-1≤0,+y+1≥0,-y+3≥0则目标函数z=2x+y的最小值是________.6.右图是一个算法的流程图,则输出的值是________.(第6题)7.已知函数f(x)=2sin(2x+φ).若=3,则________.8.已知l、m、n、β、γ①若l∥m,n⊥m,则n⊥l;②若l∥m,m⊂α,则l∥α;③若l⊂α,m⊂β,α∥β,则l∥m;④若α⊥γ,β⊥γ,α∩β=l,则l⊥γ.其中真命题是________.(填序号)9.如图,在△ABC中,∠BAC=90°,AB=6,D在斜边BC上,且CD=2DB,则AB→·AD→的值为________.(第9题)10.已知数列{a n }的前n 项和S n=2n 2+pn ,a 7=11,若a k +a k +1>12,则正整数k 的最小值为________.11.若不等式4x 2+9y 2≥2k xy 对一切正整x 、k 的最大值为________.12.已知直线y =mx (m ∈R )与函数f (x )2-12x ,x ≤0,12x 2+1,x >0的图象恰有3个不同的公共点,则实数m 的取值范围是________.13.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1、F 2,离心率为e ,若椭圆上存在点P ,使得PF 1PF 2=e ,则该椭圆离心率e 的取值范围是________.14.如图,已知正方形ABCD 的边长为1,过正方形中心O 的直线MN 分别交正方形的边AB 、CD 于点M 、N ,则当MN BN 取最小值时,CN =________.(第14题)二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤.15.(本题满分14分)已知a 、b 、c 分别为△ABC 的内角A 、B 、C 的对边,且a cos C +c cos A =2b cos B .(1)求角B 的大小;(2)求sin A +sin C 的取值范围.如图,在矩形ABCD中,AD=2,AB=4,E、F分别为边AB、AD的中点,现将△ADE 沿DE折起,得四棱锥A—BCDE.(1)求证:EF∥平面ABC;(2)若平面ADE⊥平面BCDE,求四面体FDCE的体积.2014年青奥会水上运动项目将在J地举行.截至2010年底,投资集团B在J地共投资100百万元用于房地产和水上运动两个项目的开发.经调研,从2011年初到2014年底的四年间,B集团预期可从三个方面获得利润:一是房地产项目,四年获得的利润的值为该项目投资额(单位:百万元)的20%;二是水上运动项目,四年获得的利润的值为该项目投资额(单位:百万元)的算术平方根;三是旅游业,四年可获得利润10百万元.(1)B集团的投资应如何分配,才能使这四年总的预期利润最大?(2)假设从2012年起,J地政府每年都要向B集团征收资源占用费,2012年征收2百万元,以后每年征收的金额比上一年增加10%.若B集团投资成功的标准是:从2011年初到2014年底,这四年总的预期利润中值(预期最大利润与最小利润的平均数)不低于总投资额的18%,问B集团投资是否成功?在平面直角坐标系xOy中,已知定点A(-4,0)、B(4,0),动点P与A、B连线的斜率之积为-14.(1)求点P的轨迹方程;(2)设点P的轨迹与y轴负半轴交于点C.半径为r的圆M的圆心M在线段AC的垂直平分线上,且在y轴右侧,圆M被y轴截得的弦长为3r.(ⅰ)求⊙M的方程;(ⅱ)当r变化时,是否存在定直线l与动圆M均相切?如果存在,求出定直线l的方程;如果不存在,说明理由.设等比数列{a n }的前n 项和为S n .已知a n +1=2S n +2(n ∈N *).(1)求数列{a n }的通项公式;(2)在a n 与a n +1之间插入n 个数,使这n +2个数组成一个公差为d n 的等差数列.(ⅰ)求证:1d 1+1d 2+1d 3+…+1d n <1516(n ∈N *);(ⅱ)在数列{d n }中是否存在三项d m 、d k 、d p (其中m 、k 、p 成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.已知函数f(x)=x3+x2-ax(a∈R).(1)当a=0时,求与直线x-y-10=0平行,且与曲线y=f(x)相切的直线方程;(2)求函数g(x)=f(x)x-a ln x(x>1)的单调递增区间;(3)如果存在a∈[3,9],使函数h(x)=f(x)+f′(x)(x∈[-3,b]在x=-3处取得最大值,试求b的最大值.高三数学附加题试卷第页(共2页)2011届高三第三次模拟考试数学附加题(满分40分,考试时间30分钟)21.【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.A.选修41:几何证明选讲如图,AB为⊙O的切线,A为切点,过线段AB上一点C作⊙O的割线CED(E在C、D 之间),若∠ABE=∠BDE,求证:C为线段AB的中点.B.选修42:矩阵与变换求曲线C:xy=1在矩阵M=11-11对应的变换作用下得到的曲线C1的方程.C.选修44:坐标系与参数方程在极坐标系中,已知圆C:ρ=22cosθ和直线l:θ=π4(ρ∈R)相交于A、B两点,求线段AB的长.D.选修45:不等式选讲已知a、b都是正实数,且a+b=2,求证:a2a+1+b2b+1≥1.【必做题】第22题、第23题,每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.22.在棱长为2的正方体ABCD-A1B1C1D1中,E为棱AB的中点,点P在平面A1B1C1D1内,若D1P⊥平面PCE,试求线段D1P的长.23.假设位于正四面体ABCD顶点处的一只小虫,沿着正四面体的棱随机地在顶点间爬行,记小虫沿棱从一个顶点爬到另一个顶点为一次爬行.小虫第一次爬行由A等可能地爬向B、C、D中的任意一点,第二次爬行又由其所在顶点等可能地爬向其他三点中的任意一点,如此一直爬下去,记第n(n∈N*)次爬行后小虫位于顶点A处的概率为p n.(1)求p2,p3,p4的值,并写出p n的表达式(不要求证明);(2)设S n=p1C1n+p2C2n+p3C3n+…+p n C n n(n∈N*),试求S n(用含n的式子表示).。
南京市高三第一次模拟考试(word版有答案)

南京市、盐城市2012届高三年级第一次模拟考试数 学 试 题(总分160分,考试时间120分钟)一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上. 1.已知集合{}{}1,3,1,2,A B m ==,若A B ⊆,则实数m = . 2.若(12)(,i i a bi a b -=+∈R ,i 为虚数单位),则ab = . 3.若向量a (2,3),=b (,6)x =-,且∥a b ,则实数x = . 4.袋中装有大小相同且形状一样的四个球,四个球上分别标有“2”、“3”、“4”、“6”这四个数.现从中随机选取三个球,则所选的三个球上的数恰好能构成一个等差数列的概率是 .5.某校共有400名学生参加了一次数学竞赛,竞赛成绩的频率分布直方图如图所示(成绩分组为[0,10),[10,20),,[80,90),[90,100]⋅⋅⋅).则在本次竞赛中,得分不低于80分以上的人数为 .6.在ABC ∆中,已知sin :sin :sin 2:3:4A B C =,则cos C = .7.根据如图所示的伪代码,当输入a 的值为3时,最后输出的S 的值 为 .8.已知四边形ABCD 为梯形, ∥AB CD ,l 为空间一直线,则“l 垂直于两腰,AD BC ”是“l 垂直于两底,AB DC ”的 条件(填写“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”中的一个).9.函数2()(1)xf x x x e =++()x R ∈的单调减区间为 . 10.已知1()21x f x a =--是定义在(,1][1,)-∞-+∞上的奇函数, 则()f x 的值域为 .11.记等比数列{}n a 的前n 项积为*()n T n N ∈,已知1120m m m a a a -+-=,且21128m T -=,则m = .12.若关于x 的方程1ln kx x +=有解,则实数k 的取值范围是 .13.设椭圆2222:1(0)x y C a b a b+=>>恒过定点(1,2)A ,则椭圆的中心到准线的距离的最小值 .第5题第7题14.设a b c x y ===+,若对任意的正实数,x y ,都存在以,,a b c 为三边长的三角形,则实数p 的取值范围是 .二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内. 15.(本小题满分14分)已知函数21()cos cos ()2f x x x x x R =-+∈. (1)求函数()f x 的最小正周期; (2)求函数()f x 在区间[0,]4π上的函数值的取值范围.16.(本小题满分14分)如图,在四棱锥P ABCD -中,四边形ABCD 是菱形,PA PC =,E 为PB 的中点. (1)求证:∥PD 面AEC ;(2)求证:平面AEC ⊥平面PDB .CA B D P E 第16题在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD 的三边AB 、BC 、CD 由长6分米的材料弯折而成,BC 边的长为2t 分米(312t ≤≤);曲线AOD 拟从以下两种曲线中选择一种:曲线1C 是一段余弦曲线(在如图所示的平面直角坐标系中,其解析式为cos 1y x =-),此时记门的最高点O 到BC 边的距离为1()h t ;曲线2C 是一段抛物线,其焦点到准线的距离为98,此时记门的最高点O 到BC 边的距离为2()h t . (1)试分别求出函数1()h t 、2()h t 的表达式;(2)要使得点O 到BC 边的距离最大,应选用哪一种曲线?此时,最大值是多少?第17题如图,在平面直角坐标系xoy中,已知点A为椭圆222199x y+=的右顶点, 点(1,0)D,点,P B在椭圆上,BP DA=.(1)求直线BD的方程;(2)求直线BD被过,,P A B三点的圆C截得的弦长;(3)是否存在分别以,PB PA为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.第18题对于函数()f x ,若存在实数对(b a ,),使得等式b x a f x a f =-⋅+)()(对定义域中的每一个x 都成立,则称函数()f x 是“(b a ,)型函数”.(1)判断函数()4xf x =是否为“(b a ,)型函数”,并说明理由;(2)已知函数()g x 是“(1,4)型函数”, 当[0,2]x ∈时,都有1()3g x ≤≤成立,且当[0,1]x ∈时,2()g x x =(1)1m x --+(0)m >,若,试求m 的取值范围.20.(本小题满分16分)已知数列{}n a 满足*1(0,)a a a a N =>∈,1210n n a a a pa +++⋅⋅⋅+-=*(0,1,)p p n N ≠≠-∈.(1)求数列{}n a 的通项公式n a ;(2)若对每一个正整数k ,若将123,,k k k a a a +++按从小到大的顺序排列后,此三项均能构成等差数列, 且公差为k d .①求p 的值及对应的数列{}k d .②记k S 为数列{}k d 的前k 项和,问是否存在a ,使得30k S <对任意正整数k 恒成立?若存在,求出a 的最大值;若不存在,请说明理由.南京市、盐城市2012届高三年级第一次模拟考试数学参考答案一、填空题:本大题共14小题,每小题5分,计70分.1.32. 23. -44.12 5.120 6.14- 7.21 8.充分不必要 9.(2,1)--(或闭区间)10.3113[,)(,]2222-- 11.4m = 12.21(,]e-∞2 14. (1,3)二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内.15.解: (1)因为1()2cos 222f x x x =-……………………………………………………………4分 sin(2)6x π=-……………………………………………………………………………………………6分故()f x 的最小正周期为π………………………………………………………………………………8分 (2)当[0,]4x π∈时,2[,]663x πππ-∈-…………………………………………………………………10分故所求的值域为1[,22-………………………………………………………………………………14分 16.(1)证明:设AC BD O =,连接EO,因为O,E 分别是BD,PB 的中点,所以∥PD EO …………4分 而,PD AEC EO AEC ⊄⊂面面,所以∥PD 面AEC …………………………………………………7分 (2)连接PO,因为PA PC =,所以AC PO ⊥,又四边形ABCD 是菱形,所以AC BD ⊥…………10分 而PO ⊂面PBD ,BD ⊂面PBD ,PO BD O =,所以AC ⊥面PBD ……………………………13分 又AC ⊂面AEC ,所以面AEC ⊥面PBD ……………………………………………………………14分 17.解:(1)对于曲线1C ,因为曲线AOD 的解析式为cos 1y x =-,所以点D 的坐标为(,cos 1)t t -……2分 所以点O 到AD 的距离为1cos t -,而3AB DC t ==-,则13()(3)(1cos )cos 4(1)2h t t t t t t =-+-=--+≤≤…………………………………………………4分对于曲线2C ,因为抛物线的方程为294x y =-,即249y x =-,所以点D 的坐标为24(,)9t t -………2分所以点O 到AD 的距离为249t ,而3AB DC t ==-,所以2243()3(1)92h t t t t =-+≤≤……………7分(2)因为1()1sin 0h t t '=-+<,所以1()h t 在3[1,]2上单调递减,所以当1t =时,1()h t 取得最大值为3cos1-…………………………………………………………………………………………………9分又224939()()9816h t t =-+,而312t ≤≤,所以当32t =时,2()h t 取得最大值为52……………………11分因为1cos1cos 32π>=,所以153cos1322-<-=,故选用曲线2C ,当32t =时,点E 到BC 边的距离最大,最大值为52分米……………………………14分18.解: (1)因为BP DA =,且A(3,0),所以BP DA ==2,而B,P 关于y 轴对称,所以点P 的横坐标为1,从而得(1,2),(1,2)P B -……………………………………………………………………………………3分 所以直线BD 的方程为10x y +-=………………………………………………………………………5分(2)线段BP 的垂直平分线方程为x=0,线段AP 的垂直平分线方程为1y x =-,所以圆C 的圆心为(0,-1),且圆C的半径为r =……………………………………………………8分 又圆心(0,-1)到直线BD的距离为d =所以直线BD 被圆C 截得的弦长为= ……………………………………………………………………………………10分 (3)假设存在这样的两个圆M 与圆N,其中PB 是圆M 的弦,PA 是圆N 的弦,则点M 一定在y 轴上,点N 一定在线段PC 的垂直平分线1y x =-上,当圆M 和圆N 是两个相外切的等圆时,一定有P,M,N 在一条直线上,且PM=PN …………………………………………………………………………………………12分 设(0,)M b ,则(2,4)N b -,根据(2,4)N b -在直线1y x =-上,解得3b =…………………………………………………………………………………………………14分所以(0,3),(2,1),M N PM PN ==,故存在这样的两个圆,且方程分别为22(3)2x y +-=,22(2)(1)2x y -+-=………………………………………………………………16分19.解: (1)函数()4xf x =是“(b a ,)型函数”…………………………………………………………2分 因为由b x a f x a f =-⋅+)()(,得16ab =,所以存在这样的实数对,如1,16a b ==………………6分 (2) 由题意得,(1)(1)4g x g x +-=,所以当[1,2]x ∈时, 4()(2)g x g x =-,其中2[0,1]x -∈,而[0,1]x ∈时,22()(1)110g x x m x x mx m =+-+=-++>,且其对称轴方程为2m x =,① 当12m>,即2m >时,()g x 在[0,1]上的值域为[(1),(0)]g g ,即[2,1]m +,则()g x 在[0,2]上的值域为44[2,1][,2][,1]11m m m m +=+++,由题意得13411m m +≤⎧⎪⎨≥⎪+⎩,此时无解………………………11分②当1122m ≤≤,即12m ≤≤时,()g x 的值域为[(),(0)]2mg g ,即2[1,1]4m m m +-+,所以则()g x 在[0,2] 上的值域为2244[1,1][,]4114m m m m m m +-+++-,则由题意得2431413m m m ⎧≤⎪⎪+-⎨⎪+≤⎪⎩且2114411m m m ⎧+-≥⎪⎪⎨⎪≥⎪+⎩,解得12m ≤≤……………………………………………………………………13分 ③ 当1022m <≤,即01m <≤时,()g x 的值域为[(),(1)]2mg g ,即2[1,2]4m m +-,则()g x 在[0,2]上的值域为224[1,2][2,]414m m m m +-+-=224[1,]414m m m m +-+-, 则221144314m m m m ⎧+-≥⎪⎪⎨≤⎪⎪+-⎩,解得21m ≤≤.综上所述,所求m的取值范围是223m -≤≤…………………………………………………16分 20.解:(Ⅰ)因为1210n n a a a pa +++⋅⋅⋅+-=,所以2n ≥时, 1210n n a a a pa -++⋅⋅⋅+-=,两式相减,得11(2)n n a p n a p ++=≥,故数列{}n a 从第二项起是公比为1p p+的等比数列 (3)分又当n=1时,120a pa -=,解得2a a p =,从而2(1)1()(2)n n a n a a p n p p -⎧=⎪=+⎨≥⎪⎩…………………………5分(2)①由(1)得11123111(),(),()k k k k k k a p a p a p a a a p p p p p p-+++++++===, [1]若1k a +为等差中项,则1232k k k a a a +++=+,即11p p +=或12p p +=-,解得13p =-…………6分 此时1123(2),3(2)k k k k a a a a -++=--=--,所以112||92k k k k d a a a -++=-=⋅……………………8分[2]若2k a +为等差中项,则2132k k k a a a +++=+,即11p p +=,此时无解………………………………9分 [3]若3k a +为等差中项,则3122k k k a a a +++=+,即11p p +=或112p p +=-,解得23p =-, 此时11133131(),()2222k k k k a a a a -+++=--=--,所以11391||()82k k k k a d a a -++=-=⋅……………11分综上所述,13p =-, 192k k d a -=⋅或23p =-,191()82k k a d -=⋅…………………………………12分②[1]当13p =-时,9(21)kk S a =-,则由30k S <,得103(21)ka <-, 当3k ≥时,1013(21)k <-,所以必定有1a <,所以不存在这样的最大正整数……………………14分 [2]当23p =-时,91(1())42k k a S =-,则由30k S <,得4013(1())2k a <-,因为4040133(1())2k >-,所以13a =满足30k S <恒成立;但当14a =时,存在5k =,使得4013(1())2ka >-即30k S <, 所以此时满足题意的最大正整数13a =……………………………………………………………16分。
2011-2012学年高三数学调研测试试卷(附答案)(南京市)网页版_高三试卷

2011-2012学年高三数学调研测试试卷(附答案)(南京市)网页版_高三试卷
注意事项:
1.本试卷共160分.考试用时120分钟.
2.答题前,考生务必将自己的学校、姓名、考试号写在答题纸上.考试结束后,交回答题纸.参考公式:
一组数据的方差,其中为这组数据的平均数.
一、填空题(本大题共14小题,每小题5分,共70分)
1.计算。
2.若复数为纯虚数,则m= 。
3.某人5次上班途中所花的时间(单位:分钟)分别为x,8,10,11,9.已知这组数据的平均数为10,则其方差为。
4.已知等比数列{an}的各项均为正数.若a1=3,前三项的和为21,则a4+a5+a6= 。
5.设P和Q是两个集合,定义集合.若,,则。
6.根据如图所示的伪代码,可知输出的结果I为。
7.已知扇形的周长为8cm,则该扇形面积的最大值为cm2。
8.过椭圆的左顶点A作斜率为1的直线,与该椭圆的另一个交点为M,与y轴的交点为B.若AM=MB,则该椭圆的离心率为。
点击此处下载:2011-2012学年高三数学第一次调研试卷(附答案)(南京市)。
2011高三数学文科第一次月考试题

修武一中分校2011-2012学年高三第一次月考数学试题(文)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
共150分。
考试时间120分钟。
第I 卷(选择题)60分一、选择题(本题共12个小题,每小题5分,共60分。
) 1.已知集合M ={ x|(x + 2)(x -1) < 0 },N ={ x | x + 1 < 0 },则M ∩N =( ) A. (-1,1) B. (-2,1) C 。
(-2,-1) D. (1,2)2.函数2log (2)y x =+的定义域为A .(,1)(3,)-∞-+∞B .(,1][3,)-∞-+∞C .(2,1]--D .(2,1][3,)--+∞3.已知定义在R 上的奇函数()f x 满足(2)()f x f x +=,则(5)f 的值是A . 2B .0C .1D . 1-4.若集合{}{3, xM y y N x y ====,则MN =( )A . 1[0,]3B . 1(0,]3C .(0,)+∞D . [0,)+∞5.已知函数132 (0) ()1)log (1)xx f x x x x ⎧<=>⎪⎩≤≤,当0a <时,则((()))f f f a 的值为( )AB .12- C .2- D .26.“p 或q "为真命题是“p 且q ”为真命题的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件7.不等式4x +a ·2x +1≥0对一切x ∈R 恒成立,则a 的取值范围是( )A .a ≤2B .a ≥-2C .a ≤1D .a ≥-18.下列命题中的假命题是( )A .任意x >0且x ≠1,都有x +错误!>2B .任意a ∈R ,直线ax +y =a 恒过定点(1,0)C .存在m ∈R ,使f (x )=(m -1)·xm 2-4m +3是幂函数D .任意φ∈R ,函数f (x )=sin(2x +φ)都不是偶函数 9.若关于x 的方程2sin 2sin a x x =--,则实数a 的范围是( )A .(,1]-∞B .[3,1]--C .[3,1]-D .[1,)+∞10。
2011届高三年文综模拟试卷(一)(地理部分)

子江中学2011届高三年下学期文综模拟试卷(一)(地理部分)读“世界上某种气候类型的局部分布地区示意图”,完成1-3题。
1.该种气候的分布地区中,①地区的最高纬度分布较低(低于35°S ),其主要的影响因素是( )A .海陆分布B .纬度位置C .地形D .洋流 2.②地区最热月均温约为24℃~28℃,③地区西海岸最热月均温约为16℃~21℃,产生这种气温差别的最主要因素是A .纬度位置B .海陆位置C .洋流D .地形3.该种气候条件下的农作物一般具有( ) A .耐低温干燥的特 B .耐高温干燥的特点C .喜高温多雨的特D .喜阴喜湿的特点读甲、乙、丙三个地区农业基本情况比较图,完成4~6题。
4.甲地区的农业地域类型可能是………………………………………………………………( )A .季风水田农业B .混合农业C .商品谷物农业D .种植园农业5.与乙地区农业相似的地区是…………………( )A .刚果盆地B .四川盆地C .大自流盆地D .墨累一达令盆地6.提高丙地区土地载畜量的合理措施是………( )A .提高机械化程度B .充分利用水资源C .建设高质量的人工草场D .合理开垦当地土地读“某城市A 及附近区域图”,回答7—9题。
7.A 城市所在国家………………………………………………………………………………( )A .多优良港湾,海洋运输发达B .钢铁工来为其主导产业,资源,能源丰富°26’N 90°ED.经济作物以黄麻生产为主,是世界优质黄麻的主要产区8.下列城市的形成区位与A相似的是………………………………………………………()A.天津B.石家庄C.休斯敦D.芝加哥9.关于城市A所在区域自然环境的叙述,正确的是………………………………………()A.夏季高温多雨,冬季高温少雨B.海洋性气候显著,全年温和多雨C.地形崎岖,多高原山地D.沙漠广面,多内流河下图表示6月22日三个不同地点的日出时刻与日照时数之间的关系,且这一天①、②两地同时日出。
江苏省2011届高三英语牛津版选修9综合模拟卷(含解析)
选修九综合模拟卷九第一部分:听力(共两节,满分20分)第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有l0秒钟的时间回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What does the man mean?A.He doesn’t want to buy a printer now.B.He lost the money he was saving lately.C.He doesn’t have enough money to buy a printer now.2.What does the man suggest the woman do?A.Ask Carol to play tennis.B.Get a tennis lesson from Carol.C.Ask Carol if she’s going to class.3.What can be inferred about the woman?A.She sleeps too much.B.She has bad study habits.C.She’s an excellent student.4.What will the man probably do?A.Buy the woman some magazines.B.Go to the store for some medicine.C.Help the woman find a new doctor.5.What does the man suggest they do?A.Leave early for the airport.B.Change their vacation plans.C.Check their flight schedule in the morning.第二节(共15小题,每小题1分,满分15分)听下面5段对话或独白。
江苏省重点学校2011届高三第一次调研联考数学测试试卷
江苏省重点学校2011届高三第一次调研联考数学测试试卷参考公式:一组样本数据n x x x ,,,21 ,方差2211()ni i s x x n ==-∑一、填空题:本大题共14小题,每小题5分,共70分。
请把答案填写在答题卡相应的位置上.1.命题p :2,2x R x ∃∈>,则命题p 的否定为 ▲ . 2.若复数i i i z 其中,2)1(=+是虚数单位,则复数z z ⋅= ▲ .3.已知函数2,0(),0x x f x x x ≥⎧=⎨<⎩,则((2))f f -= ▲ . 4.若123123,,,,2,3,3,3,,3n n x x x x x x x x 的方差为则的方差为 ▲ .5.一个靶子上有10个同心圆,半径依次为1、2、……、10,击中由内至外的区域的成绩依次为10、9、……、1环,则不考虑技术因素,射击一次,在有成绩的情况下成绩为10环的概率为6.已知3tan(),45παα+=则tan = ▲ .7.直线110,l x ky -+=:210l kx y -+=:,则1l ∥2l 的充要条件是 ▲ .8.已知|a |=3,|b |=4,(a +b )⋅(a +3b )=33,则a 与b 的夹角为 .9.如果执行右面的程序框图,那么输出的S = ▲ .10.设1F 和2F 为双曲线22221(0,0)x y a b a b -=>>的两个焦点,若1F ,2F ,(0,2)P b 是正三角形的三个顶点,则双曲线的离心率为 ▲ .11.函数2cos y x x =+在0,2π⎡⎤⎢⎥⎣⎦上取最大值时,x 的值是___▲___. 12.我们知道若一个边长为a ,面积为S 的正三角形的内切圆半径23Sr a =,由此类比,若一个正四面体的一个面的面积为S ,体积为V ,则其内切球的半径r = ▲ .13.设12a =,121n n a a +=+,211n n n a b a +=--,*n N ∈,则2011b =w.w ▲ .14.图为函数()(01)f x x x =<<的图象,其在点(())M t f t ,l l y 处的切线为,与轴和直线1=y 分别交于点P 、Q ,点N (0,1),若△PQN 的面积为b 时的点M 恰好有两个,则b 的取值范围为 ▲ .二、解答题:本大题共6小题,共90分,解答应写出文字说明、证明过程或演算步骤.15.(本小题满分14分) 已知函数231()sin 2cos 22f x x x x =--∈R ,.(Ⅰ)求函数()f x 的最小值和最小正周期;(Ⅱ)设△ABC 的内角A 、B 、C 的对边分别为a ,b ,c ,且3()0c f C ==,,若si n 2s i n B A =,求a ,b 的值.16.(本小题满分14分)如图,在四棱锥P ABCD -中,PD ABCD ⊥平面,AD CD =,DB 平分ADC ∠,E 为PC 的中点. (Ⅰ)证明://PA BDE 平面; (Ⅱ)证明:AC PBD ⊥平面.17. (本小题满分15分)如图,某小区准备在一直角围墙ABC 内的空地上植造一块“绿地ABD ∆”,其中AB 长为定值a ,BD 长可根据需要进行y xOP M QN GFDC A DCBP E调节(BC 足够长).现规划在ABD ∆的内接正方形BEFG 内种花,其余地方种草,且把种草的面积1S 与种花的面积2S 的比值12S S 称为“草花比y ”.(Ⅰ)设DAB θ∠=,将y 表示成θ的函数关系式; (Ⅱ)当BE 为多长时,y 有最小值?最小值是多少?18. (本小题满分15分)已知C 过点)1,1(P ,且与M :222(2)(2)(0)x y r r +++=>关于直线20x y ++=对称.(Ⅰ)求C 的方程;(Ⅱ)设Q为C 上的一个动点,求PQ MQ ⋅的最小值;(Ⅲ)过点P 作两条相异直线分别与C 相交于B A ,,且直线PA 和直线PB 的倾斜角互补,O 为坐标原点,试判断直线OP 和AB 是否平行?请说明理由.19.(本小题满分16分)已知函数()ln af x x x =-.(Ⅰ)求函数()f x 的单调增区间;(Ⅱ)若函数()f x 在[1,]e 上的最小值为32,求实数a 的值;(Ⅲ)若函数2()f x x <在(1,)+∞上恒成立,求实数a 的取值范围.20.(本小题满分16分)已知等差数列{}n a 的首项为a ,公差为b ,等比数列{}n b 的首项为b ,公比为a (其中,a b 均为正整数). (Ⅰ) 若1122,a b a b ==,求数列{}n a 、{}n b 的通项公式;(Ⅱ)在(Ⅰ)的条件下,若1213,,,k n n n a a a a a ,,,12(3)k n n n <<<<<成等比数列,求数列{}k n 的通项公式;(Ⅲ) 若11223a b a b a <<<<,且至少存在三个不同的b 值使得等式()m n a t b t N +=∈成立,试求a 、b 的值.附加题部分(满分40分) 21.【选做题】在A 、B 、C 、D 四小题中只能选做2题;每题10分,共20分;解答时应写出文字说明,证明过程或演算步骤. A .选修4-1:几何证明选讲如图,⊙O 的半径OB 垂直于直径AC ,M 为AO 上一点,BM 的延长线交⊙O 于N ,过N 点的切线交CA 的延长线于P . (1)求证:PM2=PA·PC ;(2)若⊙O 的半径为23,OA=3OM ,求MN 的长.OCM NA PB (第1题)考试证号———————————————————————B .选修4-2:矩阵与变换试求曲线sin y x =在矩阵MN 变换下的函数解析式,其中M =1002⎡⎤⎢⎥⎣⎦,N =10201⎡⎤⎢⎥⎢⎥⎣⎦.C .选修4-4:坐标系与参数方程在极坐标系下,已知圆O :cos sin ρθθ=+和直线2sin 42l ρθπ⎛⎫-=⎪⎝⎭:. (1)求圆O 和直线l 的直角坐标方程;(2)当(0,)θ∈π时,求直线l 与圆O 公共点的一个极坐标.D .选修4-5:不等式选讲用数学归纳法证明不等式:211111(1)12n n n n n n *++++>∈>++N 且.【必做题】第22题,23题,每题10分,共20分;解答时应写出文字说明,证明过程或演算步骤.22.甲、乙、丙三个同学一起参加某高校组织的自主招生考试,考试分笔试和面试两部分,笔试和面试均合格者将成为该高校的预录取生(可在高考中加分录取),两次考试过程相互独立.根据甲、乙、丙三个同学的平时成绩分析,甲、乙、丙三个同学能通过笔试的概率分别是0.6,0.5,0.4,能通过面试的概率分别是0.5,0.6,0.75.(1)求甲、乙、丙三个同学中恰有一人通过笔试的概率;(2)设经过两次考试后,能被该高校预录取的人数为ξ,求随机变量ξ的期望)(ξE .23.已知点F(0,1),点P 在x 轴上运动,M 点在y 轴上,N 为动点,且满足0PM PF ⋅=, PN PM +=0.(1)求动点N 的轨迹C 方程;(2)由直线y= -1上一点Q 向曲线C 引两条切线,切点分别为A ,B ,求证:AQ ⊥BQ .参考答案1、2,2x R x ∀∈≤ 2、2 3、4 4、18 5、1100 6、14-7、1- 8、120︒ 9、650 10、2 11、6π 12、34V S 13、201221- 14、18,427⎛⎫⎪⎝⎭ 15.解:(1)31cos21()sin 2sin 212226x f x x x +π⎛⎫=--=-- ⎪⎝⎭, (3分)则()f x 的最小值是-2,(4分)最小正周期是22T π==π;(6分)(2)()sin 210,sin 2166f C C C ππ⎛⎫⎛⎫=--=-= ⎪ ⎪⎝⎭⎝⎭则, 110,022,2666C C C ππ<<π∴<<π∴-<-<π, 2,623C C πππ∴-==, (8分)sin 2sin B A =,由正弦定理,得12a b =,① (10分) 由余弦定理,得222222cos ,33c a b ab a b abπ=+-=+-即, ②由①②解得1,2a b ==. (14分) 16.证明:(1)连结AC ,设ACBD H =,连结EH ,在ADC ∆中,因为AD CD =,且DB 平分ADC ∠,所以H 为AC 的中点,又∵E 为PC 的中点, ∴//EH PA ,……………………………4分 又EH BDE ⊂平面,且PA BDE ⊄平面, ∴//PA BDE 平面;……………………7分 (2)∵PD ABCD ⊥平面,AC ABCD ⊂平面, ∴PD AC ⊥,由(1)得BD AC ⊥, 又PDDB D =, 故AC PBD ⊥平面.……………14分17. 解:(Ⅰ)因为tan BD a θ=,所以ABD ∆的面积为21tan 2a θ((0,)2πθ∈)…(2分) 设正方形BEFG 的边长为t ,则由F G D G A BD B =,得tan tan t a t a a θθ-=,解得t a n 1t a n a t θθ=+,则2222tan (1tan )a S θθ=+…………………………………………………………(6分)所以222212211tan tan tan 22(1tan )a S a S a θθθθ=-=-+,则212(1tan )12tan S y S θθ+==- (9分)(Ⅱ)因为tan (0,)θ∈+∞,所以1111(tan 2)1(tan )2tan 2tan y θθθθ=++-=+1≥… (13分)当且仅当tan 1θ=时取等号,此时2aBE =.所以当BE 长为2a时,y 有最小值1…………………………… (15分)18. 解:(Ⅰ)设圆心C (,)a b ,则222022212a b b a --⎧++=⎪⎪⎨+⎪=⎪+⎩,解得00a b =⎧⎨=⎩…………… (3分) 则圆C 的方程为222x y r +=,将点P 的坐标代入得22r =,故圆C 的方程为222x y +=…………………… (5分) (Ⅱ)设(,)Q x y ,则222x y +=,且(1,1)(2,2)PQ MQ x y x y ⋅=--⋅++… (7分) =224x y x y +++-=2x y +-,所以PQ MQ ⋅的最小值为4-(可由线性规划或三角代换求得)…(10分)(Ⅲ)由题意知, 直线PA 和直线PB 的斜率存在,且互为相反数,故可设:1(1)PA y k x -=-,:1(1)PB y k x -=--,由221(1)2y k x x y -=-⎧⎨+=⎩,得222(1)2(1)(1)20k x k k x k ++-+--= …………………………………………(11分)因为点P 的横坐标1x =一定是该方程的解,故可得22211A k k x k --=+………… (13分) 同理,22211B k k x k +-=+, 所以(1)(1)2()1B A B A B A AB B A B A B Ay y k x k x k k x x k x x x x x x ------+====---=OP k所以,直线AB 和OP 一定平行……………………………………(15分)19、解:(1)由题意,()f x 的定义域为(0,)+∞,且221()a x af x x x x +'=+=.……2分①当0a ≥时,()0f x '>,∴()f x 的单调增区间为(0,)+∞.………………(3分) ②当0a <时,令()0f x '>,得x a >-,∴()f x 的单调增区间为(,)a -+∞.…4分(2)由(1)可知,2()x af x x +'=①若1a ≥-,则0x a +≥,即()0f x '≥在[1,]e 上恒成立,()f x 在[1,]e 上为增函数, ∴min 3[()](1)2f x f a ==-=,∴32a =-(舍去).…………… (6分)②若a e ≤-,则0x a +≤,即()0f x '≤在[1,]e 上恒成立,()f x 在[1,]e 上为减函数, ∴min 3[()]()12a f x f e e ==-=,∴2e a =-(舍去).………………………8分③若1e a -<<-,当1x a <<-时,()0f x '<,∴()f x 在(1,)a -上为减函数, 当a x e -<<时,()0f x '>,∴()f x 在(,)a e -上为增函数, ∴min 3[()]()ln()12f x f a a =-=-+=,∴a e =-综上所述,a e =-.………………………………………………………………10分(3)∵2()f x x <,∴2ln ax x x -<.∵0x >,∴3ln a x x x >-在(1,)+∞上恒成立……………………………12分令32()ln ,()()1ln 3g x x x x h x g x x x '=-==+-,则2116()6x h x x x x -'=-=. ∵1x >,∴()0h x '<在(1,)+∞上恒成立,∴()h x 在(1,)+∞上是减函数,∴()(1)2h x h <=-,即()0g x '<,∴()g x 在(1,)+∞上也是减函数,∴()(1)1g x g <=-.∴当2()f x x <在(1,)+∞恒成立时,1a ≥-.……………………………………16分20.解:(Ⅰ)由1122,a b a b ==得:a ba b ab =⎧⎨+=⎩, 解得:0a b ==或2a b ==,,a b N +∈, 2a b ∴==,从而2,2nn n a n b ==…………………………………5分(Ⅱ)由(Ⅰ)得132,6a a ==,∴1213,,,k n n n a a a a a ,,,构成以2为首项,3为公比的等比数列,即:123k k n a +=⋅ ……………………………………………………… 7分又2k n ka n =,故1223k k n +=⋅,13k k n +∴=…………………………………………10分(Ⅲ) 由11223a b a b a <<<<得:2a b a b ab a b <<+<<+,由a b ab +<得:()1a b b->;由2ab a b <+得:()12a b b-<,而*,,a b N a b ∈<,即:1b a >≥,从而得:12211241111b b a b b b b <+=<<=+≤----,2,3a ∴=,当3a =时,2b =不合题意,故舍去,所以满足条件的2a =. …………………………………………………………………12分 又2(1)m a b m =+-,12n n b b -=⋅,故()1212n b m t b -+-+=⋅,即:()1212n m b t--+=+①若1210n m --+=,则2t N =-∉,不合题意;………………………………… 14分②若1210n m --+≠,则1221n t b m -+=-+,由于121n m --+可取到一切整数值,且3b ≥,故要至少存在三个b 使得()m n a t b t N +=∈成立,必须整数2t +至少有三个大于或等于3的不等的因数,故满足条件的最小整数为12,所以t 的最小值为10,此时3b =或4或12…………………………………………………………………16分附加题部分21. A .(1)证明:连结ON .∵PN 切⊙O 于N ,∴∠ONP=90°.∴∠ONB+∠BNP=90°. ∵OB=ON ,∴∠OBN=∠ONB .∵BO ⊥AC 于O ,∴∠OBN +∠BMO=90°.∴∠BNP=∠BMO=∠PMN ,∴PM=PN . ∴PM2=PN2=PA·PC .………………………………………………………5分(2)解:OM=2,BO=23,BM=4.∵BM·MN=CM·MA=(23+2)(23-2)=8,∴MN=2.………………………………10分B .解:MN = 1002⎡⎤⎢⎥⎣⎦10201⎡⎤⎢⎥⎢⎥⎣⎦=10202⎡⎤⎢⎥⎢⎥⎣⎦,---------------------------------------------------4分即在矩阵MN 变换下122x x x y y y ⎡⎤''⎡⎡⎤⎤⎢⎥→=⎢⎢⎥⎥⎢⎥''⎦⎦⎣⎣⎢⎦⎣,-------------------------------------7分 则1sin 22y x ''''=,即曲线sin y x =在矩阵MN 变换下的函数解析式为2sin 2y x =.----------10分C .解:(1)圆O :cos sin ρθθ=+,即2cos sin ρρθρθ=+, 圆O 直角坐标方程为:22x y x y +=+, 直线2sin 42l ρθπ⎛⎫-= ⎪⎝⎭:, 即sin cos 1ρθρθ-=,则直线l 的直角坐标方程为:1y x -=; --------------------------------------6分(2)由220,10,x y x y x y ⎧+--=⎨-+=⎩得0,1,x y =⎧⎨=⎩故直线l 与圆O 公共点的一个极坐标为(1,)2π.----------------------------------10分D .证明:(1)当2n =时,左边=11113123412++=>,∴2n =时成立; ----------3分(2)假设当(2)n k k =≥时成立,即21111112k k k k ++++>++,那么当1n k =+时,左边2221111()11(1)k k k k =++++++++ 222111111()11(1)k k k k k k =++++++-+++2221111(21)111(1)k k k k k k k -->++⋅-=+>++,∴1n k =+时也成立, --------------------------------------8分根据(1)(2)可得不等式对所有的1n >都成立. ---------------------------10分22.解:(1)分别记甲、乙、丙三个同学笔试合格为事件1A 、2A 、3A ;E 表示事件“恰有一人通过笔试”,则123123123()()()()P E P A A A P A A A P A A A =++0.60.50.60.40.50.=⨯⨯+⨯⨯+⨯⨯0.38=;--------------5分(2)解法一:因为甲、乙、丙三个同学经过两次考试后合格的概率均为0.3p =,所以~(30.3)B ξ,,故()30.30.9E np ξ==⨯=.------------10分 解法二:分别记甲、乙、丙三个同学经过两次考试后合格为事件A B C ,,,则()()()0.3P A P B P C ===所以2(1)3(10.3)0.30.441P ξ==⨯-⨯=, 2(2)30.30.70.189P ξ==⨯⨯=,3(3)0.30.027P ξ===.于是,()10.44120.18930.0270.9E ξ=⨯+⨯+⨯=.23.解:(1)设N(x ,y).因PN PM +=0,故P 的坐标为(2x,0),M(0,-y),于是,(,)2x PM y =--,(,1)2x PF =-, 因0PM PF ⋅=,即得曲线C 的方程为x2=4y ; -------------------5分(2)设Q(m ,-1).由题意,两条切线的斜率k 均存在,故可设两切线方程为y=k(x-m)-1, 将上述方程代入x2=4y ,得x2-4kx+4km+4=0,依题意,∆=(-4k)2-4(4km+4)=0,即k2-mk-1=0,上述方程的两根即为两切线的斜率,其积为-1,即它们所在直线互相垂直. -------------------10分。
%80中学2011届高三第一次模拟考试(地理)
云龙一中2011届高三年级第一次模拟考试地理试题第Ⅰ卷(选择题,共60分)一、单项选择题 (在每小题的四个选项中,只有一项符合题目要求,请将正确答案的代号写在题后的括号内。
)读某地正午太阳高度年变化情况图1,回答1~2题。
1.该地位于 ( )A .南半球温带地区B .北回归线以北地区C .0°~23°26′N 之间D .0°~23°26′S 之间2.图中P 点表示的这一天 ( ) A .太阳直射南回归线 B .北半球纬度越高昼越长C .太阳直射赤道D .地球公转速度最慢图2为“近地面气压带、风带示意图”,回答3-4题。
3.图中气压带代表 ( ) A .赤道低气压带 B .副极地低气压带 C .极地高气压带 D .副热带高气压带4.图中气压带、风带对气候产生的影响,正确的是( ) A .受该气压带影响,北非地区终年高温少雨 B .受风带1影响,台湾东部夏季多暴雨 C .受风带2影响,新西兰终年温和湿润D .受气压带和风带2的交替控制,罗马夏季高温干燥,冬季温和多雨图25.2007年3月7日上午我国西北某军用机场,三架轰炸机相继升空,先后5次进入内蒙古段黄河冰凌区实施轰炸,24枚炸弹全部准确命中目标,炸凌任务圆满完成。
黄河凌汛灾情监测中可能用到的技术是 ,飞机准确轰炸目标可能用到 技术来完成空间定位。
( )A.RS GIS B.GPS GRS C.RS GPS D.GIS RS 读图3,回答6~8题。
6.一年中有两种环流影响的地区是 ( ) A .①和② B .③和④ C .②和④ D .①和③ 7.④地区的植被类型为 ( ) A .热带荒漠 B .亚热带常绿阔叶林 C .温带草原 D .亚热带常绿硬叶林 8.⑤地区炎热干燥时 ( ) A .地球到远日点附近 B .蒙古高压最强盛时期 C .②地处于多雨季节 D .我国东部盛行东南风读中国地理四大区域图4,完成9~11四大区域太阳年辐射总量由大到小的排序是( )A .abcB .adbcC .dbacD .dcba9.有关四大区域农业发展主要制约因素的叙述,错误的是( )A .a ——洪涝灾害B .b ——土壤肥力C .c ——灌溉水源D .d ——生长积温10.有关四大区域主要能源的叙述,错误的是( )A .a ——水能B .b ——煤、石油C .c ——石油、煤、天然气、水能D .d ——煤、石油、水能 11.四大区域目前以公路运输占绝对主导地位的是( )A .aB .bC .cD .d读图5回答12—13题。
数学_2011年江苏省盐城市、南京市高考数学三模试卷(含答案)
2011年江苏省盐城市、南京市高考数学三模试卷一、题空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题纸相应位置上.1. 命题“∀x ∈R ,sinx >0”的否定是________.2. 已知复数z =3+4i (i 为虚数单位),则复数z ¯+5i 的虚部为________.3. 如图,已知集合A ={2, 3, 4, 5, 6, 8},B ={1, 3, 4, 5, 7},C ={2, 4, 5, 7, 8, 9},用列举法写出图中阴影部分表示的集合为________.4. 在水平放置的长为5cm 的木杆上挂一盏灯,则悬挂点与木杆两端距离都大于2cm 的概率是________.5. 设变量x ,y 满足约束条件{x −1≤0x +y +1≥0x −y +3≥0 ,则目标函数z =2x +y 的最小值是________.6. 如图是一个算法的流程图,则输出的值是________.7. 已知函数f(x)=2sin(2x +φ),若f(π4)=√3,则f(13π4)=________.8. 已知l ,m ,n 是三条不同的直线,α,β,γ是三个不同的平面,下列命题:①若l // m ,n ⊥m ,则n ⊥l ;②若l // m ,m ⊂α,则l // α;③若l ⊂α,m ⊂β,α // β,则l // m ; ④若α⊥γ,β⊥γ,α∩β=l ,则l ⊥γ.其中真命题是________.(写出所有真命题的序号).9.如图,在△ABC 中,∠BAC =90∘,AB =6,D 在斜边BC 上,且CD =2DB ,则AB →⋅AD →的值为________.10. 已知数列{a n }的前n 项和S n =2n 2+pn ,a 7=11,若a k +a k+1>12,则正整数k 的最小值为________.11. 若不等式4x 2+9y 2≥2k xy 对一切正数x ,y 恒成立,则整数k 的最大值为________. 12. 已知直线y =mx(m ∈R)与函数f(x)={2−(12)x (x ≤0)12x 2+1(x >0)的图象恰好有三个不同的公共点,则实数m 的取值范围是________.13. 已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,离心率为e ,若椭圆上存=e,则该离心率e的取值范围是________.在点P,使得PF1PF214. 如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当MN最小时,CN=________.BN二、解答题:本大题共6小题,共计90分,请在答题纸指定的区域内作答,解答是时应写出文字说明、证明过程或演算步骤.15. 已知a,b,c分别为△ABC的三内角A,B,C的对边,且acosC+ccosA=2bcosB.(1)求角B的大小;(2)求sinA+sinC的取值范围.16. 如图1,在矩形ABCD中,AD=2,AB=4,E,F分别为边AB,AD的中点.现将△ADE沿DE折起,得四棱锥A−BCDE(如图2).(1)求证:EF // 平面ABC;(2)若平面ADE⊥平面BCDE,求四面体FDCE的体积.17. 书旗集团截止2010年底,在A市共投资100百万元用于地产和水上运动项目的开发.经调研,从2011年初到2014年底的四年间,书旗集团预期可从三个方面获得利润:一是房地产项目,四年获得的利润的值为该项目投资额(单位:百万元)的25%;二是水上运动项目,四年获得的利润的值为该项目投资额(单位:百万元)的算术平方根;三是旅游业,四年可获得利润10百万元.(1)书旗集团的投资应如何分配,才能使这四年总的预期利润最大?(2)假设2012年起,A市决定政府每年都要向书旗集团征收资源占用费,2012年征收2百万元,以后每年征收的金额比上一年增加1百万元,若书旗集团投资成功的标准是:从2011年初到2014年底,这四年总的预期利润中值(预期最大利润与最小利润的平均数)不低于投资额的18%.问书旗集团投资是否成功?18. 在平面直角坐标系xOy中,已知定点A(−4, 0),B(4, 0),动点P与A、B连线的斜率之积为−1.4(I)求点P的轨迹方程;(II)设点P的轨迹与y轴负半轴交于点C,半径为r的圆M的圆心M在线段AC的垂直平分线上,且在y轴右侧,圆M被y轴截得弦长为√3r.(1)求圆M的方程;(2)当r变化时,是否存在定直线l与动圆M均相切?如果存在,求出定直线l的方程;如果不存在,说明理由.19. 设等比数列{a n}的前n项和为S n,已知a n+1=2S n+2(n∈N+).(1)求数列{a n}通项公式;(2)在a n与a n+1之间插入n个数,使这n+2个数组成一个公差为d n的等差数列.(I)求证:1d1+1d2+1d3+⋯+1d n<1516(n∈N+)(II)在数列{d n}中是否存在三项d m,d k,d p(其中m,k,p成等差数列)成等比数列.20. 已知函数f(x)=x3+x2−ax(a∈R).(1)当a=0时,求与直线x−y−10=0平行,且与曲线y=f(x)相切的直线的方程;(2)求函数g(x)=f(x)x−alnx(x>1)的单调递增区间;(3)如果存在a∈[3, 9],使函数ℎ(x)=f(x)+f′(x)(x∈[−3, b])在x=−3处取得最大值,试求b的最大值.三、数学附加题(本试卷共40分,考试时间30分钟).(一)【选做题】在21、22、23、24四小题中只能选做2题,每小题10分.请在答题纸指定的区域内作答,解答应写出文字说明、证明过程或演算步骤.【选修4-1:几何证明选讲】21. 如图,AB为圆O的切线,A为切点,过线段AB上一点C作圆O的割线,CED(E在C、D之间),若∠ABE=∠BDE,求证:C为线段AB的中点.【选修4-2:矩阵与变换】22. 求曲线C:xy=1在矩阵M=[11−11]对应的变换作用下得到的曲线C1的方程.【选修4-4:极坐标系与参数方程】23. 在极坐标系中,已知圆C:ρ=2√2cosθ和直线l:θ=π4(ρ∈R)相交于A、B两点,求线段AB的长.【选修4-5:不等式选讲】24. 已知a,b都是正实数,且a+b=2,求证:a2a+1+b2b+1≥1.(二)【必做题】第25题、26题每题10分,共计20分,解答应写出文字说明、证明过程或演算步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京市2011届高三第一次模拟考试(数学)2011.01
参考公式:
1.样本数据12,,,nxxx的方差2211()niisxxn,其中x是这组数据的平均数。
2.柱体、椎体的体积公式:1,3VShVSh柱体椎体,其中S是柱(锥)体的底面面积,h是高。
一、填空题:(5分×14=70分)
1.函数22yxx的定义域是 .
2.已知复数z满足(2)1zii(i为虚数单位),则z的模为 .
3.
已知实数,xy满足20,0,1,xyxyx则2zxy的最小值是 .
4.如图所示的流程图,若输入的9.5x,则输出的结果为 .
5.在集合2,3A中随机取一个元素m,在集合1,2,3B中随机取一个元
素n,得到点(,)Pmn,则点P在圆229xy内部的概率为 .
6.已知平面向量,ab满足||1,||2ab,a与b的夹角为3,以,ab为邻边
作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 .
7.为了分析某篮球运动员在比赛中发挥的稳定程度,统计了该运动员在6场比赛中的
得分,用茎叶图表示如图所示,则该组数据的方差为 .
8.在△ABC中,角A、B、C所对的边分别为a、b、c,若tan21tanAcBb,则角A的大小为 .
9.已知双曲线C:22221(0,0)xyabab的右顶点、右焦点分别为A、F,它的左准线与x轴的交
点为B,若A是线段BF的中点,则双曲线C的离心率为 .
10.已知正数数列na对任意,pqN,都有pqpqaaa,若24a,则9a= .
11.已知,lm是两条不同的直线,,是两个不同的平面。下列命题:
①若,,||,||,lmlm则||; ②若,||,,llm则||lm;
③若||,||,l则||l; ④若,||,||,lml则m.
其中真命题是 (写出所有真命题的序号).
12.已知2()log(2)fxx,若实数,mn满足()(2)3fmfn,则mn的最小值是 .
13. 在△ABC中,已知BC=2,1ABAC,则△ABC面积的最大值是 .
14.若直角坐标平面内两点P、Q满足条件:①P、Q都在函数()fx的图象上;②P、Q关于原
点对称,则称点对(P,Q)是函数()fx的一个“友好点对”(点对(P,Q)与(Q,P)看
作同一个“友好点对”).已知函数2241,0,()2,0,xxxxfxxe则()fx的“友好点对”有 个.
二、解答题:(本大题共6小题,共计90分).
15.(本题满分14分)
已知函数()2sin()(0,0)fxx的最小正周期为,且()24f.
(1)求,的值;(2)若6()(0)25f,求cos2的值。
16. (本题满分14分)
如图,在棱长均为4的三棱柱111ABCABC中,D、1D分别是
BC和11BC的中点.
(1)求证:11AD∥平面1ABD;
(2)若平面ABC⊥平面11BCCB,160OBBC,求三棱锥1BABC的体积。
17. (本题满分14分)
如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点
A、B在直径上,点C、D在圆周上。
(1)怎样截取才能使截得的矩形ABCD的面积最大?并求最
大面积;
(2)若将所截得的矩形铝皮ABCD卷成一个以AD为母线的
圆柱形罐子的侧面(不计剪裁和拼接损耗),应怎样截取,才
能使做出的圆柱形形罐子体积最大?并求最大面积.
18. (本题满分16分)
在直角坐标系xOy中,中心在原点O,焦点在x轴上的椭圆C上的点(22,1)到两焦
点的距离之和为43.
(1)求椭圆C 的方程;(2)过椭圆C 的右焦点F作直线l与椭圆C分别交于A、B两点,
其中点A在x轴下方,且3AFFB.求过O、A、B三点的圆的方程.
19. (本题满分16分)
将数列na中的所有项按每一行比上一行多两项的规则排成如下数表:
1
234
56789
a
aaa
aaaaa
已知表中的第一列数125,,,aaa构成一个等差数列,记为nb,且254,10bb.表
中每一行正中间一个数137,,,aaa构成数列nc,其前n项和为nS.
(1)求数列nb的通项公式;
(2)若上表中,从第二行起,每一行...中的数按从左到右的顺序均构成等比数列,公比
为同一个正数,且131a.①求nS;②记|(1),nMnncnN,若集合M的元素
个数为3,求实数的取值范围.
20. (本题满分16分)
已知函数()1ln()fxxaxaR.
(1)若曲线()yfx在1x处的切线的方程为330xy,求实数a的值;
(2)求证:()fx≥0恒成立的充要条件是1a;
(3)若0a,且对任意12,(0,1]xx,都有121211|()()|4||fxfxxx,求实数
a
的取值范围.
南京市2011届高三第一次模拟考试 数学附加题 2011.01
21.【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
A.选修4-1:几何证明选讲
如图,AB是半圆O的直径,C是圆周上一点(异于A、
B),过C作圆O的切线l,过A作直线l的垂线AD,垂足为
D,AD交半圆于点E.求证:CB=CE.
B. 选修4-2:矩阵与变换
在平面直角坐标系xOy中,直线20xy在矩阵
14a
Mb
对应的变换作用下得到直线:40mxy,求实数,ab的值.
C. 选修4-4:坐标系与参数方程
在极坐标系中,圆C:10cos和直线:3cos4sin300l相交于A、B
两点,求线段AB的长.
D.选修4-5:不等式选讲
解不等式|24|4||xx.
【必做题】第22题、第23题,每题10分,共计20分.
22.如图,在直三棱柱111ABCABC中,190,30,1,6OOACBBACBCAA,
M是1CC的中点.
(1)求证:11ABAM;
(2)求二面角BAMC的平面角的大小.
23.已知等比数列na的首项12a,公比3q,nS是它的前n项和.求证:131nnSnSn.
