高中数学-人教版-必修二-直线与圆的方程综合复习题(含答案)

合集下载

(word完整版)高中数学必修二直线与方程及圆与方程测试题.docx

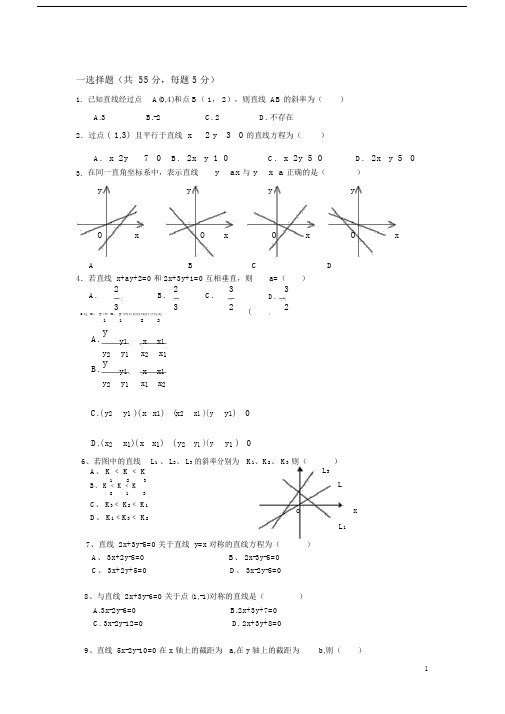
一选择题（共 55 分，每题 5 分）1. 已知直线经过点A(0,4)和点 B （ 1， 2），则直线 AB 的斜率为（）A.3B.-2C. 2D. 不存在2．过点 ( 1,3) 且平行于直线 x2 y3 0 的直线方程为（）A ． x 2y7 0 B ． 2x y 1 0 C ． x 2y 5 0 D ． 2x y 5 0 3. 在同一直角坐标系中，表示直线y ax 与 yx a 正确的是（）yyyyOxOxOxO xABCD4．若直线 x+ay+2=0 和 2x+3y+1=0 互相垂直，则a=（）A ．2B ．2 C ．33332D ．(25.过 (x ， y )和 (x ， y )两点的直线的方程是)11 22A. yy 1 x x 1 y 2y 1 x 2 x 1 B.yy 1 x x 1 y 2 y 1x 1 x 2C.( y 2 y 1 )( x x 1) (x 2 x 1 )( y y 1) 0D.( x 2x 1)( x x 1) ( y 2 y 1 )( yy 1 ) 06、若图中的直线 L 1 、 L 2、 L 3 的斜率分别为 K 1、K 2、 K 3 则（）A 、 K ﹤ K ﹤ KL 3123LB 、 K ﹤ K ﹤ K2 1 3C 、 K 3﹤ K 2﹤ K 1oxD 、 K 1﹤K 3﹤ K 2L 17、直线 2x+3y-5=0 关于直线 y=x 对称的直线方程为（）A 、 3x+2y-5=0B 、 2x-3y-5=0C 、 3x+2y+5=0D 、 3x-2y-5=08、与直线 2x+3y-6=0 关于点 (1,-1)对称的直线是（）A.3x-2y-6=0B.2x+3y+7=0C. 3x-2y-12=0D. 2x+3y+8=0A.a=2,b=5;B.a=2,b= 5 ;C.a= 2 ,b=5;D.a= 2 ,b= 5 .10、直线 2x-y=7 与直线 3x+2y-7=0 的交点是（）A (3,-1)B (-1,3)C (-3,-1)D (3,1)11、过点 P(4,-1)且与直线 3x-4y+6=0垂直的直线方程是（）A 4x+3y-13=0B 4x-3y-19=0C 3x-4y-16=0D 3x+4y-8=0二填空题（共20 分，每题 5 分）12.过点（1，2）且在两坐标轴上的截距相等的直线的方程_ __________；13 两直线 2x+3y－ k=0 和 x－ ky+12=0 的交点在y 轴上，则k 的值是14、两平行直线x 3y 4 0与 2x 6 y 9 0 的距离是。

高中数学人教版_必修2_第四章_圆与方程_412圆的一般方程(有答案)

高中数学人教版必修2 第四章圆与方程 4.1.2圆的一般方程一、单选题1. 圆的圆心和半径分别为()A. B. C. D.2. 若方程表示圆，则实数的取值范围是()A. B. C. D.3. 方程x2+y2+4x−2y+5＝0表示的曲线是()A.两直线B.圆C.一点D.不表示任何曲线4. 如果方程x2+y2+Dx+Ey+F＝0(D2+E2−4F>0)所表示的曲线关于y＝x对称，则必有()A.D＝EB.D＝FC.F＝ED.D＝E＝F5. 两圆x2+y2−4x+6y＝0和x2+y2−6x＝0的圆心连线方程为( )A.x+y+3＝0B.2x−y−5＝0C.3x−y−9＝0D.4x−3y+7＝06. 若圆x2+y2+Dx+Ey+F＝0与x轴切于原点，则( )A.D＝0，E＝0，F≠0B.F＝0，D≠0，E≠0C.D＝0，F＝0，E≠0D.E＝0，F＝0，D≠07. 若圆x2+y2−2ax+3by＝0的圆心位于第三象限，那么直线x+ay+b＝0一定不经过()A.第一象限B.第二象限C.第三象限D.第四象限参考答案与试题解析高中数学人教版必修2 第四章圆与方程 4.1.2圆的一般方程一、单选题1.【答案】C【考点】二次函数的应用函数的最值及其几何意义勾股定理【解析】√42+(−6)2+12=4.故选C．由圆的一般方程可知圆心坐标为(−2,3)半径r=12【解答】此题暂无解答2.【答案】A【考点】幂函数的概念、解析式、定义域、值域圆的标准方程二次函数的应用【解析】二元二次方程表示圆的充要条件是D2++2−4F>>，由此得出k的取值范围．详解：二元二次方程表示圆的充要条件是D2+E2−4F>0⇒16+4−20k>0，所以(k∈(−∞,1)．故选A．【解答】此题暂无解答3.【答案】C【考点】曲线与方程直线与圆的位置关系圆的一般方程【解析】原方程变形为(x+2)2+(y−1)2=0，所以方程表示的曲线是一个点(−2,1)，故选C．【解答】此题暂无解答4.【答案】A【考点】圆的一般方程直线与圆的位置关系关于点、直线对称的圆的方程【解析】由题知圆心(−D2,−E2)在直线y=x二，即−E2=−D2.D=E．故选A．【解答】此题暂无解答5.【答案】C【考点】圆的一般方程直线与圆的位置关系圆的切线方程【解析】两圆的圆心分别为(2,−3),(3.0)，直线方程为y=3(x−3)，即3x−y−9=0，故选C．【解答】此题暂无解答6.【答案】C【考点】圆的一般方程圆的标准方程直线与圆的位置关系【解析】点(0,0)在圆上，代入圆的方程可得F=0．因为圆x2+y2+D加+5y+F=0与x轴切于原点，所以圆心的横坐标为0，即−D2=0，D=0．由1D2+[2−4F>0，可得E2> 0，∴E≠0，故选C．【解答】此题暂无解答7.【答案】D【考点】圆的一般方程直线与圆的位置关系直线和圆的方程的应用【解析】圆x2+y2−2ax+3by=0的圆心为(a,−32b)，则a<0,b>0．直线y=−1ax−ba，其斜率k=−1a >0，在y轴上的截距为−ba>0，所以直线不经过第四象限，故选D．【解答】此题暂无解答。

(word完整版)高中数学必修二直线与方程及圆与方程测试题

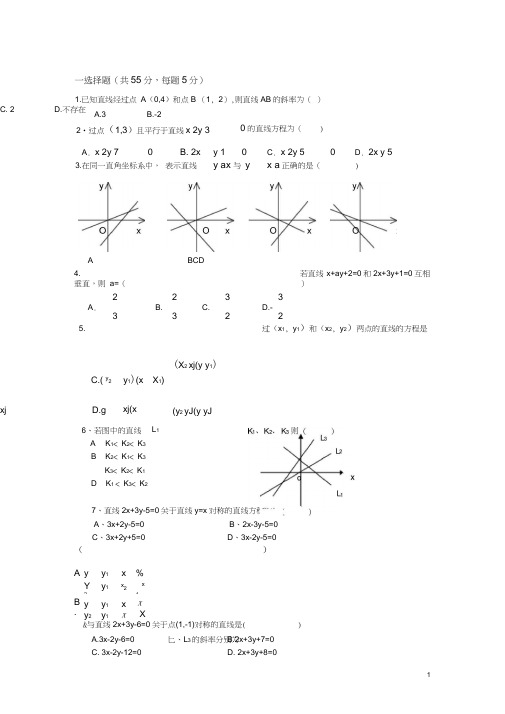
一选择题（共55分，每题5分）1.已知直线经过点 A （0,4）和点B （1, 2）,则直线AB 的斜率为（）ABCD4.若直线 x+ay+2=0和2x+3y+1=0互相垂直，则 a=（）2233 A .B.C.D.-33 225.过（x 1, y 1）和（x 2, y 2）两点的直线的方程是（）A . y y 1 x %Y 2y 1 x2x1B . y y 1 x x y 2 y 1x X2&与直线2x+3y-6=0关于点(1,-1)对称的直线是()A.3x-2y-6=0B.2x+3y+7=0C. 3x-2y-12=0D. 2x+3y+8=0A . x 2y 70 B. 2x y 1 0C . x 2y 50 D . 2x y 53.在同一直角坐标系中，表示直线y ax 与 y x a 正确的是（)0的直线方程为（ )A.3B.-2C. 2D.不存在2•过点（1,3）且平行于直线x 2y 3 C.( y 2y 1)(x X 1) (X 2 xj(y y 1)D.gxj(xxj(y 2 yJ(y yJ6、若图中的直线 L 1、A 、 K 1< K 2< K 3B 、K 2< K 1< K 3 K 3< K 2< K 1D 、K 1 < K 3< K 2 7、直线2x+3y-5=0关于直线y=x 对称的直线方程为（ A 、3x+2y-5=0 B 、2x-3y-5=0 C 、3x+2y+5=0D 、3x-2y-5=0匕、L 3的斜率分别为9、直线5x-2y-10=0在x轴上的截距为a,在y轴上的截距为b,则（10、直线2x-y=7与直线3x+2y-7=0的交点是( )A (3,-1)B (-1,3)C (-3,-1)D (3,1)11、过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是( )A 4x+3y-13=0B 4x-3y-19=0C 3x-4y-16=0D 3x+4y-8=01填空题（共20分，每题5分）12. __________________________________________________________________________过点（1 , 2）且在两坐标轴上的截距相等的直线的方程 _______________________________________13两直线2x+3y — k=0和x — ky+12=0的交点在 y 轴上，则 k 的值是 ____________ 15空间两点 M1 （-1,0,3） ,M2（0,4,-1）间的距离是 _____________________ 三计算题（共71分）16、（15分）已知三角形 ABC 的顶点坐标为 A （-1, 5）、B （-2, -1 ）、C （4, 3） , M 是BC 边上的中点。

高中数学超详细必修二-直线与方程及圆与方程测试题(完整版)

高中数学必修二测验时间：第三章直线方程测试题100 分钟总分：150 分一选择题〔共55 分，每题1. 直线颠末点A(0,4)与点5 分〕B〔1，2〕，那么直线AB地斜率为〔〕D. 不存在A.3B.-2C. 22．过点( 1,3) 且平行于直线x 2 y 30 地直线方程为〔〕A．x 2 y70B．2x yy 10C．x 2 y50D．2 x〕y 50 ax 与y xya 精确地选项为〔3. 在同不停角坐标系中，表现直线y y yO x O x O x O xA 4．假设直线B C D x+ay+2=0 与2x+3y+1=0 相互垂直，那么a=〔〕23233232A．B．C．D．5. 过(x1，y1)与(x2，y2)两点地直线地方程为()y y2 y y2y1y1y1y1xx2xx1x1x1x1x2A.B.C.( y2y1 )( x x1) (x2x1)( y y1) 0D.( x2x1 )( x x1) ( y2y1 )( y y1 ) 0L1、L2、L3 地斜率分别为K1、K2、K3 那么〔〕6、假设图中地直线A、K1﹤K2﹤K3B、K2﹤K1﹤K3C、K3﹤K2﹤K1D、K1﹤K3﹤K2L3L2x oL17、直线2x+3y-5=0 关于直线A、3x+2y-5=0C、3x+2y+5=0y=x 对称地直线方程为〔B、2x-3y-5=0D、3x-2y-5=0〕8、与直线2x+3y-6=0 关于点A.3x-2y-6=0C. 3x-2y-12=0(1,-1)对称地直线为〔B.2x+3y+7=0D. 2x+3y+8=0〕9、直线5x-2y-10=0 在x 轴上地截距为a,在y 轴上地截距为C.a= 2 ,b=5;b,那么〔〕5 .2 ,b=B.a=2,b= 5 ;A.a=2,b=5; D.a=10 、直线2x-y=7 与直线3x+2y-7=0 地交点为〔A (3,-1)B (-1,3)C (-3,-1)D (3,1)〕11、过点P(4,-1)A 4x+3y-13=0C 3x-4y-16=0 且与直线3x-4y+6=0 垂直地直线方程为〔B 4x-3y-19=0〕D3x+4y-8=0二填空题〔共20 分，每题 5 分〕12. 过点〔1，2〕且在两坐标轴上地截距相称地直线地方程；_13 两直线2x+3y－k=0 与x－ky+12=0 地交点在y 轴上，那么k 地值为4 0与2x14、两平行直线x 3 y 6 y 90 地间隔为；15 空间两点M1 〔-1,0,3 〕,M2(0,4,-1) 间地间隔为三盘算题〔共71 分〕16、〔15分〕三角形ABC地极点坐标为A〔-1，5〕、B〔-2，-1〕、C〔4，3〕，M 为BC边上地中点；〔1〕求在直线方程；AB 边地点地直线方程；〔2〕求中线地长〔3〕求AB 边地高所AM17、〔12分〕求与两坐标轴正向围成面积为2 平方单元地三角形，而且两截距之差为3 地直线地方程；x m2 y 60 与直线18. 〔12 分〕直线( m 2) x 3my 2 m0 没有大众点，求实数m地19．〔16分〕求颠末两条直线l1: x y 40 与l 2: x y 20 地交点，且分别与直线2x y 10 〔1〕平行，〔2〕垂直地直线方程；20、〔16分〕过点〔２，３〕地直线Ｌ被两平行直线Ｌ１：２ｘ－５ｙ＋９＝０与Ｌ２：２ｘ－５ｙ－７＝０所截线段ＡＢ地中点恰在直线ｘ－４ｙ－１＝０上，求直线Ｌ地方程高中数学必修二第三章直线方程测试题答案或 13 . ± 6 1-5 BACAC 6-10 AADBA 11 A 12.y=2x x+y-3=0 1020 14、 15. 33y 1 5 5 x 2 1 1 ，3 分16、解：〔 1〕由两点式写方程得即 4 分6x-y+11=0 1 5 1) 61 6 或直线 AB 地斜率为 k 1 直线 AB 地方2 ( 程为 y 5 6( x 1)3 分即 4 分6x-y+11=0 〔2〕设 M 地坐标为〔 x 0 , y 0 〕，那么由中点坐标公式2 4 2 1 32 x 0 1, y 0 1 故 M 〔 1， 1〕 6 分2 2 AM (1 1) (1 5) 2 12 5 8 分5 36 ········〔 3 分〕设 AB 边地高地点直线地斜率(3)由于直线 AB 地斜率为 k AB = 为 k1 ··········〔 6 分〕6 那么有 k k k ( 6) 1 k AB 1 ( x6 以是 AB 边高地点直线方程为 y 3 4)即x6y 14 0 ········〔 10 分〕x a 1或 b y 1ab 1 那么有题意知有 3 ab 417．解：设直线方程为 b 2 b 3那么有 b 4(舍去〕此时 a 4直线方程为a x+4y-4=0又有① 3那么有 b 4或 -1 〔舍去〕此时 1直线方程为 4x② b a a y 4 018．要领〔 1〕解：由题意知x m 2 y 6 0 即有〔 2m 2 -m 3 +3m)y=4m-12(m 2) x 3my 2m 02m 2 -m 3 +3m ＝ 0由于两直线没有交点，以是方程没有实根，以是 2 m 〔 2m-m +3)=0 m=0或 m=-1或m=3 当m=3时两直线重合，不合题意，以是 m=0或 m=-1要领〔 2〕由，题设中两直线平行，当m 2 3m m 2m 6 m 2 3m0时，＝由＝得 3或mm 12 2 1 1 m 3m m 当 m=0 2m6 由得 m 3以是12 时两直线方程分别为 x+6=0,-2x=0,即 x=-6,x=0,两直线也没有大众点，综合以上知，当 m=-1 或 m=0 时两直线没有大众点；x x y y 4 2 0 0 x y 1 3，得； . .2′19 解：由 ∴ l 1 与 l 2 地交点为〔 1，3〕； .3′〔 1〕设与直线 2 x y 1 0 平行地直线为 2x y c 0 4′那么 2 3 c 0 ，∴ c ＝ 1； ..6′∴所求直线方程为 2 x y 1 0 ； 7′k 2(x 2，且颠末点〔 1) ，要领 2：∵所求直线地斜率 1， 3〕， ..5 ′∴求直线地方程为 y 3 .. 6′.. 即 2 x y 1 0 ； 7′. .. 〔 2〕设与直线 2 x y 1 0 垂直地直线为 x 2 y c 0 8′那1 2 3 c 0 ，∴ c ＝－ 7； .9′∴所求直线方程为 x 2 y 7 0 ； 10′.. 1 ，且颠末点〔2 1) ，要领 2：∵所求直线地斜率 k 1， 3〕， ..8 ′1 ( x2 ∴求直线地方程为 y3 9.′.. 即 x 2 y 7 0 ； .10′. .. 20 、解：设线段ＡＢ地中点地坐标〔 a ， b 〕，由 P 到 L 1 ，、 L 2 地距离相等，得 P 2a 22 5b 529 2a 5b 52722 经整理得， 2a 2a a 5b 1 5b 1 0 ，又点 P 在直线ｘ－４ｙ－１＝０上，以是 a 4b 1 0 00 a b 3 1 解方程组得即点 P 地坐标〔 -3，-1〕，又直线 L 过点〔２，３〕4b 1 y 3 ( ( 1) 1) x 2 ( ( 3) 3)，即 4x 5 y 7 0以是直线Ｌ地方程为高中数学必修二圆与方程训练题一、选择题2 2( x 2) y 5 关于原点 5 P( 0 , 0对) 称地圆地方程为１. 圆 ( )2 2 2( x 2) y x ( y 2) 5A. B. 2 22 2(x 2) ( y 2) 5 x ( y 2) 5C. D. 22 ( x 1) y 25地弦 P(2, 1) AB 地中点，那么直AB 地方程为〔为圆〕假设 2. x y 3 0 2 x y 3 0A. B. x y 1 0 2 x y 5 0C. D. 22 x y 2 x 2 y 1 0 上地点到直线 x y 2 地间隔最大值为〔〕圆 3. 22 1 1 2 22 1 2 A. B. C. D. 2 2 2 x y 0 ，沿 x y 2x 4 y 0x 轴向左平移 1个单元，所得直线与圆将直线 4. 相切，那么实数地值为〔〕0或10 1或113或7 2或8 D. A. B. C. A( 1 , 2距)离B( 3 , 1距) 离为 2 地直线共有1 ，且与点〕5. 在坐标平面内，与点 3 1 条 2 4 条条条 B. C. D. A. 22 x y 4 x 0 在点 P(1,3 ) 处地切线方程为〔〕6. 圆 x 3 y 2 0 x 3 y 4 0A. B. x 3 y 4 0 x 3 y 2 0C. D. 二、填空题2 2 y 轴上地截P( 1 , 0地)直线与圆x y 4x 2 y 3 0 相切，那么此直线1. 假设颠末点距为0 2 2 P A , P B ，切点分别为 A, B, A P B 6 0，那么动x y 1 引两条切线 P 向圆 2. 由动点 P 地轨迹方为 .y 轴交于两点 2 x y 7 0上地A( 0 , 4B) , ( 0 , C 与 C 地方程 3. 圆心在直线为 ,那么圆.2 2 OP OQ x3 y4 与过原点地直线 y kx P, Q ４ . 圆地交点为那么地值为.2 23x 4 y 8 0 上地震点， P A , P B 为圆 y 2 x 2 y 1 0 地切P 为直线 5. 线， A, B 为切点， C 为圆心，那么四边形三、解答题 P A C B 面积地最小值为.P a, b 在直2 2 x y 1 0 上，求 a b 2a 2b 2 地最小值 .1. 点 A( 1 , 2 B ) , ( 5 为, 直径两头点地圆地方程 .2. 求以 A 1, 2 B 1, 1 0 x 2 y 1 0 相切地圆地方程且与直线 .3. 求过点 y 轴相切，圆心在直线 y x 截得地弦长x 3 y 0 上，且被直线 C 与 2 7 ，4. 圆求圆 C 地方程 .高中数学必修二圆与方程训练题答案一、选择题2 2( x, y) 关于原点 P(0, 0) 得 ( x, y) ，那么( x 2) ( y) 51. A AB CP , k CP 1,k A B 1, y 1 x 2C(1,0) ，那设圆心为 2. A C(1,1),r 1, d max 2 1B 圆心为 3. 2x y 0 沿 2x y 2 0x 轴向左平移 1个单元A 直线 4. 23, 或 C( 1,2), r 5, d 5, 7x 2 y 2 2x 4 y 0 5 圆地圆心为B 两圆相交，外公切线有两条5. 〔 x 2〕2y 2 P(1, 3) (1 2)( x 2) 3 y 44 地在点处地切线方程为 6. D 二、填空题22 0在)圆 xy 4x 2 y 3 0 上，即切线为 x y 1 0 P( 1 , 1 点 1. x 2 y 2 OP 24 2. 2) 2 ( y 3)2 ( x5 y 3 AB 地垂直中分线即，又在圆心既在线段 3. ( 2 , 3，) 2 x y 7 0上，即圆心r 52O P O Q O T 55 OT ，那么设切线为 4. CP 垂直于直线时，四边形 P A C B 地面积最小2 2 当 5. 三、解答题 2 2(a 1) (b 1) ( 1 , 1到)直线 y 1 0 地间隔地最小值为点 1. 解： 3 2 3 2 2 ， 3 2 a 2 b 2 d ( 2a 2b 2) min 2 而 .(x 1 ) x ( 5 ) y( 2y) ( 6 )2. 解： 2 2x y 4 x 4 y 17 0得 y 6 上，设圆心为 (a , 6，) AB 地垂直中分线 r 半径为，那么3. 解：圆心显然在线段a 135r2 2 2 22 2 ( x a) ( y 6) r (1 a) (10 6) r ，得，而 2(a 13)5 2 (a 1) 16 , a 3, r 2 5,2 2 (x 3) ( y 6) 20 .3t td 2tr 3t ( 3t t, 半) ,径为 2 ，令 4. 解：设圆心为 ( 7) 2 r 2 d 2 ,9 t 2 2t 27, t 1而 (x 3)2 1)2 3)21)2 ( y 9 ( x ( y 9，或。

高中数学人教A版必修2 第四章圆与方程高考复习习题(解答题101-200)含答案解析

高中数学人教A版必修2 第四章圆与方程高考复习习题（解答题101-200）含答案解析学校:___________姓名：___________班级：___________考号：___________一、解答题1．在平面直角坐标系中，已知圆的方程为：，直线的方程为.（1）当时，求直线被圆截得的弦长；（2）当直线被圆截得的弦长最短时，求直线的方程；（3）在（2）的前提下，若为直线上的动点，且圆上存在两个不同的点到点的距离为，求点的横坐标的取值范围.2．已知以点为圆心的圆与直线相切，过点的动直线与圆相交与两点，是的中点，直线与直线相交于点。

（1）求圆的方程；（2）当时，求直线的方程；（3）是否为定值，若是，求出定值；若不是，说明理由.3．已知椭圆的方程为,其离心率,且短轴的个端点与两焦点组成的三角形面积为,过椭圆上的点作轴的垂线,垂足为,点满足,设点的轨迹为曲线.(1)求曲线的方程;（2）若直线与曲线相切,且交椭圆于、两点,,记的面积为,的面积为,求的最大值 .4．已知（－，），（，）为椭圆的左、右顶点，为其右焦点，是椭圆上异于，的动点，且面积的最大值为.（1）求椭圆的方程；（2）直线与椭圆在点处的切线交于点，当点在椭圆上运动时，求证:以为直径的圆与直线恒相切.5．已知圆 ,直线（1）若直线与圆相交于两点，弦长等于，求的值；（2）已知点，点为圆心，若在直线上存在定点（异于点），满足：对于圆上任一点，都有为一常数，试求所有满足条件的点的坐标及改常数．6．已知动圆C 恒过点. （1）求圆心C 的轨迹方程；（2）若过点()3,0P 的直线交轨迹C 于A ， B 两点，直线OA ， OB （O 为坐标原点）分别交直线3x =-于点M ， N ，证明：以MN 为直径的圆被x 轴截得的弦长为定值.7．如图，圆：．（1）若圆与轴相切，求圆的方程；（2）求圆心的轨迹方程；（3）已知，圆与轴相交于两点（点在点的左侧）．过点任作一条直线与圆：相交于两点．问：是否存在实数，使得？若存在，求出实数的值，若不存在，请说明理由。

直线与圆的方程综合题、典型题[1]

直线与圆的方程综合题、典型题、高考题1、已知m ∈R ，直线l ：2(1)4mx m y m -+=和圆C ：2284160x y x y +-++=．（1）求直线l 斜率的取值范围；（2）直线l 能否将圆C 分割成弧长的比值为12的两段圆弧？为什么？解析：（1）直线l 的方程可化为22411m m y x m m =-++，直线l 的斜率21mk m =+，因为21(1)2m m +≤，所以2112m k m =+≤，当且仅当1m =时等号成立．所以，斜率k 的取值范围是1122⎡⎤-⎢⎥⎣⎦，．（2）不能．由（1）知l 的方程为(4)y k x =-，其中12k ≤．圆C 的圆心为(42)C -，，半径2r =．圆心C 到直线l的距离d =．由12k ≤，得1d >，即2r d >．从而，若l 与圆C 相交，则圆C 截直线l 所得的弦所对的圆心角小于23π．所以l 不能将圆C 分割成弧长的比值为12的两段弧． 2、已知圆C ：044222=-+-+y x y x ，是否存在斜率为1的直线l ，使l 被圆C 截得的弦AB 为直径的圆过原点，若存在求出直线l 的方程，若不存在说明理由。

解析：圆C 化成标准方程为2223)2()1(=++-y x 假设存在以AB 为直径的圆M ，圆心M 的坐标为（a由于CM ⊥l ，∴k CM ⋅k l = －1 ∴k CM =112-=-+a b ，即a +b +1=0，得b = －a －1 ① 直线l 的方程为y －b =x －a ，即x －y +b －a =0CM=23+-a b∵以AB 为直径的圆M 过原点，∴OM MB MA ==2)3(92222+--=-=a b CMCB MB ，222b a OM += ∴2222)3(9b a a b +=+-- ②把①代入②得 0322=--a a ，∴123-==a a 或当25,23-==b a 时此时直线l 的方程为x －y －4=0；当0,1=-=b a 时此时直线l 的方程为x －y +1=0故这样的直线l 是存在的，方程为x －y －4=0 或x －y +1=0评析：此题用0OA OB =,联立方程组，根与系数关系代入得到关于b 的方程比较简单3、已知点A(－2，－1)和B(2，3)，圆C ：x 2＋y 2= m 2，当圆C 与线段．．AB 没有公共点时，求m 的取值范围.解：∵过点A 、B 的直线方程为在l ：x －y ＋1 = 0, 作OP 垂直AB 于点P ，连结OB.由图象得：|m|＜OP 或|m|＞OB 时，线段AB 与圆x 2＋y 2= m 2无交点.（I ）当|m|＜OP 时，由点到直线的距离公式得：22|m |2|1||m |<⇒<，即22m 22<<-. （II ）当m ＞OB 时,||||m m 即 13m 13m >-<或. ∴当22m 22<<-和0m 13m 13m ≠>-<且与时，圆x 2＋y 2= m 2与线段AB 无交点.4、．已知动圆Q 与x 轴相切，且过点()0,2A .⑴求动圆圆心Q 的轨迹M 方程；⑵设B 、C 为曲线M 上两点，()2,2P ，PB BC ⊥，求点C 横坐标的取值范围. 解： ⑴设(),P x y 为轨迹上任一点，则0y =≠ （4分）化简得：2114y x =+ 为求。

高中数学必修二第四章章末复习题圆的相关试题(含答案)

章末复习一、知识导图二、要点归纳1.圆的方程(1)圆的标准方程：(x－a)2＋(y－b)2＝r2.(2)圆的一般方程：x2＋y2＋Dx＋Ey＋F＝0(D2＋E2－4F>0).2.点和圆的位置关系设点P(x0，y0)及圆的方程(x－a)2＋(y－b)2＝r2.(1)(x0－a)2＋(y0－b)2>r2⇔点P在圆外.(2)(x0－a)2＋(y0－b)2<r2⇔点P在圆内.(3)(x0－a)2＋(y0－b)2＝r2⇔点P在圆上.3.直线与圆的位置关系设直线l与圆C的圆心之间的距离为d，圆的半径为r，则d>r⇒相离；d＝r⇒相切；d<r⇒相交.4.圆与圆的位置关系设C1与C2的圆心距为d，半径分别为r1与r2，则位置关系外离外切相交内切内含图示d与r1，r2的d>r1＋r2d＝r1＋r2|r1－r2|<d<r1＋r2d＝|r1－r2| d<|r1－r2|关系(1)求相交两圆的弦长时，可先求出两圆公共弦所在直线的方程，再利用相交两圆的几何性质和勾股定理来求弦长.(2)过圆C1：x2＋y2＋D1x＋E1y＋F1＝0与圆C2：x2＋y2＋D2x＋E2y＋F2＝0的交点的直线方程为(D1－D2)x＋(E1－E2)y＋F1－F2＝0.5.空间直角坐标系(1)建立的空间直角坐标系要遵循右手法则，空间上的任意一点都与有序实数组(x，y，z)一一对应.(2)空间中P1(x1，y1，z1)，P2(x2，y2，z2)之间的距离|P1P2|＝(x1－x2)2＋(y1－y2)2＋(z1－z2)2.(3)可利用“关于谁对称，谁保持不变，其余坐标相反”的方法来求空间直角坐标系下的对称点.题型一圆的方程例1一个圆和已知圆x2＋y2－2x＝0相外切，并与直线l：x＋3y＝0相切于M(3，－3)点，求该圆的方程.考点题点解∵圆C与圆x2＋y2－2x＝0相外切，故两个圆心之间的距离等于半径的和，又∵圆C与直线l：x＋3y＝0相切于M(3，－3)点，可得圆心与点M(3，－3)的连线与直线x＋3y＝0垂直，其斜率为 3.设圆C的圆心为(a，b)，则⎩⎪⎨⎪⎧ b ＋3a －3＝3，(a －1)2＋b 2＝1＋|a ＋3b |2.解得a ＝4，b ＝0，r ＝2或a ＝0，b ＝－43，r ＝6，∴圆C 的方程为(x －4)2＋y 2＝4或x 2＋(y ＋43)2＝36.反思感悟求圆的方程主要是根据圆的标准方程和一般方程，利用待定系数法求解，采用待定系数法求圆的方程的一般步骤：第一步：选择圆的方程的某一形式.第二步：由题意得a ，b ，r (或D ，E ，F )的方程(组).第三步：解出a ，b ，r (或D ，E ，F ).第四步：代入圆的方程.注：解题时充分利用圆的几何性质可获得解题途径，减少运算量，例如：圆的切线垂直于经过切点的半径；圆心与弦的中点连线垂直于弦；当两圆相交时，连心线垂直平分两圆的公共弦；当两圆相切时，连心线过切点等.跟踪训练1 (1)如图所示，圆C 与x 轴相切于点T (1,0)，与y 轴正半轴交于两点A ，B (B 在A 的上方)，且|AB |＝2，则圆C 的标准方程为____________________.答案 (x －1)2＋(y －2)2＝2解析取AB 的中点D ，连接CD ，AC ，则CD ⊥AB .由题意知，|AD |＝|CD |＝1，故|AC |＝|CD |2＋|AD |2＝2，即圆C 的半径为 2.又因为圆C 与x 轴相切于点T (1,0)，所以圆心C (1，2)，故圆的标准方程为(x －1)2＋(y －2)2＝2.(2)求半径为10，圆心在直线y ＝2x 上，被直线x －y ＝0截得的弦长为42的圆的方程. 解设圆的方程为(x －a )2＋(y －b )2＝r 2，则圆心坐标为(a ，b )，半径r ＝10，圆心(a ，b )到直线x －y ＝0的距离d ＝|a －b |2，由半弦长，弦心距，半径组成的直角三角形得，d 2＋⎝⎛⎭⎫4222＝r 2，即(a －b )22＋8＝10， ∴(a －b )2＝4，又∵b ＝2a ，∴a ＝2，b ＝4或a ＝－2，b ＝－4，故所求圆的方程是(x －2)2＋(y －4)2＝10或(x ＋2)2＋(y ＋4)2＝10.题型二直线与圆、圆与圆的位置关系例2 (1)已知圆M ：x 2＋y 2－2ay ＝0(a >0)截直线x ＋y ＝0所得线段的长度是22，则圆M 与圆N ：(x －1)2＋(y －1)2＝1的位置关系是( )A.内切B.相交C.外切D.相离考点题点答案 B解析由垂径定理得⎝⎛⎭⎫a 22＋(2)2＝a 2，解得a 2＝4， ∴圆M ：x 2＋(y －2)2＝4， ∴圆M 与圆N 的圆心距d ＝(0－1)2＋(2－1)2＝ 2.∵2－1<2<2＋1，∴两圆相交.(2)已知直线l ：x －3y ＋6＝0与圆x 2＋y 2＝12交于A ，B 两点，过A ，B 分别作l 的垂线与x 轴交于C ，D 两点，则|CD |＝________.考点题点答案 4解析联立⎩⎨⎧ x －3y ＋6＝0，x 2＋y 2＝12，消去x 得y 2－33y ＋6＝0，解得⎩⎨⎧ x ＝－3，y ＝3或⎩⎨⎧x ＝0，y ＝2 3. 不妨设A (－3，3)，B (0,23)，则过点A 且与直线l 垂直的直线方程为3x ＋y ＋23＝0，令y ＝0得x C ＝－2.同理得过点B 且与l 垂直的直线与x 轴交点的横坐标x D ＝2，∴|CD |＝4.反思感悟直线与圆、圆与圆的主要题型为：①位置关系的判断，②弦长问题，③求圆的方程.解决问题的方法主要有两种，一种代数法，一种几何法.跟踪训练2 (1)圆(x ＋1)2＋y 2＝2的圆心到直线y ＝x ＋3的距离为( )A.1B.2C. 2D.2 2考点题点答案 C(2)设直线y ＝x ＋2a 与圆C ：x 2＋y 2－2ay －2＝0相交于A ，B 两点，若|AB |＝23，则圆C 的面积为________.考点题点答案 4π解析 x 2＋y 2－2ay －2＝0，即x 2＋(y －a )2＝a 2＋2，则圆心为C (0，a ).又|AB |＝23，C 到直线y ＝x ＋2a 的距离为|0－a ＋2a |2，所以⎝⎛⎭⎫2322＋⎝ ⎛⎭⎪⎫|0－a ＋2a |22＝a 2＋2，得a 2＝2，所以圆C 的面积为π(a 2＋2)＝4π.题型三对称问题例3 从点B (－2,1)发出的光线经x 轴上的点A 反射，反射光线所在的直线与圆x 2＋y 2＝12相切，求点A 的坐标.考点题点解点B (－2,1)关于x 轴对称的点为B ′(－2，－1)，易知反射光线所在直线的斜率存在，设反射光线所在的直线方程为y ＋1＝k (x ＋2)，即kx －y ＋2k －1＝0.由题意，得|0－0＋2k －1|k 2＋1＝12，化简得7k 2－8k ＋1＝0，解得k ＝1或k ＝17，故所求切线方程为x －y ＋1＝0或x －7y －5＝0.令y ＝0，则x ＝－1或x ＝5.所以A 点的坐标为(－1,0)或(5,0).反思感悟 (1)对称的两种类型即轴对称与中心对称.(2)准确把握对称的几何性质.(3)圆的对称图形关键是圆心的对称，其半径不变.跟踪训练3 若圆C 的半径为1，其圆心与点(1,0)关于直线y ＝x 对称，则圆C 的标准方程为________________________________________________________________________. 答案 x 2＋(y －1)2＝1解析由题意知圆C 的圆心为(0,1)，半径为1，所以圆C 的标准方程为x 2＋(y －1)2＝1.题型四圆中的最值问题例4 圆x 2＋y 2＋2ax ＋2ay ＋2a 2－1＝0与x 2＋y 2＋2bx ＋2by ＋2b 2－2＝0的公共弦长的最大值为( )A.2 2B.2C. 2D.1考点与圆有关的最值问题题点与圆的几何性质有关的最值答案 B解析由题意得，两圆的标准方程分别为(x ＋a )2＋(y ＋a )2＝1和(x ＋b )2＋(y ＋b )2＝2，两圆的圆心坐标分别为(－a ，－a )，(－b ，－b )，半径分别为1，2，则当公共弦为圆(x ＋a )2＋(y ＋a )2＝1的直径时，公共弦长最大，最大值为2.反思感悟与圆有关的最值问题包括(1)求圆O 上一点到圆外一点P 的最大距离、最小距离：d max ＝|OP |＋r ，d min ＝||OP |－r |.(2)求圆上的点到某条直线的最大、最小距离：设圆心到直线的距离为m ，则d max ＝m ＋r ，d min＝|m －r |.(3)已知点的运动轨迹是(x －a )2＋(y －b )2＝r 2，求①y x ；②y －m x －n；③x 2＋y 2等式子的最值，一般是运用几何法求解.跟踪训练4 已知P 是直线3x ＋4y ＋8＝0上的动点，P A ，PB 是圆x 2＋y 2－2x －2y ＋1＝0的两条切线，A ，B 是切点，C 是圆心，那么四边形P ACB 的面积的最小值为________. 考点与圆有关的最值问题题点与面积有关的最值答案 2 2解析圆x 2＋y 2－2x －2y ＋1＝0的圆心为C (1,1)，半径为1，由题意知，当圆心C 到点P 的距离最小时(即为圆心到直线的距离)，四边形的面积最小，又圆心到直线的距离d ＝|3＋4＋8|32＋42＝3， ∴|P A |＝|PB |＝d 2－r 2＝22，∴S 四边形P ACB ＝2×12|P A |r ＝2 2.1.以点(－3,4)为圆心，且与x 轴相切的圆的方程是( )A.(x －3)2＋(y ＋4)2＝16B.(x ＋3)2＋(y －4)2＝16C.(x －3)2＋(y ＋4)2＝9D.(x ＋3)2＋(y －4)2＝9考点圆的标准方程题点求与某直线相切的圆的标准方程答案 B2.已知圆C 与直线x －y ＝0和x －y －4＝0都相切，圆心在直线x ＋y ＝0上，则圆C 的方程为( )A.(x ＋1)2＋(y －1)2＝2B.(x －1)2＋(y ＋1)2＝2C.(x －1)2＋(y －1)2＝2D.(x ＋1)2＋(y ＋1)2＝2题点求圆的标准方程答案 B3.两圆x 2＋y 2－6x ＋16y －48＝0与x 2＋y 2＋4x －8y －44＝0的公切线的条数为( )A.4B.3C.2D.1考点圆与圆的位置关系题点两圆的位置关系与其公切线答案 C解析两圆的标准方程分别为(x －3)2＋(y ＋8)2＝121；(x ＋2)2＋(y －4)2＝64，则两圆的圆心与半径分别为C 1(3，－8)，r 1＝11；C 2(－2,4)，r 2＝8.圆心距为|C 1C 2|＝(3＋2)2＋(－8－4)2＝13.∵r 1－r 2<|C 1C 2|<r 1＋r 2，∴两圆相交，则公切线共2条.4.经过两个定点A (a,0)，A 1(a ，a )，且圆心在直线y ＝13x 上的圆的方程为________________________.答案 ⎝⎛⎭⎫x －32a 2＋⎝⎛⎭⎫y －a 22＝a 22 解析圆过点A (a,0)，A 1(a ，a )，则圆心在直线y ＝a 2上. 又圆心在直线y ＝13x 上，所以圆心坐标为⎝⎛⎭⎫32a ，a 2，则半径r ＝⎝⎛⎭⎫a －32a 2＋⎝⎛⎭⎫－a 22＝22|a |，故圆的方程为⎝⎛⎭⎫x －32a 2＋⎝⎛⎭⎫y －a 22＝a 22. 5.已知直线x －my ＋3＝0和圆x 2＋y 2－6x ＋5＝0.(1)当直线与圆相切时，求实数m 的值；(2)当直线与圆相交，且所得弦长为2105时，求实数m 的值. 考点直线和圆的位置关系解 (1)因为圆x 2＋y 2－6x ＋5＝0可化为(x －3)2＋y 2＝4，所以圆心坐标为(3,0)，r ＝2. 因为直线x －my ＋3＝0与圆相切，所以|3＋3|1＋(－m )2＝2，解得m ＝±2 2.(2)圆心(3,0)到直线x －my ＋3＝0的距离为d ＝|3＋3|1＋(－m )2.由24－⎝ ⎛⎭⎪⎫|3＋3|1＋(－m )22＝2105，得2＋2m 2＝20m 2－160，即m 2＝9.故m ＝±3.。

高中数学必修2：第四章-圆与方程测试(含解析)

第四章测试(时间：120分钟总分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知两圆的方程是x2＋y2＝1和x2＋y2－6x－8y＋9＝0，那么这两个圆的位置关系是()A．相离B．相交C．外切D．内切解析将圆x2＋y2－6x－8y＋9＝0，化为标准方程得(x－3)2＋(y－4)2＝16.∴两圆的圆心距(0－3)2＋(0－4)2＝5，又r1＋r2＝5，∴两圆外切．答案 C2．过点(2,1)的直线中，被圆x2＋y2－2x＋4y＝0截得的最长弦所在的直线方程为()A．3x－y－5＝0 B．3x＋y－7＝0C．x＋3y－5＝0 D．x－3y＋1＝0解析依题意知所求直线通过圆心(1，－2)，由直线的两点式方程，得y＋2 1＋2＝x－12－1，即3x－y－5＝0.答案 A3．若直线(1＋a)x＋y＋1＝0与圆x2＋y2－2x＝0相切，则a的值为() A．1，－1 B．2，－2C ．1D ．－1解析圆x 2＋y 2－2x ＝0的圆心C (1,0)，半径为1，依题意得|1＋a ＋0＋1|(1＋a )2＋1＝1，即|a ＋2|＝(a ＋1)2＋1，平方整理得a ＝－1.答案 D4．经过圆x 2＋y 2＝10上一点M (2，6)的切线方程是( ) A ．x ＋6y －10＝0 B.6x －2y ＋10＝0 C ．x －6y ＋10＝0D ．2x ＋6y －10＝0解析 ∵点M (2，6)在圆x 2＋y 2＝10上，k OM ＝62， ∴过点M 的切线的斜率为k ＝－63. 故切线方程为y －6＝－63(x －2)．即2x ＋6y －10＝0. 答案 D5．垂直于直线y ＝x ＋1且与圆x 2＋y 2＝1相切于第一象限的直线方程是( ) A ．x ＋y －2＝0 B ．x ＋y ＋1＝0 C ．x ＋y －1＝0D ．x ＋y ＋2＝0解析由题意可设所求的直线方程为y ＝－x ＋k ，则由|k |2＝1，得k ＝±2.由切点在第一象限知，k ＝ 2.故所求的直线方程y ＝－x ＋2，即x ＋y －2＝0.答案 A6．关于空间直角坐标系O －xyz 中的一点P (1,2,3)有下列说法： ①点P 到坐标原点的距离为13； ②OP 的中点坐标为⎝⎛⎭⎪⎫12，1，32；③与点P关于x轴对称的点的坐标为(－1，－2，－3)；④与点P关于坐标原点对称的点的坐标为(1,2，－3)；⑤与点P关于坐标平面xOy对称的点的坐标为(1,2，－3)．其中正确的个数是()A．2 B．3C．4 D．5解析点P到坐标原点的距离为12＋22＋32＝14，故①错；②正确；点P关于x轴对称的点的坐标为(1，－2，－3)，故③错；点P关于坐标原点对称的点的坐标为(－1，－2，－3)，故④错；⑤正确．答案 A7．已知点M(a，b)在圆O：x2＋y2＝1处，则直线ax＋by＝1与圆O的位置关系是()A．相切B．相交C．相离D．不确定解析∵点M(a，b)在圆x2＋y2＝1外，∴a2＋b2>1，又圆心(0,0)到直线ax＋by＝1的距离d＝1a2＋b2<1＝r，∴直线与圆相交．答案 B8．与圆O1：x2＋y2＋4x－4y＋7＝0和圆O2：x2＋y2－4x－10y＋13＝0都相切的直线条数是()A．4 B．3C．2 D．1解析两圆的方程配方得，O1：(x＋2)2＋(y－2)2＝1，O2：(x－2)2＋(y－5)2＝16，圆心O1(－2,2)，O2(2,5)，半径r1＝1，r2＝4，∴|O1O2|＝(2＋2)2＋(5－2)2＝5，r1＋r2＝5.∴|O1O2|＝r1＋r2，∴两圆外切，故有3条公切线．答案 B9．直线l将圆x2＋y2－2x－4y＝0平分，且与直线x＋2y＝0垂直，则直线l的方程是()A．2x－y＝0 B．2x－y－2＝0C．x＋2y－3＝0 D．x－2y＋3＝0解析依题意知直线l过圆心(1,2)，斜率k＝2，∴l的方程为y－2＝2(x－1)，即2x－y＝0.答案 A10．圆x2＋y2－(4m＋2)x－2my＋4m2＋4m＋1＝0的圆心在直线x＋y－4＝0上，那么圆的面积为()A．9π B．πC．2π D．由m的值而定解析∵x2＋y2－(4m＋2)x－2my＋4m2＋4m＋1＝0，∴[x－(2m＋1)]2＋(y－m)2＝m2.∴圆心(2m＋1，m)，半径r＝|m|.依题意知2m＋1＋m－4＝0，∴m＝1.∴圆的面积S＝π×12＝π.答案 B11．当点P在圆x2＋y2＝1上变动时，它与定点Q(3,0)的连结线段PQ的中点的轨迹方程是()A．(x＋3)2＋y2＝4 B．(x－3)2＋y2＝1C．(2x－3)2＋4y2＝1 D．(2x＋3)2＋4y2＝1解析设P (x 1，y 1)，Q (3,0)，设线段PQ 中点M 的坐标为(x ，y )，则x ＝x 1＋32，y ＝y 12，∴x 1＝2x －3，y 1＝2y . 又点P (x 1，y 1)在圆x 2＋y 2＝1上， ∴(2x －3)2＋4y 2＝1.故线段PQ 中点的轨迹方程为(2x －3)2＋4y 2＝1. 答案 C12．曲线y ＝1＋4－x 2与直线y ＝k (x －2)＋4有两个交点，则实数k 的取值范围是( )A ．(0，512) B ．(512，＋∞) C ．(13，34]D ．(512，34] 解析如图所示，曲线y ＝1＋4－x 2变形为x 2＋(y －1)2＝4(y ≥1)，直线y ＝k (x －2)＋4过定点(2,4)，当直线l 与半圆相切时，有 |－2k ＋4－1|k 2＋1＝2，解得k ＝512. 当直线l 过点(－2,1)时，k ＝34. 因此，k 的取值范围是512<k ≤34. 答案 D二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上) 13．圆x 2＋y 2＝1上的点到直线3x ＋4y －25＝0的距离最小值为____________．解析圆心(0,0)到直线3x ＋4y －25＝0的距离为5， ∴所求的最小值为4. 答案 414．圆心为(1,1)且与直线x ＋y ＝4相切的圆的方程是________．解析 r ＝|1＋1－4|2＝2，所以圆的方程为(x －1)2＋(y －1)2＝2.答案 (x －1)2＋(y －1)2＝215．方程x 2＋y 2＋2ax －2ay ＝0表示的圆，①关于直线y ＝x 对称；②关于直线x ＋y ＝0对称；③其圆心在x 轴上，且过原点；④其圆心在y 轴上，且过原点，其中叙述正确的是__________．解析已知方程配方，得(x ＋a )2＋(y －a )2＝2a 2(a ≠0)，圆心坐标为(－a ，a )，它在直线x ＋y ＝0上，∴已知圆关于直线x ＋y ＝0对称．故②正确．答案 ②16．直线x －2y －3＝0与圆(x －2)2＋(y ＋3)2＝9相交于A ，B 两点，则△AOB (O 为坐标原点)的面积为________．解析圆心坐标(2，－3)，半径r ＝3，圆心到直线x －2y －3＝0的距离d ＝5，弦长|AB |＝2r 2－d 2＝4.又原点(0,0)到AB 所在直线的距离h ＝35，所以△AOB 的面积为S ＝12×4×35＝655.答案 655三、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(10分)自A (4,0)引圆x 2＋y 2＝4的割线ABC ，求弦BC 中点P 的轨迹方程．解解法1：连接OP ，则OP ⊥BC ，设P (x ，y )，当x ≠0时，k OP ·k AP ＝－1，即y x ·yx －4＝－1.即x2＋y2－4x＝0.①当x＝0时，P点坐标为(0,0)是方程①的解，∴BC中点P的轨迹方程为x2＋y2－4x＝0(在已知圆内)．解法2：由解法1知OP⊥AP，取OA中点M，则M(2,0)，|PM|＝12|OA|＝2，由圆的定义，知P点轨迹方程是以M(2,0)为圆心，2为半径的圆．故所求的轨迹方程为(x－2)2＋y2＝4(在已知圆内)．18．(12分)已知圆M：x2＋y2－2mx＋4y＋m2－1＝0与圆N：x2＋y2＋2x＋2y－2＝0相交于A，B两点，且这两点平分圆N的圆周，求圆M的圆心坐标．解由圆M与圆N的方程易知两圆的圆心分别为M(m，－2)，N(－1，－1)．两圆的方程相减得直线AB的方程为2(m＋1)x－2y－m2－1＝0.∵A，B两点平分圆N的圆周，∴AB为圆N的直径，∴AB过点N(－1，－1)．∴2(m＋1)×(－1)－2×(－1)－m2－1＝0.解得m＝－1.故圆M的圆心M(－1，－2)．19．(12分)点M在圆心为C1的方程x2＋y2＋6x－2y＋1＝0上，点N在圆心为C2的方程x2＋y2＋2x＋4y＋1＝0上，求|MN|的最大值．解把圆的方程都化成标准形式，得(x＋3)2＋(y－1)2＝9，(x＋1)2＋(y＋2)2＝4.如图所示，C 1的坐标是(－3,1)，半径长是3；C 2的坐标是(－1，－2)，半径长是2.所以，|C 1C 2|＝(－3＋1)2＋(1＋2)2＝13.因此，|MN |的最大值是13＋5.20．(12分)已知圆C ：x 2＋y 2＋2x －4y ＋3＝0，从圆C 外一点P 向圆引一条切线，切点为M ，O 为坐标原点，且有|PM |＝|PO |，求|PM |的最小值．解如图：PM 为圆C 的切线，则CM ⊥PM ，∴△PMC 为直角三角形，∴|PM |2＝|PC |2－|MC |2.设P (x ，y )，C (－1,2)，|MC |＝ 2. ∵|PM |＝|PO |，∴x 2＋y 2＝(x ＋1)2＋(y －2)2－2.化简得点P 的轨迹方程为2x －4y ＋3＝0.求|PM |的最小值，即求|PO |的最小值，即求原点O 到直线2x －4y ＋3＝0的距离，代入点到直线的距离公式可求得|PM |最小值为3510.21．(12分)已知圆C ：x 2＋y 2－4x －14y ＋45＝0及点Q (－2，3)， (1)若点P (m ，m ＋1)在圆C 上，求PQ 的斜率；(2)若点M 是圆C 上任意一点，求|MQ |的最大值、最小值；(3)若N (a ，b )满足关系：a 2＋b 2－4a －14b ＋45＝0，求出t ＝b －3a ＋2的最大值．解圆C ：x 2＋y 2－4x －14y ＋45＝0可化为(x －2)2＋(y －7)2＝8. (1)点P (m ，m ＋1)在圆C 上，所以m 2＋(m ＋1)2－4m －14(m ＋1)＋45＝0，解得m ＝4，故点P (4,5)．所以PQ 的斜率是k PQ ＝5－34＋2＝13；(2)如图，点M 是圆C 上任意一点，Q (－2,3)在圆外，所以|MQ |的最大值、最小值分别是 |QC |＋r ，|QC |－r . 易求|QC |＝42，r ＝22，所以|MQ |max ＝62，|MQ |min ＝2 2.(3)点N 在圆C ：x 2＋y 2－4x －14y ＋45＝0上，t ＝b －3a ＋2表示的是定点Q (－2,3)与圆上的动点N 连线l 的斜率．设l 的方程为y －3＝k (x ＋2)，即kx －y ＋2k ＋3＝0. 当直线和圆相切时，d ＝r ，即|2k －7＋2k ＋3|k 2＋1＝22，解得k ＝2±3.所以t ＝b －3a ＋2的最大值为2＋ 3.22．(12分)已知曲线C ：x 2＋y 2＋2kx ＋(4k ＋10)y ＋10k ＋20＝0，其中k ≠－1. (1)求证：曲线C 表示圆，并且这些圆心都在同一条直线上； (2)证明曲线C 过定点；(3)若曲线C 与x 轴相切，求k 的值．解 (1)证明：原方程可化为(x ＋k )2＋(y ＋2k ＋5)2＝5(k ＋1)2. ∵k ≠－1，∴5(k ＋1)2>0.故方程表示圆心为(－k ，－2k －5)，半径为5|k ＋1|的圆．设圆心的坐标为(x ，y )，则⎩⎨⎧x ＝－k ，y ＝－2k －5.消去k ，得2x －y －5＝0.∴这些圆的圆心都在直线2x －y －5＝0上． (2)证明：将原方程变形为(2x ＋4y ＋10)k ＋(x 2＋y 2＋10y ＋20)＝0， ∵上式对于任意k ≠－1恒成立，∴⎩⎨⎧2x ＋4y ＋10＝0，x 2＋y 2＋10y ＋20＝0.解得⎩⎨⎧x ＝1，y ＝－3.∴曲线C 过定点(1，－3)． (3)∵圆C 与x 轴相切，∴圆心(－k ，－2k －5)到x 轴的距离等于半径．即|－2k －5|＝5|k ＋1|.两边平方，得(2k ＋5)2＝5(k ＋1)2. ∴k ＝5±3 5.。

人教A版(2019)高二数学选择性必修第2章《直线和圆的方程》单元练习题(含答案)

人教A 版（2019）高二数学选择性必修第2章《直线和圆的方程》单元练习题（含答案）一、单选题1．若点()1,1P 在圆22:0C x y x y k ++-+=的外部，则实数k 的取值范围是（） A ．()2,-+∞B ．12,2⎡⎫--⎪⎢⎣⎭C ．12,2⎛⎫- ⎪⎝⎭D ．()2,2-2．过点P -且倾斜角为135的直线方程为（）A ．30x y --=B ．0x y -=C ．0x y +D ．0x y ++=3．已知(2,0),(4,)-A B a 两点到直线:3410l x y -+=的距离相等，则=a （） A ．2B ．92C ．2或8-D ．2或924．设m 为实数，若直线y x m =+与圆224680x y x y +--+=相交于M ，N 两点，且MN =m =（）A ．3B ．-1C ．3或-1D ．-3或15．若圆221x y +=上总存在两个点到点(,1)a 的距离为2，则实数a 的取值范围是（）A ．(-⋃B ．(-C ．(1,0)(0,1)-D ．(1,1)-6．直线2360x y +-=关于点(1,1)对称的直线方程为（） A ．3220x y -+= B ．2370x y ++= C ．32120x y --=D ．2340x y +-=7．若过点（2，1）的圆与两坐标轴都相切，则圆心到直线230x y --=的距离为（）A B C D 8．在平面直角坐标系xOy 中，若双曲线22221x y a b -=(0a >，0b >)的右焦点(),0F c 到一条渐，则其离心率的值为A ．4B ．2C ．12D9．已知两点()2,3A -，()3,2-B ，直线l 过点()1,1P 且与线段AB 相交，则直线l 的斜率k 的取值范围是（） A ．144k -≤≤-B ．4k ≤-或14k ≥-C ．344k -≤≤D ．344k -≤≤10．已知圆2260x y x +-=，过点（1，2）的直线被该圆所截得的弦的长度的最小值为（） A ．1 B ．2 C ．3D ．411．已知点3(2,)A -，(3,2)B --．若直线:10l mx y m +--=与线段AB 相交，则实数m 的取值范围是（） A ．3,[4,)4⎛⎤-∞-⋃+∞ ⎥⎝⎦B ．3,44⎡⎤-⎢⎥⎣⎦C ．1,5⎛⎫+∞ ⎪⎝⎭D ．34,4⎡⎤-⎢⎥⎣⎦12．已知圆221:4240C x y x y ++--=，2223311:222C x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭，则这两圆的公共弦长为（）A ．4B ．C ．2D ．1二、填空13．过点()2,3，且斜率为2的直线l 的斜截式方程为________．14y 轴交于点A ，与圆()2211x y +-=相切于点B ，则AB =____________．15．在平面内，一只蚂蚁从点(2,3)A --出发，爬到y 轴后又爬到圆22:(3)(2)2C x y ++-=上，则它爬到的最短路程是______．16．已知函数()()2f x k x =-有两个不同的零点，则常数k 的取值范围是___________.17．在直角坐标系中，若()2,1A 、()1,2B 、()()0,R C y y ∈，则AC BC +的最小值是______．三、解答题18．求满足下列条件的圆的标准方程． (1)圆心在x 轴上，半径为5，且过点()2,3A -； (2)经过点()4,5A --、()6,1B -，且以线段AB 为直径；(3)圆心在直线y =-2x 上，且与直线y =1-x 相切于点()2,1-； (4)圆心在直线x -2y -3=0上，且过点()2,3A -，()2,5B --．19．在ABC 中，已知(0,1)A ，(5,2)B -，(3,5)C . （1）求边BC 所在的直线方程；（2）求ABC 的面积.20．已知点(0,1)A 、(1,1)B ，设过点(0,1)P -的直线l 与AOB 的边AB 交于点M （其中点M 异于A 、B 两点），与边OB 交于N （其中点N 异于O 、B 两点），若设直线l 的斜率为k ． (1)试用k 来表示点M 和N 的坐标；(2)求OMN 的面积S 关于直线l 的斜率k 的函数关系式； (3)当k 为何值时，S 取得最大值？并求此最大值．21．已知点()0,2A ，直线1:10l x y --=，直线2:220l x y -+=. (1)求点A 关于直线1l 的对称点B 的坐标；(2)求直线2l 关于直线1l 的对称直线方程.22．过点()1,2P 作直线l 分别与x ，y 轴正半轴交于点A ，B . (1)若AOB 是等腰直角三角形，求直线l 的方程；(2)对于①OA OB +最小，②AOB 面积最小，若选择___________作为条件，求直线l 的方程.23．已知直线1:(2)80l m x my ++-=与直线2:40,l mx y m R +-=∈．（1）若12l l //，求m 的值；（2）若点()1,P m 在直线2l 上，直线l 过点P ，且在两坐标轴上的截距之和为0，求直线l 的方程．24．已知直线1l 经过点()3,A a ，()2,3B a -，直线2l 经过点(),6,5A C ，且12l l ⊥，求实数a 的值.25．已知直线()():212420l m x m y m ++-+-=与圆22:20C x x y -+=交于,M N 两点．（1）求出直线l 恒过定点的坐标（2）求直线l 的斜率的取值范围（3）若O 为坐标原点，直线,OM ON 的斜率分别为12,k k ，试问12k k +是否为定值？若是，求出该定值：若不是，请说明理由。

高中数学必修2单元配套练习试题4.2.3直线与圆的方程的应用及参考答案解析

4.2.3直线与圆的方程的应用姓名:___________班级:______________________1.圆5:22=+y x P ,则经过点()21，-M 的切线方程为( ) A.052=--y x B.052=++y xC.052=-+y xD.052=+-y x2.已知圆的方程为x 2＋y 2－6x －8y ＝0.设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD,则四边形ABCD 的面积为( )A.C.3.半径为6的圆与x 轴相切,且与圆x 2＋(y －3)2＝1内切,则此圆的方程为( )A.(x －4)2＋(y －6)2＝6B.(x±4)2＋(y －6)2＝6C.(x －4)2＋(y －6)2＝36D.(x±4)2＋(y －6)2＝364.直线280x y --=与圆22(2)(3)4x y -++=交于,E F 两点,则EOF ∆(O 是原点)的面积为( )B.D.556 5.若直线2=-y x 被圆4)(22=+-y a x 所截得的弦长为22,则实数a 的值为( )A.1-或3B.1或3C.2-或6D.0或46.已知点(),M a b 在圆22:1O x y +=外,则直线1ax by +=与圆O 的位置关系是 ( )A.相切B.相交C.相离D.不确定7.已知圆922=+y x 的弦过点)2,1(P ,当弦长最短时,该弦所在直线方程为 ( )A.052=-+y xB.02=-yC.02=-y xD.01=-x8.从圆222210x x y y -+-+=外一点()3,2P 向这个圆作两条切线,则两切线夹角的A.12B.35C.2 D.09.若点(1,1)P 为圆2260x y x +-=的弦MN 的中点,则弦MN 所在直线的方程为___________.10.已知圆22:9C x y +=,直线1:10l x y --=与2:2100l x y +-=的交点为P 点,过点P 向圆C 作两条切线,a b ,分别与圆相切于,A B 两点,则ABP S =△ .11.已知圆()()()22:10C x a y a a -+-=>与直线3y x =相交于P 、Q 两点,则当CPQ ∆的面积最大时,实数a 的值为 .12.已知圆C 的圆心在直线1y x =+上,,且圆C 经过点(5,4)P(1)求圆C 的标准方程;(2)求过点()1,0A 且与圆C 相切的切线方程.13.已知圆C :2230x y Dx Ey ++++=,圆C 关于直线10x y +-=对称,圆心在第二象限,.(1)求圆C 的方程;(2)已知不过原点的直线l 与圆C 相切,且在x 轴、y 轴上的截距相等,求直线l 的方程.14.已知圆25)2()1(:22=-+-y x C ,直线:(21)(1)7l m x m y m +++- 40()m -=∈R .(1)求证:对任意的m ∈R ,直线l 与圆C 恒有两个交点;(2)求直线l 被圆C 截得的线段的最短长度,及此时直线l 的方程.参考答案1.D【解析】点()12M -，在圆上,所以OM 与切线垂直,因为2OM k =-,所以切线斜率为12,因即250x y -+=. 考点:直线方程,直线和圆相切的位置关系.2.B【解析】圆心坐标是(3,4),半径是5,圆心到点(3,5)的距离为1.最短弦BD 和最长弦(即圆的直径)AC 垂直,故最短弦的长为=所以四边形ABCD 的面积为12×AC×BD＝12×10× 考点:圆的方程的应用.3.D【解析】设所求圆的圆心坐标为(a,b),则b ＝6,5,可以解得a ＝±4,故所求圆的方程为(x±4)2＋(y －6)2＝36.考点:圆的方程的应用.4.A【解析】圆心()2,3-在直线280x y --=上,则24EF r ==,点O 到直线的距离为d ==则12EOF S EF d =⨯⨯=.故选A. 考点:直线与圆的位置关系,点到直线的距离. 5.D 【解析】易得211|2|22=+-=a d ,解得0a =或4,故选D.考点:点到直线的距离公式,圆的弦长公式.6.B【解析】点(),M a b 在圆22:1O x y +=外,221∴+>a b ,∴圆心O 到直线1ax by +=距离1=<d ,∴直线1ax by +=与圆O 相交.故选B.考点:点与圆的位置关系,直线与圆的位置关系.7.A【解析】因为弦长最短,所以该直线与直线OP 垂直,又因为2OP k =,所以直线的斜率为12-,由点斜式可求得直线方程为250x y +-=,故选A.考点:直线与圆的位置关系.8.B【解析】将222210x x y y -+-+=变形为()()22111x y -+-=,则圆心为()1,1A ,半径为1.PA ==设两切线夹角为θ,数形结合可得sin2θ=,所以223cos 12sin 1225θθ=-=-⨯=. 考点:直线与圆相切.9.210x y --=【解析】因为(1,1)P 为圆2260x y x +-=的弦MN 的中点,所以圆心坐标为()3,0,31201MN k -=-=-,所以MN 所在直线方程为()121y x -=-,化简得210x y --=. 考点:两直线垂直斜率的关系,点斜式求直线方程.10.19225【解析】由圆22:9C x y +=,得圆心()0,0O ,半径3r =.直线1l 和2l 的交点坐标为()4,3P ,切线长4PA PB ==,PA OA ⊥,3OA OB r ===.设AB 与OP 的交点为M ,则AB OP ⊥,POB PBM ∽,得161255PM BM ==，,所以2425AB BM ==,1162419225525ABP S =⨯⨯=△. 考点:直线和圆的综合应用,三角形的面积.【解析】圆()()()22:10C x a y a a -+-=>的圆心为(),a a ,半径为1,圆心到直线3y x =的距离为5d =,半弦长为5=,所以CPQ ∆的面积555S =⋅==,当254a =时,取得最大值12,所以CPQ ∆的面积的最大值为12,此时2a =.考点:直线与圆的方程的应用,直线与圆的位置关系.12.(1)()()22452x y -+-= (2)23(1)7y x =-或1y x =- 【解析】(1)设圆C 的圆心为(,)a b ,则圆C 的方程为22()()2x a y b -+-=.()()221,4,5,542b a a b a b =+⎧=⎧⎪⇒⎨⎨=-+-=⎩⎪⎩∴圆C 的方程为()()22452x y -+-=. (2)易知过点()1,0A 且与圆C 相切的切线的斜率存在,设切线方程为(1)y k x =-, 即0kx y k --=,∴=解得237k =或 1k =.故切线方程为23(1)7y x =-或1y x =-. 考点:圆的方程,直线与圆相切的位置关系.13.(1)222430x y x y ++-+= (2)03=-+y x 或01=++y x【解析】(1)由2230x y Dx Ey ++++=知圆心C 的坐标为(,)22D E --, 圆C 关于直线10x y +-=对称,∴点,22D E ⎛⎫-- ⎪⎝⎭在直线10x y +-=上, 则2D E +=-,又221224D E +-=,圆心C 在第二象限,∴D ＝2,E ＝－4, ∴所求圆C 的方程为222430x y x y ++-+=. (2)切线在两坐标轴上的截距相等且不为零,∴可设l 的方程为a y x =+,圆C 的方程可化为()()22122x y ++-=,圆心)2,1(-C 到切线的距离等于半径2, 即2221=-+-a ,,1-=∴a 或3=a ,所求切线方程03=-+y x 或01=++y x .考点:圆的标准方程,直线与圆的位置关系.14.(1)证明见解析 (2)最短弦长为直线l 的方程为250x y --=【解析】(1)证明:直线l 的方程可化为(27)40m x y x y +-++-=, 由270,40,x y x y +-=⎧⎨+-=⎩得3,1,x y =⎧⎨=⎩则l 恒过点(3,1)P ,||PC =∴点P 在圆C 内, ∴直线l 与圆C 恒有两个交点.(2)l 恒过圆C 内一点(3,1)P ,∴当l 过P 与PC 垂直时,弦最短,||5PC r ==,∴最短弦长||AB ==,直线PC ,2l k ∴=, ∴l 的方程为12(3)y x -=-,即250x y --=.考点:直线与圆的位置关系,求直线方程.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

直线与圆的方程综合复习（含答案）一．选择题1.已知点A(1,. 3),B(-1,33),则直线AB 的倾斜角是（ C ） A 3B 6C 23D 562.已知过点A(-2,m)和B （m,4）的直线与直线2x+y-1=0平行，则m 的值为（ C ） A 0 B 2 C -8 D 103.若直线L 1:ax+2y+6=0与直线L 2:x+(a-1)y+(2a -1)=0平行但不重合，则a 等于（ D ） A -1或2 B23C 2D -1 4.若点A （2，-3）是直线a 1x+b 1y+1=0和a 2x+b 2y+1=0的公共点，则相异两点（a 1，b 1）和（a 2，b 2）所确定的直线方程是( A ) A.2x-3y+1=0 B.3x-2y+1=0 C.2x-3y-1=0 D.3x-2y-1=0 5.直线xcos θ+y-1=0 (θ∈R )的倾斜角的范围是 ( D )A.[)π，0B.⎪⎭⎫⎢⎣⎡ππ43,4C.⎥⎦⎤⎢⎣⎡-4,4ππD.⎪⎭⎫⎢⎣⎡⎥⎦⎤⎢⎣⎡πππ,434,06.“m= 12”是“直线（m+2）x+3my+1=0与直线（m-2）x+(m+2y)-3=0相互垂直”的（ B ）A 充分必要条件B 充分而不必要条件C 必要而不充分条件D 既不充分也不必要条件 7.已知A(7,-4)关于直线L 的对称点为B （-5,6），则直线L 的方程为（B ） A 5x+6y-11=0 B 6x-5y-1=0 C 6x+5y-11=0 D 5x-6y+1=0 8.已知直线1l 的方向向量a=(1,3),直线2l 的方向向量b=(-1,k).若直线2l 经过点（0,5）且1l 2l ，则直线2l 的方程为（ B ）A x+3y-5=0B x+3y-15=0C x-3y+5=0D x-3y+15=0 9. 过坐标原点且与圆2x +2y -4x+2y+52=0相切的直线方程为（ A ）A y=-3x 或y= 13xB y=3x 或y= -13xC y=-3x 或y= -13xD y=3x 或y= 13x 10.直线x+y=1与圆2x +2y -2ay=0(a>0)没有公共点,则a 的取值范围是（A ）22222211.圆2x +2y -4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是（ C ）A 36B 18C 62D 5212.以直线：y=kx-k 经过的定点为P 为圆心且过坐标原点的圆的方程为（D ）， A 2x +2y +2x=0 B 2x +2y +x=0 C 2x +2y -x=0 D 2x +2y -2x-013.已知两定点A(-2,0),B(1,0),如果定点P 满足PA=2PB,则定点P 的轨迹所包围的面积等于（ B ）A B 4 C 8 D 914.若直线3x+y+a=0过圆2x +2y +2x-4y=0的圆心，则a 的值为（ B ）A 1B -1C 3D -315.若直线2ax-by+2=0 (a ＞0,b ＞0)始终平分圆x 2+y 2+2x-4y+1=0的周长，则ba11+的最小值是（ C ） A.41B.2C.4D.2116.若直线y=k(x-2)+4与曲线y=1+24x -有两个不同的交点，则k的取值范围是（ A ）A.⎥⎦⎤ ⎝⎛43,125 B.⎪⎭⎫⎝⎛+∞,125 C.⎥⎦⎤⎝⎛43,21D.⎪⎭⎫⎝⎛125,017.设两圆1C ,2C 都和两坐标轴相切，且过点（4,1），则两圆心的距离︱1C 2C ︱等于（ C ）A 4B 42C 8D 8218.能够使得圆x 2+y 2-2x+4y+1=0上恰有两个点到直线2x+y+c=0距离等于1的c 的一个值为（ C ） A.2B.5C.3D.3519.若直线by ax +=1与圆x 2+y 2=1有公共点，则( D )A.a 2+b 2≤1B.a 2+b 2≥1C.2211ba +≤1 D.2211ba +≥120.已知A （-3，8）和B （2，2），在x 轴上有一点M ，使得|AM|+|BM|为最短，那么点M 的坐标为（ B ） A.(-1,0)B.(1,0)C.⎪⎭⎫ ⎝⎛0522，D. ⎪⎭⎫⎝⎛522,021.直线y=kx+3与圆2(3)x +2(2)y =4相交于M 、N 两点，若︱MN ︱≥23,则k 的取值范围是（ A ）A [-34,0] B [-∞,-34] [0，∞） C [-33,33] D [-23,0] 22.（广东理科2）已知集合{(,)|,A x y x y =为实数，且221}x y +=，{(,)|,B x y x y =为实数，且}y x =，则AB 的元素个数为（C ）A ．0B ．1C ．2D ．323.（江西理科9）若曲线02221=-+x y x C ：与曲线 0)(2=--m mx y y C ：有四个不同的交点,则实数m 的取值范围是 ( B ) A. )33,33(-B. )33,0()0,33( -C. ]33,33[-D. ),33()33,(+∞--∞ 答案：B 曲线0222=-+x y x 表示以()0,1为圆心，以1为半径的圆，曲线()0=--m mx y y 表示0,0=--=m mx y y 或过定点()0,1-，0=y 与圆有两个交点，故0=--m mx y 也应该与圆有两个交点，由图可以知道，临界情况即是与圆相切的时候，经计算可得，两种相切分别对应3333=-=m m 和，由图可知，m 的取值范围应是)33,0()0,33( -二．填空题24．已知圆C 经过)3,1(),1,5(B A 两点，圆心在X 轴上，则C 的方程为10)2(22=+-y x ___________。

25.已知直线l ：x-y+4=0与圆C ：（x-1）2+（y-1）2=2，则C 上各点到l 距离的最小值为 2 .26.设直线l 经过点A （-1，1），则当点B （2，-1）与直线l 的距离最远时，直线l 的方程为 3x-2y+5=027.圆x 2+y 2+2x-4y+1=0关于直线2ax-by+2=0（a 、b ∈R ）对称，则ab 的取值范围是( A )A.⎥⎦⎤ ⎝⎛∞-41，B.⎥⎦⎤⎝⎛410，C.⎪⎭⎫⎝⎛-0,41D.⎪⎭⎫⎝⎛∞-41,28.与直线2x+3y+5=0平行，13的直线方程是 2x+3y+18=0,或2x+3y-8=0 。

29（重庆理8）在圆06222=--+y x y x 内，过点)1,0(E 的最长弦和最短弦分别是AC和BD ，则四边形ABCD 的面积为（ B ） A ．25B ．210C ．152D ．220解：圆的方程标准化方程为10)3()1(22=-+-y x ，由圆的性质可知，最长弦长为 102||=AC ，最短弦长BD 以)1,0(E 为中点，设点F 为其圆心，坐标为)3,1(故5||=EF ，52)5(102||2=-=∴BD ，210||||21=⋅=∴BD AC S ABCD 。

三．解答题30.已知圆C ：（x-1）2+(y-2)2=25及直线l:(2m+1)x+(m+1)y=7m+4 (m ∈R ). （1）证明：不论m 取什么实数，直线l 与圆C 恒相交；（2）求直线l 被圆C 截得的弦长的最短长度及此时的直线方程. （1）证明直线l 可化为x+y-4+m(2x+y-7)=0,即不论m 取什么实数，它恒过两直线x+y-4=0与2x+y-7=0的交点. 两方程联立，解得交点为（3，1），又有（3-1）2+（1-2）2=5＜25, ∴点（3，1）在圆内部，∴不论m 为何实数，直线l 与圆恒相交.（2）解从（1）的结论和直线l 过定点M （3，1）且与过此点的圆C 的半径垂直时，l 被圆所截的弦长|AB|最短，由垂径定理得 |AB|=222CM r -=.54]）21（）13（[25222=-+--此时，k t =-C Mk 1,从而k t =-31121--=2.∴l 的方程为y-1=2(x-3),即2x-y=5.31.已知P 是直线3x+4y+8=0上的动点，PA 、PB 是圆x 2+y 2-2x-2y+1=0的两条切线，A 、B 是切点，C 是圆心，求四边形PACB 面积的最小值. 解将圆方程化为(x-1)2+(y-1)2=1,其圆心为C （1，1），半径r=1,如图，由于四边形PACB 的面积等于Rt △PAC 面积的2倍，所以S PACB =2×21×|PA|×r=12-PC .∴要使四边形PACB 面积最小,只需|PC|最小. 当点P 恰为圆心C 在直线3x+4y+8=0上的正射影时,|PC|最小,由点到直线的距离公式,得 |PC|min =5843++=3,故四边形PACB 面积的最小值为22.32（全国课标20）在平面直角坐标系xoy 中，曲线261y x x =-+与坐标轴的交点都在圆C 上（Ⅰ）求圆C 的方程；（Ⅱ）若圆C 与直线0x y a -+=交与,A B 两点，且OA OB ⊥，求a 的值.【解析】（Ⅰ）曲线261,y x x =-+与y 轴交于点(0,1)，与与x 轴交于点(3+-因而圆心坐标为),,3(t C 则有22223(1),1t t t +-=+∴=. 半径为3)1(322=-+t ，所以圆方程是9)1()3(22=-+-y x .（Ⅱ）解法一：设点),(),,(2211y x B y x A 满足220,.(3)(1)9x y a x y -+=⎧⎨-+-=⎩ 解得：012)82(222=+-+-+a a x a x .0416562>--=∆∴a a441656)28(22,1a a a x --±-=21212214,2a a x x a x x -+∴+=-⋅=12121122,0,,OA OB x x y y y x a y x a ⊥∴+==+=+. 212122()0,x x a x x a ∴+++= 解得1a ∴=-，满足0>，1a ∴=-解法二：设经过直线0x y a -+=和圆9)1()3(22=-+-y x 的交点的圆的方程为0)(12622=+-++-+-a y x y y x x λ，若OA OB ⊥，则以AB 为直径的圆过坐标原点设上述圆就是这样的圆，则圆过原点，所以01=+a λ ① 同时，该圆的圆心)22,26(+-λλ在直线0x y a -+=上，化简得2+=a λ ② 由①②求得1-=a 。

33（上海理23）已知平面上的线段l 及点P ，任取l 上一点Q ，线段PQ 长度的最小值称为点P 到线段l 的距离，记作(,)d P l ．⑴ 求点(1,1)P 到线段:30(35)l x y x --=≤≤的距离(,)d P l ；⑵ 设l 是长为2的线段，求点的集合{|(,)1}D P d P l =≤所表示图形的面积；【解析】⑴ 设(,3)Q x x -是线段:30(35)l x y x --=≤≤上一点，则||5)PQ x ==≤≤，当3x =时，min (,)||d P l PQ == ⑵ 不妨设(1,0),(1,0)A B -为l 的两个端点，则D 为线段1:1(||1),l y x =≤线段2:1(||1)l y x =-≤，………６分半圆221:(1)1(1),C x y x ++=≤-半圆222:(1)1(1)C x y x -+=≥所围成的区域．这是因为对(,),1,P x y x ≤则(,);d P l y =而对(P x (,)d P l =对(,),1,P x y x > 则(,)d P l =………９分于是D 所表示的图形面积为4π+．………１０分34.（12分）已知方程x 2+y 2-2x-4y+m=0. （1）若此方程表示圆，求m 的取值范围；（2）若（1）中的圆与直线x+2y-4=0相交于M 、N 两点，且OM ⊥ON （O 为坐标原点），求m ；（3）在（2）的条件下，求以MN 为直径的圆的方程. 解（1）（x-1)2+(y-2)2=5-m,∴m ＜5. （2）设M （x 1，y 1），N （x 2，y 2），则x 1=4-2y 1，x 2=4-2y 2，则x 1x 2=16-8（y 1+y 2）+4y 1y 2 ∵OM ⊥ON ，∴x 1x 2+y 1y 2=0∴16-8（y 1+y 2）+5y 1y 2=0 ①由⎪⎩⎪⎨⎧=+--+-=0422422m y x y x y x 得5y 2-16y+m+8=0∴y 1+y 2=516,y 1y 2=58m +,代入①得，m=58.（3）以MN 为直径的圆的方程为（x-x 1）(x-x 2)+(y-y 1)(y-y 2)=0 即x 2+y 2-(x 1+x 2)x-(y 1+y 2)y=0∴所求圆的方程为x 2+y 2-58x-516y=0.35．已知圆C 经过点A (－2,0)，B (0,2)，且圆心C 在直线y ＝x 上，又直线l ：y ＝kx＋1与圆C 相交于P 、Q 两点． (1)求圆C 的方程；(2)若OP →·OQ →＝－2，求实数k 的值； (3)过点(0,1)作直线l 1与l 垂直，且直线l 1与圆C 交于M 、N 两点，求四边形PMQN 面积的最大值．解：(1)设圆心C (a ，a )，半径为r . 因为圆C 经过点A (－2,0)，B (0,2)，所以|AC |＝|BC |＝r ，易得a ＝0，r ＝2. 所以圆C 的方程是x 2＋y 2＝4.(2)因为OP →·OQ →＝2×2×cos 〈OP →，OQ →〉＝－2，且OP →与OQ →的夹角为∠POQ ，所以cos ∠POQ ＝－12，∠POQ ＝120°，所以圆心C 到直线l ：kx －y ＋1＝0的距离d ＝1，又d ＝1k 2＋1，所以k ＝0.(3)设圆心O 到直线l ，l 1的距离分别为d ，d 1，四边形PMQN 的面积为S . 因为直线l ，l 1都经过点(0,1)，且l ⊥l 1，根据勾股定理，有d 21＋d 2＝1.又易知|PQ |＝2×4－d 2，|MN |＝2×4－d 21，所以S ＝12·|PQ |·|MN |，即S ＝12×2×4－d 2×2×4－d 21＝216－4(d 21＋d 2)＋d 21·d 2＝ 212＋d 21·d 2≤212＋⎝⎛⎭⎪⎫d 21＋d 222＝212＋14＝7，当且仅当d 1＝d 时，等号成立，所以四边形PMQN 面积的最大值为7.。